For Karine
hard-working scholar who always
finds time for friendship
"Until some decades ago, it was customary to discuss much pre-Modern mathematics as "algebra", without agreement between workers about what was to be understood by that word. Then this view came under heavy fire, rarely with more precision.
Now, instead, it has become customary to classify pre-Modern practical arithmetic as "algorithmic mathematics". In so far as any computation in several steps can be claimed to follow an underlying algorithm (just as it can be explained from an "underlying theorem", for instance from proportion theory, or from a supposedly underlying algebraic calculation), this can no doubt be justified. Traditionally, however, historians as well as the sources would speak of a rule.
The paper first goes through some of the formative appeals to the algebraic interpretation – Eisenlohr, Zeuthen, Neugebauer – as well as some of the better argued attacks on it (Rodet, Mahoney).
Next it asks for the reasons to introduce the algorithmic interpretation, and discusses the adequacy or inadequacy of some uses. Finally, it investigates in which sense various pre-modern mathematical cultures can be characterized globally as "algorithmic", concluding that this characterization fits ancient Chinese and Sanskrit mathematics but neither early second-millennium Mediterranean practical arithmetic (including Fibonacci and the Italian abbacus tradition), nor the Old Babylonian corpus."
1.
Introduction
One of the main research areas of differential geometry is the characterization of curves in Euclidean, Minkowski, or other special spaces by analyzing them according to different frame such as Frenet, Bishop, etc.
Although the Serret-Frenet frame is useful for the analysis of curves, this frame cannot be defined at points where the second derivative of the curve is equal to zero. This has led to the popularization of orthonormal frame systems defined along a curve, which have been proposed as an alternative to the Frenet frame. In this way, the frame can be defined at points with this property and enables any space curve to be analyzed. One of these alternative frames, the Bishop frame, offers a more suitable option, especially when the torsion is zero or when the effect of torsion needs to be minimized. The advantages of the parallel frame and its comparison with the Frenet frame in 3-dimensional (3D) Euclidean space were given and studied by Bishop [1]. The Bishop frame has many applications in computer graphics and biology. For example, the Bishop frame can be used to predict the shape of DNA sequences or to control virtual cameras in computer graphics. It provides clearer geometric modeling by avoiding the analysis of torsional effects in the double-helical structure of DNA [2]. It is, therefore, of great importance to identify new types of curves and characterize them in different frames.
Helices appear in many applications, so the most common way to characterize curves is to determine whether they are general helices, cylindrical helices, or slant helices. A curve with a helix in E3E31 is characterized by the property that the tangent vector field forms a constant angle with a constant direction. Lancret's theorem proves that the ratio of torsion and curvature of a helix is constant [3]. The helix was generalized by Hayden in [4]. Later, with the help of the Killing vector field over a curve, the general helix was defined in 3D real space form, and in this space form, Lancret's theorem for general helices was given again by Barros [5]. Izumiya and Takeuchi named the curve whose main normal vector field makes a constant angle with a constant direction in 3D Euclidean space as a slant helix [6]. They also gave another characterization of the slant helix in [7]. Bükçü and Karacan, on the other hand, defined slant helixes in the Bishop frame and gave the necessary and sufficient condition for a curve to be a slant helix according to this frame as the ratio of Bishop curvatures of the curve being constant [8]. Another example of the classification of curves is the integral curves, which are the solution of a differential equation and define a parameterized curve. In [9,10,11,12], curves generated by the integral of the binormal vector field, which is one of the Frenet vectors of a curve given by any parameter s, are defined as associated curves.
It is possible to generate new curves from a given curve by introducing geometric features, as in integral curves. There are some special curves in this context, including the Bertrand, Mannheim, Natural Mate, Smarandache, involute, evolute, and pedal curves, etc. In the references, there are some studies on these curves in different frames such as Frenet and the Bishop frame [13,14,15,16], and these curves have important applications in physics, engineering surface modeling, and computer graphics [17,18,19].
In differential geometry, Smarandache curves are important in that they create more complex geometric structures by transitioning from one curve to another. Smarandache curves in E41 Minkowski space were introduced by Yilmaz and Turgut. By definition, Smarandache curves are included in Smarandache geometry, and if the position vector of a curve β is generated by the vectors of the Frenet frame of another curve α, then the curve β is called a Smarandache curve [20]. These curves enable in-depth analysis of the curve and surface. They are used in physics, engineering, biomechanics, robotics, and computer graphics, among other fields. Particularly in physics, they are employed in general relativity theory and space-time geometry [21]. They are used in materials science and structural analysis in engineering. They are essential to motion planning and object recognition in robotics and computer graphics [15]. They also contribute to theoretical and applied research in differential geometry by providing a more flexible and general framework than other types of curves. For example, Smarandache curves form a derived curve based on Frenet vectors since curvature and torsion are usually not constant compared to helical curves with constant curvature and constant torsion. While other curves based on curvature and torsion use only curvature and torsion, Smarandache curves directly use the other elements of the Frenet frame: the tangent, normal, and binormal vectors. Special Smarandache curves have been studied by some authors. Ali introduced special curves in Euclidean space, called Smarandache TN, NB, and TNB curves by Frenet-Serret vector fields [22]. Çetin et al. also studied Smarandache curves according to Bishop frame and made some calculations about the geometric properties of the curve [23]. Nurkan and Güven defined special curves by combining Smarandache curves and integral curves in the Frenet frame and gave some characterizations [24]. The Smarandache curves of Mannheim, Bertrand, involute and evolute curves are discussed in detail in [25,26,27,28], while their geometric properties in Minkowski space are explored in [29,30]. Recent advancements in curve and surface theories across various spaces include studies in Galilean space [31,32,33], and ruled surfaces generated from Smarandache curves are analyzed in [34,35,36].
In this paper, new adjoint curves are defined by combining special Smarandache curves and integral curves in the Bishop frame, and interesting and useful results are provided. I define these new curves as tαζα1-Bishop adjoint curve, tαζα2-Bishop adjoint curve, ζα1ζα2-Bishop adjoint curve, and tαζα1ζα2-Bishop adjoint curve. Some relationships are established between a curve in the Bishop frame and the adjoint curves generated from it. Moreover, using these relations, I give necessary and sufficient conditions for the curve to be a general helix and slant helix.
2.
Basic concepts
Some fundamental concepts related to differential geometry of space curves in Euclidean space E3 are reviewed in this section.
Consider that Euclidean 3-space E3, with the standard flat metric given by
where x1–x3 is a rectangular coordinate system of E3. The norm is defined by
A curve α is called a unit speed curve if its velocity vector α′ satisfies
When α is a unit speed curve, its unit tangent vector is
and its curvature is
and
give the principal normal vector and the unit binormal vector of α, respectively. Next, the well-known Frenet formula is shown as
where
is the torsion of α.
An alternate method for creating a moving frame that is well-defined even in cases when the curve's second derivative vanishes is the Bishop frame, also known as the parallel transport frame. To represent the parallel transport of an orthonormal frame along a curve, just parallel transport each frame component. Any convenient arbitrary basis and the tangent vector are used for the remaining section of the frame.
Although t(s) for a given curve model is unique, the parallel transport frame is based on the observation that, for the remaining portion of the frame, I can choose any convenient arbitrary basis (ζ1(s),ζ2(s)) as long as it is in the normal plane perpendicular to t(s) at each point. Regardless of the curvature of the path, (ζ1(s),ζ2(s)) may change smoothly if their derivatives only depend on t(s) and not on each other. Thus, the various frame equations are available to us
The set {t,ζ1,ζ2} is referred to as a Bishop trihedron in this case, the curvatures k1 and k2 are called Bishop curvatures. The relation matrix can be expressed
where
and
so that k1 and k2 effectively correspond to a Cartesian coordinate system for the polar coordinates κ, θ with
The orientation of the parallel transport frame includes the arbitrary choice of integration constant which θ0, which disappears from τ (and hence from the Frenet frame) due to the differentiation (see [1,23]). Here, Bishop curvatures are defined by
on the other hand, if Eq (2.3) is regularized, the following equations are obtained
When the angle between a curve's tangent lines and a fixed direction remains constant, the curve is called to general helix. The general helix's axis is the name given to this fixed direction. In 1802, Lancret articulated the definition of a helix, stating that a curve may be classified only as a general helix if the harmonic curvature or the ratio τκ remains constant, with
If both
κ≠0 and τ≠0
are constants, the general helix is referred to as a circular helix [3].
The constant geodesic curvature function of the principal image of the constant normal indicatrix characterizes a slant helix, as stated in [7]. This function that is constant is provided by
Bükçü and Karacan defined the concept of slant helix according to the Bishop frame in 3D Euclidean space E3 and stated that the necessary and sufficient condition for a curve α to be a slant helix is that the ratio of the Bishop's curvatures
should be constant.
Theorem 2.1. ([8]) Let the unit speed curve
be a slant helix with non-zero natural Bishop curvatures. Then α is slant helix if and only if k1k2 is constant.
Definition 2.2. ([12]) Let α be an s-arc length parameterized regular curve with nonvanishing torsion and {Tα,Nα,Bα} is the Frenet frame of α. The adjoint curve of α is defined as
Definition 2.3. ([22]) Let α be an s-arc length parameterized regular curve with nonvanishing torsion and {Tα,Nα,Bα} is the Frenet frame of α. Smarandache TN, NB, and TNB curves are defined by
respectively.
3.
Bishop adjoint curve in E3
In [22], the author introduced that a curve in E3 parameterized by the arc length is called a Smarandache curve whose position vector is generated by the Frenet frame vectors on another regular curve. Then, in [24], the authors adapted this definition to regular curves as integrals of Smarandache curves in Euclidean 3-space. In this paper, New curves are obtained by taking the integrals of Smarandache curves with respect to the Bishop frame in Euclidean 3-space.
Definition 3.1. Let α be an s-arc length parameterized regular curve with Bishop apparatus {tα,ζα1,ζα2,kα1,kα2}. tαζα1-Bishop adjoint curve, tαζα2-Bishop adjoint curve, ζα1ζα2-Bishop adjoint curve and tαζα1ζα2-Bishop adjoint curve of α are obtained
respectively.
Remark 3.2. ([9]) Let α be a regular curve parameterized by arc length s, and let β1−β4 be the adjoint curves of α. The arc length parameter s∗ of these adjoint curves can be taken as s∗=s.
3.1. tαζα1-Bishop adjoint curve
Theorem 3.3. Let α be an s-arc length parameterized regular curve in E3 with Bishop apparatus {tα,ζα1,ζα2,kα1,kα2} and β1 be a tαζα1-Bishop adjoint curve of α. The Frenet vector fields, curvature and torsion of β1 are given by
where
Proof. By differentiating Eq (3.1) and using Frenet formulas, I compute
if the norm of both sides of the Eq (3.6) is taken, (3.7) is obtained
also, Eq (3.8) is obtained from Eqs (3.6) and (3.7)
differentiating (3.8) with respect to s and using Eq (2.2), I obtain
Then, the curvature and principal normal vector field of the curve β1 are, respectively,
and
and besides this, I express
Thus, the binormal vector of curve β1 is
to find the torsion of β1, differentiate nβ11 and use the relation
Then, I obtain
By ordering the expressions and assuming
I arrive at the final result.
Theorem 3.4. Let α be an s-arc length parameterized regular curve in E3 with Bishop apparatus {tα,ζα1,ζα2,kα1,kα2} and β1 be a tαζα1-Bishop adjoint curve of α. The Bishop vector fields and curvatures of β1 are given by
Proof. If Eq (3.5) is substituted into Eqs (2.4) and (2.5), the proof is completed.
Corollary 3.5. Let the unit speed curve
be a slant helix with respect to the Bishop frame, tαζα1-Bishop adjoint curve of α is a general helix.
Proof. If I compute the quotient of the torsion and curvature of tαζα1-Bishop adjoint curve of α which are in Theorem 3.3, I have
Assuming that α is a slant helix, then h′=0. Thus, I get
which means τβ1κβ1 is constant.
Corollary 3.6. Let the unit speed curve
be a slant helix with the Bishop frame. If I rotate the Frenet frame around the tα axis, the angle of rotation is
Proof. According to Bishop formulas,
is known. If the value of τβ1 is written as expressed in Eq (3.9), the following expression is obtained
since α is a slant helix h′=0. Therefore
3.2. tαζα2-Bishop adjoint curve
Theorem 3.7. Let α be an s-arc length parameterized regular curve in E3 with Bishop apparatus {tα,ζα1,ζα2,kα1,kα2} and β2 be a tαζα2-Bishop adjoint curve of α. The Frenet vector fields, curvature and torsion of β2 are given by
Proof. By differentiating Eq (3.2) and using Frenet formulas, I compute
differentiating (3.12) with respect to s and using Eq (2.2), I obtain
Then, the curvature and principal normal vector field of the curve β2 are, respectively,
and
beside this, I express
Thus, the binormal vector of curve β2 is
in order to find the torsion of β2, differentiating nβ2 and use the relation
Then, I have
by ordering the expressions and assuming
I arrive at the final result.
Theorem 3.8. Let α be an s-arc length parameterized regular curve in E3 with Bishop apparatus {tα,ζα1,ζα2,kα1,kα2} and β2 be a tαζα2-Bishop adjoint curve of α. The Bishop vector fields and curvatures of β2 are given by
Proof. If Eq (3.11) is substituted into Eqs (2.4) and (2.5) the proof is completed.
Corollary 3.9. Let the unit speed curve
be a slant helix with respect to the Bishop frame, then tαζα2-Bishop adjoint curve of α is a general helix.
Proof. If I compute the quotient of the torsion and curvature of tαζα2-Bishop adjoint curve of α which are in Theorem 3.7. I have
Which means τβ2κβ2 is constant.
Corollary 3.10. Let the unit speed curve
be a slant helix with the Bishop frame. If I rotate the Frenet frame around the tα axis, the angle of rotation is
Proof. According to the Bishop formulas,
is known. If the value of τβ2 is written as expressed in Eq (3.13), the following expression is obtained
Since α is a slant helix h′=0. Therefore
3.3. ζα1ζα2-Bishop adjoint curve
Theorem 3.11. Let α be an s-arc length parameterized regular curve in E3 with Bishop apparatus {tα,ζα1,ζα2,kα1,kα2} and β3 be a ζα1ζα2-Bishop adjoint curve of α. The Frenet vector fields, curvature and torsion of β3 are given by
Proof. By differentiating Eq (3.3) and using Frenet formulas, I compute
differentiating (3.16) with respect to s and using Eq (2.2), I obtain
Then, the curvature and principal normal vector field of curve {\beta _\mathit{3}} are, respectively,
and
beside this, I express
Thus, the binormal vector of curve {\beta _\mathit{3}} is
in order to find the torsion of {\beta _\mathit{3}}, differentiating {\mathbf{n}_{{\boldsymbol{\beta} _\mathit{\pmb{3}}}}} and use the relation
Then, I obtain
by ordering the expressions and assuming
I arrive at the final result.
Theorem 3.12. Let be \alpha an s-arc length parameterized regular curve in {\mathbb{E}^\mathit{3}} with Bishop apparatus \left\{ {{\mathbf{t}_\boldsymbol{\alpha} }, \boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\alpha}, \boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\alpha}, k_1^\alpha, k_2^\alpha } \right\} and {\beta _\mathit{3}} be a \boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\alpha} \boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\alpha} -Bishop adjoint curve of \alpha . The Bishop vector fields and curvatures of {\beta _\mathit{3}} are given by
Proof. If Eq (3.15) is substituted into Eqs (2.4) and (2.5) the proof is completed.
Corollary 3.13. Let \alpha be an s-arc length parameterized regular curve in {\mathbb{E}^\mathit{3}} with Bishop frame. Then, the \boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\alpha} \boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\alpha} -Bishop adjoint curve of \alpha is a slant helix.
Proof. Let \alpha be an s-arc length parameterized regular curve in {\mathbb{E}^\mathit{3}} with Bishop frame. Using the Eq (3.18),
follows. From Bishop formulas and Eq (3.17),
is obtained. Thus,
which means \frac{{k_1^{{\beta _\mathit{3}}}}}{{k_2^{{\beta _\mathit{3}}}}} is constant, so \boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\alpha} \boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\alpha} -Bishop adjoint curve of \alpha is a slant helix.
Corollary 3.14. Let the unit speed curve
be a slant helix according to Bishop frame. Then, \boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\alpha} \boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\alpha} -Bishop adjoint curve of \alpha is involute of \alpha .
Proof. From Eq (3.15), I found that
which means the tangent vector fields of \alpha and \boldsymbol{\zeta} _{1}^\boldsymbol{\alpha} \boldsymbol{\zeta} _{2}^\boldsymbol{\alpha} -Bishop adjoint curve of \alpha are perpendicular. Thus, the \boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\alpha} \boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\alpha} -Bishop adjoint curve is involute of \alpha .
3.4. {\mathbf{t}_\boldsymbol{\alpha} }\boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\alpha} \boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\alpha} -Bishop adjoint curve
Theorem 3.15. Let \alpha be an s-arc length parameterized regular curve in {\mathbb{E}^\mathit{3}} with Bishop apparatus \left\{ {{\mathbf{t}_\boldsymbol{\alpha} }, \boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\alpha}, \boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\alpha}, k_1^\alpha, k_2^\alpha } \right\} and {\beta _\mathit{4}} be a {\mathbf{t}_\boldsymbol{\alpha} }\boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\alpha} \boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\alpha} -Bishop adjoint curve of \alpha . The Frenet vector fields, curvature and torsion of {\beta _\mathit{4}} are given by
Proof. The proof is similar to other Bishop adjoint curves.
Theorem 3.16. Let \alpha be an s-arc length parameterized regular curve in {\mathbb{E}^\mathit{3}} with Bishop apparatus \left\{ {{\mathbf{t}_\boldsymbol{\alpha} }, \boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\alpha}, \boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\alpha}, k_1^\alpha, k_2^\alpha } \right\} and {\beta _\mathit{4}} be a {\mathbf{t}_\boldsymbol{\alpha} }\boldsymbol{\zeta} _{1}^\boldsymbol{\alpha} \boldsymbol{\zeta} _{2}^\boldsymbol{\alpha} -adjoint curve of \alpha . The Bishop vector fields and curvatures of {\beta _\mathit{4}} are given by
Proof. If Eq (3.19) is substituted into Eqs (2.4) and (2.5) the proof is completed.
Corollary 3.17. Let the unit speed curve
be slant helix with respect to the Bishop frame, the {\beta _4} curve, which is the {\mathbf{t}_\boldsymbol{\alpha} }\boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\alpha} \boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\alpha} -adjoint curve of \alpha is a general helix.
Proof. If I compute the quotient of the torsion and curvature of the {\mathbf{t}_\boldsymbol{\alpha} }\boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\alpha} \boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\alpha} -Bishop adjoint curve of \alpha as expressed in Theorem 3.15., I have
which is constant.
Corollary 3.18. Let the unit speed curve
be a slant helix with the Bishop frame. If I rotate the Frenet frame around the {\mathbf{t}_\boldsymbol{\alpha} } axis, the angle of rotation is
Proof. According to the Bishop formulas,
is known. If the value of {\mathtt{τ} _{{\beta _\mathit{4}}}} is written as expressed in Eq (3.19), the following expression is obtained
since \alpha is a slant helix h' = 0. Thus
Example 3.19. Consider the unit speed curve \gamma in {\mathbb{E}^\mathit{3}}
Bishop trihedron of \gamma were found in [37]. Now let's find {\mathbf{t}_\boldsymbol{\gamma} }\boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\gamma} , {\mathbf{t}_\boldsymbol{\gamma} }\boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\gamma} , \boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\gamma} \boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\gamma} , {\mathbf{t}_\boldsymbol{\gamma} }\boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\gamma} \boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\gamma} -Bishop adjoint curves of \gamma . By using the definitions of these curves, I obtained, respectively;
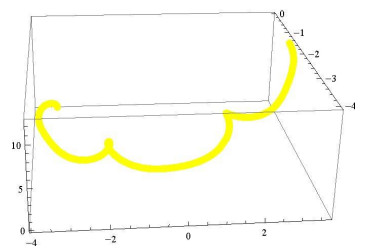
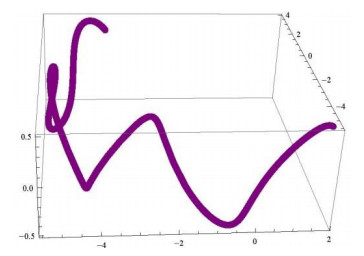
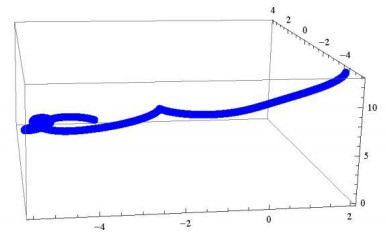
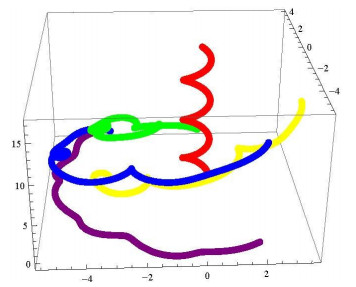
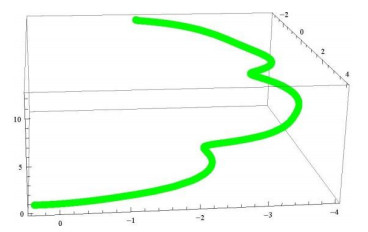
The curve \gamma and its {\mathbf{t}_\boldsymbol{\gamma} }\boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\gamma} \;{\mathbf{t}_\boldsymbol{\gamma} }\boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\gamma} , \boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\gamma} \boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\gamma} , {\mathbf{t}_\boldsymbol{\gamma} }\boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\gamma} \boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\gamma} -Bishop adjoint curves are shown in the following computer generated graphs, where Figure1 illustrates the {\mathbf{t}_\boldsymbol{\gamma} }\boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\gamma} -Bishop adjoint curve, Figure 2 the {\mathbf{t}_\boldsymbol{\gamma} }\boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\gamma} -Bishop adjoint curve, Figure 3 the \boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\gamma} \boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\gamma} -Bishop adjoint curve, Figure 4 the {\mathbf{t}_\boldsymbol{\gamma} }\boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\gamma} \boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\gamma} -Bishop adjoint curves of \gamma , and Figure 5 combines \gamma and its Bishop adjoint curves into a single visualization for comparison.
4.
Discussion
General helices are often encountered in biology for DNA structures, in engineering for pipelines, in computer graphics for 3D modeling, and in robotics for motion planning within the scope of my findings.
First, the adjoint curve {\beta _1} of the Smarandache curve {\mathbf{t}_\boldsymbol{\alpha} }\boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\alpha} , which is generated from the Bishop vectors t and {\boldsymbol{\zeta} _\mathbf{1}} of a unit-speed curve α in 3D Euclidean space, was determined. Upon analyzing the generated curve together with the main curve, it was found that when the curve α is a slant helix, the curve {\beta _1} is a general helix. In the second case, similarly, the adjoint curve {\beta _2} of the Smarandache curve {\mathbf{t}_\boldsymbol{\alpha} }\boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\alpha} , generated from the Bishop vectors t and {\boldsymbol{\zeta} _\mathbf{2}} of the curve α was determined. Upon analyzing the generated curve together with the main curve, it was found that when the curve α is a slant helix, the curve {\beta _2} is a general helix. In the third case, the adjoint curve {\beta _3} of the Smarandache curve {\boldsymbol{\zeta} _\mathbf{1}}{\boldsymbol{\zeta} _\mathbf{2}} , generated from the Bishop vectors {\boldsymbol{\zeta} _\mathbf{1}} and {\boldsymbol{\zeta} _\mathbf{2}} vectors of the curve α was determined. I found that the curve {\beta _3} is a slant helix and, at the same time, the involute of the curve α. In the fourth case, the adjoint curve {\beta _4} of the Smarandache curve {\mathbf{t}_\boldsymbol{\alpha} }\boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\alpha} \boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\alpha} , generated from the Bishop vectors t, {\boldsymbol{\zeta} _\mathbf{1}} and {\boldsymbol{\zeta} _\mathbf{2}} of the curve α was determined. Upon analyzing the generated curve together with the main curve, it was found that when the curve α is a slant helix, the curve {\beta _4} is a general helix. In the final part of the study, adjoint curves of the Smarandache curves, generated from the Bishop vectors of the helix curve \gamma , were determined, and the shapes of these curves were plotted.
My findings indicate that the adjoint of Smarandache curves, generated using the vectors of the Bishop frame, belongs to the class of general helices. Furthermore, the transition from special curves, such as slant helices, to general helices facilitates the analysis of various geometric structures of curves. Additionally, the relationship between the main curve and the new curves derived from it deepens our understanding of transformations of curves according to different frame systems.
In this study, new curves were generated using the adjoint curves of Smarandache curves based on the vectors of the Bishop frame. These generated curves could contribute to surface theory by introducing new surfaces. With the proposed method, new curves and surfaces can be produced in different frames, enriching curve and surface theories with novel geometric structures.
5.
Conclusions
In this study, I construct new adjoint curves by combining special Smarandache curves and integral curves in Bishop frame. I call these new curves {\mathbf{t}_\boldsymbol{\alpha} }\boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\alpha} -Bishop adjoint curve, {\mathbf{t}_\boldsymbol{\alpha} }\boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\alpha} -Bishop adjoint curve, \boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\alpha} \boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\alpha} -Bishop adjoint curve, and {\mathbf{t}_\boldsymbol{\alpha} }\boldsymbol{\zeta} _\mathbf{1}^\boldsymbol{\alpha} \boldsymbol{\zeta} _\mathbf{2}^\boldsymbol{\alpha} -Bishop adjoint curve. I establish some relations between a unit speed curve and its Bishop adjoint curves, and based on these relations, I provide an important characterization for a unit speed curve with respect to the Bishop frame.
Use of Generative-AI tools declaration
The author declares she has not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The author would like to thank the referees for their valuable comments and suggestions, which contributed to the improvement of this article.
Conflict of interest
The author declares no conflict of interest in this paper.









 DownLoad:
DownLoad: