1. Introduction
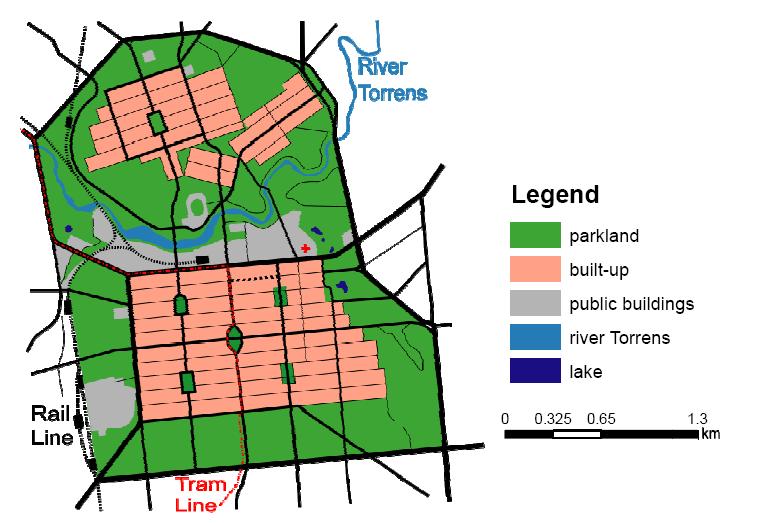
Adelaide, the capital city of South Australia, was founded in 1836 by settlers from the United Kingdom. It was formally designed by Colonel William Light, the state’s first Surveyor-General, and his deputy George Strickland Kingston, to a simple plan consisting of two main grid-iron pattern arrangements of streets (one a city centre covering one square mile) including six principal squares set in a figure of eight of open land forming a “green girdle” [1,2,3]. The latter became known as the Park Lands, and are now State Heritage listed. Beyond the city centre to the north the second area of planned residential settlement was laid out, also with Park Lands around it. Originally covering 9.31 km2, the Park Lands have lost 1.53 km2 for government purposes (mainly cultural institutions), and the remaining 7.6 km2 comprise various land uses, including a botanic gardens, sports grounds, schools’ fields and a stretch of the river Torrens, but are primarily public parks, 29 in total, some in formal or semi-planned gardens (Figure 1). This largely green space, twice the size of New York’s Central Park, encircling the city centre and the planned development north of the Torrens was described as “the green lungs of the city” by Colonel Light [4]. And indeed this ideal has featured in many of the debates and plans regarding the future of the Park Lands, so that they are a constant in any considerations of the development of the city and a model adopted elsewhere in Australasia [5,6].
This paper uses the ongoing presence of Adelaide’s Park Lands as a starting point for examining the contradictions that so often appear within debates about urban “greening”. For whilst there is a wealth of literature extolling the virtues of creating more green space in cities and for re-creating close linkages between people and nature or between people and food production, there has been a seemingly inexorable urban sprawl that challenges these ideals. Adelaide and major Australian cities in general provide excellent examples of this contradiction as low-density urban growth has swallowed up farmland and removed large swathes of native vegetation during the two centuries since initial European colonization of the continent [7,8]. Using Adelaide as a case study, the paper will consider how the arguments in favor of “greening” are competing with other ideas about future development, especially in the Australian context in which the argument that “there is plenty of land for development” frequently holds sway [9,10,11].
2. Colonizing Adelaide’s Park Lands
Despite the metaphor of “green lungs” being applied to the Park Lands, their actual use was originally unspecified beyond potential division between government and community uses (not necessarily for public amenity), with nine areas demarcated for government use in 1837. By 1840 some land had been allocated to a cemetery, a military barracks, Government House and a gaol, with much of the remainder used for grazing horses belonging to the government. From 1849 Adelaide Corporation assumed responsibility for management of most of the land, with several gardens being laid out and native and ornamental tree planting schemes [12,13], but this did not prevent substantial development of public facilities, especially on the north side closest to the city, and including the main railway. Sheep grazing was widespread elsewhere with some land allocated to local Indigenous people, the Kaurna, though Hay et al. [14] observe that the modern Park Lands, despite the use of some Aboriginal names for individual parks, “confirm a legacy of indigenous dispossession and are symbolic of ongoing marginalization”. Native forest was cleared and noxious uses such as rubbish dumps and sewage pits permitted. Subsequently, the railway yards, immediately northwest of the city represented the single biggest “land grab” by a colonial or state governments, with 10 ha, including 1.3 km of River Torrens frontage, alienated in two phases in 1880 and 1913 for the Railways Commission, despite protests from the city council and wider community [15]. Community concern over loss of public amenity in the park lands led to the founding of a Park Lands Preservation League (PLPL) in 1903 [16].
Over the course of its history there have been numerous challenges to the notion of the Park Lands as the city’s “green lungs”. In part the “lungs” have retained a green dimension by way of providing facilities for various active recreational pursuits, and this has been incorporated into city planning documents, with the Park Lands defined as “the prime open space focal point for the whole metropolitan area” [17]. Moreover, since 1997 they have been formally linked to other green space within the metropolitan area and beyond by the creation of the Torrens Linear Park, with public reserves along each riverbank [18]. Prompted by concerns about decline of natural habitat along the river, the quality of drinking water, flooding, the effects of a guided busway to the north-east suburbs (the “o”-bahn) and community demands for more recreational space, the River Torrens Acquisition Act was passed in 1970, followed a decade later by studies on flood mitigation and elaboration of the linear park concept [19,20]. Work on landscaping and construction of cycling and walking trails began in 1982 and were completed in 1997, creating a 30 km trail from the outflow to the city’s north-east suburbs. The National Heritage listing of the “Adelaide Park Lands and City Layout” was confirmed in November 2008. This acknowledged that the Park Lands are a cultural landscape comprising not just “green” space but also the five squares in the city’s layout, the tracts of State Government administered land including the Adelaide Botanic Garden, and the various individual garden designs. The significance of the Park Lands to the Garden City planning movement of the early 20th century is acknowledged in the listing [13,21,22].
The PLPL was formed in 1903 to contest further alienation of land in the Park Lands, and it was subsequently reformed in 1987 as the Adelaide Parklands Preservation Association after major commercial activities had been permitted including the Adelaide Casino, Hyatt Hotel and the Convention Centre as part of the Adelaide Station Environs Redevelopment project [23], adjacent to the Adelaide Festival Centre built in 1973. The 2005 Adelaide Park Lands Act limited further commercial uses, but has not prevented the recent building of a new hospital, new research facilities and extensions of the Convention Centre and sports stadium (the Adelaide Oval). The latter reflects the increasing use of the Park Lands for sporting activities, creating conflicts over public access and often featuring erection of specialist buildings [24]. In 1863 a portion of the eastern Park Lands (Victoria Park) was alienated by Parliamentary Act so that land could be used exclusively for horse racing. Public protest led to this land being unfenced, but from the 1980s this area has been used annually for motor racing, most recently for the Clipsal 500 (V8 Supercars) race, with the general public kept out of the area for up to four months at a time.
Overall around one-quarter of the original area of the Park Lands has been alienated from the public, with ongoing threats to add to this proportion, especially via redevelopment plans for the city’s “Riverside Precinct”, new developments for Victoria Park and by failure to return the current Royal Adelaide Hospital (built within the Park Lands) to green open space once a replacement hospital at a different site (within the designated Park Lands) has been built. It was not until 2005 that the Adelaide Parklands Authority was established (created under the Adelaide Park Lands Act 2005) to oversee a management strategy [25], a belated recognition of a need for systematic planning of this key feature of the city’s design [26].
3. “Un”greening Adelaide?
In comparison with most cities in the world, Australian cities have a low population density, with large areas devoted to low-density suburban living. Adelaide has an average residential density of 18 persons per ha, compared with 21.1 for Melbourne and 27.6 for Sydney [27]. Beyond the Park Lands there are very few pockets of high density living in the middle and outer suburbs. Of the city’s population 62% live at densities of 15 to 30 persons per ha, which is often defined as “suburbia”, compared with 26% for Sydney and 44% for Brisbane [27].
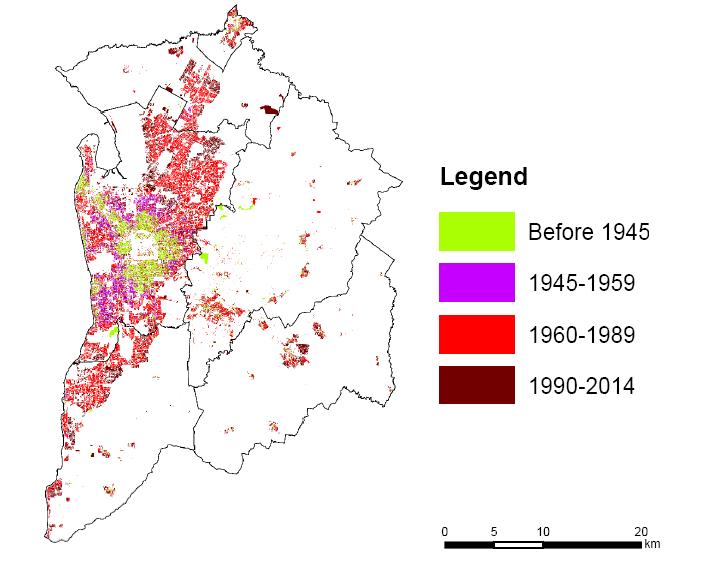
The most rapid expansion of the urban footprint occurred in the 1960s and 1970s as the seemingly inexorable sprawl of new suburbs across the plain occurred between the sea and the foothills of the Mount Lofty Ranges to the east (Figure 2). The city now sprawls along the coast for 100 km from Gawler in the north to Sellick’s Beach in the south, a point of natural constriction of the coastal plain, where the scarp face of the Mount Lofty Ranges reaches the coast in conjunction with the Onkaparinga River. The population density in the city has barely changed in the last quarter century (at around 15 persons per ha).
As shown in Table 1 the built-up area of Adelaide expanded most rapidly post-1960. The built-up area rose from 227.38 km2 in 1960 to 801.36 km2 in 1990 (an increase by a factor of 3.5) and then grew again to reach 1375.62 km2 in 2014, a rise of 72% from 1990. As shown in Figure 2, effectively this translated low-density urban development right across the Adelaide Plain. Some of the expansion also occurred into the city’s rural hinterland, where the most rapid loss of land to urban development is now happening (e.g. at Mount Barker, Gawler, and in the Fleurieu Peninsula).
Table 1. Urban Expansion of Greater Adelaide
| Source: Primary Industries and Regions, South Australia |
|
Period
|
Expansion area (km2)
|
Percent total (%)
|
Annual expansion area (km2)
|
|
Before 1945
|
53.70
|
14.57
|
|
|
1945‒1959
|
37.40
|
10.15
|
2.49
|
|
1960‒1989
|
166.80
|
45.27
|
5.56
|
|
1990‒2014
|
110.58
|
30.01
|
4.42
|
|
Total
|
368.48
|
100
|
|
Post-1945 suburbanization took place without formal planning controls, except for the limited powers of the Building Act, 1923 and the Town Planning Act, 1929. Local government had few powers to regulate the location of industry or the caliber of public housing, with broad state interests over-riding those of local residents prior to new planning laws introduced in 1962 [28]. The Report on the Metropolitan Area of Adelaide 1962 “provided a plan for the integration and guidance of the headlong growth of Adelaide which took place after the Second World War and which had tripled its population from 1945 to 1990” [29,30]: from 372, 000 in 1945 to 576, 600 in 1960 and 1, 044, 602 in 1990 [31]. Subsequently there was also creation of a State Planning Authority pursuant to the Planning and Development Act, 1967 [32]. However, the 1962 Report effectively supported continued urban expansion as a means of contributing to economic growth whilst meeting demands for single-family dwellings located on their own plot of land [33].
In part, this growth and the accompanying sprawl was encouraged by State Government attempts to promote economic development, notably through provision of funding and infrastructure (e.g. a north-south transportation corridor), and formation of a joint committee to govern planning, design and development control. A satellite town, Elizabeth, was developed 24 km north of the CBD in the late 1940s by the state’s public housing authority, the South Australian Housing Trust. This led to substantial housing and industrial development, with rapid population growth in the local government districts of Salisbury and Playford. In the 1990s a new centre for the southern suburbs 30 km south of the CBD at Noarlunga was developed, and in the north-east Modbury council took advantage of the concentration of land ownership to develop a major retail centre at Tea Tree Plaza (17 km from the CBD). These initiatives fostered decentralization of retail and industrial development for the city, but accompanied by low-density housing and reliance on privately-owned motor vehicles. Only rarely did concerns for design, visual amenity and “appropriate” development appear to hold sway [34] and strategic planning was not the prime concern in the South Australian Planning Act introduced in 1982 nor following the Planning Review of 1992 [35,36,37,38]. However, urban consolidation policies, with an increased emphasis on clearer residential design policies and neighborhood character studies (including integrated land use and transport planning) emerged in the 2003 Planning Strategy for Metropolitan Adelaide [39].
The link between deconcentration, urban expansion and economic growth remains strong in the Australian psyche, but challenges to the urban development model of the 1960s and 70s are now far more apparent in the planning of all the major cities. In the case of Adelaide the South Australian Government’s 30-Year Plan for Greater Adelaide released in 2010 invokes “Light’s vision” on numerous occasions, notably “by expanding the network of parks and greenways” and “parklands and open spaces built into new urban environments from the outset” [40].
It must also be acknowledged that there has been a prolonged debate in Australia, from the 1970s, regarding the benefits of low-density urban development and the most desirable future urban form [41]. This has focused on different aspects of urban planning, including proposals for well-planned development at the rural-urban interface to prevent the more undesirable aspects of urban sprawl [42,43], linking models of suburban form to aspects of sustainable development [44,45,46,47], advocates for higher-density housing [48], failures of planning for metropolitan regions [49] and the superiority of a polycentric form for the future of Australian cities as opposed to a continuing increase in densities around a single city centre [50,51]. Indeed, there are strong arguments acknowledging social equity concerns arising from the recent push towards high residential density inner suburbs [52,53]. So it is not possible to divorce concerns about past and future losses of greenfield sites to development without acknowledging that arguments other than just the balance sheet of land conversions to development need to be addressed. In particular, there are growing fears about increased housing inequality in Australian cities, frequently attributed to the withdrawal of state governments from land assembly and housing development [54], and the widespread adoption of a neo-liberal model in which it is assumed that markets alone can both stop urban sprawl and provide affordable housing [55,56].
The evolving national context raises concerns about the sustainability of increased reliance on the private car in the low-density metropolis as both federal and some state governments limit investment in public transport [57], though there has been some recent investment in South Australia in suburban rail lines and Adelaide’s tram line [58]. More holistic planning is needed that can balance competing demands of the environment, housing, transport, energy and economic development to produce more livable, resilient, sustainable cities [59].
This broader approach to urban planning is recognized in some aspects of the 30-Year Plan, which estimates a population increase of 560,000 by 2040, requiring an estimated 258,000 net additional dwellings in Greater Adelaide and Murray Bridge (76 km east of Adelaide). It aims for around 70% of the city’s population growth until 2040 to be housed via infill development: 134,000 infill dwellings, 85,000 fringe dwellings, and 39,000 township dwellings by 2035 [60]. This is seen by the State Government as meeting “consumer preference” for inner and middle suburban living whilst also providing more jobs than if development occurred on greenfield sites. The 30-Year Plan assumed an annual average of 400 ha per annum of broadacre land would be needed to meet the city’s demands. However, the average has been 320 ha and below since 2010‒2011 [61]. In part this reflects the impact of a series of additional and revised measures designed to increase urban population densities, which State Government has begun to implement since late 2013 (see Box 1). It also seems to reflect some greater acceptance of higher density urban living, as embodied in The City of Adelaide Strategic Plan 2012-2016, which refers to 15,040 net additional dwellings, 27,300 net additional residents and 50, 000 net additional jobs for the city by 2040 [62], which would shift some of the focus away from centrifugal urban expansion. Moreover, there are some signs that higher urban densities are linked to a range of developments that can broadly be labeled as “green” or favoring more environmentally friendly outcomes. These come in two forms: those that are being deliberately planned (including long-term expansions of green open space in the Greater Adelaide region) and those that reflect more organic tendencies within society. These will now be discussed in turn.
| Box 1. Measures designed to increase urban population densities in Adelaide. |
· Revising planning rules to help refocus private-sector interest in the CBD
· Rezoning of inner-metropolitan council areas to promote inner-city living
· Strengthen anti-development laws to the south (McLaren Vale) and north (Barossa Valley) of the city
· Developing a new 30-year transport plan for the state
· Developing a new strategy to revitalize the Park Lands
· Rezoning the Adelaide Riverbank precinct and creating a new management authority for the precinct
· New development initiatives focused on the CBD, including urban renewal legislation
· Commissioning a Planning Improvement Project to up-date 20-year old planning legislation |
Source: Derived from [127].
4. “Re”greening Adelaide?
4.1. Planned developments in new urban design and provision of green space
If the expectations of the 1960s were that centrifugal urban growth was closely equated with economic growth then it might be argued that in the new millennia there has been some reversal of this view. Greater recognition of the negative environmental consequences from limited controls on urban sprawl plus the perceived benefits from higher density development linked to “green” design features are producing new urban landscapes, often featuring partnerships between government, developers, industry, commerce and academia. Adelaide has three “living laboratories” that illustrate this.
The Low Carbon Living Co-operative Research Centre (LCLCRC), a federally-supported partnership between five universities and a range of industry partners, was formally launched in December 2012. A principal aim is to help Australia achieve its 2050 greenhouse gas emissions reduction target of an 80% reduction compared with levels in 2000 (with a 25% reduction by 2020). The realization of these targets will primarily be via developing low carbon building construction materials and increasing the evidence base for government policy and planning. This rests on research in three main areas: integrated building systems, creation of low-carbon precincts (LCPs), and “engaged” communities. Some of the early initiatives within the LCLCRC are based in Adelaide, notably work on LCPs. This reflects the creation of an Adelaide Living Laboratory Hub in December 2014 to deliver a research agenda for “three living laboratory locations” in suburban Adelaide: Tonsley, Bowden and Lochiel Park. This initiative aims to work with the local communities to develop low-carbon “solutions” for a diverse range of infrastructures and users [63]. Essentially these three showcase projects focus on reducing the carbon footprint of urban systems, through integration of the interlinked aspects of energy, water, waste, transport and buildings, to create desirable housing and high quality living with a zero carbon footprint in the long-term [64].
Tonsley, a 61 ha site 10 km south of the Adelaide CBD, is a former Mitsubishi car plant now completely re-developed. Formerly opened in February 2015, Tonsley is a collaborative and high-value industry (70% of the area), education (10%) and residential precinct (20%). With a new campus of Flinders University, a TAFESA campus and major industrial players on site (including Siemens, Zen Energy Systems and MAN Diesel & Turbo), the precinct has reused the former car plant’s Main Assembly Building to avoid loss of carbon emissions from the original construction whilst adding an “urban forest”, being highly water and energy efficient and providing new integrated transport options [65].
Lochiel Park, previously a TAFE College and Metropolitan Fire Service Training Centre, is marketed as “Australia’s model green village”, despite the fact that it is an Adelaide suburb just 8 km north-east of the CBD. It is a 106-dwellings residential development completed in 2009 by the Land Management Corporation of South Australia, at a density of 24.5 houses per ha (compared with the state average of 13). It was “planned based on sustainability principles which included addressing climate change impacts and establishing credentials for claiming carbon neutrality” [66]. The design includes servicing all houses by Solar PV cells, recycled water systems, gas boosted solar hot water systems, a minimum 7.5 star thermal performance rating, with a target of reducing potable water supply by 78%, greenhouse gases by 74% and energy use by 66%, compared with the 2004 state average. Monitoring over an initial nine-year period will focus on resource consumption in sample households to see whether residents’ behaviors show evidence of “sustainable lifestyles”. Essentially this development is a showcase for sustainable urban development, with its experience being translated into wide dissemination across various interest groups nationwide. The development cost AUD$18 million, with a subsidy paid by the State Government to builders for compliance with the green design specifications, which in the long-term should generate savings from an expected 40% reduction in water bills, and 66% in energy use bills. On the 15 ha site, just 4.25 ha is occupied by housing, the remainder being green open space (including an “urban forest”) protected by legislation from future development.
Initial evaluation of residents suggests that the keys to translating the plan into “sustainable lifestyles” will be determined by how the residents deal with their primary concerns of comfort, convenience and cost [67]. These are the biggest influences on the behavior of actual or intending residents of Lochiel Park and similar developments, and in turn these are affected by a range of factors within “the domains of work, home and community life, and the ways in which these domains intersect”. Hence, “green” design and environmentally friendly provision of water and electricity does not necessarily change overall behavior of the residents [68,69].
In Bowden, an inner suburb just 3 km north-east of the CBD, the former Clipsal and Origin Energy factories, covering 16.3 ha and abutting the Park Lands, were purchased by the State Government in 2008 to become a new “green village”. This proposal envisaged up to 1500 medium and high density multi-storey “green star” residential apartments (since revised to 2400 homes), with retail outlets and commercial offices set around a central retail development, and creating over 1200 ongoing jobs. So this is a much higher density design than that for Lochiel Park. It is also more ambitious, with total costs initially estimated at one billion dollars by including a “transport oriented development” or transit hub [70]. Renewal SA [71] is planning to create homes for 3500 residents who “will have cafes, restaurants, shops, offices, parks and gardens on their doorstep” in a largely self-contained “neighborhood”. Construction started in July 2013. However, the plans for the transit hub have already been revised, replacing an underground rail scheme with further development of the city’s tram system [72]. The Prince’s Foundation for Sustainable Communities will establish a small number of new terrace homes as part of the development in the form of showcasing “green” design [73].
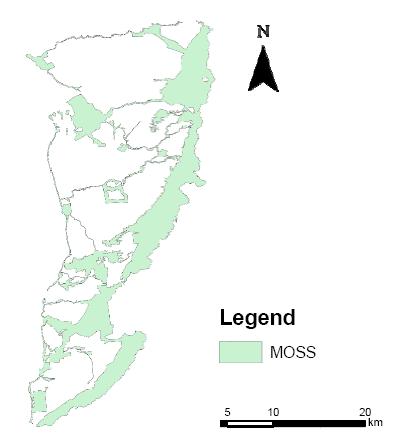
Whilst the three “living laboratories” are relatively small scale and represent experiments designed to pioneer “greener” living, a longer term and more wide-ranging planned green initiative relates directly to the Park Lands itself by extending green open space from the Park Lands to a much larger area. In the north-east suburbs the Torrens Linear Park now links to an extensive area of green space that represents an ambitious addition to the notion of “green lungs” for the city. This is the Metropolitan Open Space System (MOSS), the brainchild of 1980s State Minister for Environment and Planning, Don Hopgood [74]. His idea was to preserve the remaining natural environment in Adelaide’s rural-urban fringe and also watercourses and the coastline [75]. This idea was realized by the creation of MOSS in 1994 in the State’s planning strategy, formally implemented under the Parklands 21 Strategy [76,77]. As indicated in Figure 3, MOSS is extensive, incorporating the scarp face of the Mount Lofty Ranges and Adelaide Hills (including national and conservation parks), 70 km of metropolitan coastline (known as Coast Park), ten linear parks along the city’s rivers and some privately owned land incorporated for what Garnaut [75] describes as “its amenity value”, an increasingly important consideration in urban planning [78]. She also notes that since 1994 land has been added to MOSS by various state and local government initiatives.
In part, this reflects commitment to MOSS by State Government as set out in 2003 in its “Parklands 2036” program [76]. In this it specifically invoked the original creation of the Park Lands as a “first generation of parklands” now being followed by “a second generation of parklands” through taking MOSS “to the next level and setting the “blueprint” for open space for the next 33 years, ” and including realization of a coastal park concept [79].
4.2. Reconnecting people to nature
A common feature of life in the developed world has been for urban residents to become divorced from the physical environment, leading lives in which interactions with nature are very restricted. In particular, this “divorce” has separated people from the production of food, with food typically purchased from supermarkets sourcing their goods worldwide. However, growing concerns over food miles, the environmental dis-benefits of “industrial-style” farming, and the desire for renewing connections between food producers and consumers [80] has prompted various new “greening” initiatives that include community-supported agriculture, food production from urban gardens and allotments (often comprising small-scale organic production), creation of green roofs on buildings, and new systems of water harvesting. Whilst Australian cities have generally lagged behind those in North America and Europe in terms of manifestations of these initiatives, there are now several good examples in the major Australian cities, including Adelaide.
Community-supported agriculture (CSA) usually involves sales of produce direct from the farm to consumers, but with the consumers (i.e. the community) “adopting” farms by purchasing a share of the farm [81,82]. Under this arrangement shareholders are guaranteed weekly deliveries of seasonal produce. There are over 1500 such schemes in the USA, and now several in Australia, including Jupiter Creek Farm in the Adelaide Hills east of the city, a typical location for such ventures as it is close enough to the city to have input from city-based residents as well as locals. Subscribers to the Jupiter Creek scheme can order produce boxes of various sizes to be delivered weekly to a pick-up-point of their choice [83]. Another South Australian example is Beach Organics, a smallholding on the Fleurieu Peninsula, 85 km south of Adelaide, where subscriptions vary from $270 fortnightly for a box of organic produce for two to $495 quarterly for a box of organic produce for four [84]. Another variant is community gardens, where urban residents collectively produce fruit and vegetables for local consumption [85,86]. These have a long history in some parts of the world, e.g. the allotment gardens scheme in the United Kingdom, though they have been less common in Australian cities. Nevertheless there are currently 50 in and around Adelaide [87], including some initiatives designed to involve lower socio-economic status groups [88].
CSA is an example of “reconnection” between farmers and consumers, which has taken various guises in the past two decades, and which is at the heart of any realization of the potential for expanding organic production [89]. The term symbolizes a renewal of links between producers and consumers that some contend was lost during the last half century’s emphasis on mass food production [90,91]. Reconnection’s role in the demand for sustainable production, “natural” and organic foods, and local supply place it on the opposite pole to the expanding global food sector dominated by trans-national, supermarket-based retailing [92]. Reconnection is a key component of the growth of alternative food networks (AFNs), the polar opposite of “conventional” agri-food systems as they are often characterized by small-scale production, processing, distribution and consumption of food within a particular region [93]. This links AFNs to “short” food chains as opposed to the globally sourced, food miles-generating, long-distance supply chains typical of many products purchased from supermarkets. AFNs have grown from the late 1980s, partly through local (bottom-up) initiatives to generate closer ties between food producers and consumers in the region or locality of production [94]. In the Adelaide region they are typified by small-scale horticultural and dairying enterprises that feature direct sales to the public, including pick-your-own schemes, farm-gate sales and farmers’ markets. For example, there are now several farmers’ markets in the Adelaide region, with new ones having emerged in the last five years. Challenging the power of large supermarkets, these are offering opportunities for small farmers, especially those in the rural-urban fringe, to reconnect consumers to producers. Especially for sales of fresh produce and value-added produce, these markets are allowing certain values, such as the method or location of production, environmental benefits and high quality, peri-urban produce, to be represented in the price of marketed goods [95].
A different form of “greening” is the creation of “green roofs”, “rain gardens” and “green walls”, as encouraged by the State Government in the form of guides to “water sensitive urban design” [96], and initial trials starting in 2009 [97]. This acknowledges that a particular challenge in the Adelaide region “is to provide sufficient water to maintain the vegetation during the long inter-storm dry periods commonly experienced”. However, a key positive associated with green roofs is also identified: “if partial usage of rooftops for green roofs were to be implemented, then a considerable reduction in overall runoff volumes could be achieved”. This is important given that rooftop areas as a percentage of total impervious area can range from 30‒35% in suburban developments to as much as 70‒80% in business and industrial districts [98]. Green roofs can have important thermal insulation properties, whilst also helping to reduce temperatures, thereby impacting positively on urban heat island effects as well as enhancing amenity, reducing stormwater run-off and perhaps adding in a minor way to food production [99,100]. The experimental nature of many green roofs is reflected in another LCLCRC project, examining the mitigation of urban heat island effects through creating more green space (including green roofs) in trial areas of Sydney, Melbourne and Adelaide.
A problem with water-using initiatives in Adelaide, like green roof projects, is the small annual rainfall (average 550 mm p.a.) and long summer dry period. However, a significant “greening” initiative is the city’s wastewater crop irrigation system established in 1999, which supplies water via 100 km network of pipelines for thousands of ha of agriculture, notably to around 250 horticulturalists in the Virginia area of the northern rural-urban fringe. The Virginia Pipeline Scheme consumes a volume of water equivalent to about 10% of the wastewater generated and processed across all four of Adelaide’s wastewater treatment plants (over 22,000 ML p.a.) [101]. This pioneering scheme “is regarded as one of the great success stories of urban agriculture” [81] and potentially holds the key to the creation of more sustainable agricultural systems [102].
Since January 2010 the Park Lands has also benefited from a related “greening” initiative, with 3.8 billion liters a year of high quality recycled water piped underground 8 km from Glenelg to the west as part of a 34 km underground pipeline network around the entire Park Lands, incorporating North Adelaide and the CBD, in a $76.2 million state- and federally-funded project. Adelaide now recycles one-third of its wastewater compared with the national average of 10% [103]. This is part of an ongoing “droughtproofing” strategy, though there are concerns over the high salinity of this wastewater [104,105].
5. Conclusions: greening versus “un”greening
Adelaide’s initial design is still visible today in the form of the “green girdle” of the Park Lands surrounding the city centre. Yet, ongoing plans for development on land originally designated as open space in Colonel Light’s scheme symbolize the conflicts over green space that have been present throughout the city’s history. Today the immediate argument centers on how land already alienated from the Park Lands alongside the river Torrens should be developed, but at the same time measures to protect and enhance the remaining green space are evident. For example, in 2013 the State Government committed $20 million over four years for Park Lands revitalization projects through its Planning and Development Fund [106] and a more recent example is the State Government’s plan, announced in February 2015, to support a $160 million tunnel for the “O”-bahn bus route underneath the Park Lands, enabling two of the Park Lands’ parks (Rymill and Rundle) to be rejoined, thereby restoring over 3000 m2 of green space. Smaller interventions such as tree replanting along North Terrace and a $24 million redevelopment of Victoria Square/Tarntanyangga (one of the five original inner city squares of Light’s design) begun in 2013 are part of a management plan aimed at maintaining and enhancing landscape, recreation, natural systems, and heritage [107].
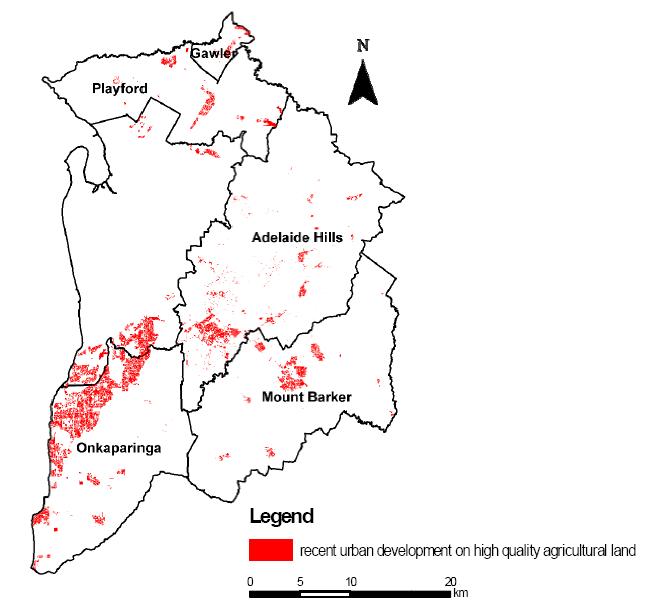
The sprawling nature of Greater Adelaide is in keeping with similar patterns of development for all major Australian cities, but despite the low-density residential development and decentralization of various industrial activities especially in the three decades following World War Two, the creation of MOSS in 1994 has produced a swathe of protected green space that has replicated and extended the “green lungs” metaphor attached to Light’s original scheme. Yet, despite the presence of the MOSS, only 13% of the original native vegetation of the Mount Lofty Ranges/Adelaide Hills to the east of the city remains intact; this is highly fragmented and only 22% is formally managed for conservation purposes [108]. It is one of 15 Australian biodiversity hotspots identified by the Australian Government’s Department of the Environment [109]. Yet, “Of the 31 species of native mammals known to reside in the Southern Mount Lofty Ranges at the commencement of European settlement in 1836, only 22 can now be confirmed as currently resident within the region” [110]. Moreover, in the Greater Adelaide area, “At least 132 native species of plants and animals have become locally extinct, and a minimum of 648 introduced species have arrived (mostly plants)” [111,112]. The consumption of this vegetation and greenfield land has slowed, but there remain major tensions between conservation and urban sprawl as new development is occurring beyond MOSS and also often on high quality farmland (Figure 4), notably in areas targeted for even more development. Farmland protection policies, such as residential exclusion zoning, have not been popular in Australia, the latest notable failure of such schemes being Sydney’s “green zones”. James [113] argues that in part this reflects a lack of proper consultation with those who could make peri-urban agriculture work: small-scale farmers and existing residents of the rural-urban fringe [114,115].
In terms of farming activity in the fringe, Butt [116,117] observes that there is a mixture of non-commercial activity interspersed with a few high value activities, such as intensive poultry, whose growth is constrained by the nature of the location. He uses the term “post-productive environment” to highlight the fact that food production is often a secondary concern in the fringe, though in Adelaide’s case there are three highly agriculturally productive areas within 50 km of the city centre (the Adelaide Hills, the Barossa Valley and McLaren Vale). However, the vulnerability of Adelaide’s urban fringe is also apparent in the recent losses of commercial horticultural land to development in the Virginia area north of Elizabeth and the expansion of Mount Barker (which had the most rapidly growing population in the state in 2014) by converting high quality farmland for development. Houston [118] estimates that whilst peri-urban land comprises just 3% of the surface area, it produces one-quarter of the gross value of agricultural production in the five mainland states. Yet protection of this valuable farmland is often submerged within broader policy deliberations [118,119,120,121].
A trend to further “un”greening may be the increased ability of developers to succeed in attempts to build on green space in the rural-urban fringe if recent recommendations to overhaul the State’s planning system are implemented. The Expert Panel on Planning Reforms (EPPR) has made 22 recommendations that if implemented could remove local council involvement in the decision-making process on key rezoning and development proposals. In particular, the proposal is to force the Development Assessment Commission (DAC) (or its successor), which hears planning appeals, to rehear contentious applications rather than, as at present, being heard in the Environment, Resources and Development Court. Developers could drive changes to zonings by preparing their own development plans, which currently is the province of councils and State Government. The underlying rationale for the proposed changes is State Government’s view that the current development assessment process is too slow and cumbersome and so needs reform. Hence the EPPR also suggests creating Regional Planning Boards covering several council areas, which would set regional planning strategies and assess changes to development plans driven by councils. Moreover, a new State Planning Commission would advise State Government on planning infrastructure and urban renewal issues, developing State Planning and design policies and replacing the DAC. Council Development Assessment Panels would be replaced with regional panels that would lack the presence of local councilors, so a local dimension could be removed from the process and opportunities for local communities to “get a fair hearing” might be reduced.
An extra dimension in the case of Adelaide’s rural-urban fringe, especially close to the MOSS in the Adelaide Hills and Mount Lofty Ranges, is the potential for conflict between new residential development and risk of bushfires. This area was the site for a major fire in 1983 when 14 people died. More recently, over 12, 500 ha were burned and 38 houses destroyed by a fire in January 2015 in the northern part of the Hills. So further urban development is not only antithetical to maintenance of biodiversity, but may pose physical risk to new inhabitants, especially as the numbers of fires and population densities are often closely related [122].
Local councils have prepared bushfire risk assessments that inform development decisions [123]. For example, within high bushfire risk areas, development proposals are assessed against bushfire protection planning provisions of the relevant local area development plan, including referral to the Country Fire Service for advice on the degree of difficulty in protecting the development from bushfire. In medium risk areas development proposals are assessed against bushfire protection planning provisions [124]. There are also strict controls on clearing vegetation under the Native Vegetation Act [125]. However, under new planning provisions, restrictions on native vegetation clearance around dwellings have been weakened so that residents are now allowed to clear vegetation 20 m from their dwelling [126], thereby potentially adversely affecting environmental assets in the rural-urban fringe.
New developments are accentuating the creation of an urban fringe landscape where it will be a proliferation of small reserves that dominate biodiversity conservation across the region, whilst a broader wider whole-of-landscape, whole-of-community approach to biodiversity conservation and fire management will be required if the probability of further extinctions is to be reduced [111]. So a real battle between “greening” and “un”greening will continue to be fought not only in the Park Lands and through introduction of new cutting edge low-carbon urban designs but via the growth of “reconnection” and conflicts in the rural-urban fringe.
Acknowledgements
The authors are most grateful for advice from Peter Houston regarding the data used in generating Figures 2 and 4.
Conflict of interest
Authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: