1. Introduction
The dynamic thermal rating (DTR) system determines the maximum capacity of overhead line conductors based on a set of weather conditions [1,2]. The IEEE 738 standard describes the DTR system in great details [3]. Parameters such as wind speed (Vw), wind angle (ϕ), air temperature (Ta), solar angle (θ), conductor resistance (R) and operating temperature (Tc), are used to determine the steady state line rating as shown in (1).
|
Qc(Tc,Ta,Vw,ϕ)+Qr(Tc,Ta)=Qs(θ)+I2R(Tc)
|
(1)
|
where Qc is the convection heat loss, Qr is the radiated heat loss, Qs is the solar heat gain, R is the conductor resistance, and I is the line thermal rating.
In more than 90% of the instances for which the measurements for DTR are taken, the DTR system can increase the line capacities by 10–30% with improvement of 50% being possible in windy areas [4]. This reduces the needs for more transmission corridors and its applications have attracted many researches. The DTR system has also been proven to be beneficial for the reliability of transmission networks in several field studies [5,6]. The reason is the DTR system clears line congestions through the redirections of power flows and this consequently provides flexibility in load shedding strategy [7]. The reliability and risk impact of DTR systems on a power network has also been evaluated [8,9]. Then, an optimum placing strategy for the DTR sensors on a long overhead transmission line was proposed due to it being impossible to deploy DTR sensors on each span of a line [10]. It has also been shown that the many successful deployments of wind farms worldwide [11,12] are due to the ability of the DTR system to facilitate the integration of wind energy [13,14,15,16]. In [11], it was shown that the strategic deployment of the DTR sensors can further improve the rating of the transmission line for accommodating higher level of wind power. In [12], a time-series model was proposed as a more suitable model for accurate analysis of the effects of the DTR system. In various studies from [13,14,15,16], they collectively agree that the DTR system can adequately improve line rating for wind power integration. Partly due to this reason, the wind power has become one of the most invested renewable sources by energy utilities worldwide [17]. As such, the reliability of wind farm operation has been heavily investigated as well. Moreover, an option-theory was used to extent the lifespan of wind turbines by minimizing their failure risk [18]. An operational and maintenance model for reducing the repair cost of wind turbine was proposed [19]. A methodology that considers the reliability impact of wind variability and wind turbine outage rate on wind farms was proposed [20] as the variability of wind power is essential towards the reliability of wind-integrated power networks [21]. All the cited studies collectively agree that the reliability benefits of the DTR system and wind energy is highly dependent on its weather parameters such as locations, the correlations among the weather parameters and the ability to collect accurate weather data. Apart from wind energy, other renewable sources such as (but not limited to) photovoltaic and fuel cell can also be incorporated to form a hybrid power supply for power systems [22,23]. In these cited studies, it was mentioned that non-conventional energy sources, namely wind power, mini-hydro, solar, and cogeneration (e.g., biomass), start having a significant contribution in the energy production matrix due to the recent restructuring of the electricity sector. It is also noted that the intermittency and stochastic behavior of renewable sources should be properly managed and be considered during power system expansion and operation in order to maintain the reliability of power supply [24].
From the above, it is clear that the DTR systems and renewable energy sources play a considerably different role in the electricity transmission and generation planning. From the transmission perspective, the implementation of the DTR system will cause the fluctuations of line rating throughout the day and this need to be considered during line expansion planning. In terms of the generation planning, the stochastic nature of the renewable sources, especially wind, is appropriately handled by the DTR system as stronger wind blows also produce higher line ratings. Despite this, all the aforementioned studies have not effectively examined transmission network expansion study for connecting renewable sources by using the benefits of the DTR systems. In view of the relationship that strong wind speed is able to produce high wind power and be able to provide maximum cooling, which in turn produces high line rating from the DTR system, this paper is focused on the transmission network expansion planning that incorporates the DTR systems and wind power. In the modelling of the DTR system and wind energy, a sequential Monte Carlo simulation (SMCS) is ideally suitable. The reason is the SMCS has the existing framework for incorporating all the chronological characteristics of weather data, load profiles, and the chronological transition of component states within a system [25]. The SMCS is, therefore, able to provide an accurate and realistic simulation involving the DTR system and wind energy.
In this paper, a bulk electric system reliability analysis considering the integration of wind energy and the DTR systems is investigated. More importantly, the possible transmission network reinforcement alternatives for absorbing a significant amount of wind energy are studied and a methodology for carrying out this type of reliability study is proposed. All the considered scenarios of transmission reinforcement planning in this paper are based on the current actual electric system practices and they are discussed in this paper. Finally, due to the characteristics of the SMCS and the studies perform in this paper, the reliability evaluations are also carried out through SMCS.
2. Methodology
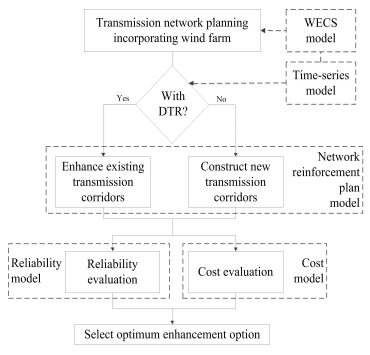
This section describes the proposed methodology of the composite power system reliability evaluation for transmission network planning. The proposed methodology is depicted in Figure 1. The figure shows that the methodology begins with the modelling of wind energy conversion system (WECS). The WECS model can be replaced with other generation models should other renewable sources or conventional generators be used. Then, the methodology identifies whether the DTR system is incorporated into the transmission network reinforcement planning process. The DTR system is modelled using the IEEE 738 standard. The time-series characteristics of wind energy and line rating given by the DTR systems are considered as well. Next, all the possible reinforcement plans are identified based on the presence of the DTR systems and these plans are evaluated from their reliability and cost perspectives—see section 2.3 for more details. In the plans that consider the DTR systems, existing transmission corridors are enhanced with the DTR systems and no new transmission lines are built. Notice that the decision to avoid building new transmission corridors when the DTR systems are installed is temporary if the load demand continue to rise into the future. In this case, the installation of the DTR system is beneficial for delaying new constructions in order to ease financial burden or to obtain approval for new land and space explorations.
In the plans that do not include the DTR systems, new transmission corridors are constructed. At the end of the methodology, a plan is suggested based on the optimum trade-off between the reliability and cost values. In addition, the proposed methodology in Figure 1 also shows that the methodology can be separated into several models, which all of them will be explained in details in the remaining of this section. These models are the WECS model, a time-series model, a network reinforcement plan model, a network reinforcement cost model and an overall reliability evaluation model.
2.1. WECS model
In this section, the wind farm or WECS model are described. This is important as wind farm is considered in the proposed transmission network planning framework. The presented WECS model will be used to determine the WECS power output. In general, WECS consists of two main parts. They are the wind speed and wind turbine generator (WTG). The modelling of wind speed is given in section 2.2 and this section describes the WTG model. The power output of a WTG depends on the amount of wind speed it receives. This relationship between the wind speed and wind power is given by [26]:
|
P(Vw)={00≤Vw<Vci(A+BVw+CV2w)PrVci≤Vw<VrPrVr≤Vw<Vco0Vw≥Vco
|
(2a)
|
where Vw is the wind velocity and Pr is the rated power output of the wind turbine. Vci, Vr and Vco are the cut-in, rated and cut-out wind speed respectively. The constant A, B and C are given as [26]:
|
A=1(Vci−Vr)2[Vci(Vci+Vr)−4(VciVr)(Vci+Vr2Vr)3]B=1(Vci−Vr)2[4(VciVr)(Vci+Vr2Vr)3−(3Vci+Vr)]C=1(Vci−Vr)2[2−4(Vci+Vr2Vr)3]
|
(2b)
|
All WTG units in this paper are assumed to have the rated capacity of 250 MW. Based on the reliability survey report [27] on the five mainstream WTG designs, this paper adopts the reliability value of the most reliable WTG design. This design is based on the directly-driven permanent magnet synchronous generator (DDPMSG) technology and it has the failure and repair rates of 1.501/year and 0.0081/year, respectively. In this paper, all WTGs are assumed to be the same and share the same reliability data.
2.2. Time-series model
The ability to realistically simulate the hourly values of wind speed and line rating is the prerequisite for power system reliability analysis that incorporate wind energy and the DTR systems using SMCS. Time-series, unlike probability samplings, can simulate random wind speed while maintaining their propagation pattern based on the wind speed historical samples. Besides, the wind speed modelled by the proposed time-series model in this section will also affect the power output of WECS as given in (2). According to [12], the weather parameters needed for calculating DTRs and wind power output varies with geographies and time and they are related to their immediate previous hours. In other words, the sampling of weather profile is not entirely random and they follow a trend that is affected by past samplings. Considering this, the conventional data samplings through probability distribution fittings are not suitable as each sampling is independent of one another. Therefore, the line ratings based on the DTR systems and wind speed in this paper are more suitably modeled using the auto-regressive moving average (ARMA) model [12]. The ARMA (n, m) model has the following general expression:
|
yt=∑ni=1αiyt−i+et−∑nj=1βjet−j
|
(3)
|
where αi(i=1,2,…,n) is the auto-regressive parameter, βj(j=1,2,…,m) is the moving average parameter. The notation et denotes white noise process with zero mean and variance of σ2 In other words, et it is normally and independently distributed (et∈NID(0,σ2)). Equation (2) shows that a future conditional mean value of yt (line ratings or wind speeds) is affected by its past observed values yt−i and past innovations et−j. In this paper, the order of the ARMA model was obtained using the educational software ARMASA [28].
It is also important to consider that the ARMA models are correlated in a way similar to their respective weather parameters from different locations. It is, therefore, important to consider such correlation relationship during the simulations of the ARMA model. In this paper, the correlation model described in [16] is used. Briefly, the correlation model shows that instead of sampling the random innovations of the ARMA models from their respective uni-variate normal distribution, an equivalent multivariate normal distribution that considers the correlations among the ARMA model can be used to simulate line ratings and wind speeds that are correlated.
2.3. Network reinforcement plan model
A number of reports indicate that the current electric system practices in most of the North American states require the generator owners to pay for all the costs of connecting their generators to the bulk electric system [29,30]. The transmission network provider (TSP), however, is responsible for all the network enhancement costs due to new or modified network connections. The TSP has the prerogative to allocate all or parts of the network enhancement costs to customers on a postage stamp basis. Similar with any commercial projects, all the connection projects are entitled to a payment scheme within an agreed timeframe. The report also mentioned that Canada adopts similar standard.
Considering the current worldwide electric system practices for managing the connections of new generators, four categories of realistic network reinforcement scenarios are identified and described as below:
(1) The wind farm owner pays for the connection paths to the transmission network and will therefore minimize the construction cost by building two shortest lines to connect the wind farms. The TSP will pay for the cost of building the new transmission corridors in the transmission network in order to absorb the additional wind energy and to increase the overall system reliability.
(2) The TSP negotiates rerouting paths for connecting the wind farms in order to improve the overall network reliability. Hence, all the additional rerouting cost of connecting the wind farms will be subsidized by the TSP. Similar to the first case, the TSP will pay for the cost of building new transmission corridors in the transmission network.
(3) This scenario is similar to the first scenario, except the TSP implements the DTR system instead of building new transmission corridors in the transmission network.
(4) This scenario is similar to the second scenario, except the TSP implements the DTR system instead of building new transmission corridors in the transmission network.
2.4. Network reinforcement cost model
All the network reinforcement costs consist of capital investment (CI) cost and operating and maintenance (O & M) cost. For simplicity, all O & M costs are included into the capital cost. The yearly payment scheme of a reinforcement plan is given by [31]:
|
Capitalrecoveryfactor(CRF)=i(1+i)n(1+i)n−1
|
(4)
|
where i is the present worth rate and n is the useful years considered. CRF adjusts the equal regular payment for a number of years that is equivalent to the current value. In short, CRF indicates an annual uniform payment of a project through n years for its useful lifetime. Considering that, the following equations calculate the annual payment (AP) cost of all the network reinforcement plans for each category.
Category 1 and 3 (Without wind farm rerouting):
|
P1,3=CI+O&MAP1,3=P1,3×CRF
|
(5)
|
Category 2 and 4 (With wind farm rerouting):
|
P2,4=(CI+O&M)−originalcostAP2,4=P2,4×CRF
|
(6)
|
The subscripts represent the category of the network reinforcement plan. Furthermore, the following assumptions are made:
(1) CI cost of a 138 kV overhead line = 0.5 M$/km [2].
(2) O & M cost of a 138 kV overhead line = 5% of its CI cost [2].
(3) CI cost of a DTR system = 20% of CI cost of a 138 kV overhead line as the DTR system incurs only a fraction of the cost of constructing new lines [2].
(4) O & M cost of a DTR system = 5% of its CI cost.
(5) Number of useful years, n = 50 years.
(6) Present worth rate, i = 10%.
2.5. Network reinforcement reliability model
The reliability evaluation of power system can be performed in three layers [25]. The first layer considers the ability of the generation to satisfy the load. The second layer expands the first layer by incorporating the adequacy problem of the transmission network and this layer is also known as the composite reliability evaluation. The third layer expands the evaluation by considering the distribution network. The third layer is not normally performed as it is time consuming and complicated [25]. In this paper, the composite reliability evaluation is performed.
In order to form an accurate network reinforcement reliability study, the possible huge number of power system states and the chronological elements of wind power and line rating have to be considered. To achieve this, the SMCS offers an effective solution [32]. The SMCS used in this paper is described below and a more detailed description can be found in [25,32].
(1) Specify the initial state of all components (generators and transmission lines). It is assumed that all components are initially in the normal up-state.
(2) Simulate the duration of each component residing in its present state base on its failure and repair rates distribution function using the inverse transform method [33]. In this paper, an exponential distribution function is assumed for all components. Hence, the sampled value of the ith component state duration (Ti) is given as:
The symbol Ui denotes the uniformly distributed random number in between 0 and 1 for the ith component. λi, depending on the current state of the component, is the failure or repair rate of the ith component.
(3) A chronological up and down-state for each component is then generated for a year with time resolution of an hour. The chronological hourly load model for each load point is constructed and incorporated into the analysis. The time-series DTR and wind speed values are generated using their ARMA models and they are updated into the power network.
(4) The simulated process is assessed for each hour by running the direct-current optimal power flow (DCOPF) [34]. Although DCOPF ignores reactive power and voltage constraint, it has less computational burden and is widely use in composite reliability analysis as the formulation is linear [25,32].
3. Test system
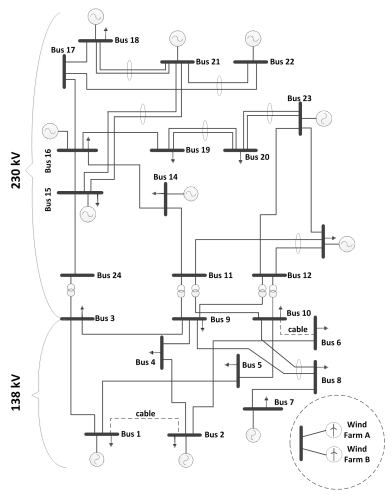
The original IEEE reliability test network (RTN) is a 24-bus system with 10 generator buses, 17 load buses, 33 transmission lines, 5 transformers and 32 generating units. The total system peak load and generation are 2850 MW and 3405 MW, respectively [35]. The test system used in this paper is a modified IEEE RTN as shown in Figure 2.
In the modified RTN, all loads and generations were increased by 2.5 times in order to stress the transmission network. As the bulk of the generator is located in the 230 kV region, there is a deficiency of power generation in the 138 kV region. Moreover, most of the power generated in the 230 kV region is unable to deliver to load points in the 138 kV region due to the highly congested network.
Consequently, two wind farms, each with a 250 MW capacity, were assumed to be connected into the grid by a wind farm company. The connections of these wind farms and the required transmission network reinforcements for absorbing the additional wind energy for improving the overall power system reliability are based on the network reinforcement plan options given in section 2.3.
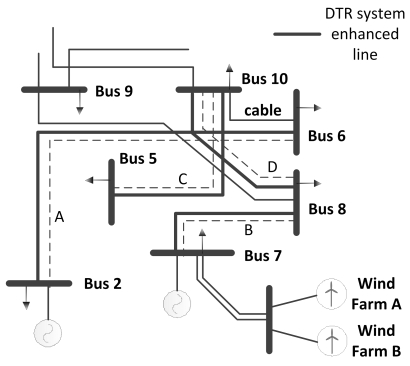
In the first and third category scenarios of the network reinforcement plan model, it is assumed in this paper that the wind farm owner chooses to connect two wind farms to bus 7 using two parallel lines as shown in Figure 3. Due to double circuit structure, the CI cost of the second line is considered to be 50% of the cost of the first line. This is the most preferable option by the wind farm owner because it is the shortest (60 km) connection path into the bulk electric system. The wind farm owner is not responsible for any possible constraints on the transmission system. Instead, the TSP is responsible for enhancing the transmission network in order to fully utilize the wind energy for improving the overall power system reliability. These enhancements are as the followings and they are also shown in Figure 3:
(1) Plan 1.1: Construct line A.
(2) Plan 1.2: Construct line B.
(3) Plan 1.3: Construct line C.
(4) Plan 1.4: Construct line D.
(5) Plan 3.1: Enhance line 2–6 with DTR system.
(6) Plan 3.2: Enhance line 7–8 with DTR system.
(7) Plan 3.3: Enhance line 5–10 with DTR system.
(8) Plan 3.4: Enhance line 8–10 with DTR system.
(9) Plan 3.5: Enhance line 2–6, 7–8, 5–10 and 8–10 with DTR systems.
Notice that the above enhancements options are only some of the actions that the TSP can take. This list does not consider all the possible enhancement options that the TSP can carry out for this network as the purpose is only to demonstrate the proposed methodology. Other enhancement options can follow the same analysis procedure that is given by the proposed methodology.
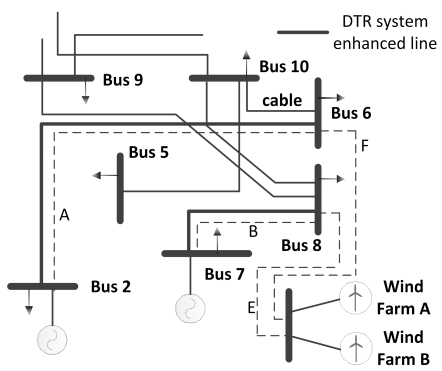
In the second and fourth category scenarios of the network reinforcement plan model, the TSP is involved in determining the connection paths of the wind farms. As the TSP is involved, the transmission network constraints and also the impact of the wind farm connection on the overall power system reliability are of concerned to the TSP. For such arrangement to occur, the TSP negotiates with the wind farm owner to reroute the wind farm connection paths. It is assumed that all the rerouted connection paths from the wind farms to the transmission network are 100 km. All the additional costs incurred due to the longer connection paths arising from the reroute will be subsidized by the TSP. This category of the reinforcement plans are shown in Figure 4 and they are designated as follows:
(1) Plan 2.1: Construct line E.
(2) Plan 2.2: Construct line E and B.
(3) Plan 2.3: Construct line F.
(4) Plan 2.4: Construct line F and A.
(5) Plan 2.5: Construct line E and F.
(6) Plan 2.6: Construct line E, F, A and B.
(7) Plan 4.1: Construct line E and enhance line 7–8 with DTR system.
(8) Plan 4.2: Construct line F and enhance line 2–6 with DTR system.
(9) Plan 4.3: Construct line E and F and enhance line 2–6 and 7–8 with DTR systems.
Similarly, this list does not consider all the possible enhancement options that the TSP can carry out for this network as the purpose is only to demonstrate the proposed methodology. Other enhancement options can follow the same analysis procedure that is given by the proposed methodology.
All the weather parameters required for the calculation of the DTR ratings and wind energy were sampled from the British Atmospheric Data Center (BADC) website [36]. All the weather data has a historic period of 20 years with hourly resolution. Due to the proximity of the transmission corridors in the IEEE RTN that are enhanced with the DTR system, the weather data was also sampled from the locations that are no further than 50 km apart. In all the plans where new transmission lines are built by the TSP within the transmission network, they are all considered to be parallel with the existing lines. For example, line A in Figure 3 and Figure 4 is parallel with the line from bus 2 to bus 6. Considering this, the length of line A, B, C and D are 50 km, 16 km, 23 km and 43 km, respectively, as given in the original IEEE RTN standard [35].
4. Results and discussions
In this section, the reliability and cost of all the transmission network reinforcement plans are evaluated. Although all the plans shown in this paper are specific, the basis on which the plans are devised and the evaluation methodology presented in this paper are not. Hence, the proposed evaluation methodology shown in this paper can be applied to the other power networks facing the same issue of connecting new generators, especially wind farm.
The evaluations of all the reinforcement plans were performed from the cost and reliability perspectives. The results are shown in Table 1 and they are discussed in this section.
4.1. Cost evaluation of reinforcement plans
The AP costs of all the network reinforcement plans were determined according to the network reinforcement cost model given in section 2.4. One network reinforcement plan from each category is selected to demonstrate the calculations and they are as follows:
Plan 1.1: Construct line A
P1.1=CI+O&M
=50×0.5+0.05(50×0.5)=26.25M$
AP1.1=26.25M$×0.1009=2.65M$/year
Plan 2.1: Construct line E
In order to calculate the AP cost of this network reinforcement plan, the original connection cost of the wind farms is first determined:
P=1.05(60×0.5+12×60×0.5)=47.25M$
then,
P2.1=1.05(100×0.5)−47.25=5.25M$
AP2.1=5.25M$×0.1009=0.53M$/year
Plan 3.1: Enhance line 2-6 with DTR system
AP3.1=0.2×AP1.1=0.53M$/year
Plan 4.1: Construct line E and enhance line 7-8 with DTR system
P4.1=1.05(100×0.5)−47.25+0.2×1.05(16×0.5)=6.93M$
AP4.1=6.93M$×0.1009=0.70M$/year
The remaining calculations for all the other network reinforcement plans follow the same procedure given by (5) and (6) according to their respective category. The costs of all the network reinforcement plans are shown in Table 1. The table shows that the construction cost of category 3 reinforcement plans is in general lower than the other categories. The reason is the category 3 reinforcement plans do not require new transmission line and the TSP is not involved in the rerouting of the wind farm connection paths. Instead, only the DTR systems are installed in this category, which cost only a fraction of the cost of building new transmission lines [2]. The table also shows the reliability cost of each reinforcement plan. This is will be discussed in detail in section 4.2.
Table 1. The cost of all the network reinforcement plans.
|
Plans |
Construction cost (M$/year) |
Reliability cost (M$/year) |
Total cost (M$/year) |
| Category 1 |
1.1 |
2.65 |
16.76 |
19.41 |
| 1.2 |
0.85 |
8.32 |
9.17 |
| 1.3 |
1.22 |
27.63 |
28.85 |
| 1.4 |
2.28 |
40.64 |
42.92 |
| Category 2 |
2.1 |
0.53 |
18.44 |
18.97 |
| 2.2 |
1.38 |
8.64 |
10.02 |
| 2.3 |
0.53 |
14.53 |
15.06 |
| 2.4 |
3.18 |
8.97 |
12.15 |
| 2.5 |
5.83 |
11.85 |
17.68 |
| 2.6 |
9.32 |
0.46 |
9.78 |
| Category 3 |
3.1 |
0.53 |
29.95 |
30.48 |
| 3.2 |
0.17 |
10.34 |
10.51 |
| 3.3 |
0.25 |
27.60 |
27.85 |
| 3.4 |
0.46 |
28.65 |
29.11 |
| 3.5 |
1.40 |
29.88 |
31.28 |
| Category 4 |
4.1 |
0.70 |
10.55 |
11.25 |
| 4.2 |
1.06 |
16.88 |
17.94 |
| 4.3 |
6.53 |
8.97 |
15.5 |
On the other hand, the category 2 reinforcement plans have some of the highest reinforcement costs due to the construction of new lines and the rerouting of the wind farms connection paths. Expectedly, the average construction cost of the plans from category 2 and category 4 are higher than the plans from the other categories. This is due to the fact that the TSP reroute the connection paths of the wind farm, which causes an increase in the construction cost.
Despite a clear indication that the plans from category 3 have low reinforcement cost, the results presented in this section do not provide enough information to determine an optimum reinforcement plan. Hence, the reliability performance of all the plans are also examined and considered.
4.2. Reliability evaluation of reinforcement plans
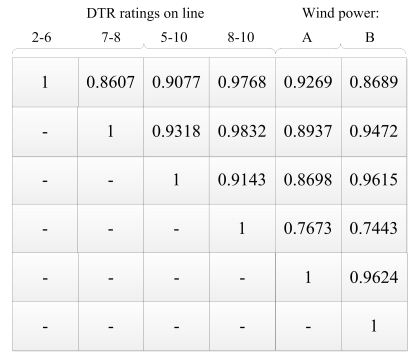
In this section, the reliability impact of all the network reinforcement plans were evaluated base on the network reinforcement reliability model given in section 2.5. In the cases where the DTR systems were used, the correlations among the time-series DTR ratings and wind energy were considered. A comprehensive matrix that shows the correlations among all the historic DTR ratings and the wind energy are shown in Figure 5.
The results show that the correlations among the line ratings and wind farm power output are in general high. The lowest recorded correlation value (0.7443) is between DTR ratings on line 8–10 and wind farm power output B. Thus, the results in Figure 5 also indicate that the inability to consider the correlation relationship during the reliability analysis of the network reinforcement plan will lead to inaccurate results.
The expected-energy-not-served (EENS MWhr/year) index was selected as the reliability performance indicator for all the network reinforcement plans as it has the longest convergence time among all the other reliability indices [25]. Hence, convergence of EENS will ensure that sufficient Monte Carlo simulations have been performed and premature convergence can be avoided. In addition, the average values of loadloss (VoLLs) from the Royal Academy of Engineering's report for the UK Prime Minister's Council of Science and Technology were also used to translate the impact of EENS into monetary cost [37]. By multiplying the interrupted energy with average VoLL, one can translate electricity lost into monetary lost. These values are given in Table 2.
Table 2. Average VoLL of various conditions.
|
Average interruption cost of, $/MWhr |
| Peak (3–6 pm) |
Off-peak |
Weekend |
| Winter |
6495.69 |
6525.70 |
5634.43 |
| Summer |
6268.91 |
5757.02 |
5178.49 |
The reliability cost of all the plans are shown in Table 1. In general, the results show that the reinforcement plans that reroute wind farm connections (category 2 and 4) have lower reliability costs than the other reinforcement plans that do not reroute wind farm connections. For example, Plan 2.6 has the lowest reliability cost. This is due to the fact that the rerouting of the wind farm connections alleviated the network congestions on the lines connected to bus 7. Besides that, the two additional transmission lines constructed in this plan also provided extra line capacities for absorbing the wind energy to satisfy more load demand. On the other hand, Plan 1.4 has the highest reliability cost despite the plan constructs an additional transmission line from bus 8 to 10. This shows that this additional transmission line is not critical in aiding the absorption of the wind energy. The reason is the impact on the overall power system reliability due to the connection of the wind farms is not considered in this plan.
4.3. Total cost of reinforcement plans
The total cost of all the reinforcement plans is obtained by summing the construction and reliability costs. The total costs of the all the plans are shown in Table 1.
The results in Table Ⅰ shows that Plan 1.2 has the lowest total cost (9.17 M$/year) following by Plan 2.6 (9.78 M$/year), Plan 2.2 (10.02 M$/year) and Plan 3.2 (10.51 M$/year). The costs of all these plans are comparable to each other. Plan 2.6 is very competitive with Plan 1.2 as its total cost is only higher by 0.61 M$/year. However, when the construction costs are examined, it shows that Plan 2.6 has a much higher value than Plan 1.2 by 8.47 M$/year. The construction costs of Plan 2.6 and Plan 1.2 are 9.32 M$/year and 0.85 M$/year, respectively. This is due to the fact that Plan 2.6 involves the constructions of two new transmission lines and an agreement between the wind farm owner and the TSP to reroute wind farm connection paths. On the other hand, Plan 1.2 requires only the construction of a short overhead line from bus 7 to bus 8. In short, Plan 2.6 has the lowest reliability cost but this benefit is negated by its high construction cost (highest among all the plans). On the contrary, Plan 1.2 has a much higher reliability cost than Plan 2.6 but this disadvantage is compensated by its low construction cost.
Among the four cheapest plans mentioned previously, Plan 3.2 offers the lowest construction cost with moderate reliability cost. Its reliability cost is only higher than Plan 1.2 by 2.02 M$/year. Besides that, it is also the only plan that utilizes the DTR systems and no new transmission lines are required in Plan 3.2. Hence, Plan 3.2 should also prove to be the most attractive when considering that it offers more space for future transmission network developments when the demand grows higher. Thus, from this perspective, Plan 3.2 is more attractive than Plan 1.2. This argument is enhanced by the fact that the total cost of Plan 3.2 is only higher than Plan 1.2 by 1.34 M$/year. All in all, based on the implementation of the proposed methodology on the IEEE-RTN, the analysis recommend the implementation of Plan 3.2.
5. Discussions
The advantages of the proposed transmission network planning are:
(1) It utilizes the line-rating enhancement benefits of the DTR systems to delay or avoid new line constructions. The DTR systems have fast implementation time and are relatively cheaper than constructing new lines. This is advantageous for quick connections of new wind farms for satisfying consumer loads. As a result, this planning methodology also has the advantage of easing the financial burden of the TSP.
(2) The use of the DTR systems is able to free up land space as new line constructions can be avoided. Hence, the DTR system is beneficial in locations where land and space are restricted.
The limitations of the proposed method are:
It is most beneficial for the planning of wind farm connections. If other renewable energy sources are to be connected, the advantages of the DTR systems are not able to be utilized fully. The reason is wind speed has strong correlations with high wind power output and high line-rating. When wind is strong, the cooling effect on transmission lines is maximized and the DTR system is able to enhance the line ratings the most. At the same time, wind farm is able to produce higher power output due to the stronger wind. The acquired new line capacity enhancement is then able to be used to connect higher level of wind energy.
6. Conclusion
A new methodology is proposed in this paper to evaluate the reliability and cost of transmission network planning involving large wind farms and the DTR systems. The studies demonstrated in this paper show that the integration of bulk wind sources can cause congestion on a weak area of a transmission network. In order to alleviate this problem, transmission network reinforcements are needed and they can be carried out through constructing new transmission corridors, rerouting of wind farm connections or implementing the state-of-the-art DTR system. Results from this paper show that the reinforcement of transmission network with the DTR systems incurs a much lower cost than building new lines although it does not necessarily provide the best reliability for the network. However, it is more desirable to implement plans that use the DTR systems as they offer more space for future transmission network development when the load demand grows higher. In addition, results also show that the transmission network planning with the DTR system (Plan 2.6) is only slightly higher than the cheapest plan (Plan 1.2) which implemented new line constructions by 0.61 M$/year. Lastly, the work in this paper has also shown that the proposed methodology can assist system planners to create potential transmission reinforcement schemes to facilitate large wind farms additions into the bulk power system.
Acknowledgments
The authors would like to thank the funding support given by the USM short term grant: PELECT/304/60313051, the Ministry of Science and Technology (MOST) in Taiwan under grant MOST106-2218-E-027-010, and the Chaoyang University of Technology in Taiwan under grant CYUT-106-7778.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: