1. Introduction

Oligomers can be regarded as molecular complexes composed of multiple subunits of polypeptide chains through non-covalent bonding with discrete protein-like structures, and they serve as valuable models for understanding the details of protein functions. Relatively little is known about the structure of oligomeric forms, and an investigation of the amyloid beta (Aβ) oligomeric form is quite important in order to control fibrillogenesis, which is regarded as a hallmark of Alzheimer’s disease [1,2,3]. (The full sequence of Aβ_1-40 is: H₂N-DAEFRHDSGYEVHHQKLVFFAEDVGSNKGAIIGLMVGGVV-COOH.) Oligomerization is essentially a functional control, such as allosteric regulation and the establishment of higher-order complexity. However, observing the details of oligomerization is a challenging task since oligomers can be unstable due to a local minimum of monomer elongation or aggregation processes, which possess relatively high DG (Gibbs energy change). Furthermore, no specific study on the binding structure of Aβ with gold surface has been conducted and the detailed binding force, therefore, has not been identified. Based on the limited studies investigating the interactions of peptides with gold surfaces in an aqueous solution, adsorption of energies can be best estimated to be broadly ranging between -9 kcal/mol and -63 kcal/mol [4]. Therefore, it is quite difficult to focus on a major conformation which plays a key role in binding with the gold surface. Since oligomers are typically a heterogeneous ensemble consisting of a multitude of distinct characterizations and properties, a general characterization is extremely difficult to determine. The oligomerization may be incidental to protein activity in certain cases [5,6,7], and no one general mechanism can account for the process. Several mechanisms in different proteins may have taken place by different routes to create the oligomerization [6,8,9,10]. The oligomerization depends on environmental conditions, such as concentration, temperature, and pH. It can take place in response to a stimulus, such as a change in nucleotide binding, nucleotide hydrolysis or phosphorylation state. Such a change can have a dramatic effect on the affinity of the subunits for one another, often by orders of magnitude [5,6].

A majority of the proteins in a cell are oligomeric [11,12], but due to experimental constraints only the lower order of oligomeric protein structures has been studied [13]. The association between subunits can vary in strength and duration. The folding pathways of a number of monomeric proteins have been studied, including b-sheet proteins and caging structure [14,15,16,17,18]. Generally, thermodynamic mechanisms involving several different conformations of in vitro protein folding are complex phenomena and often occur with the assistance of molecular chaperones after the folded subunits are released from the chaperone [19,20,21,22,23,24,25,26,27,28,29,30,31]. Most in vitro studies center on the aggregation of Ab monomers prepared in solution, and the important energetic role that exists at an interface during oligomerization has been underestimated [32]. An interfacial environment provides the significant contribution to a structural change of Aβ [33]. The proteins immobilized at an interface can possess different properties than their counterparts dispersed in solutions [34,35,36,37]. The amount of specific surface field is enough to stabilize a structure which is not otherwise prepared at interface free environments. Secondary and tertiary structures of peptides under interfacial environments have been extensively studied [38,39,40,41,42,43,44,45,46,47]. A sheet structure was confirmed on fluorinated nanoparticles, and this observation implied that self-assembly over a nanoscale interfacial environment plays a key role in fibrillogenesis [47].

Our approach is to prepare a specific type of Aβ oligomeric units on the surface of gold colloidal nanoparticles. The Aβ is a relatively small key peptide with 40 to 42 amino acid sequences that eventually irreversibly forms an insoluble fibril. By altering external pH conditions, it is possible to create a reversible self-assembly process. We have been investigating the formation of oligomers of amyloid beta peptide over gold colloidal nanoparticles (10nm-100 nm) and it has proved to be the best template for selectively assembling a specific oligomeric unit [48,49,50]. The associated nanoscale structural information of this adsorbed Aβ and the oligomeric form of Aβ is then investigated [51,52,53,54,55,56]. Nanoscale surface properties affect the adsorption of the proteins present in biological fluids, leading to the so-called protein “corona”, which determines the pharmacokinetic and pharmacodynamic properties of nanoparticles [9,10,11,12]. Site-specific targeting can be conveniently achieved by functionalizing the surface of nanoparticles with suitable ligands, such as small molecules or antibodies capable of recognizing receptors specifically located at the site of interest [13,14,15]. The clarification of peptide-heavy metal interaction can be fully utilized to design a highly sensitive optical biosensor and can quantify heavy metal pollution under aqueous environments [57]. As a great advantage, the spectral feature of gold nanocolloidal particles can be used as a marker for identifying the conformational change of the Aβ. A self-assembly of Aβ monomers was found to possess its sequence, surface size, and temperature dependence.[48,54,55,58,59,60] The surface potential prepared over nanoscale materials revealed a high possibility of controlling the reversible self-assemblypath of Aβ monomers.

2. Amyloid Beta Attachment and Occupancy Ratio

The usage of Aβ attached to goldcolloidal particles allows for a spectroscopic study to be conducted. The peak position of the surface plasmon band depends on the conformation of peptide attached on the gold colloidal surface. We prepared the folded or unfolded conformation by setting the solution to be basic or acidic. The average peak position, λ_peak(pH), of the observed band at a given pH is extracted by the weighted average of multi components as shown in Eqn. (1).

Here, λ_i(pH) and a_i(pH) are the peak position and fraction of the i-th component band, and the fraction a_i was determined by the fraction of the area, A_i (a_i = A_i /S A_i ) of the band to the total area of the entire bands. Then, the average peak position was surveyed as a function of pH, and the position of the peaks were plotted as a function of pH as shown in Figure 1a. It was analysed by a Boltzmann formula as shown in Eqn. (2).

Figure 1. a) The observation of the peak positions as a function of pH. This plot was analysed by a Boltzmann model (sigmoidal) given in Eqn. (2). b)The size dependence of the ΔpH_o. The difference of pH_o between those with or without proteins was plotted as a function of gold colloidal size for Aβ_1-40. ΔpH_o = pH_o (Aβ_1-40 coated gold a nm) - pH_o (gold a nm).

DownLoad: Full-Size ImgPowerPoint

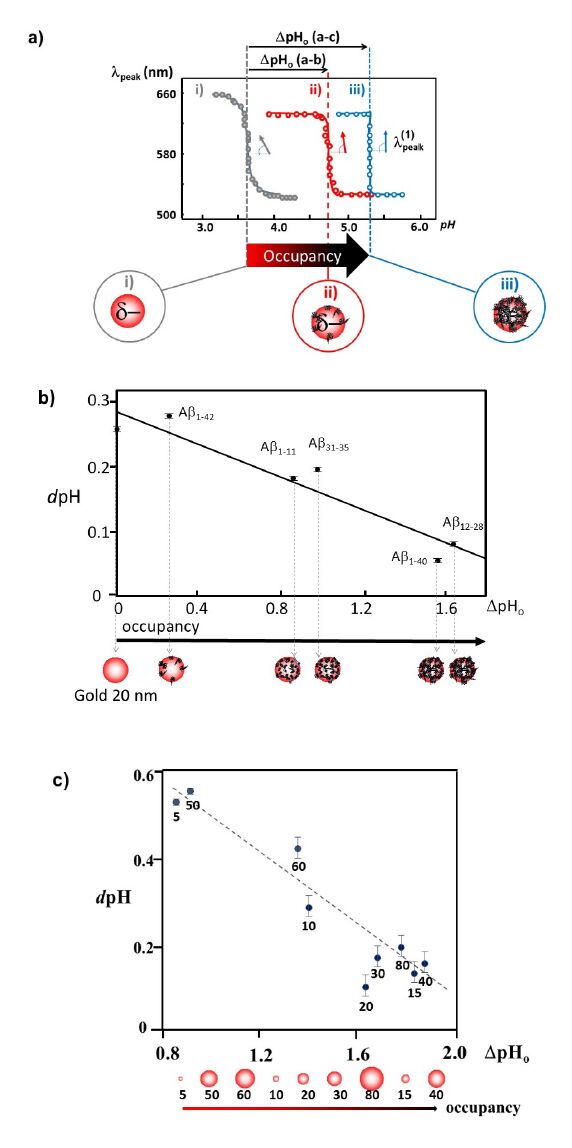
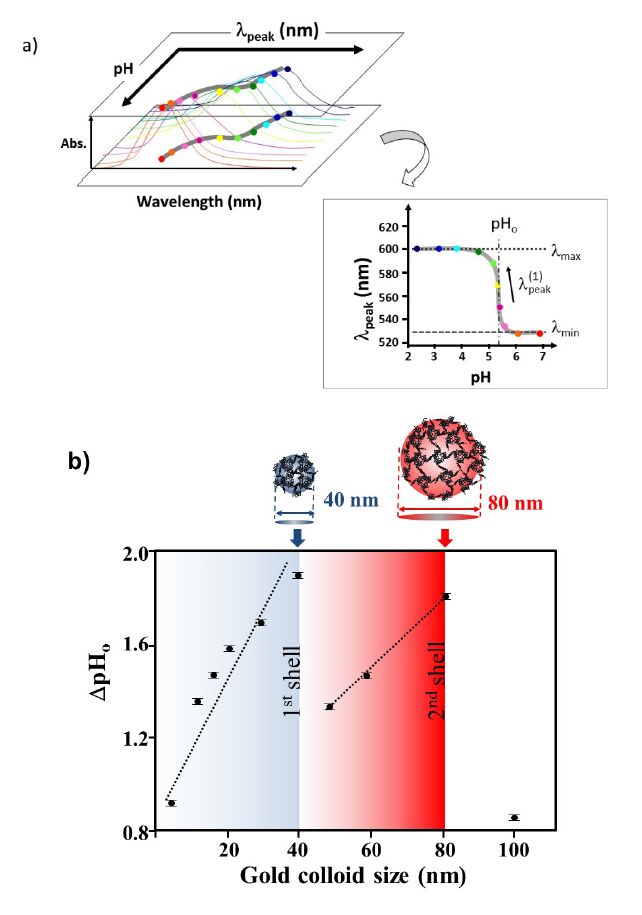
Here, the value of pH_o shows the point where a colour change takes place at which λ_peak = (λ_min + λ_max)/2. The λ_min and λ_max stand for the minimum and maximum of the band peak positions, respectively. The dpH is defined as: dpH = (λ_max - λ_min)/4λ_peak⁽¹⁾, where λ_peak⁽¹⁾ is the first derivative of the λ_peak(pH). Absorption of a collective excitation of the electrons at the interface between a conductor and an insulator is considered to account for the colour of the suspensions of these particles [61,62,63].

If the net anionic sites of the metal surface are neutralized by acid, an aggregation should be more enhanced, resulting in the solution’s colour change to blue from red. As protein covers the colloidal surface more, the less negative net ionic charge can be achieved by a shielding effect shifting pH_o to the higher value. For example, bare gold colloids (10nm-100 nm) change their colors at lower pHs (pH = 2-4) while Aβ coated colloidal surface shows the colour change at pH = 4.5-6. The difference of pH_o between bare gold (ΔpH_o) was plotted as a function of the size of gold (Figure 1b). The discontinuities were found every 40 nm (i.e., 40 nm and 80 nm). This suggests that cage structure effectively closes as the diameter takes a multiple of 40 nm.

We have discovered a clear negative correlation between dpH and ΔpH_o, where ΔpH_o is the difference between pH_o (gold alone) and pH_o (Aβ coated gold colloid). Also the effectiveness of the coverage is expected to increase as DpH_o increases. The dpH is inversely proportional to λ_peak⁽¹⁾, the first derivative of the λ_peak(pH), and the smaller value in dpH indicates the higher λ_peak⁽¹⁾. As Abcoverage or occupancy increases onto the gold surface, ΔpH_o gets higher and the slope of curve at pH_o becomes steeper (i.e., dpH gets smaller.) as illustrated in Figure 2a. The degree of coverage or occupancy of peptides reflects upon how much shielding of a partially negative charge of gold colloidal surface is obtained. By neutralizing the anionic sites of the metal surface, an aggregation is more enhanced and resulting in the solution’s colour change to blue from red. If protein covers the nanocolloidal surface more, net ionic charge can be more shielded. It means that more coverage from the peptides requires a less acidic condition to neutralize the surface. Bare gold colloids change their colors at lower pHs (pH = ~ 3) while peptide coated colloidal surfaces show the colour change at a pH = 4.5-6 depending on the degree of coverage. When dpH was examined for various Aβ on 20 nm gold colloid, a clear sequence dependence was found (Figure 2b). Since Aβ_1-42exhibited the smallest ΔpH_o, it illustrated the least effective adsorption among the tested Ab sequences. On the other hand, Aβ_12-28possessed the largest ΔpH_o implying the most effective coverage among tested Aβ sequences. This means that Aβ_12-28contains an essential secondary structure required for adsorbing onto the gold colloidal surface. It is also noteworthy that Aβ_1-40 showed a relatively high ΔpH_o (i.e., more effective shielding). Considering that the hydrophilic segments (sequences 1-16) are used for networking with other monomers, the sequences of 17-40 must be a major section interacting with the colloidal surface.

Figure 2. a) A schematic diagram explaining the shift of pH_o and an aggregation of gold colloidal particles. The pH_o values shifts to more basic position as the coverage of protein increased from i) to iii). The plot of dpH_o vs ΔpH_o for b) various Aβ sequences on 20 nm gold colloid and c) various gold colloidal surfaces of Aβ_1-40.

DownLoad: Full-Size ImgPowerPoint

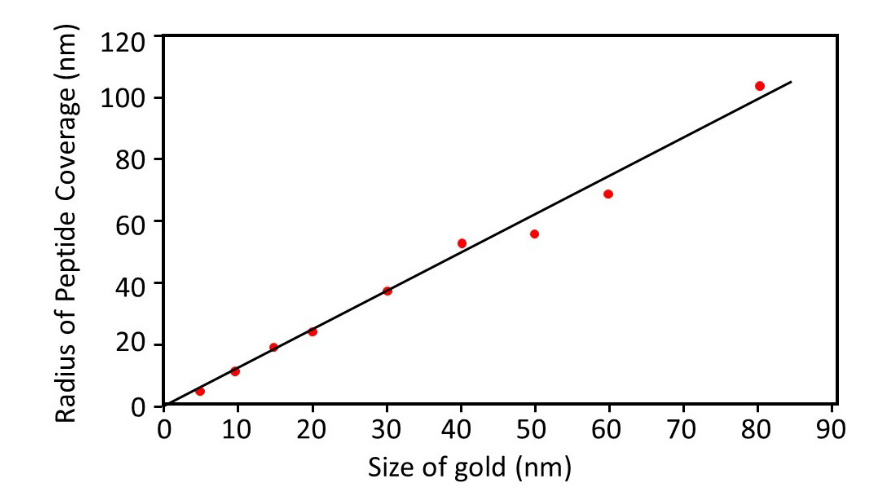
We have examined the dpH value as a function of ΔpH_o for variously sized gold colloids on Aβ_1-40. Remarkably, both plots showed a linear relationship as shown in Figure 2c. By assuming that ΔpH_o and dpH maintain a linear relationship, a linear trend line given in Figure 2c shows that the peptide coverage ratio becomes 0 % at ΔpH_o = 0, and an x-axis intercept indicates a ΔpH_o value at the peptide coverage to be a ratio of 100% (ΔpH_o = 2.11 at dpH = 0). Thus, ΔpH_o of each gold colloidal size enables us to estimate the coverage ratio as shown in Table 1. The peptides do not cover 100 % of the surface which indicates that the coverage may be monolayer. Furthermore, we calculated the coverage area for each gold colloid, and it showed a linear relationship with the size of the gold colloid (Figure 3). This means that the coverage area is determined by the size of the nanogold colloid and that there must be an equilibrium electrostatic shielding value for a given nanogold metal surface. The packing of these peptides must try to achieve a minimum potential energy on the surface of the gold by arranging themselves in a way that maximizes the occupancy of that sized particle.

Table 1. Estimated Aβ_1-40 coverage ratio over each nanogold surface.

Gold size (nm)	Coverage
5	0.43
10	0.66
15	0.86
20	0.77
30	0.80
40	0.89
50	0.63
60	0.64
80	0.85

 | Show Table

DownLoad: CSV

Figure 3. The plot of radius of Aβ_1-40 covered area versus size (diameter) of gold colloid.

DownLoad: Full-Size ImgPowerPoint

3. PH Induced Nano-Size Dependent Reversible Self-Assembly

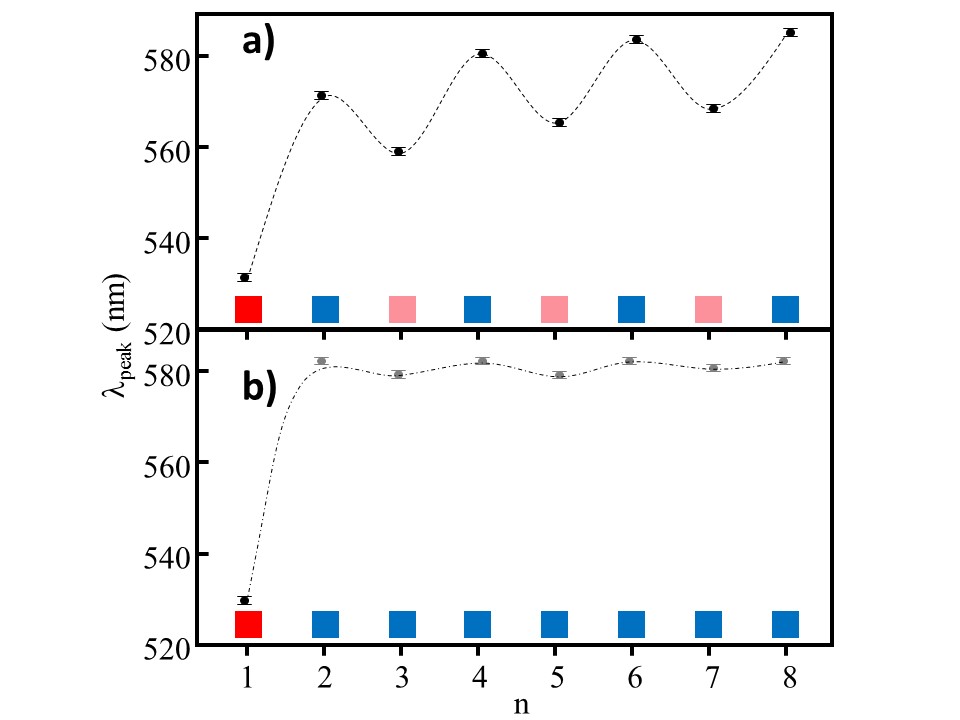
In our study, folded or unfolded conformations were induced by an external pH condition change. The pH of the solution was repeatedly altered between pH 4 (unfolded) and pH 10 (folded) as the corresponding spectrum was collected. The identification of the pH change operation was given by “n”, and n = 1 corresponds to the starting pH condition of solution (e.g., approximately pH 7). The odd numbers of n (n_odd = 3, 5, 7, ...) indicated an operation of basic addition making the pH of solution to be pH 10, and even numbers of n (n_even = 2, 4, 6, ...) indicated an acidic addition (pH 4). The feature of the reversible self-assembly was represented by band peak position, λ_peak (n, T), for each gold colloidal size using Eqn. (3).

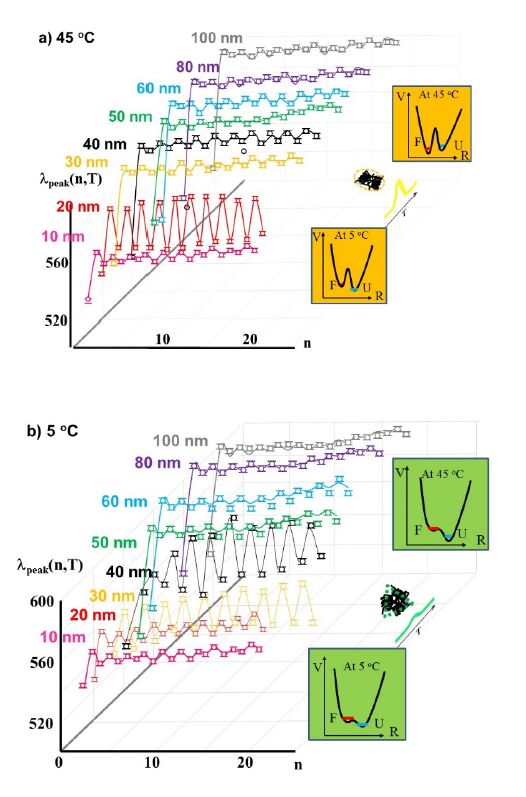
Here, n is an index showing the operation of the pH change.(n=1, 2, 3….; pH 10 at n_odd = 3, 5, 7, ...; pH 4 at n_even = 2, 4, 6, ...) An initial peak position at neutral pH (i.e., λ_peak(n = 1, T)) is given by $A_T^d - D_T^d$, and the parameters $B_T^d$ and $C_T^d$ indicate the average shift of the wavelength between pH 4 and pH 10. The parameters $D_T^d$ and $E_T^d$ are designed to represent an “amplitude of reversibility” and a “damping factor for the repetitive event”, respectively. The cosine function represents an undulation of λ_peak(n, T) between pH 4 and pH 10. Under a room temperature, most prominent quasi-reversible self-assembly was observed for Aβ_1-40adsorbed on 20 nm gold among all tested sizes of gold colloidal nanoparticles ranging from 5 nm to 100 nm (See Figure 4).

Figure 4. The demonstrations of peak position under two different cases of D parameters. Peak position λ_peak is plotted as a function of n. a) Aβ_1-40 coated 20 nm gold colloid (D > 5.5 nm), and b) Aβ_1-40 coated 15 nm gold colloid (D < 5.5 nm). The curves show the values predicted by Eqn. (3), and the squares below show the colours of each solution.

DownLoad: Full-Size ImgPowerPoint

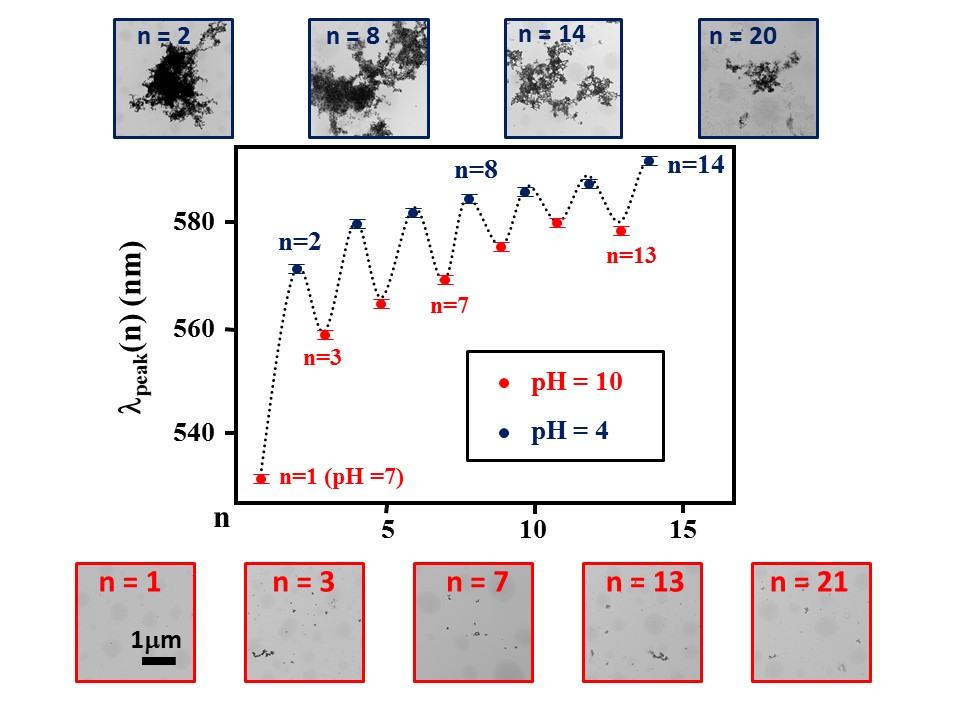
A quasi-reversible feature in λ_peak is further clarified from an analysis utilizing TEM (Transmission Electron Microscopy). As for Aβ_1-40 coated gold colloid 20 nm, the morphology of the gold colloids exhibited a dispersed feature at basic conditions, whereas a significant aggregation was observed at acidic conditions as shown in the bottom images placed in Figure 5.

Figure 5. A resulted λ_peak as a function of pH for Aβ_1-40 coated 20 nm gold colloid. Except for the n=1, the blue circle and red circles indicate the λ_peak after an injection of HCl and NaOH, adjusting the pH of the solution to pH 4 and pH 10, respectively. The dashed line is shown to provide a guide a trend of peak shift. At the above and beneath of plot, TEM images for n = 1 (pH 7), n = 2 (pH 4), n = 3 (pH 10), n = 7 (pH 10), n = 8 (pH 4), n = 13 (pH 10), n = 14 (pH 4), n = 20 (pH 4), and n = 21 (pH 10) are shown.

DownLoad: Full-Size ImgPowerPoint

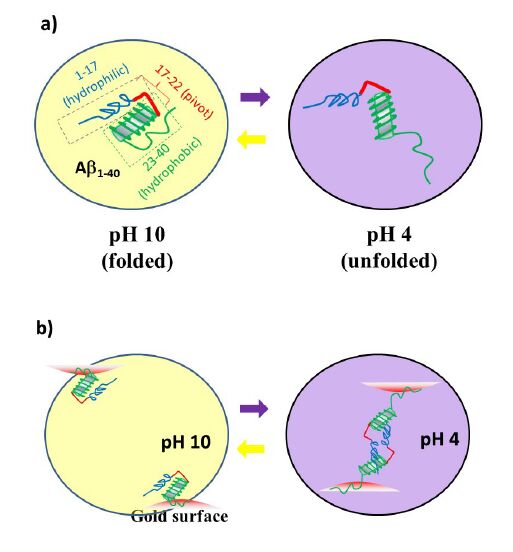
In order to investigate the number of particles consisting within an aggregate, TEM images were further analyzed by converting the image to data of pixel coordinates and corresponding color indices. The ratio of the area occupied by the particles (occupancy rate, a), and the estimated number of the particles (N) were calculated. As for Aβ_1-40 coated 20 nm gold colloid, a drastic change in a and N were repetaedly observed as the condition was changed to acidic or basic [64]. This change clearly correlate with the oscillatory change of l_peak. It is consistent with an assumption that the Aβ_1-40 prepared on the gold surface under the acidic condition constructed an unfolded conformation and the terminal sequences sticking outward were used for networking with the other monomers. Folded conformations must be prepared and no sequences are considered to be placing outword for networking under basic conditions. The number of gold particles consisting of one cluster is very high at the initial stage of cycles, and it decreased as the acidic/basic operation was repetaed implying that Aβ_1-40 was being denatured at the later stage of the cycles. In order to support the pH dependent repetitive structural change, a type of “pivotal structure model” is proposed as shown in Figure 6. In a pivotal structure model, a monomer of Aβ_1-40 is roughly described with three sections as: Aβ_1-16 (hydrophilic section), Aβ_17-22 (pivotal section), and Aβ_22-40 (hydrophobic section). Here, the sequences between 17 and 22 play as a pivot to switch between fold and unfold conformation at basic or acidic conditions, respectively.

Figure 6. a) Sketches of fold and unfold conformation of Aβ_1-40 monomer at the gold colloidal surface between pH 10 and pH 4, respectively. b) The sketches of surface adsorption of Aβ_1-40 over a nanogold colloidal surface at pH 10 and pH 4.

DownLoad: Full-Size ImgPowerPoint

Under acidic conditions, the Abmonomers coated over the colloidal surface are physically inter-connected with each other through the hydrophilic sequences. Remarkably, we did not observe any reversible aelf-assembly over silver nanocolloid’s surfaces [64]. Considering that the polarizability of silver (7.9 ų) is larger than that of gold (6.1 ų), a stronger binding of the peptide to the silver surface is plausible if an electrostatic interaction dominates the interface. The stronger polarizability of the silver interacted with both the hydrophilic and hydrophorbic segments and it prevented the peptide fr om forming the unfolded conformation even under acidic conditions.

4. Nanoscale Surface Potential Induced Oligomeric Forms

The significant quasi-reversible feature was observed for Aβ_1-40-coated 20 nm gold colloids between 20 °C and 45 °C (See Figure 7a). On the 30 nm and 40 nm gold colloidal surfaces, Aβ_1-40-monomers exhibited a prominent reversible self-assembly below 15 °C as shown in Fig 7b. It is known that Aβ_1-40monomers form β-sheets consisting of Aβ-oligomers around pH 5.4 [65,66]. The hydrophilic portion of the sequences must be exposed outside in order to make a network with other Aβ-coated gold colloids under aqueous conditions. The hydrophobic portion must be used for bonding to the gold colloidal surfaces. Structures that converge into the unfolded conformation as the cycle proceeds, and the conformation of the hydrophobic sequences (18-40) may remain unaltered. On the other hand, the hydrophilic portion may fold or unfold at basic or acidic conditions, and the hydrophilic portion determines a degree of reversibility. The surface potential prepared by the 20 nm gold colloid can support a repeating folding/unfolding process without disturbing the organization of the network of oligomers. The rest of the gold colloid can only support the cage structure, in which some of the monomers are not fully organized due to the physical area limitation. Reversible self-assembly of Aβ_1-40 over 20 nm gold colloids was significantly enhanced 15 °C and above, whereas that over 30 or 40 nm gold colloid was observed at the 15 °C and below. This opposing temperature dependence suggests that a conformation created over the 20 nm colloidal surface and those created over 30 or 40 nm colloidal surfaces are thermochemically different. The MD (Molecular Dynamics) simulation of Aβ_10-35 showed that the dimer concentration was maximized at 47 °C, while the maximum concentration of trimer was calculated to be at 17 °C [67]. Considering that Aβ_10-35 contains essential sequences of Aβ_1-40 to conduct a reversible self-assembly, we can conclude that the Aβ_1-40 dimer oligomeric form is more dominant over the 20 nm colloidal surface and the Aβ_1-40 trimer form is enhanced at the 30 nm and 40 nm gold colloidal surface.

Figure 7. The measurements of λ_peak between pH 4 and pH 10 for Aβ_1-40 coated on various gold colloidal sizes ranging from 10 nm to 100 nm at a) 45 °C and b) 5 °C. The dotted lines indicate the values predicted by Eqn. (3). The potential energy diagram for a self-assembly between folded (F) and unfolded (U) structure over a) 30 nm gold (trimer based oligomer is supported) and b) 20 nm gold (dimer based oligomer is supported).

DownLoad: Full-Size ImgPowerPoint

A key issue of a reversible self-assembly between the unfolded and the folded structure must be how much denaturization or damage to the α-helix portion of the Aβ₁₋₄₀ is minimized under an acidic condition. The hydrophilic segments (1-17) are responsible for the formation of a-coil and the hydrophobic component (18-40) plays a major role for forming the β-sheet. Aβ monomers placed at polar-nonpolar interfaces are considered to form the aggregates with β-structure rich conformations [68]. It is highly plausible that the hydrophilic segments are utilized for the networking between Aβ monomers coated over gold colloids [69,70]. At the acidic condition, the unfolded form is expected to be taken with hydrophilic portion of Aβ_1-40outward from the colloidal surface and networks with each other. In this case, an oligomeric form containing a b-pleated sheet must be structured. Thus, the hydrophobic tail must anchor on the gold colloidal surface. The hydrophobic segments of Aβ_1-40 used for binding to the gold surface are expected to remain relatively unaltered during the self-assembly, so that it must support a repetitive and quasi-organized structural change on the surface, keeping a stable frame structure. The formation of a multimeric β-sheet was found to span the central hydrophobic core sequences (17-21) [71]. Therefore, the formation of dimers or trimers can be the rate-limiting step for the networking between Ab oligomers formed over the gold surfaces. The binding enthalpy of Aβ to the anionic lipid membrane was reported to be endothermic, and this binding process is an entropy-driven reversible transition between random coil↔β-sheet [72]. Since a dimer or trimer formations need to organize cage frame structure over the colloidal surface, it is considered to be a non-spontaneous and non-entropy driven process. However, we need to speculate that a b-sheet formation involving a unfolded conformation must earn a great amount of entropy which can overcome the negative contribution of entropy in a dimer or trimer formation.

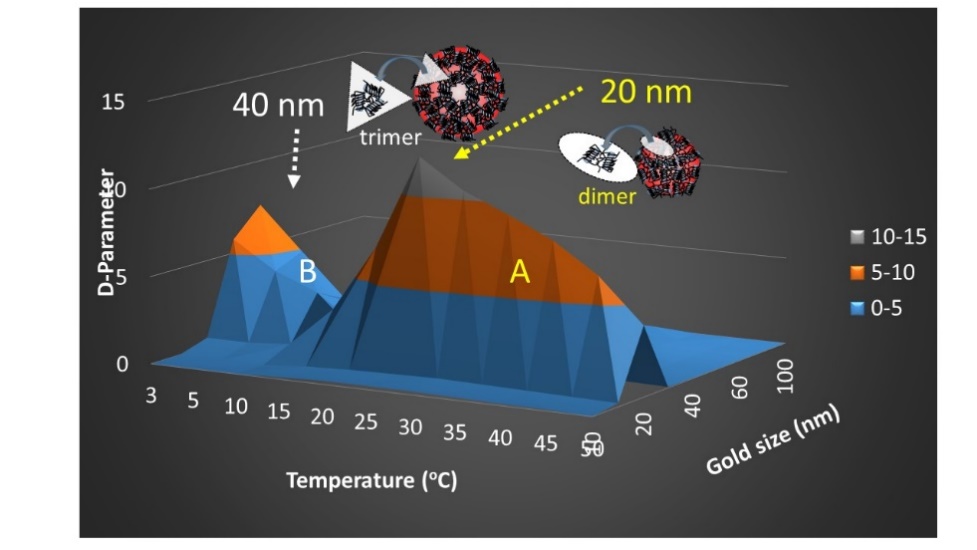
Besides a particular nanosize dependence, another notable property of the self-assembly process of Aβ_1-40 coated on gold colloid particles is the temperature dependence and size specificity in the self-assembly channel. When the observed temperature was lowered below 10 °C, a quasi-reversible self-assembly process was clearly observed for Aβ_1-40 coated on 30 and 40 nm gold colloids. A quasi-repetitive oligomerization was observed for Aβ_1-40 coated on 20 nm gold colloids above 20 °C. Reversible self-assembly channels were opened up for Aβ_1-40 coated on 30 nm and 40 nm gold colloids under 20 °C [73]. Using Eqn. (3), a series of features of λ_peak (d, n, T) were analyzed for d =10-100 nm and T = 3-50 °C; and parameter (i.e., representation of reversibility amplitude) was plotted as a function of d and T, as shown in Figure 8. This 3D plot clearly shows that there are two distinctly different regions (A and B) that support reversible-self-assembly; and these two regions are different in gold size (d) and temperature (T), implying that two intrinsically different self-assembly channels (i.e., two different oligomer units) exist. The two different oligomeric units prepared at region A and B in Figure 8 can be best explained by dimer and trimer units, respectively.

Figure 8. 3D plot for -parameter (Eqn. 1) of various Aβ_1-40-coated gold colloid particles as a function of temperature.

DownLoad: Full-Size ImgPowerPoint

Our study showed that a reversible self-assembly process over a nanoscale surface depends on both the size of particle and temperature. A certain oligomer has a unique optimum condition of gold size and temperature for its formation. Thus, a potential barrier for a self-assembly must be minimized at a corresponding temperature for each size. The nucleation of Aβ monomers follows the Arrhenius law and its activation energy was estimated to be 311.2 kJ mol⁻¹ at pH 7.4 over the temperature range from 0 °C to 45 °C [40,74,75]. Since a nucleation over the surface can gain surface potential from the gold colloid, the surface potential must lower the activation energy. The localized minima of the dimer form must exist with a relatively higher transition barrier between 5 °C and 45 °C. It is consistent with our observation, in which a reversible self-assembly took place within the potential created at the initial temperature condition. On the other hand, the relatively lower transition barrier was expected between 5 °C and 45 °C for Aβ_1-40 monomers coated over 30 or 40 nm gold colloidal surface. This is because a reversible self-assembly must be dominated by the final temperature.

5. Conclusions

We investigated the interaction of the Aβ_1-40 monomers with nanogold colloidal surfaces and the formations of oligomers. In aqueous conditions, the hydrophobic segment of Aβ_1-40 is believed to be interacting with the gold surface. It was found that the surface area coverage can be determined by the size of the nanogold colloid. The coverage ratio was proportional to surface area. Since no full coverage was achieved within the size of gold colloid tested in this study, monolayer formation was speculated. Furthermore, two thermochemically different Aβ_1-40 oligomer formation paths were identified over nanogold colloids. The potential surface over the 20 nm gold colloidsupports dimer based oligomers, and trimer based oligomers were believed to be formed over the 30 or 40 nm gold colloid. While a relatively high barrier height was expected for dimer or trimer formation, nanoscale surface potential must enhance a formation of β-sheets resulting in a spontaneous oligomerization as an entropy driven process. Our study showed a high potential of selective formation of a particular oligomeric form by pairing a specific nanogold size and temperature condition.

Acknowledgments

This work is supported by the National Science Foundation under Grant NSF-NER 0508240 and NSF 0929615. The Geneseo Foundation is greatly appreciated for their generous contribution towards this project. TEM measurements were conducted under the supervision of Professor Harold Hoops of SUNY Geneseo. The following individuals also should be recognized for their involvement of this project listed here: D. R Welchons, N. B. Gaulin, N. M. Briglio, H. Cho, D. S. Hartati, S. M. Tsang, W. W. Eng, G. T. Nguyen, K. Chung, C. A. Heimburger, M. R. Spencer, H. Chen, K. Brown, L. M. Morrow, and A. L. Tran.

Conflict of Interest

The author declares that there is no conflict of interests regarding the publication of this paper.