Effect of Self-Directed Learning on Knowledge Acquisition of Undergraduate Nursing Students in Albaha University, Saudi Arabia

Waled Amen Mohammed Ahmed; Ziad Mohammad Yousef Alostaz; Ghassan Abd AL- Lateef Sammouri; Waled Amen Mohammed Ahmed; Ziad Mohammad Yousef Alostaz; Ghassan Abd AL- Lateef Sammouri

doi:10.3934/medsci.2016.3.237

AIMS Medical Science

2016, Volume 3, Issue 3: 237-247. doi: 10.3934/medsci.2016.3.237

Previous Article Next Article

Research article

Effect of Self-Directed Learning on Knowledge Acquisition of Undergraduate Nursing Students in Albaha University, Saudi Arabia

Nursing Department, Faculty of Applied Medical Sciences, Albaha University, Al-Baha, Kingdom of Saudi Arabia

Received: 23 July 2016 Accepted: 02 September 2016 Published: 06 September 2016

Objective:The study aimed to assess the effect of self-directed learning on knowledge acquisition (first and second exam) among undergraduate nursing students at Albaha University.Methods:A quasi-experimental design was used to compare two unequal groups of nursing students in Albaha University. A convenience sampling technique was used to select the undergraduate nursing students at Al-Baha, Saudi Arabia during the 2014/2015 academic year. Students (n= 65) were recruited through an on-campus advertisement campaign either to register in traditional subjects or self-directed learning subjects. The selected students were assigned to an experimental group (23 students) and a comparison group (42 students) according to their interests. Both groups received same topics by either traditional or self-directed learning. Students’ knowledge acquisition was assessed through exams. Data was analysed by Statistical Package for the Social Sciences, version 20.Results:The results of students in pediatric nursing were (60.2% and 67.3%) in the first exam in traditional learning and self-learning respectively. The students’ scores in the second exam were (57.4% and 70%) in traditional learning and self-learning respectively (p= 0.03). In the first exam of medical-surgical nursing II, the students scored 29.6% in comparison group and 40% in the experimental group (p= 0.025). In the second exam of medical-surgical nursing II, the students scored (35.2% and 51.4%) in the comparison and experimental groups respectively. In the first exam of medical-surgical nursing I, the students scored (50% and 61.6%) in comparison and experimental groups respectively (p= 0.04). In the second exam of medical-surgical nursing I, the students scored(61% and 65.6%) in the comparison and experimental groups respectively. Conclusion: Self-learning was found to be better than traditional learning for nursing students in Albaha University. Therefore, the study findings are useful to improve nursing curricula.

Keywords:

Citation: Waled Amen Mohammed Ahmed, Ziad Mohammad Yousef Alostaz, Ghassan Abd AL- Lateef Sammouri. Effect of Self-Directed Learning on Knowledge Acquisition of Undergraduate Nursing Students in Albaha University, Saudi Arabia[J]. AIMS Medical Science, 2016, 3(3): 237-247. doi: 10.3934/medsci.2016.3.237

Related Papers:

[1]	Ting Guo, Zhipeng Qiu . The effects of CTL immune response on HIV infection model with potent therapy, latently infected cells and cell-to-cell viral transmission. Mathematical Biosciences and Engineering, 2019, 16(6): 6822-6841. doi: 10.3934/mbe.2019341
[2]	Cameron Browne . Immune response in virus model structured by cell infection-age. Mathematical Biosciences and Engineering, 2016, 13(5): 887-909. doi: 10.3934/mbe.2016022
[3]	Tinevimbo Shiri, Winston Garira, Senelani D. Musekwa . A two-strain HIV-1 mathematical model to assess the effects of chemotherapy on disease parameters. Mathematical Biosciences and Engineering, 2005, 2(4): 811-832. doi: 10.3934/mbe.2005.2.811
[4]	Ran Zhang, Shengqiang Liu . Global dynamics of an age-structured within-host viral infection model with cell-to-cell transmission and general humoral immunity response. Mathematical Biosciences and Engineering, 2020, 17(2): 1450-1478. doi: 10.3934/mbe.2020075
[5]	A. M. Elaiw, N. H. AlShamrani, A. D. Hobiny . Stability of an adaptive immunity delayed HIV infection model with active and silent cell-to-cell spread. Mathematical Biosciences and Engineering, 2020, 17(6): 6401-6458. doi: 10.3934/mbe.2020337
[6]	Jiawei Deng, Ping Jiang, Hongying Shu . Viral infection dynamics with mitosis, intracellular delays and immune response. Mathematical Biosciences and Engineering, 2023, 20(2): 2937-2963. doi: 10.3934/mbe.2023139
[7]	Abdessamad Tridane, Yang Kuang . Modeling the interaction of cytotoxic T lymphocytes and influenza virus infected epithelial cells. Mathematical Biosciences and Engineering, 2010, 7(1): 171-185. doi: 10.3934/mbe.2010.7.171
[8]	Yan Wang, Tingting Zhao, Jun Liu . Viral dynamics of an HIV stochastic model with cell-to-cell infection, CTL immune response and distributed delays. Mathematical Biosciences and Engineering, 2019, 16(6): 7126-7154. doi: 10.3934/mbe.2019358
[9]	Chunyang Qin, Yuming Chen, Xia Wang . Global dynamics of a delayed diffusive virus infection model with cell-mediated immunity and cell-to-cell transmission. Mathematical Biosciences and Engineering, 2020, 17(5): 4678-4705. doi: 10.3934/mbe.2020257
[10]	Bing Li, Yuming Chen, Xuejuan Lu, Shengqiang Liu . A delayed HIV-1 model with virus waning term. Mathematical Biosciences and Engineering, 2016, 13(1): 135-157. doi: 10.3934/mbe.2016.13.135

Abstract

1. Introduction

The human immunodeficiency virus (HIV) is a lentivirus that causes HIV infection and over time acquired immunodeficiency syndrome (AIDS). AIDS leads to progressive failure of the immune system, which allows life-threatening opportunistic infections and cancers to thrive. In the past decades, within host virus models have been investigated in some literatures, which helps us understand the biological interactions between viruses and host cells. Nowak et al. ^[20] designed a mathematical model including uninfected cells $x(t)$ , infected cells $y(t)$ and free virus $v(t)$ to describe the viral dynamics in HIV-1 infection:

$\begin{equation}\label{101} \begin{aligned} &\dot x(t) = s - dx(t) - {\beta _1}x(t)v(t), \\ &\dot y(t) = {\beta _1}x(t)v(t) - ay(t), \\ &\dot v(t) = ky(t) - uv(t), \end{aligned} \end{equation}$

(1.1)

where uninfected cells $x(t)$ are produced at rate $s$ and die at rate $d$ ; ${\beta _1}$ is the infection rate of virus-to-cell infection; $a$ is the death rate of infected cells; $k$ denotes the number of free virus particles produced by per infected cell; $u$ is the remove rate of virus. System (1.1) has been further investigated by Perelson and Nelson ^[21] and Cangelosi et al. ^[1].

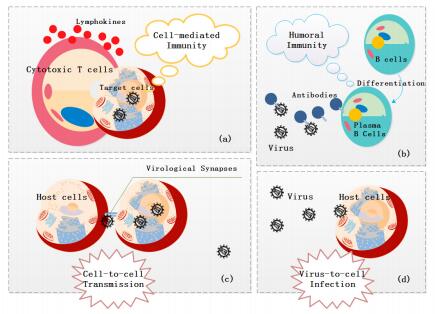
Faced with different virus infections, immunity system protects us against pathogens. Human specific immunity can be classified into cell-mediated immunity, for which the protective function is associated with cells and humoral immunity, where the protective function exists in the humor ^[2]. As for cell-mediated immunity, activated effector T cells can detect peptide antigens originating from various types of pathogens and remove virus-infected cells. Some HIV-1 infection models have been proposed to describe the virus dynamics with cell-mediated immune response (see, for example, ^{[15,19,24,26,34]}). While, in humoral immunity, matured B cells migrate from bone marrow to lymph nodes or other lymphatic organs, where they begin to eliminate pathogens ^[23]. There have been several works on virus models with humoral immune response (see, for example, ^{[4,14,28,29,30]}). In ^[6], Fouts et al. pointed out that a guiding principle for HIV vaccine design has been that cellular and humoral immunities work together to provide the strongest degree of efficacy. In ^[33], Yan and Wang considered both cell-mediated and humoral immune responses and put forward an HIV-1 infection model including both T cells and B cells, which only involves virus-to-cell infection mechanism.

It is mentioned in ^[17] that cell-to-cell transmission is a more potent and efficient means of virus propagation than the virus-to-cell infection mechanism. Cell-to-cell spread not only facilitates rapid viral dissemination but also reduce the effectiveness of neutralizing antibodies and viral inhibitors by immune evasion. In ^[25], Sigal et al. proved that cell-to-cell spread of HIV-1 does reduce the efficacy of antiretroviral therapy, since cell-to-cell transmission can cause multiple infections of target cells, which can in turn reduce the sensitivity to the antiretroviral drugs. In view of this, some mathematical analysis of virus models with cell-to-cell transmission has been performed. For instance, Li and Wang ^[13] dealt with the global dynamics of an HIV infection model which incorporated direct cell-to-cell transmission. Meanwhile, Lai and Zou ^[11,12] studied the effect of cell-to-cell transfer of HIV-1 on the virus dynamics.

It was assumed in system (1.1) that the infection process is governed by the mass-action principle, namely, the infection rate per host or per virus is a constant. In ^[22], Regoes et al. illustrated that the infection rate is often found to be a sigmoidal rather than a linear function of the parasite dose to which it is exposed, and presented a dose-dependent infection rate ${{(v/\rm{ID}_{50})}^\kappa}/[1 + {{(v/\rm{ID}_{50})}^\kappa}]$ , where $\rm{ID}_{50}$ denotes the infectious dose at which $50\%$ of the hosts are infected and $\kappa$ measures the slope of the sigmoidal curve at $\rm{ID}_{50}$ . In ^[10], Huang et al. indicated that the bilinear incidence rate is insufficient to describe the infection process in detail and proposed a class of nonlinear incidence. Besides, to place the model on more sound biological grounds, Xu ^[31] and Elaiw et al. ^[5] incorporated a saturation incidence ${{\beta _1}v(t)}/{(1 + \alpha v(t))}$ to replace the mass-action infection rate.

Motivated by the works of Fouts et al. ^[6], Yan and Wang ^[33], Sigal et al. ^[25] and Regoes et al. ^[22], in the present paper, we are concerned with the effects of cell-to-cell transmission, saturation incidence, both cell-mediated and humoral immune responses on the global dynamics of HIV-1 infection model. To this end, we consider the following delay differential equations:

$\begin{equation}\label{102} \begin{aligned} \dot x(t) = & s - dx(t) - \frac{{{\beta _1}x(t)v(t)}}{{1 + \alpha v(t)}} - {\beta _2}x(t)y(t), \\ \dot y(t) = & \frac{{{\beta _1}{e^{ - m\tau }}x(t - \tau )v(t - \tau )}}{{1 + \alpha v(t - \tau )}} + {\beta _2}{e^{ - m\tau }}x(t - \tau )y(t - \tau ) - ay(t) - {p_1}y(t)z(t), \\ \dot v(t) = & ky(t) - uv(t) - {p_2}v(t)w(t), \\ \dot z(t) = & {c_1}y(t)z(t) - {b_1}z(t), \\ \dot w(t) = & {c_2}v(t)w(t) - {b_2}w(t), \end{aligned} \end{equation}$

(1.2)

where $x(t)$ , $y(t)$ , $v(t)$ , $z(t)$ , $w(t)$ denote the concentration of uninfected cells, infected cells, virus, T cells and B cells at time $t$ , respectively, and other parameters are described in Table 1. A simple schematic diagram for the virus infection corresponding to system (1.2) is shown in Figure 1.

Table 1. Definitions of frequently used symbols.

Symbols	Description
$s$	recruitment rate of uninfected cells
$d$	death rate of uninfected cells
${\beta}_1$	infection rate of virus-to-cell infection
${\beta}_2$	transmission rate of cell-to-cell transmission
$\alpha$	saturation infection rate coefficient
$\tau$	the time between viral entry into a cell and the production of new
	free virus or the time between infected cells spreading virus into
	uninfected cells and the production of new free virus ^[8]
$e^{ - m\tau }$	the probability of surviving the time period from $t-\tau$ to $t$
$a$	death rate of infected cells
$u$	removal rate of virus
$k$	average number of free virus particles produced by per infected cell
${p_1}$	kill ratio of infected cells by T cells
${p_2}$	kill ratio of virus by B cells
${b_1}$	death rate of T cells
${b_2}$	death rate of B cells
${c_1}$	maturing rate of new T cells from thymocytes in the thymus
${c_2}$	production rate of new B cells by antigenic stimulation

| Show Table

DownLoad: CSV

Figure 1. Simple schematic diagram of the HIV-1 infection model. (a), (b), (c) and (d) depict the process of cell-mediated immunity, humoral immunity, cell-to-cell infection and virus-to-cell transmission, respectively.

DownLoad: Full-Size Img PowerPoint

The initial condition for system (1.2) takes the form

$\begin{equation}\label{103} x(\theta ) = {\phi _1}(\theta ), ~ y(\theta ) = {\phi _2}(\theta ), ~ v(\theta ) = {\phi _3}(\theta ), ~ z(\theta ) = {\phi _4}(\theta ), ~ w(\theta ) = {\phi _5}(\theta ), \end{equation}$

(1.3)

where it satisfies that ${\phi _i}(\theta ) \ge 0, ~\theta \in [ - \tau , 0), ~{\phi _i}(0)>0$ , where ${\phi _i} \in \mathbf{C}([ - \tau , 0], \mathbb{R}_{ + 0}^5)$ , $i = 1, 2, 3, 4, 5$ , the Banach space of continuous functions mapping the interval $[ - \tau , 0]$ into $\mathbb{R}_{ + 0}^5$ , where ${\mathbb{R}_{ + 0}^5} = {\{(x_1, x_2, x_3, x_4, x_5):x_i \ge 0, i = 1, 2, 3, 4, 5\}}$ .

It can be proved by the fundamental theory of functional differential equations ^[7] that system (1.2) has a unique solution $(x(t), y(t), v(t), z(t), w(t))$ satisfying the initial condition (1.3). It is easy to show that all solutions of system (1.2) with initial condition (1.3) are defined on $[0, + \infty )$ and remain positive for all $t\ge0$ .

This paper is organized as follows. In Section 2, we calculate the reproduction ratios to system (1.2) and establish the existence of feasible equilibria. In Section 3, the local asymptotic stability of each of feasible equilibria is studied. In Section 4, we investigate the global asymptotic stability of each of feasible equilibria. In Section 5, we present numerical simulations to illustrate the theoretical results and study the effects of cell-to-cell transmission, viral production rate, death rate of infected cells and viral removal rate on viral dynamics, respectively. Besides, we perform a sensitivity analysis of reproduction ratios. The paper ends with a conclusion in Section 6.

2. Reproduction ratios and feasible equilibria

Clearly, system (1.2) always has an infection-free equilibrium ${E_0}(s/d, 0, 0, 0, 0)$ . Denote

${\mathcal R}_0 = \frac{{\left( {{\beta _1}k + {\beta _2}u} \right)s{e^{ - m\tau }}}}{{aud}},$

where ${{\mathcal R}_0}$ is called immunity-inactivated reproduction ratio of system (1.2), which represents the number of newly infected cells produced by one infected cell during its lifespan ^[3]. It is easy to show that if ${{\mathcal R}_0}>1$ , system (1.2) has an immunity-inactivated equilibrium ${E_1}({x_1}, {y_1}, {v_1}, 0, 0)$ , where

${x_1} = \frac{{s\left( {u + \alpha k{y_1}} \right)}}{{\left( {d + {\beta _2}{y_1}} \right)\left( {u + \alpha k{y_1}} \right) + {\beta _1}k{y_1}}}, \quad {v_1} = \frac{{k{y_1}}}{u},$

and

${y_1} = \frac{{ - \left( {{\beta _1}ak + {\beta _2}au + \alpha adk - \alpha {\beta _2}ks{e^{ - m\tau }}} \right) + \sqrt \Delta }}{{2\alpha {\beta _2}ak}},$

in which,

$\begin{align*} \Delta = {\left( {{\beta _1}ak + {\beta _2}au + \alpha adk - \alpha {\beta _2}ks{e^{ - m\tau }}} \right)^2} - 4\alpha {\beta _2}ak\left( {adu - {\beta _1}ks{e^{ - m\tau }} - {\beta _2}su{e^{ - m\tau }}} \right). \end{align*}$

Denote

${\mathcal R}_1 = \frac{{{c_1}s{e^{ - m\tau }}\left[ {{\beta _2}\left( {{c_1}u + \alpha {b_1}k} \right) + {\beta _1}{c_1}k} \right]}}{{a\left[ {\left( {{c_1}d + {\beta _2}{b_1}} \right)\left( {{c_1}u + \alpha {b_1}k} \right) + {\beta _1}{b_1}{c_1}k} \right]}} = \frac{{{\mathcal R}_0}}{{1 + {X_1}{\mathcal R}_0}},$

where

${X_1}{\rm{ = }}\frac{{a{b_1}\left( {{\beta _1}k + {\beta _2}u} \right)\left[ {{c_1}\left( {{\beta _1}k + {\beta _2}u} \right) + \alpha {\beta _2}{b_1}k} \right] + \alpha {\beta _1}a{b_1}{c_1}d{k^2}}}{{{c_1}s{e^{ - m\tau }}\left( {{\beta _1}k + {\beta _2}u} \right)\left[ {{c_1}\left( {{\beta _1}k + {\beta _2}u} \right) + \alpha {\beta _2}{b_1}k} \right]}} \gt 0.$

${{\mathcal R}_1}$ is called cell-mediated immunity-activated reproduction ratio, which denotes the average number of T cells activated by infectious cells when virus infection is successful and humoral immune response has not been established. If ${{\mathcal R}_1}>1$ , in addition to $E_0$ and $E_1$ , system (1.2) has a cell-mediated immunity-activated equilibrium ${E_2} ({x_2}, {y_2}, {v_2}, {z_2}, 0)$ , where

${x_2} = \frac{{{c_1}s\left( {{c_1}u + \alpha {b_1}k} \right)}}{{\left( {{c_1}d + {\beta _2}{b_1}} \right)\left( {{c_1}u + \alpha {b_1}k} \right) + {\beta _1}{b_1}{c_1}k}}, \quad {y_2} = \frac{{{b_1}}}{{{c_1}}}, \quad {v_2} = \frac{{{b_1}k}}{{{c_1}u}},$

and

${z_2} = \frac{{c_1}s{e^{ - m\tau }}\left[ {{\beta _2}{b_1}\left( {{c_1}u + \alpha {b_1}k} \right) + {\beta _1}{b_1}{c_1}k} \right]}{{b_1}{p_1}\left[ {\left( {{c_1}d + {\beta _2}{b_1}} \right)\left( {{c_1}u + \alpha {b_1}k} \right) + {\beta _1}{b_1}{c_1}k} \right]} - \frac{a{b_1}}{{b_1}{p_1}}.$

We further denote

${\mathcal R}_2 = \frac{{{c_2}ks{e^{ - m\tau }}\left[ {{\beta _2}u\left( {{c_2} + \alpha {b_2}} \right) + {\beta _1}{c_2}k} \right]}}{{au\left( {{c_2} + \alpha {b_2}} \right)\left( {{\beta _2}{b_2}u + {c_2}dk} \right) + {\beta _1}a{b_2}{c_2}ku}} = \frac{{{\mathcal R}_0}}{{1 + {X_2}{\mathcal R}_0}},$

in which

${X_2} = \frac{{a{b_2}u\left( {{\beta _1}k + {\beta _2}u} \right)\left[ {{\beta _2}u\left( {{c_2} + \alpha {b_2}} \right) + {\beta _1}{c_2}k} \right] + \alpha {\beta _1}a{b_2}{c_2}d{k^2}u}}{{{c_2}ks{e^{ - m\tau }}\left( {{\beta _1}k + {\beta _2}u} \right)\left[ {{\beta _2}u\left( {{c_2} + \alpha {b_2}} \right) + {\beta _1}{c_2}k} \right]}}.$

${{\mathcal R}_2}$ is called humoral immunity-activated reproduction ratio, which denotes the average number of B cells activated by viruses when virus infection is successful and cell-mediated response has not been established. When ${{\mathcal R}_2}>1$ , system (1.2) has a humoral immunity-activated equilibrium ${E_3}({x_3}, {y_3}, {v_3}, 0, {w_3})$ , where

$\begin{align*} &{x_3} = \frac{{{c_2}ks\left( {{c_2} + \alpha {b_2}} \right)}}{{\left( {{c_2} + \alpha {b_2}} \right)\left( {{\beta _2}{b_2}{p_2}{w_3} + {\beta _2}{b_2}u + {c_2}kd} \right) + {\beta _1}{b_2}{c_2}k}}, \quad {y_3} = \frac{{{b_2}{p_2}}}{{{c_2}k}}{w_3} + \frac{{{b_2}u}}{{{c_2}k}}, \quad {v_3} = \frac{{{b_2}}}{{{c_2}}}, \end{align*}$

where $w_3$ is the positive real root of the following quadratic equation:

$\begin{align*} &w_3^2 + \frac{{\left( {{c_2} + \alpha {b_2}} \right)\left( {2{\beta _2}a{b_2}u + a{c_2}dk - {\beta _2}{c_2}ks{e^{ - m\tau }}} \right) + {\beta _1}a{b_2}{c_2}k}}{{{\beta _2}a{b_2}{p_2}\left( {{c_2} + \alpha {b_2}} \right)}}{w_3} \\ &+ \frac{{au\left( {{c_2} + \alpha {b_2}} \right)\left( {{\beta _2}{b_2}u + {c_2}dk} \right) + {\beta _1}a{b_2}{c_2}ku}}{{{\beta _2}a{b_2}p_2^2\left( {{c_2} + \alpha {b_2}} \right)}}\left( {1 - {\mathcal R}_2} \right) = 0.\\ \end{align*}$

Denote

${\mathcal R}_3 = \frac{{{b_1}{c_2}k}}{{{b_2}{c_1}u}}, \quad {\mathcal R}_4 = \frac{{{c_1}s{e^{ - m\tau }}\left[ {{\beta _2}{b_1}\left( {{c_2} + \alpha {b_2}} \right) + {\beta _1}{b_2}{c_1}} \right]}}{{a{b_1}\left[ {\left( {{c_1}d + {\beta _2}{b_1}} \right)\left( {{c_2} + \alpha {b_2}} \right) + {\beta _1}{b_2}{c_1}} \right]}},$

where ${\mathcal R}_3$ is called humoral immunity-competed reproduction ratio and represents the average number of B cells activated by viruses under the condition that cell-mediated immune response has been established, while, ${\mathcal R}_4$ is called cell-mediated immunity-competed reproduction ratio and represents the average number of T cells activated by infectious cells under the condition that humoral immune response has been established. If ${\mathcal R}_3>1$ and ${\mathcal R}_4>1$ , system (1.2) has an immunity-activated equilibrium $E^*({{x^*}, {y^*}, {v^*}, {z^*}, {w^*}})$ , where

$\begin{align*} {x^*} = \frac{{{c_1}s\left( {{c_2} + \alpha {b_2}} \right)}}{{\left( {{c_1}d + {\beta _2}{b_1}} \right)\left( {{c_2} + \alpha {b_2}} \right) + {\beta _1}{b_2}{c_1}}}, \quad {y^*} = \frac{{{b_1}}}{{{c_1}}}, \quad {v^*} = \frac{{{b_2}}}{{{c_2}}}, \quad {w^*} = \frac{{{b_1}{c_2}k - {b_2}{c_1}u}}{{{b_2}{c_1}{p_2}}}, \end{align*}$

and

${z^*} = \frac{{{c_1}s{e^{ - m\tau }}\left[ {{\beta _2}{b_1}\left( {{c_2} + \alpha {b_2}} \right) + {\beta _1}{b_2}{c_1}} \right] - a{b_1}\left[ {\left( {{c_1}d + {\beta _2}{b_1}} \right)\left( {{c_2} + \alpha {b_2}} \right) + {\beta _1}{b_2}{c_1}} \right]}}{{{b_1}{p_1}\left[ {\left( {{c_1}d + {\beta _2}{b_1}} \right)\left( {{c_2} + \alpha {b_2}} \right) + {\beta _1}{b_2}{c_1}} \right]}},$

in which cell-mediated and humoral immune responses take effect simultaneously.

3. Local asymptotic stability

In this section, we are concerned with the local asymptotic stability of each of feasible equilibria to system (1.2) by analyzing the distribution of roots of corresponding characteristic equations.

Theorem 3.1. If ${{\mathcal R}_0} < 1$ , the infection-free equilibrium ${E_0}(s/d, 0, 0, 0, 0)$ of system (1.2) is locally asymptotically stable; if ${{\mathcal R}_0} > 1$ , ${E_0}$ is unstable.

Proof. The characteristic equation of system (1.2) at $E_0$ is

$\begin{equation}\label{301} \begin{aligned} \left( {\lambda + {b_1}} \right)\left( {\lambda + {b_2}} \right)\left( {\lambda + d} \right)\left( {\lambda + a} \right)\left( {\lambda + u} \right) - \frac{s}{d}{e^{ - (\lambda + m)\tau }}\left( {\lambda + {b_1}} \right)\left( {\lambda + {b_2}} \right)\left( {\lambda + d} \right)\left( {{\beta _2}\lambda + {\beta _1}k + {\beta _2}u} \right) = 0. \end{aligned} \end{equation}$

(3.1)

It is clear that (3.1) has negative real roots ${\lambda} = -b_1, ~{\lambda} = - b_2, ~{\lambda} = -d$ and other roots are determined by the following equation:

$\begin{equation}\label{302} \left( {\lambda + a} \right)\left( {\lambda + u} \right) -\frac{s}{d}\left( {{\beta _2}\lambda + {\beta _1}k + {\beta _2}u} \right){e^{ - (\lambda + m)\tau }} = 0. \end{equation}$

(3.2)

Denote ${{\mathcal R}_0} = {{\mathcal R}_{01}} + {{\mathcal R}_{02}}$ , where

${{\mathcal R}_{01}} = \frac{{{\beta _1}ks{e^{ - m\tau }}}}{aud} \quad {\rm and} \quad {{\mathcal R}_{02}} = \frac{{{\beta _2}s{e^{ - m\tau }}}}{{ad}}.$

Substituting ${{\mathcal R}_{0}}$ and ${{\mathcal R}_{02}}$ into (3.2) yields

$\begin{equation}\label{303} \left( {\frac{\lambda }{a} + 1} \right)\left( {\frac{\lambda }{u} + 1} \right) = {e^{ - \lambda \tau }}\left( {\frac{\lambda }{u}{\mathcal R}_{02} + {\mathcal R}_{0}} \right). \end{equation}$

(3.3)

Now, we claim that all roots of (3.3) have negative real parts. Otherwise, there exists a root ${\lambda _1} = {\mathop{\rm Re}\nolimits} {\lambda _1} + i{\mathop{\rm Im}\nolimits} {\lambda _1}$ with ${\mathop{\rm Re}\nolimits} {\lambda _1} \ge 0$ . In this case, if ${{\mathcal R}_{0}} < 1$ , it is easy to see that

$\left| {\frac{\lambda_1 }{a} + 1} \right| \ge \left|{e^{ - \lambda_1 \tau }}\right|, \quad \left| {\frac{\lambda_1 }{u} + 1} \right| \gt \left| \frac{\lambda_1 }{u}{{\mathcal R}_{02}} + {{\mathcal R}_{0}} \right|.$

It follows that

$\left| {\left(\frac{\lambda_1 }{a} + 1\right)\left(\frac{\lambda_1 }{u} + 1\right)} \right| \gt \left| {{e^{ - \lambda_1 \tau }}\left(\frac{\lambda_1 }{u}{{\mathcal R}_{02}} + {{\mathcal R}_{0}}\right)} \right|,$

which contradicts to (3.3). Therefore, if ${{\mathcal R}_{0}} < 1$ , all roots of (3.1) have negative real parts and $E_0$ is locally asymptotically stable. If ${{\mathcal R}_{0}} > 1$ , we denote the left side of (3.2) by $G(\lambda)$ :

$\begin{equation}\label{304} G(\lambda ) = \left( {\lambda + a} \right)(\lambda + u) - {e^{ - (\lambda + m )\tau }}\frac{s}{d}({\beta _2}\lambda + {\beta _1}k+{\beta _2}u), \end{equation}$

(3.4)

where $G(0) = au(1 - {{\mathcal R}_{0}}) < 0$ and $G(\lambda ) \to \infty$ as $\lambda \to \infty$ . Noting that $G(\lambda)$ is a continuous function in respect to $\lambda$ , if ${{\mathcal R}_{0}} > 1$ , Eq. (3.1) has a positive real root, then $E_0$ is unstable.

Theorem 3.2. If ${{\mathcal R}_{0}} > 1$ , ${{\mathcal R}_{1}} < 1$ and ${{\mathcal R}_{2}} < 1$ , the immunity-inactivated equilibrium ${E_1}({x_1}, {y_1}, {v_1}, 0, 0)$ of system (1.2) is locally asymptotically stable.

Proof. The characteristic equation of system (1.2) at $E_1$ is

$\begin{equation}\label{305} \begin{aligned} &\left( {\lambda + a} \right)\left( {\lambda + u} \right)\left[ {\lambda - \left( {{c_1}{y_1} - {b_1}} \right)} \right]\left[ {\lambda - \left( {{c_2}{v_1} - {b_2}} \right)} \right]\left( {\lambda + d + \frac{{{\beta _1}{v_1}}}{{1 + \alpha {v_1}}} + {\beta _2}{y_1}} \right) \\ & = {e^{ - (\lambda + m)\tau }}{\beta _2}{x_1}\left( {\lambda + u} \right)\left( {\lambda + d} \right)\left[ {\lambda - \left( {{c_1}{y_1} - {b_1}} \right)} \right]\left[ {\lambda - \left( {{c_2}{v_1} - {b_2}} \right)} \right] \\ &\quad + {e^{ - (\lambda + m)\tau }}\left( {\lambda + d} \right)\left[ {\lambda - \left( {{c_1}{y_1} - {b_1}} \right)} \right]\left[ {\lambda - \left( {{c_2}{v_1} - {b_2}} \right)} \right]\frac{{{\beta _1}k{x_1}}}{{{{\left( {1 + \alpha {v_1}} \right)}^2}}}. \\ \end{aligned} \end{equation}$

(3.5)

Note that

$\begin{equation}\label{306} \begin{aligned} {{\mathcal R}_1} = {H_1}\left( {{c_1}{y_1} - {b_1}} \right) + 1 \lt 1, \end{aligned} \end{equation}$

(3.6)

in which

${H_1} = \frac{{{y_1}\left( {1 + \alpha {v_1}} \right)\left[ {{\beta _2}a\left( {{c_1}u + \alpha {b_1}k} \right) + {\beta _1}a{c_1}k} \right] + \alpha {\beta _1}{c_1}dk{x_1}{v_1}{e^{ - m\tau }}}}{{a{y_1}\left( {1 + \alpha {v_1}} \right)\left[ {\left( {{c_1}d + {\beta _2}{b_1}} \right)\left( {{c_1}u + \alpha {b_1}k} \right) + {\beta _1}{b_1}{c_1}k} \right]}},$

and

$\begin{equation}\label{307} {{\mathcal R}_2} = {H_2}\left( {{c_2}{v_1} - {b_2}} \right) + 1 \lt 1, \end{equation}$

(3.7)

where

${H_2} = \frac{{{y_1}\left( {1 + \alpha {v_1}} \right)\left[ {{\beta _2}a{u^2}\left( {{c_2} + \alpha {b_2}} \right) + {\beta _1}a{c_2}ku} \right] + \alpha {\beta _1}{c_2}dku{x_1}{v_1}{e^{ - m\tau }}}}{{{y_1}\left( {1 + \alpha {v_1}} \right)\left[ {au\left( {{c_2} + \alpha {b_2}} \right)\left( {{\beta _2}{b_2}u + {c_2}dk} \right) + {\beta _1}a{b_2}{c_2}ku} \right]}}.$

It is clear that (3.5) has negative real roots ${\lambda} = {{c_1}{y_1} - {b_1}}$ and ${\lambda} = {{c_2}{v_1} - {b_2}}$ , and other roots are determined by the following equation:

$\begin{equation}\label{308} \begin{aligned} \left( {\lambda + a} \right)\left( {\lambda + u} \right)\left( {\lambda + d + \frac{{{\beta _1}{v_1}}}{{1 + \alpha {v_1}}} + {\beta _2}{y_1}} \right) - {e^{ - (\lambda + m)\tau }}\left( {\lambda + d} \right)\left[ {{\beta _2}{x_1}\left( {\lambda + u} \right) + \frac{{{\beta _1}k{x_1}}}{{{{\left( {1 + \alpha {v_1}} \right)}^2}}}} \right] = 0. \end{aligned} \end{equation}$

(3.8)

For the sake of contradiction, let ${\lambda _2} = {\mathop{\rm Re}\nolimits} {\lambda _2} + i{\mathop{\rm Im}\nolimits} {\lambda _2}$ with ${\mathop{\rm Re}\nolimits} {\lambda _2} \ge 0$ . In this case, it is easy to see that

$\left| {\lambda_2 + d + \frac{{{\beta _1}{v_1}}}{{1 + \alpha {v_1}}} + {\beta _2}{y_1}} \right| \gt \left| {{e^{ - \lambda_2 \tau }}\left( {\lambda_2 + d} \right)} \right|.$

Direct calculation shows that

$\begin{align*} &\Big| {\left( {\lambda_2 + a} \right)\left( {\lambda_2 + u} \right)} \Big| - \bigg| {{\beta _2}{e^{ - m\tau }}{x_1}\left( {\lambda_2 + u} \right) + \frac{{{\beta _1}{e^{ - m\tau }}k{x_1}}}{{{{\left( {1 + \alpha {v_1}} \right)}^2}}}} \bigg| \\ & = {\lambda _2}\left[ {{\lambda _2} + u + \frac{{{\beta _1}{e^{ - m\tau }}k{x_1}}}{{u\left( {1 + \alpha {v_1}} \right)}}} \right] + \frac{{{\beta _1}{e^{ - m\tau }}k{x_1}}}{{1 + \alpha {v_1}}} - \frac{{{\beta _1}{e^{ - m\tau }}k{x_1}}}{{{{\left( {1 + \alpha {v_1}} \right)}^2}}} \\ & \gt {\lambda _2}\left[ {{\lambda _2} + u + \frac{{{\beta _1}{e^{ - m\tau }}k{x_1}}}{{u\left( {1 + \alpha {v_1}} \right)}}} \right] \gt 0, \end{align*}$

which contradicts to (3.8). Thus, if ${{\mathcal R}_{0}} > 1$ , ${{\mathcal R}_{1}} < 1$ and ${{\mathcal R}_{2}} < 1$ , all roots of Eq. (3.5) have negative real parts, and $E_1$ is locally asymptotically stable.

Theorem 3.3. If ${{\mathcal R}_{1}} > 1$ and ${{\mathcal R}_{3}} < 1$ , the cell-mediated immunity-activated equilibrium ${E_2} ({x_2}, {y_2}, {v_2}$ , ${z_2}, 0)$ of system (1.2) is locally asymptotically stable.

Proof. The characteristic equation of system (1.2) at $E_2$ is

$\begin{equation}\label{309} \begin{aligned} &\left( {\lambda + u} \right)\left[ {\lambda - \left( {{c_2}{v_2} - {b_2}} \right)} \right]\left[ {\lambda \left( {\lambda + a + {p_1}{z_2}} \right) + {c_1}{p_1}{y_2}{z_2}} \right] \left( {\lambda + d + \frac{{{\beta _1}{v_2}}}{{1 + \alpha {v_2}}} + {\beta _2}{y_2}} \right) \\ & = {e^{ - (\lambda + m)\tau }}\left( {\lambda + d} \right)\left[ {\lambda - \left( {{c_2}{v_2} - {b_2}} \right)} \right]\left[ {{\beta _2}{x_2}\lambda \left( {\lambda + u} \right) + \frac{{{\beta _1}k{x_2}}}{{{{\left( {1 + \alpha {v_2}} \right)}^2}}}\lambda } \right]. \\ \end{aligned} \end{equation}$

(3.9)

Note that ${\mathcal R}_3 = \left( {{c_2}{v_2} - {b_2}} \right)/{b_2} + 1 < 1$ . It is clear that (3.9) has negative real root ${\lambda} = {{c_2}{v_2} - {b_2}}$ , and other roots are determined by the following equation:

$\begin{equation}\label{310} \begin{aligned} &\left( {\lambda + u} \right)\left[ {\lambda \left( {\lambda + a + {p_1}{z_2}} \right) + {c_1}{p_1}{y_2}{z_2}} \right]\left( {\lambda + d + \frac{{{\beta _1}{v_2}}}{{1 + \alpha {v_2}}} + {\beta _2}{y_2}} \right) \\ & = {e^{ - (\lambda + m)\tau }}\left( {\lambda + d} \right)\left[ {{\beta _2}{x_2}\lambda \left( {\lambda + u} \right) + \frac{{{\beta _1}k{x_2}}}{{{{\left( {1 + \alpha {v_2}} \right)}^2}}}\lambda } \right]. \\ \end{aligned} \end{equation}$

(3.10)

Similarly, we claim that all roots of (3.10) have negative real parts. Otherwise, there exists a root ${\lambda _3} = {\mathop{\rm Re}\nolimits} {\lambda _3} + i{\mathop{\rm Im}\nolimits} {\lambda _3}$ with ${\mathop{\rm Re}\nolimits} {\lambda _3} \ge 0$ . In this case, it is obvious that

$\left| {\lambda_3 + d + \frac{{{\beta _1}{v_2}}}{{1 + \alpha {v_2}}} + {\beta _2}{y_2}} \right| \gt \left| {{e^{ - \lambda_3 \tau }}\left( {\lambda_3 + d} \right)} \right|.$

It follows that

$\begin{align*} &\left|\left( {{\lambda _3} + u} \right)\left[ {{\lambda _3}\left( {{\lambda _3} + a + {p_1}{z_2}} \right) + {c_1}{p_1}{y_2}{z_2}} \right]\right| - \left|{\beta _2}{e^{ - m\tau }}{x_2}{\lambda _3}\left( {{\lambda _3} + u} \right) + \frac{{{\beta _1}{e^{ - m\tau }}k{x_2}}}{{{{\left( {1 + \alpha {v_2}} \right)}^2}}}{\lambda _3}\right| \\ & = \lambda _3^2\left[ {{\lambda _3} + u + \frac{{{\beta _1}{e^{ - m\tau }}{x_2}{v_2}}}{{{y_2}\left( {1 + \alpha {v_2}} \right)}}} \right] + {p_1}{c_1}{y_2}{z_2}\left( {{\lambda _3} + u} \right) + \frac{{{\beta _1}{e^{ - m\tau }}k{x_2}}}{{1 + \alpha {v_2}}}{\lambda _3} - \frac{{{\beta _1}{e^{ - m\tau }}k{x_2}}}{{{{\left( {1 + \alpha {v_2}} \right)}^2}}}{\lambda _3} \\ & \gt \lambda _3^2\left[ {{\lambda _3} + u + \frac{{{\beta _1}{e^{ - m\tau }}{x_2}{v_2}}}{{{y_2}\left( {1 + \alpha {v_2}} \right)}}} \right] + {p_1}{c_1}{y_2}{z_2}\left( {{\lambda _3} + u} \right) \gt 0, \end{align*}$

which contradicts to (3.10). Hence, if ${{\mathcal R}_{1}} > 1$ and ${{\mathcal R}_{3}} < 1$ , all roots of Eq. (3.9) have negative real parts, and $E_2$ is locally asymptotically stable.

Theorem 3.4. If ${{\mathcal R}_{2}} > 1$ and ${{\mathcal R}_{4}} < 1$ , the humoral immunity-activated equilibrium ${E_3}({x_3}, {y_3}, {v_3}, 0, {w_3})$ of system (1.2) is locally asymptotically stable.

Proof. The characteristic equation of system (1.2) at $E_3$ is

$\begin{equation}\label{311} \begin{aligned} &\left( {\lambda + a} \right)\left[ {\lambda - \left( {{c_1}{y_3} - {b_1}} \right)} \right]\left[ {\lambda\left( {\lambda + u + {p_2}{w_3}} \right) + {c_2}{p_2}{v_3}{w_3}} \right] \left( {\lambda + d + \frac{{{\beta _1}{v_3}}}{{1 + \alpha {v_3}}} + {\beta _2}{y_3}} \right) \\ & = {e^{ - \left( {\lambda + m} \right)\tau }}{x_3}\left( {\lambda + d} \right)\left[ {\lambda - \left( {{c_1}{y_3} - {b_1}} \right)} \right]\left[{{\beta _2}\lambda\left( {\lambda + u + {p_2}{w_3}} \right) + {\beta _2}{c_2}{p_2}{v_3}{w_3} + \frac{{{\beta _1}k\lambda }}{{{{\left( {1 + \alpha {v_3}} \right)}^2}}}} \right]. \\ \end{aligned} \end{equation}$

(3.11)

Note that

$\begin{equation}\label{312} {\mathcal R}_4 = \left( {{c_1}{y_3} - {b_1}} \right)\frac{{{y_3}\left[ {{\beta _2}a{b_1}\left( {{c_2} + \alpha {b_2}} \right) + {\beta _1}a{b_2}{c_1}} \right] + {\beta _1}{e^{ - m\tau }}{b_2}{c_1}d{x_3}}}{{a{b_1}{y_3}\left[ {\left( {{c_1}d + {\beta _2}{b_1}} \right)\left( {{c_2} + \alpha {b_2}} \right) + {\beta _1}{b_2}{c_1}} \right]}} + 1 \lt 1. \end{equation}$

(3.12)

It is obvious that (3.11) has negative real root ${\lambda} = {{c_1}{y_3} - {b_1}}$ , and other roots are determined by the following equation:

$\begin{equation}\label{313} \begin{aligned} &\left( {\lambda + a} \right)\left[ \lambda{\left( {\lambda + u + {p_2}{w_3}} \right) + {c_2}{p_2}{v_3}{w_3}} \right]\left( {\lambda + d + \frac{{{\beta _1}{v_3}}}{{1 + \alpha {v_3}}} + {\beta _2}{y_3}} \right) \\ & = {e^{ - \left( {\lambda + m} \right)\tau }}{x_3}\left( {\lambda + d} \right)\left[ {{\beta _2}\lambda\left( {\lambda + u + {p_2}{w_3}} \right) + {\beta _2}{c_2}{p_2}{v_3}{w_3} + \frac{{{\beta _1}k\lambda }}{{{{\left( {1 + \alpha {v_3}} \right)}^2}}}} \right]. \\ \end{aligned} \end{equation}$

(3.13)

Similarly, we claim that all roots of (3.13) have negative real parts. If not, there exists a root ${\lambda _4} = {\mathop{\rm Re}\nolimits} {\lambda _4} + i{\mathop{\rm Im}\nolimits} {\lambda _4}$ with ${\mathop{\rm Re}\nolimits} {\lambda _4} \ge 0$ . In this case, it is easy to see that

$\left| {\lambda_4 + d + \frac{{{\beta _1}{v_3}}}{{1 + \alpha {v_3}}} + {\beta _2}{y_3}} \right| \gt \left| {{e^{ - \lambda_4 \tau }}\left( {\lambda_4 + d} \right)} \right|.$

Direct calculation yields

$\begin{align*} &\Big| {\left( {\lambda_4 + a} \right)\left[ {\lambda_4\left( {\lambda_4 + u + {p_2}{w_3}} \right) + {c_2}{p_2}{v_3}{w_3}} \right]} \Big| \\ &- \left| {{e^{ - m\tau }}{x_3}\left[ {{\beta _2}\lambda_4 \left( {\lambda_4 + u + {p_2}{w_3}} \right) + {\beta _2}{c_2}{p_2}{v_3}{w_3} + \frac{{{\beta _1}k\lambda_4 }}{{{{\left( {1 + \alpha {v_3}} \right)}^2}}}} \right]} \right| \\ = & \lambda_4 \left[ {\lambda_4\left( {\lambda _4 + u + {p_2}{w_3}} \right) + {c_2}{p_2}{v_3}{w_3}} \right] + \frac{{{\beta _1}{e^{ - m\tau }}{x_3}{v_3}}}{{{y_3}\left( {1 + \alpha {v_3}} \right)}}\left( {{\lambda_4 ^2} + {c_2}{p_2}{v_3}{w_3}} \right) \\ & + \frac{{{\beta _1}{e^{ - m\tau }}{x_3}{v_3}}}{{{y_3}\left( {1 + \alpha {v_3}} \right)}}\left( {u + {p_2}{w_3}} \right)\lambda_4 - \frac{{{\beta _1}{e^{ - m\tau }}k{x_3}}}{{{{\left( {1 + \alpha {v_3}} \right)}^2}}}\lambda_4 \\ \gt & \lambda_4 \left[ {\lambda_4\left( {\lambda_4 + u + {p_2}{w_3}} \right) + {c_2}{p_2}{v_3}{w_3}} \right] + \frac{{{\beta _1}{e^{ - m\tau }}{x_3}{v_3}}}{{{y_3}\left( {1 + \alpha {v_3}} \right)}}\left( {{\lambda_4 ^2} + {c_2}{p_2}{v_3}{w_3}} \right) \gt 0, \end{align*}$

which contradicts to (3.13). Therefore, if ${{\mathcal R}_{2}} > 1$ and ${{\mathcal R}_{4}} < 1$ , all roots of Eq. (3.11) have negative real parts, and $E_3$ is locally asymptotically stable.

Theorem 3.5. If ${{\mathcal R}_{3}} > 1$ and ${{\mathcal R}_{4}} > 1$ , the immunity-activated equilibrium $E^*({x^*}, {y^*}, {{v^*}, {z^*}, {w^*}})$ of system (1.2) is locally asymptotically stable.

Proof. The characteristic equation of system (1.2) at $E^*$ is

$\begin{equation}\label{314} \begin{aligned} &\left( {\lambda + d + \frac{{{\beta _1}{v^*}}}{{1 + \alpha {v^*}}} + {\beta _2}{y^*}} \right)\left[ {\lambda \left( {\lambda + a + {p_1}{z^*}} \right) + {c_1}{p_1}{y^*}{z^*}} \right] \left[ {\lambda\left( {\lambda + u + {p_2}{w^*}} \right) + {c_2}{p_2}{v^*}{w^*}} \right] \\ & = {e^{ - \left( {\lambda + m} \right)\tau }}{x^*}\left( {\lambda + d} \right)\left\{ {{\beta _2}\lambda \left[ {\lambda\left( {\lambda + u + {p_2}{w^*}} \right) + {c_2}{p_2}{v^*}{w^*}} \right] + \frac{{{\beta _1}k{\lambda ^2}}}{{{{\left( {1 + \alpha {v^*}} \right)}^2}}}} \right\}.\\ \end{aligned} \end{equation}$

(3.14)

Similarly, we claim that all roots of (3.14) have negative real parts. Otherwise, there exists a root ${\lambda _5} = {\mathop{\rm Re}\nolimits} {\lambda _5} + i{\mathop{\rm Im}\nolimits} {\lambda _5}$ with ${\mathop{\rm Re}\nolimits} {\lambda _5} \ge 0$ . In this case, it is clear that

$\left|{\lambda_5 + d + \frac{{{\beta _1}{v^*}}}{{1 + \alpha {v^*}}} + {\beta _2}{y^*}} \right| \gt \left| {{e^{ - \lambda_5 \tau }}\left( {\lambda_5 + d} \right)} \right|.$

Direct calculation shows that

$\begin{align*} &\Big| {\left[ {\lambda_5 \left( {\lambda_5 + a + {p_1}{z^*}} \right) + {c_1}{p_1}{y^*}{z^*}} \right]\left[ {\lambda_5 \left( {\lambda_5 + u + {p_2}{w^*}} \right) + {c_2}{p_2}{v^*}{w^*}} \right]} \Big| \\ &- \bigg| {{\beta _2}{e^{ - m\tau }}{x^*}\lambda_5 \left[ {\lambda_5 \left( {\lambda_5 + u + {p_2}{w^*}} \right) + {c_2}{p_2}{w^*}{v^*}} \right] + \frac{{{\beta _1}{e^{ - m\tau }}k{x^*}{\lambda_5 ^2}}}{{{{\left( {1 + \alpha {v^*}} \right)}^2}}}} \bigg| \\ = & \left( {{\lambda_5 ^2} + {c_1}{p_1}{y^*}{z^*}} \right)\left[ {\lambda_5 \left( {\lambda_5 + u + {p_2}{w^*}} \right) + {c_2}{p_2}{v^*}{w^*}} \right] \\ & + \frac{{{\beta _1}{e^{ - m\tau }}{x^*}{v^*}}}{{{y^*}\left( {1 + \alpha {v^*}} \right)}}\lambda_5 \left( {{\lambda_5 ^2} + {c_2}{p_2}{v^*}{w^*}} \right) + \frac{{{\beta _1}{e^{ - m\tau }}{x^*}{\lambda_5 ^2}}}{{{y^*}\left( {1 + \alpha {v^*}} \right)}}\left( {u{v^*} + {p_2}{v^*}{w^*} - \frac{{k{y^*}}}{{1 + \alpha {v^*}}}} \right) \\ \gt & \left( {{\lambda_5 ^2} + {c_1}{p_1}{y^*}{z^*}} \right)\left[ {\lambda_5 \left( {\lambda_5 + u + {p_2}{w^*}} \right) + {c_2}{p_2}{v^*}{w^*}} \right] \\ &+ \frac{{{\beta _1}{e^{ - m\tau }}{x^*}{v^*}}}{{{y^*}\left( {1 + \alpha {v^*}} \right)}}\lambda_5 \left( {{\lambda_5 ^2} + {c_2}{p_2}{v^*}{w^*}} \right) \gt 0, \end{align*}$

which contradicts to (3.14). Therefore, if ${{\mathcal R}_{3}} > 1$ and ${{\mathcal R}_{4}} > 1$ , all roots of Eq. (3.14) have negative real parts, and $E^*$ is locally asymptotically stable.

4. Global asymptotic stability

In this section, we study the global stability of each of feasible equilibria to system (1.2) by suitable Lyapunov functionals and LaSalle's invariance principle. First, we discuss the boundedness of solutions.

Lemma 4.1. Any solution of system (1.2) with initial condition (1.3) is bounded for all $t \ge 0$ .

Proof. Let $(x(t), y(t), v(t), z(t), w(t))$ be any solution of system (1.2) with initial condition (1.3). Denote

${B_1}(t) = x(t - \tau ) + {e^{m\tau }}y(t) + \frac{{{p_1}}}{{{c_1}}}{e^{m\tau }}z(t), \quad {B_2}(t) = v(t) + \frac{{{p_2}}}{{{c_2}}}w(t).$

Calculating the derivatives of $B_1(t)$ and $B_2(t)$ in respect to $t$ yields

${{\dot B}_1}(t) = s - dx(t - \tau ) - a{e^{m\tau }}y(t) - {b_1}\frac{{{p_1}}}{{{c_1}}}{e^{m\tau }}z(t) \le s - \min \{ a, {b_1}, d\} {B_1}(t),$

and

${{\dot B}_2}(t) = y(t) - uv(t) - {b_2}\frac{{{p_2}}}{{{c_2}}}w(t) \le \frac{{{e^{ - m\tau }}s}}{{\min \{ a, {b_1}, d\} }} - \min \{ {b_2}, u\} {B_2}(t).$

Therefore, the following set is positively invariant set for system (1.2) :

$\begin{align*} {\bf\Omega} = \bigg\{(x, y, v, z, w)\bigg|&x + {e^{m\tau }}y+\frac{{{p_1}}}{{{c_1}}}{e^{m\tau }}z \le \frac{s}{{\min \{ a, {b_1}, d\} }}, v + \frac{p_2}{c_2}w \le \frac{{{e^{ - m\tau }}s}}{{\min \{ a, {b_1}, d\} \min \{ {b_2}, u\} }}\bigg\}. \end{align*}$

It is easy to see that $x(t), y(t), v(t), z(t)$ and $w(t)$ are bounded in the invariant set ${\bf\Omega}$ .

Next, define a function $g(x) = x-1-\rm{ln}x$ , which will be used in Lyapunov functionals of this section.

Theorem 4.2. If ${{\mathcal R}_{0}} < 1$ , the infection-free equilibrium ${E_0}(s/d, 0, 0, 0, 0)$ of system (1.2) is globally asymptotically stable.

Proof. Let $(x(t), y(t), v(t), z(t), w(t))$ be any positive solution of system (1.2) with initial condition (1.3). Define

$\begin{align*} {V_1}(t) = & {x_0}g\left( {\frac{{x(t)}}{{{x_0}}}} \right) + {l_{11}}y(t) + {l_{12}}v(t) + {l_{13}}z(t) + {l_{14}}w(t) + \int_{t - \tau }^t {\left( {\frac{{{\beta _1}x(s)v(s)}}{{1 + \alpha v(s)}} + {\beta _2}x(s)y(s)} \right)ds}, \end{align*}$

where $x_0 = s/d$ , and constants $l_{11}$ , $l_{12}$ , $l_{13}$ , $l_{14}$ will be determined later. Calculating the derivative of $V_1(t)$ along positive solutions of system (1.2) yields

$\begin{align*} {{\dot V}_1}(t) = & \left( {1 - \frac{{{x_0}}}{{x(t)}}} \right)\left( {s - dx(t) - \frac{{{\beta _1}x(t)v(t)}}{{1 + \alpha v(t)}} - {\beta _2}x(t)y(t)} \right) \\ &+ {l_{11}}\left( {\frac{{{\beta _1}{e^{ - m\tau }}x(t - \tau )v(t - \tau )}}{{1 + \alpha v(t - \tau )}} + {\beta _2}{e^{ - m\tau }}x(t - \tau )y(t - \tau )- ay(t) - {p_1}y(t)z(t)} \right) \\ & + {l_{12}}\left( {ky(t) - uv(t) - {p_2}v(t)w(t)} \right) + {l_{13}}\left( {{c_1}y(t)z(t) - {b_1}z(t)} \right) + {l_{14}}\left( {{c_2}v(t)w(t) - {b_2}w(t)} \right) \\ &+ \frac{{{\beta _1}x(t)v(t)}}{{1 + \alpha v(t)}} + {\beta _2}x(t)y(t) - \frac{{{\beta _1}x(t - \tau )v(t - \tau )}}{{1 + \alpha v(t - \tau )}} - {\beta _2}x(t - \tau )y(t - \tau ). \end{align*}$

Direct calculation yields

$\begin{equation}\label{401} \begin{aligned} {{\dot V}_1}(t) = & d{x_0}\left( {2 - \frac{{{x_0}}}{{x(t)}} - \frac{{x(t)}}{{{x_0}}}} \right) + \frac{{{\beta _1}{x_0}v(t)}}{{1 + \alpha v(t)}} - {l_{12}}uv(t) - {l_{13}}{b_1}z(t) - {l_{14}}{b_2}w(t) \\ &+ \left( {{l_{11}}{e^{ - m\tau }} - 1} \right)\left( {\frac{{{\beta _1}x(t - \tau )v(t - \tau )}}{{1 + \alpha v(t - \tau )}} + {\beta _2}x(t - \tau )y(t - \tau )} \right) \\ &+ \left( {{\beta _2}{x_0} + {l_{12}}k - {l_{11}}a} \right)y(t) + \left( {{l_{13}}{c_1} - {l_{11}}{p_1}} \right)y(t)z(t) + \left( {{l_{14}}{c_2} - {l_{12}}{p_2}} \right)v(t)w(t). \\ \end{aligned} \end{equation}$

(4.1)

Choose

$\begin{equation}\label{402} {l_{11}}{\rm{ = }}{e^{m\tau }}, \quad {l_{12}}{\rm{ = }}\frac{{{e^{m\tau }}a - {\beta _2}{x_0}}}{k} \gt 0, \quad {l_{13}}{\rm{ = }}\frac{{{e^{m\tau }}{p_1}}}{{{c_1}}}, \quad {l_{14}}{\rm{ = }}{p_2}\frac{{{e^{m\tau }}a - {\beta _2}{x_0}}}{{{c_2}k}} \gt 0. \end{equation}$

(4.2)

Thus, we obtain from (4.1) and (4.2) that

${{\dot V}_1}(t) \le d{x_0}\left( {2 - \frac{{{x_0}}}{{x(t)}} - \frac{{x(t)}}{{{x_0}}}} \right) + \left( {{\mathcal{R}_0} - 1} \right)\frac{{{e^{m\tau }}au}}{k}v(t) - {l_{13}}{b_1}z(t) - {l_{14}}{b_2}w(t).$

It follows that $\dot V_1(t) \le 0$ with equality holding if and only if $x = {x_0}, y = v = z = w = 0$ . It can be verified that ${M_0} = \{ {E_0}\} \subset {\bf\Omega}$ is the largest invariant subset of $\{(x(t), y(t), v(t), z(t), w(t)):\dot V_1(t) = 0\}$ . Noting that if ${{\mathcal R}_{0}} < 1$ , $E_0$ is locally asymptotically stable, thus we obtain the global asymptotic stability of $E_0$ from LaSalle's invariance principle.

Theorem 4.3. If ${{\mathcal R}_{0}} > 1$ , ${{\mathcal R}_{1}} < 1$ and ${{\mathcal R}_{2}} < 1$ , the immunity-inactivated equilibrium ${E_1}({x_1}, {y_1}, {v_1}, 0, 0)$ of system (1.2) is globally asymptotically stable.

Proof. Let $(x(t), y(t), v(t), z(t), w(t))$ be any positive solution of system (1.2) with initial condition (1.3). Define

$\begin{align*} {V_2}(t) = & {x_1}g\left( {\frac{{x(t)}}{{{x_1}}}} \right) + {l_{21}}{y_1}g\left( {\frac{{y(t)}}{{{y_1}}}} \right) + {l_{22}}{v_1}g\left( {\frac{{v(t)}}{{{v_1}}}} \right) + {l_{23}}z(t) + {l_{24}}w(t) \\ &+ \frac{{{\beta _1}{x_1}{v_1}}}{{1 + \alpha {v_1}}}\int_{t - \tau }^t {g\left( {\frac{{x(s)v(s)\left( {1 + \alpha {v_1}} \right)}}{{{x_1}{v_1}\left( {1 + \alpha v(s)} \right)}}} \right)ds} + {\beta _2}{x_1}{y_1}\int_{t - \tau }^t {g\left( {\frac{{x(s)y(s)}}{{{x_1}{y_1}}}} \right)ds}, \end{align*}$

where constants $l_{21}$ , $l_{22}$ , $l_{23}$ and $l_{24}$ will be determined later. Calculating the derivative of $V_2(t)$ along positive solutions of system (1.2), we have

$\begin{equation}\label{403} \begin{aligned} {{\dot V}_2}(t) = &\left( {1 - \frac{{{x_1}}}{{x(t)}}} \right)\left( {s - dx(t) - \frac{{{\beta _1}x(t)v(t)}}{{1 + \alpha v(t)}} - {\beta _2}x(t)y(t)} \right) \\ &+ {l_{21}}\left( {1 - \frac{{{y_1}}}{{y(t)}}} \right)\left( {\frac{{{\beta _1}{e^{ - m\tau }}x(t - \tau )v(t - \tau )}}{{1 + \alpha v(t - \tau )}} + {\beta _2}{e^{ - m\tau }}x(t - \tau )y(t - \tau ) - ay(t) - {p_1}y(t)z(t)} \right)\\ &+ {l_{22}}\left( {1 - \frac{{{v_1}}}{{v(t)}}} \right)\left( {ky(t) - uv(t) - {p_2}v(t)w(t)} \right) \\ &+ {l_{23}}\left( {{c_1}y(t)z(t) - {b_1}z(t)} \right) + {l_{24}}\left( {{c_2}v(t)w(t) - {b_2}w(t)} \right) \\ &+ \frac{{{\beta _1}{x_1}{v_1}}}{{1 + \alpha {v_1}}}\left[g\left( {\frac{{x(t)v(t)\left( {1 + \alpha {v_1}} \right)}}{{{x_1}{v_1}\left( {1 + \alpha v(t)} \right)}}} \right) - g\left( {\frac{{x(t - \tau )v(t - \tau )\left( {1 + \alpha {v_1}} \right)}}{{{x_1}{v_1}\left( {1 + \alpha v(t - \tau )} \right)}}} \right)\right] \\ &+ {\beta _2}{x_1}{y_1}\left[ {g\left( {\frac{{x(t)y(t)}}{{{x_1}{y_1}}}} \right) - g\left( {\frac{{x(t - \tau )y(t - \tau )}}{{{x_1}{y_1}}}} \right)} \right]. \end{aligned} \end{equation}$

(4.3)

Substituting $s = d{x_1} + {{{\beta _1}{x_1}{v_1}}}/({1 + \alpha {v_1}}) + {\beta _2}{x_1}{y_1}$ , ${{{\beta _1}{e^{ - m\tau }}{x_1}{v_1}}}/({1 + \alpha {v_1}}) + {\beta _2}{e^{ - m\tau }}{x_1}{y_1} = a{y_1}$ , $k{y_1} = u{v_1}$ into (4.3) yields

$\begin{equation}\label{404} \begin{aligned} {{\dot V}_2}(t) = & d{x_1}\left( {2 - \frac{{{x_1}}}{{x(t)}} - \frac{{x(t)}}{{{x_1}}}} \right) + {l_{21}}a{y_1} + {l_{22}}u{v_1} - {l_{22}}{v_1}\frac{{u{v_1}}}{{{y_1}}}\frac{{y(t)}}{{v(t)}} - {l_{22}}uv(t) \\ &+ \frac{{{\beta _1}{x_1}{v_1}}}{{1 + \alpha {v_1}}}\left[ {1 + \frac{{v(t)\left( {1 + \alpha {v_1}} \right)}}{{{v_1}\left( {1 + \alpha v(t)} \right)}} - \frac{{{x_1}}}{{x(t)}}} \right] - {l_{21}}{e^{ - m\tau }}\frac{{{\beta _1}{x_1}{v_1}}}{{1 + \alpha {v_1}}}\frac{{x(t - \tau )v(t - \tau )\left( {1 + \alpha {v_1}} \right){y_1}}}{{{x_1}{v_1}\left( {1 + \alpha v(t - \tau )} \right)y(t)}} \\ &+ \frac{{{\beta _1}{x_1}{v_1}}}{{1 + \alpha {v_1}}}\ln \frac{{x(t - \tau )v(t - \tau )\left( {1 + \alpha v(t)} \right)}}{{x(t)v(t)\left( {1 + \alpha v(t - \tau )} \right)}} + {\beta _2}{x_1}{y_1}\left( {1 - \frac{{{x_1}}}{{x(t)}} - {l_{21}}{e^{ - m\tau }}\frac{{x(t - \tau )y(t - \tau )}}{{{x_1}y(t)}}} \right)\\ & + {\beta _2}{x_1}{y_1} \ln \frac{{x(t - \tau )y(t - \tau )}}{{x(t)y(t)}} + \left( {{l_{21}}{e^{ - m\tau }} - 1} \right)\left( {\frac{{{\beta _1}x(t - \tau )v(t - \tau )}}{{1 + \alpha v(t - \tau )}} + {\beta _2}x(t - \tau )y(t - \tau )} \right) \\ &+ \left( {{\beta _2}{x_1} + {l_{22}}k - {l_{21}}a} \right)y(t) + \left( {{l_{21}}{p_1}{y_1} - {l_{23}}{b_1}} \right)z(t) + \left( {{l_{22}}{p_2}{v_1} - {l_{24}}{b_2}} \right)w(t) \\ &+ \left( {{l_{23}}{c_1} - {l_{21}}{p_1}} \right)y(t)z(t) + \left( {{l_{24}}{c_2} - {l_{22}}{p_2}} \right)v(t)w(t). \end{aligned} \end{equation}$

(4.4)

Choose

$\begin{equation}\label{405} {l_{21}} = {e^{m\tau }}, \quad {l_{22}} = \frac{{{\beta _1}{x_1}{v_1}}}{{k{y_1}\left( {1 + \alpha {v_1}} \right)}}, \quad {l_{23}} = \frac{{{e^{m\tau }}{p_1}}}{{{c_1}}}, \quad {l_{24}} = \frac{{{\beta _1}{p_2}{x_1}{v_1}}}{{{c_2}k{y_1}\left( {1 + \alpha {v_1}} \right)}}. \end{equation}$

(4.5)

From (4.4) and (4.5), we obtain that

$\begin{equation}\label{406} \begin{aligned} {{\dot V}_2}(t) = & d{x_1}\left( {2 - \frac{{{x_1}}}{{x(t)}} - \frac{{x(t)}}{{{x_1}}}} \right) + {e^{m\tau }}{p_1}\frac{{{c_1}{y_1} - {b_1}}}{{{c_1}}}z(t) + \frac{{{\beta _1}{p_2}{x_1}{v_1}}}{{k{y_1}\left( {1 + \alpha {v_1}} \right)}}\frac{{{c_2}{v_1} - {b_2}}}{{{c_2}}}w(t) \\ &- \frac{{\alpha {{\left( {v(t) - {v_1}} \right)}^2}}}{{{v_1}\left( {1 + \alpha {v_1}} \right)\left( {1 + \alpha v(t)} \right)}} - g\left( {\frac{{1 + \alpha v(t)}}{{1 + \alpha {v_1}}}} \right) - \frac{{{\beta _1}{x_1}{v_1}}}{{1 + \alpha {v_1}}}\left[ g\left( {\frac{{{x_1}}}{{x(t)}}} \right) + g\left( {\frac{{y(t){v_1}}}{{{y_1}v(t)}}} \right) \right] \\ &- \frac{{{\beta _1}{x_1}{v_1}}}{{1 + \alpha {v_1}}} g\left( {\frac{{x(t - \tau )v(t - \tau )\left( {1 + \alpha {v_1}} \right){y_1}}}{{{x_1}{v_1}\left( {1 + \alpha v(t - \tau )} \right)y(t)}}} \right) - {\beta _2}{x_1}{y_1}\left[ {g\left( {\frac{{{x_1}}}{{x(t)}}} \right) + g\left( {\frac{{x(t - \tau )y(t - \tau )}}{{{x_1}y(t)}}} \right)} \right]. \end{aligned} \end{equation}$

(4.6)

From (3.6) and (3.7), we derive that ${c_1}{y_1} < {b_1}$ and ${c_2}{v_1} < {b_2}$ . Since function $g(x) = x - 1 - \ln x$ is always positive except for $x = 1$ where $g(x) = 0$ . It follows from (4.6) that $\dot V_2(t) \le 0$ with equality holding if and only if $x = {x_1}, y = {y_1}, v = {v_1}, z = w = 0$ . It can be proved that ${M_1} = \{{E_1}\} \subset {\bf\Omega}$ is the largest invariant subset of $\{ (x(t), y(t), v(t), z(t), w(t)):\dot V_2(t) = 0\}$ . Noting that if ${{\mathcal R}_{0}} > 1$ , ${{\mathcal R}_{1}} < 1$ and ${{\mathcal R}_{2}} < 1$ , $E_1$ is locally asymptotically stable, hence we obtain the global asymptotic stability of $E_1$ from LaSalle's invariance principle.

Theorem 4.4. If ${{\mathcal R}_{1}} > 1$ and ${{\mathcal R}_{3}} < 1$ , the cell-mediated immunity-activated equilibrium ${E_2}({x_2}, {y_2}, {v_2}$ , ${z_2}, 0)$ of system (1.2) is globally asymptotically stable.

Proof. Let $(x(t), y(t), v(t), z(t), w(t))$ be any positive solution of system (1.2) with initial condition (1.3). Define

$\begin{align*} {V_3}(t) = & {x_2}g\left( {\frac{{x(t)}}{{{x_2}}}} \right) + {l_{31}}{y_2}g\left( {\frac{{y(t)}}{{{y_2}}}} \right) + {l_{32}}{v_2}g\left( {\frac{{v(t)}}{{{v_2}}}} \right) + {l_{33}}{z_2}g\left( {\frac{{z(t)}}{{{z_2}}}} \right) + {l_{34}}w(t) \\ &+ \frac{{{\beta _1}{x_2}{v_2}}}{{1 + \alpha {v_2}}}\int_{t - \tau }^t {g\left({\frac{{x(s)v(s)\left( {1 + \alpha {v_2}} \right)}}{{{x_2}{v_2}\left( {1 + \alpha v(s)} \right)}}} \right)ds} + {\beta _2}{x_2}{y_2}\int_{t - \tau }^t {g\left( {\frac{{x(s)y(s)}}{{{x_2}{y_2}}}} \right)ds}, \end{align*}$

where constants $l_{31}$ , $l_{32}$ , $l_{33}$ and $l_{34}$ will be determined later. Calculating the derivative of $V_3(t)$ along positive solutions of system (1.2), we obtain that

$\begin{equation}\label{409} \begin{aligned} {{\dot V}_3}(t) = & \left( {1 - \frac{{{x_2}}}{{x(t)}}} \right)\left( {s - dx(t) - \frac{{{\beta _1}x(t)v(t)}}{{1 + \alpha v(t)}} - {\beta _2}x(t)y(t)} \right) \\ &+ {l_{31}}\left( {1 - \frac{{{y_2}}}{{y(t)}}} \right) \left( {\frac{{{\beta _1}{e^{ - m\tau }}x(t - \tau )v(t - \tau )}}{{1 + \alpha v(t - \tau )}} + {\beta _2}{e^{ - m\tau }}x(t - \tau )y(t - \tau ) - ay(t) - {p_1}y(t)z(t)} \right) \\ &+ {l_{32}}\left( {1 - \frac{{{v_2}}}{{v(t)}}} \right)\left( {ky(t) - uv(t) - {p_2}v(t)w(t)} \right) \\ &+ {l_{33}}\left( {1 - \frac{{{z_2}}}{{z(t)}}} \right)\left( {{c_1}y(t)z(t) - {b_1}z(t)} \right) + {l_{34}}\left( {{c_2}v(t)w(t) - {b_2}w(t)} \right) \\ &+ \frac{{{\beta _1}{x_2}{v_2}}}{{1 + \alpha {v_2}}}\left[g\left( {\frac{{x(t)v(t)\left( {1 + \alpha {v_2}} \right)}}{{{x_2}{v_2}\left( {1 + \alpha v(t)} \right)}}} \right) - g\left( {\frac{{x(t - \tau )v(t - \tau )\left( {1 + \alpha {v_2}} \right)}}{{{x_2}{v_2}\left( {1 + \alpha v(t - \tau )} \right)}}} \right)\right] \\ &+ {\beta _2}{x_2}{y_2}\left[ {g\left( {\frac{{x(t)y(t)}}{{{x_2}{y_2}}}} \right) - g\left( {\frac{{x(t - \tau )y(t - \tau )}}{{{x_2}{y_2}}}} \right)} \right]. \end{aligned} \end{equation}$

(4.7)

Substituting $s = d{x_2} + {\beta _1}{x_2}{v_2}/({1 + \alpha {v_2}}) + {\beta _2}{x_2}{y_2}$ , ${\beta _1}{e^{ - m\tau }}{x_2}{v_2}/({1 + \alpha {v_2}}) + {\beta _2}{e^{ - m\tau }}{x_2}{y_2} = a{y_2} + {p_1}{y_2}{z_2}$ , $k{y_2} = u{v_2}$ , ${c_1}{y_2}{z_2} = {b_1}{z_2}$ into (4.7) yields

$\begin{equation}\label{410} \begin{aligned} {{\dot V}_3}(t) = & d{x_2}\left( {2 - \frac{{{x_2}}}{{x(t)}} - \frac{{x(t)}}{{{x_2}}}} \right) + {l_{31}}a{y_2} + {l_{32}}u{v_2} + {l_{33}}{b_1}{z_2} - {l_{32}}{v_2}\frac{{u{v_2}}}{{{y_2}}}\frac{{y(t)}}{{v(t)}} - {l_{32}}uv(t) \\ &+ \frac{{{\beta _1}{x_2}{v_2}}}{{1 + \alpha {v_2}}}\left[ {1 + \frac{{v(t)\left( {1 + \alpha {v_2}} \right)}}{{{v_2}\left( {1 + \alpha v(t)} \right)}} - \frac{{{x_2}}}{{x(t)}}} \right] - {l_{31}}{e^{ - m\tau }}\frac{{{\beta _1}{x_2}{v_2}}}{{1 + \alpha {v_2}}}\frac{{x(t - \tau )v(t - \tau )\left( {1 + \alpha {v_2}} \right){y_2}}}{{{x_2}{v_2}\left( {1 + \alpha v(t - \tau )} \right)y(t)}} \\ &+ \frac{{{\beta _1}{x_2}{v_2}}}{{1 + \alpha {v_2}}}\ln \frac{{x(t - \tau )v(t - \tau )\left( {1 + \alpha v(t)} \right)}}{{x(t)v(t)\left( {1 + \alpha v(t - \tau )} \right)}} + {\beta _2}{x_2}{y_2}\left( {1 - \frac{{{x_2}}}{{x(t)}} - {l_{31}}{e^{ - m\tau }}\frac{{x(t - \tau )y(t - \tau )}}{{{x_2}y(t)}}} \right) \\ &+ {\beta _2}{x_2}{y_2}\ln \frac{{x(t - \tau )y(t - \tau )}}{{x(t)y(t)}} + \left( {{l_{31}}{e^{ - m\tau }} - 1} \right)\left( {\frac{{{\beta _1}x(t - \tau )v(t - \tau )}}{{1 + \alpha v(t - \tau )}} + {\beta _2}x(t - \tau )y(t - \tau )} \right)\\ &+ \left( {{\beta _2}{x_2} + {l_{32}}k - {l_{33}}{c_1}{z_2} - {l_{31}}a} \right)y(t) + \left( {{l_{32}}{p_2}{v_2} - {l_{34}}{b_2}} \right)w(t) \\ &+ \left( {{l_{31}}{p_1}{y_2} - {l_{33}}{b_1}} \right)z(t) + \left( {{l_{33}}{c_1} - {l_{31}}{p_1}} \right)y(t)z(t) + \left( {{l_{34}}{c_2} - {l_{32}}{p_2}} \right)v(t)w(t). \end{aligned} \end{equation}$

(4.8)

Choose

$\begin{equation}\label{411} {l_{31}} = {e^{m\tau }}, \quad {l_{32}} = \frac{{{\beta _1}{x_2}{v_2}}}{{k{y_2}\left( {1 + \alpha {v_2}} \right)}}, \quad {l_{33}} = \frac{{{e^{m\tau }}{p_1}}}{{{c_1}}}, \quad {l_{34}} = \frac{{{\beta _1}{p_2}{x_2}{v_2}}}{{{c_2}k{y_2}\left( {1 + \alpha {v_2}} \right)}}. \end{equation}$

(4.9)

From (4.8) and (4.9), we obtain that

$\begin{equation}\label{412} \begin{aligned} {{\dot V}_3}(t) = & d{x_2}\left( {2 - \frac{{{x_2}}}{{x(t)}} - \frac{{x(t)}}{{{x_2}}}} \right) + \frac{{{\beta _1}{p_2}{x_2}{v_2}}}{{k{y_2}\left( {1 + \alpha {v_2}} \right)}}\frac{{{c_2}{v_2} - {b_2}}}{{{c_2}}}w(t) \\ &- \frac{{\alpha {{\left( {v(t) - {v_2}} \right)}^2}}}{{{v_2}\left( {1 + \alpha {v_2}} \right)\left( {1 + \alpha v(t)} \right)}} - g\left( {\frac{{1 + \alpha v(t)}}{{1 + \alpha {v_2}}}} \right) - \frac{{{\beta _1}{x_2}{v_2}}}{{1 + \alpha {v_2}}}\left[ {g\left( {\frac{{{x_2}}}{{x(t)}}} \right) + g\left( {\frac{{y(t){v_2}}}{{{y_2}v(t)}}} \right)} \right] \\ &- \frac{{{\beta _1}{x_2}{v_2}}}{{1 + \alpha {v_2}}}g\left( {\frac{{x(t - \tau )v(t - \tau )\left( {1 + \alpha {v_2}} \right){y_2}}}{{{x_2}{v_2}\left( {1 + \alpha v(t - \tau )} \right)y(t)}}} \right) - {\beta _2}{x_2}{y_2}\left[ {g\left( {\frac{{{x_2}}}{{x(t)}}} \right) + g\left( {\frac{{x(t - \tau )y(t - \tau )}}{{{x_2}y(t)}}} \right)} \right]. \end{aligned} \end{equation}$

(4.10)

Noting that ${\mathcal{R}_3} = \left( {{c_2}{v_2} - {b_2}} \right)/{b_2} + 1 < 1$ , it is clear that ${c_2}{v_2} < {b_2}$ . It follows from (4.10) that $\dot V_3(t) \le 0$ with equality holding if and only if $x = {x_2}, y = {y_2}, v = {v_2}, z = {z_2}, w = 0$ . It can be verified that ${M_3} = \{ {E_2}\} \subset {\bf\Omega}$ is the largest invariant subset of $\{ (x(t), y(t), v(t), z(t), w(t)):\dot V_3(t) = 0\}$ . Noting that if ${{\mathcal R}_{1}} > 1$ and ${{\mathcal R}_{3}} < 1$ , $E_2$ is locally asymptotically stable, thus we obtain the global asymptotic stability of $E_2$ from LaSalle's invariance principle.

Theorem 4.5. If ${{\mathcal R}_{2}} > 1$ and ${{\mathcal R}_{4}} < 1$ , the humoral immunity-activated equilibrium ${E_3}({x_3}, {y_3}, {v_3}, 0, {w_3})$ of system (1.2) is globally asymptotically stable.

Proof. Let $(x(t), y(t), v(t), z(t), w(t))$ be any positive solution of system (1.2) with initial condition (1.3). Define

$\begin{align*} {V_4}(t) = & {x_3}g\left( {\frac{{x(t)}}{{{x_3}}}} \right) + {l_{41}}{y_3}g\left( {\frac{{y(t)}}{{{y_3}}}} \right) + {l_{42}}{v_3}g\left( {\frac{{v(t)}}{{{v_3}}}} \right) + {l_{43}}z(t) + {l_{44}}{w_3}g\left( {\frac{{w(t)}}{{{w_3}}}} \right) \\ &+ \frac{{{\beta _1}{x_3}{v_3}}}{{1 + \alpha {v_3}}}\int_{t - \tau }^t {g\left( {\frac{{x(s)v(s)\left( {1 + \alpha {v_3}} \right)}}{{{x_3}{v_3}\left( {1 + \alpha v(s)} \right)}}} \right)ds} + {\beta _2}{x_3}{y_3}\int_{t - \tau }^t {g\left( {\frac{{x(s)y(s)}}{{{x_3}{y_3}}}} \right)ds}, \end{align*}$

where constants $l_{41}$ , $l_{42}$ , $l_{43}$ and $l_{44}$ will be determined later. Calculating the derivative of $V_4(t)$ along positive solutions of system (1.2), we obtain that

$\begin{equation}\label{413} \begin{aligned} {{\dot V}_4}(t) = & \left( {1 - \frac{{{x_3}}}{{x(t)}}} \right)\left( {s - dx(t) - \frac{{{\beta _1}x(t)v(t)}}{{1 + \alpha v(t)}} - {\beta _2}x(t)y(t)} \right) \\ &+ {l_{41}}\left( {1 - \frac{{{y_3}}}{{y(t)}}} \right)\left( {\frac{{{\beta _1}{e^{ - m\tau }}x(t - \tau )v(t - \tau )}}{{1 + \alpha v(t - \tau )}} + {\beta _2}{e^{ - m\tau }}x(t - \tau )y(t - \tau ) - ay(t) - {p_1}y(t)z(t)} \right) \\ &+ {l_{42}}\left( {1 - \frac{{{v_3}}}{{v(t)}}} \right)\left( {ky(t) - uv(t) - {p_2}v(t)w(t)} \right) \\ &+ {l_{43}}\left( {{c_1}y(t)z(t) - {b_1}z(t)} \right) + {l_{44}}\left( {1 - \frac{{{w_3}}}{{w(t)}}} \right)\left( {{c_2}v(t)w(t) - {b_2}w(t)} \right) \\ &+ \frac{{{\beta _1}{x_3}{v_3}}}{{1 + \alpha {v_3}}}\left[g\left( {\frac{{x(t)v(t)\left( {1 + \alpha {v_3}} \right)}}{{{x_3}{v_3}\left( {1 + \alpha v(t)} \right)}}} \right) - g\left( {\frac{{x(t - \tau )v(t - \tau )\left( {1 + \alpha {v_3}} \right)}}{{{x_3}{v_3}\left( {1 + \alpha v(t - \tau )} \right)}}} \right)\right] \\ &+ {\beta _2}{x_3}{y_3}\left[ {g\left( {\frac{{x(t)y(t)}}{{{x_3}{y_3}}}} \right) - g\left( {\frac{{x(t - \tau )y(t - \tau )}}{{{x_3}{y_3}}}} \right)} \right]. \end{aligned} \end{equation}$

(4.11)

Substituting $s = d{x_3} + {{\beta _1}{x_3}{v_3}}/({1 + \alpha {v_3}}) + {\beta _2}{x_3}{y_3}$ , ${{\beta _1}{e^{ - m\tau }}{x_3}{v_3}}/({1 + \alpha {v_3}}) + {\beta _2}{e^{ - m\tau }}{x_3}{y_3} = a{y_3}$ , $k{y_3} = u{v_3} + {p_2}{v_3}{w_3}$ , ${c_2}{v_3}{w_3} = {b_2}{w_3}$ into (4.11) yields

$\begin{equation}\label{414} \begin{aligned} {{\dot V}_4}(t) = & d{x_3}\left( {2 - \frac{{{x_3}}}{{x(t)}} - \frac{{x(t)}}{{{x_3}}}} \right) + {l_{41}}a{y_3} + {l_{42}}u{v_3} + {l_{44}}{b_2}{w_3} \\ &- {l_{42}}k{v_3}\frac{{y(t)}}{{v(t)}} - \left( {{l_{42}}u + {l_{44}}{c_2}{w_3}} \right)v(t) + \frac{{{\beta _1}{x_3}{v_3}}}{{1 + \alpha {v_3}}}\left[ {1 + \frac{{v(t)\left( {1 + \alpha {v_3}} \right)}}{{{v_3}\left( {1 + \alpha v(t)} \right)}} - \frac{{{x_3}}}{{x(t)}}} \right] \\ &- {l_{41}}{e^{ - m\tau }}\frac{{{\beta _1}{x_3}{v_3}}}{{1 + \alpha {v_3}}}\frac{{x(t - \tau )v(t - \tau )\left( {1 + \alpha {v_3}} \right){y_3}}}{{{x_3}\left( {1 + \alpha v(t - \tau )} \right){v_3}y(t)}} + \frac{{{\beta _1}{x_3}{v_3}}}{{1 + \alpha {v_3}}}\ln \frac{{x(t - \tau )v(t - \tau )\left( {1 + \alpha v(t)} \right)}}{{x(t)v(t)\left( {1 + \alpha v(t - \tau )} \right)}} \\ &+ {\beta _2}{x_3}{y_3}\left( {1 - \frac{{{x_3}}}{{x(t)}} - {l_{41}}{e^{ - m\tau }}\frac{{x(t - \tau )y(t - \tau )}}{{{x_3}y(t)}}} \right) + {\beta _2}{x_3}{y_3} \ln \frac{{x(t - \tau )y(t - \tau )}}{{x(t)y(t)}} \\ &+ \left( {{l_{41}}{e^{ - m\tau }} - 1} \right)\left( {\frac{{{\beta _1}x(t - \tau )v(t - \tau )}}{{1 + \alpha v(t - \tau )}} + {\beta _2}x(t - \tau )y(t - \tau )} \right) \\ &+ \left( {{\beta _2}{x_3} + {l_{42}}k - {l_{41}}a} \right)y(t) + \left( {{l_{41}}{p_1}{y_3} - {l_{43}}{b_1}} \right)z(t) + \left( {{l_{42}}{p_2}{v_3} - {l_{44}}{b_2}} \right)w(t) \\ & + \left( {{l_{43}}{c_1} - {l_{41}}{p_1}} \right)y(t)z(t) + \left( {{l_{44}}{c_2} - {l_{42}}{p_2}} \right)v(t)w(t). \end{aligned} \end{equation}$

(4.12)

Choose

$\begin{equation}\label{415} {l_{41}} = {e^{m\tau }}, \quad {l_{42}} = \frac{{{\beta _1}{x_3}{v_3}}}{{k{y_3}\left( {1 + \alpha {v_3}} \right)}}, \quad {l_{43}} = \frac{{{e^{m\tau }}{p_1}}}{{{c_1}}}, \quad {l_{44}} = \frac{{{\beta _1}{p_2}{x_3}{v_3}}}{{{c_2}k{y_3}\left( {1 + \alpha {v_3}} \right)}}. \end{equation}$

(4.13)

It follows from (4.12) and (4.13) that

$\begin{equation}\label{416} \begin{aligned} {{\dot V}_4}(t) = & d{x_3}\left( {2 - \frac{{{x_3}}}{{x(t)}} - \frac{{x(t)}}{{{x_3}}}} \right) + {e^{m\tau }}{p_1}\frac{{{c_1}{y_3} - {b_1}}}{{{c_1}}}z(t) - \frac{{\alpha {{\left( {v(t) - {v_3}} \right)}^2}}}{{{v_3}\left( {1 + \alpha {v_3}} \right)\left( {1 + \alpha v(t)} \right)}} - g\left( {\frac{{1 + \alpha v(t)}}{{1 + \alpha {v_3}}}} \right) \\ &- \frac{{{\beta _1}{x_3}{v_3}}}{{1 + \alpha {v_3}}}\left[ {g\left( {\frac{{{x_3}}}{{x(t)}}} \right) + g\left( {\frac{{y(t){v_3}}}{{{y_3}v(t)}}} \right) + g\left( {\frac{{x(t - \tau )v(t - \tau )\left( {1 + \alpha {v_3}} \right){y_3}}}{{{x_3}{v_3}\left( {1 + \alpha v(t - \tau )} \right)y(t)}}} \right)} \right] \\ &- {\beta _2}{x_3}{y_3}\left[ {g\left( {\frac{{{x_3}}}{{x(t)}}} \right) + g\left( {\frac{{x(t - \tau )y(t - \tau )}}{{{x_3}y(t)}}} \right)} \right]. \end{aligned} \end{equation}$

(4.14)

According to (3.12), it is easy to see that ${c_1}{y_3} < {b_1}$ . It follows from (4.14) that $\dot V_4(t) \le 0$ with equality holding if and only if $x = {x_3}, y = {y_3}, v = {v_3}, z = 0, w = {w_3}$ . It can be proved that ${M_4} = \{ {E_3}\} \subset {\bf\Omega}$ is the largest invariant subset of $\{ (x(t), y(t), v(t), z(t), w(t)):\dot V_4(t) = 0\}$ . Noting that if ${{\mathcal R}_{2}} > 1$ and ${{\mathcal R}_{4}} < 1$ , $E_3$ is locally asymptotically stable, hence we obtain the global asymptotic stability of $E_3$ from LaSalle's invariance principle.

Theorem 4.6. If ${{\mathcal R}_{3}} > 1$ and ${{\mathcal R}_{4}} > 1$ , the immunity-activated equilibrium $E^*({x^*}, {y^*}, {v^*}, {z^*}, {w^*})$ of system (1.2) is globally asymptotically stable.

Proof. Let $(x(t), y(t), v(t), z(t), w(t))$ be any positive solution of system (1.2) with initial condition (1.3). Define

$\begin{align*} {V_5}(t) = & {x^*}g\left( {\frac{{x(t)}}{{{x^*}}}} \right) + {l_{51}}{y^*}g\left( {\frac{{y(t)}}{{{y^*}}}} \right) + {l_{52}}{v^*}g\left( {\frac{{v(t)}}{{{v^*}}}} \right) + {l_{53}}{z^*}g\left( {\frac{{z(t)}}{{{z^*}}}} \right) + {l_{54}}{w^*}g\left( {\frac{{w(t)}}{{{w^*}}}} \right) \\ &+ \frac{{{\beta _1}{x^*}{v^*}}}{{1 + \alpha {v^*}}}\int_{t - \tau }^t {g\left({\frac{{x(s)v(s)\left( {1 + \alpha {v^*}} \right)}}{{{x^*}{v^*}\left( {1 + \alpha v(s)} \right)}}} \right)ds} + {\beta _2}{x^*}{y^*}\int_{t - \tau }^t {g\left( {\frac{{x(s)y(s)}}{{{x^*}{y^*}}}} \right)ds}, \end{align*}$

where constants $l_{51}$ , $l_{52}$ , $l_{53}$ and $l_{54}$ will be determined later. Calculating the derivative of $V_5(t)$ along positive solutions of system (1.2), we have

$\begin{equation}\label{417} \begin{aligned} {{\dot V}_5}(t) = & \left( {1 - \frac{{{x^*}}}{{x(t)}}} \right)\left( {s - dx(t) - \frac{{{\beta _1}x(t)v(t)}}{{1 + \alpha v(t)}} - {\beta _2}x(t)y(t)} \right) \\ &+ {l_{51}}\left( {1 - \frac{{{y^*}}}{{y(t)}}} \right)\left( {\frac{{{\beta _1}{e^{ - m\tau }}x(t - \tau )v(t - \tau )}}{{1 + \alpha v(t - \tau )}} + {\beta _2}{e^{ - m\tau }}x(t - \tau )y(t - \tau ) - ay(t) - {p_1}y(t)z(t)} \right) \\ &+ {l_{52}}\left( {1 - \frac{{{v^*}}}{{v(t)}}} \right)\left( {ky(t) - uv(t) - {p_2}v(t)w(t)} \right) \\ &+ {l_{53}}\left( {1 - \frac{{{z^*}}}{{z(t)}}} \right)\left( {{c_1}y(t)z(t) - {b_1}z(t)} \right) + {l_{54}}\left( {1 - \frac{{{w^*}}}{{w(t)}}} \right)\left( {{c_2}v(t)w(t) - {b_2}w(t)} \right) \\ &+\frac{{{\beta _1}{x^*}{v^*}}}{{1 + \alpha {v^*}}}\left[g\left( {\frac{{x(t)v(t)\left( {1 + \alpha {v^*}} \right)}}{{{x^*}{v^*}\left( {1 + \alpha v(t)} \right)}}} \right) - g\left( {\frac{{x(t - \tau )v(t - \tau )\left( {1 + \alpha {v^*}} \right)}}{{{x^*}{v^*}\left( {1 + \alpha v(t - \tau )} \right)}}} \right)\right] \\ &+ {\beta _2}{x^*}{y^*}\left[ {g\left( {\frac{{x(t)y(t)}}{{{x^*}{y^*}}}} \right) - g\left( {\frac{{x(t - \tau )y(t - \tau )}}{{{x^*}{y^*}}}} \right)} \right]. \end{aligned} \end{equation}$

(4.15)

Substituting $s = d{x^*} + {{\beta _1}{x^*}{v^*}}/({1 + \alpha {v^*}}) + {\beta _2}{x^*}{y^*}$ , ${{\beta _1}{e^{ - m\tau }}{x^*}{v^*}}/({1 + \alpha {v^*}}) + {\beta _2}{e^{ - m\tau }}{x^*}{y^*} = a{y^*} + {p_1}{y^*}{z^*}$ , $k{y^*} = u{v^*} + {p_2}{v^*}{w^*}$ , ${c_1}{y^*}{z^*} = {b_1}{z^*}$ , ${c_2}{v^*}{w^*} = {b_2}{w^*}$ into (4.15) yields

$\begin{equation}\label{418} \begin{aligned} {{\dot V}_5}(t) = & d{x^*}\left( {2 - \frac{{{x^*}}}{{x(t)}} - \frac{{x(t)}}{{{x^*}}}} \right) + \frac{{{\beta _1}{x^*}{v^*}}}{{1 + \alpha {v^*}}}\left[ {1 + \frac{{v(t)\left( {1 + \alpha {v^*}} \right)}}{{{v^*}\left( {1 + \alpha v(t)} \right)}} - \frac{{{x^*}}}{{x(t)}}} \right] \\ & + \frac{{{\beta _1}{x^*}{v^*}}}{{1 + \alpha {v^*}}}\left[\ln \frac{{x(t - \tau )v(t - \tau )\left( {1 + \alpha v(t)} \right)}}{{x(t)v(t)\left( {1 + \alpha v(t - \tau )} \right)}}- {l_{51}}{e^{ - m\tau }}\frac{{x(t - \tau )v(t - \tau ){y^*}\left( {1 + \alpha {v^*}} \right)}}{{{x^*}{v^*}y(t)\left( {1 + \alpha v(t - \tau )} \right)}}\right] \\ &+ {\beta _2}{x^*}{y^*}\left( {1 - \frac{{{x^*}}}{{x(t)}} - {l_{51}}{e^{ - m\tau }}\frac{{x(t - \tau )y(t - \tau )}}{{{x^*}y(t)}}} + \ln \frac{{x(t - \tau )y(t - \tau )}}{{x(t)y(t)}} \right) \\ &+ {l_{51}}a{y^*} + {l_{52}}u{v^*} + {l_{53}}{c_1}{y^*}{z^*} + {l_{54}}{c_2}{v^*}{w^*}- {l_{52}}{v^*}\frac{{u{v^*} + {p_2}{v^*}{w^*}}}{{{y^*}}}\frac{{y(t)}}{{v(t)}} \\ &+ \left( {{l_{51}}{e^{ - m\tau }} - 1} \right)\left( {\frac{{{\beta _1}x(t - \tau )v(t - \tau )}}{{1 + \alpha v(t - \tau )}} + {\beta _2}x(t - \tau )y(t - \tau )} \right) \\ &+ \left( {{\beta _2}{x^*} + {l_{52}}\frac{{u{v^*} + {p_2}{v^*}{w^*}}}{{{y^*}}} - {l_{51}}a - {l_{53}}{c_1}{z^*}} \right)y(t) \\ &- \left( {{l_{54}}{c_2}{w^*} + {l_{52}}u} \right)v(t) + \left( {{l_{51}}{p_1} - {l_{53}}{c_1}} \right){y^*}z(t) + \left( {{l_{52}}{p_2} - {l_{54}}{c_2}} \right){v^*}w(t)\\ & + \left( {{l_{53}}{c_1} - {l_{51}}{p_1}} \right)y(t)z(t)+ \left( {{l_{54}}{c_2} - {l_{52}}{p_2}} \right)v(t)w(t). \end{aligned} \end{equation}$

(4.16)

Choose

$\begin{equation}\label{419} {l_{51}} = {e^{m\tau }}, \quad {l_{52}} = \frac{{{\beta _1}{x^*}}}{{\left( {1 + \alpha {v^*}} \right)\left( {u + {p_2}{w^*}} \right)}}, \quad {l_{53}} = \frac{{{p_1}}}{{{c_1}}}{e^{m\tau }}, \quad {l_{54}} = \frac{{{\beta _1}{p_2}{x^*}}}{{{c_2}\left( {1 + \alpha {v^*}} \right)\left( {u + {p_2}{w^*}} \right)}}. \end{equation}$

(4.17)

From (4.16) and (4.17), we can obtain that

$\begin{equation}\label{420} \begin{aligned} {{\dot V}_5}(t) = & d{x^*}\left( {2 - \frac{{{x^*}}}{{x(t)}} - \frac{{x(t)}}{{{x^*}}}} \right) - \frac{{\alpha {{\left( {v(t) - {v^*}} \right)}^2}}}{{{v^*}\left( {1 + \alpha {v^*}} \right)\left( {1 + \alpha v(t)} \right)}}- g\left( {\frac{{1 + \alpha v(t)}}{{1 + \alpha {v^*}}}} \right)\\ &- \frac{{{\beta _1}{x^*}{v^*}}}{{1 + \alpha {v^*}}}\left[ {g\left( {\frac{{{x^*}}}{{x(t)}}} \right) + g\left( {\frac{{y(t){v^*}}}{{{y^*}v(t)}}} \right) + g\left( {\frac{{x(t - \tau )v(t - \tau ){y^*}\left( {1 + \alpha {v^*}} \right)}}{{{x^*}{v^*}y(t)\left( {1 + \alpha v(t - \tau )} \right)}}} \right)} \right] \end{aligned} \end{equation}$

(4.18)

$- {\beta _2}{x^*}{y^*}\left[ {g\left( {\frac{{{x^*}}}{{x(t)}}} \right) + g\left( {\frac{{x(t - \tau )y(t - \tau )}}{{{x^*}y(t)}}} \right)} \right].$

It follows from (4.18) that $\dot V_5(t) \le 0$ with equality holding if and only if $x = {x^*}, y = {y^*}, v = {v^*}, z = {z^*}, w = {w^*}$ . It can be verified that ${M_5} = \{ {E^*}\} \subset {\bf\Omega}$ is the largest invariant subset of $\{ (x(t), y(t), v(t), z(t), w(t)):\dot V_5(t) = 0\}$ . Noting that if ${{\mathcal R}_{3}} > 1$ and ${{\mathcal R}_{4}} > 1$ , $E^*$ is locally asymptotically stable, we therefore obtain the global asymptotic stability of $E^*$ from LaSalle's invariance principle.

5. Numerical simulations

In this section, we want to illustrate the theoretical results for system (1.2) by numerical simulations. Besides, we investigate the effects of cell-to-cell transmission, viral production rate, death rate of infected cells and viral remove rate on viral dynamics. Furthermore, sensitivity analysis is used to quantify the range of variables in reproduction ratios and identify the key factors giving rise to reproduction ratios, which can be helpful to design treatment strategies and provide insights on evaluating effective antiviral drug therapies.

Following ^{[18,26,27,32]}, we choose appropriate parameters and simulate each of feasible equilibria, respectively.

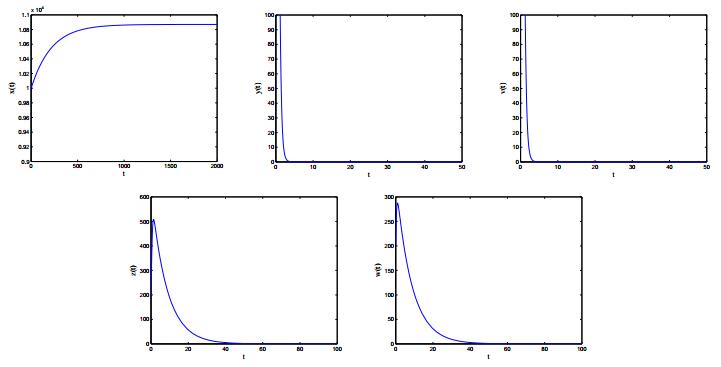
Case 1: Corresponding parameters are listed in Case 1 of Table 2. The immunity-inactivated reproduction ratio is calculated as ${\mathcal R}_{0} = 0.5640 < 1$ . From Theorem 3.1, we derive that infection-free equilibrium $E_0$ is locally asymptotically stable, which is illustrated in Figure 2.

Table 2. List of parameters.

Parameters (units)	Case 1	Case 2	Case 3	Case4	Case5	Source
$s~$ $(\rm{cells}\cdot\rm{ml}/\rm{day})$	$50$	$23$	$100$	$23$	$100$	Assumed
$d$ $(/\rm{day})$	$0.0046$	$0.0065$	$0.0046$	$0.0046$	$0.0046$	^[26]
$\beta_1$ $(\rm{ml}\cdot\rm{virion}/\rm{day})$	$4.8\times10^{-7}$	$4.8\times10^{-7}$	$4.8\times10^{-7}$	$4.8\times10^{-7}$	$4.8\times10^{-7}$	^[26]
$\beta_2$ $(\rm{ml}\cdot\rm{virion}/\rm{day})$	$4.7\times10^{-7}$	$4.7\times10^{-9}$	$4.7\times10^{-7}$	$4.7\times10^{-7}$	$4.7\times10^{-7}$	^[26]
$\alpha$	$0.01$	$0.0001$	$0.01$	$0.01$	$0.01$	Assumed
$m$	$1.39$	$1.39$	$1.39$	$1.39$	$1.39$	^[26]
$\tau$ $\rm{(day)}$	$0.5$	$0.3$	$0.5$	$0.5$	$0.5$	^[26]
$a$ $(/\rm{day})$	$0.015$	$0.032$	$0.008$	$0.01$	$0.008$	Assumed
$p_1$ $(\rm{cells}\cdot\rm{ml}/\rm{day})$	$0.005$	$0.005$	$0.001$	$0.005$	$0.001$	^[27]
$k$ $(\rm{cells}\cdot\rm{virion}/\rm{day})$	$1.1349$	$7.3$	$1.1349$	$11.349$	$11.349$	^[26]
$u$ $(/\rm{day})$	$0.5$	$0.25$	$0.05$	$0.05$	$0.05$	^[26]
$p_2$ $(\rm{{{\mu}g/day}})$	$0.01$	$0.01$	$0.01$	$0.01$	$0.01$	^[27]
$c_1$ $(\rm{cells}\cdot\rm{ml}/\rm{day})$	$0.002$	$0.021$	$0.002$	$0.002$	$0.002$	Assumed
$b_1$ $(/\rm{day})$	$0.12$	$0.25$	$0.02$	$0.12$	$0.02$	Assumed
$c_2$ $(\rm{cells}\cdot\rm{virion}/\rm{day})$	$0.0006$	$0.0013$	$0.00013$	$0.0013$	$0.0013$	^[27]
$b_2$ $(/\rm{day})$	$0.12$	$0.46$	$0.12$	$0.12$	$0.12$	Assumed

| Show Table

DownLoad: CSV

Figure 2. The temporal solutions of

$x(t)$ ,

$y(t)$ ,

$v(t)$ ,

$z(t)$ and

$w(t)$ versus

$t$ of system (1.2) where

${\mathcal R}_{0} = 0.5640 < 1$ .

DownLoad: Full-Size Img PowerPoint

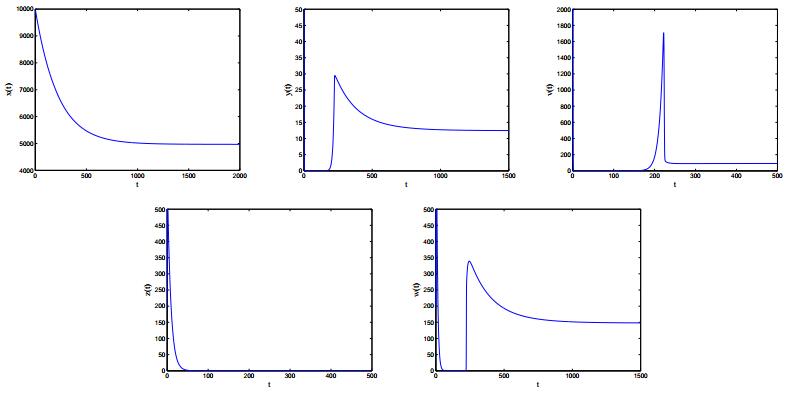
Case 2: Corresponding parameters are listed in Case 2 of Table 2. By simple computing, we obtain that ${\mathcal R}_{0} = 1.0217 > 1$ , ${\mathcal R}_{1} = 0.9635 < 1$ and ${\mathcal R}_{2} = 0.9625 < 1$ . From Theorem 3.2, we derive that immunity-inactivated equilibrium $E_1$ is locally asymptotically stable, which is in accord with Figure 3.

Figure 3. The temporal solutions of

$x(t)$ ,

$y(t)$ ,

$v(t)$ ,

$z(t)$ and

$w(t)$ versus

$t$ of system (1.2) where

${\mathcal R}_{0} = 1.0217 > 1$ ,

${\mathcal R}_{1} = 0.9635 < 1$ and

${\mathcal R}_{2} = 0.9625 < 1$ .

DownLoad: Full-Size Img PowerPoint

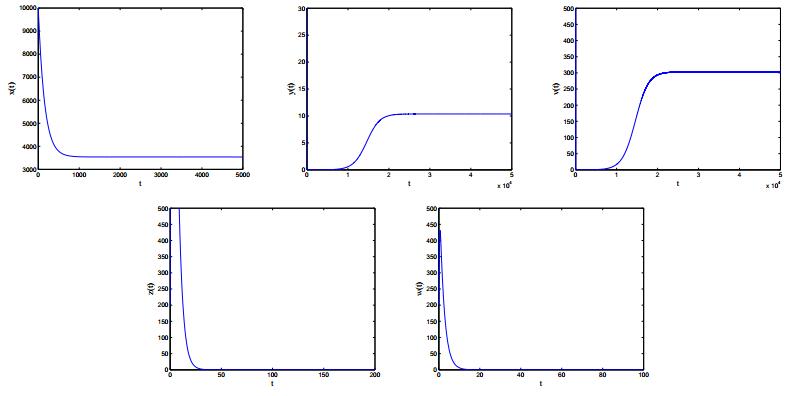
Case 3: Corresponding parameters are listed in Case 3 of Table 2. Similarly, we obtain that ${\mathcal R}_{1} = 5.1140 > 1$ and ${\mathcal R}_{3} = 0.2459 < 1$ . From Theorem 3.3, we derive that cell-mediated immunity-activated equilibrium $E_2$ is locally asymptotically stable, which is illustrated in Figure 4.

Figure 4. The temporal solutions of

$x(t)$ ,

$y(t)$ ,

$v(t)$ ,

$z(t)$ and

$w(t)$ versus

$t$ of system (1.2) where

${\mathcal R}_{1} = 5.1140 > 1$ and

${\mathcal R}_{3} = 0.2459 < 1$ .

DownLoad: Full-Size Img PowerPoint

Case 4: Corresponding parameters are listed in Case 4 of Table 2. Likewise, we obtain that ${\mathcal R}_{2} = 14.1830 > 1$ and ${\mathcal R}_{4} = 0.2108 < 1$ . From Theorem 3.4, we derive that humoral immunity-activated equilibrium $E_3$ is locally asymptotically stable, which is in keeping with in Figure 5.

Figure 5. The temporal solutions of

$x(t)$ ,

$y(t)$ ,

$v(t)$ ,

$z(t)$ and

$w(t)$ versus

$t$ of system (1.2) where

${\mathcal R}_{2} = 14.1830 > 1$ and

${\mathcal R}_{4} = 0.2108 < 1$ .

DownLoad: Full-Size Img PowerPoint

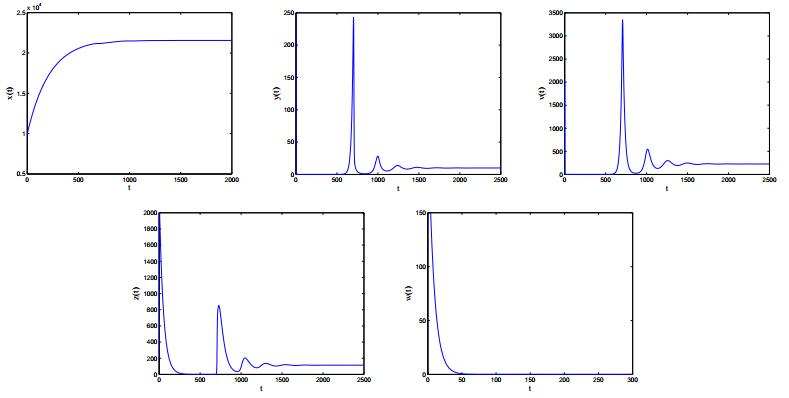
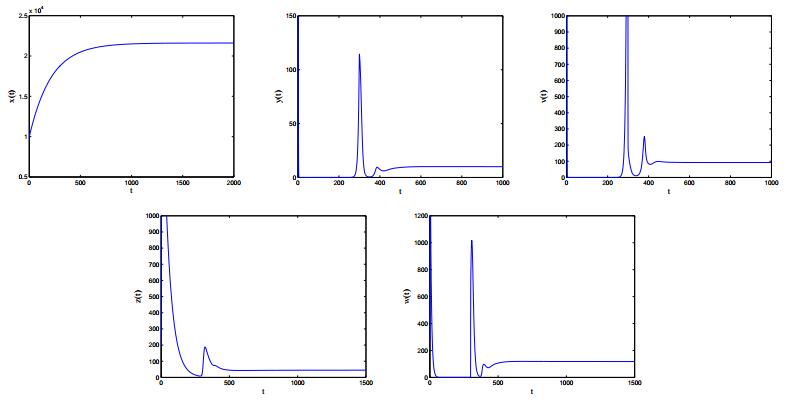
Case 5: Corresponding parameters are listed in Case 5 of Table 2. By calculation, we obtain that ${\mathcal R}_{3} = 24.5895 > 1$ and ${\mathcal R}_{4} = 3.7395 > 1$ . From Theorem 3.5, we derive that immunity-activated equilibrium $E^*$ is locally asymptotically stable, which is consistent with observation in Figure 6.

Figure 6. The temporal solutions of

$x(t)$ ,

$y(t)$ ,

$v(t)$ ,

$z(t)$ and

$w(t)$ versus

$t$ of system (1.2) where

${\mathcal R}_{3} = 24.5895 > 1$ and

${\mathcal R}_{4} = 3.7395 > 1$ .

DownLoad: Full-Size Img PowerPoint

5.1. Effect of cell-to-cell transmission

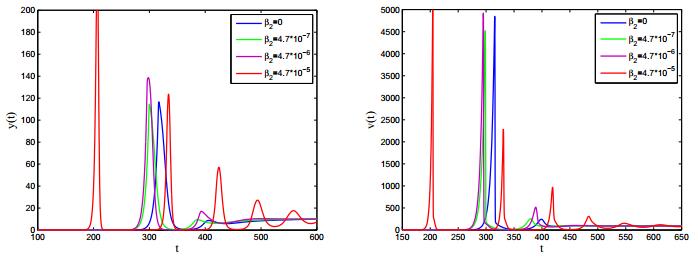
In order to investigate the effect of cell-to-cell transmission, we carry out some numerical simulations to show the contribution of cell-to-cell transmission during the whole infection. First, we let $\beta_2$ as zero to compare the virus infection without cell-to-cell transmission with the infection which has both transmissions. Figure 7 ( $\beta_2 = 0, ~\beta_2 = 4.7 \times {10^{ - 7}}$ ) shows that cell-to-cell transmission is of benefit to HIV-1 transmission and the time to reach the peak level of virus is shorter. Then, we increase $\beta_2$ to study the change of the peak level of infected cells and virus, and the time to reach the peak level. Figure 7 ( $\beta_2 = 4.7 \times {10^{ - 7}}, ~\beta_2 = 4.7 \times {10^{ - 6}}, ~\beta_2 = 4.7 \times {10^{ - 5}}$ ) shows that infected cells and virus reach the peak level more quickly as $\beta_2$ increases, meanwhile, the peak level become larger as $\beta_2$ increases, too. Therefore, cell-to-cell transmission plays an important role in the whole virus infection.

Figure 7. The effect of

${\beta}_2$ on the dynamical behavior of system (1.2).

DownLoad: Full-Size Img PowerPoint

5.2. Effect of viral production rate

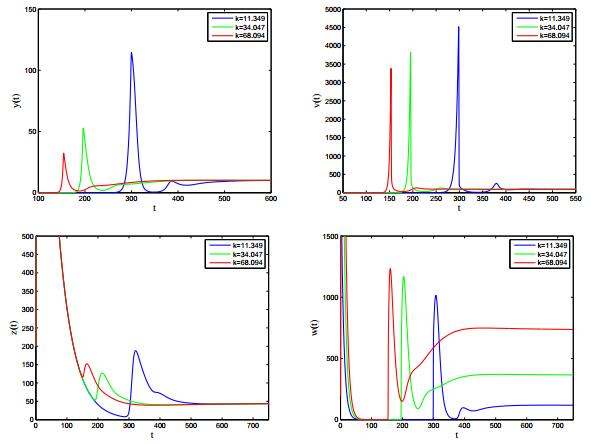
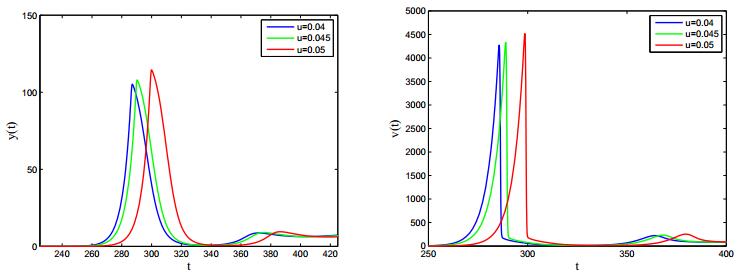
Viral production rate also has great influence on the dynamical behavior of the model. We set the viral production rate $k$ as 11.349, 34.047, 68.094. In Figure 8, we observe that the time to reach the peak level of infected cells and virus becomes shorter as $k$ increases, which means that larger viral production rate contributes to the viral infection. Meanwhile, T cells and B cells increase more quickly as $k$ increases, especially, larger viral production rate can stimulate more B cells. Hence, the peak level of infected cells and virus decreases as $k$ increases. In terms of the prevention and treatment of HIV, it implies that antiretroviral therapies, such as, reverse transcriptase inhibitors and protease inhibitors are effective methods to decrease $k$ , namely, to inhibit virus reproduction.

Figure 8. The effect of

$k$ on the dynamical behavior of system (1.2).

DownLoad: Full-Size Img PowerPoint

5.3. Effect of death rate of infected cells and viral remove rate

Usually, the death rate of infected cells is larger than the death rate of uninfected cells due to the fact that HIV infection can kill more host cells. We present some numerical simulations to study the effect of death rate of infected cells on the dynamical behavior of the model. We can observe from Figure 9 that, infected cells and virus increase more slowly as $a$ increases, which indicates that increasing the death rate of infected cells can slow down the virus infection. Humoral immunity is mainly used to clear virus in our humor, so the viral remove rate has an effect on viral infection as well. Figure 10 implies that as the viral remove rate increases, infected cells and virus increase more slowly, which has the similar results to $a$ . In the clinic treatment of HIV, promoting body's immune capacity contributes to increasing the death rate of infected cells and viral remove rate.

Figure 9. The effect of

$a$ on the dynamical behavior of system (1.2).

DownLoad: Full-Size Img PowerPoint

Figure 10. The effect of

$u$ on the dynamical behavior of system (1.2).

DownLoad: Full-Size Img PowerPoint

5.4. Sensitivity analysis

Sensitivity analysis is used to quantify the range of variables in reproduction ratios and to identify the key factors giving rise to reproduction ratios. In ^[9,16], Latin hypercube sampling (LHS) is found to be a more efficient statistical sampling technique which has been introduced to the field of disease modelling.

LHS allows an un-biased estimate of the reproduction ratios, with the advantage that it requires fewer samples than simple random sampling to achieve the same accuracy. For each parameter of reproduction ratios, a probability density function is defined based on experimental data and stratified into N equiprobable serial intervals. A single value is then selected randomly from every interval and this is done for every parameter. In this way, an parameter value from each sampling interval is used only once in the analysis but the entire parameter space is equitably sampled in an efficient manner. Distributions of the reproduction ratios can then be derived directly by running the model N times with each of the sampled parameter sets.

In terms of the prevention and treatment of HIV, we pay more attention to antiretroviral therapies, which is directly related to viral production rate and viral remove rate. Figure 11 shows the scatter plots of ${\mathcal R}_{0}$ , ${\mathcal R}_{1}$ and ${\mathcal R}_{2}$ in respect to $k$ and $u$ , which implies that $k$ is a positively correlative variable with ${\mathcal R}_{0}$ and ${\mathcal R}_{2}$ , while $u$ is a negatively correlative variable. As for ${\mathcal R}_{1}$ , we find that the correlation between $k$ and ${\mathcal R}_{1}$ or $u$ and ${\mathcal R}_{1}$ is not clear.

Figure 11. Scatter plots of

${\mathcal R}_{0}$ ,

${\mathcal R}_{1}$ and

${\mathcal R}_{2}$ in respect to

$k$ and

$u$ .

DownLoad: Full-Size Img PowerPoint

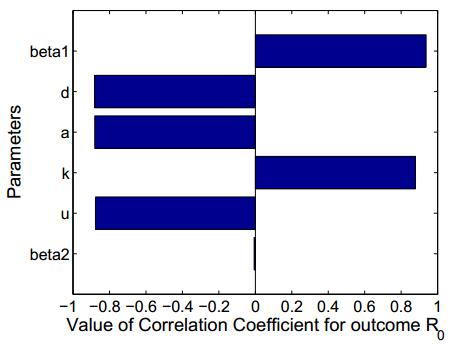
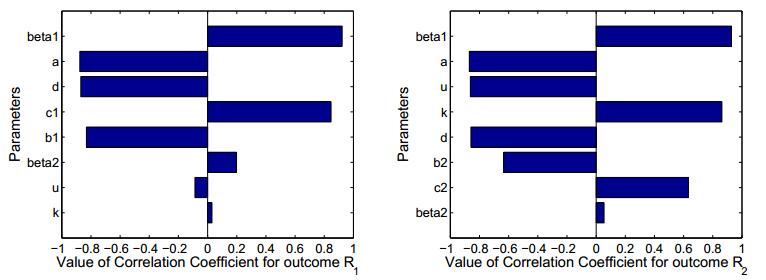
In ^[16], Marino et al. mentioned that Partial Rank Correlation Coefficients (PRCCs) provide a measure of the strength of a linear association between the parameters and the reproduction ratios. Furthermore, PRCCs are useful for identifying the most important parameters. The positive or negative of PRCCs respectively denote the positive or negative correlation with the reproduction ratios, and the sizes of PRCCs measure the strength of the correlation. First, we investigate the immunity-inactivated reproduction ratio ${\mathcal R}_{0}$ , as we can see in Figure 12, ${\beta}_1$ and $k$ are positively correlative variables with ${\mathcal R}_{0}$ while others are negatively correlative variables. In order of correlative strength, it goes: ${\beta}_1$ , $d$ , $a$ , $k$ , $u$ and ${\beta}_2$ . Similarly, we obtain the PRCCs of ${\mathcal R}_{1}$ and ${\mathcal R}_{2}$ (see Figure 13). Specially, we observe that $k$ and $u$ is weakly correlative in respect to ${\mathcal R}_{1}$ , which accords with the scatter plots of ${\mathcal R}_{1}$ .

Figure 12. Tornado plot of PRCCs in regard to

${\mathcal R}_{0}$ .

DownLoad: Full-Size Img PowerPoint

Figure 13. Tornado plots of PRCCs in regard to

${\mathcal R}_{1}$ and

${\mathcal R}_{2}$ .

DownLoad: Full-Size Img PowerPoint

6. Conclusion

In this paper, we have considered an HIV-1 infection model to describe cell-to-cell transmission, saturation incidence, both cell-mediated and humoral immune responses. By a complete mathematical analysis, the threshold dynamics of the model is established and it can be fully determined by reproduction ratios. If ${{\mathcal R}_{0}} < 1$ , the infection-free equilibrium $E_0$ is locally and globally asymptotically stable; if ${{\mathcal R}_{0}} > 1$ , ${{\mathcal R}_{1}} < 1$ and ${{\mathcal R}_{2}} < 1$ , the immunity-inactivated equilibrium $E_1$ is locally and globally asymptotically stable; if ${{\mathcal R}_{1}} > 1$ and ${{\mathcal R}_{3}} < 1$ , the cell-mediated immunity-activated equilibrium $E_2$ is locally and globally asymptotically stable; if ${{\mathcal R}_{2}} > 1$ and ${{\mathcal R}_{4}} < 1$ , the humoral immunity-activated equilibrium $E_3$ is locally and globally asymptotically stable; if ${{\mathcal R}_{3}} > 1$ and ${{\mathcal R}_{4}} > 1$ , the immunity-activated equilibrium $E^*$ is locally and globally asymptotically stable.

Numerical simulations vividly illustrate our main results of stability analysis for system (1.2). Besides, we have investigated the effects of cell-to-cell transmission, viral production rate, death rate of infected cells and viral remove rate on viral dynamics. It is worth mentioning that as the infection rate of cell-to-cell transmission ${\beta}_2$ increases, virus load rises quickly and largely, which implies that cell-to-cell transmission facilitates virus spread. Furthermore, we perform a sensitivity analysis of reproduction ratios, which implies some useful consequences on the prevention and treatment of HIV-1.

It is easy to see that immunity-inactivated reproduction ratios ${{\mathcal R}_{0}}$ is the sum of the reproduction ratio determined by virus-to-cell infection, ${{\mathcal R}_{01}}$ , and that determined by cell-to-cell transmission, ${{\mathcal R}_{02}}$ . In other words, immunity-inactivated reproduction ratio ${{\mathcal R}_{0}}$ becomes larger when the model includes cell-to-cell transmission. Meanwhile, we find that our research includes some existing work. When $\beta_2 = 0$ and $\alpha = 0$ , our virus model is similar to the model in ^[33] and the immunity-inactivated reproduction ratio ${{\mathcal R}_{0}}$ reduces to ${{\mathcal R}_{01}}$ . Based on the model in ^[33], Wang et al. ^[27] consider nonlinear incidence and continuous intracellular delay, which is similar to our model with $\beta_2 = 0$ only. Besides, when we only consider one of the immune responses, our model reduces to the models in ^[14] and ^[26].

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Nos.11871316, 11801340, 11371368, 11331009), Shanxi Scientific Data Sharing Platform for Animal Diseases (201605D121014), and the Science and Technology Innovation Team of Shanxi Province (201605D131044-06).

Conflict of interest

The authors declare there is no conflict of interest.

References

[1]	Aldossary A, While A, Barriball L (2008) Health care and nursing in Saudi Arabia. Int Nursing Rev 55: 125-128. doi: 10.1111/j.1466-7657.2007.00596.x
[2]	Tumulty G (2001) Professional development of nursing in Saudi Arabia. J Nursing Scholarship 33: 285-290.
[3]	Miller-Rosser K, Chapman Y, Francis K (2006) Historical, cultural, and contemporary influences on the status of women in nursing in Saudi Arabia. Online J Issues Nursing 11.
[4]	Chambers D, Thiek?tter A, Chambers L (2013) Preparing student nurses for contemporary practice: The case for discovery learning. J Nursing Edu Prac 3: p106.
[5]	Hiemstra R (2004) Self-directed learning lexicon. Int J Self-Directed Learning 1: 1-6.
[6]	Knowles MS (1970) The modern practice of adult education: New York Association Press New York.
[7]	Guglielmino LM (2008) Why self-directed learning. International J Self-directed Learning 5: 1-14.
[8]	O'Shea E (2003) Self‐directed learning in nurse education: a review of the literature. J Advanced Nursing 43: 62-70. doi: 10.1046/j.1365-2648.2003.02673.x
[9]	Kuiper RA, Pesut DJ (2004) Promoting cognitive and metacognitive reflective reasoning skills in nursing practice: self‐regulated learning theory. J Advanced Nursing 45: 381-391. doi: 10.1046/j.1365-2648.2003.02921.x
[10]	Al‐Qahtani AA, Higgins SE (2013) Effects of traditional, blended and e‐learning on students' achievement in higher education. J Computer Assist Learning 29: 220-234. doi: 10.1111/j.1365-2729.2012.00490.x
[11]	Nolan J, Nolan M (1997) Self-directed and student-centred learning in nurse education. British J Nursing 6: 103-107.
[12]	Dauna Crooks DNS R, Ellis PJ, Cottie Ofosu EdD R, et al. (2001) Self-directed learning: Faculty and student perceptions. J Nursing Edu 40: 116.
[13]	Ramnarayan K, Hande S (2005) Thoughts on self-directed learning in medical schools: Making students more responsible. New Horizons 11.
[14]	Díaz JL, Leal C, García JA, et al. (2016) Self-Learning Methodology in Simulated Environments [MAES?]: Elements and Characteristics. Clin Simulation Nursing 12: 268-274. doi: 10.1016/j.ecns.2016.02.011
[15]	El-Gilany A-H, Abusaad FES (2013) Self-directed learning readiness and learning styles among Saudi undergraduate nursing students. Nurse Edu Today 33: 1040-1044. doi: 10.1016/j.nedt.2012.05.003
[16]	Soliman M, Al-Shaikh G (2015) Readiness for self-directed learning among First Year Saudi Medical students: A descriptive study. Pakistan J Med Sci 31: 799.
[17]	Said AB, Ghani N, Khan A, et al. (2015) Examination of Self-Directed Learning Readiness among Baccalaureate Nursing Students in Peshawar Pakistan. Int J Innovative Res Develop 4.
[18]	Gagnon M-P, Gagnon J, Desmartis M, et al. (2013) The impact of blended teaching on knowledge, satisfaction, and self-directed learning in nursing undergraduates: a randomized, controlled trial. Nursing Edu Perspectives 34: 377-382. doi: 10.5480/10-459
[19]	Phillips BN, Turnbull BJ, He FX (2015) Assessing readiness for self-directed learning within a non-traditional nursing cohort. Nurse Edu Today 35: e1-e7.
[20]	Kocaman G, Dicle A, Ugur A (2009) A longitudinal analysis of the self-directed learning readiness level of nursing students enrolled in a problem-based curriculum. J Nursing Edu 48: 286-290.
[21]	Guglielmino LM (1978) Development of the self-directed learning readiness scale: ProQuest Information & Learning.
[22]	Shahin ES, Tork HM (2013) Critical thinking and self-directed learning as an outcome of problem-based learning among nursing students in Egypt and Kingdom of Saudi Arabia. J Nursing Edu Practice 3: p103.
[23]	Alzahrani I (2013) The impact of using wiki technology in learning biology among Al-Baha University students: perceptions, knowledge, e-learning skills and attitudes: University of Southampton.
[24]	Prabjandee D, Inthachot M (2013) Self-Directed Learning Readiness of College Students in Thailand. J Edu Res Innovation 2.
[25]	Bulik RJ (2013) Faculty Reflection on Teaching: Walking The Walk. Int J Self-directed Learning 5.
[26]	Murad MH, Coto‐Yglesias F, Varkey P, et al. (2010) The effectiveness of self‐directed learning in health professions education: a systematic review. Med Edu 44: 1057-1068.
[27]	Ozuah PO, Curtis J, Stein RE (2001) Impact of problem-based learning on residents' self-directed learning. Arch Pediatrics Adolescent Med 155: 669-672.
[28]	Klunklin A, Viseskul N, Sripusanapan A, et al. (2010) Readiness for self‐directed learning among nursing students in Thailand. Nursing Health Sci 12: 177-181. doi: 10.1111/j.1442-2018.2010.00515.x
[29]	LeFlore JL, Anderson M, Michael JL, et al. (2007) Comparison of self-directed learning versus instructor-modeled learning during a simulated clinical experience. Simulation Healthcare 2: 170-177. doi: 10.1097/SIH.0b013e31812dfb46

This article has been cited by:

1.	Yan Wang, Minmin Lu, Daqing Jiang, Viral dynamics of a latent HIV infection model with Beddington-DeAngelis incidence function, B-cell immune response and multiple delays, 2021, 18, 1551-0018, 274, 10.3934/mbe.2021014
2.	Ahmed Elaiw, Noura AlShamrani, Stability of a general adaptive immunity virus dynamics model with multistages of infected cells and two routes of infection, 2020, 43, 0170-4214, 1145, 10.1002/mma.5923
3.	N.H. AlShamrani, Stability of a general adaptive immunity HIV infection model with silent infected cell-to-cell spread, 2021, 09600779, 110422, 10.1016/j.chaos.2020.110422
4.	A. M. Elaiw, N. H. AlShamrani, A. D. Hobiny, I. A. Abbas, Global stability of an adaptive immunity HIV dynamics model with silent and active cell-to-cell transmissions, 2020, 10, 2158-3226, 085216, 10.1063/5.0017214
5.	Ahmed M. Elaiw, Matuka A. Alshaikh, Global stability of discrete pathogen infection model with humoral immunity and cell-to-cell transmission, 2020, 130, 09600779, 109458, 10.1016/j.chaos.2019.109458
6.	A. M. Elaiw, N. H. AlShamrani, STABILITY OF A DELAYED ADAPTIVE IMMUNITY HIV INFECTION MODEL WITH SILENT INFECTED CELLS AND CELLULAR INFECTION, 2021, 11, 2156-907X, 964, 10.11948/20200124
7.	Najmeh Akbari, Rasoul Asheghi, Optimal control of an HIV infection model with logistic growth, celluar and homural immune response, cure rate and cell-to-cell spread, 2022, 2022, 1687-2770, 10.1186/s13661-022-01586-1
8.	A. M. Elaiw, N. H. AlShamrani, E. Dahy, A. A. Abdellatif, Aeshah A. Raezah, Effect of Macrophages and Latent Reservoirs on the Dynamics of HTLV-I and HIV-1 Coinfection, 2023, 11, 2227-7390, 592, 10.3390/math11030592
9.	Najmeh Akbari, Rasoul Asheghi, Maryam Nasirian, Stability and Dynamic of HIV-1 Mathematical Model with Logistic Target Cell Growth, Treatment Rate, Cure Rate and Cell-to-cell Spread, 2022, 26, 1027-5487, 10.11650/tjm/211102
10.	Noura H. AlShamrani, Matuka A. Alshaikh, Ahmed M. Elaiw, Khalid Hattaf, Dynamics of HIV-1/HTLV-I Co-Infection Model with Humoral Immunity and Cellular Infection, 2022, 14, 1999-4915, 1719, 10.3390/v14081719
11.	Ahmed M. Elaiw, Abdualaziz K. Aljahdali, Aatef D. Hobiny, Discretization and Analysis of HIV-1 and HTLV-I Coinfection Model with Latent Reservoirs, 2023, 11, 2079-3197, 54, 10.3390/computation11030054
12.	Lili Yuan, Xiao-Dong Gao, Yufei Xia, Optimising the oil phases of aluminium hydrogel-stabilised emulsions for stable, safe and efficient vaccine adjuvant, 2022, 16, 2095-0179, 973, 10.1007/s11705-021-2123-1
13.	A. M. Elaiw, N. H. Alshamrani, E. Dahy, A. A. Abdellatif, Stability of within host HTLV-I/HIV-1 co-infection in the presence of macrophages, 2023, 16, 1793-5245, 10.1142/S1793524522500668
14.	Rui Xu, Chenwei Song, Dynamics of an HIV infection model with virus diffusion and latently infected cell activation, 2022, 67, 14681218, 103618, 10.1016/j.nonrwa.2022.103618
15.	Ahmed M. Elaiw, Abdulaziz K. Aljahdali, Aatef D. Hobiny, Dynamical Properties of Discrete-Time HTLV-I and HIV-1 within-Host Coinfection Model, 2023, 12, 2075-1680, 201, 10.3390/axioms12020201
16.	Noura H. AlShamrani, Reham H. Halawani, Ahmed M. Elaiw, Analysis of general HIV-1 infection models with weakened adaptive immunity and three transmission modalities, 2024, 106, 11100168, 101, 10.1016/j.aej.2024.06.033
17.	Chong Chen, Yinggao Zhou, Dynamic analysis of HIV model with a general incidence, CTLs immune response and intracellular delays, 2023, 212, 03784754, 159, 10.1016/j.matcom.2023.04.029
18.	Shan Hu, Ruiqi Liu, Sheng Hu, Jianfeng Ye, Sheng Chen, Xiaozhou Ye, Yun Wang, Preparation of OVA‐loaded γ‐PGA/CS nanocomposite delivery vector and its immune response, 2024, 141, 0021-8995, 10.1002/app.54949
19.	Ke Guo, Donghong Zhao, Zhaosheng Feng, Lyapunov functionals for a virus dynamic model with general monotonic incidence, two time delays, CTL and antibody immune responses, 2024, 158, 08939659, 109212, 10.1016/j.aml.2024.109212
20.	Ahmed M. Elaiw, Aeshah A. Raezah, Matuka A. Alshaikh, Global Dynamics of Viral Infection with Two Distinct Populations of Antibodies, 2023, 11, 2227-7390, 3138, 10.3390/math11143138
21.	Noura H. AlShamrani, Reham H. Halawani, Ahmed M. Elaiw, Effect of Impaired B-Cell and CTL Functions on HIV-1 Dynamics, 2023, 11, 2227-7390, 4385, 10.3390/math11204385
22.	A. M. Elaiw, E. A. Almohaimeed, A. D. Hobiny, Modeling the co-infection of HTLV-2 and HIV-1 in vivo, 2024, 32, 2688-1594, 6032, 10.3934/era.2024280
23.	Alberto Vegas Rodriguez, Nieves Velez de Mendizábal, Sandhya Girish, Iñaki F. Trocóniz, Justin S. Feigelman, Modeling the Interplay Between Viral and Immune Dynamics in HIV: A Review and Mrgsolve Implementation and Exploration, 2025, 18, 1752-8054, 10.1111/cts.70160
24.	A. M. Elaiw, E. A. Almohaimeed, Within-host dynamics of HTLV-2 and HIV-1 co-infection with delay, 2025, 19, 1751-3758, 10.1080/17513758.2025.2506536

Reader Comments

Your name:*

Email:*
© 2016 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Medical Science

0.4

Metrics

Article views(5506) PDF downloads(1168) Cited by(8)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(1) / Tables(2)

AIMS Medical Science

Effect of Self-Directed Learning on Knowledge Acquisition of Undergraduate Nursing Students in Albaha University, Saudi Arabia

Related Papers:

Abstract

1. Introduction

2. Reproduction ratios and feasible equilibria

3. Local asymptotic stability

4. Global asymptotic stability

5. Numerical simulations

5.1. Effect of cell-to-cell transmission

5.2. Effect of viral production rate

5.3. Effect of death rate of infected cells and viral remove rate

5.4. Sensitivity analysis

6. Conclusion

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Medical Science

Effect of Self-Directed Learning on Knowledge Acquisition of Undergraduate Nursing Students in Albaha University, Saudi Arabia

Related Papers:

Abstract

1. Introduction

2. Reproduction ratios and feasible equilibria

3. Local asymptotic stability

4. Global asymptotic stability

5. Numerical simulations

5.1. Effect of cell-to-cell transmission

5.2. Effect of viral production rate

5.3. Effect of death rate of infected cells and viral remove rate

5.4. Sensitivity analysis

6. Conclusion

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog