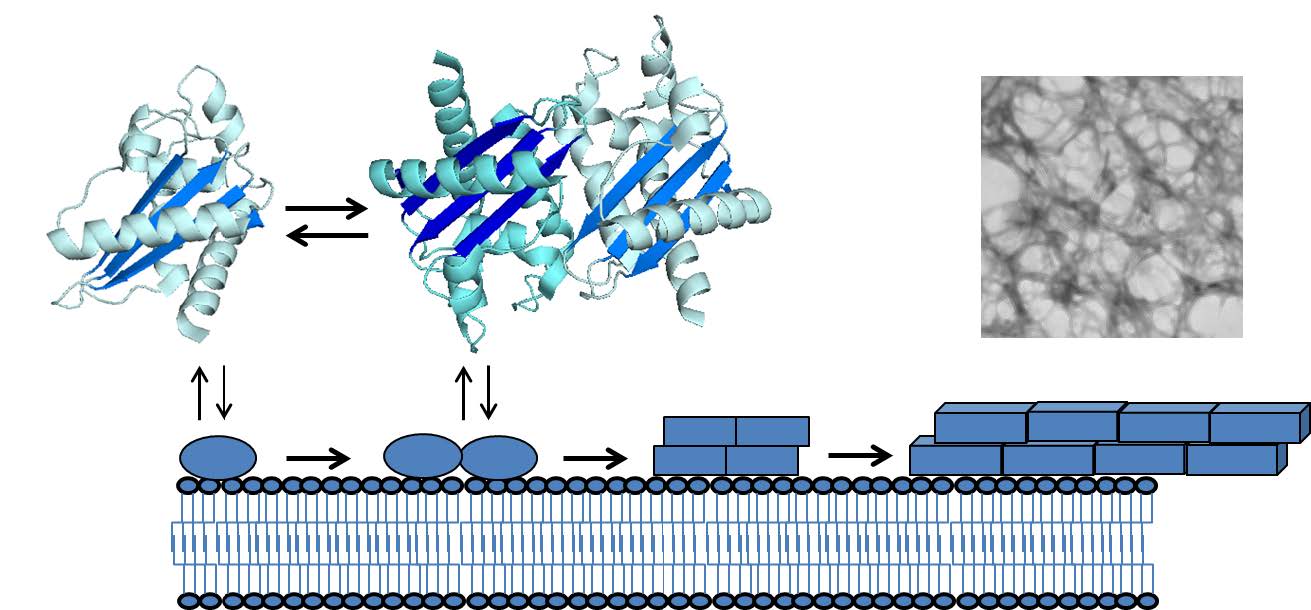
Members of the Cysteine-rich secretory proteins, Antigen 5, and Pathogenesis-related 1 proteins (CAP) superfamily are found in a remarkable variety of biological species. The presence of a highly conserved CAP domain defines the CAP family members, which in many cases is linked to other functional protein domains. As a result, this superfamily of proteins is involved in a large variety of biological processes such as reproduction, tumor suppression, and immune regulation. The role of the CAP domain and its conserved structure throughout evolution in relation to the diverse functions of CAP proteins is, however, poorly understood. Recent studies on the mammalian Golgi-Associated plant Pathogenesis Related protein 1 (GAPR-1), which consists almost exclusively of a CAP domain, may shed new light on the function of the CAP domain. GAPR-1 was shown to form amyloid fibrils but also to possess anti-amyloidogenic properties against other amyloid forming peptides. Amyloid prediction analysis reveals the presence of potentially amyloidogenic sequences within the highly conserved sequence motifs of the CAP domain. This review will address the structural properties of GAPR-1 in combination with existing knowledge on CAP protein structure-function relationships. We propose that the CAP domain is a structural domain, which can regulate protein-protein interactions of CAP family members using its amyloidogenic properties.
1.
Introduction
With rapid development of the Internet, information technology, and digital communications, the status of multimedia data transmission is increasing in modern society. Image is an important information carrier in human life to display or describe directly the objective phenomena. In recent years, owing to leakages of digital image information, serious consequences have occurred. Thus, image encryption protection has become particularly important. Traditional encryption algorithms store and encrypt data as a one-dimensional string. As to images, due to the large amount of data, the calculation of encryption schemes is complicated, and the high correlation between the adjacent pixels requires a sufficient long keystream for a high security level. Therefore, a new encryption algorithm needs to be proposed for the secure communication of images.
A chaotic system refers to a deterministic system with seemingly random irregular movements, and its behavior is uncertain, unrepeatable, and unpredictable. Chaotic system is sensitive to initial conditions, and exhibits pseudorandom, ergodicity, and aperiodicity [1]. The combination of an image encryption algorithm and a chaotic system can effectively improve security and anti-cracking ability. Therefore, chaotic systems have been widely used in image encryption algorithms since they were proposed. For example, in [2], an algorithm with one-time-keys was proposed to resist brute-force attack. Albahrani et al. [3] designed a block method based image encryption with a cross map as a kind of chaotic map. To improve the robustness against common attacks, Yu et al. [4] proposed a new image encryption algorithm based on a short-time fractional Fourier transform (FrFT) and a hyperchaotic system. The diffusion operation and feedback system were designed to improve the anti-interference ability. Moreover, the use of the hyperchaotic system increases the key space and enhances sensitivity to all keys. In [5], a color image encryption algorithm was proposed by using a hyperchaotic system, of which can compress and encrypt an image according to the requirements of the reconstructed image quality. To hide efficiently the pixel distribution for the plain image, DNA based method was employed in [6] with the help of DNA random encoding rules. A generalized chaotic map and operation of fractional-order edge dection were applied into image encryption algorithm [7]. Besides of time domain encryption, Borujeni and Eshghi [8] suggested a hybrid domain based image encryption scheme including both frequency and time domains. Hybrid chaotic systems [9,10] were also be designed and applied for color image encryption Liu et al. [11] designed a new pathological image encryption scheme to ensure the secure transmission of pathological images in a telemedicine system. To effectively resist the plaintext attacks, Feng et al. [12] combined the discrete logarithm with a memristor-based chaotic system and proposed an image reconstruction encryption algorithm. The finite multiplication group used in this study has up to 128 generators, which can expand the key space and enhance the ability of the image encryption algorithm in resisting plaintext attacks. To compress multiple images into a small amount of data for the convenience of image transmission, Huang et al. [13] presented a nonlinear optical image encryption scheme that can encrypt images in both spatial and frequency domains, in which phase truncation and bitwise exclusive-OR (XOR) operation improve the robustness of the multi-image encryption scheme. In [14], a simple and efficient image encryption scheme was designed based on multiple piece-wise linear chaotic map systems. Rotational permutation operations and block diffusion operations were implemented to reach good encryption effect. Wang and Gao [15] studied the application of matrix semi-tensor product theory in a new chaotic image encryption with a Boolean network, scrambling, and diffusion. A new method of global pixel diffusion [16] by chaotic sequences was proposed for image encryption with a high security. In [17], a three-dimensional bit-level based image encryption algorithm was presented. Both the Rubik's cube method and the bit-level encryption principle were taken to realize scrambling operation. Some other image encryption algorithms [18,19,20] also show good performance by different hyeer-chaotic system, coupled map, and 2D chaotic map.
Arnold transformation is a common image pixel scrambling algorithm used to reduce the high correlation between pixels. Based on Arnold transformation and singular value decomposition (SVD) in the fractional Hartley domain, a new phase image encryption scheme was proposed in [21]. Liu et al. [22] suggested a color image encryption algorithm using Arnold transformation and color mixing operation in the discrete cosine transform (DCT) domain. Arnold transformation was used to scramble the pixels of the three channels in color image, and the DCT was used to change the pixel values in the entire spatial distribution. Sui and Gao [23] proposed a color image encryption scheme using Gyrator transform and Arnold transformation, which has two security levels to protect image content. In the encryption and decryption processes, the rotation angle of the gyrator, number of iterations in Arnold transformation, parameters of the chaotic mapping, and generated accompanying phase function were all treated as the secret keys, thereby improving the security of the system. In [24], an optical color image encryption technique based on Arnold transformation and interferometry was proposed. Color image was decomposed into three channels R, G, B, and then each channel was encrypted into two random phase masks using Arnold transformation and interference method. Chen [25] used Arnold transformation to perturb the matrix pixels by encoding a single parameter, to form an image similar to color noise and to reduce the key space for storage and transmission applications. Wang et al. [26] suggested a fast algorithm for image encryption by parallel computing, in which parallelism of diffusion is designed to implement fast operation.
According to the classification of cryptosystems, cryptography can be divided into symmetric cryptography [27,28,29,30] and asymmetric (public key) cryptography [31,32,33,34,35,36]. In an asymmetric encryption algorithm, different keys are used for encrypting and decrypting, thereby realizing the nonlinearity of the algorithm, higher security, and convenient implementation of digital signature and verification. In [33], a scalable method of asymmetric image compression and encryption was proposed based on a discrete wavelet transform (DWT) and nonlinear operations in the cylindrical diffraction domain. DWT reduces the amount of data and is more conducive to data transmission. To enhance an encryption scheme with a larger key space than traditional cryptographic systems in the FT and FrFT fields, Ren et al. [37] designed an asymmetric image encryption scheme using a phase-truncated discrete multi-parameter FrFT. After a pixel scrambling and a random-phase mask, the asymmetric ciphertext with stable white noise was obtained through phase truncation.
In order to reduce the redundancy of image transmission, compression was also considered in image encryption. For example, Chai et al. [38] proposed a visually meaningful cipher image encryption by using technology of compressive sensing. Chaotic system, kronecker product, and singular value decomposition were all combined to produce the measurement matrix. In [39], a new chaotic color image encryption scheme was presented by multi-embedding strategy and compressive sensing. Each channel of R, G, and B were compressed to obtain measurements. Although there are many new image encryption algorithms have been published, some of them still have defects, for example, (i) The keystream is generated only dependent on the secret keys; (ⅱ) It is hard to ensure the secure management of keys. In view of this, this paper combines quantum logistic map, Arnold transformation, and diffusion technology together with RSA to design an asymmetric encryption scheme, aiming to carry out high security, strong anti-attack and more suitable for network transmission. The innovations of this paper are: 1) Extract the text information of the plain image to be plain message. 2) Generate the cipher message by RSA and produce the initial conditions for quantum system by a new mathematical model. 3) Update the initial conditions by the text information of the plain image to enhance the plaintext dependence. 4) Build an end-to-start cyclic modulo diffusion operation.
The rest of this article is organized as follows. Section 2 briefly introduces the public key RSA algorithm, Arnold transformation, and quantum logistic map. Section 3 gives the image encryption and decryption processes. Section 4 displays some experimental results. Section 5 discusses the various analytical tests of the encryption results. Section 6 presents the conclusions of this study.
2.
Preparatory knowledges
2.1. RSA encryption algorithm
The public key RSA cryptosystem was proposed in 1978 by Rivest, Shamir, and Adleman. RSA encryption algorithm is an asymmetric encryption structure, which can complete the decryption operation without directly passing the keys. This method ensures security and avoids the risk of keys being cracked, which typically happens when keys are transmitted directly. In the whole encryption process, the key and algorithm are independently separated. Therefore, the key can be distributed more effectively. The specific description of the RSA algorithm is as follows:
Step 1: Randomly and secretly choose two large prime numbers $p$ and $q$.
Step 2: Compute $n = p \times q$, $\varphi (n) = (p - 1)(q - 1)$, where $\varphi (n)$ is the Euler function of $n$.
Step 3: Randomly select $e$ in range $1 < e < \varphi (n)$, satisfying $\gcd (e, \varphi (n)) = 1$, where $e$ and $\varphi (n)$ are prime numbers.
Step 4: Calculate the decryption key $d$, where $e \times d = 1\bmod (\varphi (n))$.
Step 5: Open integers $n$ and $e$, and keep $d$ in secret.
Step 6: Encrypt plaintext $m$ to be ciphertext $c$ by $c = {m^e}\bmod n$.
Step 7: Decrypt ciphertext $c$ to be plaintext $m$ by $m = {c^d}\bmod n$.
2.2. Quantum logistic map
Logistic map is a classical mathematical model used to study the behaviors of complex systems, such as dynamic systems, fractals, and chaos. In physics, if a physical quantity has the smallest indivisible basic unit, then this physical quantity is quantized, and the smallest unit is called a quantum. The quantum state is introduced into the chaotic system to form a quantum logistic map. The coupling of the system and harmonic oscillator path will produce a quantum logistic map with quantum correction. Akhshani et al. [40] applied quantum logistic map for image encryption, and its quantum logistic map is defined as,
where $\beta $ and $r$ represent the dissipation parameter and adjustable parameter, respectively, and $x_n^*$, $z_n^*$ are the conjugate complex numbers of ${x_n}$ and ${z_n}$, respectively. When one sets $r = 3.99$ and $\beta \geqslant 6$, the quantum logistic map shows higher chaotic characteristics [40]. So, in this study, $r = 3.99$ and $\beta = 7$ are set with all initial parameters be real numbers. As pointed by [40]: classical nonlinear chaotic systems are famous because of their exponential sensitivity to each initial condition. However, the linearity of quantum mechanics not only shows such sensitivity to each initial condition, and also the Heisenberg uncertainty principle (HUP) prevents us from talking about initial conditions in quantum mechanics. Therefore, for this interesting property, quantum logistic map can also be used in cryptography, for example image encryption. In view of these good characteristics of quantum logistic map, many image encryption algorithms [41,42,43] based on it have been proposed.
2.3. Arnold transformation
Arnold transformation is a scrambling operation that can randomly change the pixel position for an image, which is also called a cat map. By rearranging the pixels in a digital image matrix, the originally meaningful image will become a meaningless image. Arnold transformation is defined as follows:
By replacing the matrix of above Arnold transformation, a generalized Arnold transformation can be obtained, which is defined as
where $a, b$ and $N$ are positive integers, $({x_n}, {y_n})$ are the coordinates of the pixel in the original image, and $({x_{n + 1}}, {y_{n + 1}})$ are the coordinate positions after transformation. Arnold transformation is a reversible mapping, and its corresponding inverse transformation is defined as
Arnold transformation is reversible, and it is easy to be implemented. Therefore, this study combines Arnold transformation with the quantum logistic system and other technologies to design a new image encryption scheme.
3.
The proposed image encryption scheme
3.1. Image encryption process
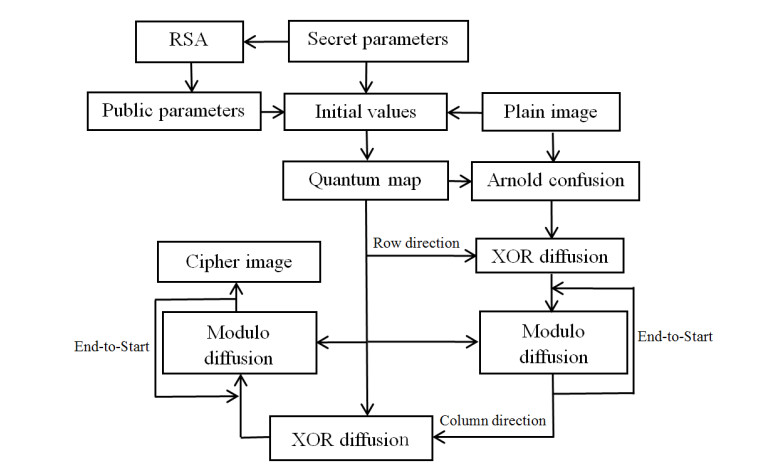
This study integrates the quantum logistic map, the RSA algorithm, the Arnold transformation, and the diffusion operation to realize a new asymmetric image encryption scheme. The framework of the proposed image encryption scheme is shown in Figure 1. The detail encryption steps are as follows:
Step 1: Select large prime numbers $p$ and $q$, and calculate public key $e$ and private key $d$.
Step 2: Read plain image $P$ with size $M \times N$.
Step 3: Extract the text information of the image, i.e., $R = \sum\nolimits_{i = 1}^M {\sum\nolimits_{j = 1}^N {P(i, j)} } $, for public information.
Step 4: Select three plain parameters ${a_i}(i = 1, 2, 3)$ and encrypt them with the public key to obtain the public parameters ${c_i} = a_i^e\bmod n$.
Step 5: Calculate the initial values: ${x_0} = ({c_1} + {a_1})/({k_1}{c_1} + {k_2}{a_1})$, ${y_0} = ({c_2} + {a_2})/({k_1}{c_2} + {k_2}{a_2})$, ${z_0} = ({c_3} + {a_3})/({k_1}{c_3} + {k_2}{a_3})$, where ${k_1} = 3, {k_2} = 5$.
Step 6: Update the initial values: ${x'_0} = \bmod ({x_0} + {R_1}, 1)$, ${y'_0} = \bmod ({y_0} + {R_1}, 1)$, ${z'_0} = \bmod ({z_0} + {R_1}, 1)$, where ${R_1} = (R + 1)/(255 \times M \times N + 1)$.
Step 7: The updated initial values are substituted into quantum logistic map. After discarding the first 500 values of the sequence, the chaotic sequences $x, y, z$ are obtained.
Step 8: Process the sequences as,
Step 9: Perform Arnold scrambling operation on the plain image to obtain the scrambled image . The values of , , and in the Arnold map are calculated as
where $mc = \bmod (sum(Z), R) + 1$.
Step 10: For the image $A$, perform XOR diffusion operation by row for it to obtain image $B$ as,
where $i = 1, 2, \cdots, M$.
Step 11: Perform diffusion under modulo operation by row again to obtain image $C$ as,
where $i = 1, 2, \cdots , M$. ${C_0}$ is a constant.
Step 12: Connect the last row of image $C$ with the first row of $C$ and perform diffusion under modulo operation for rows again to obtain image $D$ as,
where $i = 2, 3, \cdots, M$.
Step 13: The column direction is similar to the row direction. For image $D$, take the column as a unit and perform the XOR diffusion operation on the corresponding component of each column and $Y$ to obtain image $E$ as,
where $j = 1, 2, \cdots, N$.
Step 14: Perform modulo diffusion to each column to obtain image $F$ as,
where $j = 1, 2, \cdots , N$. ${F_0}$ is a constant.
Step 15: Connect the last column of the image $F$ with the first column of $F$ and perform modulo diffusion in the column direction again to obtain the cipher image $G$ as,
where $j = 2, 3, \cdots, N$.
3.2. Image decryption process
The receiver has a cipher image $G$, public parameters ${c_1}, {c_2}, {c_3}, r, \beta $, and $R$, and private key $(d, n)$. Figure 2 is the decryption flowchart of the proposed algorithm. The specific steps of decryption are as follows:
Step 1: Use the private key $(d, n)$ to decrypt the public parameters ${a_i} = c_i^d\bmod n$.
Step 2: Read the cipher image $G$ with size $M \times N$.
Step 3: Calculate the initial value ${x_0} = ({c_1} + {a_1})/(3{c_1} + 5{a_1})$, ${y_0} = ({c_2} + {a_2})/(3{c_2} + 5{a_2})$, ${z_0} = ({c_3} + {a_3})/(3{c_3} + 5{a_3})$.
Step 4: Update the initial values ${x_0}^\prime = \bmod ({x_0} + {R_1}, 1)$, ${y_0}^\prime = \bmod ({y_0} + {R_1}, 1)$, ${z_0}^\prime = \bmod ({z_0} + {R_1}, 1)$, where ${R_1} = (R + 1)/(255 \times M \times N + 1)$.
Step 5: By iterating quantum logistic map, and discarding the first 500 values of the sequence, obtain the chaotic sequence $x', y', z'$.
Step 6: Use Eq (5) to process the sequence and get $X', Y', Z'$.
Step 7: Calculate the two control parameters $ma'$ and $mb'$ of the Arnold map using Eqs (6) and (7).
Step 8: Use images $G$ and $Z'$ to perform the inverse modulo operation of the corresponding columns to derive image $F'$ as,
where $j = 2, 3, \cdots, N$.
Step 9: Use image $F'$ to perform the inverse modulo operation of the corresponding columns to derive image $E'$ as,
where $j = 1, 2, \cdots , N$. ${F'_0}$ is a constant.
Step 10: Use images $E'$ and $Y'$ to perform the XOR diffusion operation of the corresponding column to derive image $D'$ as,
where $j = 1, 2, \cdots, N$
Step 11: The row direction is similar to the column direction. Use $Z'$ to perform the inverse modulo diffusion operation in the row direction, and then use $X'$ to perform the XOR diffusion of the corresponding rows to derive image $A'$.
Step 12: According to the parameter values $ma'$ and $mb'$, use Eq (4) to perform the inverse operation of the Arnold map and obtain the plain image $P'$.
4.
Experimental tests
Grayscale and color images (some from the USC-SIPI database) are taken for testing. Windows 10 operating system is used with an AMD Ryzen 7 1700 8-core processor and 8 GB memory, and the simulations are performed on MATLAB R2017b. Table 1 shows the values of each parameter in our test. Among them, ${a_1}, {a_2}, {a_3}, q, p$ and $d$ are the private keys, as well as $e, r, \beta , {c_1}, {c_2}$ and ${c_3}$ are the public keys. Figures 3 and 4 present the test images and their corresponding cipher images, respectively. So, no useful information about the plain image can be seen from these cipher images. Figure 5 shows the corresponding correct decrypted images. So, the proposed cryptographic scheme can be applied to both grayscale and color images. Table 2 shows the time required to encrypt images of different sizes. As we see that our scheme can be implemented by a fast way.
5.
Security analysis
5.1. Histogram analysis
Histogram analysis [44,45] shows how pixels are distributed in an image by plotting the number of observations for each brightness level. The frequency distribution of pixel values implies the statistical correlation between the plain images and the cipher images. A good image encryption system should have the ability to hide correlations; that is, the frequency distribution of the cipher on the pixel value is uniform, and the attacker cannot infer the plain information from it. To verify the uniformity of the pixel distribution of the proposed encryption algorithm, Figure 6 (a)–(c) and (d)–(f) show the histograms of the grayscale and encrypted images, respectively. Figure 7 is the histogram of the Baboon color image with three channels. To further evaluate the uniformity of the histogram, the statistical chi-square test was also performed, which is defined as,
where $L$ is the intensity level, ${o_L}$ and ${e_L}$ are the observation reference and expected reference of the $L$ gray level in the cipher image, respectively. The results of evaluating the uniformity of cipher images based on the chi-square values are shown in Table 3. Table 4 shows the chi-square comparison results. The smaller the chi-square value, the more uniform the pixel distribution and the higher the security. The histogram of the cipher image is evenly distributed, and the chi-square value is much smaller than the value of the plain image, which effectively improves resistivity against statistical attacks.
5.2. Correlation coefficient
Another measurement of statistical analyses is correlation [47,48,49,50]. For a natural digital image, there is a strong correlation between adjacent pixels in the horizontal, vertical, and diagonal directions. The lower correlation of adjacent pixels in a cipher image, the better performance of an encryption algorithm. A good cryptographic scheme should eliminate this correlation in a quantitative way to ensure security. The correlation coefficient is defined as
where ${R_{x'y'}}$ represents the correlation coefficient, $x'$ and $y'$ are the gray values of two adjacent pixels, and $N$ is the total logarithm. Figure 8 shows the correlation of three directions of the grayscale image sailboat. Tables 5 and 6 show the correlation coefficient values of the test images. Table 7 shows the correlation coefficient comparisons of Baboon. The data in the tables show that the correlation coefficient of the plain images is close to 1, which means that the correlation coefficient between adjacent pixels is very strong. By using the proposed scheme, the values become close to 0, which means that our scheme can eliminate the strong correlation.
5.3. Information encryption
In information theory, entropy is an important index to measure the degree of randomness of a message. Ideally, each pixel of an 8-bit cipher image has a theory entropy value of 8. The higher the information entropy value, the more uniform of gray value distribution and the more random of an image. The calculation formula of information entropy is,
where $p({x_i})$ is the probability of the occurrence of ${x_i}$, and $N$ is the total number of ${x_i}$. Tables 8 and 9 show the information entropy tests for different images. These results tell us that the information entropy values of the cipher image are very close to 8, indicating that the encryption scheme has strong randomness.
5.4. Local information encryption
Usually, an image has high data redundancy; therefore, its pixels have a high correlation with neighboring pixels. For a secure cipher image, the pixel values should be evenly distributed to achieve high randomness and high security. Local information entropy is another qualitative criterion for evaluating the randomness of an image, which is defined as,
where ${S_i}$ represents the optional $k$ groups of pixels in the image, and $TB$ represents the number of pixels in ${S_i}$. The local information entropy values of the grayscale and color images are tested and shown in Tables 10 and 11, respectively. Based on these results, it can be seen that the local information entropy of the cipher image has surpassed 7.95, indicating that the distribution of pixel values inside the image is very uniform and random.
5.5. Differential attack analysis
The ideal property of a good encryption method should be sensitive to any small change in the plain image. That is, when the plain image has a small change in any pixel, the difference of the cipher image is analyzed to evaluate the diffusion performance of the encryption algorithm and should have the ability to resist differential attacks. The number of pixel change rate (NPCR) and unified average changing intensity (UACI) are two standards used for testing. The formulas are,
where ${C_1}$ is one cipher image, ${C_2}$ is another cipher image with one pixel in the same plain image changes. The theory values for NPCR and UACI are 99.6093 and 33.4635% respectively. Tables 12 and 13 present the average values of NPCR and UACI for grayscale and color images, respectively. Table 14 lists the comparisons by testing image Lena. All these test results show that the proposed asymmetric image encryption scheme has the ability to resist differential attacks.
5.6. Key sensitivity analysis
An extremely high key sensitivity can guarantee the security of an encryption system against the brute force attacks. To evaluate the sensitivity of keys, the $512 \times 512$ image Sailboat is used as an example for testing. Figure 9 shows the key sensitivity analysis results. Moreover, Figure 9(d) shows that even if a small key change occurs, the cipher image experiences a big difference. These test results show that only the correct key can decrypt the image, and the image encryption algorithm is highly sensitive to the keys and has the ability to resist brute force attacks.
5.7. Comparisons
The asymmetric image encryption algorithm proposed in this paper is suitable for grayscale and color images. Taking color image as an example, Table 15 shows the information entropy comparisons with other image encryption algorithms. The values in the table express that the information entropy result of the proposed scheme in this paper is closer to 8, indicating that the gray value distribution in the proposed asymmetric encryption scheme is more uniform and random than that of other algorithms.
5.8. Conclusion and perspectives
This study employed a chaotic quantum logistic map, combining with both scrambling and diffusion operations, to propose a new asymmetric image encryption algorithm. First, the Arnold map was used to scramble the pixel positions of the plain images to achieve information hiding in the first layer. In the diffusion stage, different from the conventional point-to-point diffusion method, our solution took each row and each column as different units to perform diffusion operation. As to the row direction, the data in each row are first XOR-diffused. Then, each row in the image and the corresponding row in the keystream matrix are modulated and diffused; that is, two cyclic diffusions are realized by connecting the start and end. Operations to the column direction use a similar process to obtain the cipher image. Among them, the initial values of the quantum logistic map are related to the plain image, which can resist the known plaintext attack and chosen plaintext attack. Experimental tests and analyses show that the new asymmetric image encryption scheme proposed in this paper is suitable for both grayscale and color images, can better distribute pixel values be uniform, reduce high correlation, is highly sensitive to keys, and has the ability to resist various attacks.
However, there is still some disadvantages, for example, the compression operation was not considered in our scheme. So, in the future work, image can be compressed to reduce data redundancy, and how to achieve a good balance between the security and the complexity of image reconstruction should be taken into consideration. In addition, fast implement of encryption scheme is also an important issue in the future research.
Acknowledgments
The authors would like to thank the reviewers for their valuable comments and the editor's helpful suggestions. This work was supported in part by the National Natural Science Foundation of China (No.61972103), the Natural Science Foundation of Guangdong Province of China (No.2019A1515011361), and the Key Scientific Research Project of Education Department of Guangdong Province of China (No.2020ZDZX3064).
Conflict of interest
The authors declare that they have no conflict of interest.









 DownLoad:
DownLoad: