1. Introduction
Proteins exist in conformational ensembles around their native states (the conformational selection and population shift model), many of which are functionally relevant [1,2]. The ensemble can present a large number of substates. The population of each substate is not static; it changes dynamically with the conditions. This dynamic landscape is the outcome of environmental fluctuations that physically perturb the protein structure [3,4]. Population shift of dynamic conformational ensembles is the origin of allosteric effect—perturbation from effector binding propagating throughout the structure, leading to active site conformational changes. In hemoglobins (Hbs), these perturbations occur as allosteric perturbations, which can arise from binding of small or large molecules; from temperature, pH, concentration, or ionic strength [4] changes, even of 2, 3 diphosphoglycerate (DPG) [5,6], or mutational events [7]. The HbS differs from the HbA by a point mutation on the surface of the HbS, which results in the replacement of the surface exposed, negatively charged glutamic acid on the HbA by the apolar valine on the HbS, with consequent susceptibility of the HbS to sickling while reportedly been resistant to Plasmodium falciparum attack [8,9] - a typical case of pleiotropy and balanced polymorphism.
Structure is related to function, and a single amino acid substitution can result in population shifts away from the native state well, especially if the mutational event lies along a major pathway—which can break native state interactions and make new interactions [3]. Could this, probably, be the case for the HbS and if true, could it be possible, that the same factor(s) that predispose the HbS to sickling in the homozygous state might also be responsible for resistance to the Plasmodium spp. attack? Recently, it was proposed [10,11,12] that there could be some “shared metabolic factors” between the HbS and the parasite, such that these factors would act as allosteric modulators, which can tune the HbS, when homozygous, to sickle under specified conditions while conferring resistance to malaria. For e.g., some cations that modulate R ↔ T transitions in Hb [13] have also been implicated in parasite survival and HbS polymerization. An example is the Magnesium ion (Mg2+).
Magnesium is the fourth most abundant cation in the body and the second most prevalent intracellular cation [14,15]. This element is of vital importance to both the proper functioning of the host (man) [16,17,18] as well as the parasite (Plasmodium spp) [19]. Additionally, in the parasite, magnesium is important in regulating the abundance of [Ca2+] [20,21], which is of holistic importance in the parasite metabolism [see refs 10 - 12 and references therein].
In the human erythrocyte, the intracellularly located neutral Mg2+ dependent sphingomyelinase is activated in the intraerythrocytic stage of the P. falciparum life cycle only in the presence of Mg2+ [22]. The parasite utilizes the enzyme to breakdown sphingomyelin into ceramide, which is necessary for the tubovesicular membrane (TVM) formation. The TVM extends from the parasitophorous vacuole to the erythrocyte membrane delivering essential extracellular nutrients to the parasite [23]. On the other hand, Mg2+, is involved in over 300 enzymatic reactions [24] including glycolysis, pentose phosphate pathway, membrane sealing or stabilization, transmembrane ion flux, nucleic acid metabolism, acid/alkaline balance, calcium channels’ gating, calcium metabolismand regulation of blood sugar levels in the human erythrocyte [25]. Additionally, Mg2+ is used in the inhibition of the Psickle pathway and the electro-diffusional anion conductance pathway, KCC [26] to prevent dehydration that could trigger HbS polymerization.
Another Hb allosteric modulator, which is a “shared metabolic factor” is the human erythrocyte membrane. Membranes have been implicated in the HbS secondary polymer nucleation [27]. Furthermore, biomolecules important in both the patho-physiology of sickling [28,29,30] and the Plasmodium spp survival [31,32] such as ion channels and pumps are localized on membranes. Since the parasite genes do not encode for the desired number of pumps required to maintain the parasite metabolism, the parasite endocytosis into the cell by membrane invagination so as to reside in an immunologically privileged intracellular parasitophorous vacuolar membrane (PVM) [33]. Thus, ion paths such as the calcium pumps [31,32] and Mg2+ influxing ion channels [34] are incorporated into the PVM: to deliver their contents into the vacuole’s confines. This makes Mg2+ readily available for the parasite’s TVM generation. Besides, the PVM also constitutes the parasite’s digestive or food vacuolar membranes [35,36].
Within the food vacuoles are the hemoglobinases for Hb catalysis. Even though the optimal catalytic pH of the Plasmodium proteases is far below pH 7.2, some of the proteases exhibit catalytic activities at neutral pH [37]. We deem it fit to start our enquiry from this pH since it is the optimal shortly before and even on infection of the parasite. Besides, what is/are the nature of the proteins’ conformation(s) at this pH prior to low pH that favors both sickling and optimal protease activities? We investigate the proteins’ interactions with the 0.50 mM- and 2.30 mM Mg2+, been the ionizable and total erythrocyte [Mg2+] respectively [38]. We also employed the use of the sodium n-dodecyl sulfate (SDS) to model membranes, since the effects of SDS on the protein conformations are very similar to those of unilamellar phospholipid vesicles on protein conformation [39]. This can then allow the study of simple models involving the correlation between structure, function and stability in the presence of biological membranes [40]. Besides, at high concentrations, SDS denature proteins, providing information on the structural energetics of globular proteins such as cooperativity and intrinsic stability; thus providing test data to elucidate the contributions of the various interactions that stabilize protein structures [41,42,43] and possibly how site-directed mutagenesis (or point mutations) can affect this [44]. These prompted the study of the interaction of Mg2+ with the proteins in a membrane and protease modelled environments at pH 7.20.
2. Materials and Methods
The chemicals, apparatus, buffers (and their preparations), and the experimental procedures used in this study are as previously described [10]. However, we shall briefly describe the methods utilized.
2.1. Collection of blood sample and Hemoglobin extraction
In brief, blood (3 ml) was collected via venipuncture from a healthy, non-alcoholic and non-smoker donor of genotype Hemoglobin AS (HbAS) - into a sterile bottle containing two drops of 1% EDTA. The method of William and Tsay [45] was employed to separate the R state HbA and HbS from the heterozygous genotype (HbAS). The blood sample was spun in a cold centrifuge, the serum discarded, and the packed erythrocyte cells were then washed with ten volumes of cold 1 mM Tris buffer-saline, pH 8.5 by entrifuging at 4 oC for 25 minutes at 10000 rpm. The supernatant was then discarded. This procedure was repeated thrice until the buffer above the packed cells became clear. The packed cells were then lysed with an equal volume of cold 1 mM Tris buffer, pH 8.5 and left to stand for 10 minutes at 4 oC. The lysed cells were then spun at 4 oC for 25 minutes at 10000 rpm to recover the crude Hb while the membrane “ghosts” was discarded.
2.2. Purification of Hemoglobins
The crude Hb was then made 5% NaCl (w/v) and allowed to stand for 10 minutes at 4 oC after which it was centrifuged and the precipitates discarded. The recovered supernatant was then dialysed in the cold, for 12 hours with a change at the seventh hour, in 2 L of 1 mM Tris buffer, pH 8.5 with continuous stirring. The dialyzed hemoglobins (a mixture of HbA and HbS) were separated using the DEAE-cellulose ion-exchange chromatography. The DEAE-cellulose gel was packed and equilibrated in a column. The dialyzed Hb (3 ml) was carefully and evenly introduced onto the column head and allowed to adsorb onto the gel. Then, Tris buffer (100 ml) of 1 mM, pH 8.5 was also gradually introduced onto the column to wash off any unbound protein. Using the methods of Riggs [46], a pH gradient from 8.5 to 6.5 was generated by a gradient mixer, using 250 ml of 50 mM Tris buffer, pH 8.5 and 250 ml of 50 mM Tris buffer, pH 6.5. The eluates were collected in 5 ml fractions. The HbS and HbA fractions with high absorbance values at 541 nm were pooled and dialyzed at 4 oC for 12 hours, with two changes, against a 2 L solution of 50 mM Tris buffer, pH 7.2 containing 10−5 M EDTA and 0.5 M NaCl. The protein concentrations were determined by the method of Antonini and Brunori [47] (ε415 nm = 125 mM−1 cm−1 or ε541 nm =13.8 mM−1 cm−1 per heme) and were high enough (i.e. ≥ 100 mM) to avoid the formation of a considerable amount of dimmers, which should always be ≤ 5% [48].
2.3. Electronic absorption spectrophotometry and data processing
Spectroscopic studies were carried out in a UNICO-2LO2 PC UV-visible scanning spectrophotometer on the proteins were carried out for two Mg2+ (0.50- and 2.30 mM) in the presence and absence of two [SDS] (0.60 and 5.0 mM). Baseline spectral scans were carried out with the Tris buffers, in the presence and absence of Mg2+ and or SDS prior, to the introduction of the hemoglobins, to assay for their possible absorbance. This baseline solutions were used, subsequently, as blanks for the scans involving the introduction of the hemoglobins. Spectral readings were recorded after 3 min on addition of the components: Hb to the SDS-buffer and then Mg or Hb to the Mg-buffer mixture. The obtained spectra were smoothened using the smoothing software of the UNICO-2LO2 PC, stored and subsequently processed on a Pentium-based computer using the 2003 edition of the Microsoft Excel package. The results were studied by comparison of the convoluted acquired spectra as well as the calculated second-derivative and difference second-derivative spectra. The second derivative spectra were calculated on a 2013 edition of the Microsoft Excel package. This was carried out by taking the first derivative of the absorbance values with respect to the wavelengths and then repeating this same procedure on the obtained first derivative so as to generate the second derivative. The difference second derivative spectra were obtained by subtracting the value of the second derivatives from each other.
3. Results
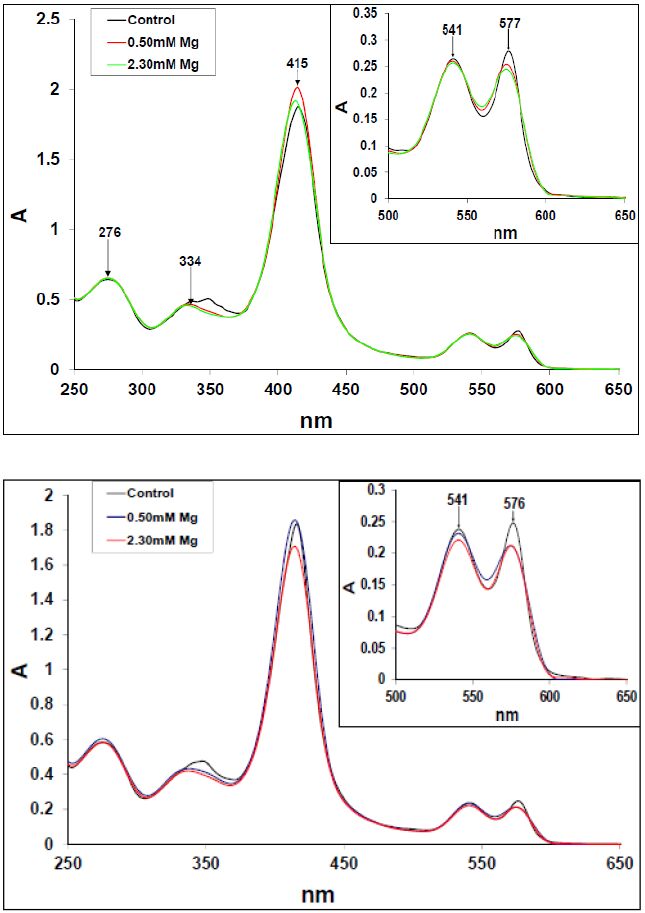
3.1. The interaction of [Mg] with the hemoglobins at pH 7.20
The spectra depicting the interaction of [Mg2+] with the HbA and HbS are shown in Figures 1a and 1b respectively. In Figure 1a, all three spectra had near perfect overlap for the aromatic- (λmax = 276 nm) and d- (λmax = 334 nm) regions. In Figure 1b, both the control spectrum and that of the 2.30 mM Mg-HbS were hypochromic to that of the 0.50 mM Mg-HbS for the aromatic region. The 0.50 mM Mg2+-protein spectrum in each of the Figures was hyperchromic to the other spectra at the Soret peak while the 2.30 mM Mg2+-HbA was blue-shifted to 412 nm. For the Q bands, the [Mg2+] resulted in the hypochromicity of both the α (576 nm) and β (541 nm) bands with the effects been more on the α bands. The more pronounced effect of the 2.30 mM Mg2+ in decreasing the α to β peak values (α/β ) of the proteins’ Q bands, and in particular those of the HbS spectra, suggests a reduced ability to bind or retain bound oxygen by the proteins in the presence of the [Mg2+].
3.2. The Interaction of Low SDS (0.60 mM) and [Mg2+] on the Proteins at pH 7.20
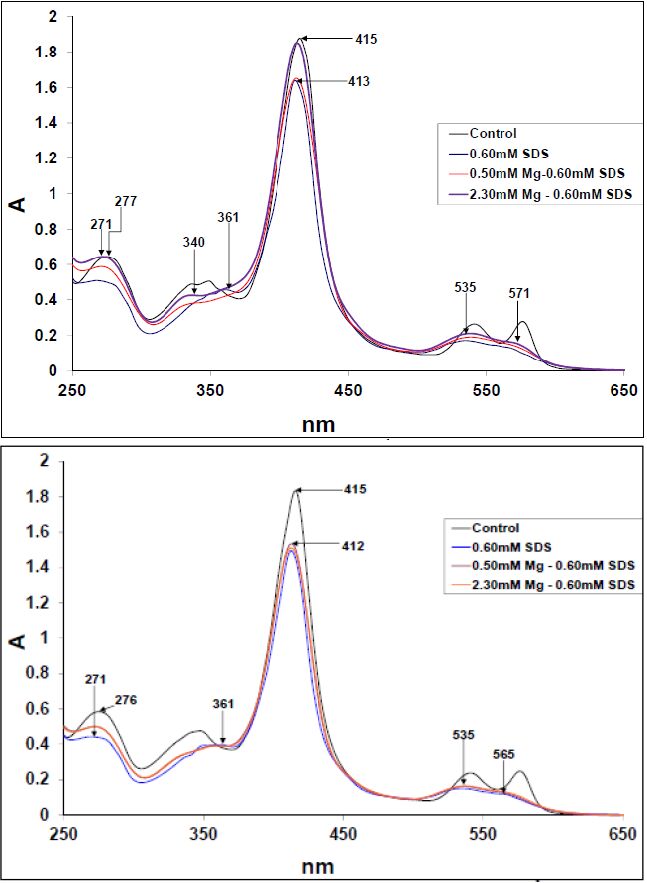
The spectral representation of the interaction of the 0.60 mM SDS with the proteins in the presence and absence of [Mg2+] are shown in Figures 2a and 2b for the HbA and HbS respectively. The 0.60 mM SDS-proteins’ spectra were hypochromic to all other spectra for both proteins. Furthermore, in the presence of SDS, the aromatic regions were slightly flattened, suggesting a loosening of the proteins’ cores. In Figure 2a, the HbA-SDS-2.30 mM Mg2+ spectrum was hyperchromic to that of the HbA-SDS-0.50 mM Mg2+ for both the aromatic and d- regions with the d- regions having a shoulder at ca. 340 nm, while the HbA-0.60 mM SDS spectrum had a peak at 361 nm. In Figure 2b, the HbS-SDS-[Mg2+] spectra overlapped at both their aromatic and d- regions, while been hypochromic and hyperchromic to the control and HbS-SDS spectra respectively. As in Figure 2a, the HbS aromatic region peaks, in the presence of the [Mg2+] and or [SDS] were hypsochromic with respect to the control with λmax = 271 nm. All three HbS related spectra had shoulders at 361 nm. The HbA spectra, in the presence of SDS were blue-shifted to 413 nm (that of the HbS was at 412 nm) for the Soret peaks. While the HbA-SDS-2.30 mM Mg2+ Soret peak was slightly hypochromic to that of the control but pronouncedly hyperchromic to those of the HbA-SDS and HbA-SDS-0.50 mM Mg2+ spectra, all three spectra in Figure 2b had about the same Soret band λmax and were markedly hypochromic to the control spectrum. In the visible regions of both Figure, peaks appeared at 535- and 635 nm with the proteins-SDS spectra been hypochromic to all the other spectra. The HbA-SDS-2.30 mM Mg2+ spectrum was hyperchromic to that of the HbA-SDS-0.50 mM Mg2+ while those of the HbS-SDS-[Mg2+] overlapped well.
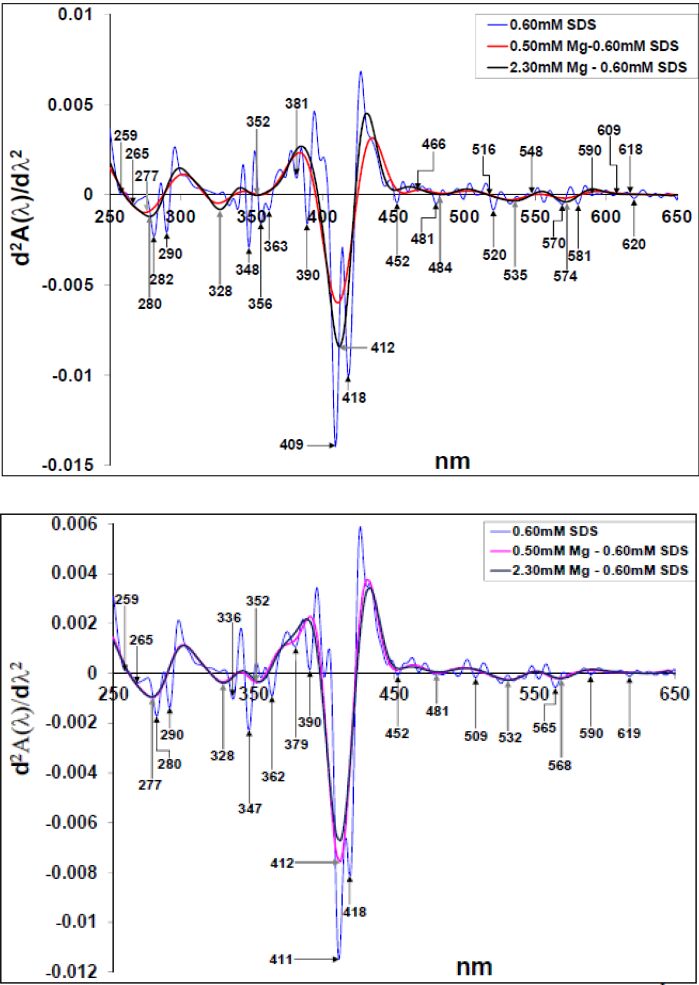
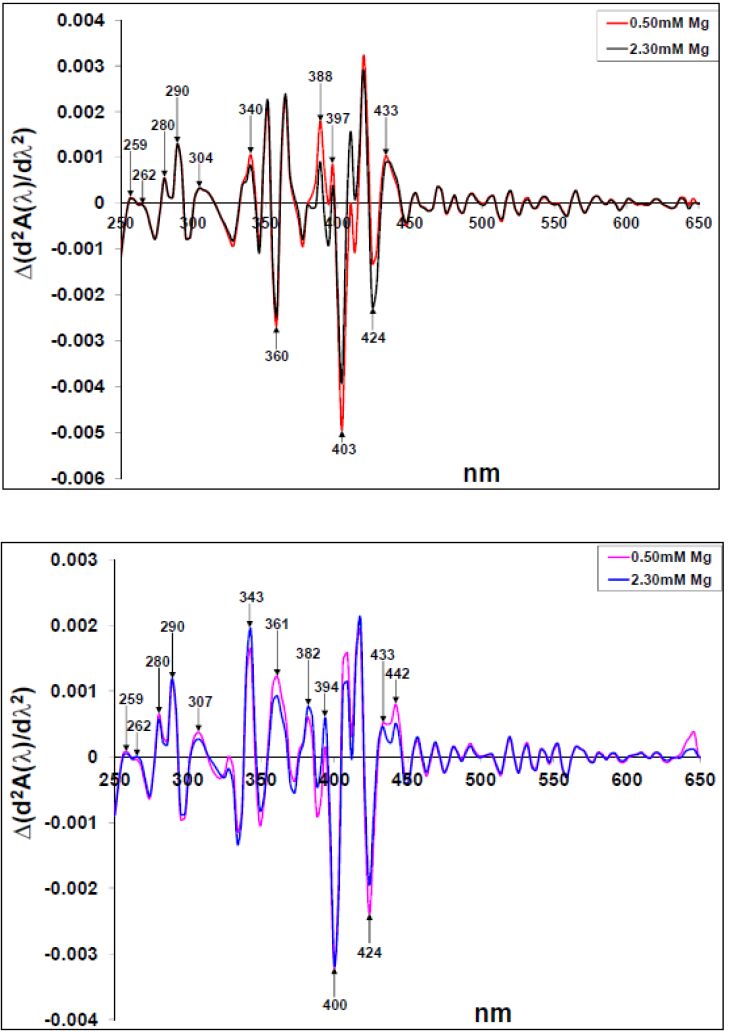
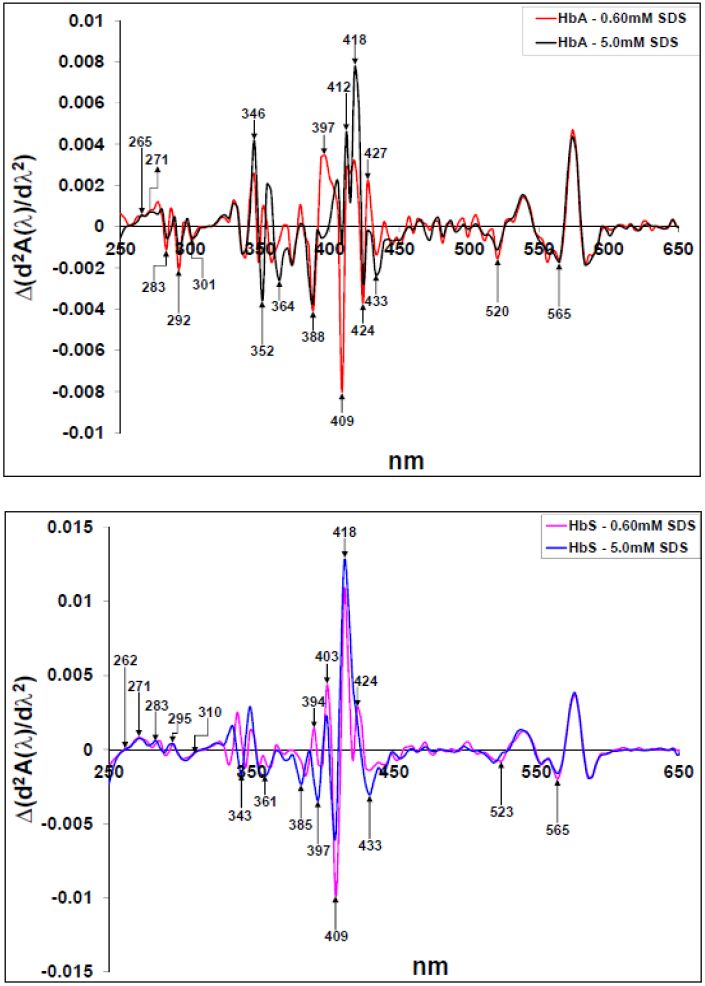
The second derivative spectra of Figures 2a and b are shown in Figures 3a (i) and 3b (i) respectively. The proteins-0.60 mM SDS spectra had λmin at 259-, 265-, 282- (280 nm for the HbS-SDS spectrum), and 290 nm (aromatic region). Their d regions had numerous peaks with prominent ones at 348-, 356- and 363 nm for Figure 3a(i) and 336-, 348- and 361 nm for Figure 3b(i). At the Soret region, the HbA-SDS spectrum had two minima at 381- and 390 nm, while that of the HbS-SDS occurred at 379- and 390 nm. The 409 nm peak of Figure 3ai (HbA spectra) is more pronounced to that of the 411 nm peak of the HbS (Figure 3bi). Besides, the SDS-HbA spectrum had more pronounced λmin at 418 nm in comparison to that of the HbS. In the visible region, the Hb-SDS spectra had noticeable peaks, conspicuously different from several “wiggles” that appeared in this region. While the HbA-SDS had pronounced λmin at 452-, 481-, 520-, 570- and 581 nm, that of the HbS-SDS spectrum had a pronounced λmin at 509- and 565 nm. The HbA spectra had isobestic points at 466-, 516-, 609- and 618 nm suggesting the transient formation of another absorbing species. Thus, it could be deduced that there were more protein products from the HbA-0.60mM SDS interaction in comparison to that of the HbS-0.60 mM SDS interaction. The second derivative of the [Mg2+]-SDS-protein spectral interactions (Figures 3ai and 3bi) have peaks at (for ease, the arrows for the [Mg2+]-SDS interaction are gray colored and bold) 277 nm (280 nm for the 2.30 mM Mg2+-SDS-HbA), 328 nm, 352 nm, 412 nm, ≈ 481 nm, ≈ 535 nm and ≈ 565 nm. A λmin at 379 nm occurred for the 0.50 mM Mg2+-[SDS]-HbS spectrum, which did not appear in that of the HbA. The 2.30 mM Mg2+-SDS had slightly more pronounced peaks in the HbA spectra while the 0.50 mM Mg2+-SDS had a more pronounced Soret peak for the HbS spectra. Thus, while the 2.30 mM Mg2+ played a more prominent role in the HbA spectra, both [Mg2+] played about the same role in the HbS spectra suggesting that the interaction of the Mg2+ with the HbS was concentration independent while that with the HbA was sensitive to concentration.
The intrinsic [Mg2+] contributions to the proteins in a 0.60 mM SDS milieu is shown in the difference second derivative spectra of Figures 3a (ii) and 3b (ii) for the HbA and HbS respectively. The HbA spectra (Figure 3a (ii)) had about the same minima and maxima values as in the HbS spectra. However, the HbA spectra had more peaks to the HbS especially at the Soret region.
3.3. The Interaction of High SDS (5.0 mM) and [Mg2+] on the Proteins at pH 7.20
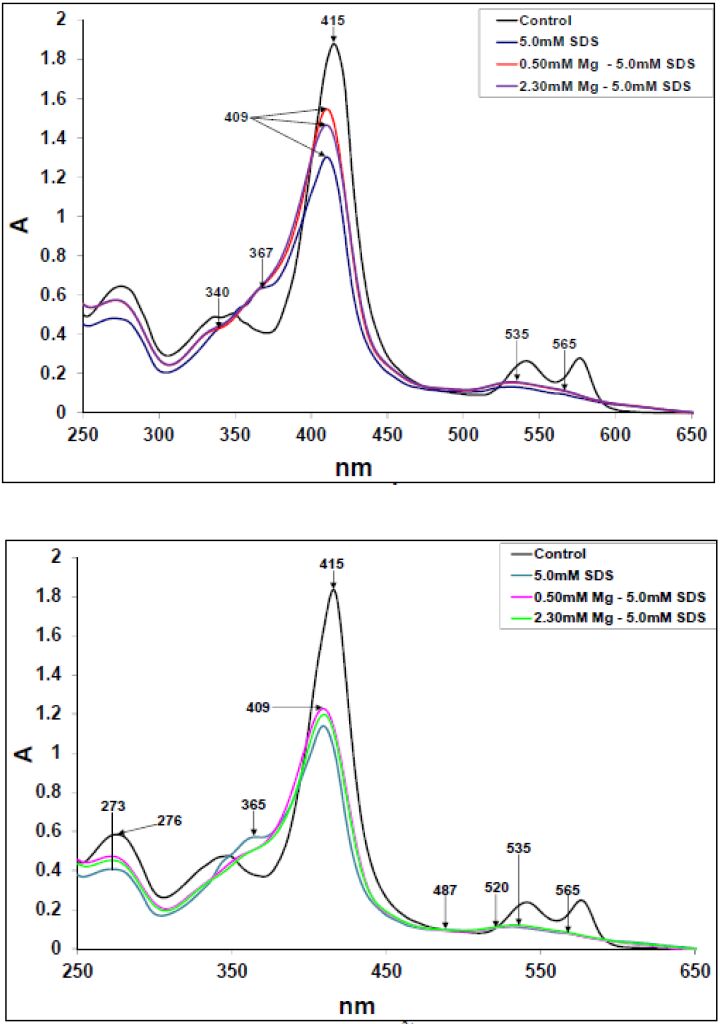
The spectra representing the 5.0 mM SDS-protein-(Mg2+) interactions are shown in Figures 4a and b for the HbA and HbS respectively. In Figure 4a, the 5.0 mM SDS-[Mg2+]-HbA spectra overlapped well except at the Soret peak, where the 0.50 mM Mg2+-SDS-HbA spectrum was hyperchromic to those of the 2.30 mM Mg2+-SDS-HbA and SDS-HbA spectra. The 0.50 mM Mg2+-SDS-HbS spectrum, in Figure 4b, was hyperchromic to those of the SDS-HbS and 2.30 mM Mg2+-SDS-HbS spectra from the aromatic to the Soret regions.
However, from ca. 450 nm to the end, the 2.30 mM Mg2+-SDS-HbS spectrum had either insignificantly higher absorbance to that of the SDS-HbS spectrum or that all three spectra overlapped fairly well. In both Figs, their control spectrum had the most - and the [SDS]-proteins, the least - absorbance. The peaks for the [Mg2+]-SDS-proteins and SDS-proteins were blue shifted to 273 nm while their d bands fused with the Soret regions. While the HbA spectra had shoulders at 340 nm and 367 nm (the 367 nm maximum is well pronounced for the SDS-HbA spectrum), that of the HbS spectra had shoulders at 365 nm: the SDS-HbS spectrum been pronounced compared to those of the [Mg2+]-SDS-HbS. Their Soret peaks (λmax = 409 nm) were considerably hypochromic to their control spectra. This hypochromicity been more pronounced for the HbS spectra. Additionally, the Soret peaks hypochromicity roughly correlated inversely with the emergence of the ca. 365 nm shoulders for both Figures At the visible regions, the SDS-proteins and [Mg2+]-SDS-proteins spectra had peaks at 535- and 565 nm. The [Mg2+]-SDS-HbA spectra were slightly hyperchromic to the [SDS]-HbA spectrum at the 535- and 565 nm peaks. Isosbestic points appeared at ca. 487 nm and 520 nm for the HbS spectra.
The second derivative of the proteins-SDS and protein-SDS-[Mg2+] spectral interactions are shown in Figures 5a (i) and 5b (i) for the HbA and HbS respectively. The 5.0 mM SDS-HbA and 5.0 mM SDS-HbS spectra, had minima at 259-, ca. 268-, 281-, and 290 nm. Their d regions had numerous peaks with broad ones at ca. 325 nm. The HbA-5.0 mM SDS spectrum had pronounced minima at 351- and 364 nm while that of the HbS was at 342- and 360 nm. Their Soret regions had small peaks at 397 nm, and prominent ones at ca. 408-, and 416 nm. Their visible wavelengths had several peaks occurring at λmin ≈ 454-, 518-, 532-, 541-565-, ca. 578- and 589 nm. In the presence of [Mg2+]-5.0 mM, the proteins’ spectra had aromatic regions with single peaks at 277 nm. Minima occurred at 328- and ≈ 355 nm with the 0.50 mM Mg2+ spectrum having the greater effect for the HbA spectra. While the 0.50 mM Mg2+-SDS-HbA spectrum had a more prominent 409 nm Soret maximum, the 2.30 mM Mg2+-SDS-HbS spectrum had the more prominent Soret peak at the same λmax. In both Figs, peaks occurred at 484-, ca. 526-, 565- and ca. 628 nm.
The difference second derivative highlighting the intrinsic contributions of the [Mg2+] to the proteins in an 5.0 mM SDS milieu are shown in Figures 5a (ii) and 5b (ii) for the HbA and HbS respectively. Minima and maxima occurred at 360 nm and 361 nm for the HbA and HbS spectra respectively. In Figure 5a (ii), the 0.50 mM Mg2+ spectrum had greater Δ absorbance λmin at 403 nm, while the 2.30 mM Mg2+ spectrum had the greater Δ absorbance λmin at 424 nm. In Figure 5b (ii), both [Mg2+] had similar magnitude at their 400 nm minima while the 0.50 mM Mg2+ had slightly greater Δ absorbance at the 424 nm minimum. Both Figs had a Δ λmax at 433 nm and an additional Δ λmax at 442 nm for the HbS spectra. However, both Figures exhibited similar minima and maxima.
The second derivative difference spectra comparing the impact of the 0.60 mM- and 5.0 mM SDS interactions on the proteins are shown in Figures 6a and 6b for the HbA and HbS respectively. Both Figures had Δ λmax at ca. 262- and 271 nm. The HbA spectra had Δ λmin at 283-, 292- and 301 nm, while the HbS spectra had Δ λmax at 283-, 295- and 310 nm. The 0.60 mM SDS exhibited slightly more pronounced aromatic peaks for the HbA spectra but with no significant difference(s) of both [SDS] on the HbS spectra. In the d region, the HbA-5.0 mM SDS spectrum had pronounced minima and maxima magnitude relative to that of the HbA-0.60 mM SDS. In Figure 6b, the HbS-5.0 mM SDS spectrum had slightly pronounced minima to that of the HbS-0.60 mM SDS. The HbS-5.0 mM SDS spectrum had a greater Δ absorbance minimum at 409 nm when compared to the HbA-5.0 mM SDS spectrum. Yet, both [SDS] had similar effects on the proteins’ visible region spectra.
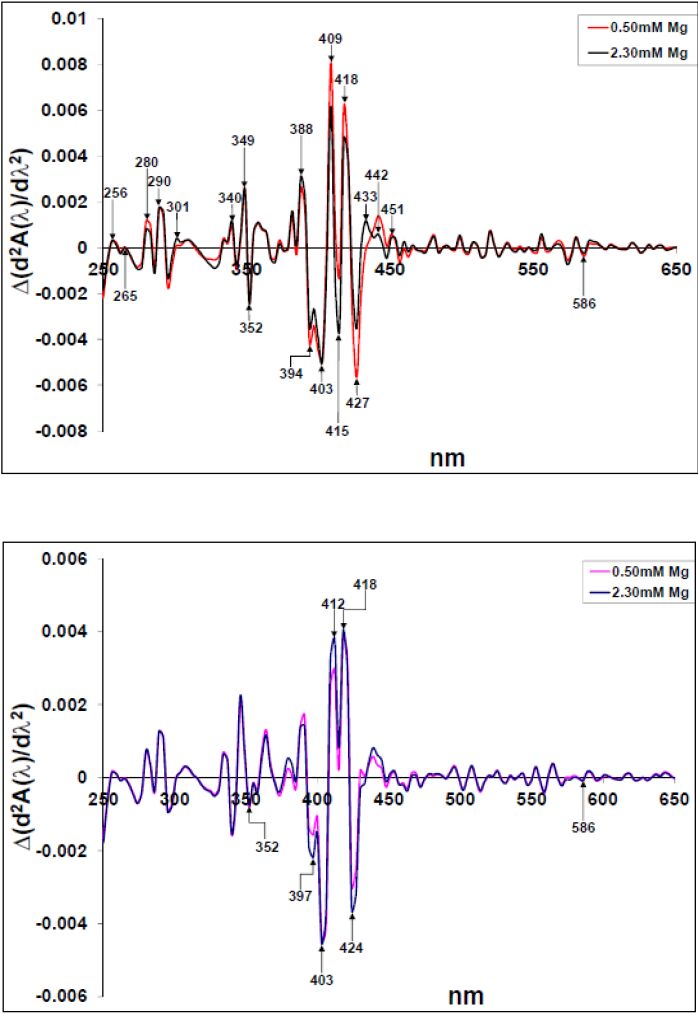
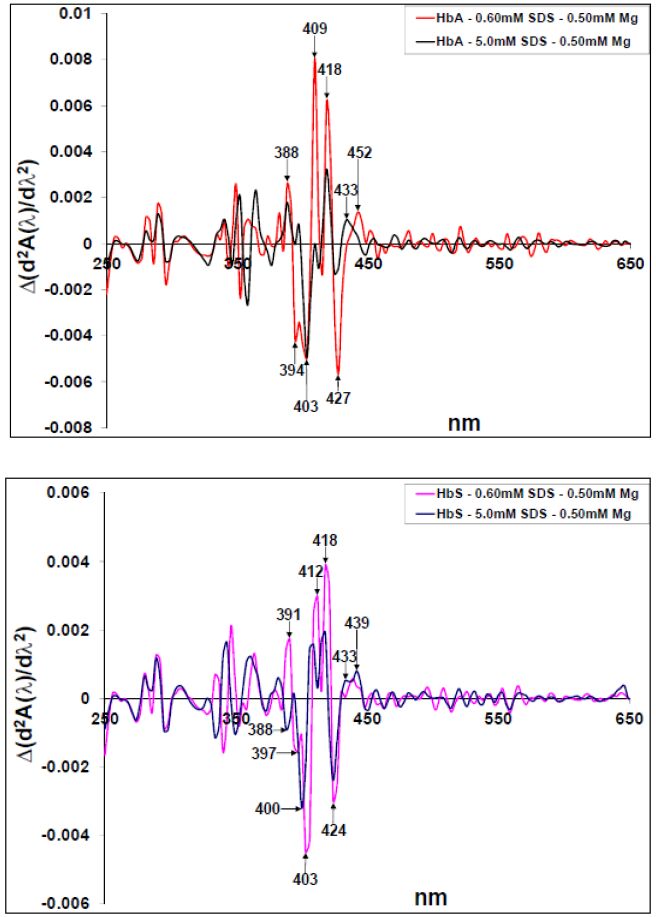
The difference second derivative highlighting the 0.60 mM- and 5.0 mM SDS influence on the 0.50 mM Mg2+-protein interactions are shown in Figures 7a and 7b for the HbA and HbS spectra respectively. In both Figs, the 0.60 mM SDS-protein-0.50 mM Mg2+ spectra had greater Δ λmax and Δ λmin in comparison to the 5.0 mM SDS-protein-0.50 mM Mg2+ spectra. In Figure 7a, both spectra had maxima at 388- and 418 nm, with additional Δ λmax at 409- and 433 nm for the 0.60 mM SDS-HbA-0.50 mM Mg2+ spectrum. The 5.0 mM SDS-HbA-0.50 mM spectrum had a 433 nm shoulder and a λmax at 452 nm. In Figure 7b, the 0.60 mM SDS-HbS-0.50 mM Mg2+ spectrum had a maximum at 391 nm. Both spectra had additional maxima at 412-, 418-, 433- and 452 nm even though the 5.0 mM SDS-HbS-0.50 mM Mg2+ spectrum had the greater Δ λmax at 433- and 452 nm. Both Figures had minima at 403 nm and 427 nm (424 nm in Figure 7b). While the 5.0 mM SDS-HbA-0.50 mM Mg2+ spectrum had Δ λmin at 403 nm, the corresponding HbS spectrum had Δ λmin at388- and 400 nm. These results suggest that the 0.60 mM SDS-proteins-0.50 mM Mg2+ interactions enhanced product formation comparative to the 5.0 mM SDS-proteins-0.50 mM Mg2+ interactions. Additionally, these effects were more pronounced for the 0.60mm SDS-0.50 mM Mg2+-HbA spectrum relative to the 0.60mm SDS-0.50 mM Mg2+-HbS spectrum.
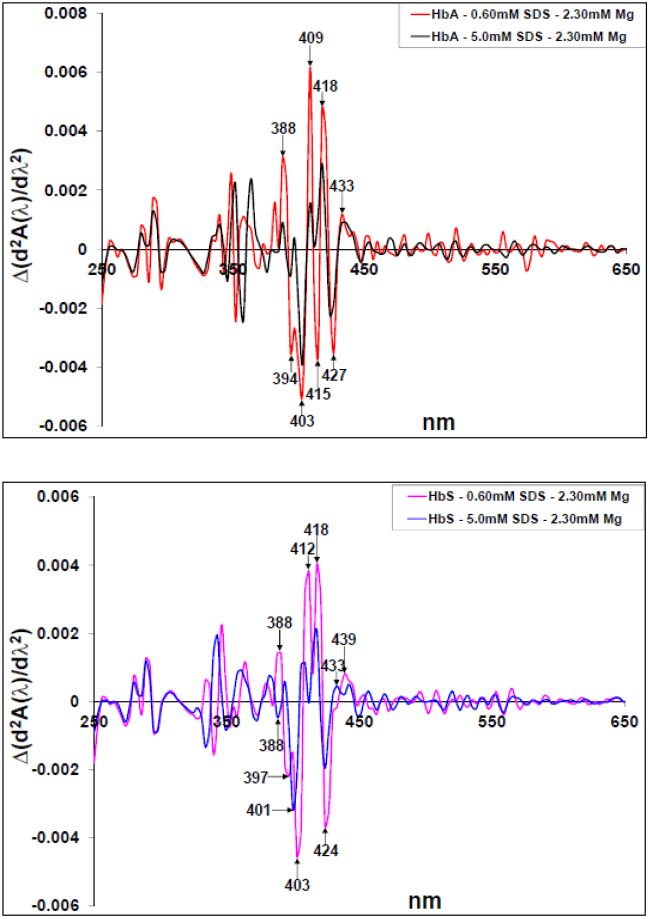
The difference second derivative highlighting the 0.60 mM- and 5.0 mM SDS influence on the 2.30 mM Mg2+-protein interactions are shown in Figures 8a and 8b for the HbA and HbS spectra respectively. The 0.60 mM SDS-protein-2.30 mM Mg2+ spectrum had greater Δ λmax and Δ λmin in comparison to the 5.0 mM SDS-protein-2.30 mM Mg2+ spectrum. Figure 8a had similar Δ λmax and Δ λmin as in Figure 7a, except that there was no 452 nm Δ λmax in Figure 8a and the appearance of a Δ λmin at 415 nm for the 0.60 mM SDS-HbA-2.30 mM Mg2+ spectrum. The same λmax and λmin appeared in Figure 8b as did in Figure 7b. These results suggest that the 0.60 mM SDS - protein-2.30 mM Mg2+ interaction promoted increased Hb breakdown products as compared to the 5.0 mM SDS-protein-2.30 mM Mg2+ interactions. These effects were pronounced in the HbA spectra in comparison to the HbS. Summarily, these results suggest an enhancement of the 0.60 mM SDS-2.30 mM Mg2+ interaction on the HbA relative to that of the 0.60 mM SDS-0.50 mM Mg2+.
4. Discussion
The proteins-[Mg2+] interaction resulted in reduced oxygen affinity while the proteins-SDS-[Mg2+] interactions suggests some sort of intrinsic conformational disorder for the HbS [11] as explained below.
On interacting with the 0.60 mM SDS in the presence and or absence of the [Mg2+], the proteins’ cores were loosened as revealed by their aromatic regions. Since, the aromatic amino acids absorption are sensitive to changes in their environment, the blue-shift -from 277 nm to 271 nm- in the absolute spectra is due to increase in the solvent polarity [49], in this case, by the addition of SDS to the protein-[Mg2+] mixtures. Second derivatives with λmin at 259- and 265 nm are typical of phenylalanine exposure [50,51,52]; 277-, 280- and 282 nm are attributed to tyrosine exposure while 290, 292-, 301 and 310 nm are attributes of tryptophan exposure in proteins [52]. These spectral features have been ascribed to perturbation of the optical spectrum of the aromatic side chain residues at the α1b2 interface, namely α42 (C7) Tyr, b37 (C3) Trp, and b41 (C7) Phe [53]. The α1b2 interface, where the quaternary transition is associated with the largest reorganization of contacts, mediates cooperativity in Hbs via allosteric transitions [54,55,56]. Buried within the hydrophobic core are the cysteine residues with low molar absorptivity in comparison to the aromatic residues. Even though cysteine residues are assumed to exist in the reduced state in intracellular proteins [57], Wetlaufer [58] in his classic review some 53 years ago, reported a λmax of 350 nm for some oxidized sulfyhydryl containing amino acids. Besides, we had suggested that the delta (δ) band in Hb correlates with the redox states of both the aromatic and sulfur-containing amino acid residues in the haem environment; that the overlap of electron dense clouds from these residues is not only responsible for the δ band formation but also contributes substantially to the phenomenon of cooperativity in Hbs; and that both the δ band and cooperative oxygen binding in Hb are abolished by oxidation, which would disperse the dense electron clouds [59]. Thus, we attribute the 328 nm to the <350 nm to oxidation of the aromatic and sulfur containing amino acid residues, which correlates to the loss of the d band on the absolute spectra of the proteins. Various Tryptophan (Trp) derivatives were reported to have peaks between 352- and 355 nm [52]. The addition of [Mg2+] and 0.60 mM SDS resulted in λmin at 352 nm for both proteins. We suggest that the λmin at 356 nm for the 0.60 mM SDS-HbA would also depict Trp derivative, which could result from the endogenous production of hydrogen peroxide (H2O2) from the SDS-heme interaction [10,60,61]. We would discuss the likely implication of these Trp derivatives as we discuss other spectral peaks. The Soret λmin at ≈ 365 and 394 nm, are indicative of monomer and μ-oxo-dimer hemes respectively [62]. From the study of Polet and Steinhardt [63], free hemes liberated during the proteins’ oxidative denaturation would undergo further dimerization reactions. Also, these expulsed hemes interact further with the proteins, forming hemichrome [64], which is accelerated by denaturing agents [65,66] such as SDS.
The HbA-SDS had pronounced 390 nm minimum compared to the HbS-SDS spectrum. This suggests that the HbA-SDS interaction formed more dimers, which should potentially cut down on heme toxicity. However, this was not the case. The peaks at ≈ 410 and 417 nm are characteristic of heme oxidation [63,67]; with the HbA-SDS interaction in the presence and or absence of [Mg2+] been more pronounced to those corresponding to HbS interaction. These results suggest enhanced HbA oxidation over the HbS under the given conditions. The visible parts of the spectra show numerous peaks for both the SDS and or SDS-Mg2+-protein spectra. The less but broad proteins-SDS-Mg2+ peaks indicate “rigidification” and “structuredness” of the proteins on Mg2+addition. The various peaks represent different oxidation states and products of the proteins with the HbA having more products to the HbS. Common to both proteins, on Mg2+ addition, are the pronounced 532- to 535 nm and 565- to 574 nm peaks, indicative of hemichrome formation [61,65,68]. For the second derivative HbA-0.60 mM SDS spectrum, λmin at 418 nm, 548 nm (which is partially occluded by the broad HbA-0.60 mM SDS-[Mg2+] spectra), 581 nm and 590 nm [61,69,70,71]; isobestic points at 466-, 516-, 609 nm and 618 nm [70] are characteristic of oxoferrylHb (•HbFe (IV) = O) species. The reducing equivalent on this species is probably on a Trp radical as can be deduced from the prominent 356 nm peak, which is indicative of Trp derivative. This, is in comparison to the diminutive 418 nm and 590 nm minima of the HbS. These results suggest less HbS oxoferryl sp formation with respect to the HbA. OxoferrylHb (•HbFe (IV) = O) radical species is stable at equilibrium conditions and is a strong oxidizing agent [67], capable of promoting oxidation, peroxidation and epoxidation of various biomolecules [70]. A Trp radical would suggest a peroxidative pathway [72] is the main enzymatic path to the oxoferryl heme generation since ferryl intermediates could be formed from enzymes such as peroxidases and catalases as part of their primary catalytic pathways [73]. Thus, even though the HbA formed more heme dimers, a great deal of its undimerized heme (monomers) were funneled into oxoferryl production [10]. Moreover, the heme dimers still possess enzymatic properties, albeit less than the monomers [74]. In contrast, since the HbS had less heme dimers and less oxoferryl formation, the interaction of the HbS with the ligands (SDS and Mg2+) lead to some sort of structural reorganization that made the HbS heme less accessible to the endogenously formed H2O2.
The maxima in the second derivative difference spectra denotes a decrease in the protein derivatives formation rate on [Mg2+] addition to the SDS-protein while a minima indicates an increase and thus represents an intrinsic [Mg2+] contribution to the proteins’ spectra in the given [SDS] environment. While the 388 nm, 409 nm (hemin) and 418 nm (oxoferryl) maxima in the HbA spectra indicates that the [Mg2+] introduction reduced these derivative formation comparative to that of the 0.60 mM SDS alone, the HbA spectra still had the higher 352- and 586 nm minima magnitude and more Soret derivatives relative to the HbS. Thus, [Mg2+] introduction to both protein-0.60 mM SDS ameliorated the SDS effects, though the amelioration was more pronounced in the HbS spectra.
The proteins’ aromatic regions absolute spectra on 5.0 mM SDS and 5.0 mM SDS-[Mg2+] introduction showed hypsochromic shifts, characteristic of polarity increases on protein-ligand interactions. Additionally, the proteins are transformed to entirely new species with no capability for oxygen binding, accompanied by pronounced hypochromic and blue-shifted Soret peaks. Under the given conditions, their Soret peaks fused with their d bands. The HbS Soret peaks were more hypochromic to those of the HbA.
The fact that the Soret peak hypochromicity correlated roughly with the shoulder emergence at 365- to 370 nm suggests that the greater the heme oxidation, the more monomer heme formation. Even though the HbA Soret peaks from the [Mg2+]-5.0 mM SDS or 5.0 mM SDS interacting alone were hyperchromic to those of the HbS, the HbA spectra had, in all cases, pronounced 367 nm shoulders relative to those of the HbS. This suggests less fusogenicity of the HbA and or its denaturation products with the SDS and supports the findings of LaBrake and Fung [75] on the greater HbS fusogenicity with membranes, at physiological pH, comparative to the HbA. The fact that the HbA-[Mg2+]-5.0 mM SDS spectra had the greater hemichrome formation (535- and 565 nm) and less heme oxidation products relative to the HbA-5.0 mM SDS spectrum indicates that the [Mg2+] protected the HbA somewhat from the SDS. This is even more obvious from their second derivative spectra where the SDS-HbA spectrum had pronounced λmin at 351- and 361 nm in comparison to the SDS-[Mg2+] spectra.
Observably, the proteins-5.0 mM SDS spectra (the HbA in particular) had pronounced λmin at352- and 360 nm relative to the protein-0.60 mM SDS spectra and less oxoferrylheme formation (as is evidence in the peak sizes). This suggests that even though the HbA-5.0 mM interaction had more Trp derivatives and monomer hemes relative to the 0.60 mM-HbA, the excess SDS in the HbA-5.0 mM SDS interaction would have blocked the heme active sites, preventing further conversion of the met state to the oxoferryl Hb state. An alternative explanation is that since there were considerable λmin magnitude at 351- and 361 nm in the HbA-5.0 mM SDS spectrum, then there was substantial oxoferryl Hb formed but the excess [SDS] served as a “sink” for this oxidizing species, probably by blocking the heme from pooling electrons from nearby amino residues, as reducing species, to reduce the FeIV. Thus, even with evidence for spectral derivatives suggesting oxoferryl Hb formation, the spectral depiction of the species proper is weak. In a like manner, the HbS-[Mg2+]-5.0 mM SDS spectra had λmin at 352 nm, which is absent from that of the HbS-5.0 mM SDS. This suggests Trp derivative formation on [Mg2+] addition, which was not seen for the 5.0 mM SDS alone. Additionally, the HbA-5.0 mM SDS explanation still holds true for this situation too.
Intrinsically, in a 5.0 mM SDS milieu, both [Mg2+] contributed to free hemin (λmin at 360 nm) increase during the HbA denaturation. The exact opposite occurred in the HbS denaturation. Besides, [Mg2+] minimized the Hb denaturation products. We assayed for the low and high [SDS] intrinsic contributions, in the presence and absence of [Mg2+], on the proteins in order to clarify on how [Mg2+] moderated the SDS ionic and or hydrophobic interactions and on how these interactions affected Hb denaturation. The [SDS] intrinsic contribution suggests, as previously noted [43,44], that the SDS binding at low concentration is essentially electrostatic (with minor hydrophobic contributions), and purely hydrophobic at higher [SDS]. At the low [SDS], the HbS denaturation decreased. The high [SDS] contributed more to the Hb denaturation products. For the HbA, both [SDS] had, on the average, about the same effect; contributing to the formation and or disappearance of the multiple Soret peaks. Summarily, the 0.60 mM SDS, had less destructive tendencies on the HbS in comparison to the HbA.
The [SDS]-0.50 mM Mg2+ interactions on the proteins show that the 0.60 mM SDS effect is exacerbated comparative to the 5.0 mM SDS for both proteins. This suggests enhancement of electrostatic interactions over hydrophobicity. In fact, relative to the 5.0 mM SDS intrinsic contributions, the 5.0 mM SDS effects were stifled, suggesting that the 0.50 mM Mg2+ contributed to some coulombic interactions and or masked some hydrophobic interactions on the protein surface. The greater “stifling” effect of the 0.50 mM Mg2+ on the 5.0 mM SDS for the HbA in comparison to the HbS suggests that hydrophobicity is a crucial interaction for the HbS at neutral pH and is little-masked by ionic, electrostatic or coulombic interactions. The intrinsic contribution of the 2.30 mM Mg2+ in a 0.60 mM SDS milieu suggests more coulombic interactions (in comparison to the 0.50 mM Mg2+-0.60 mM SDS) for the HbA, with apparently no additional effect of the 5.0 mM SDS (in comparison to the 2.30 mM Mg2+-0.60 mM SDS) on the protein. The results of the HbS for these same situations are no different from those of the 0.50 mM Mg2+ in the presence of the 0.60- or 5.0 mM SDS, thus suggesting no new ionic interactions for an increase in [Mg2+] to either of the [SDS]. Thus, the results suggest that while the ionic or coulombic interactions for the HbA, in the presence of the surfactants, are [Mg2+] dependent, those of the HbS are not.
Our findings show that increased [Mg2+] on the HbS did not have much influence on its outcome with membrane interaction. Could this suggest less [Mg2+] on the functioning of the HbS if the pH is kept constant? Probably yes! Thus, the importance of increased Mg administration on sickle cell patients to prevent dehydration [76] may be overtly exaggerated even though it could be beneficial provided the erythrocyte pH is maintained at 7.20. This is not guaranteed since at physiological conditions, the fully oxygenated sickle erythrocytes are more acidic by pH 0.11-0.15 units than normal erythrocytes [5], suggesting that the acid/alkaline balance in the HbS is a big issue, which, unfortunately has received less attention over the years. In terms of parasite survival, less toxic heme species would be formed at neutral pH to combat parasite metabolism. In our next discuss, we would be interrogating the consequences of these “players” on the dynamics of the proteins at pH 5.0, which is the pH of the parasite’s digestive vacuole [77,78].
5. Conclusion
In conclusion, the 0.60 mM SDS- and [SDS]-[Mg2+] brought about a structural reorganization of the HbS that made the heme less accessible to SDS, the oxoferryl heme and or the H2O2 formed by the interaction of the SDS with the heme. Additionally, our results show that the [SDS], in particular the 0.60 mM SDS had less destructive tendencies on the HbS in comparison to the HbA. Furthermore, the interaction of the HbA-SDS and [Mg2+] showed Mg2+ concentration-dependency while the HbS-SDS interactions were [Mg2+]-independent - suggesting some intrinsic unstructuredness in the HbS. On the other hand, the interaction of the [Mg2+] and [SDS] on the proteins suggests that while the ionic or coulombic interactions for the HbA are [Mg2+] dependent, those of the HbS are not. On the other hand, hydrophobicity is a crucial force for the HbS interaction at neutral pH and is little-masked by ionic, electrostatic or coulombic interactions.
Conflict of Interest
All authors declare no conflict of interest in this paper.









 DownLoad:
DownLoad: