A scalable learning approach for user equilibrium traffic assignment problem using graph convolutional networks

1.   Introduction

Neural network dynamics have attracted much attention owing to the wide applications in associative memory ^[1], signal processing ^[2], intelligent control ^[3], and so on. The mainly dynamical behaviours in neural network systems include stability ^{[4,5,6,7,8,9,10]}, synchronization ^[11,12], bifurcation ^[13], chaos ^[14] and reaction-diffusion^[15], which reflect the characteristics of network systems. Fractional calculus has good free space and infinite storage space in many fields, such as artificial neural networks ^[16], genetic algorithm ^[17] and image enhancement ^[18].

Time delay is an interesting phenomenon in network systems, resulting from differences in the efficiency of signal transmission from the point of generation to the point of reception during network transmission, as well as interference from other external factors. Recently, the results with regard to time delay phenomena are extensively reported including leakage time delay^[19], discrete time delay^[20], distributed time delay^[21] and so on. In actual industrial operation, uncertainties in the parameters associated with the model coefficients can arise due to operational errors, incomplete considerations and model construction. Therefore, the models with uncertain parameters will further improve the robustness of systems in ^[22,23,24].

Synchronization, as one of the typical dynamical behaviours, such as collective recitations, military parades and resonance phenomena, and has become a hot topic ^{[15,22,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43]} including Fin-TS ^{[22,26,27,28,29]}, Fix-TS ^{[22,25,26,30]}, exponential synchronization^{[31,32,33,34,35]}, Mittag-Leffler synchronization^[36,37,38], projective synchronization^[36,39], quasi-synchronization^[40,41], global synchronization^[42]. Lin et al. ^[15] explored the synchronization of directly coupled QDNNs based on pinning control. Li et al. ^[22] investigated Fin-TS and Fix-TS of Caputo QVNNs by employing feedback and adaptive controllers. Wei et al. ^[25] studied Fix-TS of QNNs by a pure power-law control design. Kashkynbayev et al. ^[26] discussed Fin-TS and Fix-TS of DNNs by designing proper control functions. Hu et al.^[43] used an adaptive distributed approach at the edge to study the synchronization of spatio-temporal networks. In fact, Fin-TS and Fix-TS are more relevant to realistic control requirements. However, very few research results on Fin-TS and Fix-TS for fractional order NNs are reported except ^[44,45], where the controller designs for Fix-TS are denoted in fractional order form, then this will undoubtedly increase the difficulty to explore the dynamics of systems.

Inspired by these works, this paper focuses on Fin-TS and Fix-TS issues on Caputo QDNNs with uncertainty. Different from the decomposition method ^{[23,25,35,46]}, Laplace transform ^[40,47,52], comparison principle ^[23,48,49] and linear matrix inequality (LMI) ^[30,41,50], we apply the quaternion direct method, the Lyapunov stability method and the quaternion inequality method to establish the synchronization criterion for Caputo QDNNs. It is worth noting that a new Caputo differential inequality is constructed, then the fixed time of the positive definite function is estimated. The propoesd method can greatly simplify the complexity of the calculation and solve the complexity of controller design caused by the immaturity of the fractional fixed time stability theory, which is very convenient to derive Fix-TS condition to Caputo QDNNs.

The main innovations and highlights of this paper are presented below.

$\bullet$ The model includes the discrete and distributed delays, uncertain term and Caputo derivative operator.

$\bullet$ A new Caputo differential inequality is constructed, then the fixed time of the positive definite function is estimated.

$\bullet$ Applying quaternion direct method rather than the decomposition method, the algebraic discriminant conditions to achieve Fin-TS and Fix-TS on Caputo QDNNs are proposed.

$\bullet$ The control strategies to design the appropriate self feedback and adaptive controllers can effectively reduce the consumption of control costs caused by the time delay term.

2.   Preliminary and model presentation

In this section, the basic definitions, related lemmas and model introduction are described.

Definition 2.1. Fractional integral of the order $\mu$ of $k(t)$ is defined as ^[51]

Definition 2.2. The Caputo-type fractional-order derivative of the function $k(t)$ is defined as ^[51]

where $t > t_0, \ n = [\mu]+1$.

Lemma 2.1. If $0 < \mu < 1$, $\alpha \in \mathbb{R}$, then ^[49]

Lemma 2.2. Let $k(t)$ be a differentiable function over the quaternion field $\mathbb{Q}$, then ^[22]

Lemma 2.3. Let $\chi$ and $\varphi$ be any constant in the quaternion field $\mathbb{Q}$, for any positive number $\theta$ in the real number field $\mathbb{R}$, then ^[44]

Lemma 2.4. If $\xi_i \geqslant 0, \ 0 < \theta \leqslant 1, \ \gamma > 1,$ for $i = 1, 2, \cdots, s$, then ^[25]

Lemma 2.5. Suppose the positive definite function $V(t)$ is a continuously differentiable function on $[0, +\infty)$, if there are positive numbers $0 < \mu < 1, \ \lambda > 0, \ v\geqslant 1, \ \gamma > 0$, such that ^[22]

then when $t \rightarrow \overline{T}$, $\lim\limits_{t \to \overline{T}}V(t) = 0$, and for any $t\geqslant \overline{T}$, $V(t) = 0$ holds, where

Lemma 2.6. Suppose $k(t)$ is a continuously differentiable function on $[t_0, \xi)$, for any constant $\zeta$ on interval $[t_0, \xi)$, then ^[22]

In this paper, a class of Caputo QDNNs with delays and uncertain coefficients is considered as the drive system

where $0 < \mu < 1$, $k_p(t)$ is the state vector representing the $p$-th neuron, $a_p$ is the self feedback regulation coefficient, $g_w(\cdot)$ is the activation function, $b_{pw}+\Delta b_{pw}(t), \ c_{pw}+\Delta c_{pw}(t)$ and $d_{pw}+\Delta d_{pw}(t)$ are connection weights, $\Delta b_{pw}(t), \ \Delta c_{pw}(t), \ \Delta d_{pw}(t)$ are the uncertain coefficients, $I_p(t)$ is an external input, $\tau_1(t), \ \tau_2(t)$ are time-varying delays, $a_p \in \mathbb{R}$, the other coefficients belong to quaternion field $\mathbb{Q}$.

The response system associated with System (2.1) is

where $U_p(t) \in \mathbb{Q}$ stands for controller, $k_p(t_0) \in \mathbb{Q}$ and $o_w(t_0) \in \mathbb{Q}$ are the initial conditions of derive-response Systems $(2.1)$ and $(2.2)$.

Let $\widetilde{\Im_p(t)} = o_p(t)-k_p(t)$, then error system of derive-response Systems $(2.1)$ and $(2.2)$ is:

then the initial condition to System $(2.3)$ is $\widetilde{\Im_p(t_0)} = o_p(t_0)-k_p(t_0).$

Throughout this paper, the following assumptions and synchronization definitions are given:

Assumption 2.1. For any $k_i, o_i$, there exists a positive number $l_i$, such that

where $g(\cdot) = {\Big({g_1}(\cdot), {g_2}(\cdot), ..., {g_n}(\cdot)\Big)^T} \in {\mathbb{Q}^n}$ is the activation function in System $(2.1)$.

Assumption 2.2. For uncertain coefficients $\Delta(t), \ \Delta {c_{pw}}(t), \ \Delta {d_{pw}}(t)$, there exist constants $\hat{b_{pw}}, \ \hat{c_{pw}}, \ \hat{d_{pw}}$, such that$\Delta {b_{pw}}(t) = \hat b_{pw} \alpha _{pw}(t), \ \Delta{c_{pw}}(t) = \hat c_{pw} \beta _{pw}(t), \Delta {d_{pw}}(t) = \hat d_{pw} \omega _{pw}(t)$, where $\alpha _{pw}(t), \beta _{pw}(t), \ \omega _{pw}(t)$ are uncertain quantities under $\overline{\alpha _{pw}(t)}\alpha _{pw}(t) \leqslant 1, \ \overline{\beta _{pw}(t)}\beta _{pw}(t) \leqslant 1, \ \overline{\omega _{pw}(t)}\omega _{pw}(t) \leqslant 1$.

Definition 2.3. For Systems $(2.1)$ and $(2.2)$, if there exists a positive constant $\overline{T}$ related to the initial condition, such that $\mathop {\lim }\limits_{t \to \overline T } ||\widetilde{\Im_p(t)}|| = 0$, $||\widetilde{\Im_p(t)}|| = 0$ holds for any $t \geqslant \overline{T}$, then Systems $(2.1)$ and $(2.2)$ are said to reach Fin-TS ^[22].

Definition 2.4. For Systems $(2.1)$ and $(2.2)$, if there exists a positive constant $T$ independent of the initial condition, such that $\mathop {\lim }\limits_{t \to T } ||\widetilde{\Im_p(t)}|| = 0$, for any $t \geqslant T$, $||\widetilde{\Im_p(t)}|| = 0$ holds, then Systems $(2.1)$ and $(2.2)$ are said to reach Fix-TS ^[44].

Remark 2.1. The models with uncertain parameters can further improve the robustness of systems in ^[22,23,24]. In this paper, the model $(2.1)$ includes the discrete and distributed delays, uncertain term and Caputo derivative operator. Different from the constant time delays in ^[23,34,47], the time delays in model $(2.1)$ are variable, which can enhance the applicability of the model and enrich the results of Fin-TS and Fix-TS.

3.   Main results

In this section, we mainly establish Fin-TS and Fix-TS criteria between Systems $(2.1)$ and $(2.2)$.

Firstly, we construct a Caputo derivative differential inequality to estimate Fix-TS time for the positive definite function $V(t)$.

Theorem 3.1. Let $V(t)\triangleq V(t, \varphi(t))$ be a continuously positive definite and radially unbounded function, and $V(t, \varphi (t)) = 0$ if and only if $\varphi(t) = 0$. If

where $0 < \varepsilon < \alpha < 1, \ 1 < \delta < 1 + \alpha, \ \xi > 0, \ \eta > 0$, then for any $t\geqslant T = t_0+T_1+T_2$, the equality $V(t) = 0$ holds, where

Proof. We first prove that when $t\geqslant t_0$, there exists a $t^*$, such that $V(t^*)\leqslant 1$. Otherwise, for any $t\geqslant t_0, \ V(t) > 1$. From inequality $(3.1)$, we can get that the following two differential inequalities are simultaneously true

Taking the Caputo derivative of order $\alpha$ on $t_0 \to t$ for $V^{\alpha-\delta}(t)$, from Lemma 2.1, then we get

For both sides of inequality $(3.4)$, we take $\alpha$-order fractional integral on $t_0 \to t$ below

Then, we have

From inequality $(3.8)$, we know that $V(t)$ is monotonically decreasing. Take

then the inequality $V({t^*}) \leqslant 1$ holds. Let

thus we have $T_1 > t^*$. Similarly, we can also get

Let

when $t = t^*+T_2$, then the right hand side of inequality $(3.10)$ is equal to $0$. Furthermore, we can get that $V(t) \leqslant 0$ when $t = t^*+T_2$. Since $V(t)$ is a positive definite function, when $t = t^*+T_2$, $V(t)\equiv 0$. Let $t = t_0+T_1+T_2$, then we can get $V(t) = 0$ holds. When $t \geqslant t_0+T_1+T_2$, we have $\varphi(t) = 0$, and the settling time is estimated as $T$.

Remark 3.1. Recently, many synchronization results have been reported in ^{[15,22,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43]} including Fin-TS ^[22,26], Fix-TS ^[22,25,26], exponential synchronization^{[31,32,33,34,35]}, Mittag-Leffler synchronization^[36,37,38], projective synchronization^[36,39] and quasi-synchronization^[40,41]. In Theorem 3.1, a new Caputo differential inequality is constructed, then the fixed time of the positive definite function is estimated, which is very convenient to derive Fix-TS conditions between Systems $(2.1)$ and $(2.2)$.

To achieve Fin-TS between Systems $(2.1)$ and $(2.2)$, the self feedback controller is designed

where $\varepsilon \geqslant 2, \alpha_p, \delta$ and $\sigma$ are positive constants.

Theorem 3.2. Under Assumptions 2.1, 2.2 and controller $(3.11)$, if there exist positive constants $h > 1$ and $r > 1$, such that

then Systems $(2.1)$ and $(2.2)$ can achieve Fin-TS, and the settling time of Systems $(2.1)$ and $(2.2)$ is

where$\Omega = |{b_{pw}}|^2 + \hat{|{b_{pw}}|}^2, \ \Pi = |{c_{pw}}|^2 + \hat{|{c_{pw}}|}^2, \ \Psi = |{d_{pw}}|^2 + \hat{|{d_{pw}}|}^2$, $l_p, {l'_p}$ and ${l''_p}$ are Lipschitz coefficients.

Proof. Choosing the following Lyapunov function

From Lemma 2.2, we have

By computation, we further get

According to controller (3.11), we have

In terms of Lemma 2.3, Assumptions 2.1 and 2.2, we have

Similarly, we can get

Substituting $(3.17)$–$(3.19)$ to $(3.16)$, we can get

where $\Omega = |{b_{pw}}|^2 + \hat{|{b_{pw}}|}^2, \ \Pi = |{c_{pw}}|^2 + \hat{|{c_{pw}}|}^2, \ \Psi = |{d_{pw}}|^2 + \hat{|{d_{pw}}|}^2$. From $(3.12)$, Lemma 2.4, fractional-order Razumikhin theorem and Jensen Inequality, there exist $h > 1$ and $r > 1$, such that

According to Lemma 2.5, Systems $(2.1)$ and $(2.2)$ can realize Fin-TS under controller $(3.11)$, and the settling time of Systems $(2.1)$ and $(2.2)$ is estimated as

Therefore, when $t \geqslant \overline{T}$, we have $||\widetilde{\Im_p(t)}|| = 0$, then Systems $(2.1)$ and $(2.2)$ can realize Fin-TS under controller $(3.11)$.

In order to realize Fix-TS of Systems $(2.1)$ and $(2.2)$, the following adaptive controller is designed

where $- \mu < \delta < 0, \ 1-\mu < \varepsilon < 1, k_{1p} > 0, k_{2p} > 0,$ and $\sigma_p(t)$ is the adaptive control gain satisfying

Theorem 3.3. Under Assumptions 2.1, 2.2 and controller $(3.23)$, if there exist positive constants $h > 1$ and $r > 1$, such that

then Systems $(2.1)$ and $(2.2)$ can realize Fix-TS, and the settling time of Systems $(2.1)$ and $(2.2)$ is

where ${l_p}, {l'_p}$ and ${l''_p}$ are Lipschitz coefficients.

Proof. Take into account the following Lyapunov function

Similar to the proof Theorem 3.2, by Lemma 2.6 we have

Under adaptive controller (3.23), we have

By fractional-order Razumikhin theorem, there are $h > 1, r > 1$, The following formula holds:

An application of Lemma 2.4 yields that

Similarly, one can get

where ${H_1} = \mathop {\min }\limits_{1 \leqslant p \leqslant n} \left\{ {2{k_{1p}}\lambda _p^\delta, 2{S_p}\lambda _p^\delta } \right\}, {H_2} = \mathop {\min }\limits_{1 \leqslant p \leqslant n} \left\{ {2{k_{2p}}\lambda _p^\varepsilon, 2{R_p}\lambda _p^\varepsilon } \right\}$. Substituting $(3.31)$ and $(3.32)$ to $(3.30)$, from $(3.25)$, we have

According to Theorem $3.1$, Systems $(2.1)$ and $(2.2)$ can achieve Fix-TS under controller $(3.23)$, and the settling time is estimated as

Therefore, when $t\geqslant T$, we have $\mathop {\lim }\limits_{t \to T} ||\widetilde {{\Im_p}(t)}|| = 0$. Thus, Systems $(2.1)$ and $(2.2)$ can realize Fix-TS under controller $(3.23)$.

Remark 3.2. Different from other synchronization controller designs such as exponential synchronization ^{[31,32,33,34,35]}, quasi-synchronization ^[40,41] and global synchronization ^[42], the Fin-TS and Fix-TS controllers $(3.11)$ and $(3.23)$ are designed in two steps including the synchronization control term and stability control term, which can greatly improve the performance of the controller, enhance the operability and system stability, and also allow the synchronization term gain and stability term gain to be adjusted.

Remark 3.3. In contrast to the decomposition method ^[46], Laplace transform ^[47], comparison principle ^[48,49] and linear matrix inequality (LMI) ^[50], the algebraic condition $(3.12)$ in Theorem 3.2 is proposed to realize Fin-TS based on the quaternion direct method, Lyapunov stability theory, extended Cauchy Schwartz inequality and Jensen inequality.

4.   Examples

In this section, two numerical examples are given to verify the correctness and validity of Theorems 3.1–3.3 under the different derivative orders.

Consider the following Caputo QDNN model:

where

The response system is

where ${o_p}(t) = o_p^R(t) + Io_p^I(t) + Jo_p^J(t) + Ko_p^K(t) \in \mathbb{Q}.$ The initial conditions of Systems $(4.1)$ and $(4.2)$ are chosen as

Example 4.1. To realize Fin-TS of Systems $(4.1)$ and $(4.2)$, for the self feedback controller $(3.11)$, the following control gains are taken as $\delta = 0.9, \ \sigma = 0.1, \ \varepsilon = 2.1, \ h = r = 1.5, \ {l_p} = {l'_p} = {l''_p} = 1.$ By calculation, we can get

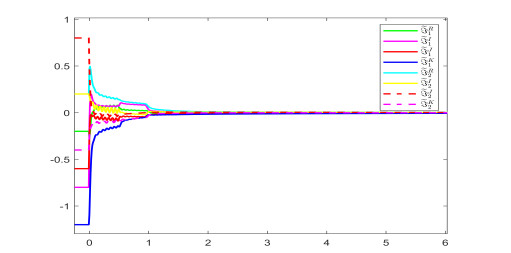
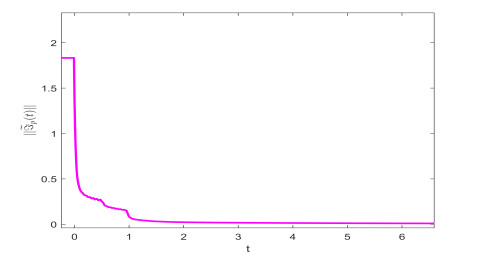
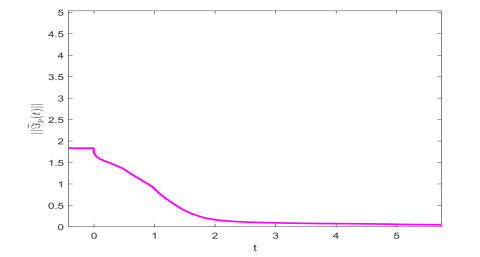
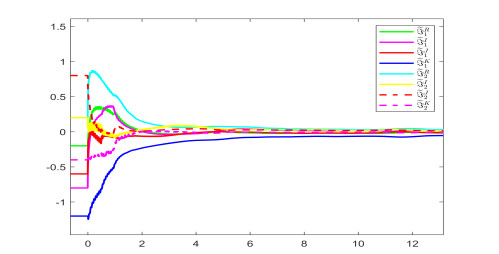
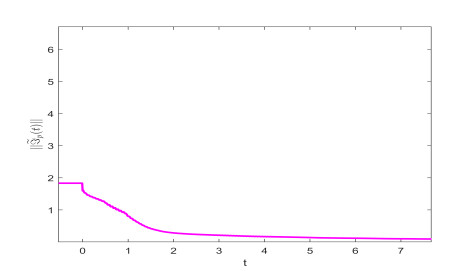
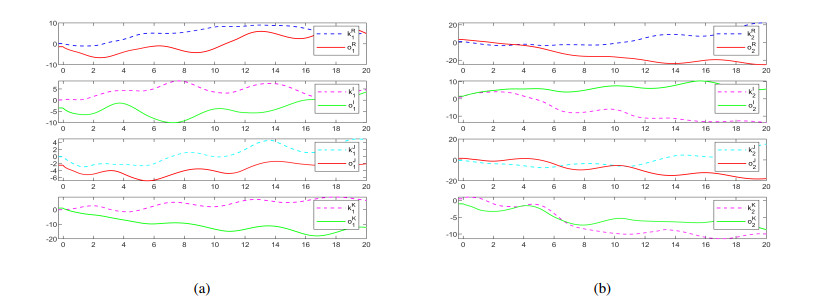
From Theorem 3.2, the settling time can be estimated as $\overline T \approx 4.5123$. Figure 1 shows the state trajectories of derive-response Systems $(4.1)$ and $(4.2)$ without controller. Figures 2 and 3 describe Fin-TS trajectories and error norm of Systems $(4.1)$ and $(4.2)$ under controller $(3.11)$ when the order is 0.73. Figures 4 and 5 depict Fin-TS trajectories and error norm of Systems $(4.1)$ and $(4.2)$ under controller $(3.11)$ when the derivative order is 0.53. Figures 2–5 reveal that the numerical simulations are consistent with Theorem 3.2.

Example 4.2. To realize Fix-TS between Systems $(4.1)$ and $(4.2)$, an adaptive controller $(3.20)$ is designed based on Theorem 3.1. Taking

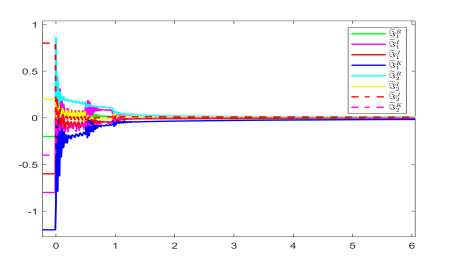
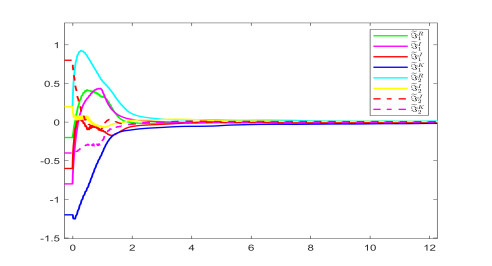
the other model parameters are consistent with Example 4.1. By computation, the conditions of Theorem 3.3 are satisfied. The settling time can be estimated as $T\approx5.2198$. Figures 6 and 7 show Fix-TS trajectories and error norm of Systems $(4.1)$ and $(4.2)$ under controller $(3.23)$ when the order is 0.73. Figures 8 and 9 characterize Fix-TS trajectories and error norm of Systems $(4.1)$ and $(4.2)$ under controller $(3.23)$ when the derivative order is 0.53. Figures 6–9 verify that the numerical simulations are coincident with Theorems 3.1 and 3.3.

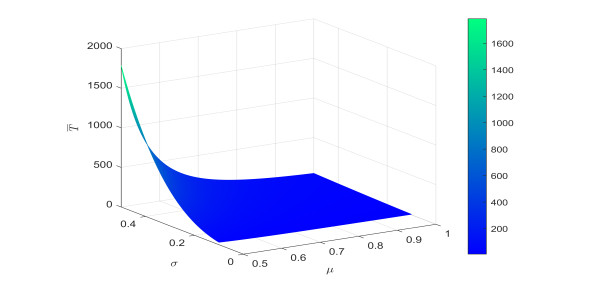
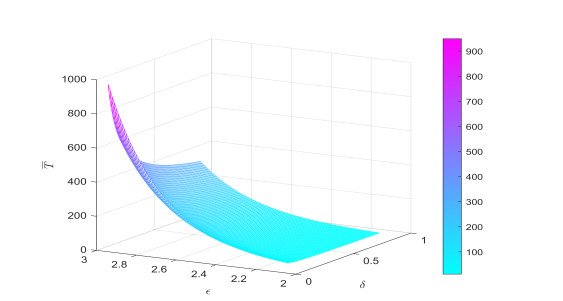
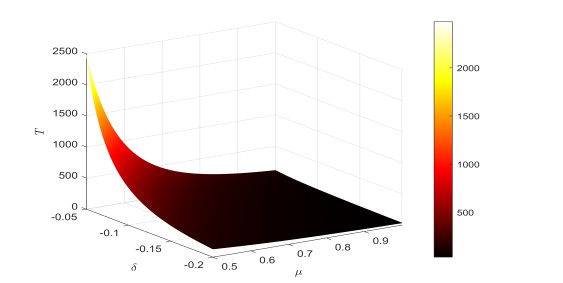
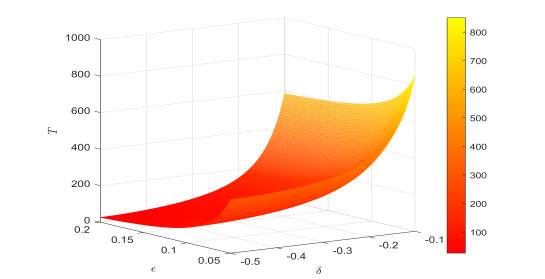
Remark 4.1. Figures 10 and 11 depict the relationship between the settling time $\overline{T}$ of Fin-TS with the order $\mu$ and the parameters $\sigma$, $\delta$ and $\varepsilon$. Figures 12 and 13 illustrate the relationship between the settling time $T$ of Fix-TS with the order $\mu$ and the parameters $\delta$, $\varepsilon$. For Fin-TS, it can be observed from Figures 10 and 11 that the settling time is positively correlated with $\sigma$, $\varepsilon$ and negatively correlated with $\delta$, $\mu$. For Fix-TS the settling time is positively correlated with $\delta$ and negatively correlated with $\varepsilon$, $\mu$. Therefore, the settling time of synchronisation is closely related to the order of the equation, regardless of whether it is Fin-TS or Fix-TS.

5.   Conclusions

This paper has investigated Fin-TS and Fix-TS issues for derive-response Systems $(2.1)$ and $(2.2)$. Firstly, a new Caputo fractional differential inequality $(3.1)$ is constructed, then Fix-TS settling time of the positive definite function $V(t)$ is estimated, which is very convenient to derive Fix-TS condition to Systems $(2.1)$ and $(2.2)$. By designing the appropriate self feedback controller $(3.11)$ and adaptive controller $(3.23)$, the algebraic discriminant conditions $(3.12)$ and $(3.25)$ to achieve Fin-TS and Fix-TS on Systems $(2.1)$ and $(2.2)$ are established in terms of quaternion direct method, Lyapunov stability theory, extended Cauchy Schwartz inequality, Jensen inequality. Finally, the correctness and validity of Theorems 3.1–3.3 under the orders $\mu = 0.53$ and $\mu = 0.73$ are verified by two numerical examples. The dynamics of QDNNs models including impulsive effect and multiple time delays will be our next research issue.

Acknowledgments

This work was supported by the Natural Science Foundation of Anhui Province of China (No. 1908085MA01) and Research on green prevention and control of tea diseases and insect pests and automatic processing technology based on 5G network (No. 200118).

Conflict of interest

The authors declare that they have no conflict of interest.