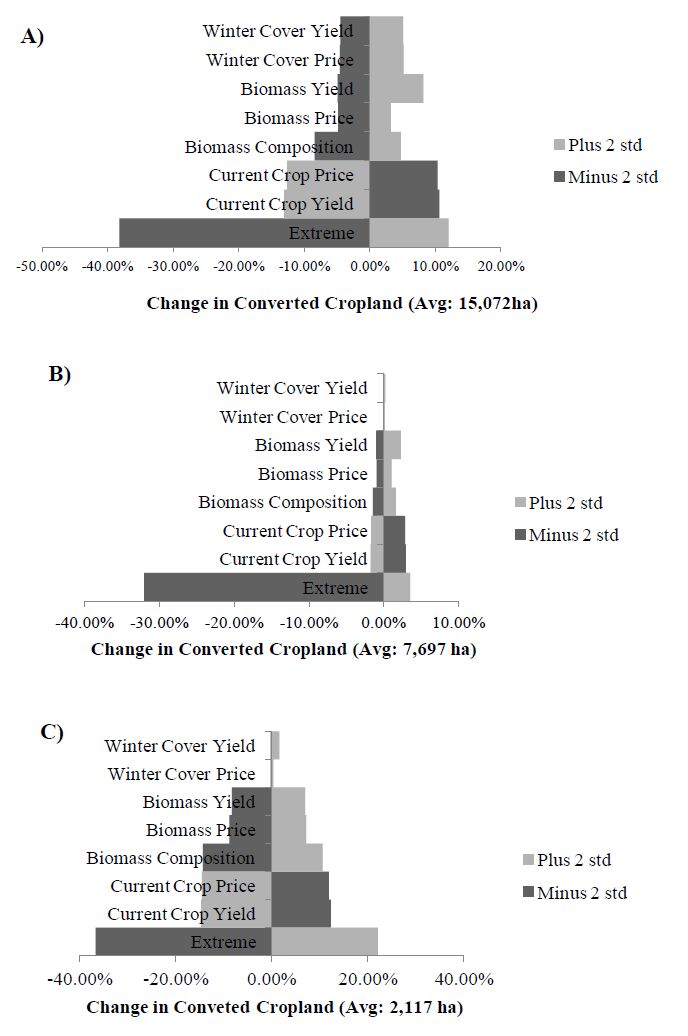
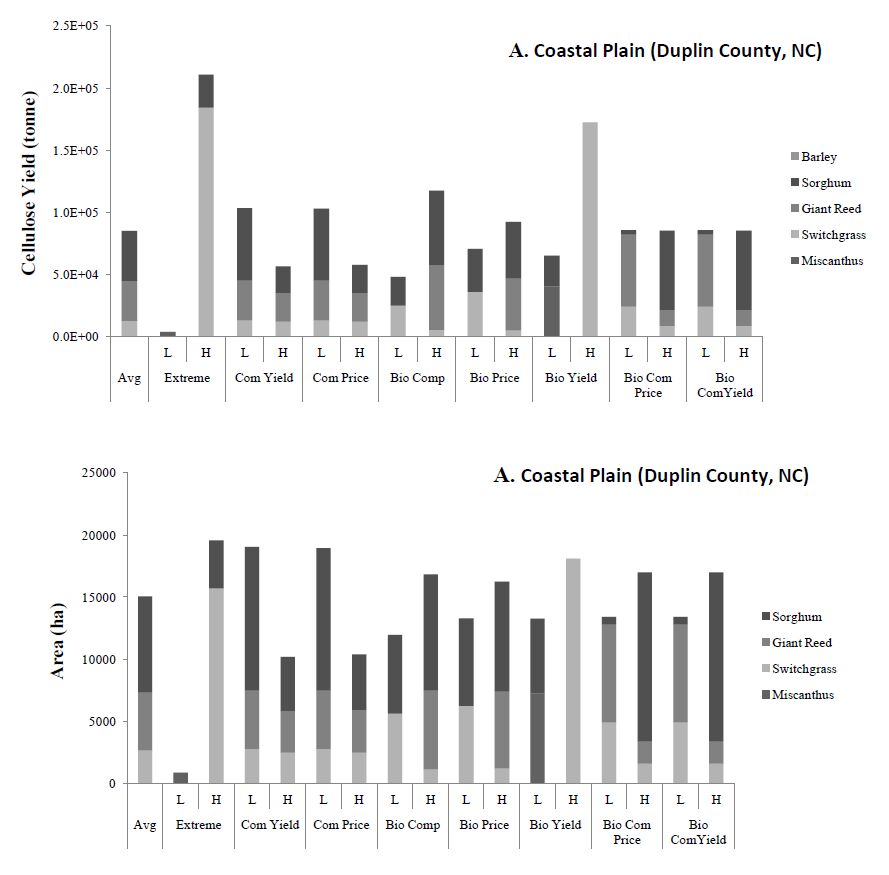
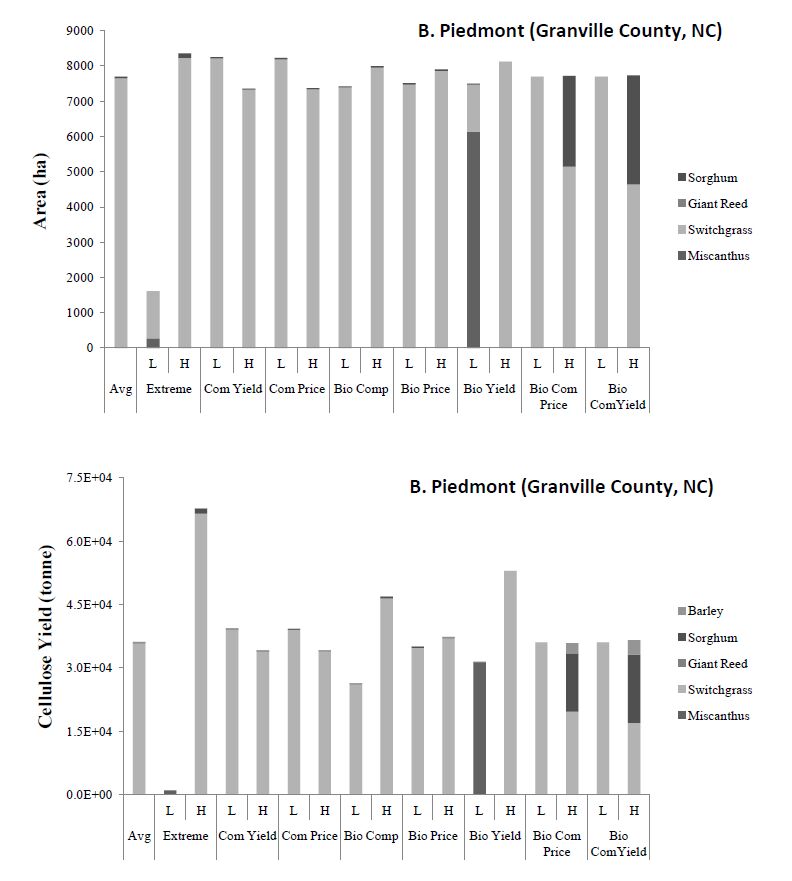
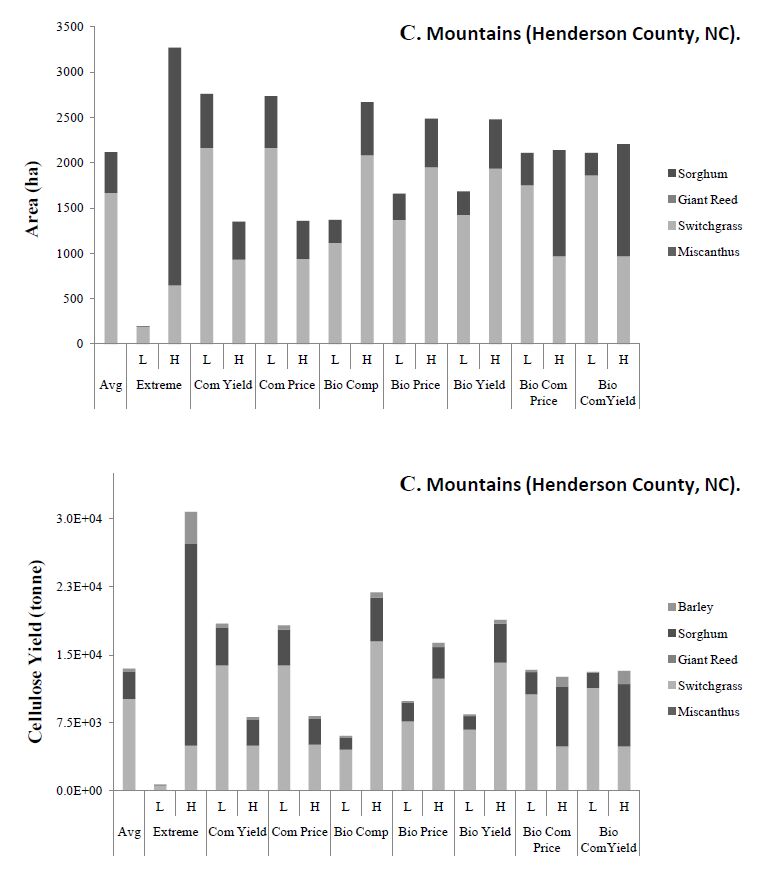
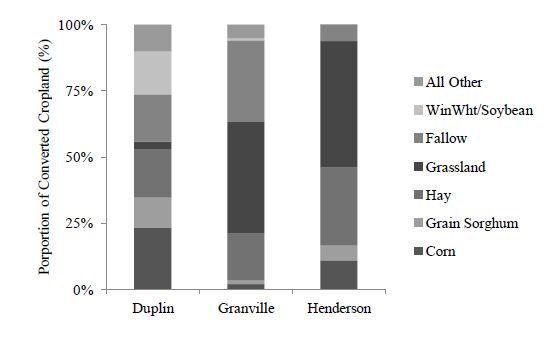
Increased interest in biomass cultivation requires detailed analysis of spatial production potential of possible biorefinery locations, with emphasis on feedstock production cost minimization. Integrated assessment of publicly available spatial data on current crop production, soil type, and yield potential, coupled with techno-economic production cost estimates, can support a functional method for rapid analysis of potential biorefinery sites. A novel predictive model was developed to determine cropland conversion using a probabilistic profit based equation for multiple biomass crops: giant reed, miscanthus, switchgrass, and sorghum (with either canola or barley as a winter crop). The three primary regions of North Carolina (Mountains, Piedmont, and Coastal Plain) were used as a case study and with a single parameter uncertainty analysis was completed. According to the model, the county chosen to represent the Coastal Plain (Duplin County) had the largest potential acreage that would be converted (15,071 ha, 7.1% total land, 9.3% of cropland) primarily to sorghum with canola as a winter crop. Large portions were also predicted to convert to giant reed and switchgrass, depending on the price and yield parameters used. The Piedmont (Granville County, 7697 ha, 5.5% total land, 6.9% cropland) and Mountain (Henderson County, 2117 ha, 2.2% total land, 2.3% cropland) regions were predicted to convert primarily to switchgrass acreage for biomass production, with much less available biomass overall compared to the Coastal Plain. This model provided meaningful insight into regional cropping systems and feedstock availability, allowing for improved business planning in designated regions. Determination of cropland conversion is imperative to develop realistic biomass logistical operations, which in conjunction can assist with rapid determination of profitable biomass availability. After this rapid analysis method is conducted in-depth on-ground biorefinery feasibility analysis can occur, ensuring resource are used only in locations with a high potential for available low cost biomass feedstocks.
1.
Introduction
Predator-prey models are highly important in general and mathematical ecology [1]. In the past decades, many factors have been considered to describe the ecological predator-prey system more correctly and reasonably [2,3]. Notably, population models in the real world is inevitably influenced by numerous unpredictable environmental noise, and deterministic systems are fairly challenged in describing the fluctuation accurately [4,5]. Hence, an increasing number of researchers have paid attention to stochastic models and proposed various population models with stochastic perturbations, such as in [6,7,8,9,10]. Liu and Wang [10] introduced a stochastic non-autonomous predator-prey model for one species with white noise as follows:
The group analyzed the conditions for extinction and species persistence in Eq (1.1). On the basis of the theoretical and practical significance of this stochastic model, many results have been presented, particularly, in [11,12,13]. However, the influence of the functional response to systems has been rarely considered in previous stochastic population models.
Generally, two types of functional response exist, that is, prey- and predator-dependent responses. The first functional response considers only the prey density, whereas the other accounts for both prey and predator densities [2]. When investigating biological phenomena, one must not ignore the predator's functional response to prey because of such response's effect on dynamical system properties [14,15,16,17,18]. Among many different forms of predator-dependent functional responses, the three classical ones include the Beddington-DeAngelis, Hassell-Varley and Crowley-Martin types. We let $ x_{1}(t) $ and $ x_{2}(t) $ denote the prey and predator population densities, respectively, at time $ t $. Then, $ \frac{\omega(t) x_{1}(t)}{1+a(t)x_{1}(t)+b(t)x_{2}(t)+a(t)b(t)x_{1}(t)x_{2}(t)} $ becomes the Crowley-Martin functional response, where $ a(t) $, $ b(t) $ and $ \omega(t) $ represent the effects of handling time, the magnitude of interference among predators, and capture rate, respectively. Interestingly, if $ a(t) = 0 $ and $ b(t) = 0 $, then the Crowley-Martin functional response becomes a linear mass-action functional response. If $ a(t) = 0 $ and $ b(t) > 0 $, the response represents a saturation response; if $ a(t) > 0 $ and $ b(t) = 0 $, then the response becomes a Michaelis-Menten functional response (or Holling type-II functional response) [1,19,20]. Given its importance and appeal, some scholars have studied stochastic predator-prey models incorporating Crowley-Martin functional response [21,22,23] and in this paper, we consider the Crowley-Martin functional response to embody interference among predators and provide insight into the dynamics of the predator-prey population model.
Meanwhile, the theory of impulsive differential equation was well developed recently, and impulsive differential equations were found as a more effective method for describing species and the ecological systems more realistically. Many important and peculiar results have been obtained regarding the dynamical behavior of these systems, including the permanence, extinction of positive solution and dynamical complexity. However, few studies have addressed the population dynamics of two species both with stochastic and impulsive perturbations, except in [24,25,26]. In [25], Zhang and Tan considered a stochastic autonomous predator-prey model in a polluted environment with impulsive perturbations and analyzed the extinction and persistence of the system. By contrast, the model proposed is autonomous, that is, the parameters are assumed as constants and independent of time. In [26], Wu, Zou, and Wang proposed a stochastic Lotka-Volterra model with impulsive perturbations. The asymptotic properties of the model were examined. However, their model was based on the prey-dependent functional response and did not consider the predator's functional response to prey. In addition, there are four approaches to introduce stochastic perturbations to the model as usual, through time Markov chain model, parameter perturbation, being proportional to the variables, and robusting the positive equilibria of deterministic models [27]. In this paper, we adopt the third approach to include stochastic effects to Eq (1.2).
Inspired by the above discussion and [11,25,26], we consider the possible effects of impulsive and stochastic perturbations on the system and propose the following non-autonomous stochastic differential equation:
The parameters are defined as follows: $ r(t) $ and $ g(t) $ denote the intrinsic growth rate of the prey and predator population at time $ t $; $ k(t) $ and $ h(t) $ are the density-dependent coefficients of prey and predator populations, respectively; $ f(t) $ represents the conversion rate of nutrients into the reproductive predator population; $ \sigma_{i}^{2}(t) $ $ (i = 1, 2) $ refers to the intensities of the white noises at time $ t $; $ \dot{B}_{1}(t) $ and $ \dot{B}_{2}(t) $ are standard white noises, in particular, $ B_{1}(t), B_{2}(t) $ are Brownian motions defined on a complete probability space $ (\Omega, \mathcal{F}, \mathbb{ P}) $ [6].
Throughout this paper, all the coefficients are assumed to be positive and continuously bounded on $ \mathbb{R}_{+} = [0, +\infty) $. The impulsive points satisfy $ 0 < \tau_{1} < \tau_{2} < \ldots < \tau_{k} < \ldots $ and $ \lim\limits_{k\rightarrow +\infty} \tau_{k} = +\infty $. According to biological meanings, $ \rho_{1k} > -1, \rho_{2k} > -1 $. Moreover, we assume that there are some positive constants $ m $, $ M $, $ \widetilde{m} $ and $ \widetilde{M} $ that satisfy $ 0 < m\leq \prod\limits_{0 < \tau_{k} < t} (1+\rho_{1k})\leq M $ and $ 0 < \widetilde{m}\leq \prod\limits_{0 < \tau_{k} < t} (1+\rho_{2k})\leq \widetilde{M} $, for all $ t > 0 $.
The remaining portion of this paper is arranged as follows. In the next section, some preliminaries are introduced. We analyze the impulsive stochastic differential model and obtain the existence, uniqueness and stochastically ultimate boundness of the positive solution in Section 3. In Section 4, sufficient conditions for extinction and a set of persistence in the mean, including non-persistence, weak persistence, and strong persistence in the mean, are presented. Additionally, we provide conditions to guarantee the stochastic permanence of the system. In Section 5, the global attractiveness of Eq (1.2) is studied. Finally, some numerical simulations, which verify our theoretical results, are given in Section 6. We compare the results of stochastic models under positive or negative impulsive perturbations with those without such disturbances, as well as, the figures with different stochastic perturbations and same impulse. By doing so, we clearly show that the impulsive and stochastic perturbations are of great importance to species permanence and extinction.
2.
Preliminaries
To proceed, we list some appropriate definitions, notations, and lemmas as follows. For convenience, we denote
where $ f(t) $ is a continuous and bound function defined on $ [0, +\infty) $. $ X(t) $ represents $ (x_{1}(t), x_{2}(t)) $ and $ |X(t)| = (x_{1}^{2}(t)+x_{2}^{2}(t))^{\frac{1}{2}} $. $ \mathbb{N} $ is the set of positive integers and $ \mathbb{R}_{+}^{n} = \{x\in \mathbb{R}^{n}: x_{i} > 0, i = 1, 2, 3...n\} $.
Definition 2.1.
(a) If $ \lim\limits_{t\rightarrow +\infty}x(t) = 0 $ a.s., then the species $ x(t) $ is said to go to extinction.
(b) If $ \langle x\rangle^{*} = 0 $ a.s., then the population $ x(t) $ is said to be non-persistent in the mean.
(c) If $ \langle x\rangle^{*} > 0 $ a.s., then the population $ x(t) $ is said to be weakly persistent in the mean.
(d) If $ \langle x\rangle_{*} > 0 $ a.s., then the population $ x(t) $ is said to be strongly persistent in the mean.
(e) If $ x^{*} > 0 $ a.s., then the population $ x(t) $ is said to be weakly persistent.
Definition 2.2 ([28]) Solution $ X(t) = (x_{1}(t), x_{2}(t)) $ of Eq (1.2) is said to be stochastically ultimately bound, if for arbitrary $ \varepsilon \in (0, 1) $, a positive constant $ \delta = \delta(\varepsilon) $ exists, such that for any given initial value $ X_{0} = (x_{1}(0), x_{2}(0)) \in \mathbb{R}_{+}^{2} $, the solution $ X(t) $ to Eq (1.2) satisfies $ \limsup\limits_{t\rightarrow\infty} \text{P}\{|X(t)| > \delta\} < \varepsilon. $
Definition 2.3 ([28]) Solution $ X(t) = (x_{1}(t), x_{2}(t)) $ of Eq (1.2) is said to be stochastically permanent, if for any $ \varepsilon \in (0, 1) $, there is a pair of positive constants $ \delta = \delta(\varepsilon) $ and $ \chi = \chi(\varepsilon) $ such that for any initial value $ X_{0} = (x_{1}(0), x_{2}(0))\in \mathbb{R}_{+}^{2} $, the solution $ X(t) $ to Eq (1.2) satisfies $ \liminf\limits_{t\rightarrow\infty} \text{P}\{|X(t)|\geq\delta\}\geq 1-\varepsilon $, $ \liminf\limits_{t\rightarrow\infty} \text{P}\{|X(t)|\leq\chi\}\geq 1-\varepsilon $.
Definition 2.4. Eq (1.2) is said to be globally attractive if
for any two solutions $ (x_{1}(t), x_{2}(t)) $, $ (\overline{x}_{1}(t), \overline{x}_{2}(t)) $ of Eq (1.2).
Definition 2.5. ([29]) Consider the impulsive stochastic equation
with the initial value $ x(0) = x_{0}\in \mathbb{R}^{n} $. A stochastic process $ x(t) = (x_{1}(t), x_{2}(t), \cdots, x_{n}(t))^{T} $, $ t\in[0, +\infty) $ is the solution of Eq (2.1) if
(a) $ x(t) $ is $ \mathcal{F}_{t} $ adapted and continuous on $ (0, t_{1}) $ and each interval $ (t_{k}, t_{k+1}) $, $ k\in \mathbb{N} $ and $ F(t, x(t))\in L^{1}(\mathbb{R}^{+}, \mathbb{R}^{n}) $, $ G(t, x(t))\in L^{2}(\mathbb{R}^{+}, \mathbb{R}^{n}) $.
(b) For each $ t_{k} $, $ x(t^{+}_{k}) = \lim\limits_{t\rightarrow t^{+}_{k}}x(t) $ and $ x(t^{-}_{k}) = \lim\limits_{t\rightarrow t^{-}_{k}}x(t) $ and $ x(t_{k}) = x(t^{-}_{k}) $ a.s..
(c) $ x(t) $ obeys the equivalent integral Eq (2.1) for almost every $ t\in \mathbb{R}_{+}\setminus t_{k} $ and satisfies the impulsive conditions at $ t = t_{k} $ a.s..
Lemma 2.1. ([5]) Suppose that $ x(t) \in \bf{C}[\Omega \times\mathbb{ R}_{+}, \mathbb{R}_{+}^{0}] $, where $ \mathbb{R}_{+}^{0} = (0, +\infty) $ and $ B_{i}(t) $ $ (i = 1, 2, 3, \ldots, n) $ are independent Brownian motions defined on a complete probability space $ (\Omega, \mathcal{F}, \mathbb{ P}) $, then
$ (a) $ If there are positive constants $ \lambda_{0}, T $ and $ \lambda \geq 0 $ satisfying
for all $ t \geq T $, where $ \beta_{i} $ is a constant, $ 1\leq i\leq n $, then, $ \langle x\rangle^{*} \leq \lambda/\lambda_{0} $ a.s.
$ (b) $ If there are positive constants $ \lambda_{0}, T $ and $ \lambda \geq 0 $ satisfying
for all $ t \geq T $, where $ \beta_{i} $ is a constant, $ 1\leq i\leq n $, then, $ \langle x\rangle_{*} \geq \lambda/\lambda_{0} $ a.s.
Lemma 2.2. ([30]) Let $ f $ be a non-negative function defined on $ \mathbb{R}_{+} $ such that $ f $ is integrate and is uniformly continuous. Then $ \lim\limits_{t\rightarrow +\infty} f(t) = 0 $.
3.
Properties of the solution
In this section, the existence, uniqueness, and stochastically ultimate boundedness of the global positive solution are obtained.
Firstly, we denote
then by virtue of Lemma 2.1 in [30], the following lemma can be obtained.
Lemma 3.1. For the stochastic equations without impulses
$ (y_{1}(t), y_{2}(t)) $ is a solution of Eq (3.1) if and only if $ (x_{1}(t), x_{2}(t)) $ is a solution of Eq (1.2) with initial value $ (x_{1}(0), x_{2}(0)) = (y_{1}(0), y_{2}(0)) $.
The proof can be given easily as in [31], but such approach is not applied herein.
Theorem 3.1 For any given value $ (x_{1}(0), x_{2}(0)) = X_{0} $$ \in \mathbb{R}_{+}^{2} $, a unique solution $ (x_{1}(t), x_{2}(t)) $ exists for Equation (1.2) on $ t\geq 0 $ and the solution will remain in $ \mathbb{R}_{+}^{2} $ with probability one.
The proof of Theorem 3.1 is standard and is presented in Appendix A.
Theorem 3.2 The solutions of Eq (1.2) are stochastically ultimately bounded for any initial value $ X_{0} = (x_{1}(0), x_{2}(0))\in \mathbb{R}_{+}^{2} $.
The proof of Theorem 3.2 is presented in Appendix A.
4.
Long time behavior of Eq (1.2)
In this section, sufficient conditions for extinction and a series of persistence in the mean, such as non-persistence, weak persistence and strong persistence in the mean, are established. Furthermore, we obtain conditions to guarantee the stochastic permanence of the system. Before giving the main theorems, we introduce a lemma essential to our proofs.
Lemma 4.1. If $ \limsup\limits_{t\rightarrow\infty}\frac{\prod\limits_{0 < \tau_{k} < t}(1+\rho_{1k})}{ \text{ln}t} < \infty $, $ \limsup\limits_{t\rightarrow\infty}\frac{\prod\limits_{0 < \tau_{k} < t}(1+\rho_{2k})}{ \text{ln}t} < \infty $ hold, then for any initial value $ (x_{1}(0), x_{2}(0)) \in \mathbb{R}_{+}^{2} $, the solution $ X_{1}(t) = (x_{1}(t), x_{2}(t)) $ of Eq (1.2) satisfies
The proof of Lemma 4.1 is given in Appendix A.
4.1. Extinction and persistence of the system
The results about persistence in the mean and extinction of the prey and predator populations are presented in Theorems 4.1.1 and 4.1.2.
Theorem 4.1.1 For the prey population $ x_{1} $ of Eq (1.2), we have
(a) If $ \widehat{r}_{1} < 0 $, then the prey population $ x_{1} $ is extinct with probability 1, where $ r_{1}(t) = r(t)-0.5\sigma_{1}^{2}(t) $, $ \widehat{r}_{1} = \limsup\limits_{t\rightarrow+\infty}\frac{1}{t}[\sum\limits_{0 < \tau_{k} < t} \text{ln}(1+\rho_{1k})+\int_{0}^{t}r_{1}(s)ds] $.
(b) If $ \widehat{r}_{1} = 0 $, then the prey population $ x_{1} $ is non-persistent in the mean with probability 1.
(c) If $ \widehat{r}_{1} > 0 $ and $ \widehat{r}_{2} < 0 $, then the prey population $ x_{1} $ is weakly persistent in the mean with probability 1, where $ \widehat{r}_{2} = \limsup\limits_{t\rightarrow+\infty}\frac{1}{t}[\sum\limits_{0 < \tau_{k} < t} \text{ln}(1+\rho_{2k})+\int_{0}^{t}r_{2}(s)ds] $.
(d) If $ \check{r}_{1}-\langle \frac{\omega}{b}\rangle^{*} > 0 $, then the prey population $ x_{1} $ is strongly persistent in the mean with probability 1, where $ \check{r}_{1} = \liminf\limits_{t\rightarrow+\infty}\frac{1}{t}[\sum\limits_{0 < \tau_{k} < t} \text{ln}(1+\rho_{1k})+\int_{0}^{t}r_{1}(s)ds] $.
(e) If $ \widehat{r}_{1} > 0 $, the prey population $ x_{1}(t) $ holds a superior bound in time average, that is, $ \langle x_{1}(t)\rangle^{*}\leq\frac{\widehat{r_{1}}}{k^{l}}\triangleq M_{x} $.
Proof. (a) According to $ It\hat{o} $'s formula and Eq (3.1), the function can be expressed as
Taking integral on both sides of Eq (4.1) results in
We let $ N_{1}(t) = \int_{0}^{t}\sigma_{1}(s) \text{d}B_{1}(s) $, $ N_{2}(t) = \int_{0}^{t}\sigma_{2}(s) \text{d}B_{2}(s) $, where $ N_{i}(t) (i = 1, 2) $ is a local martingale with a quadratic variation satisfying $ \langle N_{1}, N_{1}\rangle_{t} = \int_{0}^{t}\sigma^{2}_{1}(s)ds\leq (\sigma^{u}_{1})^{2}t $, $ \langle N_{2}, N_{2}\rangle_{t} = \int_{0}^{t}\sigma^{2}_{2}(s)ds\leq (\sigma^{u}_{2})^{2}t $. Using the strong law of large numbers for martingales, we show that
Thus
Therefore,
Making use of Eq (4.2) and the superior limit as $ t\rightarrow\infty $ in Eq (4.4), we get $ \Big[\frac{ \text{ln}x_{1}(t)- \text{ln}x_{1}(0)}{t}\Big]^{*}\leq \widehat{r}_{1} < 0 $ which results in $ \lim\limits_{t\rightarrow\infty}x_{1}(t) = 0 $.
(b). According to the definition of superior limit and Eq (4.2), for an arbitrary $ \varepsilon > 0 $, there is a $ T > 0 $ satisfying $ \frac{1}{t}[\sum_{0 < \tau_{k} < t} \text{ln}(1+\rho_{1k})+\int_{0}^{t}r_{1}(s) \text{d}s]\leq \widehat{r}_{1}+\frac{\varepsilon}{2} $, $ \frac{N_{1}(t)}{t}\leq \frac{\varepsilon}{2} $ for all $ t > T $. Substituting the above inequalities into the first equation of (4.4), we easily show that
By virtue of Lemma 2.1, we obtain $ \langle x_{1}(t)\rangle^{*}\leq\frac{\varepsilon}{k_{*}} $. In accordance with the arbitrariness of $ \varepsilon $, we achieve the result.
(c). By virtue of Eq (4.2), superior limit and Lemma 4.1, we show that
Thus, $ \langle x_{1}(t)\rangle^{*} > 0 $ a.s. By reduction to absurdity, we can assume that for any $ \upsilon\in \{\langle x_{1}(t, \upsilon)\rangle^{*} = 0\} $, by Equation (4.6), we obtain $ \langle x_{2}(t, \upsilon)\rangle^{*} > 0 $. Meanwhile, using the superior limit for the second equation of (4.3) and $ \langle x_{1}(t, v)\rangle^{*} = 0 $ leads to
Therefore, $ \lim\limits_{t\rightarrow\infty} x_{2}(t, \upsilon) = 0 $. This expression is a contradiction. Then, $ \langle x_{1}(t)\rangle^{*} > 0 $ a.s.
(d). Under the condition $ \check{r}_{1}-\langle \frac{\omega}{b}\rangle^{*} > 0 $, an arbitrary $ \varepsilon > 0 $ satisfying $ \check{r}_{1}-\langle \frac{\omega}{b}\rangle^{*}-\varepsilon > 0 $ exists. According to the definition of superior limit, interior limit and Eq (4.2), for the above-mentioned positive constant $ \varepsilon $, there is a $ T > 0 $ satisfying $ \frac{1}{t}\big(\sum\limits_{0 < \tau_{k} < t} \text{ln}(1+\rho_{1k})+\int_{0}^{t}r_{1}(s) \text{d}s\big) > \check{r}_{1}-\frac{\varepsilon}{3}, \langle \frac{\omega}{b}\rangle < \langle \frac{\omega}{b}\rangle^{*}+\frac{\varepsilon}{3}, \frac{N_{1}(t)}{t} > -\frac{\varepsilon}{3} $, for all $ t > T $. Then, from Eq (4.3),
Using Lemma 2.1 and the arbitrariness of $ \varepsilon $, we have that
(e). Passing to the first equation of (4.3), we yield
Thus, $ \langle x_{1}(t)\rangle^{*}\leq\frac{\widehat{r}_{1} }{k^{l}}\triangleq M_{x} $, which is obtained by a similar process in the proof of conclusion (2) and is omitted.
Let $ (\bar{x}_{1}(t), \bar{x}_{2}(t)) $ be the solution of the following comparison equation
with initial value $ (x_{1}(0), x_{2}(0))\in \mathbb{R}_{+}^{2} $, then we hold the following theorem.
Theorem 4.1.2. For the predator population $ x_{2} $ of Eq (1.2),
(a) if $ k_{*}\widehat{r}_{2}+f^{*}\widehat{r}_{1} < 0 $, then the predator population $ x_{2} $ is extinct with probability 1;
(b) if $ k_{*}\widehat{r}_{2}+f^{*}\widehat{r}_{1} = 0 $, then the predator population $ x_{2} $ is non-persistent in the mean with probability 1;
(c) if $ \widehat{r}_{2}+\langle \frac{f\bar{x}_{1}}{1+a\bar{x}_{1}+b\bar{x}_{2}+ab\bar{x}_{1}\bar{x}_{2}}\rangle^{*} > 0 $, then the predator population $ x_{2} $ is weakly persistent in the mean with probability 1;
(d) if $ \widehat{r}_{2}+\langle \frac{f}{a}\rangle^{*} > 0 $, then the predator population $ x_{2}(t) $ has a superior bound in time average, that is, $ \langle x_{2}(t)\rangle^{*}\leq\frac{\widehat{r}_{2}+\langle \frac{f}{a}\rangle^{*}}{h^{l}}\triangleq M_{y} $;
(e) if $ \widehat{r}_{2} > 0, \widehat{r}_{1}\leq0 $, then the predator population $ x_{2} $ is weakly persistent.
Proof. (a). Case I. If $ \widehat{r}_{1}\leq 0 $, then by virtue of Theorem 4.1.1, we obtain $ \langle x_{1}(t)\rangle^{*} = 0 $. According to the definition of superior limit, for an arbitrary $ \varepsilon > 0 $, there is a $ T > 0 $ satisfying $ \frac{1}{t}[\sum\limits_{0 < \tau_{k} < t} \text{ln}(1+\rho_{2k})+\int_{0}^{t}r_{2}(s) \text{d}s] < \widehat{r}_{2}+\frac{\varepsilon}{2} $, $ \frac{N_{2}(t)}{t} < \frac{\varepsilon}{2} $ for all $ t > T $. By the second equation of (4.3), we noted
then $ \lim\limits_{t\rightarrow\infty}x_{2}(t) = 0 $.
Case II. If $ \widehat{r}_{1} > 0 $, by Eq (4.3), for the above constant $ \varepsilon > 0 $, there is a $ T_{1} > 0 $ such that $ \frac{ \text{ln}x_{1}(t)- \text{ln}x_{1}(0)}{t}\leq \widehat{ r}_{1}- k_{*}\langle x_{1}(t)\rangle +\varepsilon $, for all $ t > T_{1} $. Applying Lemma 2.1, we show that
Substituting the above inequality into the second equation of (4.3) and using the arbitrariness of $ \varepsilon $, we yield
Thus, $ \lim\limits_{t\rightarrow\infty}x_{2}(t) = 0 $.
(b). In (1), we prove that if $ \widehat{r}_{1}\leq 0 $, then $ \lim\limits_{t\rightarrow\infty}x_{2}(t) = 0 $, consequently, $ \langle x_{2}(t)\rangle^{*} = 0 $. At this point, we only need to show that if $ \widehat{r}_{1} > 0 $, then $ \langle x_{2}(t)\rangle^{*} = 0 $ is also valid. Otherwise, $ \langle x_{2}(t)\rangle^{*} > 0 $, and by Lemma 4.1, we obtain that $ [\frac{ \text{ln}x_{2}(t)}{t}]^{*} = 0 $. From Eq (4.11), we note that
Meanwhile, for any constant $ \varepsilon > 0 $, there is a $ T > 0 $ satisfying $ \frac{1}{t}[\sum_{0 < \tau_{k} < t} \text{ln}(1+\rho_{2k})+\int_{0}^{t}r_{2}(s) \text{d}s] < \widehat{r}_{2}+\frac{\varepsilon}{3} $, $ \langle f(t) x_{1}(t)\rangle \leq f^{*}\langle x_{1}(t)\rangle^{*}+\frac{\varepsilon}{3} $, $ \frac{N_{2}(t)}{t}\leq \frac{\varepsilon}{3} $ for all $ t > T $. By the second equation of (4.3),
Then, making use of Lemma 2.1, we achieve $ \langle x_{2}(t)\rangle^{*}\leq\frac{\widehat{r}_{2} +f^{*}\langle x_{1}(t)\rangle^{*}+\varepsilon}{h_{*}} $, which indicates that $ \langle x_{2}(t)\rangle^{*}\leq\frac{\widehat{r}_{2} +f^{*}\langle x_{1}(t)\rangle^{*}}{h_{*}} $. By virtue of Eq (4.10) and the arbitrariness of $ \varepsilon $, we obtain $ \langle x_{2}(t)\rangle^{*}\leq\frac{k_{*}\widehat{r}_{2} +f^{*}\widehat{r}_{1}}{h_{*}k_{*}} = 0 $. This is a contradiction. Therefore, $ \langle x_{2}(t)\rangle^{*} = 0 \quad a.s. $
(c). In the following, we show that $ \langle x_{2}(t)\rangle^{*} > 0 $ a.s.. By reduction to absurdity, for arbitrary $ \varepsilon_{1} > 0 $ and initial value $ (x_{1}(0), x_{2}(0))\in \mathbb{R}_{+}^{2} $, there is a solution $ (\check{x}_{1}(t), \check{x}_{2}(t)) $ of Eq (1.2) satisfying $ P\{\langle \check{x}_{2}(t)\rangle^{*} < \varepsilon_{1}\} > 0. $ Let $ \varepsilon_{1} $ be sufficiently small that
From the second equation of (4.3), it can be shown that
Herein, $ \check{x}_{1}(t)\leq \bar{x}_{1}(t) $, $ \check{x}_{2}(t)\leq \bar{x}_{2}(t) $, a.s. for $ t\in [0, +\infty) $. Note that
then
Construct the Lyapunov function $ V_{3}(t) = | \text{ln}\bar{x}_{1}(t)- \text{ln}\check{x}_{1}(t)| $, where $ V_{3}(t) $ is a positive function on $ \mathbb{R}_{+} $. By virtue of It$ \hat{o} $'s formula and Eq (4.9), we achieve the following expression:
Moreover, integrating the above inequality from 0 to $ t $ and dividing by $ t $ on both sides of the above inequality result in $ \frac{V_{3}(t)-V_{3}(0)}{t}\leq \omega^{u}\langle \check{x}_{2}(t)\rangle-k^{l}\langle |\bar{x}_{1}-\check{x}_{1}|\rangle $. Then we achieve
By substituting the above inequality into Eq (4.12) and taking the superior limit of the inequality, we obtain
Equation (4.14) contradicts Lemma 4.1, therefore $ \langle x_{2}(t)\rangle^{*} > 0 $ a.s. The proof is hence completed.
(d). By the second equation of (4.3), we obtain the following equation
Moreover, from the definition of superior limit and Eq (4.2), for the given positive number $ \varepsilon $, there is a $ T_{2} > 0 $ satisfying $ \frac{1}{t}[\sum\limits_{0 < \tau_{k} < t} \text{ln}(1+\rho_{2k})+\int_{0}^{t}r_{2}(s) \text{d}s] < \widehat{r}_{2}+\frac{\varepsilon}{3}, \langle \frac{f}{a}\rangle < \langle \frac{f}{a}\rangle^{*}+\frac{\varepsilon}{3}, \frac{N_{2}(t)}{t} < \frac{\varepsilon}{3} $, for all $ t > T_{2} $. In accordance with Lemma 2.1 and the arbitrariness of $ \varepsilon $, we easily achieve
The desired result is obtained.
(e). If $ x_{2}^{*} > 0 $ a.s is false, let $ \Omega = \{x_{2}^{*} = 0\} $, then $ P(\Omega) > 0 $. For an arbitrary $ \nu \in \Omega $, we have $ \lim\limits_{t\rightarrow\infty}x_{2}(t, \nu) = 0 $. From the second equation of (4.3) and by virtue of Eq (4.2), we show that $ [\frac{ \text{ln}x_{2}(t, \nu)}{t}]^{*} = \widehat{r_{2}} > 0 $ a.s. Then we follow that $ P\{[\frac{ \text{ln}x_{2}(t, \nu)}{t}]^{*} > 0\} > 0 $, which contradicts with Lemma 4.1. The result is then concluded.
Remark 1. By the proof of Theorem 4.1.2, we observe that if $ \widehat{r}_{1} < 0 $, then $ k_{*}\widehat{r}_{2}+f^{*} \widehat{r}_{1} < 0 $. Thus, if the prey species is extinct, then the predator species will also be extinct. This notion is consistent with the reality. Moreover, if $ \widehat{r}_{1} > 0 $ and $ k_{*}\widehat{r}_{2}+f^{*} \widehat{r}_{1} < 0 $, then even if the prey population is persistent, the predators end in extinction because of an excessively large diffusion coefficient $ \sigma_{2}^{2} $.
Remark 2. According to conclusion (5) of Theorem 4.1.2, with the effect of impulsive perturbations despite the regression of the prey population to extinction, the predator may remain weakly persistent.
4.2. Stochastic permanence
Theorem 4.2.1 If $ (\max\{\sigma_{1}^{u}, \sigma_{2}^{u}\})^{2}+2(\frac{\omega^{u}}{b^{l}}+g^{u}) < 2 \min\{r^{l}, \frac{f^{l}}{a^{u}}\} $ holds, then Eq (1.2) is stochastically permanent.
Proof. The whole proof is divided into two parts. First, we must prove that for arbitrary $ \varepsilon > 0 $, there is a constant $ \delta > 0 $ satisfying $ \text{P}_{*}\{|X_{1}(t)|\geq \delta\}\geq 1-\varepsilon $, where $ X_{1}(t) = (x_{1}(t), x_{2}(t)) $.
At this point, we show that for any initial value $ \overline{X}(0) $ $ = (y_{1}(0), y_{2}(0))\in \mathbb{R}_{+}^{2} $, the solution $ \overline{X}(t) = (y_{1}(t), y_{2}(t)) $ holds the property that
where $ \theta > 0 $ is a sufficiently small constant, such that
By virtue of Eq (4.16), there is an arbitrary constant $ p > 0 $ such that
Define $ V(y_{1}, y_{2}) = y_{1}+y_{2} $, then
Let $ U(y_{1}, y_{2}) = \frac{1}{V(y_{1}, y_{2})} $, according to the $ It\hat{o} $'s formula, we obtain
Under the condition of this theorem, a positive constant $ \theta $ can be chosen to satisfy Eq (4.16). By the Itô formula,
Then we choose $ p > 0 $ to be sufficiently small such that the term satisfies Eq (4.17). We define $ W(\overline{X}) = e^{pt}(1+U(\overline{X}))^{\theta} $ and consequently achieve
By Eq (4.17), a positive constant $ S $ satisfying $ \text{L}W(\overline{X})\leq Se^{pt} $ is easily noted. Consequently, $ \text{E}[e^{pt}(1+U(\overline{X}))^{\theta}]\leq (1+U(0))^{\theta}+\frac{S(e^{pt}-1)}{p} $ and then
Notably, $ (y_{1}+y_{2})^{\theta}\leq 2^{\theta}(y_{1}^{2}+y_{2}^{2})^{\frac{\theta}{2}} = 2^{\theta}|\overline{X}|^{\theta} $, where $ \overline{X} = (y_{1}, y_{2})\in \mathbb{R}_{+}^{2} $. Then, we obtain
and
where $ \overline{m} = \min\{m, \widetilde{m}\} $. Therefore, for arbitrary $ \varepsilon > 0 $, we let $ \delta = (\varepsilon\setminus \overline{M_{0}})^{\frac{1}{\theta}} $ in accordance with Chebyshev's inequality, thereby yielding
thus, $ \text{P}_{*}\{|X_{1}(t)|\geq\delta\}\geq 1-\varepsilon $.
In the following relations, we prove that for any $ \varepsilon > 0 $, there exists $ \chi > 0 $ satisfying $ \text{P}_{*}\{|X_{1}(t)|\leq\chi\}\geq 1-\varepsilon $. Define $ V_{4}(\overline{X}) = y_{1}^{q}+y_{2}^{q} $, herein $ 0 < q < 1 $ and $ \overline{X} = (y_{1}, y_{2})\in \mathbb{R}_{+}^{2} $, then by virtue of $ It\hat{o} $'s formula, we obtain the expression
Let $ n_{0} $ be a sufficiently large constant, such that $ y_{1}(0) $, $ y_{2}(0) $ remain within the internal $ [\frac{1}{n_{0}}, n_{0}] $. For each integer $ n\geq n_{0} $, we define the stopping time $ t_{n} = \inf \{t\geq 0: y_{1}(t) {\not \in}(1/n, n)\, \, or \, \, y_{2}(t) {\not \in}(1/n, n)\} $. Obviously, $ t_{n} $ increases as $ n\rightarrow +\infty $. Using $ It\hat{o} $'s formula again for $ \exp\{t\}V_{4}(\overline{X}) $ and accounting for the expectations on both sides, we show that
where $ K_{1}, K_{2} $ are positive constants. Letting $ n\rightarrow +\infty $ yields
Then, we achieve $ \limsup\limits_{t\rightarrow+\infty} \text{E}[\overline{X}^{q}(t)]\leq K_{1}+K_{2} $ and $ \limsup\limits_{t\rightarrow+\infty} \text{E}[X_{1}^{q}(t)]\leq \overline{M}^{q}(K_{1}+K_{2}) $, where $ \overline{M} = \max\{M, \widetilde{M}\} $. Therefore, at any given $ \varepsilon > 0 $, we let $ \chi = \frac{\overline{M}(K_{1}+K_{2})^{1/q}}{\varepsilon^{1/q}} $, by virtue of the Chebyshev inequality, we easily show that
Consequently, $ \text{P}_{*}\{|X_{1}(t)|\leq\chi\}\geq 1-\varepsilon $.
Theorem 4.2.1 is proven.
Remark 3. From the conditions of Theorem 4.2.1, we find that although the stochastic disturbance greatly influence the dynamical property of the system, the bounded impulsive perturbations do not affect the stochastic permanence of the model.
Remark 4. We should point out that the definition of stochastically permanent which requires that all species have positive upper bounds and at least one species has a positive lower bound, cannot demonstrate the permanence of all species. It has some limitations and deficiency. If there is only one species having a positive lower bound and all the other species go extinction, the system is still permanent. A new definition of stochastic permanence [31] may be more appropriate.
5.
Global attractiveness
In this section, we provide some sufficient criteria to ensure the global attractiveness of the Equation (1.2).
Theorem 5.1. For any initial value $ (y_{1}(0), y_{2}(0))\in \mathbb{R}_{2}^{+} $, $ (y_{1}(t), y_{2}(t)) $ is a solution of Eq (3.1) on $ [0, +\infty) $. Then almost every sample path of $ (y_{1}(t), y_{2}(t)) $ is uniformly continuous.
The proof of Theorem 5.1 is given in Appendix A.
Theorem 5.2. Suppose that constants $ \mu_{i} > 0 \, (i = 1, 2) $ satisfying $ \liminf\limits_{t\rightarrow \infty} A_{i}(t) > 0 $ exist, where
then Eq (1.2) is globally attractive.
Proof. Let $ (y_{1}(t), y_{2}(t)) $, $ (\tilde{y}_{1}(t), \tilde{y}_{2}(t)) $ be two arbitrary solutions of Eq (3.1) with initial value $ (y_{1}(0), y_{2}(0)) $, $ (\tilde{y}_{1}(0), \tilde{y}_{2}(0))\in \mathbb{R}_{+}^{2} $. Denote $ \tilde{\lambda}(t) = 1+a(t)\prod\limits_{0 < \tau_{k} < t}(1+\rho_{1k})\tilde{y}_{1}+b(t)\prod\limits_{0 < \tau_{k} < t}(1+\rho_{2k})\tilde{y}_{2} +a(t)b(t)\prod\limits_{0 < \tau_{k} < t}(1+\rho_{1k})\prod\limits_{0 < \tau_{k} < t}(1+\rho_{2k})\tilde{y}_{1}\tilde{y}_{2} $ and define a Lyapunov function as follows:
Then,
By the condition $ \liminf\limits_{t\rightarrow \infty} A_{i}(t) > 0 \, (i = 1, 2) $, constants $ \alpha > 0 $ and $ T_{0} > 0 $ satisfying $ A_{i}(t)\geq \alpha \, (i = 1, 2) $ exist for all $ t\geq T_{0} $. Moreover, we obtain the following relation
for all $ t\geq T_{0} $. By integrating Eq (5.2) from $ T_{0} $ to $ t $, we achieve
Consequently,
Then by $ V(t)\geq 0 $, we note that $ |y_{1}(t)-\tilde{y}_{1}(t)|\in \text{L}^{1}[0, +\infty), \quad|y_{2}(t)-\tilde{y}_{2}(t)|\in \text{L}^{1}[0, +\infty) $. Thus,
Next,
Therefore, the desired assertion is obtained by Theorem 5.1 and Lemma 2.2.
6.
Numerical simulations
In this section, some numerical simulations and examples are given to illustrate and augment our theoretical findings of Eq (1.2) by means of the Milstein method mentioned in Higham [35]. Moreover, the effects of impulsive and stochastic perturbations on population dynamics are discussed.
Example 1.
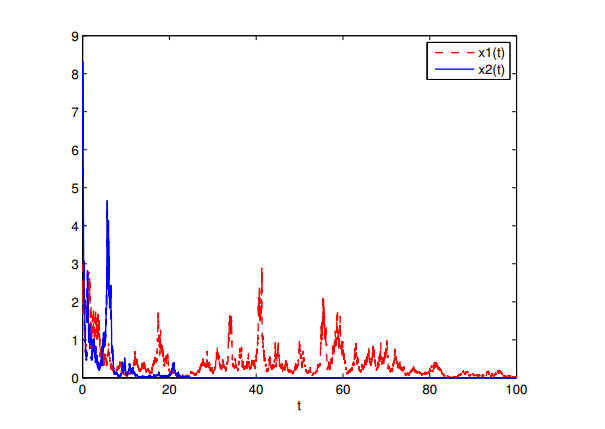
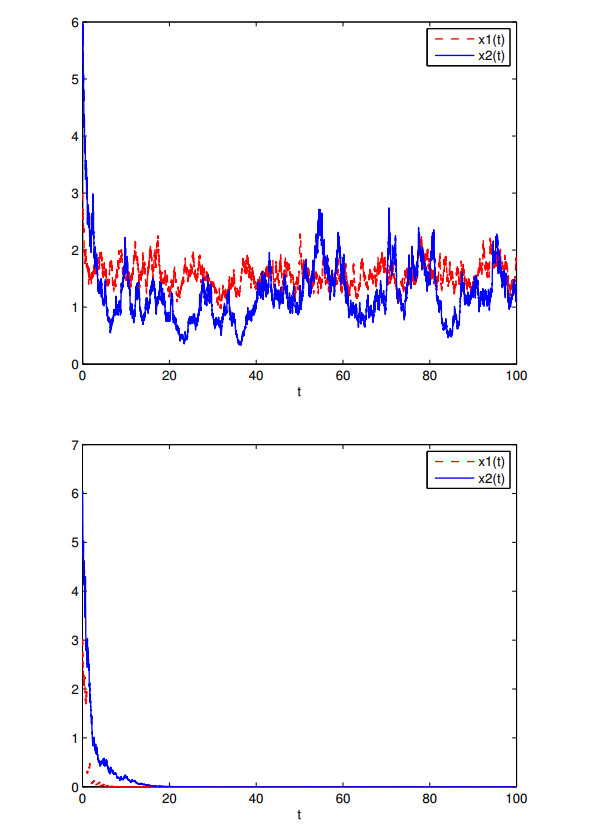
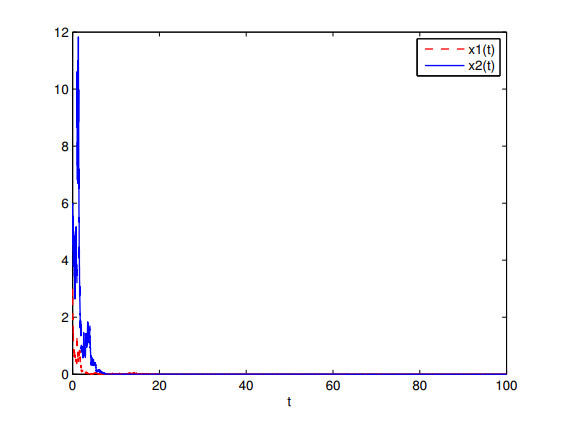
We set $ r(t) = 0.2+0.01 \sin t $, $ a(t) = 0.1+0.04 \sin t $, $ b(t) = 0.5+0.05 \sin t $, $ \frac{\sigma_{1}^{2}(t)}{2} = \frac{\sigma_{2}^{2}(t)}{2} = 0.3+0.02\sin t $, $ \rho_{1k} = \rho_{2k} = e^{(-1)^{k+1}\frac{1}{k}}-1 $ and $ \tau_{k} = k $, then it can be obtained that $ \widehat{r}_{1} = -0.1 < 0 $. By Theorems 4.1.1 and 4.1.2, both prey and predator populations ($ x_{1} $ and $ x_{2} $, respectively) regress to extinction, which is also further confirmed by Figure 1.
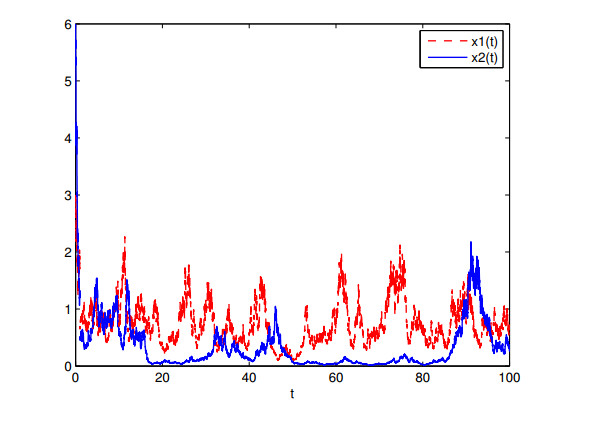
We then choose $ \frac{\sigma_{1}^{2}(t)}{2} = 0.3+0.02\sin t $, $ \frac{\sigma_{2}^{2}(t)}{2} = 0.4+0.02\sin t $, $ \rho_{1k} = \rho_{2k} = e^{(-1)^{k+1}\frac{1}{k}}-1 $, and $ r(t) = 0.4+0.01 \sin t $. The other parameters are the same as that in example 1, then $ \widehat{r}_{1} = 0.1 > 0 $, $ \widehat{r}_{2} = -0.6 < 0 $, and $ k_{*}\widehat{r}_{2}+f^{*}\widehat{r}_{1} = -0.116 < 0 $. In Figure 2, although the prey population $ x_{1} $ is weakly persistent in the mean, the predator population $ x_{2} $ end in extinction because of the effects of the white noises, which are of great importance in maintaining the coexistence of populations.
Example 2.
We let $ \frac{\sigma_{1}^{2}(t)}{2} = 0.1+0.05\sin t $, $ \frac{\sigma_{2}^{2}(t)}{2} = 0.1+0.02\sin t $, $ a(t) = 0.1+0.04 \sin t $, $ b(t) = 0.5+0.05 \sin t $ $ \rho_{1k} = \rho_{2k} = e^{-\frac{1}{k^{2}}}-1 $, and $ \tau_{k} = k $, then $ \widehat{r}_{1} = 0.5 > 0 $, $ \widehat{r}_{2} = -0.3 < 0 $. Both the prey and predator populations ($ x_{1} $ and $ x_{2} $, respectively) are weakly persistent in the mean of Figure 3.
Example 3.
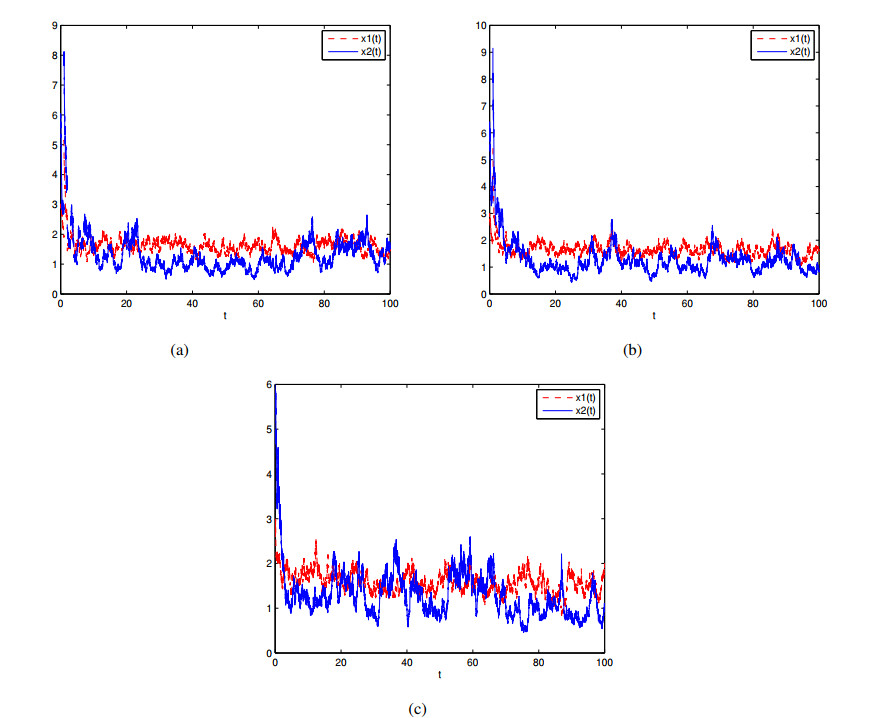
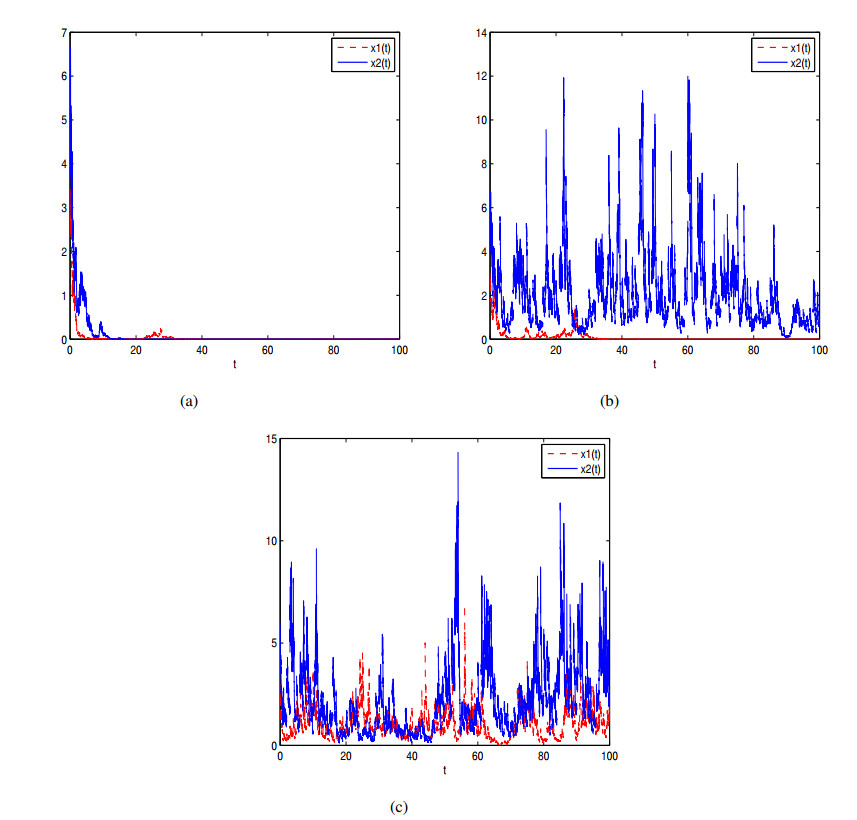
In Figure 4, we choose $ \sigma_{1}(t) = 0.2+0.02\sin t $, $ \sigma_{2}(t) = 0.3+0.02\sin t $, $ a(t) = 0.1+0.04 \sin t $, $ b(t) = 0.5+0.05 \sin t $, and the impulsive perturbations are (a) $ \rho_{1k} = \rho_{2k} = e^{\frac{(-1)^{k+1}}{k}}-1 $, (b)$ \rho_{1k} = \rho_{2k} = e^{\frac{1}{k^{2}}}-1 $, (c)$ \rho_{1k} = \rho_{2k} = 0 $. The conditions of Theorem 4.2.1 are satisfied in all of those cases and the Eq (1.2) displays stochastic permanence in Figure 4. Moreover, in Figure 4(a)-4(c), the bounded impulsive perturbations do not affect the stochastic permanence of the model.
Example 4.
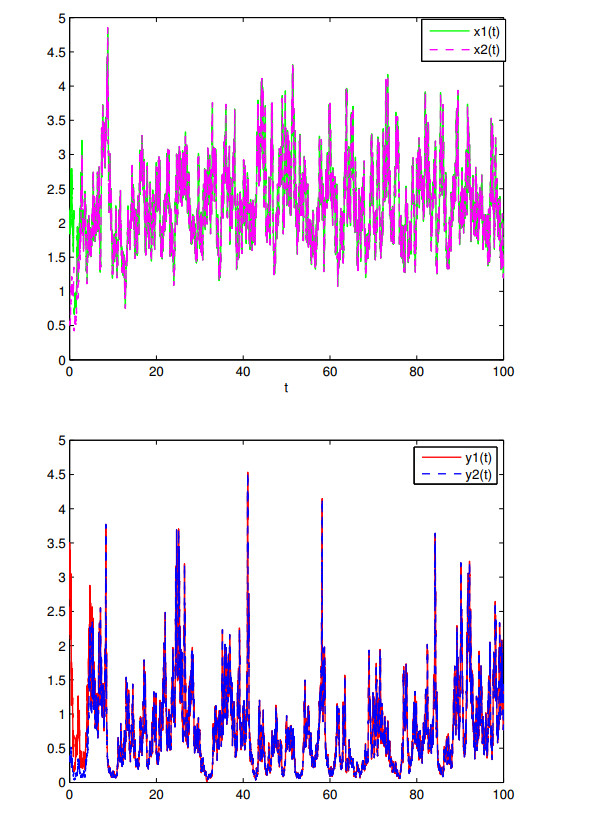
Set $ \frac{\sigma_{1}^{2}(t)}{2} = 0.1+0.05\sin t $, $ \frac{\sigma_{2}^{2}(t)}{2} = 0.6+0.02\sin t $, $ x_{1}(0) = 2 $, $ x_{2}(0) = 3 $, $ \tilde{x}_{1}(0) = 0.5 $, and $ \tilde{x}_{2}(0) = 0.3 $. We then observe from Figure 5 that Eq (1.2) is globally attractive.
In the following instance, the effects of negative and positive impulses on the species are investigated. We let $ \rho_{1k} = e^{-1.92}-1 $, $ \rho_{2k} = e^{-0.02}-1 $, and $ \tau_{k} = k $. The other parameters are the same as those in Example 3, then we obtain that $ \widehat{r}_{1} = -0.03 < 0 $ and $ \widehat{r}_{2} = -0.36 < 0 $. On the basis of Theorems 4.1.1 and 4.1.2, both the prey and predator populations end in extinction, which is further confirmed by Figure 6(b). By comparing Figure 6(a) with Figure 6(b), we observe that the negative impulses do not benefit species coexistence. Moreover, considering the impulsive perturbations are (a) $ \rho_{1k} = \rho_{2k} = 0 $, (b) $ \rho_{1k} = e^{\frac{1}{k^{2}}}-1 $, $ \rho_{2k} = e^{0.8}-1 $, (c) $ \rho_{1k} = \rho_{2k} = e^{0.8}-1 $ and the other parameters are the same as those in Example 1. Hence, the system can be altered from extinction to persistence with the effects of positive impulsive perturbations (Figure 7(a)-7(c)). Herein, persistence can be divided into two cases as follows: first, the predator population $ x_{2}(t) $ is weakly persistent and the prey population $ x_{1}(t) $ proceeds to extinction and second, both of the populations are persistent. Therefore, positive impulses are advantageous for the coexistence of ecosystems. Moreover, comparing figures 3 and 6, figures 1 and 7, we can derive that if the impulsive perturbations are unbounded, some properties may be changed significantly.
7.
Conclusions
In this paper, we propose a stochastic non-autonomous predator-prey system with impulsive perturbations and investigate the qualitative dynamic properties of the model. Under some sufficient conditions, we present the extinction and a series of persistence in the mean of the system, including non-persistence, weak persistence and strong persistence in the mean. Furthermore, we obtain the global attractivity of the model. From the assumptions of Theorems 4.1.1, 4.1.2 and 4.2.1, we demonstrate that the stochastic and impulsive disturbances greatly influence the extinction and persistence of the system. Positive impulses are advantageous for the coexistence of ecosystem, whereas negative impulses are not beneficial for species coexistence. Moreover, the results show that the bounded impulsive perturbations do not affect all the properties, such as the stochastic permanence of the model. However, if the impulsive perturbations are unbounded, some properties may be changed significantly.
Some interesting topics require further investigations. If we also consider the effects of time delays and telephone noise [36,37,38] on Eq (1.2) to propose a more realistic model, then how will the properties change? We leave it for future investigation.
Acknowledgments
This work is supported by The National Natural Science Foundation of China (11901110, 11961003), and the National Natural Science Foundation of Jiangxi (20192BAB211003, 20192ACBL20004).
Conflict of interest
The authors declare that they have no competing of interests regarding the publication of this paper.
Appendix A
Proof of Theorem 3.1. From Lemma 3.1, it suffices to show that Eq (3.1) has a unique solution, $ (y_{1}(t), y_{2}(t)) $, for all $ t\geq 0 $ and will remain in $ \mathbb{R}_{+}^{2} $ with probability one. The proof of this theorem is standard.
Let $ n_{0} > 0 $ be sufficiently large such that $ y_{1}(0) $, $ y_{2}(0) $ lie within the interval $ [1/n_{0}, n_{0}] $. For each integer $ n > n_{0} $, define the stopping times $ t_{n} = \inf \{t \in[0, t_{e}]: y_{1}(t) {\not \in}(1/n, n) \, or\, y_{2}(t) {\not \in}(1/n, n)\} $. Obviously, $ t_{n} $ is increasing as $ n\rightarrow +\infty $. Denote $ t_{+\infty} = {\lim\limits_{n\rightarrow +\infty}}t_{n} $, thus $ t_{+\infty}\leq t_{e} $. To complete the proof, it only needs to show $ t_{+\infty} = +\infty $ a.s. If the statement is not true, there exist two constants $ T > 0 $ and $ \varepsilon \in (0, 1) $, such that $ \text{P}\{t_{+\infty} < + \infty\} > \varepsilon $. Therefore, there is an integer $ n_{1}\geq n_{0} $ satisfying $ \text{P}\{t_{n}\leq T\}\geq\varepsilon $, for all $ n > n_{1} $.
Define a $ \bf{C}^{2} $-function $ V: \mathbb{R}_{+}^{2}\rightarrow \mathbb{R}_{+} $ by $ V(y_{1}, y_{2}) = (y_{1}-1- \text{ln}y_{1})+(y_{2}-1- \text{ln}y_{2}) $, then we obtain that $ V(y_{1}, y_{2}) $ is nonnegative. By virtue of $ It\hat{o} $'s formula, we achieve that
According to the negative coefficients of the quadratic terms, there is a positive number $ G $ satisfying
Thus
where $ t_{n}\wedge T = \min\{t_{n}, T\} $. Taking expectation yields that
Let $ \Omega_{n} = \{t_{n}\leq T\} $, then $ \text{P}(\Omega_{n})\geq \varepsilon $. For any $ w \in \Omega_{n} $, $ y_{1}(t_{n}, w) $ or $ y_{2}(t_{n}, w) $ equals either $ n $ or $ 1/n $, thus
Therefore it can be shown that
where $ 1_{\Omega_{n}} $ is the indicator function of $ \Omega_{n} $. Letting $ n \rightarrow +\infty $ leads to the contradiction.
So we obtain that $ t_{+\infty} = +\infty $ a.s. This completes the proof.
Proof of Theorem 3.2. Define $ V_{1}(y_{1}) = y_{1}^{p} $ and $ V_{2}(y_{2}) = y_{2}^{p} $, respectively, for $ (y_{1}, y_{2})\in \mathbb{R}_{+}^{2} $ and $ p > 1 $. According to the $ It\hat{o} $'s formula, we have
and
Taking expectation and then
and
For Eq (A.1), considering the following equation
with initial value $ v(0) = v_{0} $. Obviously, we can obtain that
Let $ t\rightarrow \infty $ and thus $ \lim\limits_{t\rightarrow +\infty}v(t) = \Big(\frac{r^{u}+0.5p(\sigma_{1}^{u})^{2}}{mk^{l}}\Big)^{p} $. Using the comparison theorem yields that $ \limsup\limits_{t\rightarrow +\infty} \text{E}[y_{1}^{p}(t)]\leq G_{1} < +\infty $, where $ G_{1} = (\frac{r^{u}+0.5p(\sigma_{1}^{u})^{2}}{mk^{l}})^{p} $. In the same way, we can achieve $ \limsup\limits_{t\rightarrow +\infty} \text{E}[y_{2}^{p}(t)]\leq G_{2} < +\infty $ and $ G_{2} = (\frac{f^{u}/a^{l}+0.5p(\sigma_{2}^{u})^{2}}{\widetilde{m}h^{l}})^{p} $.
Consequently, for a given constant $ \varepsilon > 0 $, there is a $ T > 0 $ satisfying $ \text{E}[y_{1}^{p}(t)]\leq G_{1}+\varepsilon $, $ \text{E}[y_{2}^{p}(t)]\leq G_{2}+\varepsilon $, for all $ t > T $. Considering the continuity of $ \text{E}[y_{1}^{p}(t)] $ and $ \text{E}[y_{2}^{p}(t)] $, there exist $ \overline{G_{1}}(p), \overline{G_{2}}(p) > 0 $ such that $ \text{E}[y_{1}^{p}(t)]\leq \overline{G_{1}}(p) $ and $ \text{E}[y_{2}^{p}(t)] \leq \overline{G_{2}}(p) $ for $ t\leq T $. Denote $ M_{1}(p) = \max\{\overline{G_{1}}(p), G_{1}+\varepsilon\} $, $ M_{2}(p) = \max\{\overline{G_{2}}(p), G_{2}+\varepsilon\} $, then for all $ t\in \mathbb{R}_{+} $,
and
Thus, for $ X_{1}(t) = (x_{1}(t), x_{2}(t))\in \mathbb{R}_{+}^{2} $, it is obvious that $ |X_{1}(t)|^{p}\leq 2^{\frac{p}{2}}[x_{1}^{p}(t)+x_{2}^{p}(t)] $. Therefore,
herein, $ M_{p} = 2^{\frac{p}{2}}(M^{p}M_{1}(p)+\widetilde{M}^{p}M_{2}(p)) $. By virtue of the Chebyshev inequality, the proof is completed.
Proof of Theorem 4.2. From Eq (3.1), we have
Construct the comparison equation
where $ (\bar{y}_{1}(t), \bar{y}_{2}(t)) $ is a solution of Eq (A.4) with initial value $ (y_{1}(0), y_{2}(0))\in \mathbb{R}_{2}^{+} $. According to the comparison theorem for stochastic differential equations ([33]) and Theorem 4.1 ([34]), we can obtain that $ \limsup\limits_{t\rightarrow\infty}\frac{ { \text{ln}}y_{1}(t)}{ \text{ln}t} \leq \limsup\limits_{t\rightarrow\infty}\frac{ \text{ln}\bar{y}_{1}(t)}{ \text{ln}t}\leq 1 $, $ \limsup\limits_{t\rightarrow\infty}\frac{ \text{ln}y_{2}(t)}{ \text{ln}t}\leq \limsup\limits_{t\rightarrow\infty}\frac{ \text{ln}\bar{y}_{2}(t)}{ \text{ln}t}\leq 1 $, a.s. Then,
Similarly, we have that $ \limsup\limits_{t\rightarrow\infty}\frac{ \text{ln}y_{2}(t)}{t}\leq 0 $. Therefore,
The proof is completed.
Proof of Theorem 5.1. The first equation of Eq (3.1) is equivalent to the following stochastic integral equation
Denote $ f_{1}(s) = y_{1}(s)\big(r(s)-k(s)\prod\limits_{0 < \tau_{k} < s}(1+\rho_{1k})y_{1}(s) -\frac{\omega(s)}{\lambda(s)}\prod\limits_{0 < \tau_{k} < s}(1+\rho_{2k})y_{2}(s)\Big) $, $ f_{2}(s) = y_{1}(s)\sigma_{1}(s), $ then
By virtue of the moment inequality for stochastic integrals, we can show that for $ 0\leq t_{1}\leq t_{2} $ and $ p > 2 $,
Thus, for $ 0 < t_{1} < t_{2} < \infty $, $ t_{2}-t_{1}\leq 1 $, $ \frac{1}{p}+\frac{1}{q} = 1 $ and by Eqs (A.6) and (A.7), we achieve
where $ F(p) = \max\{F_{1}(p), F_{2}(p)\} $. By Lemma 5 in [11] and the definition in [30], we obtain that almost every sample path of $ y_{1}(t) $ is locally but uniformly $ H\ddot{o}lder $-continuous with exponent $ \upsilon $ for every $ \upsilon \in (0, \frac{p-2}{2p}) $. Similarly, it can be proved that almost every sample path of $ y_{2}(t) $ is also uniformly continuous on $ t\geq 0 $. The proof is completed.









 DownLoad:
DownLoad: