Synchronization of the generalized Kuramoto model with time delay and frustration

1.   Introduction

Asymptotic collective behaviors of complex dynamical systems have recently attracted an increasing research interest in diverse disciplines such as physics, biology, engineering, ecology and social sciences ^{[1,2,3,4,29,30,31]}. The Kuramoto model has been proposed and studied ^[22,23,36] as a prototype model for synchronization, namely for phenomena where coupled oscillators adjust their rhythms through weak interactions. Due to the potential applications, there have been extensive studies on the emergent dynamics of the Kuramoto model ^{[5,8,11,13,15]}. The original Kuramoto model assumed the interactions between oscillators were instantaneous on an all-to-all network and depended sinusoidally on the phase difference. Later on, for the need of modeling real-world systems, more physical effects have been incorporated into the original Kuramoto model and have been widely investigated; for instance, frustration and inertia effects ^{[12,16,25,33]}, time-delayed interactions ^{[10,24,27,34]} and network topology ^[17,18,38].

In this paper, our interest lies in the emergent dynamics of the time-delayed Kuramoto model with frustration under general network topology. To fix the idea, we consider a weighted graph $\mathcal{G} = (\mathcal{V}, E, A)$, where $\mathcal{V} = \{1, \ldots, N\}$ and $E \subset \mathcal{V}\times \mathcal{V}$ are vertex and edge sets, respectively, and $A = (a_{ij})$ is an $N \times N$ capacity matrix whose element $a_{ij} \ge 0$ denotes the communication weight flowing from agent $j$ to $i$. More precisely, we assume the Kuramoto oscillators are located at the vertices of graph $\mathcal{G}$, and mutual interactions between oscillators are registered by $E$ and $A$. Let $\theta_i = \theta_i(t)$ be the phase of the $i$-th Kuramoto oscillator, $\tau_{ij} \ge 0$ the communication time delay and $\alpha_{ij}$ the frustration both flowing from $j$ to $i$. The dynamics of Kuramoto oscillators is governed by the following system

where $\tau : = \max_{1 \le i, j\le N} \tau_{ij}$, $\Omega_i$ and $K$ represents the natural frequency of $i$-th oscillator and the coupling strength, respectively, and the initial datum $\theta^0_i \in C^1[-\tau, 0]$ satisfies

Note that the well-posedness of the time-delayed system (1.1) can be found in ^[19], which proves the existence and uniqueness of the classical solutions to (1.1) for any continuous initial data.

Time delay effects are inevitably present due to the finite transmission of information in the real world; for instance, in the neural populations, arrays of lasers and microwave oscillators ^[32,37]. Moreover, vast studies on the Kuramoto model with time delays from the numerical and theoretical level indicate that the time-delayed interactions can induce rich dynamics such as multistability ^[21], multiple stable solutions ^[35], bistability between synchronized and incoherent states ^[37], discontinuous phase transitions ^[6] and more ^[27,28]. Additionally, it has been observed that the frustration effects are common and can generate richer dynamical phenomenon for the Kuramoto oscillators than those without frustration ^[9,39]. On the other hand, all-to-all coupling is a relatively ideal setting, and the non-all-to-all and asymmetric interactions are ubiquitous in the natural world. Hence, it is natural to take the time delay interactions, frustration effects and network topology into account in large coupled oscillator systems. However, the interplay of these effects increases the complexity of the Kuramoto system and causes difficulties in the analysis, mainly due to the lack of mean phase conservation law.

The closely related work to this paper can be found in ^{[7,10,14,20,34]}. More precisely, in the absence of time delay, the authors in ^[14] considered the Kuramoto model with heterogeneous frustrations on a complete network that is a small perturbation of the all-to-all coupling. It was shown that the initial configuration distributed in a half circle tends to the complete synchronization under the smallness assumption of frustrations. Moreover, in the presence of time delay, for an all-to-all coupled network, the Kuramoto oscillators with heterogeneous time delays were shown to achieve the frequency synchronization for the initial data restricted in a quarter circle ^[34]. Subsequenntly, for the initial phase configuration distributed in a half circle, under a sufficient regime in terms of small time delay and large coupling strength, synchronization of the Kuramoto model with uniform time delay was shown to occur ^[7] by using a Lyapunov functional approach. Moreover, in ^[20] the authors discussed the synchronized phenomenon for the Kuramoto oscillators with heterogeneous time delays and frustrations. For the initial data confined in a half circle, they showed the emergence of synchronization by the inductive analysis on the phase and frequency diameter. On the other hand, for general network topology, the authors in ^[10] investigated the emergent behaviors of the Kuramoto model with heterogeneous time delays on a general digraph containing a spanning tree. They required the initial configuration to be confined in a quarter circle for the frequency synchronization. To the best of our knowledge, there are few works on the emergent dynamics of the Kuramoto model with time delay interactions and frustration effects under general network topology.

The contributions of this paper are twofold. First, when the initial configuration is distributed in a half circle, we consider the asymptotic dynamics of (1.1) under the locally coupled network structure:

Note that under this network, all distinct vertices are reachable through at most two edges. In this case, we provide sufficient frameworks leading to the complete frequency synchronization in terms of small time delay and frustration and large coupling strength. To be more precise, we first show the existence of an invariant set, which suggests that the phase diameter is uniformly bounded by its initial one as time evolves. Next, we verify that all oscillators will be trapped into a small region confined in a quarter circle in finite time. Under this setting, we take a Lyapunov functional approach ^[7] to derive that the frequency diameter decays to zero exponentially fast. Second, for the initial data restricted in a half circle, we deal with a network topology of system (1.1) which is a small perturbation of the all-to-all coupled case:

where $\varepsilon$ is a small positive constant. Under this network structure, we apply the similar argument as in the aforementioned coupled case and present sufficient conditions on system parameters and initial data, which ultimately yields the emergence of frequency synchronization.

The rest of this paper is organized as follows. In Section 2, we provide the descriptions of our frameworks and main results. In Section 3, for the time-delayed Kuramoto model with frustration under the network structure (1.2), we present the exponential emergence of synchronization when the initial configuration is distributed in a half circle. In Section 4, under the network structure (1.3), we show that the frequency synchronization occurs exponentially fast for the initial data confined in a half circle. In Section 5, we present some numerical simulations and compare them with the analytic results. Section 6 is devoted to a brief summary of our work and some discussions on future issues.

2.   Frameworks and main resluts

In this section, we first introduce some notation which will be frequently used throughout the paper. Then we give our frameworks and provide main results on the frequency synchronization for the time-delayed Kuramoto model with frustration under different network structures.

Consider the Kuramoto model with heterogeneous time-delayed interactions and frustration effects under the locally coupled network:

with initial data $\theta^0_i(t) \in C^1[-\tau, 0]$. For a solution $\theta(t) = (\theta_1(t), \ldots, \theta_N(t))$ to (2.1), we introduce a frequency variable $\omega(t) = (\omega_1(t), \ldots, \omega_N(t))$ where we define $\omega_i(t) : = \dot{\theta}_i(t)$ for all $1 \le i \le N$. Next, for notational simplicity, we set several extremal and diameter functions and some other parameters as given below:

Assume there is no self time delay and self frustration, i.e., for all $1 \le i \le N$,

Moreover, we define by $D^\infty$ the dual angle of $D(\theta(0))$ satisfying

Note that the case $D(\theta(0)) = \frac{\pi}{2}$ will be studied separately (see Remark 3.1).

Now, we introduce the concept of complete frequency synchronization.

Definition 2.1. ^[7] Let $\theta(t) = (\theta_1(t), \ldots, \theta_N(t))$ be a solution to Kuramoto system (2.1), then the system exhibits a complete frequency synchronization iff the relative frequency differences tend to zero asymptotically:

2.1.   Preparatory estimates

In this part, we provide a preparatory estimate that states the frequency variable can be bounded from above.

Lemma 2.1. Let $\theta(t) = (\theta_1(t), \ldots, \theta_N(t))$ be a global classical solution to system (1.1), then the frequency variable is uniformly bounded from above:

where $\mathcal{M}$ is a positive constant depending on initial data and system parameters.

Proof. Due to the assumption on initial data, for $t \in [-\tau, 0]$, we see that

which implies that there exists a positive constant $\mathcal{M}_0$ such that

Next, for $t \in (0, +\infty)$, it follows from Eq (2.1) that for all $1 \le i \le N$,

Set

then we have

which derives the desired result.

2.2.   Main results

In this part, for the Kuramoto model (2.1) with frustration in the presence of time delay, we present our synchronization estimates under different network topology.

In what follows, we first introduce the framework $(\mathcal{A})$:

● ($\mathcal{A}_1$): The network structure of system (1.1) satisfies

Note that in this situation, the graph diameter, i.e., the largest distance between pairs of node, is no greater than two.

● ($\mathcal{A}_2$): The initial data and system parameters are subject to the following constraints:

Here, $\delta$ is a small positive constant and other parameters are defined in Eqs (2.2) and (2.3).

Remark 2.1. We make some comments on the framework $(\mathcal{A})$.

1. Note that the parameter $\delta$ is a suitable positive constant satisfying the condition (2.6). Remark that the choice of smallness of $\delta$ and $\alpha$ can guarantee the validity of condition (2.6).

2. Under the network structure (2.4), if there are no effects of time delay and frustration, i.e., $\tau = 0$ and $\alpha = 0$, then the constant $\delta$ in Eqs (2.6)–(2.9) can be zero. Moreover, the assumptions (2.6) and (2.8) can be removed. That is to say, the assumption $\mathcal{A}_2$ can be reduced to the following assumptions

This gives exactly the same assumptions on the complete frequency synchronization for the generalized Kuramoto model with absence of time delay and frustration in ^[11].

Now, we present our first theorem on the complete frequency synchronization for the time-delayed Kuramoto model (2.1) with frustration under the network structure ($\mathcal{A}_1$).

Theorem 2.1. Let $\theta(t) = (\theta_1(t), \ldots, \theta_N(t))$ be a solution to system (2.1) and suppose the framework $(\mathcal{A})$ holds. Then, there exists time $T^* \ge 0$ such that

where $C, \Lambda$ are positive constants.

In the following, we consider an interaction network concerning a small perturbation of an all-to-all coupled case, and discuss the collective synchronized behavior of the time-delayed Kuramoto oscillator with frustration. The framework $(\mathcal{B})$ is given as follows:

● $(\mathcal{B}_1)$: The network structure of system (2.1) satisfies

where $\varepsilon$ is a small positive constant. Note that in this setting, the network structure is close to the all-to-all network (i.e., $a_{ij} = \frac{1}{N}$) for small positive constant $\varepsilon$.

● $(\mathcal{B}_2)$: The initial configuration and system parameters satisfy the following conditions:

where $\tilde{\delta}$ is a small positive constant and other parameters are defined in Eqs (2.2) and (2.3).

Remark 2.2. We make some comments on the framework $(\mathcal{B}_2)$.

1. Note that the suitable choices of smallness of positive constants $\varepsilon, \tilde{\delta}$ and frustration $\alpha$ can guarantee the validity of condition (2.12).

2. If there is no perturbation of all-to-all coupling for the interaction network and no effects of time delay and frustration, i.e., $\varepsilon = \tau = \alpha = 0$, then the constant $\tilde{\delta}$ can be zero. Moreover, the assumptions (2.12), (2.14) and (2.15) can be gotten rid of, which means that the assumption (2.16) can be further reduced to the following form

This leads to exactly the same assumptions on the complete frequency synchronization for the original Kuramoto model in ^[5].

Actually, if we consider the all-to-all case, i.e., $a_{ij} = \frac{1}{N}$, which is a special case for network settings (2.4) and (2.10), then we have $\tilde{a} = 1$, $\bar{a} = \frac{1}{N}$ in Eq (2.6), and $\varepsilon$ in Eq (2.12) can be zero. Moreover, we see that the assumptions $(\mathcal{A}_2)$ and $(\mathcal{B}_2)$ can be reduced to exactly the same expressions as below,

Next, under the setting of framework $(\mathcal{B})$, we give our second theorem on the synchronization estimates for the Kuramoto model (2.1).

Theorem 2.2. Let $\theta(t) = (\theta_1(t), \ldots, \theta_N(t))$ be a solution to system (2.1) and suppose the framework $(\mathcal{B})$ holds. Then, there exists time $\tilde{T}^* \ge 0$ such that

where $\tilde{C}$ and $\tilde{\Lambda}$ are positive constants.

Subsequently, we will show our two main results in Theorem 2.1 and Theorem 2.2 in the following two sections.

3.   Synchronization estimate: Proof of Theorem 2.1

In this section, for the time-delayed Kuramoto model (2.1) with frustration and under the assumption $\mathcal{A}_1$ on the network structure, we will show the exponential emergence of frequency synchronization stated in Theorem 2.1. More precisely, under the sufficient regime in terms of small time delay and frustration and large coupling strength, we prove that all Kuramoto oscillators will concentrate into a small region in finite time. Moreover, based on the small uniform bound of phase diameter, we will show the frequency diameter tends to zero exponentially fast by taking a Lyapunov functional approach.

3.1.   Uniform bound estimate on the phase diameter

For this, we first present a lemma on the existence of an invariant set, which states that the phase diameter can be bounded by its initial one less than $\pi$. In general, the phase diameter $D(\theta(t))$ is not $\mathcal{C}^1$, so for the time derivative of $D(\theta(t))$, we use the upper Dini derivative defined by (see ^[26])

Lemma 3.1. Let $\theta(t) = (\theta_1(t), \ldots, \theta_N(t))$ be a solution to system (2.1) and suppose the framework $(\mathcal{A})$ holds, then we have

Moreover, we have

Proof. According to (1.1), it follows that

Here, we used

Moreover, owing to Lemma 2.1 and the facts that for all $t \ge 0$

it yields from (3.4) that

where we use the concave property of $\sin x, x \in [0, \pi]$, i.e.,

Due to the assumptions (2.9) and (3.5), one has

This together with (3.6) yields that

which means that $D(\theta(t))$ is strictly decreasing at $t = 0^+$. Next, we claim that

Suppose the contrary, i.e., there exists a time $t_*$ such that

which means that

Then, we apply Eq (3.7) and the similar analysis as in Eq (3.8) to get

This leads to a contradiction. Thus, we have

Moreover, based on the above estimate, we can follow the similar analysis in Eq (3.8) to obtain

Therefore, we combine Eqs (3.9) and (3.10) to derive the desired results.

Next, we show that under the framework $(\mathcal{A})$, the Karumoto oscillators will be trapped into a region confined in a quarter circle in finite time.

Lemma 3.2. Let $\theta(t) = (\theta_1(t), \ldots, \theta_N(t))$ be a solution to system (2.1) and suppose the framework $(\mathcal{A})$ holds, then there exists a time $T^* \ge 0$ such that

where $D^\infty$ is defined in Eq (2.3).

Proof. We consider two cases separately.

Case (i): If $D(\theta(0)) \in \left(0, \frac{\pi}{2}\right)$, then we have $D^\infty = D(\theta(0))$. Thus, the desired result yields from Eq (3.2) where we set $T^* = 0$.

Case (ii): If $D(\theta(0)) \in \left(\frac{\pi}{2}, \pi\right)$, in this case, when $D(\theta(t)) \in [D^\infty, D(\theta(0))]$ for $t \ge 0$, it follows from Lemma 3.1 and the assumptions on $K, \tau, \alpha$ in framework $(\mathcal{A}_2)$ that for $t \ge 0$,

where the second inequality holds using $\sin D(\theta(t)) \ge \sin D(\theta(0))$. This implies that $D(\theta(t))$ will strictly decrease into the interval $[0, D^\infty)$ at a speed greater than $K \tilde{a}\cos (\mathcal{M} \tau + \alpha) \sin D(\theta(0)) - D(\Omega) - 2KN\bar{a} \sin (\mathcal{M}\tau + \alpha)$. Therefore, it follows that

where

Remark 3.1. We discuss the case $D(\theta(0)) = \frac{\pi}{2}$ for the proof of Lemma 3.2. In fact, in this case, we can apply the the same argument as in Eq (3.8) to see that

where we use the assumptions in (2.6) and (2.9), which now become

This means that $D(\theta(t))$ starts to strictly decrease at $t = 0^+$. Therefore, together with the facts from (3.11), we can find a time $0 < t_0 \ll 1$ and a constant $\eta < \frac{\pi}{2}$ close to $\frac{\pi}{2}$ such that

As the system is autonomous, we can set the time $t_0$ as the initial time and replace the conditions on $D(\theta(0))$ in framework $(\mathcal{A}_2)$ by the above conditions on $\eta$. Then, we apply the same argument as in Lemma 3.1 and finally obtain

3.2.   Frequency synchronization estimate

In this part, under the conditions in framework $(\mathcal{A})$, we will show the exponential decay of frequency diameter by taking a Lyapunov functional approach.

To this end, we differentiate the system (1.1) with respect to time $t$ to obtain

It follows from Lemma 3.2 that there exists $T^* > 0$ such that

Then, for $t \ge T^*$, we further estimate $\theta_j(t-\tau_{ij}) - \theta_i(t) + \alpha_{ij}$ in the cosine function of system (3.12),

where we use the assumptions (2.6) and (2.8) in framework $(\mathcal{A}_2)$. Thus, for any $1 \le i, j\le N$, one has

where $\xi$ is defined in Eq (2.7). For the estimate of the dynamics of frequency diameter, we set

Similarly, the frequency diameter $D(\omega(t))$ is not $\mathcal{C}^1$ in general, thus we use the upper Dini derivative defined in Eq (3.1) for the time derivative of $D(\omega(t))$. Now based on the estimate in Eq (3.13), we present a differential inequality on the frequency diameter in the lemma below.

Lemma 3.3. Let $\theta(t) = (\theta_1(t), \ldots, \theta_N(t))$ be a solution to system (2.1) and suppose the framework $(\mathcal{A})$ holds, then we have

where $\Delta_\tau(t)$ is defined in Eq (3.14).

Proof. According to Eq (3.12), we estimate the dynamics of frequency diameter for $t \ge T^*$,

For the estimate of $\mathcal{I}_1$ in Eq (3.15), we have

{where we used that, by Eq (3.14), for any $1 \le i, j \le N$, }

For the estimate of $\mathcal{I}_2$ in Eq (3.15), similarly, we get

Then, we combine Eqs (3.15), (3.16) and (3.18) to obtain

which finishes the proof.

We next provide a rough estimate on the time derivative of frequency variables which is presented in the following lemma.

Lemma 3.4. Let $\theta(t) = (\theta_1(t), \ldots, \theta_N(t))$ be a solution to Eq (2.1) and suppose the framework $(\mathcal{A})$ holds, then we have

where $\Delta_\tau(t)$ is defined in Eq (3.14).

Proof. We see from Eq (3.12) that

Taking the maximum on both sides of the above inequality for $1 \le i \le N$, we obtain

Now we are ready to prove our one main result in Theorem 2.1 on the asymptotic frequency synchronization for the Kuramoto model (2.1) under the framework $(\mathcal{A})$. We follow ^[7] to define a Lyapunov functional

where the parameter $\mu$ is a positive constant satisfying

Note that the inequalities

are guaranteed by the assumption on $\tau$ in $(2.8)_2$, i.e.,

Actually, the argument on the Lyapunov functional approach in ^[7] is generalized here to the more general setting.

Proof of Theorem 2.1:

Proof. It follows from Lemma 3.3 and Lemma 3.4 that

In what follows, we estimate the sign of coefficients of $\Delta_\tau(t)$ and $D(\omega(t))$ in Eq (3.21). In fact, it can be seen from Eq (3.20) that

and

Hence, we combine Eqs (3.19), (3.21)–(3.23) to get

where

Then, it follows from Eqs (3.19) and (3.24) that

Therefore, we complete the proof of Theorem 2.1.

4.   Synchronization estimate: Proof of Theorem 2.2

In this section, under the network structure $(\mathcal{B}_1)$, we will provide a detailed proof of our second main result in Theorem 2.2 for the Kuramoto model (2.1) with frustration in the presence of time delay. The presentation in this section will be similar to that in Section 3.

4.1.   Uniform bound estimate on the phase diameter

In this part, we first show the existence of an invariant set for the Kuramoto flow (2.1) under the framework $(\mathcal{B})$.

Lemma 4.1. Let $\theta(t) = (\theta_1(t), \ldots, \theta_N(t))$ be a solution to system (2.1) and suppose the framework $(\mathcal{B})$ holds, then we have

Moreover, we have

where $\mathcal{M}$ is given in Lemma 2.1.

Proof. According to Eq (2.1), it follows that

Owing to the network structure assumption (2.10) and following form (4.3), one has

Moreover, we can apply the similar argument in Eqs (3.4)–(3.6) to derive

where we used the Lemma 2.1 and assumptions (2.12), (2.15), and the last inequality holds due to the assumption (2.16) on $K$. This means that $D(\theta(t))$ starts to strictly decrease at $t = 0^+$. We claim that

Suppose the contrary, i.e., there exists a time $t_*$ such that

which implies that

Then, we apply the similar analysis from Eq (4.5) together with Eq (4.6) to obtain

This contradicts to Eq (4.7). Thus, we have

Moreover, owing to Eq (4.8), we can follow the similar analysis as in Eq (4.5) to derive

Therefore, we combine Eqs (4.8) and (4.9) to complete the proof of this lemma.

Next, we present that under the restriction of framework $(\mathcal{B})$, all Kuramoto oscillators will shrink to a region with a geometric length less than $\frac{\pi}{2}$ in finite time.

Lemma 4.2. Let $\theta(t) = (\theta_1(t), \ldots, \theta_N(t))$ be a solution to system (2.1) and suppose the framework $(\mathcal{B})$ holds, then there exists time $\tilde{T}^* \ge 0$ such that

where $D^\infty$ is defined in Eq (2.3).

Proof. We consider two cases seperately.

Case (i): If $D(\theta(0)) \in \left(0, \frac{\pi}{2} \right)$, then we have $D(\theta(0)) = D^\infty$. Thus, the desired result yields from Eq (4.1) where we set $T^* = 0$.

Case (ii): If $D(\theta(0)) \in \left(\frac{\pi}{2}, \pi\right)$, in this case, when $D(\theta(t)) \in [D^\infty, D(\theta(0))]$ for $t\ge0$, it follows from Eq (4.2) and assumptions in Eqs (2.15) and (2.16) that

where the second inequality holds using $\sin D(\theta(t)) \ge \sin D(\theta(0))$. This implies that $D(\theta(t))$ will strictly decrease into the interval $[0, D^\infty]$ at a speed greater than $K \cos (\mathcal{M}\tau + \alpha) \sin D(\theta(0)) - (D(\Omega) + 2K \varepsilon + 2K \sin (\mathcal{M}\tau + \alpha))$. Then, it follows that

where

Remark 4.1. In the proof of Lemma 4.2, for the case $D(\theta(0)) = \frac{\pi}{2}$, we can use the similar analysis as in Remark 3.1 to find a time $\tilde{t}_0$ and a constant $\tilde{\eta} < \frac{\pi}{2}$ such that

4.2.   Frequency synchronization estimate

In this part, under the assumptions in framework $(\mathcal{B})$, we will present that the frequency diameter decays to zero exponentially fast by taking a similar method used in subsection 3.2.

For this, we differentiate the system (2.1) to obtain

Combing Lemma 4.2 and the assumptions in Eqs (2.12) and (2.15), we apply the similar argument in Eq (3.13) to obtain

where $\zeta$ is defined in Eq (2.14).

We now provide a differenital inequality for the frequency diameter $D(\omega(t))$ in the lemma below.

Lemma 4.3. Let $\theta(t) = (\theta_1(t), \ldots, \theta_N(t))$ be a solution to system (2.1) and suppose the framework $(\mathcal{B})$ holds, then we have

where $\Delta_\tau(t)$ is defined in Eq (3.14).

Proof. We see from Eq (4.10) that

where we applied Eq (3.17). Similarly, one has

Then, it yields from Eqs (4.11)–(4.13) that

This completes the proof.

We next provide a rough estimate on the time derivative of frequency variables.

Lemma 4.4. Let $\theta(t) = (\theta_1(t), \ldots, \theta_N(t))$ be a solution to system (2.1) and suppose the framework $(\mathcal{B})$ holds, then we have

Proof. According to Eqs (4.10) and (3.17), we see that

Taking the maximum on both sides of above inequality for $1 \le i \le N$, we derive

This yields the desired result.

Now we are ready to prove our second main result in Theorem 2.2 for the Kuramoto model (2.1) under the framework $(\mathcal{B})$.

Proof of Theorem 2.2:

Proof. Similarly, we define the Lyapunov functional

Here, the parameter $\mu$ is a positive constant satisfying the following constraints

Note that the above formula is well defined since

are ensured by the assumption on $\tau$ in Eq $(2.15)_2$, namely,

Then, according to Lemma 4.3 and Lemma 4.4, we have

In the following, we study the sign of coefficients of $\Delta_\tau(t)$ and $D(\omega(t))$ in Eq (4.16). Actually, owing to Eq (4.15), one has

and

Therefore, we combine Eqs (4.16)–(4.18) to get

where

Then, it yields from Eqs (4.14) and (4.19) that

which completes the proof of Theorem 2.2.

5.   Simulations

In this section, we provide several numerical simulations and compare them with the analytic results in Theorem 2.1 and Theorem 2.2. For the numerical examples, we use the fourth-order Runge-Kutta method and choose the number of oscillators $N = 5$ with the constant initial data.

We first give the examples concerning our main result in Theorem 2.1. For this, the network topology is given as below

which satisfies the network structure $\mathcal{A}_1$ since $\tilde{a} = 1 > 0$. Note that $\bar{a} = 1$. Moreover, we use the parameters

Once the above parameters are fixed, we choose the following small frustration, small time delay and large coupling strength

which satisfy the conditions in framework $(\mathcal{A}_2)$:

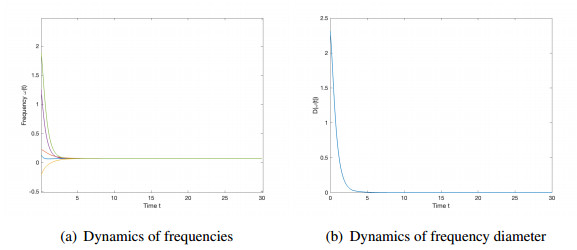
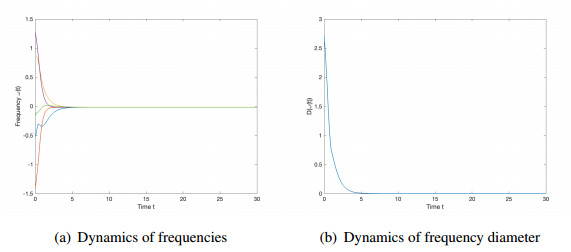
Then, based on the settings (5.1)–(5.3), the synchronized behavior can be seen from Figure 1, which supports Theorem 2.1.

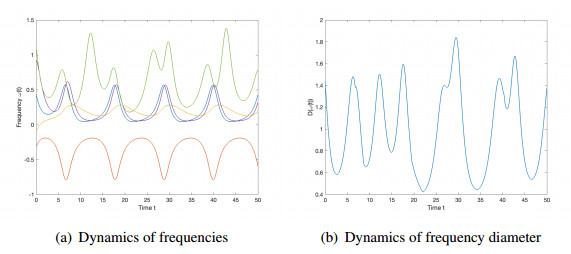
When other parameters in Eqs (5.1) and (5.2) do not change, we take relatively small coupling strength $K = 0.3$ with $\alpha = 0.005, \tau = 0.001$ and thus the condition in Eq (2.9) is not satisfied, i.e.,

Then, we observe from Figure 2 that frequency synchrony is not reached. However, our assumptions in $(\mathcal{A}_2)$ are not optimal. For example, it can be observed from Figure 3 that synchronized behavior can also emerge for the selected parameters $\alpha = 1, \tau = 0.1, K = 1$ which do not fit the framework $(\mathcal{A}_2)$.

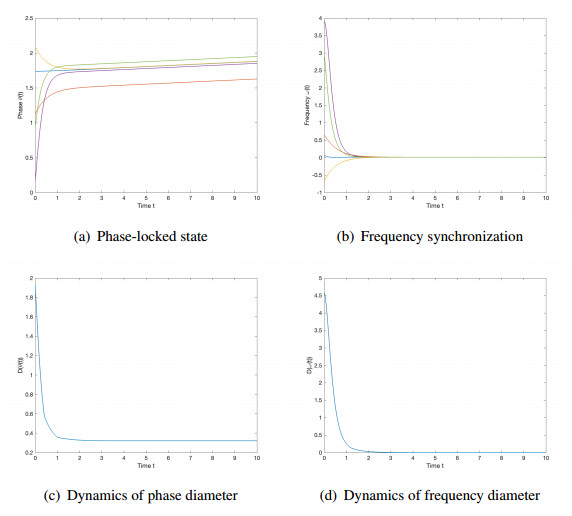
Next, we present simulation examples related to the main result in Theorem 2.2. We choose $\varepsilon = 0.1$ and the adjacency matrix is given as below

which satisfies the network structure $(\mathcal{B}_1)$. Moreover, we use the parameters

For the above fixed parameters, we further select small frustration, small time delay and large coupling strength as below

which are subject to the conditions in the framework $(\mathcal{B}_2)$:

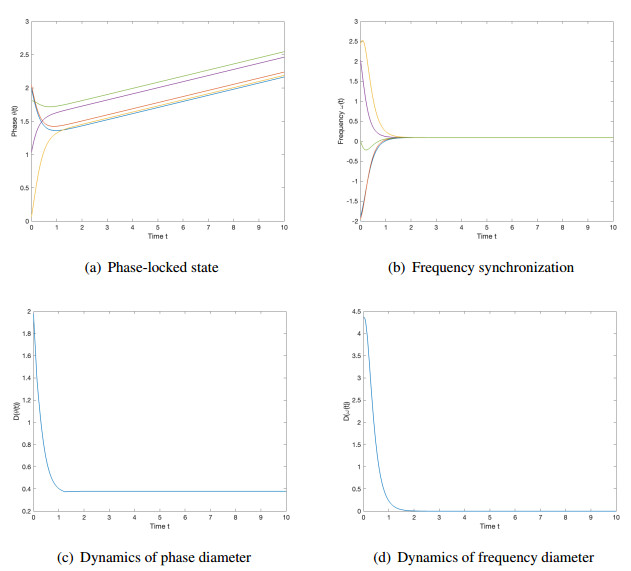
Then, based on the settings in Eqs (5.5)–(5.7), we observe from Figure 4 that frequency synchronization occurs which supports Theorem 2.2. On the other hand, based on the unchanged settings (5.5) and (5.6), we choose relatively small coupling strength $K = 1$ with $\alpha = 0.05, \tau = 0.005$, which does not cater to the condition in Eq (2.16) since

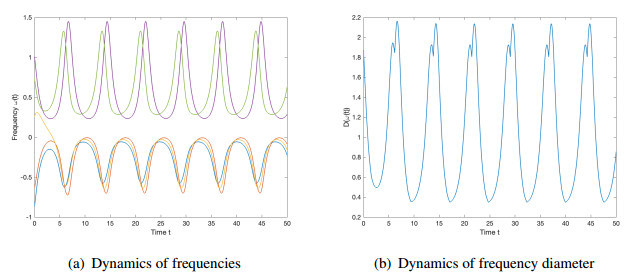
Then, it is observed from Figure 5 that the complete synchronization does not occur. Similarly, our assumptions in $(\mathcal{B}_2)$ are not optimal. For instance, when we select the parameters $\alpha = 1, \tau = 0.5, K = 2$ which do not fit the framework $(\mathcal{B}_2)$, we see from Figure 6 that synchronized behavior also occurs.

6.   Summary

In this paper, we studied the synchronized behaviors of the generalized Kuramoto model with heterogeneous time delay and heterogeneous frustration. More precisely, for the time-delayed Kuramoto model with frustration whose initial configuration is confined in a half circle, under two different network structures, we presented sufficient conditions leading to the exponential occurrence of complete frequency synchronization. Our frameworks related to the case with small time delay, small frustration and large coupling strength. As the network structures we considered here were limited, in our future work, we will continue to investigate the asymptotic behaviors on a more generally digraph such as containing a spanning tree.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The work of T. Zhu is supported by the National Natural Science Foundation of China (Grant/Award Number: 12201172), the Natural Science Research Project of Universities in Anhui Province, China (Project Number: 2022AH051790) and the Talent Research Fund of Hefei University, China (Grant/Award Number: 21-22RC23).

Conflict of interest

The authors declare there is no conflict of interest.