1. Introduction
In the past decade, information technology has gotten a rapid development, and is playing an important role in industry, commerce and humans' daily life. Computers, the most primary carriers of the advanced technique, are the requisite hardware of the modern science. However, computers have to face the threaten of worm and virus which are the biggest menace to the normal operation[16,14]. Generally, the operators do not know the existence of the computer worm, least of all how and when their computers have been infected. Worm and virus are always attached to a junk mail, masqueraded as innocent files for downloading, even ensconced in a code spreading through the Internet[5]. The dissemination of the worm and virus only needs someone to open the host file, then the worm and virus can transmit automatically without any additional operation[30]. Up to now, computer worm and virus can averagely cause billions of economic damage every year. To the operators, the direct results caused by infectious, such as causing system collapse, occupying computer RAM and demolishing existence data etc, always make them pay a heavy price. In response, updating antivirus software and patching operating system are two primary protections.
Recently, some researchers described the transmission and prevention of computer worm and virus with the state feedback compulsive model, and they have got some interesting results[7,12,27]. In their models, when the number of infected computers reaches a certain level the impulsive control will be triggered. Then new antivirus software will be published and installed, operating system will be patched to the latest version. All those activities happened instantaneously, and they are depicted as an impulse in the model.
However, the published researches all assume the diffusion of worm and virus is linear with the number of infected and susceptible computers which goes against the truth. In fact, at the initial period of a certain transmission, among the huge number of healthy computers connected with the Internet, only few of them have the opportunity to touch the virus[9,22,31]. And following the development, the infectious rate can not keep being linear with the infected and susceptible ones if the infected computers are numerically superior. So it is proper to describe the infectious with saturated transmission, and we will study the impulsive control of computer virus under this spreading fashion.
The remaining of this paper is arranged as follows: we set up the model and introduce some preliminaries in section 2; the existence, uniqueness and stability of order-1 limit cycle are analyzed in section 3; finally, some numerical simulation are showed to confirm the result and some deeper discussion is carried out in section 4.
2. Modeling and preliminaries
Enlightened by the development in the field of impulsive control and the progress of infectious disease study [19,29,25,26], all the computers connected with the Internet are divided into two disjoint groups: S(t) and I(t), which also present the number of individuals in each group at time t. The computers in group S are healthy ones and can be infected by the computer worm and virus, and group I is made up of individuals that are infected and they can transform worm and virus to members of S. In the present research[12,27], the incidence form are assumed as the simple item βSI which is contravened with the truth. In fact, the incidence is not remarkably effected by the number of susceptible ones when S occupies a considerable large proportion of the population, especially during the first spreading stage of a certain computer worm or virus. According to these truth, saturated incidence coincides with the real situation more closely.
Considering objectively, we make the following assumptions:
(1) all the new emerging computers are susceptible ones, and the rate is K;
(2) rejection rate is not affected by the computer worm and virus, and both suceptibles and infectives are sifted out from the Internet at rate μ;
(3) the transmission incidence is βSI1+αS which means the incidence is approximately βαI when the number of susceptibles S is relatively large;
(4) ˉI is assumed as the threshold that the computer virus can be discovered.
When infectives is less than ˉI, the computer virus spreads freely, and in case the number of infectives reaches ˉI, the computer worm and virus can be detected. Then the super-version antivirus software and operating system patch program will be published and a percentage of computers (both suceptibles and infectives) will upgrade their antivirus softwares and patch their operating systems. After these operations, those computers are immune to the certain computer worm or virus and get away from the virus spreading system. We define the upgrading rate of suceptibles and infectives are σ1 and σ2 separately. Following these assumptions, the spreading and control process can be explicated with the state feedback impulsive model
|
{dSdt=K−βSI1+αS−μS,dIdt=βSI1+αS−μI,I<ˉI, ΔS=−σ1S, ΔI=−σ2I,I=ˉI.
|
(1)
|
Considering the practical significance, all the parameters in this paper are positive, σ1∈(0,1), σ2∈(0,1) and system (1) is only considered in space R+2={(S,I)|S≥0,I≥0}.
In the reminder part of this section, we introduce some definitions and lemmas to support the proof of the existence and stability of the order-1 limit cycle of system (1).
Definition 2.1 (19-25) A typical state feedback impulsive differential model can be defined as
|
{dxdt=P(x,y), dydt=Q(x,y), (x,y)∉M{x,y},Δx=α(x,y), Δy=β(x,y), (x,y)∈M{x,y},
|
(2)
|
and can be denoted by (Ω,f,φ,M). The solution sources from any point P in the plane R2∖M{x,y}, i.e. P∈Ω=R2∖M{x,y}. φ(x,y)=(α(x,y),β(x,y)) is defined as an impulsive mapping, φ is continuous. After the impulsive mapping, x+=x+α(x,y) and y+=y+β(x,y), (x,y)∈M, all the points (x+,y+) form a set N. Here, we call M and N impulse set and phase set respectively, and they can be lines or curves in the plane R2.
Definitions of successor function and order-1 periodic solution of state feedback impulsive dynamic system are also vitally important in the research.
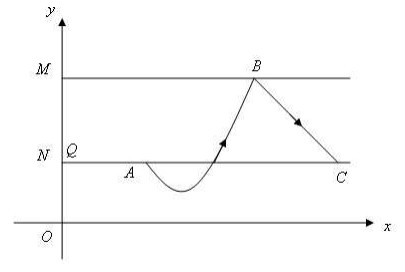
Definition 2.2. [2,21,15] Simply suppose the impulse set M and the phase set N of system (2) are two straight lines respectively(see Fig. 1), and the intersection of phase set N and y axis is Q. To any point A∈N, the coordinate of A, denoted by a, can be defined as the distance between A and Q. The solution trajectory originating from A intersects impulse set M at point B, then the impulsive function φ maps B to point C in phase set N, then C is called the subsequent point of A, and its coordinate is c. The successor function of A is defined as a continuous function F(A)=c−a. If C locates in the same point of A, then the trajectory segment ^AB is an order-1 periodic solution, and the orbit ^AB∪¯BA is said to be an order-1 limit cycle.
Remark 1. The necessary and sufficient condition that the solution passing point A forms an order-1 periodic solution is F(A)=0.
Lemma 2.3. [2,21,15] To a state feedback impulsive dynamic system (Ω,f,φ,M), there exist two points B and C in phase set N, if F(B)⋅F(C)<0, then there must exist a point A between B and C satisfying F(A)=0, and the solution f(A,t) forms an order-1 periodic solution.
3. Qualitative analysis of the uncontrolled system
Without counting the impulsive control measure, system (1) can be simplified as
|
{dSdt=K−βSI1+αS−μS,dIdt=βSI1+αS−μI,
|
(3)
|
system (3) is called uncontrolled system of (1). Change the variables with linear transform t=(1+αS)τ and still use t as the independent variable, then system (3) changes into
|
{dSdt=−βSI+(K−μS)(1+αS),dIdt=βSI−μI(1+αS).
|
(4)
|
3.1. Equilibria
It is obvious that system (4) has two equilibria E1(Kμ,0) and E2(S∗,I∗), where
|
S∗=μβ−μα and I∗=(K−μS∗)(1+αS∗)βS∗=Kμ−μβ−μα.
|
E1 is a marginal equilibrium, while E2 is the only positive equilibrium in case of
In the following discussions, we assume condition (5) is satisfied consistently. The Jacobian matrix of E1 is
|
JE1=(−μ−αK−βKμ0βKμ−μ−αK),
|
D<0, so E1 is a saddle. To positive equilibrium E2(S∗,I∗), its Jacobian matrix is
|
JE2=(−Kμ(β−μα)−αμ2β−μα−βμβ−μαKμ(β−μα)−μ0).
|
Assume λ1 and λ2 are two roots of the characteristic equation, then
|
λ1+λ2=−Kμ(β−μα)−αμ2β−μα<0 and λ1⋅λ2=βμβ−μα(Kμ(β−μα)−μ)>0,
|
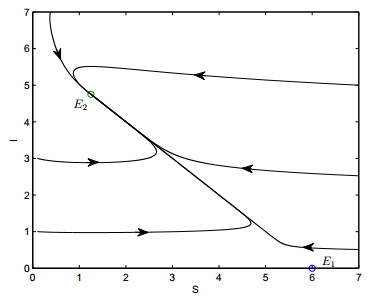
so E2 is a locally stable node or focus (see Fig. 2).
3.2. Uniform boundedness
In this part, we will consider the uniform boundedness in the first quadrant. From system (4), we can find that
is vertical isoclinic line, and
are horizontal isoclinic lines.
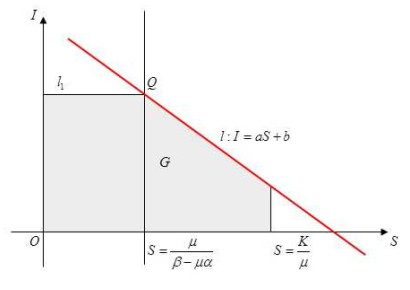
Following the succeeded statement, we select a piece of bounded region (see Fig. 3). Designate a line l:I=aS+b, where a<0,b>0. Line l intersects S=μβ−μα at point Q, and then make a horizontal straight line l1 passing point Q. Denote the region bounded by l,l1,S=0,I=0 and S=Kμ as G. Then we discuss the existence of proper a and b satisfying that G is attracted.
Assume φ=I−aS−b, then
|
dφdt=dIdt−adSdt=(1+a)aβ⋅x2+[bβ(1+a)−α(aK+bμ)]⋅x−(aK+bμ).
|
(6)
|
Set a=−1 and b=Kμ+1>0, then dφdt<0,∀S∈(μβ−μα,Kμ). Considering the character of system (4), bounded region G is attracted.
3.3. Inexistence of limit cycle
Assume Dulac function u(S,I)=1SI, and let
|
{dSdt=−βSI+(K−μS)(1+αS)Δ=P(S,I),dIdt=βSI−μI(1+αS)Δ=Q(S,I),
|
(7)
|
then
|
{dSdt=u(S,I)P(S,I)=−βSI+(K−μS)(1+αS)Δ=P1(S,I),dIdt=u(S,I)Q(S,I)=βSI−μI(1+αS)Δ=Q1(S,I).
|
(8)
|
It is obvious that ∂P1∂S+∂Q1∂I=−μαI−KS2I<0, then following Dulac Theorem system (4) has no limited cycle.
Basing on the above discussion, if condition (5) is satisfied, then there exists only one positive equilibrium E2(S∗,I∗) and E2(S∗,I∗) is globally asymptotically stable.
4. Order-1 limit cycle of System(1)
In this section, we will certificate the existence and uniqueness of order-1 limit cycle of system (1). In reality, it is unreasonable that a single kind of computer virus lasts for long time without being detected. So we assume ˉI<I∗ without loss of generality, i.e. the impulsive set M:I=ˉI is a horizontal line beneath the positive equilibrium E2. The existence, uniqueness and stability of the order-1 limit cycle will be proved progressively in this section.
4.1. Existence of order-1 limit cycle
The existence of order-1 limit cycle is studied in this subsection.
Theorem 4.1. If condition (5) holds, for any σ1∈(0,1) and σ2∈(0,1), system (1) has an order-1 limit cycle.
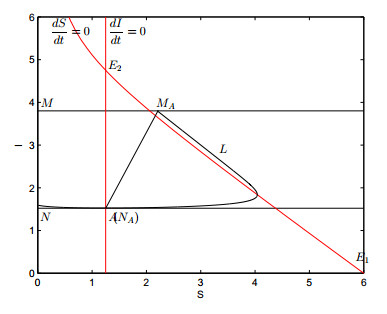
Proof. In system (1), to any σ2∈(0,1), imagine set N:I=(1−σ2)ˉI appears as another horizontal line under the impulsive set M:I=ˉI. In the following part, we prove that to any σ2∈(0,1) there exists a corresponding σ1 forming an order-1 periodic solution.
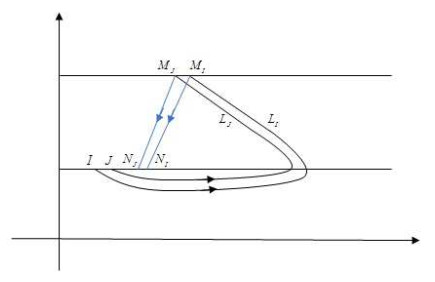
Assume the intersection of imagine set N:I=(1−σ2)ˉI and the horizontal isoclinic line dIdt=0 is A, and the coordinate is A(S∗,(1−σ2)ˉI). According to the fundamental theorem of ODE, there must exist a trajectory passing point A, denote it as L. After a period movement, trajectory L can reach the impulsive set M, and we assume the intersection is MA and its coordinate is MA(xMA,ˉI). Then the impulsive function φ maps MA to a point NA(xNA,(1−σ2)ˉI) in imagine set N. If xNA=S∗, i.e. point A and point NA are the same point, then the trajectory L and the impulsive mapping φ form an order-1 periodic solution (see Fig. 4). Let σ∗1=xMA−S∗, then we prove there exists order-1 periodic solution while 0<σ1<σ∗1 and σ∗1<σ1<1.
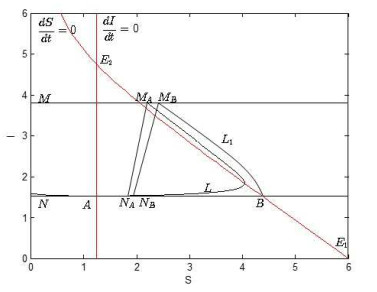
Case of 0<σ1<σ∗1. When 0<σ1<σ∗1, it means imagine point NA locates on the right side of A (see Fig 5). Then the successor function of A is F(A)=xNA−S∗>0. Consider another point B which is the intersection of imagine set N and the vertical isoclinic line dSdt=0. For point B(xB,(1−σ2)ˉI) locates on the vertical isoclinic line, the trajectory L1 initiating from point B moves upside left until it reaches the impulsive set M at MB. So xMB<xB. Then the impulsive function φ maps MB to the imagine point NB which is on left side of MB horizontally. Subsequently the successor function of point B is F(B)=xNB−xB<0. Following the continuous of successor function, there must exist a point C between A and B satisfying F(C)=0, and the trajectory initiating from C and the corresponding impulsive mapping form the order-1 periodic solution.
Case of σ∗1<σ1<1. When σ∗1<σ1<1, it means that the impulsive function φ controls the imagine point NA to fall on left side of A(see Fig 6), and the coordinate is NA((1−σ1)xMA,ˉI). So the successor function of A is F(A)=xNA−S∗<0. Then consider the trajectory L2 initiating from NA, it moves adhering the uncontrolled system (3) until intersects the impulsive set M at point MD. According to the non-intersecting feather of ODE trajectories, MD must locate on the right side of MA, i.e. xMD>xMA. Denote the imagine point of MD is ND, and its coordinate is ND((1−σ1)xMD,(1−σ2)ˉI). Then the successor function of NA is F(NA)=xND−xNA=(1−σ1)xMD−(1−σ1)xMA=(1−σ1)(xMD−xMA)>0. Still following the continuous of successor function, there must exist a point C between A and NA satisfying F(C)=0, that is to say the trajectory initiating from C and the corresponding impulsive mapping form the order-1 periodic solution.
Basing on the above discussion, to any σ1∈(0,1) and σ2∈(0,1), there exist an order-1 periodic solution of system (1).
Since the order-1 periodic solution is isolated, its trajectory and the proper impulsive line can form order-1 limit cycle of system(1).
4.2. Uniqueness of order-1 limit cycle
In this part we prove the uniqueness of the order-1 limit cycle with the homogeneous of successor function.
Theorem 4.2. The order-1 limit cycle of system (1) is unique.
Proof. Select two points I and J in phase set N arbitrarily, and assume xI<xJ (see Fig. 7). There must exist trajectories initiating from I and J, and we denote them as LI and LJ respectively. These two trajectories can reach the impulse set M, and we denote the intersections as MI and MJ respectively. It is obvious that MI must locate on the right side of MJ, i.e. xMI>xMJ. Then the impulse function φ maps them to NI and NJ respectively. xNI=(1−σ1)xMI and xNJ=(1−σ1)xMJ, it is easy to obtain xNI>xNJ. I and J have NI and NJ as their subsequent points respectively, F(I) and F(J) are their successor functions. Then F(I)−F(J)=(xNI−xI)−(xNJ−xJ)=(xNI−xNJ)+(xJ−xI)>0. Basing on the previous discussion, we can draw the conclusion that the successor function F(⋅) of system (1) is monotonically decreasing. Thus to any σ1∈(0,1) and σ2∈(0,1), there exists only one point C in imagine set satisfying F(C)=0. Therefore the order-1 limit cycle of system (1) is unique.
4.3. Stability of order-1 limit cycle
The above content has proved the existence and uniqueness of order-1 limit cycle. In this subsection, we discuss the stability of the order-1 limit cycle of system (1). Unlike the case of continuous dynamic system, the stability proof of impulsive dynamic system is quite complex. Some definition and lemma which are significant in the proof will be illustrated first.
Definition 4.3. [24] The order-1 limit cycle Γ is stable, if it is the ω limit set for those trajectories initiating from any point of its small enough neighborhood U(Γ). Otherwise, Γ is unstable.
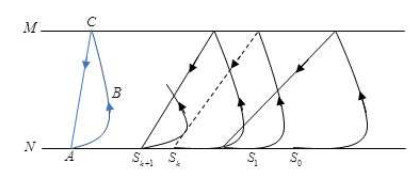
Basing on the theorem of subsection 4.1 and 4.2, to any σ1∈(0,1) and σ2∈(0,1), system (1) has a unique order-1 limit cycle, here we denote it as Γ. We also assume that Γ intersects the imagine set N at point A (see Fig. 8). Then to any point S0 that locates in the small neighborhood of A, define a point series
where Si+1 is the subsequent point of Si, i=0,1,⋯,k,⋯, and their coordinates s0,s1,⋯,sk,sk+1,⋯ are defined as
|
sk={−dk,Sk is on left side of A,dk,Sk is on right side of A,
|
where dk is the distance between Sk and A. Under this rule, it is obvious that the coordinate of A is 0.
Lemma 4.4. [24] Denote the mapping of the general impulsive dynamic system (2) as f, and suppose function ˉs=f(s) is derivative at s=0. Then s=0 is stable (unstable), if
It is not easy to prove the stability of order-1 limit cycle of system (2) only with the previous lemma, so we set up an orthogonal coordinate (s,n) in the nearby area of Γ as an auxiliary tool.
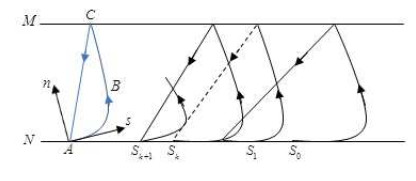
Without loss of generality, we assume that functions P(x,y) and Q(x,y) of system (2) have arbitrary order partial derivatives. Since the impulse mapping is quick enough, the period of order-1 limit cycle is the same with the time interval between A and C on a certain trajectory of corresponding uncontrolled system, and we denote it as T.
To any point in that region, there exists a certain point in the closed orbit Γ and its normal line passes the certain point. The first coordinate s of the new coordinate is defined as the length of the trajectory from A to the certain point on Γ, while the second coordinate n is defined as the number of the normal vector(upside is the positive direction)(See Fig. 9). Rewrite the rectangular equation of curve ^ABC into the parametric equation
where s is the parameter.
Then the rectangular coordinate (x,y) can be expressed with the orthogonal coordinate (s,n) as
|
x=ϕ(s)−nψ′(s),y=ψ(s)+nϕ′(s),
|
(10)
|
Following (2) and (10), we have
|
dnds=Qϕ′−Pψ′−n(Pϕ″+Qψ″)Pϕ′+Qψ′Δ=F(s,n).
|
(11)
|
It is apparent that n=0 is a solution of (11). We also assume that F(s,n) is biased derivative, and the first-order partial derivative of F(s,n) is continuous with respect to n, then (11) can be expressed briefly as
|
dnds=Fn′(s,n)|n=0⋅n+o(n).
|
(12)
|
Following (11), we can calculate
|
Fn′(s,n)|n=0=P20Qy0−P0Q0(Py0+Qx0)+Q20Px0(P20+Q20)32Δ=H(s),
|
where P0 and Q0 are the values of P and Q at point A, Px0, Py0, Qx0 and Qy0 represent the partial derivatives of P and Q at n=0 with respect to x,y respectively. It is obvious that P0ϕ″+Q0ψ″=0. Then the order-1 linear approximate equation of (12) is
and its solution is
|
n=n0e∫T0H(s′)ds′,n0=n(0).
|
(14)
|
Theorem 4.5. Assume h is the length of curve ^ABC which is a segment of the order-1 periodic solution Γ to system (2), then Γ is stable (unstable) if integration of H(s) along ^ABC is negative (positive), i.e.
Theorem 4.6. Suppose the region closed by order-1 periodic solution Γ is convex. If T∫0(Px0+Qy0)dt<0 is satisfied, then Γ is stable.
The proofs of Theorem 4.5 and Theorem 4.6 are similar with that in [27], and omitted here.
Then we can draw the corollary naturally.
Corollary 1. Suppose the area closed by order-1 limit cycle Γ is convex. If Px0+Qy0<0(>0) holds, then Γ is stable(unstable).
5. Simulation and discussion
In this section, we present and discuss a special example to check the theoretical results in section 3 and section 4.
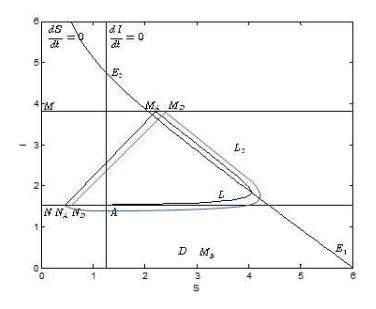
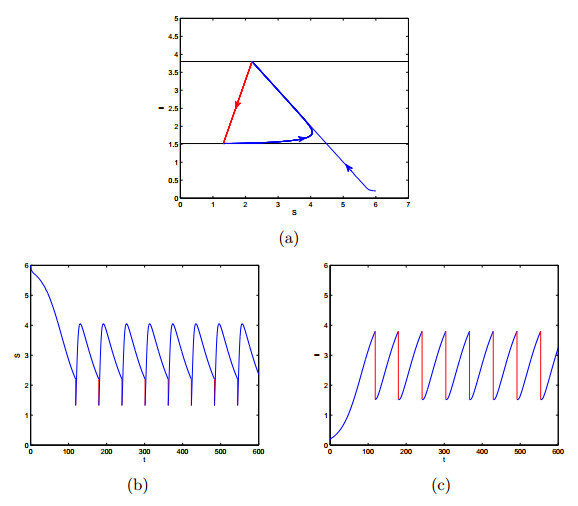
The uncontrolled part of system (1) is numerically calculated with fourth-order Runge-Kutta of Matlab software package. In the following, we discuss the solution of system (1), considering the parameters K=0.06, β=0.09, α=8.2 and μ=0.01. After a simple calculation, the corresponding uncontrolled system has a steady state (x∗,y∗)=(1.25,4.75). We also assume the threshold value that triggers patching operating system and updating the antivirus software is 3.8. Then the instantaneous impulse comes into force on 40% of susceptible ones and 60% of infected ones respectively. The trajectory of system (1) and time series of S and I are listed in Fig. (10).
From Fig. (10), it is obvious that system (1) has an order-1 limit cycle with the parameters mentioned above. We can also find that the limit cycle forms soon after the trajectory initiate from the original point which means that the impulsive patching and updating of antivirus software is quite effective. During the first period of the transmission, the worm or the virus spreads freely, the number represents susceptible computers decreases rapidly and the number stands for the infectious ones increased sharply. The developing trend of S and I(subplots (b) and (c) of Fig. (10)) indicates that the worm or virus erodes the computers ferociously, and most of the healthy computers will be infected without any intervention. After patching the system or updating the antivirus software, the infected computers will drop down instantly. Then it rises again according to the uncontrolled propagation. However, impulsive treatment triggered by the state of infected computers can prevent the deluge of worms and the collapse of the Internet. Enhancing the Internet monitor, publishing new version operating system patch, and developing efficient antivirus software can make the Internet operating normally.
Acknowledgments
We would like to sincerely thank the reviewers for their careful reading and constructive opinions of the original manuscript. This work is supported by NSFC(No.11671346, No.61751317, No.11701026), the Twin Tower Excellent Teacher supporting program (BUCEA2016) and the Fundamental Research Funds for Beijing University of Civil Engineering and Architecture (X18225, X18080) for M. Zhang. M. Zhang would like to thank the China Scholarship Council for financial support of her overseas study(No.201808110071).









 DownLoad:
DownLoad: