Design and optimization of grid Integrated hybrid on-site energy generation system for rural area in AJK-Pakistan using HOMER software

1.   Introduction

The overall energy demand of the world is increasing with growing population and with the pace it is developing. A major part of this demand is acquired by the conventional method of burning fossil fuels which is adversely affecting our surroundings ^[1].

Shortfall of electricity among developing nations especially in Pakistan is rising dramatically because of population growth. Pakistan relies on fossil fuels for most of its energy requirements ^[2]. At present Pakistan is producing 35,972 MW, out of which 30.9% of total is shared by hydroelectric, 8.2% by nuclear energy, 58.4% by thermal energy and 2.4% by other renewable resources. Three out of five parts of total generation capacity relies on fossil fuels. Annually, Pakistan consumes 19.68 million tonnes petroleum products. 58.8% of this demand is attained by local refineries and remaining 41.2% is imported at high rates which puts an extra burden on economy ^[3]. Highly expensive oil import increases the charges per unit of electricity and possibly can make this sector defenceless to variations of fossil fuels fares internationally ^[4].

According to Pakistan economic survey report 2019–20 total electric capacity installed in country till April 2020 was 35,972 MW ^[5] after the addition of 13,298 MW in last four years which made the country capable of generating surplus electricity than demand. Total electricity generated by the country in year 2019–20 was 134,745 GWh and cumulative peak demand as calculated by different DISCOs under central grid was 25,068 MW and total energy consumption by different entities was 107066.75 GWh but despite of surplus production we still come to see electricity shortage which results in several hours long load-shedding. One reason for this shortage is the long and musty infrastructure. In year 2019–20, total losses calculated were 20% (2.5% transmission and 17.9% distribution losses). Besides this government is also purchasing electricity from IPPs (Independent power producers) but due to circular debts and delay in payments these plants stop production and shortfall occurs ^[6]. These IPPs mostly use fossil fuels for electricity generation and hence give rise to economic and environmental concerns ^[7].

Such consequences have made it inevitable to think about renewable natural resources to fulfil energy demands. Renewable energy is clean, more eco-friendly, sustainable and secure ^[8]. Rebuilding the transmission and distribution infrastructure is quite costly and time taking process. Instead, using renewable energy for distributed energy generation in areas with enough potential can unburden the central grid, reduce per unit cost and can ensure the maximum availability of electricity. In last few years, many small and micro energy generation plants are installed in areas with enough potential of hydal, wind, biomass, biogas and solar energies. Some of these plants are working independently for local use and some are integrated with central grid. Geographically, Pakistan is affluent in renewable energy potential in form of solar, hydel, wind and biomass that can be used to meet its energy demand ^[4].

Topography of Pakistan makes it rich in renewable energy generation potential. Pakistan lays in latitudes 24°–37° North, and in East between longitudes 62°–75° having a total area 8, 81,913 km². In Pakistan on flat surface the average global irradiation ranges between 200–250 W/m² with sunshine of 8–10 hours daily. On average out of total area of Pakistan, 95% area gets solar insolation of 5 to 7 kWh/m²/day with more than 85% persistence factor ^[9]. Melting glaciers and rain water are main sources of running rivers in Pakistan. These rivers provide an efficient potential of hydal energy. In case of wind energy, the studies show that 9700 km² coastal belt of Pakistan has the potential of generating 43,000 MW energy from wind with power density of 4 MW/km². However, usage of land has restrained it to 11,000 MW ^[10]. Being an agricultural country Pakistan has high potential of biomass. Pakistan has almost 172 million cattles which produce 0.71 million ton dung daily. By collecting just 50% of total dung and agricultural wastes, 27.5 Mm³ biogas can be produced providing capacity of generating 1900 MW energy per day ^[11,12].

Despite of having excellent potential, most of renewable energy in Pakistan is unexploited. Some sources having small potential remain neglected due to intermittency and high initial cost. Instead, combining two or more renewable sources to make a hybrid system and using it to serve electricity in its surroundings can reduce a huge load from central grid. In this way large as well as small sources can be used for generation.

A large number of researches have been purposed for employing HRES in remote and difficult terrains, where grid extension is either hard or uneconomical. Jinze Li et al. ^[13] raised the issues of extending central grid to remote areas having terrain which is unsuitable and uneconomical to construct transmission line infrastructure. As a solution a hybrid system using locally available renewable resources (solar-wind-biomass) is purposed and analysed using HOMER software. Shehzad et al. ^[14] presented a hybrid PV-biomass system for a remote village to meet agricultural and domestic load of residential households and a cattle form. Jameel et al. ^[15] made a technical feasibility analysis of HRES for a rural site including biomass, wind and solar energy. Using these resources, a grid integrated hybrid system is purposed and analysed using HOMER software. This system resulted to generate 50 MW electricity for local community. WT chong et al. ^[16] and MS Islam ^[17] utilized combination of solar and wind energy for composition of a hybrid system for commercial high raised building and domestic load respectively Krishan et al. ^[18] utilized a hybrid PV-WE-hydro system with diesel engine backup to electrify a remote site. Khan et al. ^[19] and utilized the combination of PV-WE-biomass to design a hybrid system. Antonio et al. ^[20] purposed PV-hydrokinetic based hybrid system for an island. In ^[21] conceptual model of standalone HRES based on PV-wind hybridized system is proposed for 375 houses for an island. In ^[22], the authors presented an optimal model of micro-grid HRES to be utilized for household needs. A hybrid Wind-PV-grid-storage based optimal model in respect of cost and its impact on environment is presented using Matlab, iHoga and HOMER simulation softwares. The authors in ^[23] proposed the use of supercapistor for storage instead of expensive battery storage for an on-grid PV system for a single household. Using a control strategy based on fuzzy logic the power flow among different components of system is controlled to optimize the size and enhance the performance of the system. In reference ^[24], the authors did a techno-economic analysis for a PV system used to fulfil electricity demands of a households and compared the systems for on grid and of grid configurations through simulations and modelling. Similarly, a variety of research has been made globally for using local natural resources to meet energy demands instead of just relaying on grid. Keeping in view the potential benefits of various natural resources in context of Pakistan, a scheme to produce energy from locally available renewable potential is purposed in this study. The main idea is to exploit every available renewable resource having potential to generate electricity and consume it locally to reduce grid's burden to some extent along with uninterrupted electric supply. Using two or more RES or hybrid system will cope with the intermittent nature of renewable resources as unavailability of one resource can be compensated by other source operating parallel in system. Grid backup is used, one to reduce the size of the system and save economy and second either to sell electricity at time when system generates excess electricity than demand or to purchase electricity when demand is more than generation. In the literature, ^[14,15,25] the authors have used various combinations of solar wind biomass and diesel generation. The use of hydro-kinetic energy source is not considered. The hydro-kinetic energy source is naturally available specially in hilly areas. Therefore, the optimal design should consider this energy source. This design is purposed for district kotli a hilly area enriched with natural resources like river (hydrokinetic), solar and biomass in Pakistan. This combination is rarely considered in studies to best of our knowledge. The potential of renewables in fore named site is assessed and a feasible HRES is analysed and designed using HOMER software based simulation.

The structure of the paper is as follow: section 2 describes the material and method, simulation and design is presented in section 3 whereas results discussion is given in section 4 and conclusion of this research is made in section 5.

2.   Materials and method

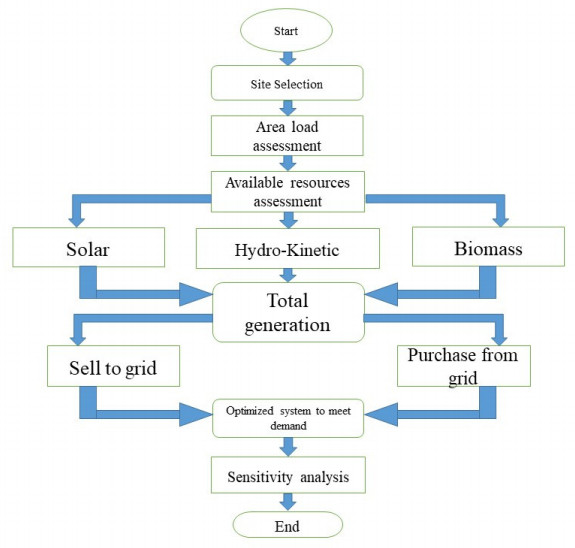
The proposed method is presented Figure 1 and the relevant detail is provided in following sub sections.

2.1.   Site description

The site for which this study is purposed is located in district Kotli of Azad Kashmir, Pakistan. The site is surrounded by mountains having 33⁰.30‵N latitude and 73⁰.54‵E longitude. HRES design is presented and evaluated for a town (Thalair) and two villages (Baila and Dakhari), having almost 237 households. River Poonch is flowing through the area. Moving from north to south, the town is located on the left bank and villages are situated on right bank of the Poonch river.

2.2.   Electricity consumption data

The total energy demand of the area is obtained from electricity department of Kotli. Table 1 shows the list of most probably used appliances and their maximum operation duration in a house according to need of its residents.

According to survey maximum temperature occurred at site is 38.4 ℃ during the month of June. Most common loads in summer are lighting and fans. There is low energy requirement during day time in winters. Mostly peak occurs when all family members are at home. It happens during morning or evening time. Load curves for two random days of both seasons are depicted in Figure 2.

There are some appliances which are kept by few houses like geysers, vacuum cleaners, water pumps, Electric owens. Sandwich makers etc. These loads are covered in simulation by having extra generation as that of required demand. Figure 3 shows monthly maximum and minimum load profile.

2.3.   Solar energy potential and technologies

Solar radiations data for these co-ordinates is obtained from NASA Surface meteorology and solar energy database Figure 4 shows average monthly irradiance received by the area.

To design most favourable and economic PV generation for desired system two important factors are considered. First one is the total consumption demand for which system is being designed and second is PV panel generation capacity. These factors assist us to figure out size and quantity of PV system significantly.

Using Shockley's diode equations, following expression is derived to draw Ⅰ-Ⅴ characteristics of a single cell.

$Here:$

● ${I}_{ph} = Photo\;current\;\left(A\right).$

● ${I}_{o} = Saturation\;current\;of\;diode\;\left(A\right).$

● ${R}_{s} = Series\;resistance\;\left(\mathit{\Omega }\right).$

● ${R}_{sh} = Parallel\;resistance\;\left(\mathit{\Omega } \right).$

$Vt = thermal\;voltage\;of\;diode$

$Here:$

● $n = ideality\;factor$

● $K = Boltzmann's\;constant$

● $T = solar\;cell\;temperature\;\left(K\right)$

● $q = electron\;charge$

These equations can be used to determine the parameters of single PV cell. Making above equations ground ^[26] developed an expression to calculate these parameters for PV array.

In above equation, Ns and Np represent the strings of PV cells in series and parallel respectively. This equation can be used for any number of PV cells. In case of PV array, Ns in above equation can be replaced with the product of total modules and cells in series (Nm*Nc).

Total power output of PV can be determined using power equation.

Iph, Io, V_t, Rs, and R_sh are major parameters in above equation. Using developer's provided specs these parameters can be measured numerically by following equations under STC (standard test conditions).

$where:$ G is solar irradiance, ${\alpha }_{{I}_{sc}}$ is coefficient of temperature for short-circuit current, Eg is bandgap energy, Tm is temperature of back side of module, ΔT is temperature difference between back and front side.

2.4.   Biomas resources and technologies

Agricultural wastes, animal dung, woods and plantation wastes and municipal wastes are some sources of biogas generation. According to ^[4] a single dairy animal produces about 10 kg manure daily and according to ^[27] one animal produces 15 kg manure a day. However, the average amount of manure an animal produces daily depends on its weight, size, amount of milk it produces, feed and physique ^[28]. The authors in ^[29] presented a method to calculate manure amount from milk production. Following expression can be used to calculate annual manure production of a dairy cow:

$where:$

$m1 = manure\;produced\;annually\;in\;tons.$

$Yd = milk\;produced\;by\;cow,\; kg/yr.$

Total manure produced by N animals can be obtained by:

$where:$

$M = manure\;produced\;by\;N\;animals\;t/y$

$n = specific\;group\;of\;animals$

$N = number\;of\;animals$

Biogas produced annually from total available manure can be estimated using following equation.

$where:$

$VB = Biogas\;obtained\;\left(m3\right)$

${k}_{{DM}_{i}} = Dry\;solids\;fraction$

${k}_{{OM}_{i}} = Organic\;matter\;fraction$

${v}_{{B}_{i}} = specific\;biogas\;\left({m}^{3}/t\right)$

From ^[29], fraction of dry solids and organic solids in manure is 0.18 and 0.86 respectively and from ^[30] the value of biogas obtained from one kg organic solids of manure is 0.30. Energy potential (kWh) of obtained biogas can be calculated using following expression;

$where$

${e}_{{B}_{i}} = calorific\;value\;\left(6KWh/{m}^{3}\right)$

Total power (kW) generation per day is calculated by:

${K}_{e} = Plants\;efficiency\;taken\;as\;40\% \;\left(0.4\right)$

${T}_{c} = annual\;operational\;time\;of\;plant$ (hrs)

From above equations we have calculated the size of generator required for this study in Table 2.

Biogas produced from animal manure composed mainly of methane CH₄ (50–75%), carbon dioxide CO₂ (25–50%) and nitrogen N₂ (0–10%). Beside this some traces of hydrogen H₂, hydrogen sulphide H₂S and oxygen O₂ (0–3% each) are also present ^[11].

2.5.   Hydrokinetic potential and technologies

Hydropower is the most abundantly used renewable source in world with 16% shares in global electricity production, which is 85% of total renewable energy being produced ^[31]. Hydal energy can be extracted, either by static mood, where by building dam water head is created and potential energy of water is converted into electrical energy or by kinetic mood, where water current is directly employed to move turbine. Out of these two methods, kinetic is comparatively simple and economic ^{[32,33,34,35]}.

Hydrokinetic device's construction and operation is similar as that of wind energy devices ^[36]. Table 3 presents comparison between the two sources. A tree diagram of different types of hydrokinetic turbines is shown in Figure 5 ^[37].

For a constant speed of flowing water, the total power produced can be calculated using following expression.

$where:$

${\rm{ \mathsf{ ρ} }} = density\;of\;water\;\left(1000\;kg/{m}^{3}\right)$

$v = velocity\;of\;flowing\;water\;\left(m/s\right)$

$A = \pi {r}^{2}\;is\;area\;swept\;by\;turbine\;blades\;\left({m}^{2}\right)$

Electricity generation from HKT is related directly to the velocity of flowing water. Flow velocity varies based on time and location throughout the cross section of river ^[38]. The authors in ^[39] presented Manning-Strickler equation to calculate river water flow speed across the cross section of specific site.

$where$

RH is hydraulic radius (m), v is the velocity (m/s), S is river-bed slope (m), n is river-bed surface roughness, A is cross-sectional area of site and P is wetted parameter. With an assumption that river bed shape for specific site is rectangular, the refence ^[40] presented Eq (20) in terms of width (W) and depth (D) of the river site.

Using the discharge rate of the river, the authors in ^[41] introduced the expressions to find the width and depth of the river bed cross section.

W and D are width and depth in feet and Q is discharge rate in cubic feet per second. The authors in ^[42] undertook a study on cross sectional dataset for 674 rivers across Canada and USA and derived the values of co-efficients and exponents used in Eqs (22) and (23).

In the reference ^[41], it is also presented an expression to determine mean velocity of river flow using discharge rate for which ^[42] calculated the values of co-efficient and exponent.

A 100 MW hydal power plant is installed at Gulpur in Kotli Mean monthly flow rate of Poonch river and rainfall in area is shown in Figure 6. According to ^[43] there is an average elevation of 800 m in 17 km from tatta pani to kotli town and according to ^[44], from tatta pani to town there is slope of 6.9–8.3 m/km which provides a good chance to exploit the potential of hydrokinetic energy. The selection of technology can be made depending upon the characteristics of site and using Eqs (18) and (19) the potential of hydrokinetic can be found for any site. However, using Eq (26) mean velocity of Poonch river in meter per second is calculated in Table 4.

3.   Simulation and design

A hybrid energy system is composed by the combination of two or more generation systems. So its bit complicated to analyse system viability. This process is carried out using some powerful software. Here, HOMER software is used to model and simulate the system to get optimized design. The software modelled diagram of purposed system is presented in Figure 7.

3.1.   System settings

The optimization settings of the system kept to run the simulations are listed below in the Table 5.

3.2.   PV module

In this study, PV module of 50 kW capacity with life time of 25 years is used. Solar irradiance data of site is used as input for which PV generation and its respective cost is obtained at output. PV module SPR-X21-335-BLK (SunPower) is employed. PV module in Pakistan is installed at cost up to 110,000 PKR/kW ^[14]. Detailed information of selected PV panel is provided in Table 6.

3.3.   Biogas generator

As calculated in table total potential of area to produce electricity using manure is 24.2 kW, so a 25 kW biogas-fuelled generator is used. The manure locally available is assumed to purchase at 5.8$/ton and is taken as input data for which we got biogas generator's cost and generation at output Cost detail of biogas generator is given in Table 7 ^[14].

3.4.   Hydro-kinetic turbine

In this study, two 40 kW Generic hydrokinetic turbines are used. For hydrokinetic the generation cost (cost/kW) has inverse relation with flow speed of water ^[45]. Water flow velocity is used as input for which we got hydro-kinetic turbine's generation and cost at output. Authors in ^[46] presented a system consisted of 16 HKT turbines fulfilling the electricity need for 693 households in Ghana, estimated total cost and divided the cost in three categories, installation cost, labour cost and material cost. Maintenance cost is estimated as 5.5% of total cost. Total cost of system per site is estimated to be $12,743. Other work ^[47] discussed about the studies of five hydrokinetic projects at different locations in Alaska. Each site has different estimation for installation cost and cost/kW. This shows that project site has an impact on system cost. In this study the hydrokinetic turbine cost is kept as given by HOMER which is updated according to NREL reports.

3.5.   Converter

As we get DC output from PV module so an inverter is needed to convert the output to AC. Converters are the most imperative components for the future prospects of hybrid AC/DC systems to provide a controlled energy conversion among different components and systems at different levels of voltage ^[48]. In HOMER this conversion is carried out by a converter which is the combination of rectifier and inverter. In case when DC output from PV is added to system the inverter does its job to convert it into AC and when excess generation is needed to store in case when battery backup is provided the rectifier converts it into DC. The model used in this study is generic system converter whose efficiencies of inverter and rectifier are 90% and 85% respectively.

3.6.   Storage

The major concern while talking about an energy storage system (ESS) is the cost of the system. Many techniques and researches have been proposed to reduce the size and cost of ESS. In this regard, it is proposed in ^[49] a double layered optimization technique based on particle swarm optimization as outer and Mixed integer quadratic programming as inner layer optimization technique to optimally size an ESS for a Micro grid. In another study ^[50] focused to optimize the size of ESS based on uncertainties that most probably exist and then applying decision theory. The authors in ^[51] proposed optimized size ESS of a MG for both on-grid and islanded system using unit commitment technique. ESS in stand-alone system is provided for two purposes, one to store excess energy generated during time when generation is more than demand and second to compensate intermittency of renewable resources. In this study, battery backup is considered to study the effect of off-grid system.

4.   Results and discussion

For given values of load requirements and potential of renewables present in area, HOMER software evaluated several configurations in order to find most suitable and optimized system. The system which HOMER choses to be most optimal is the one which achieves following properties.

1. The proposed system should be capable of meeting the load demand. HOMER automatically removes infeasible configurations and provides only the feasible results.

2. Initial capital cost required for the system to install should be lowest.

3. Total NPC (net present cost) of the system should be lowest. NPC of the system is the cost obtained by deducting the maintenance and running cost of the system from present total investment cost of the system throughout its life. It is derived using following equation.

where

C_t = Total annualized cost ($/year)

CF_R = Capital recovery factor

i = interest rate (%)

4. LT_P = Life time of project (year)

5. COE (cost of energy) or price per unit of energy for the system must be smallest. Homer derives the COE using following equation.

where

C_t = Total annual cost of system [$/year]

Cm_b = boiler marginal cost [$/kWh]

L_t = Total thermal load served [kWh/year]

L_e = Total electrical load served [kWh/year]

6. OC (operating cost) of the system must be low. Homer derives the operational cost of system through following equation.

where

C_t = total annual cost [$/year]

C_c = total annual capital cost [$/year]

7. HOMER provides mean value of unit cost for every configuration.

The simulation process carried out by HOMER provides two types of analysis:

● Optimization analysis

● Sensitivity analysis

4.1.   Optimization analysis

Optimization analyses of the purposed system is procured in two steps. In first step three different strategies (based on available systems that can be conceived to meet demand) are tested and in second step the best solution obtained is further investigated based on optimal combination of different generating units. By modelling the systems in HOMER the obtained results are analysed and compared in terms of capital cost, cost per unit, operational cost, NPC and emissions as shown to get economically as well as ecologically optimized system.

4.1.1.   Optimal system selection

Based on available options to electrify the area, the energy management system is categorized into three strategies and result of cost analysis performed on it is shown in Figure 8.

Case 1: Just grid system.

Case 2: Standalone PV-Biogas-HKT system with ESS.

Case 3: PV-Biogas-HKT system integrated with grid.

In first case whole demand is set to fulfil by grid. The cost per unit is kept according to tariff provided by distribution company. In second case a system composed of a standalone PV-Biogas-HKT hybrid system with batteries backup is designed to meet demand. In third case the system consists of PV-Biogas-HKT hybrid system with grid integration. However, small ESS may also be provided for backup in case if for some reason grid is unavailable the HRES might be able to meet the demand for some extent.

For grid the capital cost is zero as it is already available and requires no initial set up for its installation. In Second case, as it is a standalone system so it requires more CC due to enlarged generation capacity and huge batteries backup as ESS. For case 3, the capital cost is lower than the case 2 as it is integrated with grid and requires no storage hence reduces the cost. For operation, case 1 has the highest cost as grid has a huge network which requires more maintenance, case 2 has second highest cost because ESS puts extra burden of maintenance on the system, while case 3 has the least cost due to its direct integration with grid and low maintenance requirements. Similarly, for unit cost and NPC case 1 and 2 have highest costs since the initial and maintenance costs increase total annual expenses of the system, however for case 3 the total annual expenses are quite low due to free energy resources and less maintenance requirements. Here the cost is taken as the optimization variable so based on results case 3 is the most optimized and economical system provided by HOMER which is the purposed system of this study.

4.1.2.   Optimal combination of components

In this step various combinations of REGUs are configured and their effects on economy and system's operation are inquired. Seven configurations of different combinations of REGUs listed on basis of economy (high cost to low cost) are presented in Table 8. System without HKT is most expensive while system operated without grid but small battery backup is required to run on 11% capacity shortage and system without grid but no battery backup is required to run on 20% capacity shortage. On grid HKT-Biogas-PV system proved most economic. In terms of emissions, the systems without grid are more environmental.

4.1.3.   Optimal system details

HOMER simulation results provided on grid HKT-PV-Biogas system to be most economical. Figure 9(a) shows the detailed contribution of different REGUs and Grid in the system. The results revealed that 49.6% (324,422 kWh/yr) which is almost the half of the total electricity produced is provided by hydrokinetic unit, biogas generator contributed 33.5% (219,000 kWh/yr), PV system held 10.9% (71,061 kWh/yr) shares and grid contributed only 6% (39,178 kWh/yr) in annual electricity production. Grid input is required when system is operating on full load demand. Besides this the system sells 26.4% back to grid when it is operating at low load. Figure 9(b) shows total renewable fraction.

Cost comparison of various components employed in this study is presented in Figure 10.

4.2.   Sensitivity Analysis

To test the proficiency of the system under different constraints, here is performed a sensitivity analysis on the purposed system. To evaluate the load variations renewable resources intermittency effect, system is investigated under different load demand, solar intensity and water flow velocity. Annual load is set for three values (1100, 1200, 1300) kWh/yr. Solar radiation intensity variations is also set for maximum, minimum and average values appearing at site throughout the year and similarly for water flowing speed variations. HOMER derived 8744 feasible simulations of system for given constraints. Based on site location and provided data 27 most obvious cases and their effects on system economy is listed in Table 9.

5.   Conclusions

Continuous increase in consumption demand is exerting extra pressure on central grid. This demand is catered by operating fossil fuel based power plants. More than half of electricity in Pakistan is generated by these conventional plants and it requires a plenteous amount to import the fuel which puts extra burden on economy. Beside this any issue in system may result in complete shutdown as whole system is dependent on central grid. In this study, a hybrid PV/HKT/Biomass on grid system is purposed. The site selected for this project is a small town and two villages situated on the bank of Poonch river in district Kotli in AJK Pakistan. The climate, habitat and geography provides the site enough potential to exploit the available renewable resources. By practicing various simulations on HOMER different strategies and configurations are analysed. The simulation results are compared out of which the purposed system came out to be most optimized solution to meet consumption demand. The system includes 40 kW PV, 25 kW biomass generator and two HKT turbines of rating 40 kW each integrated with grid to sell or purchase electricity according to situation. The system achieved 94% renewable fraction annually. 6% of total load is entertained by grid and 26.4% of total generation is sell back to grid annually. Hybrid system is found to provide energy at rate of $0.012 per unit and$106,156 NPC.

Pakistan is blessed with vast potential of renewable resources so using such decentralized system to exploit the renewable resources can help to reduce energy crises of country.

Conflict of interest

The authors have no conflict of interest.