Determination of transmission reliability margin for brownout

1.   Introduction

Even though when significant uncertainty occurs during power transfer, the power network system needs to keep secure. For this reason, it is crucial in calculating transmission reliability margin (TRM) to quantify the intensively significant uncertainty precisely. For an effective power system, one needs to upgrade the calculation of available transfer capability (ATC) integrating the TRM. There are some fundamental differences between reliability and security. Reliability describes the ability of continuous service without an outage. Security is the ability of the power system to continue to operate normally even with specified interruptions. According to the North American Electric Reliability Council (NERC), TRM is the amount of transmission capability which ensures the safety of the network of the power system under any reasonable range of disturbances in the system operating components. Besides, adequacy and availability also have their differences; the term adequacy means having a sufficient margin between generating capacity and maximum load, and availability is the steady-state probability that a system or equipment is in service satisfactorily performing its intended function. TRM is the amount of transmission capability, not transfer capability, so the term transfer capability is the ability to transfer power from one area to another reliably. Some techniques are explained to determine TRM ^{[1,2,3,4,5,6,7,8,9,10,11,12]}. Now, ATC can be defined as the additional amount of power flows after the base one, and this flow must be done without jeopardizing the system's security. A couple of methods are discussed to determine ATC ^{[13,14,15,16,17,18,19,20,21,22]}. In any power system network, sensitive parameters are essential because disruptions can occur at any time in the system. To find out the sensitive parameters in the system, the sensitivity of the available transfer capability (SATC) term is very accommodating ^[23].

Recent blackouts happen because constantly increasing the load causes transmission lines near the safety limit levels; therefore, the prerequisite to gauge the distribution factors such as outage distribution factors or power transfer distribution factors. A new DC Q flow (DCQF) model was proposed for market clearing and settlement of pure Q market ^[24,25]. Moreover, if the load change frequently, then it will affect the voltage level too. In this work, the main observation is: how the margin will be affected if the voltage level changes. Besides, the change in any bus voltage magnitude for a transaction between a seller bus and a buyer bus is known as voltage distribution factors (VDFs). These factors aid in calculating ATC; fundamentally, in this work, ATC is determined for voltage magnitudes. After that, to determine TRM needs another term to compute, known as Sensitivity ^[26]. There is a relation between sensitivity/uncertainty and TRM ^[27]. Moreover, a power outage is the loss of the electrical power supply to a consumer. There are many power outages in an electric system network, such as transient fault, brownout, blackout, etc. Brownout causes by huge energy demand, which is above the capacity. When this happens, the flow of electricity is reduced in certain areas to prevent a blackout. The fading of incandescent lighting occurs because of voltage reduction; this phenomenon is known as brownout. Besides, blackout is the disruption of an electrical grid, which can also happen for voltage trimming ^[28,29].

Although reliability assessment research has been underway in composite energy systems since the 1960s, the practical applicability of the issue is still restricted. As a crucial element in operational and planning phases in the contemporary power system, the reliability evaluation of composite power systems has been deep attention by the power system engineers ^[30,31]. In order to calculate the transmission reliability margin, an effective technique is desirable with the progress of contemporary technology ^{[32,33,34,35]}. However, due to various variables, such as unpredictable failures of system components, intermittent electricity sources, and unsafe load profiles, entirely dependable power systems do not exist. Reference ^[36] provides a critical and systematic evaluation of transmission reliability margin to improve the understanding of reliability studies of composite power systems. To evaluate the quality and trustability of the electric power system, authors in ^[37,38] addressed the different types of contingencies considering the IEEE 30 bus system. Here, a confidence interval based on bootstrap is proposed to calculate not only the coefficients of thermal security region boundary (TSRB) but also the standard deviations and confidence intervals of the coefficients. Reference ^[39] proposed a modified affine arithmetic (AA) method to estimate the bounds of the PV curve based on continuation power flow (CPF) by considering the uncertainty of real and reactive power at all buses in the power system. In ^[40], a reactive power compensation policy is developed addressing the challenges of voltage stability in the dynamic load power system. It is intended to identify the best placement of dynamic VAR sources while meeting the voltage stability margin and transient voltage drop requirements following a set of criteria.

In the assessment of the reliability of power transmission networks, dynamic thermal rating (DTR) play an important role as reported in ^{[41,42,43,44,45,46,47]}. A novel model is presented in ^[43] to study the confidence implications of the DTR system on power grids, taking into account the network of wireless communications. For the composite reliability study of the wind-integrated power systems, reference ^[44] introduces the holistic confidence modeling of the DTR system and battery energy storage system (BESS). Authors in ^[45] studied the probabilistic peak demand matching of energy-storage batteries along with the improved network reliability of dynamic thermal ratings and demand responses. In addition, the dynamic thermal rating system and the static VAR (SVC) compensator were found as useful methods to improve network load capacity ^[46]. A multi-objective framework that optimizes the increase of the battery storage and dependability of the line's real-time thermal rating is presented in ^[47]. These reports also examine the uncertainty effects of the model failure of the line parameters and the effects of the weather information on the power system's dependability. All these works of reliability evaluation based on DTR can increase the capacity and reliability of transmission lines and estimate the line rating at distinct conditions by focusing on system transmission lines. In the end, the Internet of Things and other modern technology can be used to enhance the performance of the transmission line ^[48,49,50]. This will help power system operators make cost-effective decisions on power grid management.

The focus of this paper is to determine TRM by AC and DCQ load flow method for brownout using Gamma distribution incorporating with ATC, as well as to show how TRM is affected by the variation of probability of sensitivity. In this research work, bus voltage magnitude is considered for brownout problem means if there is any power shortage in the system at that moment, what TRM has to maintain in case of continuous power supply. This paper is organized as follows. In section 2, the determination of ATC for Brownout by AC load flow for voltage only has been discussed. Then, the sensitivity and TRM calculation for brownout are explained in section 3. Section 3 also has presented the calculation of ATC, sensitivity, and TRM by DCQF load flow. Then, the results and discussion for both methods are shown in section 4. Finally, validation of this work and conclusion are presented in section 5 and section 6, respectively.

2.   AC load flow

2.1.   ATC calculation for brownout

The determination of ATC must accommodate reasonable uncertainties in system conditions and provide operating flexibility to ensure the secure operation of the interconnected network. Probability theory is necessary because it gives a mathematical expression of the outcomes of any experiments. Besides, the probability distribution function describes the concept of recovery times and collapse times of a system. Expected values and standard deviation values help to understand the position of all data, whether they dissipated quickly or gradually. The ATC calculation process by AC load flow for brownout is described in detail below:

Run N-R load flow newly updated angles and voltage magnitudes have obtained from the following equation: used only Decoupled Jacobian Matrix:

For this work, only the updated voltage values are used to determine the voltage distribution factor (VDFs_{m, kl}) for each bus and each transaction:

Here, $\Delta {V_m} = {V_{m, kl}} - V_m^0$

$V_m^0$ = base case voltage magnitudes for each bus 'm'

${V_{m, kl}}$ = new voltage magnitudes for each bus 'm' under the change in a transaction (∆kl)

∆kl = change in a transaction of a line between two buses

Voltage distribution factors are needed for brownout conditions because it's the only term that helps to give information about the changes in voltage magnitudes after a transaction happened in the system.

Determine ATC for each transaction:

Here, $V_{\min }^m$ = minimum voltage limit at bus 'm'.

This would denote by $AT{C_{old}}$.

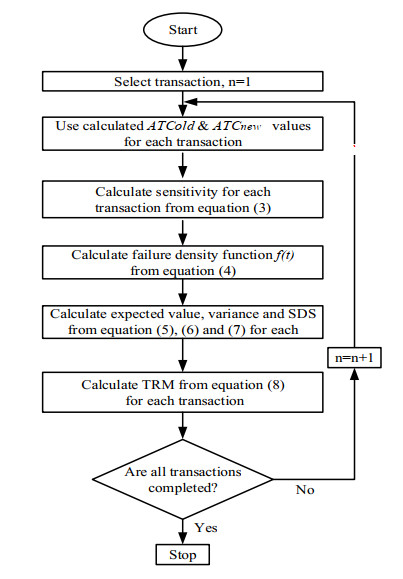
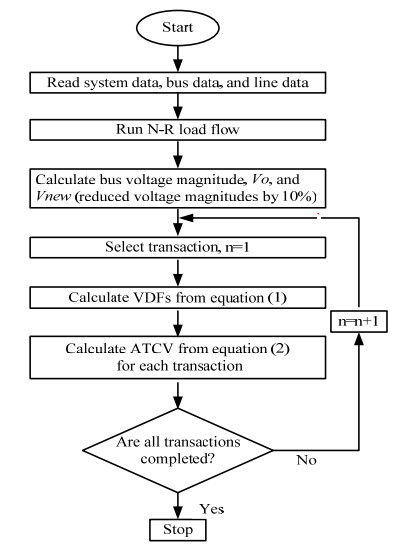
As refer to ^[24], it is considered that the bus voltage magnitudes decreased by 10% for PV bus-2, 3 and PQ bus-4, 5; rerun the load flow, utilize the new voltage values for recalculated ATC from Eq (2) for each transaction that would be denoted by $AT{C_{new}}$. Figure 1 presents the determination of ATC by AC load flow for brownout step by step.

2.2.   Sensitivity calculation for brownout

In any power system network, if any parameter changes its level or causes disturbances that will affect the whole system; so, sensitivity can define the change in a parameter. Fundamentally, the voltage will change if any load is changed in the system. In this work, two generator buses and two load bus voltages are considered uncertain parameters. Those uncertainty aids in determining the sensitivity for each transaction. As mentioned earlier about brownout reduces voltage level by about 10%; so, the whole calculation is done for brownout, and the process is discussed below:

Decreased the bus voltage magnitudes by 10% for each bus and calculated the sensitivity of ATC w.r.t voltage for each transaction from Eq (3):

Here, the ${V_{old}} =$ Base voltage magnitude

${V_{new}} =$ New calculated voltage after reduced by 10%

$AT{C_{old}}$ = Base ATC magnitude

$AT{C_{new}}$ = New calculated ATC after reduced by 10%

$\frac{{dAT{C_{kl}}}}{{dV}}$ = Sensitivity of ATC w.r.t voltage for each transaction

2.3.   TRM calculation for brownout

A formula for TRM is developed in ^[4] based on the first-order sensitivity of transfer capability for normal distribution. In this paper, a modified TRM formula is used for Gamma distribution but considered the sensitivity of ATC. In other words, the TRM values are referred to as the standard deviation of ATC. The steps to calculate TRM for Brownout are discussed below:

The first parameter that needs to determine is the failure density function, f(t) for Gamma distribution:

For this work, 95% and 99% are considered (%FDF), also known as the probability of sensitivity. Determine t from the Eq (4); because t needs to determine the TRM.

Here, α = Scale parameter = 3; β = Shape parameter = 0.5; Г(β) = √π

Now, the Expected value,

Variance,

Standard Deviation,

Equation (7) is also known as Standard Deviation of Sensitivity (S.D.S).

Here, ${c_i}$ = parameter distribution = 0.05

$\frac{{dAT{C_{kl}}}}{{dV}}$ = sensitivity of each transaction

Here, m = is a certain number that keeps the margin greater than the S.D.S to ensure the reliability of the system.

= 1.65, for 95% probability of sensitivity

= 2.33, for 99% probability of sensitivity

The algorithm for the determination of TRM by AC load flow is shown in Figures 1 and 2.

3.   DCQF load flow

3.1.   ATC calculation for brownout

Most of the ATC calculation, voltage—reactive power phenomenon is neglected. Still, in any power system network, reactive power is necessary to transfer real power through the transmission and distribution system to the customer. Besides, if there is insufficient reactive power, the voltage sags down and cannot fulfill the power demanded by loads through the lines. To maintain proper stability in the system, it needs to compensate voltage and reactive power. ATC determination by linear methods faces many errors for neglecting reactive power ^[51,52]. Reactive power is a consequential parameter of changes inflows in the lines, which also provides the action of voltage and other safety restrictions of the system. The process of calculating ATC for brownout by DCQF load flow is mentioned below:

Run fast decoupled power flow (FDPF) to get the value of all bus voltage magnitude except the slack one; during this power flow, all active power demand, generation, voltage angels, and resistances in the lines are considered zero similarly for DCQF (DC Reactive power flow). First, run DCQF flow utilized those calculated bus voltage magnitudes from FDPF flow and then calculated the bus matrix from the bus data, determined reactive power flow for each transaction and calculated DCQTDFs (DC VAR transfer distribution factors) and finally ATC for each transaction. The formulation of this flow is: $[B][V] = [{Q^{sh}}] + [{B_s}]{V_s}$; here, $B$ is the bus susceptance matrix; $V$ is the bus voltage magnitude; ${Q^{sh}} = {Q_g} - {Q_d}$ = Scheduled bus injection (difference between bus generation and demand); ${B_s}$ is the last column bus susceptance matrix; V_s is the slack bus voltage magnitude.

Here, ${V_0} =$ the bus voltage magnitude of the base case when no transaction happens, ${V_{new}} =$ new voltage magnitude after a transaction, ${B_{ij}} =$ susceptance value for the i-j line from the bus matrix.

Here, tx = the amount of transaction, ${Q_{tx}} =$ reactive power when no transaction happens, ${Q_{txn}} =$ reactive power when a transaction happens.

Now, calculate ATC for each transaction:

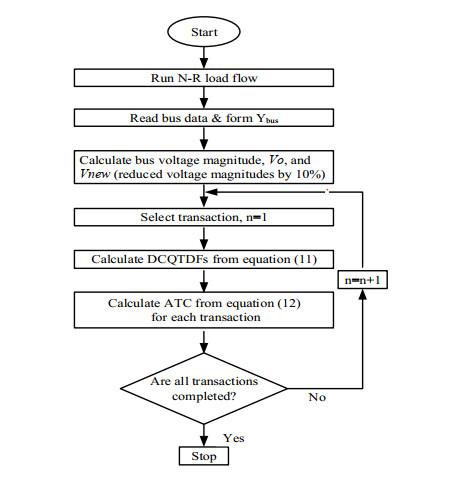
This would denote by $AT{C_{old}}$. Moreover, decreased the bus voltage magnitudes by 10% for PV bus-3 and PQ bus-5; rerun the load flow, utilize the new voltage values for recalculated $AT{C_{tx}}$ from Eq (12) for each transaction denote by $AT{C_{new}}$. Figure 3 presents the determination of ATC by DCQF load flow considered only reactive power for brownout step by step.

3.2.   Sensitivity calculation for brownout

Sensitivities of any parameter can be reflected in the discrepancy of ATC, even if it's minor. Furthermore, by sensitivity analysis, we can effectively identify ATC gridlock and get crucial convoy information for performance and planning. The definition of ATC clarifies that the value of ATC depends on both the topology of a network and the system components. The sensitivity of ATC aid in revealing the weakness of the system. If the sensitivity of ATC w.r.t any parameter in the system is bigger, that parameter significantly impacts ATC's need to improve the maintenance and investment. If it's small, then it has less effect on ATC no need to enhance investment. The formula of sensitivity for brownout by the DCQF method is given below:

Here, $\frac{{\partial ATC}}{{\partial V}}$ = sensitivity of ATC w.r.t voltage parameter for each transaction.

3.3.   TRM calculation for brownout

ATC should embody TRM because the transmission network needs to be secure when a rational range of disturbances occurs during power transmit. Likewise, Gamma distribution is used to determine TRM for DCQF load flow. The process is given below:

The first parameter that needs to determine is the failure density function, f(t) for Gamma distribution:

For this work, 95% and 99% are considered as (%FDF). Determine t from the Eq (14); because t needs to determine the TRM.

Here, α = Scale parameter = 3; β = Shape parameter = 0.5; Г(β) = √π

Now, the Expected value,

Variance,

$$

Standard Deviation,

Equation (17) is also known as Standard Deviation of Sensitivity (S.D.S).

Here, ${p_i}$ = parameter distribution = 0.05

$\frac{{\partial ATC}}{{\partial V}}$ = sensitivity of each transaction

Here, m = is a certain number that keeps the margin greater than the S.D.S to ensure that the system is reliable, a straightforward calculation from the consulting table.

= 1.65, for 95% probability of sensitivity

= 2.33, for 99% probability of sensitivity

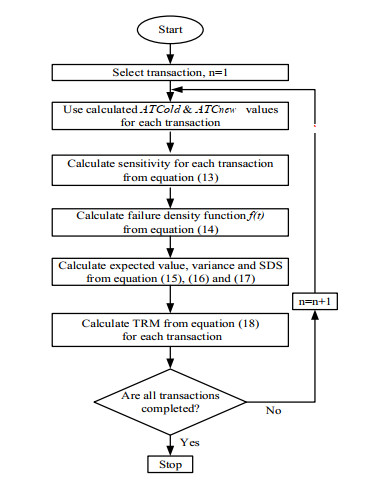
In Figures 3 and 4, the determination of TRM by DCQF load flow for brownout is presented step by step.

4.   Results and discussion

4.1.   AC load flow

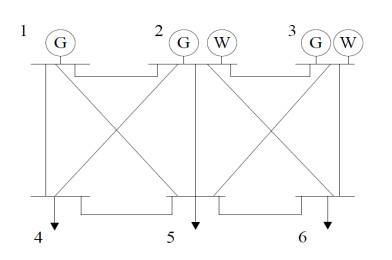
To demonstrate the proposed technique for ATC and TRM determination IEEE 6 bus system is used. Figure 5 is the schematic diagram of the IEEE 6 bus system, where bus-1, 2, and 3 are the generator buses. On the other hand, bus-4, 5, 6 are the load buses. Moreover, multi-transactions are taken for this methodology which is given below.

T14: a transaction between seller bus 1 and buyer bus 4

T15: a transaction between seller bus 1 and buyer bus 5

T16: a transaction between seller bus 1 and buyer bus 6

T24: a transaction between seller bus 2 and buyer bus 4

T25: a transaction between seller bus 2 and buyer bus 5

T35: a transaction between seller bus 3 and buyer bus 5

T36: a transaction between seller bus 3 and buyer bus 6

In Table 1, the bus data is given for the six bus systems where the first bus is the slack bus, the second and third buses are the generator buses, and buses 4, 5, and 6 are the load buses. Moreover, real power generation for PV buses is 50 and 60 MW, respectively. For each load, the bus power is 70 MW. The voltage magnitude for the slack bus is 1.05 p.u, PV 2 and PV 3 buses are 1.05 and 1.07, respectively. All PQ buses are 1 p.u.

Table 2 represents the ATCV values; determine the base values without changing any parameter in the system for each transaction. The ATC PV2 and PV3 values are calculated from the proposed technique for brownout; that means reduced voltage magnitudes of the generator buses (PV-2 and PV-3) by 10%. These values are far too small than the base one, which means if voltage magnitudes reduce, it highly affects the power transfer in the network.

Table 3 shows the sensitivity values for bus-2 and bus-3; these values are calculated from Eq (3). After that, the TRM values from Eq (8) for 95% and 99% probability of sensitivity for each transaction. This table shows that TRM is rising with the rising probability of sensitivity. To keep a reliable system, TRM must exceed the uncertainty of any parameter that can occur in the system.

In Table 4, ATC values are determined from the same Eq (2) for load bus-4 and 5 after reduced bus voltage magnitudes by 10%. This table shows that ATC values decrease after reducing the bus voltage magnitudes from their base values but are not too small compare with the ATC values in Table 2, which deduces that if voltage level changes, it affects the available transfer capability of generator buses more than the load buses.

Table 5 presents sensitivity and TRM values for PQ bus-4 and bus-5. Similarly, TRM values are increased with the probability of sensitivity. The reliability margin is the safety margin that keeps the system safe, and this is possible only then when $TRM\rangle \rangle S.D.S$. If a system is called reliable, then TRM must increase with the probability of sensitivity. In this table, the values of TRM for 99% probability are more significant than the 95% probability. This indicates that the system is reliable even after any disturbances occur in the power system network.

4.2.   DCQF load flow

In Table 6, ATC results are presented for the base case, load bus-5, and generator bus-3; these results show that ATC values are decreased with the decrease in voltage magnitude. This proved that whenever a system faced disruption, it would affect the flow through the line. Besides, if the voltage gets reduce, the current will too, which causes a reduction in the transfer capability. Therefore, in this method, the ATC values are not significantly decreased like in the AC method.

Table 7 represents sensitivity and TRM results for two different probabilities of sensitivity (95% and 99%). So, TRM is more significant than sensitivity values; that's how a system can be reliable TRM is that margin that keeps securing the network and all the transfers in it even any disruption occurs. Moreover, TRM results get increased with the increased probability of sensitivity. So, TRM must exceed the uncertainty of any parameters; otherwise, no system can be reliable.

5.   Validation

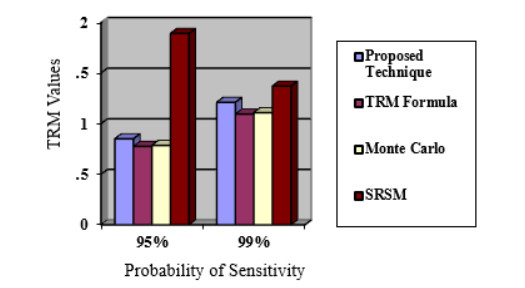
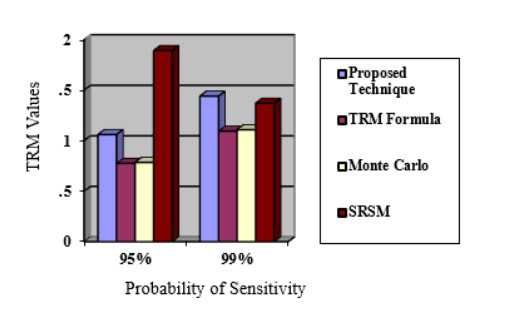
In Tables 8 and 9, the results of TRM, which are obtained from the proposed technique, are compared with the results of ^[3,4], which are pretty close. In ^[4], the TRM formula and Monte Carlo both are done for Normal distribution, and in ^[3], that's also done for Normal distribution but adds the wind farm. Moreover, the proposed technique is done for Gamma distribution using a modified TRM formula which is very facile, and the whole process is done for the IEEE-6 bus system. Tables 8 and 9 show that TRM values increase with the rise of the probability of sensitivity (95% and 99%). The growth of the probability of sensitivity causes the increase in the TRM, which proves that the system is reliable. The validation of the TRM values of the proposed technique for two different probabilities of sensitivities is presented in Figures 6 and 7.

6.   Conclusions

ATC must assist with TRM in a power transmission network so that the transmission network will be stable from any disturbances or be aware of any uncertainty of transfer capability that may happen during power transfer. In this work, TRM is calculated for brownout because, in the power system, the disturbance in voltage is very crucial; any system will be collapsed inadequately if voltage goes unstable. ATC calculation can be done for various methods such as AC, DC load flow, etc.; here, ATC is calculated by AC, and DCQF load flows for bus voltage magnitudes using VDFs and DCQTFs. Standard Deviation of Sensitivity (S.D.S) is also important for any system because of lower the S.D (standard deviation), lower the sensitivity, and thus more confidence which means higher reliability in the experiment. Numerical results reveal that the ATC values decrease when voltage magnitudes declined, affected the generator buses more than the load buses. Still, in the DCQF method, ATC values get affected too but not like the AC method. Besides, TRM values linearly vary with the probability of sensitivity. Moreover, if sensitivity rises and the TRM does not increase the system will crumble. Finally, the validation of this work is quite close to the published ones.

Acknowledgments

The author gratefully acknowledges the support of A.H. Chowdhury, Professor, Dept. of EEE, Bangladesh University of Engineering and Technology, in writing this paper.

Conflict of interest

The authors declare no conflicts of interest in this paper.