In recent years, the amount of available data is growing exponentially, and large-scale data is becoming ubiquitous. Machine learning is a key to deriving insight from this deluge of data. In this paper, we focus on the large-scale data analysis, especially classification data, and propose an online conjugate gradient (CG) descent algorithm. Our algorithm draws from a recent improved Fletcher-Reeves (IFR) CG method proposed in Jiang and Jian[13] as well as a recent approach to reduce variance for stochastic gradient descent from Johnson and Zhang [15]. In theory, we prove that the proposed online algorithm achieves a linear convergence rate under strong Wolfe line search when the objective function is smooth and strongly convex. Comparison results on several benchmark classification datasets demonstrate that our approach is promising in solving large-scale machine learning problems, viewed from the points of area under curve (AUC) value and convergence behavior.
1.
Introduction
We first establish the key notations to make them consistent in this paper. Vectors are denoted by boldface letters, e.g., w, and ∇f(w) denotes the gradient of function f at point w. Superscript "T" is the transpose operation of a vector. We use ‖w‖ as a shorthand for the l2-norm of w. Given a dataset D={(zi,yi)mi=1}, where zi∈Rn and yi∈R, the focus of this paper is structural risk minimization [28], a fundamental subject in machine learning, which is a combination of two terms
Here, w is the optimization variable (usually called weight vector in the research area of machine learning), l:Rn→R is the loss function associated with sample pair (zi,yi), and the regularization function r:Rn→R is a penalty on the complexity of w.
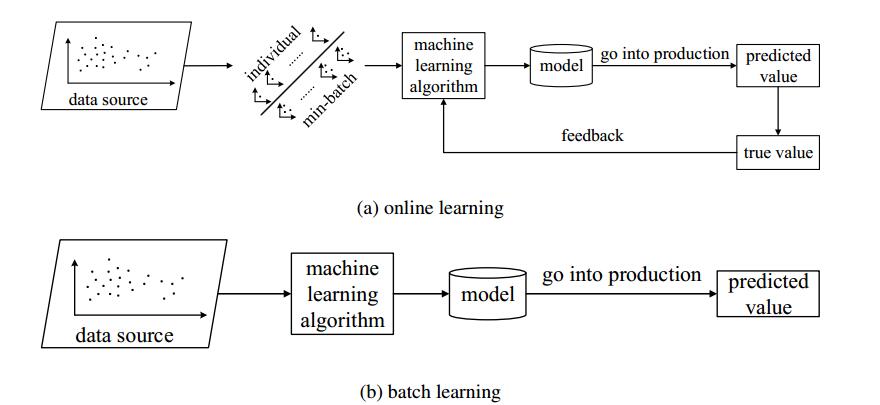
Optimization learning algorithms for solving (1.1) mainly fall into two broad categories, namely, online learning and batch learning. The two learning mechanisms are illustrated in Figure 1. In online learning, data streams (either individually or in mini-batches) into the learning algorithm and updates the prediction model. We just need to use the new (real-time) data to build a model. However, in batch learning, the model is trained using the entire dataset. This process is also called offline learning. In batch learning, if there is need to update the learning model based on new data, the model should be trained from scratch all over again using both the previous data and the new data [2].
The prototypical online learning algorithm is stochastic gradient descent (SGD) method [23], which is defined as
where ηk is the learning rate (also known as stepsize in numerical optimization), and the index ik, corresponding to the sample pair (zik,yik), is randomly chosen from {1,2,…,m}. We describe the standard SGD method in Algorithm 1. It is observed that each iteration of SGD only involves the computation of ∇fik(wk) corresponding to one sample, resulting in a very cheap iteration cost. The gradient information is obtained from only one sample at each iteration. Further, one can use a mini-batch method, in which a small subset of all samples is randomly selected per iteration and employ the iteration.
where |Sk| denotes the number of elements in the set Sk.
In recent years, SGD has been widely studied in machine learning and optimization community; see [5,16,19,22,27,29,32] for example. The standard SGD can quickly reach a proximate optimum solution during the learning process, but its convergence rate may slow down when more accurate solutions are required. Due to the variance of random sampling, with a suitably chosen ηk=O(1/k), SGD achieves a sub-linear convergence rate of O(1/k).
In order to improve the convergence of SGD, Johnson and Zhang [15] proposed a stochastic variance reduced gradient (SVRG) method to reduce the variance of random sampling. The description of SVRG is in Algorithm 2. As argued by Bottou et al. [3], for the first epochs, SGD is more efficient, but once the iterations approach the solution the benefits of the fast convergence rate of SVRG can be observed. In [21], Nguyen et al. introduced a stochastic recursive gradient algorithm (SARAH). Different from SVRG, SARAH employs a simple recursive approach to update stochastic gradient and uses more stable gradient estimates than SVRG. But the choice of the learning rate η depends on a Lipschitz constant of the objective function. Without explicit knowledge of this constant, η is typically chosen by experimentation in both SVRG and SARAH. By incorporating the idea of variance reduction, Moritz et al. [20] proposed a stochastic L-BFGS method and proved a linear rate of convergence. In [26], Tan et al. used the well-known Barzilai-Borwein (BB) method [1] to automatically compute the learning rate for SVRG, and established a linear convergence rate. Recently, based on the BB method, an improved SVRG, named stochastic two-point stepsize gradient method, has been proposed by Shao et al. [25], which also achieves a linear convergence rate for smooth and strongly convex functions. Liu et al. [17] used the BB approach to adaptively compute the learning rate for SARAH. In [14], Jin et al. proposed a stochastic CG method with variance reduction, which converges more quickly than SVRG. Actually, the idea of stochastic CG has been studied before. Schraudolph and Graepel [24] combined the idea of CG with stochastic setting to optimize unconstrained quadratic problems, and the resulting algorithms converge orders of magnitude faster than ordinary SGD. In [30], Xu and Dai employed CG to accelerate the convergence of stochastic approximation algorithm, Robbins-Monro method. Jiang and Wilford [12] proposed a stochastic CG method for the approximation of functions, which performs the CG steps by using an inner product that is based on stochastic sampling.
Motivated by this, we propose in this paper a new online variance reduced CG method and prove that the proposed method converges linearly for strongly convex and smooth objective functions. The remainder of this paper is organized as follows. In Section 2, we give a brief introduction of the IFR CG method used in batch optimization. And then, we present the proposed method along with the theoretical analysis in Section 3. Numerical experiments are reported in Section 4. Finally, we conclude this paper in Section 5.
2.
Brief introduction of IFR CG
Due to the low memory requirement and strong convergence property, CG method is a very efficient batch algorithm, and it is still one of the most active research fields of optimization [6,7,11,13,18,31]. Take (1.1) as an example. Suppose that f is differentiable, then given an initial point w0, a CG method generates a sequence {wk} by using the recurrence
where αk is the stepsize usually obtained by a line search, and the search direction dk is computed by
βk is the CG update parameter. Different choices of βk yield different CG methods. Some well-known formulas for βk are βHSk, βFRk, βPRk, βCDk, βLSk, and βDYk, see the comprehensive review [10] for details. Here, we focus on βFRk proposed by Fletcher and Reeves [8], which takes the form of
Another important issue related to the performance of CG is the line search, which requires sufficient accuracy to ensure dk satisfies the descent condition ∇f(wk)Tdk<0, ∀k. A common criteria for line search is the Wolfe line search
where 0<c1<c2<1. In the strong Wolfe line search, the second condition in (2.4) is replaced by
It has been shown that the strong Wolfe line search for βFRk may not yield a descent direction unless c2≤1/2 [4]. In practice, it is often most efficient to choose c2 close to 1. Hence, the constraint c2≤1/2, needed to ensure descent, is a significant restriction in the choice of parameter c2 in the Wolfe line search. Note that Gilbert and Nocedal [9] gave the convergent scope τk∈[−1,1] for τkβFRk. Based on this, Jiang and Jian [13] considered τk=−|∇f(wk)Tdk−1|∇f(wk−1)Tdk−1 and introduced an improved FR (IFR) formula
The following lemma shows that the search directions yielded by IFR CG are all sufficient descent, and the IFR CG method is globally convergent under the strong Wolfe line search.
Lemma 1 (Theorem 3 [13]). Suppose that f(w) is differentiable, ∇f(w) is Lipschitz continuous, and 0<c2<√2/2, then it holds that
Further, IFR CG is globally convergent by the way of lim infk→∞‖∇f(wk)‖=0.
3.
Proposed method and theoretical analysis
3.1. SIFR CG method
Based on the theories mentioned above, we now describe the core of the proposed online CG algorithm, called stochastic improved Fletcher-Reeves conjugate gradient (SIFR CG for short) method, for solving (1.1) in detail and provide the pseudo-code.
SIFR CG operates in cycles. At the beginning of each cycle, an iteration point wk is available at which the method computes a batch gradient uk←∇f(wk). Then, after initializing x0←wk, g0←hk, and d0←−g0, a set of T inner iterations indexed by t with an update xt+1←xt+αtdt are performed, where αt is chosen according to the strong Wolfe line search. We define the subsampled function fS(w) as:
where |Sk| denotes the number of elements in the set Sk.The search direction dt is computed by −gt+βtdt−1, where gt+1←∇fS(xt+1)−∇fS(wk)+uk, and S is chosen randomly. The pseudo-code of SIFR CG is given in Algorithm 3.
There are a couple of things to note about this algorithm.
Remark 1. To mitigate the effects of some outliers in the training data, we restrict αt and βt by adding some additional constraints.
Remark 2. For convenience, we use the condition |gTt+1dt|≤−c2gTtdt in the theoretical analysis.
Remark 3. The following experiments are carried out using wk+1←xT.
3.2. Theoretical analysis
In this section we analyze the convergence property of the proposed method SIFR CG. Our analysis makes use of the following assumptions.
Assumption 1. ∀i, fi:Rn→R is twice continuously differentiable.
Assumption 2. ∀w∈Rn and S⊆D, there exist two positive constants ϕ and φ such that ϕI≤∇2fS(x)≤φI, where I denotes the identity matrix, and ∇2fS(x) is the Hessian matrix of f at point x.
For Algorithm 3, we immediately have the following result.
Theorem 1. Suppose that Assumptions 1 and 2 hold, and let ξ>0 be an upper bound on −gTtdt/|gTt+1dt|, then, ∀t, we have
where ρ(t)=(ξ+43)(ϵξ)t−(ϵ2)tξ−ϵ+(ϵ2)t.
Proof. It follows from the lines 14–16 in Algorithm 3 that βt+1≤ϵ, therefore,
From the definition of dt, we have
The last inequality follows from Lemma 1 and Remark 2. Using 0<c2<1/2, it follows that
The second inequality follows from d0=g0. Observing (3.4), we immediately get ‖gt‖2≤(ϵξ)t‖g0‖2, and (3.6) can be rewritten as
which completes the proof.
The following two lemmas show a lower bound on ‖∇f(x)‖2 and an upper bound on the variance reduced gradient estimates gt, respectively.
Lemma 2 (Lemma 5 [20], Lemma 1 [14]). Let w∗ be the unique minimizer of f, and suppose that f is strongly convex with parameter σ, then, ∀x, we have ‖∇f(x)‖2≥2σ[f(x)−f(w∗)].
Lemma 3 (Lemma 6 [20], Lemma 2 [14]). Let w∗ be the unique minimizer of f, uk=∇f(wk), and gt=∇fS(xt−∇fS(wk)+uk, then by taking an expectation w.r.t. S, we have E[‖gt‖2]≤4φ[f(xt)−f(w∗)+f(wk)−f(w∗)].
Based on the above theoretical basis, we now state our main result in the following theorem.
Theorem 2. Suppose that Assumptions 1 and 2 hold, and let x∗ be the unique minimizer of f, then, ∀k, we have
Here, the convergence rate θ is given by
with Λ=ξ+4/3ξ−ϵ×1−(ξϵ)T1−ξϵ−ϵ+4/3ξ−ϵ×1−(ϵ2)T1−ϵ2, assuming that we choose 8φϵαmax<3σαmin and that we choose T large enough to satisfy
Proof. Using the Lipschitz continuity of ∇f, which follows from Assumption 2, we have
Taking expectations of (3.11) and using Lemma 2 gives
Using Theorem 1 and Lemma 3, (3.12) becomes
By summing (3.13) over t=0,1,…,T−1, we obtain
Rearranging (3.14) gives
Further, we have
The second inequality follows from f(w∗)≤f(xT). Note that ∑T−1t=0ρ(t)=ξ+4/3ξ−ϵ×1−(ξϵ)T1−ξϵ−ϵ+4/3ξ−ϵ×1−(ϵ2)T1−ϵ2 and denote this result by Λ, then we have
on condition that αmax/αmin<0.75σ/(φϵ), where θ=1+8φϵαmaxT3+4φ2α2maxΛ2σαminT−8φϵαmaxT3. Since we chose T to satisfy (3.10), it follows that the rate θ is less than one. Thus, we get the result as desired.
4.
Comparative experiments
To show the efficiency and effectiveness of the proposed method, we compare it with SVRG [15] (a stochastic learning algorithm) and IFR CG [13] (a batch learning algorithm) on five classification datasets, as shown in Table 1. These datasets are obtained from the LIBSVM database*. All experiments are implemented using the Armadillo C++ library on a PC (Core i9-9900X CPU$ @.50GHz, 64 GB of memory) with Ubuntu 18.04.1 operating system.
*http://www.csie.ntu.edu.tw/ cjlin/libsvmtools/datasets
4.1. Problem setup
We evaluate these methods on three popular machine learning problems, including
∙l2-logistic regression
∙l1-SVM
∙l2-SVM
where λ>0 is the regularization parameter.
We set λ={0.01,0.001,0.0001} and set |S|=√m during the whole experiments. We set the number of iterations of the outer loop to 25, and set the inner loop index T to 30 and 50, respectively. For SVRG, we set η={0.1,0.05,0.001,0.005,0.01,0.05}. For IFR CG and SIFR CG, we set c1=10−4 and c2=0.1. Additionally, in SIFR CG, we set αmax=1/αmin=105 and ϵ=10. We randomly divide each dataset into three parts, 1/3 for test, 1/5 for validation, and the rest for training. After finding the optimal parameters that maximize the AUC values on validation set, we employ the corresponding model to the test set.
4.2. Experimental results
We first adopt the the cross validation technique to obtain the optimal parameters for each learning model, and the cross validation results are summarize in Tables 2 and 3. We can see that for different learning models and different datasets, the optimal parameters are often data-dependent and should be tuned correspondingly.
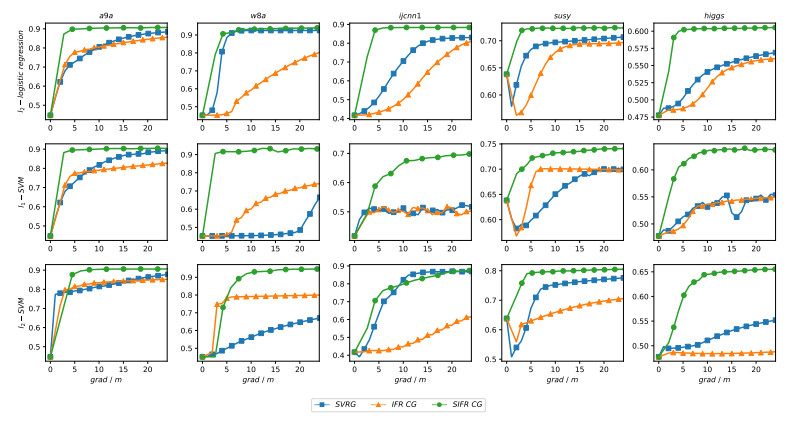
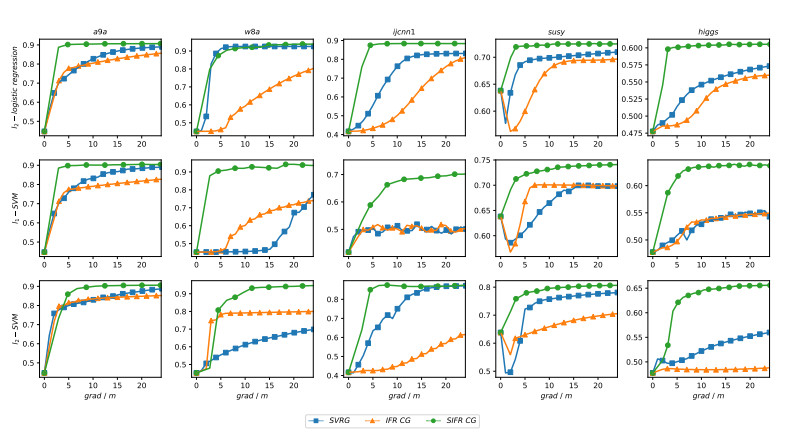
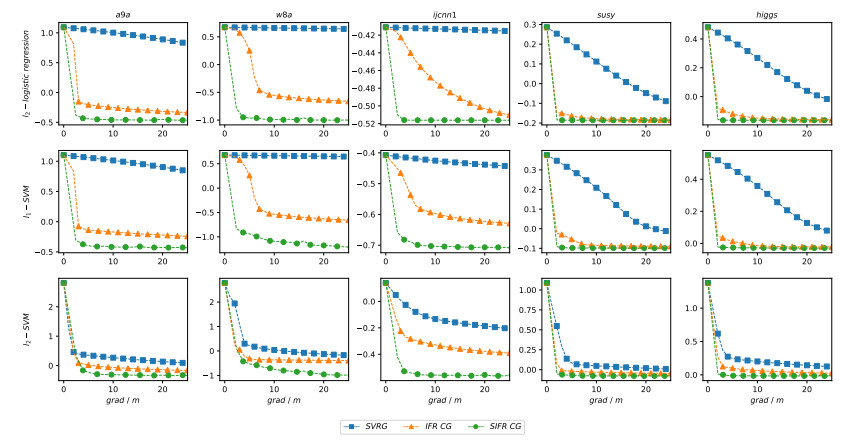
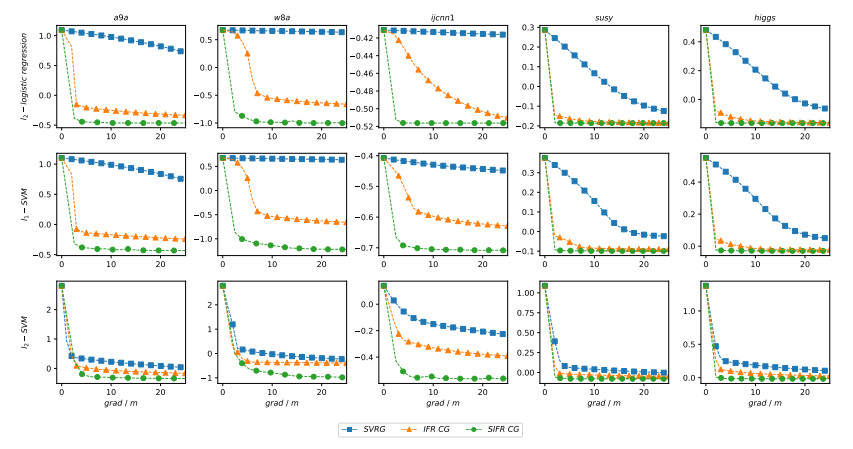
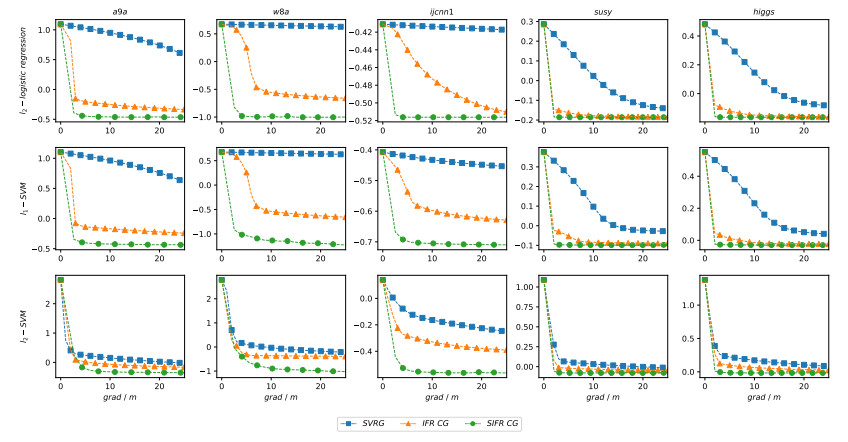
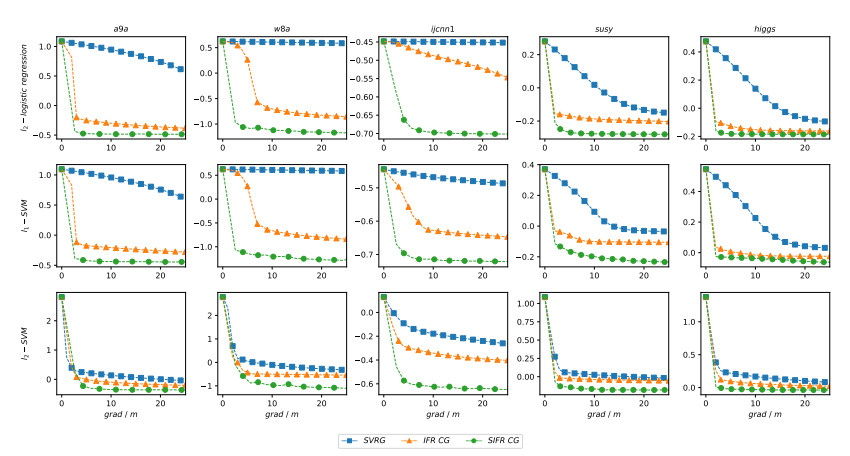
After getting the optimal learning rates for SVRG and the optimal regularization parameters for all the methods, we report the changing curves of AUC values on each test datasets obtained by different method with increasing computational cost in Figures 2-5. In order to fairly compare the performance of different methods, all the x-axes represent the computational cost that is measured by the number of gradient computations divided by m, and all the y-axes represent the AUC value. In general, the closer the AUC is to 1, the higher the accuracy of the method is. Figures 2-5 show the changing results when T=30, T=40, T=50, and T=60, respectively. Firstly, we can see from the four figures that the proposed method SIFR CG significantly outperforms SVRG and IFR CG on the whole test datssets. That is, the classification accuracy of our method is the highest. Secondly, SVRG and IFR CG have their own advantages and disadvantages on different datasets, therefore, they are hard to differentiate. Thirdly, unlike SVRG and IFR CG, we find that the role of increasing the number of loops to improve the performance of SIFR CG is less obvious. In other words, the SIFR CG method takes fewer iterations to get the optimal solution.
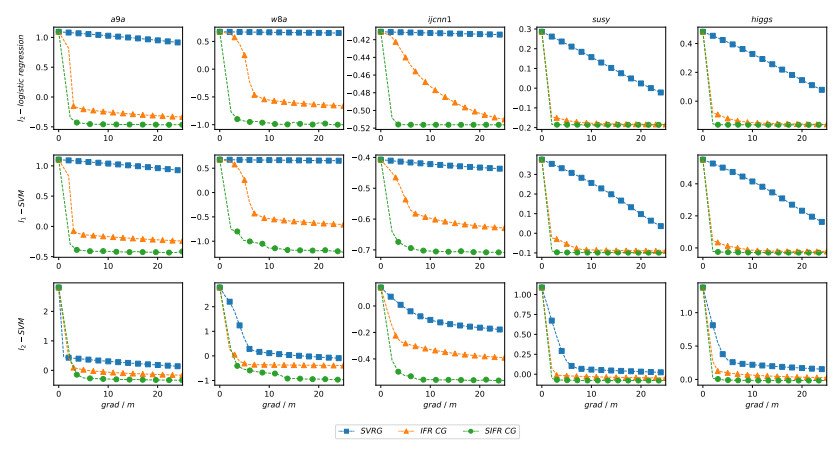
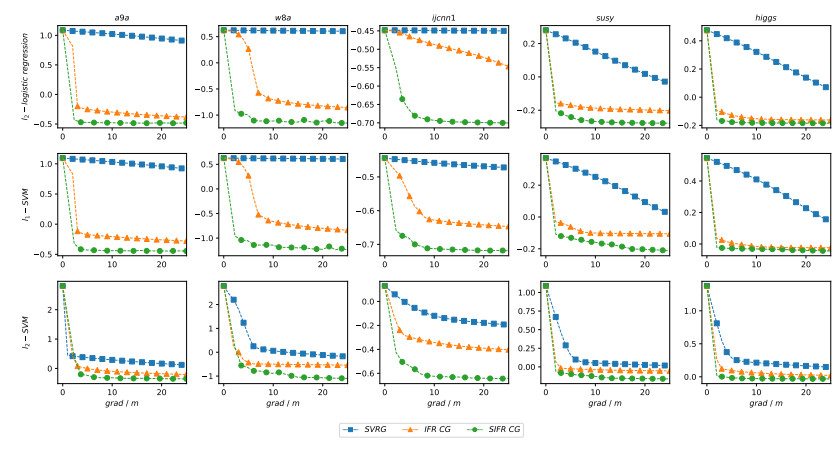
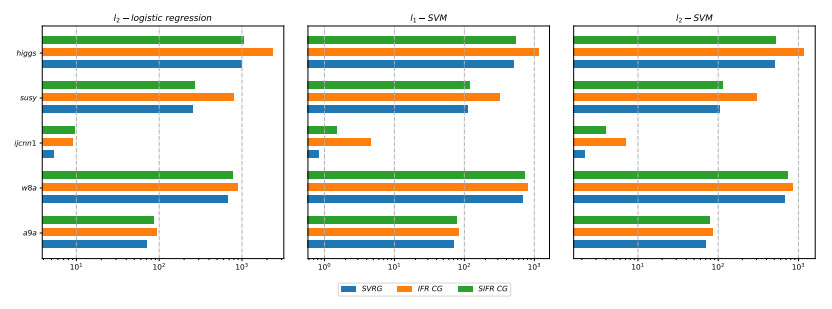
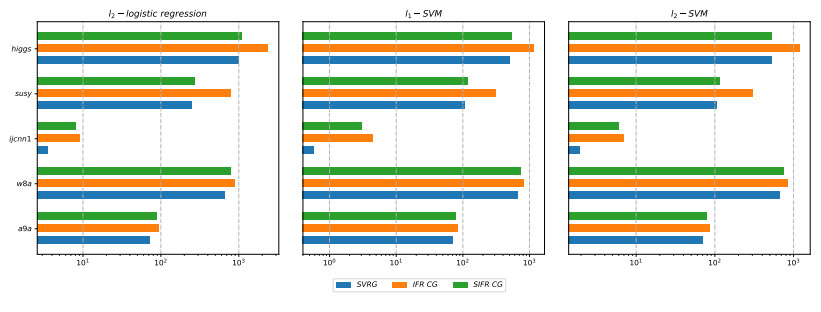
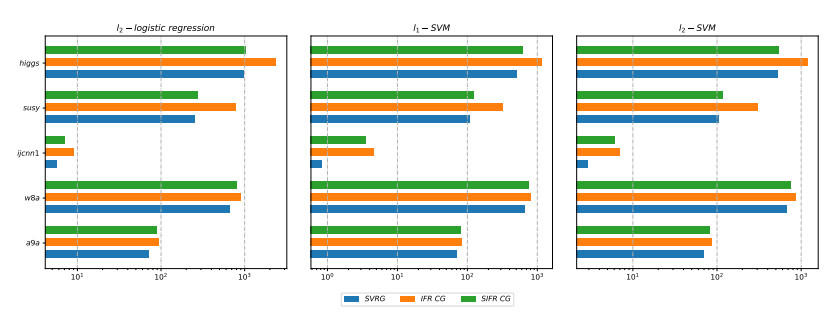
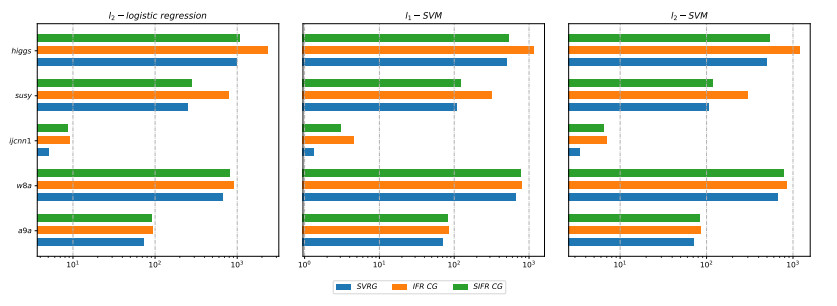
Additionally, Figures 6-17 show the convergence behaviors and the corresponding average computing time (the numbers of iterations of the outer loop is set to 25) of the three methods on each training dataset. In the convergence behavior figures (see Figures 6, 7, 9, 10, 12, 13, 15 and 16), all the x-axes also represent the computational cost that is measured by the number of gradient computations divided by m, and all the y-axes represent the logarithm of objective function value (base 10). We see that the convergence rate of the SVRG is not as fast as the other two methods because SVRG is sensitive to the learning rate. However, for all test environments, the proposed method SIFR CG has the fastest convergence speed and reaches the smallest objective function value, which is consistent with the AUC results shown in Figures 2-5. In the average computing time figures (see Figures 8, 11, 14, and 17), all the x-axes are in logarithmic time (base 10). We can see that SVRG has the least computing time on these datasets. On the contrary, IFR CG employs the entire dataset to conduct the line search to select the learning rate at each iteration, resulting in a heavy computing burden. The computing time of SIFR CG is between SVRG and IFR CG, and it can be observed that the computing time of SIFR CG is close to IFR CG when the dataset is small and is close to SVRG when the data is large.
Overall, preliminary experiments show that the proposed method SIFR CG not only has better learning performance, but converges speedily. And The advantage of SIFR CG is more obvious on large-scale datasets.
5.
Conclusions
In this paper, we proposed a stochastic Fletcher-Reeves conjugate gradient algorithm and proved a linear rate of convergence in the strongly convex case. Comparative experiments on several benchmark datasets demonstrate that the proposed algorithm performs well on large-scale smooth and nonsmooth machine learning problems.
There are several interesting issues to study in future work. For example, we can replace the Wolfe line search by a nonmonotone line search to find the optimal solution faster or propose more effective conjugate gradient update parameters.
Acknowledgments
The authors thank the editor and the reviewers for their constructive comments and suggestions that greatly improved the quality and presentation of this paper. This work was partly supported by the National Natural Science Foundation of China (Grant Nos. 11661007, 61671456 and 61806004), the China Postdoctoral Science Foundation (Grant No. 2020T130767), the Natural Science Foundation of the Anhui Higher Education Institutions of China (Grant No. KJ2019A0082), and the Natural Science Foundation of Zhejiang Province, China (Grant No. LD19A010002).
Conflict of interest
The authors declare that there is no conflict of interests regarding the publication of this article.









 DownLoad:
DownLoad: