The aim of this article is to introduce a new algorithm by integrating a viscosity-type method with the subgradient extragradient algorithm to solve the equilibrium problems involving pseudomonotone and Lipschitz-type continuous bifunction in a real Hilbert space. A strong convergence theorem is proved by the use of certain mild conditions on the bifunction as well as some restrictions on the iterative control parameters. Applications of the main results are also presented to address variational inequalities and fixed-point problems. The computational behaviour of the proposed algorithm on various test problems is described in comparison to other existing algorithms.
1.
Introduction
Assume that C is a closed and convex subset of a real Hilbert space H with the inner product and the induced norm are denoted by ⟨⋅,⋅⟩ and ‖⋅‖, respectively. Moreover, R be a set of real numbers during whole article. Let f:H×H→R be a bifunction and satisfy f(v,v)=0 for all v∈C, the equilibrium problem (EP) [6,11] for a bifunction f on C is defined in the following way:
Moreover, SEP(f,C) denotes the solution set of an equilibrium problem over the set C and u∗ is an arbitrary element of SEP(f,C). A metric projection PC(u) of u∈H onto a closed and convex subset C of H is defined by PC(u)=argminv∈C‖v−u‖.
In this article, the equilibrium problem is studied based on the following hypothesis:
(a1) A bifunction f:H×H→R is said to be (see [3,6]) pseudomonotone on C if
(a2) A bifunction f:H×H→R is said to be Lipschitz-type continuous [21] on C if there exist two constants c1,c2>0 such that
(a3)lim supn→∞f(un,v)≤f(p∗,v) for all v∈C and {un}⊂C satisfies un⇀p∗;
(a4)f(u,⋅) is subdifferentiable and convex on H for every each u∈H.
The above-defined problem (EP) is a general mathematical problem in the sense that it unifies a number of mathematical problems, i.e., the fixed point problems, the vector and scalar minimization problems, the problems of variational inequalities (VIP), the complementarity problems, the saddle point problems, the Nash equilibrium problems in non-cooperative games and the inverse optimization problems [4,6,24,41]. The problem (EP) is also known as the well-known Ky Fan inequality due to his initial contribution [11]. Many authors have developed and generalized many results on the existence and nature of the solution of an equilibrium problem (see for more detail [2,4,11]). Due to the significance of the problem (EP) and its applications in both pure and applied sciences, many researchers have studied it extensively in recent years [5,10,14].
A proximal point method is used to solve the problem (EP) based on mathematical programming [13]. This method was also known as the two-step extragradient method in [34] due to initial contribution of Korpelevich [18] to solve saddle point problems. Tran et al. in [34] established an iterative sequence {un} in the following way:
where 0<ρ<min{12c1,12c2}. Recently, many existing methods have been extended in the case of problem (EP) in finite and infinite-dimensional spaces, such as the proximal point-like methods [13,22], the extragradient-like methods [17,19,26,27,32], the subetaadient extragradient methods [1,29,36,37], the inertial methods [35,39] and others in [9,12,16,25,30,33,38].
Inspired by the results in [8,16,23], in this paper, we introduce a viscosity-type subetaadient extragradient algorithm to solve the equilibrium problems involving pseudomonotone bifunction. A strong convergence theorem for the proposed algorithm is well-established by considering certain mild conditions on bifunction and control parameters. Some applications for our main results are studied to solve two particular classes of an equilibrium problem. In the end, the computational studies show that the new method is more efficient than the existing ones [16,34].
The remainder of this article has been organized as follows: Section 2 includes some preliminary and basic results. Section 3 contains proposed algorithm and corresponding strong convergence result. Section 4 contains applications of our main results. Section 5 involves the numerical discussion of the proposed method compared to existing ones.
2.
Background
A normal cone of C at u∈C is defined by
Let φ:C→R is convex function. The subdifferential of φ at u∈C is defined by
Lemma 2.1. [15] Assume that PC:H→C is a metric projection such that
(ⅰ)
(ⅱ) u3=PC(u1) if and only if
(ⅲ)
Lemma 2.2. [40] Assume that {an}⊂(0,+∞) is a sequence satisfying
where {γn}⊂(0,1) and {δn}⊂R satisfies the following conditions:
Then, limn→∞an=0.
Lemma 2.3. [20] Assume that a sequence {an}⊂R and there exists a subsequence {ni} of {n} such that ani<ani+1, for all i∈N. Then, there is a non decreasing sequence {mk}⊂N such that mk→+∞ as k→∞, and the following conditions are fulfilled by all (sufficiently large) numbers k∈N,
In fact mk is the largest number n in the set {1,2,⋯,k} such that an≤an+1.
Lemma 2.4. [15] For each u1,u2∈H and δ∈R, then the following relationships are true.
(ⅰ)
(ⅱ)
Lemma 2.5. (Theorem 27.4 [28]) Let φ:C→R be a proper convex, subdifferentiable and lower semi-continuous function on C. An element u∈C is a minimizer of a function φ iff
where ∂φ(u) stands for the sub-differential of φ at u∈C and NC(u) the normal cone of C at u.
3.
Main results
In this section, we present an iterative scheme for solving pseudomonotone equilibrium problems that is based on Tran et al. in [34] and viscosity scheme [23]. It is important to note that the proposed method has a straightforward structure for achieving strong convergence. Suppose that g:H→H be a strict contraction function with constant ξ∈[0,1). The main algorithm has been presented as follows:
Remark 3.1. It can be easily prove that C⊂Hn. By vn and Lemma 2.5, we have
Indeed, for ωn∈∂f(un,vn) there exists ¯ωn∈NC(vn) such that
Thus, we have
Due to ¯ωn∈NC(vn) means that ⟨¯ωn,v−vn⟩≤0, for all v∈C. It implies that
which imply that ⟨un−ρωn−vn,v−vn⟩≤0,∀v∈C. It proves that C⊂Hn for each n∈N.
Theorem 3.1. Assume that {un} is a sequence generated by Algorithm 1 and for some u∗∈SEP(f,C)≠∅. Then, {un} converges strongly to u∗=PSEP(f,C)∘g(u∗).
Proof. Claim 1: The {un} sequence is bounded.
By Lemma 2.5, we have
Thus, there exists ωn∈∂f(vn,tn) and ¯ωn∈NHn(tn) such that ρωn+tn−un+¯ωn=0. Thus,
Since ¯ωn∈NHn(tn) follows that ⟨¯ωn,v−tn⟩≤0, for all v∈Hn. Thus, we have
Since ωn∈∂f(vn,tn) and using the subdifferential definition, we get
Combining expressions (3.1) and (3.2), we obtain
Substituting v=u∗ in expression (3.3), we obtain
Since u∗∈SEP(f,C), it follows that f(u∗,vn)≥0, implies that f(vn,u∗)≤0 due to the pseudomonotonicity of the bifunction f. From expression (3.4), we have
Due to the Lipschitz-type condition on a bifunction f, we obtain
Combining expressions (3.5) and (3.6), we have
Since tn∈Hn and it gives that ⟨un−ρωn−vn,tn−vn⟩≤0, which implies that
Since ωn∈∂2f(un,vn) and using the subdifferential definition, we obtain
Substituting v=tn in the above expression, we get
It follows from inequalities (3.8) and (3.9) that
From (3.7) and (3.10), we have
We have the following equalities:
and
The above facts and (3.11) implies that
It is given that u∗∈SEP(f,C). From the definition of sequence {un+1} and due to the fact that g is a contraction with ξ∈[0,1), we have
Combining expressions (3.12) and (3.13) and χn⊂(0,1), we deduce that
Thus, we conclude that the {un} is bounded sequence. Due to the reflexivity of H and the boundedness of {un} guarantees that there exists a subsequence {unk} of {un} such that {unk}⇀u∗∈H as k→∞.
Claim 2: The sequence {un} is strongly convergent.
Next, we prove the strong convergence of the iterative sequence {un} generated by Algorithm 1. The Lipschitz-continuity and pseudomonotone property of the bifunction f implies that the solution set SEP(f,C) is a closed and convex set (for more details see [34]). Since the mapping is a contraction and so does PSEP(f,C)∘g. Now, we are in position to use the Banach contraction theorem for the existence of a unique fixed point u∗∈SEP(f,C) such that
By using Lemma 2.1 (ⅱ), we have
By Lemma 2.4 (ⅰ) and (3.12), we have
The remainder of the proof shall be split into the following two parts:
Case 1: Assume that there is a fixed number N1∈N such that
Thus, above implies that limn→∞‖un−u∗‖ exists and let limn→∞‖un−u∗‖=l. From (3.16), we get
Due to the existence of limn→∞‖un−u∗‖=l and χn→0, we infer that
It follows that
We can also obtain
The above expression implies that
Thus, implies that the sequences {vn} and {tn} are bounded. Let {unk} be subsequence of {un} such that {unk} converges weakly to ˆu∈H. Next, we need to prove that ˆu∈SEP(f,C). Due to the inequality (3.3), the Lipschitz-like condition of f and (3.10), we obtain
where v is an arbitrary member in Hn. From (3.19), (3.20) and the boundedness of {un} imply that right-hand side goes to zero. From ρ>0, the condition (a3) and vnk⇀ˆu, we obtain
It follows that f(ˆu,v)≥0, for all v∈C, and hence ˆu∈SEP(f,C). Next, we consider
We have limn→∞‖un+1−un‖=0. We can deduce that
From Lemma 2.4(ⅱ) and (3.12), we have
It follows from expressions (3.26) and (3.27), we obtain
Choose n≥N2∈N (N2≥N1) large enough such that 2χn(1−ξ)<1. By using (3.27), (3.28) and applying Lemma 2.2, we conclude that ‖un−u∗‖→0 as n→∞.
Case 2: Assume there is a subsequence {ni} of {n} such that
Thus, by Lemma 2.3 there is a sequence {mk}⊂N as {mk}→∞, such that
Similar to Case 1, the expression (3.16) provides that
Due to χmk→0, we deduce the following:
Also, we can obtain
We have to use the same justification as in the Case 1, such that
By using expressions (3.27) and (3.29), we have
It follows that
Since χmk→0, and ‖umk−u∗‖ is a bounded. Thus, expressions (3.33) and (3.35) implies that
The above implies that
Consequently, un→u∗. This completes the proof of the theorem.
Remark 3.2. If we define g(u)=u0 in Algorithm 1, we obtain the Halpern subetaadient extragradient method in [16].
4.
Applications
Now, we consider the application of our main results to solve the problem of classic variational inequalities [31] for an operator G:H→H is defined in the following way:
We consider the following conditions to study variational inequalities.
(b1) The solution set of the problem (VIP) denoted by VI(G,C) is nonempty.
(b2)G:H→H is said to be a pseudomonotone, i.e.,
(b3) G:H→H is said to be a Lipschitz continuous if there exits a constants L>0 such that
(b4)G:H→H is called to be sequentially weakly continuous, i.e., {G(un)} weakly converges to G(u) for every sequence {un} converges weakly to u.
If we define f(u,v):=⟨G(u),v−u⟩, for all u,v∈C. Then, the equilibrium problem becomes the problem of variational inequalities described above where L=2c1=2c2. From the above value of the bifunction f, we have
As a consequence of the results in Section 3, we have the following results:
Corollary 4.1. Let G:C→H be a mapping satisfying the conditions (b1)–(b4). Choose u0∈C, 0<ρ<1L and a sequence χn⊂(0,1) satisfying the conditions, i.e.,
Assume that {un} is the sequence generated in the following way:
where
Then, the sequence {un} converges strongly to u∗∈VI(G,C).
Note that condition (b4) can be deleted in the case when G is monotone. Indeed, this condition is a particular case of condition (a3) is used to prove (3.24). Without condition (b4), the inequality (3.23) is obtained by imposing the monotonocity on G. In that case, we obtain
By the use f(u,v)=⟨G(u),v−u⟩ in (3.23), we get
Combining (4.2) with (4.3), we obtain
Let vs=(1−s)ˆu+sy, for all s∈[0,1]. Due to convexity of C implies that vs∈C for any s∈(0,1). Since vnk⇀ˆu∈C and ⟨G(v),v−ˆu⟩≥0 for every v∈C. Thus, we have
Therefore, ⟨G(vs),v−ˆu⟩≥0, for all s∈(0,1). Since vs→ˆu as s→0 and due to continuity of G, we have ⟨G(ˆu),v−ˆu⟩≥0, for all v∈C, which implies that ˆu∈VI(G,C).
Remark 4.1. From the above discussion, it can be concluded that the Corollary 4.1 still holds, even if we remove the condition (b4) in case of monotone variational inequaltiy.
Next, we consider the application of our results to solve fixed-point problems involving κ-strict pseudocontraction mapping and the fixed point problem for an operator T:H→H is defined in the following way:
We assume that the following requirements have been met to study fixed point problems.
(c1)T:C→C is said to be a κ-strict pseudo-contraction [7] on C if
(c2) weakly sequentially continuous on C if
If we consider that the mapping T is a κ-strict pseudocontraction and weakly continuous then f(u,v)=⟨u−Tu,v−u⟩ satisfies the conditions (a1)–(a4) and 2c1=2c2=3−2κ1−κ. The values of vn and tn in Algorithm 1, we have
Corollary 4.2. Let C be a nonempty, convex and closed subset of a Hilbert space H and T:C→C is a κ-strict pseudocontraction and weakly continuous with solution set Fix(T)≠∅. Choose u0∈C, 0<ρ<1−κ3−2κ and sequence χn⊂(0,1) satisfies the conditions, i.e.,
Let {un} be the sequence generated in the following way:
where
Then, sequence {un} strongly converges to u∗∈Fix(T).
5.
Numerical illustrations
Numerical results are presented in this section to show the efficiency of the proposed method. The MATLAB codes was run in MATLAB version 9.5 (R2018b) on the Intel(R) Core(TM)i5-6200 CPU PC @ 2.30GHz 2.40GHz, RAM 8.00 GB.
Example 5.1. Assume that f:C×C→R is defined by
where c∈Rn and P, Q are matrices of order n. The matrix P is symmetric positive semi-definite and the matrix Q−P is symmetric negative semi-definite with Lipschitz-type constants c1=c2=12‖P−Q‖ (see [34] for details). The matrices P,Q and vector c are defined by
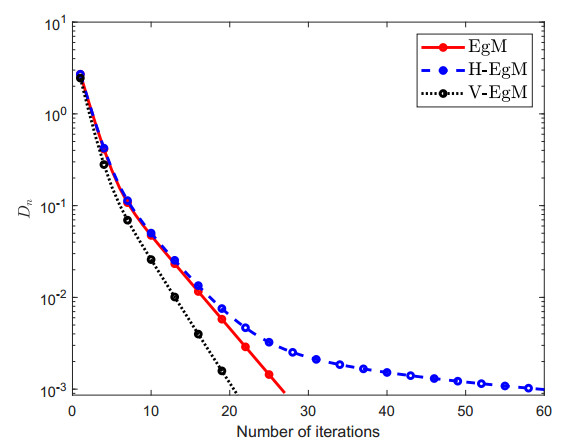
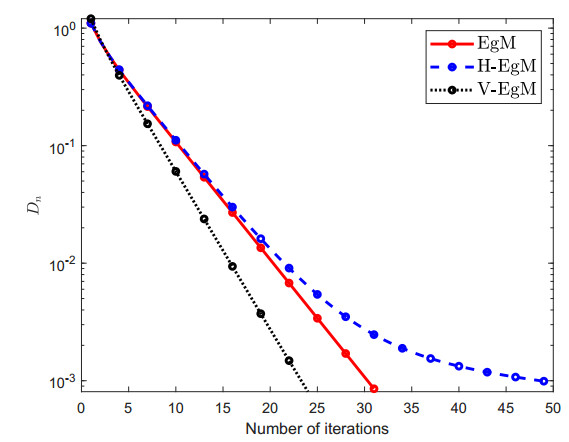
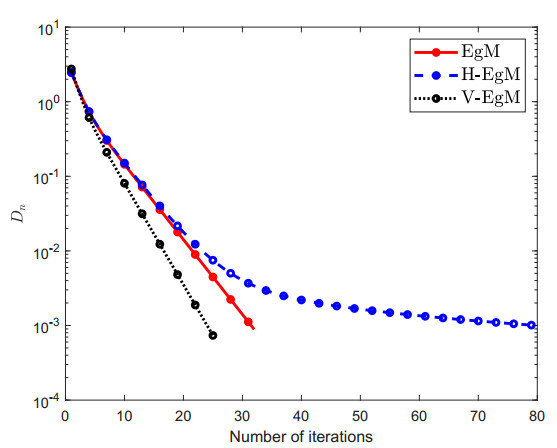
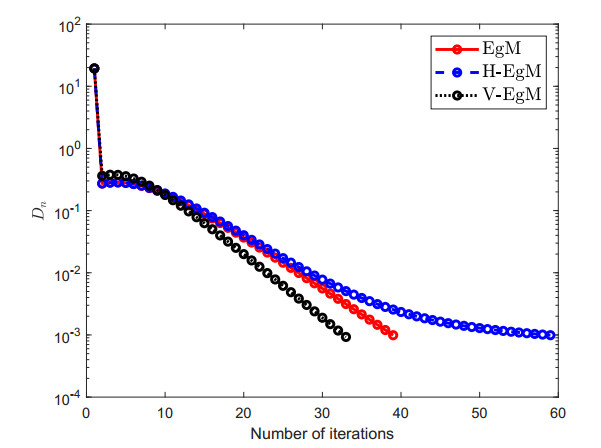
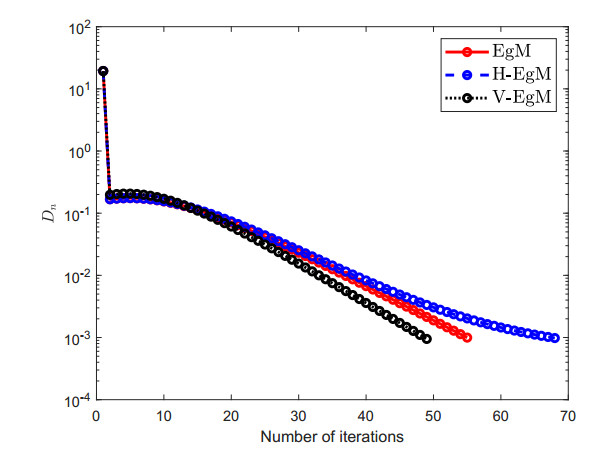
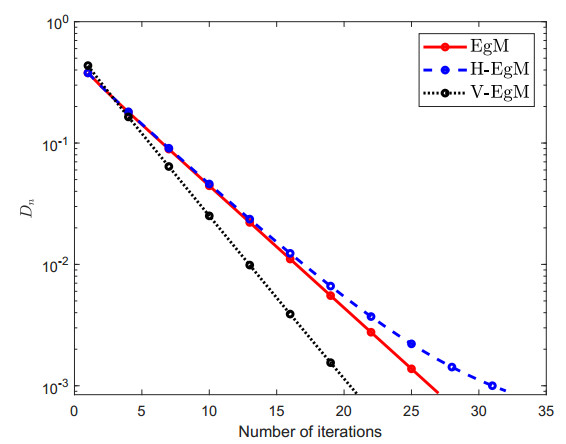
The constraint set C⊂Rn is considered as C:={u∈Rn:−5≤ui≤5}. Furthermore, control parameters conditions are taken as follows: ρ=14c1 and Dn=‖un−vn‖ for Algorithm 1 (EgM) in [34]; ρ=14c1, χn=1100(n+2) and Dn=‖un−vn‖ for Algorithm 2 (H-EgM) in [16]; ρ=14c1,χn=1100(n+2), g(u)=u2 and Dn=‖un−vn‖ for Algorithm 1 (V-EgM). The numerical and graphical results of three methods are shown in Figures 1–4 and Table 1.
Example 5.2. Let f:C×C→R defined in the following way:
where C={(u1,⋯,u5):u1≥−1,ui≥1,i=2,⋯,5}. Thus, the bifunction f is Lipschitz-type continuous with c1=c2=2, and satisfies the conditions (a1)–(a4). The solution set of an equilibrium problem is EP(f,C)={(u1,1,1,1,1):u1>1}. Furthermore, the control conditions ρ=16c1 for Algorithm 1 (EgM) in [34]; ρ=16c1 and χn=1200(n+2) for Algorithm 2 (H-EgM) in [16]; ρ=16c1,χn=1100(n+2) and g(u)=u3 for Algorithm 1 (V-EgM). The numerical results of three methods are shown in Tables 2–4.
Example 5.3. Suppose that H=L2([0,1]) is a Hilbert space with the inner product ⟨u,v⟩=∫10u(t)v(t)dt, for all u,v∈H and the induced norm is
Moreover, assume that C:={u∈L2([0,1]):‖u‖≤1}. Assume that G:C→H is defined by
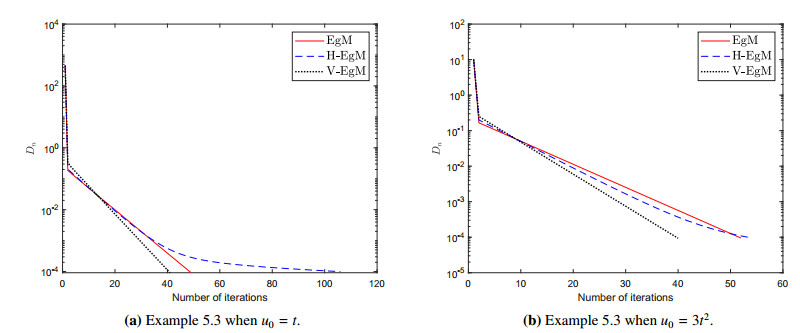
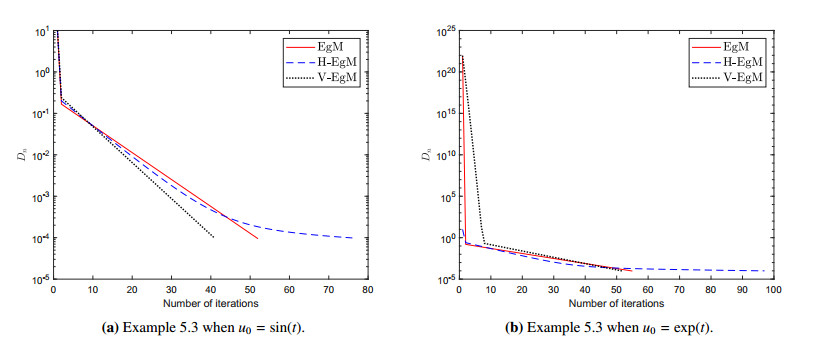
where H(t,s)=2tse(t+s)e√e2−1,f(u)=cos(u) and g(t)=2tete√e2−1. We consider the bifunction f(u,v)=⟨G(u),v−u⟩ with the Lipschitz-type continuous with c1=c2=1. Furthermore, control conditions ρ=15c1 for Algorithm 1 (EgM) in [34]; ρ=15c1 and χn=1300(n+2) for Algorithm 2 (H-EgM) in [16]; ρ=15c1,χn=1100(n+2) and g(u)=u2 for Algorithm 1 (V-EgM). The numerical results of three methods are shown in Figures 5 and 6 and Table 5.
Example 5.4. Assume that f:H×H→R is defined by
where H=l2 is a real Hilbert space having the elements are square-summable sequences and C={u∈H:‖u‖≤3}. The bifunction f is Lipschitz-type continuous and value of Lipschitz-constants are c1=c2=112. Furthermore, control conditions ρ=14c1 for Algorithm 1 (EgM) in [34]; ρ=14c1 and χn=1200(n+2) for Algorithm 2 (H-EgM) in [16]; ρ=14c1,χn=1100(n+2) and g(u)=u2 for Algorithm 1 (V-EgM). The numerical results of three methods are shown in Figures 7 and 8 and Table 6. The projection onto C is evaluated in the following way:
6.
Conclusion
We have studied a viscosity type extragradient-like method for determining the solution of pseudomonotone equilibrium problem in real Hilbert spaces and also prove that the generated sequence converges strongly to the solution. Numerical conclusions were drawn to explain the numerical efficiency of our algorithms in comparison to other methods. These numerical studies showed that viscosity influences improve the efficiency of the iterative sequence in this context.
Acknowledgements
This research work was financially supported by King Mongkut's University of Technology Thonburi through the "KMUTT 55th Anniversary Commemorative Fund". In particular, Habib ur Rehman was financed by the Petchra Pra Jom Doctoral Scholarship Academic for Ph.D. Program at KMUTT [grant number 39/2560]. Moreover, this project was supported by Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT. Also, this project was financially supported by King Mongkut’s University of Technology North Bangkok, Contract no. KMUTNB-BasicR-64-22.
The first author would like to thank the "Petchra Pra Jom Klao Ph.D. Research Scholarship from King Mongkut’s University of Technology Thonburi". We are very grateful to the editor and the anonymous referees for their valuable and useful comments, which helps in improving the quality of this work.
Conflict of interest
No potential conflict of interest was reported by the author(s).









 DownLoad:
DownLoad: