Implementing health policy: lessons from the Scottish Well Mens policy initiative

Flora Douglas; Edwin van Teijlingen; Cairns Smith; Mandy Moffat; Flora Douglas; Edwin van Teijlingen; Cairns Smith; Mandy Moffat

doi:10.3934/publichealth.2015.4.887

AIMS Public Health

2015, Volume 2, Issue 4: 887-905. doi: 10.3934/publichealth.2015.4.887

Previous Article Next Article

Research article Special Issues

Implementing health policy: lessons from the Scottish Well Mens policy initiative

1.
Public Health Nutrition, University of Aberdeen, Aberdeen, Scotland;
2.
Health and Social Care, University of Bournemouth, Bournemouth, England;
3.
Public Health, University of Aberdeen, Aberdeen, Scotland;
4.
Academic Primary Care, University of Aberdeen, Aberdeen, Scotland.

Received: 14 September 2015 Accepted: 11 December 2015 Published: 21 December 2015

Background: Little is known about how health professionals translate national government health policy directives into action. This paper examines that process using the so-called Well Men's Services (WMS) policy initiative as a ‘real world’ case study. The WMS were launched by the Scottish Government to address men's health inequalities. Our analysis aimed to develop a deeper understanding of policy implementation as it naturally occurred, used an analytical framework that was developed to reflect the ‘rational planning' principles health professionals are commonly encouraged to use for implementation purposes. Methods and materials: A mixed-methods qualitative enquiry using a data archive generated during the WMS policy evaluation was used to critically analyze (post hoc) the perspectives of national policy makers, and local health and social care professionals about the: (a) ‘policy problem’, (b) interventions intended to address the problem, and (c) anticipated policy outcomes. Results and conclusions: This analysis revealed four key themes: (1) ambiguity regarding the policy problem and means of intervention; (2) behavioral framing of the policy problem and intervention; (3) uncertainty about the policy evidence base and outcomes, and; (4) a focus on intervention as outcome. This study found that mechanistic planning heuristics (as a means of supporting implementation) fails to grapple with the indeterminate nature of population health problems. A new approach to planning and implementing public health interventions is required that recognises the complex and political nature of health problems; the inevitability of imperfect and contested evidence regarding intervention, and, future associated uncertainties.

Keywords:

Citation: Flora Douglas, Edwin van Teijlingen, Cairns Smith, Mandy Moffat. Implementing health policy: lessons from the Scottish Well Mens policy initiative[J]. AIMS Public Health, 2015, 2(4): 887-905. doi: 10.3934/publichealth.2015.4.887

Related Papers:

[1]	Jiazhe Lin, Rui Xu, Xiaohong Tian . Transmission dynamics of cholera with hyperinfectious and hypoinfectious vibrios: mathematical modelling and control strategies. Mathematical Biosciences and Engineering, 2019, 16(5): 4339-4358. doi: 10.3934/mbe.2019216
[2]	Lili Liu, Xi Wang, Yazhi Li . Mathematical analysis and optimal control of an epidemic model with vaccination and different infectivity. Mathematical Biosciences and Engineering, 2023, 20(12): 20914-20938. doi: 10.3934/mbe.2023925
[3]	Pannathon Kreabkhontho, Watchara Teparos, Thitiya Theparod . Potential for eliminating COVID-19 in Thailand through third-dose vaccination: A modeling approach. Mathematical Biosciences and Engineering, 2024, 21(8): 6807-6828. doi: 10.3934/mbe.2024298
[4]	Zhiping Liu, Zhen Jin, Junyuan Yang, Juan Zhang . The backward bifurcation of an age-structured cholera transmission model with saturation incidence. Mathematical Biosciences and Engineering, 2022, 19(12): 12427-12447. doi: 10.3934/mbe.2022580
[5]	Amira Bouhali, Walid Ben Aribi, Slimane Ben Miled, Amira Kebir . Impact of immunity loss on the optimal vaccination strategy for an age-structured epidemiological model. Mathematical Biosciences and Engineering, 2024, 21(6): 6372-6392. doi: 10.3934/mbe.2024278
[6]	Martin Luther Mann Manyombe, Joseph Mbang, Jean Lubuma, Berge Tsanou . Global dynamics of a vaccination model for infectious diseases with asymptomatic carriers. Mathematical Biosciences and Engineering, 2016, 13(4): 813-840. doi: 10.3934/mbe.2016019
[7]	Tingting Xue, Long Zhang, Xiaolin Fan . Dynamic modeling and analysis of Hepatitis B epidemic with general incidence. Mathematical Biosciences and Engineering, 2023, 20(6): 10883-10908. doi: 10.3934/mbe.2023483
[8]	Jinliang Wang, Ran Zhang, Toshikazu Kuniya . A note on dynamics of an age-of-infection cholera model. Mathematical Biosciences and Engineering, 2016, 13(1): 227-247. doi: 10.3934/mbe.2016.13.227
[9]	Majid Jaberi-Douraki, Seyed M. Moghadas . Optimal control of vaccination dynamics during an influenza epidemic. Mathematical Biosciences and Engineering, 2014, 11(5): 1045-1063. doi: 10.3934/mbe.2014.11.1045
[10]	Linhua Zhou, Meng Fan, Qiang Hou, Zhen Jin, Xiangdong Sun . Transmission dynamics and optimal control of brucellosis in Inner Mongolia of China. Mathematical Biosciences and Engineering, 2018, 15(2): 543-567. doi: 10.3934/mbe.2018025

Abstract

1. Introduction

Cholera is a waterborne disease caused by Vibrio cholera ^[1]. It is well known that it can spread rapidly in countries without clean drinking water and developed public health infrastructure ^[2,3,4]. In 2017, Somalia faced one of the largest outbreaks in history, with 78,784 suspected cases, including 1,159 related deaths. A year later, the number of suspected cases and related deaths reported in Somalia fell due to improved disease surveillance and case management. However, a new cholera outbreak in Somalia began in January 2019 ^[5].

For cholera, the interaction between environment and human is the most common pathway of transmission, that is, human typically is infected by ingesting water or food contaminated by vibrios from the environment ^[6,7,8]. On the other hand, close contacts with infected individuals (such as shaking hands and hugging) can also cause human infection, which indicates that the transmission route of human-to-human also exists ^[9]. A number of studies have shown that human-to-human transmission has a great impact on human infection that can not be ignored ^[10,11,12].

In 2010, Tien et al. formulated a model with multiple pathways ^[13]. It was assumed that the incidence rate is bilinear, indicating that the incidence rate increases with the number of infected individuals and the concentration of vibrio in the environment. However, for environment-to-human transmission, considering the fact that the inhibition effect from behavioral changes of susceptible individuals and the swarming effect of vibrios, the bilinear incidence rate is unreasonable. In 2011, based on the work in ^[13], by introducing a saturation incidence rate $ \beta_{1}B /(K+B) $ to describe the inhibition effect, in ^[9], Mukandavire et al. analyzed the following model:

$\begin{equation} \begin{aligned} \dot S& = \mu N-\beta SI-\frac{\beta_{1}S B}{K+B}-\mu S,\\ \dot I& = \beta SI+\frac{\beta_{1}S B}{K+B}-(\gamma+\mu)I,\\ \dot B& = \xi I-\delta B,\\ \dot R& = \gamma I-\mu R,\\ \end{aligned} \end{equation}$ $

(1.1)

where $ S $, $ I $ and $ R $ stand for the densities of the susceptible, infected and removed individuals, respectively, and $ B $ stands for the concentration of V. cholera in contaminated environment. The parameter $ \mu $ denotes the natural birth and death rates of human, $ \beta $ and $ \beta_{1} $ are the transmission rates of human-to-human and environment-to-human, respectively, $ K $ is the pathogen concentration that yields 50% chance of catching cholera, $ \gamma $ denotes the recovery rate, $ \xi $ is the contribution rate of each infected individual to the concentration of V. cholera shedding from infected individuals and $ \delta $ is the net death rate of V. cholerae.

In 2010, WHO recommended the oral vaccines should be used in areas with endemic cholera ^[14]. Subsequently, a number of cholera models with vaccination strategy have been proposed and analysed ^[15,16,17]. In 2015, Posny et al. proposed a new cholera model consisting of vaccination ^[18]. Model analysis shows that the vaccine can effectively control the spread of cholera. However, vaccine protection is not permanent. The existing oral cholera vaccine (OCV) can provide > % continuous protection, lasting for 2 years in the epidemic population ^[14].

Motivated by the works of the WHO report ^[14] and Posny et al. ^[18], in this paper, we focus on the influence of multiple pathways, imperfect vaccination on cholera infection, and analyze the following model:

$\begin{equation} \begin{aligned} \dot S& = A-\mu S-\phi S-\left(\beta I+\frac{\beta_{1}B}{K+B}\right)S +\eta V,\\ \dot V& = \phi S-\left(\beta I+\frac{\beta_{1}B}{K+B}\right)\sigma V-(\mu+\eta)V,\\ \dot I& = \left(\beta I+\frac{\beta_{1}B}{K+B}\right)(S+\sigma V)-(\mu+\gamma+d)I,\\ \dot B& = \xi I-\delta B,\\ \dot R& = \gamma I-\mu R, \end{aligned} \end{equation}$ $

(1.2)

where $ V $ stands for the density of vaccinated individuals. Vaccination rate of susceptible individuals is $ \phi $, vaccine efficiency is $ \sigma $ and $ 1/\eta $ is the duration of vaccine protection. And other parameters have the same biological meanings as in system (1.1).

The initial condition of system (1.2) is

$\begin{equation} \begin{aligned} S(0)\geq0,\quad V(0)\geq0,\quad I(0)\geq0, \quad B(0)\geq0, \quad R(0)\geq0, \end{aligned} \end{equation}$ $

(1.3)

and we can obtain that all solutions of system (1.2) remain positive for all $ t \geq 0 $.

The organization of this paper is as follows. In Section 2, we show the existence of feasible equilibria. In Section 3, we establish the global stability of each of feasible equilibria of system (1.2) by constructing Liapunov functions. In Section 4, we consider the optimal control problem of cholera model with vaccination, quarantine, treatment and sanitation control strategies. In order to determine the optimal control strategy, we use Pontryagin's minimum principle. In Section 5, the model is used to fit the real disease situation of cholera outbreak in Somalia. Besides, we analyze the sensitivity of the basic reproduction number and solve the resulting optimality problem numerically. Finally, a brief discussion is given in Section 6 to end this work.

2. Equilibria and boundedness of solutions

For system (1.2), it is easy to conclude that there is always a disease-free equilibrium $ E_{0}(S_{0}, V_{0}, 0, 0, 0) $, where

$ S_{0} = \frac{A(\mu+\eta)}{\mu(\mu+\eta+\phi)}, \quad V_{0} = \frac{A\phi}{\mu(\mu+\eta+\phi)}. $

Below, we first calculate the basic reproduction number $ R_{0} $ by using the method of the next generation matrix ^[19]. Let

$\begin{gathered} \mathcal{F} = \left( \begin{array}{c} \left(\beta I+\frac{\beta_{1}B}{K+B}\right)(S+\sigma V)\\ 0 \\ \end{array} \right), \quad \mathcal{V} = \left(\begin{array}{c} (\mu+\gamma+d)I\\ -\xi I+\delta B \\ \end{array} \right). \end{gathered}$ $

Computing the Jacobian Matrix at $ E_{0} $, we have

$\begin{aligned} F = \begin{pmatrix} \beta S_{0}+\sigma \beta V_{0} & \frac{\beta_{1} S_{0}+\sigma \beta_{1} V_{0}}{K}\\ 0 & 0\\ \end{pmatrix}, \quad V = \begin{pmatrix} \mu+\gamma+d & 0 \\ -\xi & \delta\\ \end{pmatrix}. \end{aligned}$ $

It follows that

$\begin{gathered} FV^{-1} = \begin{pmatrix} \frac{\beta S_{0}+\sigma \beta V_{0}}{\mu+\gamma+d }+\frac{(\beta_{1} S_{0}+\sigma\beta_{1} V_{0})\xi}{K\delta(\mu+\gamma+d )}& \frac{\beta_{1} S_{0}+\sigma \beta_{1} V_{0}}{K\delta}\\ 0 & 0\\ \end{pmatrix}. \end{gathered}$ $

We obtain:

$ R_{0} = \frac{A\beta(\mu+\eta+\sigma\phi) }{\mu (\mu+\gamma+d)(\mu+\eta+\phi)}+\frac{A\beta_{1}\xi(\mu+\eta+\sigma\phi)}{\mu K \delta(\mu+\gamma+d)(\mu+\eta+\phi)}. $

If $ R_{0} > 1 $, system (1.2) has a disease-free equilibrium $ E_{0}(S_{0}, V_{0}, 0, 0, 0) $ and an endemic equilibrium $ E^{*}(S^{*}, V^{*}, I^{*}, B^{*}, R^{*}) $, where

$\begin{aligned} S^{*}& = \frac{a_{0}(K+B^{*})^{2}+a_{1}(K+B^{*})}{ a_{2}(K+B^{*})^{2}+a_{3}(K+B^{*})+a_{4}},\; V^{*} = \frac{A\phi\xi^{2}(K+B^{*})^{2}}{a_{2}(K+B^{*})^{2}+a_{3}(K+B^{*})+a_{4}},\\ I^{*}& = \frac{\delta}{\xi}B^{*},\quad\quad\quad\quad \quad \quad R^{*} = \frac{\gamma \delta}{\mu \xi}B^{*},\\ \end{aligned}$ $

here

$\begin{aligned} a_{0}& = A(\mu+\eta)\xi^{2},\quad \quad\quad\quad \\ a_{1}& = A\xi\sigma B^{*}(\delta\beta+\beta_{1}\xi),\\ a_{2}& = \beta\delta B^{*}[\sigma\delta\beta B^{*}+(\mu+\eta)\xi]+(\phi+\mu+\eta)\mu,\\ a_{3}& = \sigma\beta_{1}B^{*}\xi[\beta\delta B^{*}+(\phi+\mu)\xi]+\beta_{1} B^{*}\xi[\sigma\delta\beta B^{*}+(\mu+\eta)\xi],\\ a_{4}& = \sigma\beta_{1}^{2}B^{*2}\xi^{2}, \end{aligned}$ $

and $ B^{*} $ is the positive real root of the equation $ h(B) = 0 $, where

$\begin{equation} \begin{aligned} h(B) = b_{4}B^{4}+b_{3}B^{3}+b_{2}B^{2}+b_{1}B+b_{0}, \end{aligned} \end{equation}$ $

(2.1)

in which

$\begin{aligned} b_{0} = &k^{2}\delta\mu\xi^{2}(\mu+\gamma+d)(\mu+\phi+\eta)(1-R_{0}),\\ b_{1} = &(\mu+\gamma+d)[K^{2}\beta\delta^{2}(\mu+\eta)\xi+K^{2}\beta\sigma\delta^{2}(\phi+\mu)\xi +2K\delta\mu(\mu+\phi+\eta)\xi^{2}\\ &+K\delta\beta_{1}\xi^{2}(\mu+\eta)+K\sigma\delta\beta_{1}\xi^{2}(\mu+\phi)] -K^{2}A\xi\beta^{2}\sigma\delta^{2}-2KA\xi^{2}\beta\delta(\mu+\eta+\phi\sigma)\\ &-2KA\beta\beta_{1}\xi^{2}\sigma\delta-A\xi^{3}\beta_{1}(\mu+\eta+\phi\sigma) -A\xi^{3}\beta_{1}^{2}\sigma,\\ b_{2} = &(\mu+\gamma+d)[K^{2}\beta^{2}\sigma\delta^{3}+2K\beta\delta^{2}(\mu+\eta)\xi +2K\beta\sigma\delta^{2}(\phi+\mu)\xi+\delta\mu(\mu+\phi+\eta)\xi^{2}\\ &+2K\xi\beta\beta_{1}\sigma\delta^{2}+(\phi+\mu)\xi^{2}\beta_{1}\delta\sigma +\beta_{1}\delta\xi^{2}(\mu+\eta)+\sigma\beta_{1}^{2}\delta\xi^{2}]-2kA\xi\beta^{2}\sigma\delta^{2}\\ &-2A\xi^{2}\beta\beta_{1}\delta\sigma-A\beta\delta\xi^{2}(\mu+\eta+\phi\sigma),\\ b_{3} = &(\mu+\gamma+d)[2K\beta^{2}\sigma\delta^{3}+\beta\delta^{2}(\mu+\eta)\xi +\beta\sigma\delta^{2}(\phi+\mu)\xi+2\beta\beta_{1}\sigma\delta^{2}\xi]-A\xi\sigma\beta^{2}\delta^{2},\\ b_{4} = &(\mu+\gamma+d)\beta^{2}\sigma\delta^{3}.\\ \end{aligned}$ $

Note that $ \lim_{B\rightarrow+\infty}h(B) = +\infty $, $ h(0) = b_0 < 0 $ if $ R_{0} > 1 $, in this case, system (1.2) has a positive equilibrium $ E^{*} $.

Let $ N = S+V+I+R. $ Then $ \dot{N} = A-\mu(S+V+I+R)-dI \leq A-\mu N $. It follows that

$ \limsup\limits_{t\rightarrow+\infty} N(t)\leq A/\mu. $

Furthermore, we derive from the fourth equation of system (1.2),

$ \limsup\limits_{t\rightarrow+\infty} B(t)\leq A\xi/\mu\delta. $

We therefore conclude that the set

$ \Omega = \left\{(S, V, I, B, R)\in R_{+}^{5}: 0 \leq S(t)+V(t)+I(t)+R(t)\leq\frac{A}{\mu}, 0 \leq B(t)\leq\frac{A\xi}{\mu\delta} \right\} $

is positively invariant.

3. Global stability

In this section, we study the global stability of each of the equilibria to system (1.2). The approach of proofs is to use suitable Lyapunov function.

Theorem 3.1. If $ R_{0} < 1 $, the disease-free equilibrium $ E_{0}(S_{0}, V_{0}, 0, 0, 0) $ of system (1.2) is globally asymptotically stable.

Proof. Define

$\begin{aligned} W(t)& = S_{0}\left(\frac{S}{S_{0}}-1-\ln\frac{S}{S_{0}}\right)+V_{0}\left(\frac{V}{V_{0}}-1-\ln\frac{V}{V_{0}}\right)+I+\frac{\beta_{1}S_{0}+\sigma \beta_{1}V_{0}}{K\delta}B.\\ \end{aligned}$ $

Calculating the derivative of $ W(t) $ along positive solutions of system (1.2), one has

$\begin{equation} \begin{aligned} \dot{W}(t)& = \left(1-\frac{S_{0}}{S}\right)\left(A-\mu S-\phi S-\left(\beta I+\frac{\beta_{1}B}{K+B}\right)S+\eta V\right)\\ &+\left(1-\frac{V_{0}}{V}\right)\left(\phi S-\left(\beta I+\frac{\beta_{1}B}{K+B}\right)\sigma V-(\mu+\eta)V\right)\\ &+\left(\beta I+\frac{\beta_{1}B}{K+B}\right)(S+\sigma V)-(\mu+\gamma+d)I\\ &+\frac{\beta_{1}S_{0}+\sigma \beta_{1}V_{0}}{K\delta}(\xi I-\delta B). \end{aligned} \end{equation}$ $

(3.1)

On substituting $ A = \mu S_{0}+\mu V_{0} $, $ \phi S_{0} = (\mu + \eta)V_{0} $ into (3.1), we obtain that

$\begin{aligned} \dot{W}(t)& = \mu S_{0}\left(2-\frac{S_{0}}{S}-\frac{S}{S_{0}}\right)+\eta V_{0}\left(2-\frac{S_{0}V}{V_{0}S}-\frac{V_{0}S}{S_{0}V}\right)\\ &{+\mu V_{0}\left(3-\frac{S}{S_{0}}-\frac{V}{V_{0}}-\frac{V_{0}S}{S_{0}V}\right) +(\mu+\gamma+d)\left(R_{0}-1\right)I}\\ &-\frac{(\beta_{1}S_{0}+\sigma \beta_{1}V_{0})B^{2}}{K(K+B)}\leq0, \end{aligned}$ $

and $ \dot{W}(t) < 0 $ for all $ (S, V, I, B, R)\neq(S_{0}, V_{0}, 0, 0, 0) $. Therefore, by Lyapunov's stability Theorem ^[20], the equilibrium $ E_{0} $ is globally asymptotically stable.

Theorem 3.2. If $ R_{0} > 1 $, the endemic equilibrium $ E^{*}(S^{*}, V^{*}, I^{*}, B^{*}, R^{*}) $ of system (1.2) is globally asymptotically stable.

Proof. Define

$\begin{aligned} W_{1}(t)& = S^{*}\left(\frac{S}{S^{*}}-1-\ln\frac{S}{S^{*}}\right)+V^{*}\left(\frac{V}{V^{*}}-1-\ln\frac{V}{V^{*}}\right)\\ &+I^{*}\left(\frac{I}{I^{*}}-1-\ln\frac{I}{I^{*}}\right)+\frac{\beta_{1}S^{*}+\sigma\beta_{1}V^{*}}{(K+B^{*})\delta} B^{*}\left(\frac{B}{B^{*}}-1-\ln\frac{B}{B^{*}}\right).\\ \end{aligned}$ $

Calculating the derivative of $ W_{1}(t) $ along positive solutions of system (1.2), one has

$\begin{equation} \begin{aligned} \dot{W_{1}}(t)& = \left(1-\frac{S^{*}}{S}\right)\left(A- \mu S-\phi S-\left(\beta I+\frac{\beta_{1}B}{K+B}\right)S+\eta V\right)\\ &+\left(1-\frac{V^{*}}{V}\right)\left(\phi S-\left(\beta I+\frac{\beta_{1}B}{K+B}\right)\sigma V-(\mu+\eta)V\right)\\ &+\left(1-\frac{I^{*}}{I}\right)\left(\left(\beta I+\frac{\beta_{1}B}{K+B}\right)(S+\sigma V)-(\mu+\gamma+d)I\right)\\ &+\frac{\beta_{1}S^{*}+\sigma\beta_{1}V^{*}}{(K+B^{*})\delta}\left(1-\frac{B^{*}}{B}\right)(\xi I-\delta B). \end{aligned} \end{equation}$ $

(3.2)

On substituting

$\begin{aligned} &A = (S^{*}+\sigma V^{*})\left(\beta I^{*}+\frac{\beta_{1}B^{*}}{K+B^{*}}\right)+\mu S^{*}+\mu V^{*},\\ &\phi S^{*} = \sigma V^{*}\left(\beta I^{*}+\frac{\beta_{1}B^{*}}{K+B^{*}}\right)+(\mu+\eta) V^{*},\\ &(\mu+\gamma+d)I^{*} = (S^{*}+\sigma V^{*})\left(\beta I^{*}+\frac{\beta_{1}B^{*}}{K+B^{*}}\right),\\ &\delta B^{*} = \xi I^{*} \end{aligned}$ $

into (3.2), we have

$\begin{aligned} \dot{W_{1}}(t)& = (\mu+\beta I^{*}) S^{*}\left(2-\frac{S}{S^{*}}-\frac{S^{*}}{S}\right) +\eta V^{*}\left(2-\frac{S^{*}V}{V^{*}S}-\frac{V^{*}S}{S^{*}V}\right)\\ &+(\mu+\sigma\beta I^{*}) V^{*}\left(3-\frac{S^{*}}{S}-\frac{V}{V^{*}}-\frac{V^{*}S}{S^{*}V}\right)\\ &+\frac{\beta_{1}S^{*}B^{*}}{K+B^{*}}\left(4-\frac{S^{*}}{S}-\frac{B^{*}I}{I^{*}B} -\frac{K+B}{K+B^{*}}-\frac{(K+B^{*})I^{*}SB}{S^{*}B^{*}(K+B)I}\right)\\ &+\frac{\sigma\beta_{1} V^{*}B^{*}}{K+B^{*}}\left(5-\frac{S^{*}}{S}-\frac{V^{*}S}{S^{*}V} -\frac{B^{*}I}{I^{*}B}-\frac{K+B}{K+B^{*}}-\frac{(K+B^{*})I^{*}VB}{V^{*}B^{*} (K+B)I}\right)\\ &-\frac{K\beta_{1}(S^{*}+\sigma V^{*})(B^{*}-B)^{2}}{(K+B^{*})^{2}(K+B)}\leq0, \end{aligned}$ $

and $ \dot{W_{1}}(t) < 0 $ for all $ (S, V, I, B, R)\neq(S^{*}, V^{*}, I^{*}, B^{*}, R^{*}) $. Therefore, by Lyapunov's stability Theorem ^[20], the equilibrium $ E^{*} $ is globally asymptotically stable.

4. Optional control strategies

We consider the optimal control problem of cholera model with vaccinate, quarantine, treatment and sanitation control strategies:

$\begin{equation} \begin{aligned} \dot S& = A-(\mu+u_{1}(t)) S-\left(\beta(1-u_{2}(t))I+\frac{\beta_{1}(1-u_{3}(t))B}{K+B}\right)S+\eta V,\\ \dot V& = u_{1}(t)S-\left(\beta (1-u_{2}(t))I+\frac{ \beta_{1}(1-u_{3}(t))B}{K+B}\right)\sigma V-(\mu+\eta)V,\\ \dot I& = \left(\beta(1-u_{2}(t))I+\frac{\beta_{1}(1-u_{3}(t))B}{K+B}\right)(S+\sigma V)-(\mu+d+\gamma+u_{4}(t))I,\\ \dot B& = \xi I-(\delta+u_{5}(t)) B,\\ \dot R& = (\gamma+u_{4}(t))I-\mu R.\\ \end{aligned} \end{equation}$ $

(4.1)

Where $ u_{1}(t) $ is a vaccination strategy aimed to the susceptible individuals; $ u_{2}(t) $ is a quarantine strategy that can reduce the transmission of human-to-human; $ u_{3}(t) $ is another kind of quarantine strategy that can reduce the transmission of environment-to-human; $ u_{4}(t) $ is therapeutic treatment aimed to the infected people, $ u_{5}(t) $ is a sanitation strategy aimed at killing vibrios in contaminated water.

Define a control function set as $ \textbf{U} = \{u_{i}(t)\mid i = 1, \cdots, 5\}, $ and $ \textbf{X} = (S, V, I, B, R). $ The admissible trajectories of set $ \mathcal{\textbf{X}} $ are given by

$ \mathcal{X} = \{\textbf{X}(.)\in W^{1,1}([0,T);R^{5})\mid\;(1.3)\; \rm{and}\;(4.1)\; \rm{are\; satisfied}\}. $

Define

$ \mathcal{U} = \{\textbf{U}(\cdot)\in L^{\infty}([0,T];R^{5})\;| 0\leq u_{i}(t)\leq u_{imax}\leq1,\;i = 1,\cdots,5, \; {\forall}\;t\;\in[0,T]\}, $

where $ u_{imax}\; (i = 1, \cdots, 5) $ denote the upper bounds for the efforts of vaccination, quarantine strategy, another kind of quarantine strategy, treatment and sanitation, respectively.

The objective functional

$\begin{aligned} &Q(\textbf{X}(\cdot),\textbf{U}(\cdot)) = \int_{0}^{T}g(\textbf{X}(t),\textbf{U}(t))dt.\\ \end{aligned}$ $

The function $ g $ is called the running payoff function ^[20]. The objective of the optimal control problem is to minimize the objective functional

$\begin{equation} \begin{aligned} Q(\textbf{X}^{*}(\cdot),\textbf{U}^{*}(\cdot)) = \min\limits_{\textbf{X}(\cdot),\textbf{U}(\cdot) \in\mathcal{X}\times\mathcal{U}}Q(\textbf{X}(\cdot),\textbf{U}(\cdot)). \end{aligned} \end{equation}$ $

(4.2)

The first question that must be addressed is the existence of the optimal control pair. According to the Filippov-Cesari existence theorem ^[20], we obtain the following result.

Theorem 4.1. There exists a $ \boldsymbol{U}^{*}(\cdot) $ such that the objective functional in (4.2) is minimized.

To apply Pontryagin's minimum principle ^[21], we need to introduce the adjoint vector function $ \lambda(t) = (\lambda_{S}(t), \lambda_{I}(t), \lambda_{V}(t), \lambda_{B}(t), \lambda_{R}(t)), $ to define the Hamiltonian:

$\begin{aligned} H(\textbf{X},\textbf{U},\lambda)& = g(\textbf{X}(t),\textbf{U}(t))\\ &+\lambda_{S}\left(A-(\mu+u_{1}(t)) S-\left(\beta(1-u_{2}(t))I+\frac{\beta_{1}(1-u_{3}(t))B}{K+B}\right)S+\eta V\right)\\ &+\lambda_{V}\left(u_{1}(t)S- \left(\beta (1-u_{2}(t))I+\frac{ \beta_{1}(1-u_{3}(t))B}{K+B}\right)\sigma V-(\mu +\eta)V\right)\\ &+\lambda_{I}\left[\left(\beta(1-u_{2}(t))I+\frac{\beta_{1}(1-u_{3}(t))B}{K+B}\right)(S +\sigma V)-(\mu+d+\gamma+u_{4}(t))I\right]\\ &+\lambda_{B}\left[\xi I-(\delta+u_{5}(t))B\right]\\ &+\lambda_{R}\left[(\gamma+u_{4}(t))I-\mu R\right]. \end{aligned}$ $

The adjoint functions must satisfy

$ \lambda_{S}^{'} = -\frac{\partial H}{\partial S},\quad \lambda_{V}^{'} = -\frac{\partial H}{\partial V},\quad \lambda_{I}^{'} = -\frac{\partial H}{\partial I}, \quad \lambda_{B}^{'} = -\frac{\partial H}{\partial B}, \quad \lambda_{R}^{'} = -\frac{\partial H}{\partial R}. $

That is,

$\begin{equation} \begin{aligned} \frac{d\lambda_{S}}{dt}& = (\mu+u_{1}(t))\lambda_{S} +\left(\beta(1-u_{2}(t))I+\frac{\beta_{1}(1-u_{3}(t))B}{K+B}\right)(\lambda_{S}-\lambda_{I}) -u_{1}(t)\lambda_{V}-\frac{\partial g}{\partial S}\\ \frac{d\lambda_{V}}{dt}& = (\mu+\eta)\lambda_{V}+\left(\sigma\beta(1-u_{2}(t))I +\frac{\sigma\beta_{1}(1-u_{3}(t))B}{K+B}\right)(\lambda_{V}-\lambda_{I})-\eta\lambda_{S}-\frac{\partial g}{\partial V},\\ \frac{d\lambda_{I}}{dt}& = \beta(1-u_{2}(t))S(\lambda_{S}-\lambda_{I})+ \sigma\beta(1-u_{2}(t))V(\lambda_{V}-\lambda_{I})+(\mu+\gamma+u_{4}(t)+d)\lambda_{I}\\ &-\xi\lambda_{B}-u_{4}(t)\lambda_{R}-\frac{\partial g}{\partial I},\\ \frac{d\lambda_{B}}{dt}& = \frac{\beta_{1}(1-u_{3}(t))S K}{(K+B)^{2}}(\lambda_{S}-\lambda_{I})+\frac{\sigma\beta_{1}(1-u_{3}(t))V K}{(K+B)^{2}}(\lambda_{V}-\lambda_{I})+(\delta+u_{5}(t))\lambda_{B}-\frac{\partial g}{\partial B},\\ \frac{d\lambda_{R}}{dt}& = \mu\lambda_{R}-\frac{\partial g}{\partial R}, \end{aligned} \end{equation}$ $

(4.3)

with transversality condition

$\begin{equation} \begin{aligned} \lambda_{S}(T) = \lambda_{V}(T) = \lambda_{I}(T) = \lambda_{B}(T) = \lambda_{R}(T) = 0, \quad j = 1, 2. \end{aligned} \end{equation}$ $

(4.4)

Moreover, the characterizations of the optimal controls are based on

$\begin{aligned} \frac{\partial H}{\partial u_{i}} = 0, \quad \quad\quad\;\; i = 1,\cdots,5. \end{aligned}$ $

In order to explore the sensitivity of the cost function to the optimal control solution, we consider two different cost functions for the running payoff function $ g(\textbf{X}(t), \textbf{U}(t)) $. If we choose the running payoff function

$\begin{equation} \begin{aligned} g_{1}(\textbf{X}(t),\textbf{U}(t)) = I+\frac{C_{11}}{2}u_{1}(t)^{2}+\frac{C_{21}}{2}u_{2}(t)^{2} +\frac{C_{31}}{2}u_{3}(t)^{2}+\frac{C_{41}}{2}u_{4}(t)^{2}+\frac{C_{51}}{2}u_{5}(t)^{2}, \end{aligned} \end{equation}$ $

(4.5)

where $ C_{i1}(i = 1, \cdots, 5) $ are the weight constants for the control strategies. The $ C_{11}u_{1}^{2}/2 $, $ C_{21}u_{2}^{2}/2 $, $ C_{31}u_{3}^{2}/2 $, $ C_{41}u_{4}^{2}/2 $, $ C_{51}u_{5}^{2}/2 $ define the appropriate costs function associated with these controls ^[20]. We can obtain that

$\begin{equation} \begin{aligned} \widetilde{u}_{11}& = \frac{(\lambda_{S1}-\lambda_{V1})S}{C_{11}}, \quad \widetilde{u}_{21} = \frac{\beta SI(\lambda_{I1}-\lambda_{S1})+\sigma\beta VI(\lambda_{I1}-\lambda_{V1})}{C_{21}},\\ \widetilde{u}_{31}& = \frac{\beta_{1} SB(\lambda_{I1}-\lambda_{S1})+\sigma\beta_{1} VB(\lambda_{I1}-\lambda_{V1})}{C_{31}(K+B)},\quad \widetilde{u}_{41} = \frac{(\lambda_{I1}-\lambda_{R1})I}{C_{41}},\\ \widetilde{u}_{51}& = \frac{\lambda_{B1}B}{C_{51}}. \end{aligned} \end{equation}$ $

(4.6)

In addition, if we choose another running payoff function

$\begin{equation} \begin{aligned} g_{2}(\textbf{X}(t),\textbf{U}(t))& = I+C_{12}\left(u_{1}(t)+u_{1}(t)^{2}\right)+C_{22}\left(u_{2}(t)+u_{2}(t)^{2}\right)+C_{32}\left(u_{3}(t)+u_{3}(t)^{2}\right)\\ &+C_{42}\left(u_{4}(t)+u_{4}(t)^{2}\right)+C_{52}\left(u_{5}(t)+u_{5}(t)^{2}\right), \end{aligned} \end{equation}$ $

(4.7)

where $ C_{i2}(i = 1, \cdots, 5) $ are the weight constants for the control strategies. $ C_{12}\left(u_{1}(t)+u_{1}(t)^{2}\right) $, $ C_{22}\left(u_{2}(t)+u_{2}(t)^{2}\right) $, $ C_{32}\left(u_{3}(t)+u_{3}(t)^{2}\right) $, $ C_{42}\left(u_{4}(t)+u_{4}(t)^{2}\right) $, $ C_{52}\left(u_{5}(t)+u_{5}(t)^{2}\right) $ define the appropriate costs function associated with these controls ^[23]. We can obtain that

$\begin{equation} \begin{aligned} \widetilde{u}_{12}& = \frac{(\lambda_{S2}-\lambda_{V2})S-C_{12}}{2C_{12}}, \quad \widetilde{u}_{22} = \frac{\beta SI(\lambda_{I2}-\lambda_{S2})+\sigma\beta VI(\lambda_{I2}-\lambda_{V2})-C_{22}}{2C_{22}},\\ \widetilde{u}_{32}& = \frac{\beta_{1} SB(\lambda_{I2}-\lambda_{S2})+\sigma\beta_{1} VB(\lambda_{I2}-\lambda_{V2})-C_{32}}{2C_{32}(K+B)},\quad \widetilde{u}_{42} = \frac{(\lambda_{I2}-\lambda_{R2})I-C_{42}}{C_{42}},\\ \widetilde{u}_{52}& = \frac{\lambda_{B2}B-C_{52}}{2C_{52}}. \end{aligned} \end{equation}$ $

(4.8)

Where $ \lambda_{Sj}, \lambda_{Vj}, \lambda_{Ij}, \lambda_{Bj}, \lambda_{Rj}(j = 1, 2) $ satisfy the equations (4.3) and (4.4). Based on this fact, we obtain $ \widetilde{u}_{ij}(i = 1, \cdots, 5, j = 1, 2) $. Further, we have

$ u_{ij}^{*} = \max[0,\min(\widetilde{u}_{ij},u_{imax})]. $

Next, in Section 5, we apply the forward-backward sweep method to solve it numerically ^[15,20].

5. Numerical simulations

In this section, system (1.2) is used to fit the real disease situation of cholera outbreak in Somalia. Besides, we analyze the sensitivity of $ R_{0} $. As mentioned in Section 4, the optimal control problem needs to be solved by numerical simulation, we will show the numerical result. In addition, we list the values of parameters in Table 1.

Table 1. Table of biologically relevant parameter values (week).

Parameter	Description	Value	Source
$ A $	Constant birth rate	7342	^[5]
$ \phi $	Vaccinate rate of susceptible	$ 4.2836\times10^{-3} $	fitting
$ \beta $	Transmission rate of human-to-human	$ 4.3771\times10^{-10} $	fitting
$ \beta_1 $	Transmission rate of environment-to-human	$ 0.5959\times10^{-4} $	fitting
$ K $	Concentration of V. cholera in environment	$ 10^{6} $	^[8]
$ \mu $	Natural death rate of human	0.00038	^[5]
$ \eta $	Waning rate of vaccinate	0.0104	^[14]
$ \sigma $	Reduction rate of vaccine efficacy	0.5	^[14]
$ \gamma $	Recovery rate of infected individuals	1.5	^[8]
$ d $	Cholera mortality	0.006	^[5]
$ \xi $	Rate of release of V. cholerae	70	^[8]
$ \delta $	Natural death rate of V. cholera	0.197	^[8]
Initial values	Description	Value	Source
$ S(0) $	Initial susceptible population	12316000	^[22]
$ V(0) $	Initial vaccinated population	0	^[22]
$ I(0) $	Initial infected population	$ 192 $	^[22]
$ B(0) $	Initial concentration of vibrios	$ 205740 $	fitting
$ R(0) $	Initial recovered population	$ 147 $	fitting

| Show Table

DownLoad: CSV

5.1. Data fitting

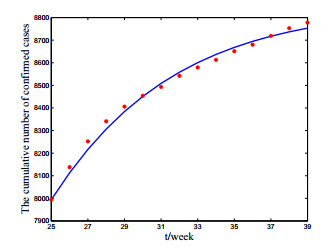
In this subsection, we use system (1.2) to fit the real disease situation of cholera outbreak in Somalia. The new cholera outbreak in Somalia began in January 2019, and the first round of oral cholera vaccination (OCV) activity started on June 22, 2019, the 25th week of 2019, so our numerical simulation starts from the 25th week of 2019.

In addition, the data we obtained is the cumulative number of cases since December 2017, so our initial case number is 7,994 ^[22]. By using the Markov Chain Monte Carlo method, we can get fitting results (see Figure 1). It is shown that the solutions of system (1.2) are in good agreement with the actual cholera cases, which verifies the rationality of the model established in this paper.

Figure 1. Cumulative cases in Somalia between weeks 25 and 39 of 2019, in which the red dots represent the reported data, the blue curve is the solution of model (1.2).

DownLoad: Full-Size Img PowerPoint

5.2. Sensitivity analysis

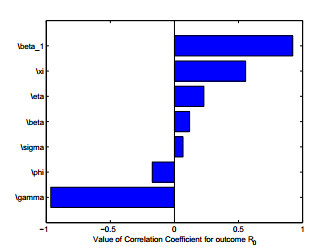
In this subsection, we use the Latin hypercube sampling (LHS) method to analyze the sensitivity of $ R_{0} $ ^[24]. Through the analysis of LHS samples, we obtain the Partial Rank Correlation Coefficients (PRCC) with respect to $ R_{0} $ (see Figure 2). It is easy to see that $ \beta_{1}, \xi, \eta, \beta, \sigma $ are positive correlative variables with $ R_{0} $; and $ \phi, \gamma $ are negative correlative variables with $ R_{0} $.

Figure 2. Tornado plot of partial rank correlation coefficients in respect to $ R_{0} $.

DownLoad: Full-Size Img PowerPoint

5.3. Optimal control solution

In this subsection, we will show the optimal control results. Based on empirical values, we set $ u_{1max} = 0.7, u_{2max} = 0.9, u_{3max} = 0.6, u_{4max} = 0.5, u_{5max} = 0.8 $, respectively. Meanwhile, we assume that the costs for vaccination, treatment, quarantine and sanitation per unit of time is roughly the same.

We first consider the running payoff function $ g_{1}(\textbf{X}(t), \textbf{U}(t)) $. The following set of values for the cost parameters

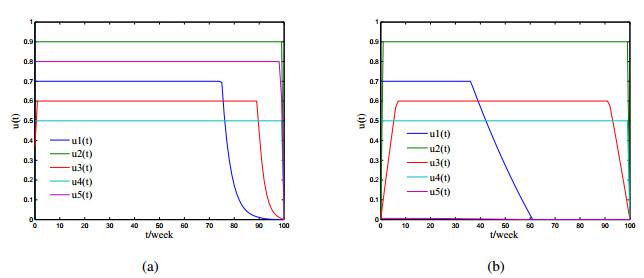
$\begin{equation*} \label{51} \begin{split} C_{11} = 1,\quad C_{21} = 1,\quad C_{31} = 1,\quad C_{41} = 1, \quad C_{51} = 1. \end{split} \tag{5.1} \end{equation*}$ $

(5.1)

The optimal control solution is shown in Figure 3(a). The vaccination strategy $ u_{1}(t) $ can be reduced 80 weeks later from the beginning of the cholera break, and the quarantine strategy $ u_{2}(t) $, treatment strategy $ u_{4}(t) $ and sanitation strategy $ u_{5}(t) $ should be maintained in the whole process. Another quarantine strategy $ u_{3}(t) $ should be gradually increased over 1 weeks and maintained at a high level until 90 weeks.

Figure 3. The graph trajectories of five optimal control strategies based on different running payoff function, in which (a) $ g_{1}(\textbf{X}(t), \textbf{U}(t)) $ with the cost parameter (5.1), (b) $ g_{2}(\textbf{X}(t), \textbf{U}(t)) $ with the cost parameter (5.2).

DownLoad: Full-Size Img PowerPoint

Next, we consider the running payoff function $ g_{2}(\textbf{X}(t), \textbf{U}(t)) $. The following set of values for the cost parameters

$\begin{equation*} \label{52} \begin{split} C_{12} = 1,\quad C_{22} = 1,\quad C_{32} = 1,\quad C_{42} = 1, \quad C_{52} = 1. \end{split} \tag{5.2} \end{equation*}$ $

(5.2)

Similarly, the optimal control solution is shown in Figure 3(b). The vaccination strategy $ u_{1}(t) $ can be reduced 40 weeks later from the beginning of the cholera break, and the quarantine strategy $ u_{2}(t) $, treatment strategy $ u_{4}(t) $ should be maintained in the whole process. Another quarantine strategy $ u_{3}(t) $ should be gradually increased over 10 weeks and maintained at a high level until 90 weeks. In addition, the sanitation strategy $ u_{5}(t) $ is not recommended.

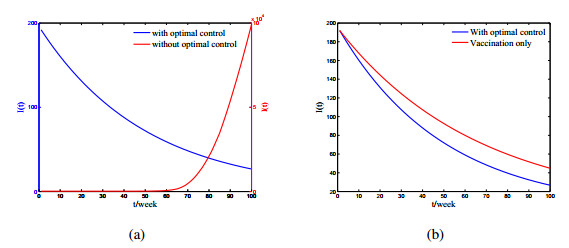
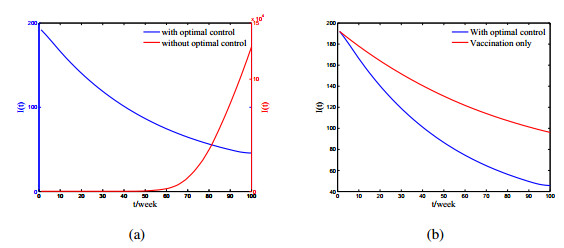
As shown in Figure 3, the values obtained on the optimal control analysis is sensitive to the selected cost function. Therefore, there are different optimal control measures when considering different cost functions. Further, based on the optimal control measures, we can get the effects of the control strategies for the infected individuals. In order to make a comparison, we consider the effects of without any control measures (see Figure 4(a), Figure 5(a)). It is well known that vaccination is a effective measure for cholera prevention and control in a short term. In the following, we explore the influence of vaccine control alone for the infected individuals (see Figure 4(b), Figure 5(b)). By Figure 4 and Figure 5, we can conclude that combining multiple control strategies are most likely to yield the best results in fighting cholera, and the vaccine has a significant control effect on cholera.

Figure 4. The graph trajectories of $ I(t) $ based on the running payoff function $ g_{1}(\textbf{X}(t), \textbf{U}(t)) $ with the cost parameter (5.1).

DownLoad: Full-Size Img PowerPoint

Figure 5. The graph trajectories of $ I(t) $ based on the running payoff function $ g_{2}(\textbf{X}(t), \textbf{U}(t)) $ with the cost parameter (5.2).

DownLoad: Full-Size Img PowerPoint

Therefore, with sufficient costs, vaccination should be combined with other prevention and control strategies to achieve better control in complex emergencies and endemic areas, as recommended by WHO in 2010. With limited costs, only vaccination strategy can control cholera to a great extent. Therefore, vaccination strategy is a feasible and effective method for countries such as Somalia and Yemen with high cholera prevalence and poor economy.

6. Discussion

In this paper, a cholera infection model with vaccination and transmission pathway has been discussed. Here, the total human population is divided into four subpopulation such as susceptible individuals, infected individuals, recovered individuals and vaccinated individuals. In addition, the vibrios in contaminated environment is introduced in the model. Furthermore, the global asymptomatic stability of the disease-free equilibrium and the endemic equilibrium have been completely established by using the Lyapunov's Stability Theorem. If $ R_{0} < 1 $, the disease-free equilibrium is globally asymptomatically stable. If $ R_{0} > 1 $, the endemic equilibrium is globally asymptomatically stable.

In our paper, we consider the saturation incidence rate to describe the environment-to-human transmission way of cholera. However, if the incidence rate is considered as traditional bilinear, the system (1.2) becomes:

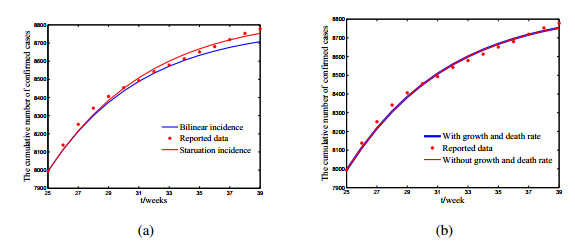
$\begin{equation} \begin{aligned} \dot S& = A-\mu S-\phi S-\left(\beta I+\beta_{1}B\right)S +\eta V,\\ \dot V& = \phi S-\left(\beta I+\beta_{1}B\right)\sigma V-(\mu+\eta)V,\\ \dot I& = \left(\beta I+\beta_{1}B\right)(S+\sigma V)-(\mu+\gamma+d)I,\\ \dot B& = \xi I-\delta B,\\ \dot R& = \gamma I-\mu R. \end{aligned} \end{equation}$ $

(6.1)

In the following, we use the system (6.1) to fit the number of cases in Somalia from 25 to 39 weeks in 2019, and the parameter values obtained are shown in case 1 of Table 2. Further, the fitting results of systems (1.2) and (6.1) are shown in Figure 6(a). By calculating, we obtain the sum-of-squares error of system (1.2) is 6493.4, and that of system (6.1) is 16822. Therefore, it could be more practical to consider the saturation incidence rate to describe the environment-to-human transmission pathway to some extent.

Table 2. List of parameters.

Parameter	Case 1	Case 2	Source
$ A $	7342	-	^[5]
$ \phi $	$ 0.5135\times10^{-3} $	$ 4.2836\times10^{-3} $	fitting
$ \beta $	$ 2.4712\times10^{-10} $	$ 4.3771\times10^{-10} $	fitting
$ \beta_1 $	$ 0.0540\times10^{-9} $	$ 0.5959\times10^{-4} $	fitting
$ \mu $	0.00038	-	^[5]
$ B(0) $	$ 189340 $	$ 205740 $	fitting
$ R(0) $	155	$ 146 $	fitting

| Show Table

DownLoad: CSV

Figure 6. Cumulative cases in Somalia between weeks 25 and 39 of 2019, in which the red dots represent the reported data, the blue curve is the solution of system.

DownLoad: Full-Size Img PowerPoint

If we remove the growth and death rate, the system (1.2) becomes:

$\begin{equation} \begin{aligned} \dot S& = -\phi S-\left(\beta I+\frac{\beta_{1}B}{K+B}\right)S +\eta V,\\ \dot V& = \phi S-\left(\beta I+\frac{\beta_{1}B}{K+B}\right)\sigma V-\eta V,\\ \dot I& = \left(\beta I+\frac{\beta_{1}B}{K+B}\right)(S+\sigma V)-(\gamma+d)I,\\ \dot B& = \xi I-\delta B,\\ \dot R& = \gamma I. \end{aligned} \end{equation}$ $

(6.2)

The parameter values are shown in case 2 of Table 2, and the results of system (1.2) and system (6.2) are shown in Figure 6(b). From Figure 6(b), we see that there is a small difference in our fitting results. Further, by calculating, we obtain that the sum-of-squares error of system (6.2) is 6481.3, which is close to system (1.2). The reason is that in the 14 weeks of fitting, the growth and death changes of individuals can be ignored. However, the threshold that determines whether a disease is prevalent changes with the growth and death rate. Compared with system (6.2), our model can more accurately describe the spread of cholera, and have more realistic representations of biological cholera infection.

Acknowledgment

The authors wish to thank the reviewers and the Editor for their careful reading, valuable comments and suggestions that greatly improved the presentation of this work. This work was supported by the National Natural Science Foundation of China (Nos. 11871316, 11801340, 11371368), and the Natural Science Foundation of Shanxi Province (Nos. 201801D121006, 201801D221007).

Conflict of interest

All authors declare no conflicts of interest in this paper.

References

[1]	Nutbeam D. (1996) Achieving ‘best practice’ in health promotion: improving the fit between research and practice. Health Educ Res, 11: 317-326. doi: 10.1093/her/11.3.317
[2]	Killoran A, & Kelly M. (2004) Towards an evidence-based approach to tackling health inequalities: The English experience. Health Educ J,;63: 7-14.
[3]	Perkins N, Smith K, Hunter DJ, Bambra C & joyce K. (2010) What counts is what works'? New Labour and partnerships in public health. Policy & Politic,s 38: 101-107.
[4]	Tones K & Green J. (2004) A systematic approach to health promotion planning. Chapter 4. In Health Promotion: Planning and Strategies, London: Sage Publications, 105-142.
[5]	Green LW & Kreuter MW. (1999) Health Promotion Planning: An Educational and Ecological Approach, 3rd ed. Boston: Mayfield.
[6]	Bartholomew LK, Parcel GS, Kok G & Gotteliob NH. (2006) Planning Health Promotion Programs, San Francisco: Jossey-Bass.
[7]	Sanderson, C, Haglund, BJA, Tillren, P, Svanstrom, L, Holm, L et al. (1996) Effect and stage models in community intervention programmes; and the development of the Model for Management of Intervention Programme Preparation (MMIPP). Health Promot Int, 11:143-156. doi: 10.1093/heapro/11.2.143
[8]	Nutely S, Walter I, Davies HTO. (2007) Chapter 10 Drawing some conclusions on using evidence. In Using evidence, 1st ed. Bristol: Policy Press, 297-320.
[9]	Petticrew M, Platt S, McCollam A, Wilson S, Thomas S. (2008) "We're not short of people telling us what the problems are. We're short of people telling us what to do". An appraisal of public policy and mental health. BMC Public Health, 8 : 314. http://bmcpublichealth.biomedcentral.com/articles/10.1186/1471-2458-8-314
[10]	Hill M. (2009) The Public Policy Process, Harlow: Pearson Longman.
[11]	Galt G. (1994) Health Policy: An Introduction to Process and Power, London : Zed Books.
[12]	Lipsky M. (1980) Street Level Bureaucracy: Dilemmas of the Individual in Public Services, 1st ed, New York: Russell Sage Foundation.
[13]	Pawson R, Greenhalgh T, Harvey G & Walshe K. (2005) Realist review--a new method of systematic review designed for complex policy interventions.[see comment]. J Health Services & Research Policy, 10 : 21-34.
[14]	Exworthy M, Berney L & Powell M. (2002) 'How great expectations in Westminster may be dashed locally: The local implementation of national policy on health inequalities. Policy & Politics, 30 : 79-96.
[15]	Alvarez-Rosete A & Mays N. (2008) Reconciling two conflicting tales of the English health policy process since 1997. Brit Politics, 3: 183-203. doi: 10.1057/bp.2008.2
[16]	Sanderson I. (2004) Getting evidence into practice: Perspectives on rationality. Evaluation, 10 :366-379.
[17]	Carlisle S. (2001) Inequalities in health: Contested explanations, shifting discourses and ambiguous policies. Critical Public Health, 11 : 267-281.
[18]	Scottish Executive. (2005b). Funding boost for men's health. Retrieved 1^st Nov 2015 from http://www.scotland.gov.uk/News/Releases/2003/10/4298
[19]	Douglas F, Amaya A, Greener J, Ludbrook A, Reid G, Robertson L & van Teijlingen, E. (2008) Evaluation of Well Men Health Service Pilots. Scottish Government Social Research. http://www.scotland.gov.uk/Publications/2008/04/01091641/0
[20]	Macintyre S. (2007) Briefing paper on health inequalities in Scotland. Scottish Government : Edinburgh.
[21]	Office of National Statistics. Life expectancy statistical bulletin - figures for Scotland. Available at: http://www.statistics.gov.uk/StatBase/Product.asp?vlnk=8841&Pos=1&ColRank=1&Rank=272. Accessed June 9th, 2010.
[22]	Walsh D, Taulbut M & Hanlon P. (2009) The aftershock of deindustrialization--trends in mortality in Scotland and other parts of post-industrial Europe. Eur J Public Health, 1-7.
[23]	Hanlon P, Walsh C & Whyte B. (2006) Let Glasgow flourish: A comprehensive report on health and its determinants in Glasgow and West Central Scotland, Glasgow: Glasgow Centre for Population Health.
[24]	Lohan M. (2007) How might we understand men's' health better? Integrating explanations from critical studies on men and inequalities in health. Soc Sci Med, 65 : 493-504.
[25]	Payne S, Doyal L.(2010) Gender equity or gender inequality in health? Policy& Politics 38 : 171-175.
[26]	Hayes BC & Prior PM. (2003) Researching gender and health hare. In: Campling J, Ed Gender and Health Care in the United Kingdom: Exploring the Stereotypes. 1st ed. Basingstoke : Palgrave MacMillan.
[27]	Mansfield AK, Addis ME & Mahalik J. (2008) Why won't he go to the doctor? The psychology of help seeking. Int J Men's Health, 2 : 93-109.
[28]	Sharpe S. (2002) Attitudes and beliefs of men and their health. Men's Health J, 1 : 118-120.
[29]	Galdas PM, Cheater F & Marsahll P. (2005) Men and health help-seeking behaviour: Literature review. J Adv Nursing, 49 : 616-622.
[30]	Wilkins D. (2005) "Getting it sorted": Identifying and implementing practical solutions to men's health. J Men's Health and Gender, 2 : 13-16.
[31]	Robertson, LM, Douglas F, Ludbrook A, Reid G & van Teijlingen ER. (2008) What works with men? A systematic review of health promoting interventions targeting men. BMC Health Services Research 8 : 141 http://www.biomedcentral.com/1472-6963/8/141.
[32]	Scottish Government. Gender influences on health Accessed 24th November 2015. http://www.healthscotland.com/equalities/gender/health-issues.aspx
[33]	Carlisle S. (2010) Tackling inequalities and social inclusion through partnership and community engagement? A reality check for policy and practice aspirations for a Social Inclusion Partnerships in Scotland. Crit Public Health,1 : 117-127.
[34]	Macdonald JJ. (2006) Shifting paradigms: a social-determinants of health approach to solving problems in men's health policy and practice. MedJAustralia, 185 : 456-458.
[35]	Bird CE & Reiker PP. (1999) Genders matters: An integrated model for understanding men's and women's health. Soc Sci Med, 48 : 745-755.
[36]	Smith JA, Robertson S. (2008) Men's health promotion: a new frontier in Australia and the UK? Health Promot.Internation, 23 : 283-289.
[37]	Campbell M, Ballas D, Dorling D & Mitchell R. (2013) Mortality inequalities: Scotland versus England and Wales. Health & Place, 23 : 179-186.
[38]	Wilkinson R, Pickett KE. (2009) The Spirit Level: Why More Equal Societies Almost Always Do Better,1st ed, : London: Allen Lane.
[39]	Kawachi I, Kennedy BP. (2002) The Health of Nations: Why Inequalities is Harmful to Your Health, New York: New Press.
[40]	O'Brien R, Hunt K & Hart G. (2005) 'It's caveman stuff, but that is to a certain extent how guys still operate': Men's accounts of masculinity and help seeking. Soc Sci Med, 61 : 503-516.
[41]	Scottish Executive. Improving health in Scotland: The challenge. Retrieved 3rd September, 2005 from http://www.scotland.gov.uk/library5/health/ihis-00.htm 211 2005
[42]	Scottish Executive. Funding boost for men's health. Retrieved 3rd September, 2005 from http://www.scotland.gov.uk/News/Releases/2003/10/429. 2005
[43]	Scottish Executive. A partnership for a better Scotland: A partnership agreement. Retrieved 12th March, 2005 from http://www.scotland.gov.uk/library5/government/pfbs-00.asp. 2005
[44]	Scottish Executive. (2004) Evaluation of the Well Men Services Pilots: Research Specification. Edinburgh: Scottish Executive.
[45]	Leishman, J. (2008) Around the world with men's health and women's health organisations: Healthy Scottish men? J Men's Health, 2 : 133-134.
[46]	W.K. Kellogg Foundation. (2004). Logic model development guide, Available at http://www.wkkf.org/resource-directory/resource/2006/02/wk-kellogg-foundation-logic-model-development-guide.
[47]	National Cancer Institute. (2005) Theory at a glance: A guide for health promotion practice.;05-3896. Available athttp://www.sneb.org/2014/Theory%20at%20a%20Glance.pdf
[48]	Naidoo J & Wills J (2009) Health Promotion; Foundations for Practice. 3rd ed, Balliere Tindall : Royal College of Nursing.
[49]	Jayasinghe S. (2011) Conceptualising population health: from mechanistic thinking to complexity science. Emerg Themes Epidemiol, 8 :1-7.
[50]	Hill PS. (2000) Planning and change: a Cambodian public health case study. Soc Sci Med, 51 : 1711-1722.
[51]	MacDonald MA & Green LW. (2001) Reconciling concept and context: the dilemma of implementation in school-based health promotion. Health Edu& Behav, 28 : 749-768.
[52]	Royal Society for Public Health. A planning guide: health inequalities and the voluntary and community sector. Available at: http://www.healthscotland.com/topics/settings/community-voluntary/oa.aspx. Accessed 15th June, 2014.
[53]	Moore N. (2007) (Re)Using Qualitative data? Sociological Research Online Accessed: 7th September, 2009.
[54]	Strauss A, Corbin J. (1998) Basics of qualitative research: Techniques and procedures for developing grounded theory, Thousand Oaks : Sage.
[55]	Ritchie J & Lewis J. (2003) Qualitative Research Practice. 1st ed, London : Sage.
[56]	Craig P, Hanlon P & Morrison J. (2008) Can primary care reduce inequalities in mental health? Public Health (e-supplement), 1-5.
[57]	Elston J, Fulop N. (2002) Perceptions of partnership. A documentary analysis of Health Improvement Programmes. Public Health, 116 : 207-213.
[58]	Denzin NK, Lincoln YS. (1998) Methods of analysing and interpreting qualitative materials. In: Denzin NK, Lincoln YS, Eds Collecting and Interpreting Qualitative Material, s London : Sage, 35-45.
[59]	Chun YH & Rainey HG. (2005) Goal ambiguity in U.S. federal agencies. J Public Administration Research & Theory, 15 : 1-30.
[60]	Lee JW, Rainey GH & Chun YH. (2009) Of politics and purpose: Political salience and goal ambiguity of US federal agencies. Public Administration, 87 : 457-484.
[61]	Pandey SK & Wright BE. (2006) Connecting the dots in public management: Political environment, organisational goal ambiguity, and the public manager's role ambiguity. J of Public Administration Research& Theory, 16 : 511-532.
[62]	Feldman MS. (1989) Order Without Design: Information Production and Policy Making. Stanford: California: Stanford University Press..
[63]	Oliver TR. (2006) The politics of public health policy. Annu Rev Public Health, 27 : 195-233.
[64]	Gordon D, Graham L, Robinson M & Taulbut M. (2010) Dimensions of Diversity: Population differences and health improvement opportunities, Edinburgh : NHS Health Scotland.
[65]	Cabinet Office. (2007) Fairness and Freedom: The Final Report of the Inequalities Review. Available at http://webarchive.nationalarchives.gov.uk/20100807034701/http:/archive.cabinetoffice.gov.uk/equalitiesreview/upload/assets/www.theequalitiesreview.org.uk/equality_review.pdf
[66]	Godin G, Gagnon H, Alary M, Levy JL & Otis J. (2007) The degree of planning; an indicator fo the potential success of health education programs. Promotion & Education, XIV : 138-142.
[67]	De Leeuw E. (1993) Health policy, epidemiology and power: the interest web. Health Promotion International, 8 : 49-52.
[68]	Marks L. (2006) An evidence base for tackling inequalities in health: Distraction or necessity? Critical Public Health, 16 : 16-17.
[69]	Smith KE. (2007) Health inequalities in Scotland and England: the contrasting journeys of ideas from research into policy. Soc Sci Med, 64 : 1438-1449.
[70]	Aronowitz R. (2008) Framing disease: An underappreciated mechanism for the social patterning of disease. Soc Sci Med, 67 : 1-9.
[71]	Nutbeam D. 1998) Evaluating health promotion - progress, problems and solutions. Health Promot.Int, 13 :27-44.
[72]	Raphael D. (2008) Getting serious about the social determinants of health: new directions for public health workers. Promotion & Education, 15 : 15-20.
[73]	Chan CC. (2009) Choosing health, constrained choices. Global Health Promotion, 16 : 54-57.
[74]	Green J. (2014) What kind of research does public health need? Critical Public Health, 24 : 249-252.
[75]	Hanlon P, McEwen J, Carey L, Gilmour H, Tannahill C, Tannahill A, et al. (1995) Health checks and coronary risk: further evidence from a randomised controlled trial. BMJ, 311 : 1609-1613.
[76]	Fitzpatrick M. (2001) The Tyranny of Health, London : Routledge.
[77]	Popay J, Whitehead M & Hunter DJ. (2010) Injustice is killing people on a large scale--but what is to be done about it? J Public Health, 2 : 148-149.
[78]	Baum F. (2011) From Norm to Eric: avoiding lifestyle drift in Australian health policy. Aust N Z J Public Health,35 : 404-406.
[79]	Baum F & Fisher M. (2014) Why behavioural health promotion endures despite its failure to reduce health inequities. Sociol Health Illn, 36 : 213-225.
[80]	Kim SH, Willis LA. (2007) Talking about Obesity: News Framing of Who is Responsible for Causing and Fixing the Problem.J Health Communication,;12 : 359-376.
[81]	King D. (2007) Foresight report on obesity. Lancet, 70 : 1754.
[82]	Friedli L. (2012) ‘What we've tried, hasn't worked': the politics of assets-based public health 1. Critical Public Health, 12 :1-15.
[83]	Mitzenberg H. (1994) The Rise and Fall of Strategic Planning, Harlow Essex: Prentice Hall.
[84]	Brassolotto J, Raphael D, Baldeo N. (2013) Epistemological barriers to addressing the social determinants of health among public health professionals in Ontario, Canada: A qualitative inquiry. Critical Public Health, 24 : 321-336.
[85]	Chambers D & Thompson S. (2009) Empowerment and its application in health promotion in acute care settings: nurses' perceptions. J Adv Nursing, 65 : 130-138.
[86]	Starfield B, Hyde J, Health I. (2008) The concept of prevention: a good idea gone astray? J Epidemiology & Community Health, 62 : 580-583.
[87]	NHS Health Scotland. Logic Models. 28th April 2010; Available at: http://www.healthscotland.com/understanding/planning/logic-models.aspx. Accessed June 8th, 2010.
[88]	NHS Health Scotland. Outcome focussed approaches. Available at: http://www.healthscotland.com/topics/settings/community-voluntary/oa.aspx. Accessed 15th June, 2014.
[89]	Buse K, Mays N & Walt G. (2005) Making Health Policy, Maidenhead: Open University Press.
[90]	Rittel HW & Webber M. (1973) Dilemmas in a General Theory of Planning. Policy Sciences, 4 : 155-169.
[91]	Rod MH, Ingholt L, Bang Sørensen B, Tjørnhøj-Thomsen T. (2013) The spirit of the intervention: reflections on social effectiveness in public health intervention research. Critical Public Health , 24 : 296-307.
[92]	Cohn S, Clinch M, Bunn C & Stronge P. (2013) Entangled complexity: why complex interventions are just not complicated enough. J Health Serv Res Policy, 18 : 40-43.
[93]	Mackenbach JP. (2012) From deep-fried Mars bars to neoliberal political attacks: explaining the Scottish mortality disadvantage. Eur J Public Health, 22 : 751-751.
[94]	Marmot M. (2012) Health equity: the challenge. Aust N Z J Public Health, 36 : 513-514.
[95]	Bambara C, Fox D & Scott-Samuel A. (2005) Towards a politics of health. Health Promot.Internation, 20 : 187-193.

This article has been cited by:

1.	Harendra Pal Singh, Sumit Kaur Bhatia, Riya Jain, Yashika Bahri, 2021, Chapter 1, 978-981-16-1695-2, 1, 10.1007/978-981-16-1696-9_1
2.	Hongyan Zhao, Shaofen Zou, Xia Wang, Yuming Chen, Dynamic behaviors of a cholera model with nonlinear incidences, multiple transmission pathways, and imperfect vaccine, 2024, 70, 1598-5865, 917, 10.1007/s12190-024-01994-9
3.	Jingyun Shen, Shengfu Wang, Linfei Nie, Dynamics of a reaction–diffusion epidemic model with general incidence and protection awareness for multi-transmission pathways, 2023, 74, 0044-2275, 10.1007/s00033-023-02144-0

Reader Comments

Your name:*

Email:*
© 2015 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Public Health

2.7 5.3

Metrics

Article views(6860) PDF downloads(1072) Cited by(1)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

AIMS Public Health

Implementing health policy: lessons from the Scottish Well Mens policy initiative

Related Papers:

Abstract

1. Introduction

2. Equilibria and boundedness of solutions

3. Global stability

4. Optional control strategies

5. Numerical simulations

5.1. Data fitting

5.2. Sensitivity analysis

5.3. Optimal control solution

6. Discussion

Acknowledgment

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Other Articles By Authors

Catalog

AIMS Public Health

Implementing health policy: lessons from the Scottish Well Mens policy initiative

Related Papers:

Abstract

1. Introduction

2. Equilibria and boundedness of solutions

3. Global stability

4. Optional control strategies

5. Numerical simulations

5.1. Data fitting

5.2. Sensitivity analysis

5.3. Optimal control solution

6. Discussion

Acknowledgment

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog