1.
Introduction
In 1999, Fallat and Johnson [1] introduced the concept of k-subdirect sums of square matrices, which generalizes the usual sum and the direct sum of matrices [2], and has potential applications in several contexts such as matrix completion problems [3,4,5], overlapping subdomains in domain decomposition methods [6,7,8], and global stiffness matrices in finite elements [7,9], etc.
Definition 1.1. [1] Let A∈Cn1×n1 and B∈Cn2×n2, and k be an integer such that 1≤k≤min{n1,n2}. Suppose that
where A22 and B11 are square matrices of order k. Then
is called the k-subdirect sum of A and B and is denoted by C=A⨁kB.
For the k-subdirect sums of matrices, one of the important problems is that if A and B lie in a certain subclass of H-matrices must a k-subdirect sum C lie in this class, since it can be used to analyze the convergence of Jacobi and Gauss-Seidel methods in solving the linearized system of nonlinear equations [10]. Here, a square matrix A is called an H-matrix if there exists a positive diagonal matrix X such that AX is a strictly diagonally dominant matrix [11]. To answer this question, several results about subdirect sum problems for H-matrices and some subclasses of H-matrices have been obtained, such as S-strictly diagonally dominant matrices [12], doubly diagonally dominant matrices [13], Σ-strictly diagonally dominant matrices [14], α1 and α2-matrices [15], Nekrasov matrices [16], weakly chained diagonally dominant matrices [17], QN-(quasi-Nekrasov) matrices [18], SDD(p)-matrices [10], and H-matrices [19]. Besides, the subdirect sum problems for some other structure matrices, including B-matrices, BRπ-matrices, P-matrices, doubly non-negative matrices, completely positive matrices, and totally non-negative matrices, were also studied; for details, see [1,20,21,22] and references therein.
In 2009, Cvetković, Kostić, and Rauški [23] introduced a new subclass of H-matrices called S-Nekrasov matrices.
Definition 1.2. [23] Given any nonempty proper subset S of N:={1,2,…,n} and ¯S=N∖S. A matrix A=[aij]∈Cn×n is called an S-Nekrasov matrix if |aii|>hSi(A) for all i∈S, and
where hS1(A)=∑j∈S∖{1}|a1j| and
Specially, if S=N, then Definition 1.2 coincides with the definition of Nekrasov matrices [23], that is, a matrix A=[aij]∈Cn×n is called a Nekrasov matrix if |aii|>hi(A) for all i∈N, where hi(A):=hNi(A). It is worth noticing that the class of S-Nekrasov matrices has many potential applications in scientific computing, such as estimating the infinity norm for the inverse of S-Nekrasov matrices [24], estimating error bounds for linear complementarity problems [25,26,27], and identifying nonsingular H-tensors [28], etc. However, to the best of the author's knowledge, the subdirect sum problem for S-Nekrasov matrices remains unclear. In this paper, we introduce the class of {i0}-Nekrasov matrices and prove that it is a subclass of S-Nekrasov matrices, and then we focus on the subdirect sum problem of {i0}-Nekrasov matrices. We provide some sufficient conditions such that the k-subdirect sum of {i0}-Nekrasov matrices and Nekrasov matrices belongs to the class of {i0}-Nekrasov matrices. Numerical examples are presented to illustrate the corresponding results.
2.
Subdirect sums of {i0}-Nekrasov matrices
We start with some notations and definitions. For a non-zero complex number z, we define arg(z)={θ:z=|z|exp(iθ),−π<θ≤π}. As is shown in [12], if we let C=A⨁kB=[cij], where A=[aij]∈Cn1×n1 and B=[bij]∈Cn2×n2, then
where t=n1−k and
with n=n1+n2−k. Obviously, S1⋃S2⋃S3=N.
We introduce the following subclass of S-Nekrasov matrices by requiring S is a singleton.
Definition 2.1. A matrix A=[aij]∈Cn×n is called an {i0}-Nekrasov matrix if there exists i0∈N such that |ai0,i0|>ηi0(A), and that for all j∈N∖{i0},
where ηi(A)=0 for all i∈N if i0=1, otherwise, η1(A)=|ai,i0| and
Remark 2.1. (i) If A is an {i0}-Nekrasov matrix, then A is an S-Nekrasov matrix for S={i0}. In fact, using recursive relations (1.2) and (2.2), it follows that hSi0(A)=0=ηi0(A) if i0=1, otherwise, hS1(A)=η1(A) and
In addition, h¯Si(A)=hi(A)−ηi(A) follows from the fact that hi(A)=hSi(A)+h¯Si(A) for each i∈N. These imply that an {i0}-Nekrasov matrix is an S-Nekrasov matrix for S={i0}.
(ii) Since a Nekrasov matrix is an S-Nekrasov matrices for any S, it follows that a Nekrasov matrix is an {i0}-Nekrasov matrices.
The following example shows that the k-subdirect sum of two {i0}-Nekrasov matrices may not be an {i0}-Nekrasov matrix in general.
Example 2.1. Consider the {i0}-Nekrasov matries A and B for i0=2, where
Then, the 3-subdirect sum C=A⨁3B gives
It is easy to check that C=A⨁3B is not an {i0}-Nekrasov matrix for neither one index i0. This motivates us to seek some simple conditions such that C=A⨁kB for any k is an {i0}-Nekrasov matrix. First, we provide the following conditions such that A⨁1B is an {i0}-Nekrasov matrix, where A is an {i0}-Nekrasov matrix and B is a Nekrasov matrix.
Theorem 2.1. Let A=[aij]∈Cn1×n1 be an {i0}-Nekrasov matrix with i0∈S1 and B=[bij]∈Cn2×n2 be a Nekrasov matrix, partitioned as in (1.1), which defines the sets S1, S2 and S3 as in (2.1), and let t=n1−1. If arg(aii) = arg(bi−t,i−t) for all i∈S2 and B21=0, then the 1-subdirect sum C=A⨁1B is an {i0}-Nekrasov matrix.
Proof. Since A is an {i0}-Nekrasov matrix and i0∈S1, it follows that if i0=1 then |c11|=|a11|>η1(A)=0=η1(C), otherwise,
Case 1: For i∈S1, we have
and if i0=1, then ηi(C)=0=ηi(A), and if i0≠1, then η1(C)=|ci,i0|=|ai,i0|=η1(A) and
Hence, for all j∈S1∖{i0},
Case 2: For i∈S2={n1}, we have
and
So,
Case 3: For i∈S3={n1+1,…,n}, we have
It follows from B21=0 that
and for each i=n1+2,…,n,
So, for all j∈S3,
The conclusion follows from (2.3), Case 1–3.
Next, we give some conditions such that C=A⨁kB for any k is an {i0}-Nekrasov matrix, where A is an {i0}-Nekrasov matrix and B is a Nekrasov matrix. First, a lemma is given which will be used in the sequel.
Lemma 2.1. Let A=[aij]∈Cn1×n1 be an {i0}-Nekrasov matrix with i0∈S1∪S2 and B=[bij]∈Cn2×n2 be a Nekrasov matrix, partitioned as in (1.1), k be an integer such that 1≤k≤min{n1,n2}, which defines the sets S1, S2 and S3 as in (2.1), let t=n1−k and C=A⨁kB. If arg(aii) = arg(bi−t,i−t) for all i∈S2, B12=0, and |aij+bi−t,j−t|≤|aij| for i≠j,i,j∈S2, then
Proof. If i0∈S1, then it follows from the proof of Case I in Theorem 2.1 that hi(C)−ηi(C)=hi(A)−ηi(A) for all i∈S1, and thus hi0(C)−ηi0(C)=hi0(A)−ηi0(A).
If i0∈S2={n1−k+1,…,n1}, then from the assumptions and t=n1−k we have
Suppose that hi(C)−ηi(C)≤hi(A)−ηi(A) for all i<t+m, where m is a positive integer and 1<m≤k. We next prove that ht+m(C)−ηt+m(C)≤ht+m(A)−ηt+m(A). Since
it follows that hi(C)−ηi(C)≤hi(A)−ηi(A) for all i∈S2. Hence, hi0(C)−ηi0(C)≤hi0(A)−ηi0(A). The proof is complete.
Theorem 2.2. Let A=[aij]∈Cn1×n1 be an {i0}-Nekrasov matrix with i0∈S1 and B=[bij]∈Cn2×n2 be a Nekrasov matrix, partitioned as in (1.1), k be an integer such that 1≤k≤min{n1,n2}, which defines the sets S1, S2 and S3 as in (2.1), and let t=n1−k. If arg(aii) = arg(bi−t,i−t) for all i∈S2, A21=0, and |aij+bi−t,j−t|≤|bi−t,j−t| for i≠j,i,j∈S2, then the k-subdirect sum C=A⨁kB is an {i0}-Nekrasov matrix.
Proof. Since A is an {i0}-Nekrasov matrix and i0∈S1, it is obvious that |ci0,i0|>ηi0(C).
Case 1: For i∈S1, since hi(C)=hi(A) and ηi(C)=ηi(A), it holds that for all j∈S1∖{i0},
Case 2: For i∈S2, by the assumptions, we have
Similarly, for i=n1−k+2,…,n1,
And for i=n1−k+1, by A21=0,
implying that for all i∈S2,
So, for all j∈S2,
Analogously to the proof of Case 2, we can easily obtain that (2.4) holds for all j∈S3. Combining with Case 1 and Case 2, the conclusion follows.
Example 2.2. Consider the following matrices:
It is easy to verify that A is an {i0}-Nekrasov matrix for i0∈S1={1,2} and B is a Nekrasov matrix, which satisfy the hypotheses of Theorem 2.2. So, by Theorem 2.2, A⨁2B is an {i0}-Nekrasov matrix for i0∈S1={1,2}. In fact, let C=A⨁2B. Then,
and from Definition 2.1, one can verify that C is an {i0}-Nekrasov matrix for i0∈S1={1,2}.
Theorem 2.3. Let A=[aij]∈Cn1×n1 be an {i0}-Nekrasov matrix with i0∈S1∪S2 and B=[bij]∈Cn2×n2 be a Nekrasov matrix, partitioned as in (1.1), k be an integer such that 1≤k≤min{n1,n2}, which defines the sets S1, S2 and S3 as in (2.1), and let t=n1−k. If arg(aii) = arg(bi−t,i−t) for all i∈S2, B12=B21=0, and |aij+bi−t,j−t|≤|aij| for i≠j,i,j∈S2, then the k-subdirect sum C=A⨁kB is an {i0}-Nekrasov matrix.
Proof. Since A is an {i0}-Nekrasov matrix, it follows that if i0∈S1, then |ci0,i0|>ηi0(C), and if i0∈S2, then
Similarly, we can obtain that ηj(C)≤ηj(A) for all j∈{n1−k+2,…,n1}. Therefore,
and
Case 1: For i∈S1, proceeding as in the proof of Case 1 in Theorem 2.1, we have hi(C)=hi(A) and ηi(C)=ηi(A), which implies that for all j∈S1∖{i0},
Case 2: For i∈S2, by the assumptions, we have
and
Hence, by Lemma 2.1, it follows that for all j∈S2∖{i0},
Case 3: For i∈S3, similarly to the proof of Case 3 in Theorem 2.1, we show that for all i∈S3,
which implies that for all j∈S3,
From the above three cases, the conclusion follows.
Example 2.3. Consider the following matrices:
where A is an {i0}-Nekrasov matrix for i0∈S1∪S2={1,2,3,4} and B is a Nekrasov matrix, and they satisfy the hypotheses of Theorem 2.3. Then, from Theorem 2.3, we get that the 3-subdirect sum C=A⨁3B is also an {i0}-Nekrasov matrix for i0∈S1∪S2={1,2,3,4}. Actually, by Definition 2.1, one can check that
is an {i0}-Nekrasov matrix for i0∈S1∪S2={1,2,3,4}.
Theorem 2.4. Let A=[aij]∈Cn1×n1 be an {i0}-Nekrasov matrix for some i0∈S2 and B=[bij]∈Cn2×n2 be a Nekrasov matrix, partitioned as in (1.1), k be an integer such that 1≤k≤min{n1,n2}, which defines the sets S1, S2 and S3 as in (2.1), and let t=n1−k. If
(i) arg(aii) = arg(bi−t,i−t) for all i∈S2,
(ii) B12=0, hi(A)≤hi−t(B), ηi(A)≤ηi−t(B), and |aij+bi−t,j−t|≤|aij| for i≠j,i,j∈S2,
(iii) (hi0−t(B)−ηi0−t(B))(|ai0,i0|−ηi0(A))≥(|bi0−t,i0−t|−ηi0−t(B))(hi0(A)−ηi0(A)),
then the k-subdirect sum C=A⨁kB is an {i0}-Nekrasov matrix.
Proof. Due to A is an {i0}-Nekrasov matrix and i0∈S2, it follows from the proof of Case 2 in Theorem 2.3 that ηi(C)≤ηi(A) for all i∈S2, which leads to
Case 1: For i∈S1, it is obvious that hi(C)=hi(A) and ηi(C)=ηi(A). Hence, for all j∈S1,
Case 2: For i∈S2, it follows from B12=0 and |aij+bi−t,j−t|≤|aij| for i≠j,i,j∈S2 that hi(C)≤hi(A), and thus for all j∈S2∖{i0}, (2.5) also holds.
Case 3: For i=n1+1∈S3, by the assumption, it follows that
which recursively yields that for i=n1+2,…,n,
Similarly, we have
and for all i=n1+2,…,n,
Hence, for all j∈S3,
From Case 1, Case 2 and Case 3, we can conclude that C=A⨁kB is an {i0}-Nekrasov matrix.
Example 2.4. Consider the following matrices:
where A is an {i0}-Nekrasov matrix for i0=2 and B is a Nekrasov matrix. By computation, we have h1(A)=3,h2(A)=5, h3(A)=1.25,h4(A)=0.75, h1(B)=5,h2(B)=1.5556,h3(B)=0.8667,h4(B)=0, η1(A)=1,η2(A)=0.3333,η3(A)=0.0167,η4(A)=0.1767, η1(B)=4,η2(B)=0.4444,η3(B)=0.5333, and η4(B)=0, which satisfy the hypotheses of Theorem 2.4. Hence, from Theorem 2.4, we have that A⨁3B is also an {i0}-Nekrasov matrix for i0=2. In fact, let C=A⨁3B. Then
and one can verify that C is an {i0}-Nekrasov matrix for i0=2 from Definition 2.1.
3.
Conclusions
In this paper, for an {i0}-Nekrasov matrix A as a subclass of S-Nekrasov matrices and a Nekrasov matrix B, we provide some sufficient conditions such that the k-subdirect sum A⨁kB lies in the class of {i0}-Nekrasov matrices. Numerical examples are included to illustrate the advantages of the given conditions. {The results obtained here have potential applications in some scientific computing problems such as matrix completion problem and the convergence of iterative methods for large sparse linear systems. For instance, consider large scale linear systems
Note that if the coefficient matrix C in (3.1) is an H-matrix, then the iterative methods of Jacobi and Gauss-Seidel associated with (3.1) are both convergent [29], but it is not easy to determine C as an H-matrix in general. However, if C is exactly the subdirect sum of matrices A and B, i.e., C=A⨁kB, where A and B satisfy the sufficient conditions given here, then it is easy to see that C is an {i0}-Nekrasov matrix, and thus an H-matrix.
Acknowledgments
The author wishes to thank the three anonymous referees for their valuable suggestions to improve the paper. The research was supported by the National Natural Science Foundation of China (31600299), the Natural Science Foundations of Shaanxi province, China (2020JM-622), and the Projects of Baoji University of Arts and Sciences (ZK2017095, ZK2017021).
Conflict of interest
The author declares no conflict of interest.









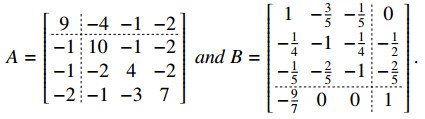

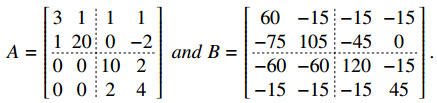

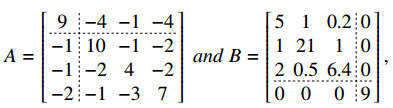
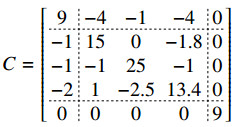
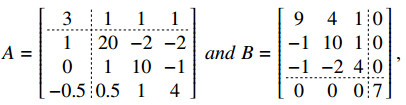















 DownLoad:
DownLoad: