RodZ: a key-player in cell elongation and cell division in Escherichia coli

1.   Introduction

One of the goals in analyzing theoretical infectious disease models is to obtain conditions that may either spread or suppress infectious diseases. Such conditions are often reported as the critical value of a parameter that would lead to a drastic qualitative change of a system—the threshold phenomenon. A central concept of the threshold phenomena in the theory of infectious disease epidemiology is the basic reproduction number ($ R_0 $), which indicates the number of consequential secondary cases in a completely susceptible population due to the introduction of a single primary case. If the $ R_0 $ value is larger than one under suitable assumptions, then the infectious disease invades a population, otherwise, the spread of the infectious disease is suppressed ^[1,2]. Furthermore, some other types of thresholds of epidemic models have been obtained under various settings: Time-delayed epidemic models ^[3,4], a malaria model considering dilution effect of animal population ^[5], a cholera model with periodic transmission rate ^[6], a time-delayed SEIRS model with pulse vaccination ^[7], a pertussis model with seasonality ^[8], a stochastic avian-human influenza model with psychological effect ^[9], among others.

Depopulation is one of the important interventions for an outbreak of animal disease, which is essentially different from that for human disease. Clearly, the faster the initiation of depopulation is, the better the outcome is. However, studies on the possible qualitative change in the model due to the delays in the depopulation are limited. Based on state-transition such as the SEIR (susceptible-exposure-infectious-recovered) model, in the present study, we developed a simple deterministic model of foot-and-mouth disease (FMD) and conduct a numerical investigation concerning threshold phenomena.

FMD is a transboundary animal disease caused by a virus of the genus Aphthovirus in the family Picornaviridae. FMD is so highly contagious that $ R_0 $ value for intra-farm transmission has been reported being as high as $ 38.4 $ ^[10]. A single confirmed case is almost equivalent to a farm-wide infection. Modes of FMD transmission include contact with infected animals or inanimate objects and exposure to the aerosolized virus ^[11,12,13]. The virus is known to exist in seven serotypes (i.e., O, A, C, SAT 1, SAT 2, SAT 3 and Asia 1) with the O serotype being the most common worldwide. In 2010, this serotype was implicated in sporadic outbreaks in East Asia ^[14,15,16] including Japan. To define the model settings and parameters, we deal with the FMD epidemic in Japan 2010 which was mainly localized in Miyazaki Prefecture. The economic damage was massive involving 292 farms and the culling of approximately 290,000 animals in a short span of two and a half months ^[17].

Depopulation is the primary intervention of choice in Japan to eradicate FMD according to the nation's legislation ^[18,19]. Measures like vaccination, traffic restriction, and quarantine are regarded as supplementary strategies only. This view is shared by 65 other countries belonging to the OIE list of "FMD free countries where vaccination is not practiced" (a total of 66 countries including Japan). When countries in the list conduct vaccination, they will be removed from the list and should depopulate all the vaccinated animals to be listed again ^[20]. In contrast, only two nations are listed as "FMD free countries where vaccination is practiced" ^[21]. Countries in the former list implemented stringent import and cross-border animal movement control and surveillance to maintain such status, which in turn grants trading privileges among them. Aside from historical accounts, compelling evidence from research employing epidemiological simulations agrees that depopulation is the most effective intervention to control and eradicate FMD, the importance of the combination of it and supplementary measures was also stated though ^[22].

The timing of the implementation of depopulation has emerged as a critical element for a successful outcome. The retrospective simulations conducted on the 2002 and 2010 FMD epidemic in Korea and Japan, respectively reported that a prompt depopulation within 48 h or less following confirmed detection would have reduced the number of infected farms to less than half of those reported ^[23,24]. Although it is ideal, the countries that had experienced the pandemic of FMDs revealed that the depopulation of all infected farms within this time frame is difficult to achieve in the case of outbreaks in a highly dense area ^[25,26,27].

Hayama et al. ^[24] presented retrospective modelling scenarios for a 1-day, 2-day, or 3-day prompt depopulation after detection of an index case; while Yoon et al. ^[23] simulated for 2 days or 5 days of prompt depopulation, as well as for a 5-day pre-emptive depopulation. In contrast, a long delay (median, 9 days) in the depopulation of infected farms was reported in the Miyazaki outbreak in 2010, because of depopulation with a full of capacity due to difficulties in identifying and accessing acceptable burial sites ^[28]. Similarly, both Great Britain and the Netherlands in 2001 also reported delays in conducting a full-fledged depopulation due to an overwhelming of the country's capacity during the first outbreaks since the epidemic affected a farm-dense area ^[25,26,27]. The scenarios presented in the previous retrospective modeling studies were not reflective of the actual delays in the implementation of depopulation. Clearly, further analysis is needed to better characterize the epidemiological repercussions of such delays. This information are important inputs for decision makers in designing contingent measures to enhance national preparedness in the event of another outbreak.

The previous retrospective studies were interested in the quantitative outcome of depopulation, but the present study aims at the qualitative revelation of the threshold phenomena in the timing of depopulation in relation to the final size of the epidemics and the timing of depopulation.

This paper is organized as follows. In section 2, we explain the methods of our study: Data, model, and numerical calculation. In section 3, we present numerical results about a threshold phenomenon. Discussion and conclusion are given in section 4 and section 5, respectively.

2.   Materials and method

2.1.   Data

Miyazaki Prefecture, one of Japan's primary livestock-producing areas, was used as the area for the present study. The densities of cattle and swine farms here are among the highest in the country at 165 cattle and 9.8 pig farms per 100 km$ ^{2} $ in 2010 ^[17]. Data obtained for the development of the model included farm location, species and number of animals for each farm. Information pertaining to the 2010 FMD epidemic was also obtained which accounted for the dates when the infection was reported to the prefectural office, dates for the start and completion of depopulation, and dates when disinfection of farm facilities and equipment was completed ^[15,29].

2.2.   Model description and formulation

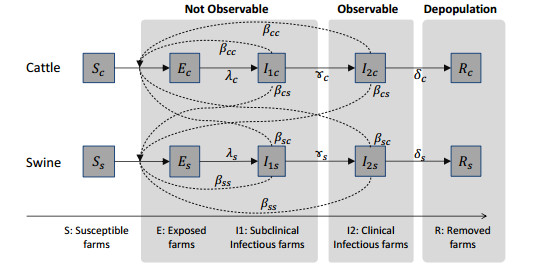
The established methodological approach for modelling FMD is by grouping the animals based on the infection stage—susceptible, exposure, infectious, or recovered (SEIR) ^[30]. This model has wide applications and had been used to model infectious diseases not only in animals ^[25] but in humans, as well ^[31]. The SEIR model has been applied to FMD previously ^[25]. We made a distinction between the asymptomatic ($ I_1 $) and symptomatic ($ I_2 $) infectious stages of the disease as a modification. This modified model, hereafter referred to as the SEIIR model, was then used to run several scenarios to simulate the epidemiological impact of delays in the implementation of depopulation and the likely effect of other secondary control strategies. Because it is assumed that if animals of the symptomatic stage do not exist, the farms are not depopulated even when infectious animals exist, we need to separate an infectious stage to subclinical and clinical stages ^[30]. The second modification was the setting of the study unit; considering that FMD virus spreads within a farm so rapidly ^[10] that a single case is nearly equivalent to farm-wide infection. We used a single farm as the basic unit of study instead of individual animals. Thus, we mainly considered direct or indirect transmission among farms via contaminated environments ^[11,12]. Thirdly, we did not consider natural recovery as the final stage of infection because once a farm is infected, the contaminated water, soils, and other equipment on the farm can cause new infections even when all the animals recovered. In our model, infected farms were considered non-infectious only after depopulation and the disinfection of the facilities and equipment. As such, the $ R $ stage of infection in our SEIIR model refers to "removed" instead of "recovered". Both cattle and swine herds were affected during the 2010 epidemic in Miyazaki, so each farm was supposed to possess either cattle or swine only and represented by the subscripts "$ c $" and "$ s $", respectively. Based on these, farms were categorized using the following compartments (Figure 1): $ S $ (susceptible farms; no animal in the farm is infected), $ E $ (exposed farms; more than one animal is infected but none is infectious), $ I_1 $ (subclinically infectious farms; more than one animal is infectious but none is symptomatic), $ I_2 $ (clinically infectious farms; more than one animal is infectious and symptomatic), and $ R $ (removed farms; depopulated farms).

Figure 1.  Compartmental model for the spread of FMD virus. Infection caused by $ I_1 $ and $ I_2 $ farms transfers $ S $ farms to $ E $ compartment, where $ \beta_{cc} $, $ \beta_{cs} $, $ \beta_{ss} $ and $ \beta_{sc} $ are transmission coefficients. $ E $ and $ I_1 $ farms transfer to $ I_1 $ and $ I_2 $ with transition rates of $ \lambda $ and $ \gamma $ respectively. $ I_2 $ farms transfer to $ R $ compartment by depopulation.

DownLoad: Full-Size Img PowerPoint

In the model, ordinary differential equations were used to describe the indirect transmission among farms.

$ \beta_{cc} $, $ \beta_{cs} $, $ \beta_{ss} $ and $ \beta_{sc} $ are transmission coefficients. $ \lambda $, $ \gamma $ and $ \delta $ are transition rates from $ E $ to $ I_1 $, from $ I_1 $ to $ I_2 $, and from $ I_2 $ to $ _r $ respectively. $ \delta (t) $ is the depopulation capacity, which is the maximum number of farms to be depopulated each day. The probability of causing new infection, represented by the transmission rate among farms ($ \beta $), was constant regardless of the number of infected animals since a single infected animal is all that is needed for inter-farm transmission. This assumption is further supported by the high $ R_0 $ value of FMD. Data on FMD transmission rate inter-farm which accounts for the heterogeneity of cattle and swine herds are yet unavailable, but such data for intra-farm transmission has been reported by Hayama et al. ^[24]. We assumed that inter- and intra-farm transmission rates were proportional. Indirect transmission of the FMD virus between farms (inter-farm transmission) is caused by the movement of the contaminated vehicle, soil, and other equipment from infected farms.

The infection of $ S $ farms was assumed to be caused by indirect transmission from either $ I_1 $ or $ I_2 $ farms. The consequent decline in the number of $ S $ farms due to this is represented by (2.1) and (2.5). In the subsequent $ E $ compartment, the increase, due to recategorization of the infected $ S $ farms, and decrease, due to the progression of the infection to the subclinical stage ($ I_1 $), are given by (2.2) and (2.6), respectively. The increase in the number of farms in the $ I_1 $ compartment and its decrease when farms start manifesting the symptoms of infection (transition to $ I_2 $) is represented by (2.3) and (2.7). The Eqs (2.4) and (2.8) give the resulting increase in the number of farms in the $ I_2 $ compartment and the decrease by depopulation explained below.

Depopulation is implemented on a farm by farm basis following the stipulations of the Japanese national legislation ^[18,19]. Since $ I_1 $ farms were asymptomatic of the infection, only the $ I_2 $ farms manifesting the symptoms were subsequently depopulated. The decrease in the number of $ I_2 $ due to this depopulation is represented by (2.4) and (2.8). While, (2.9) and (2.10) reflect the increase in the number of removed farms ($ R $) by depopulation. The depopulation capacity was set as a step function of time that was used to determine the maximum number of farms that can be depopulated each day. When the number of $ I_2 $ farms exceeds the depopulation capacity, swine farms should be depopulated preferentially because FMD in this species was shown to be highly infectious compared to cattle ^[29,32]. The depopulation factor in (2.4), (2.8), (2.9) and (2.10) were not linear functions seen in natural phenomena, but rather represent the artificial control.

2.3.   Model parameters and settings

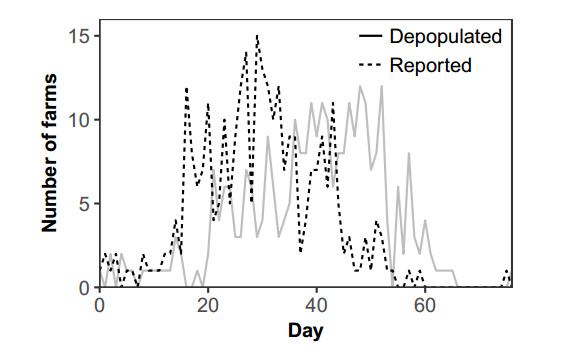
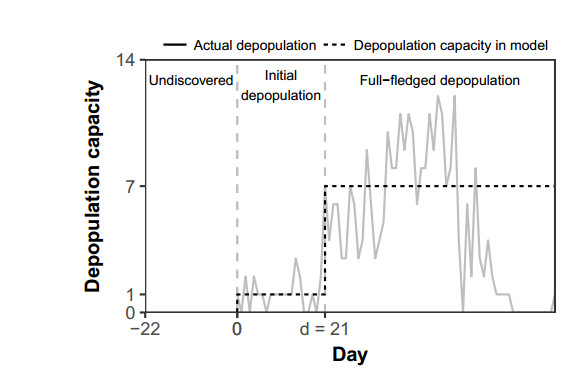
In the task of defining the parameters and settings, it is important that our model closely simulates the actual depopulation pattern during the 2010 FMD outbreak in Miyazaki which was characterized as having two phases (Figure 2) ^[29]. In fact, the number of depopulated farms per day increased only after about 5 days since the number of farms reported to have been infected increased at day 15. The first phase was the 20-day period after detection of the index case. The average depopulation at this phase, which we refer to as the "initial" depopulation phase, was 1.27 farms/day; while the second phase, referred to as the "full-fledged" depopulation phase, was the period characterized by an increased depopulation capacity of 6.89 farms/day.

Figure 2.  Epidemic and depopulation curve in Miyazaki outbreak in 2010. The number of farms reported to have infected animals at each day is shown in dashed line and that of farms where depopulation was completed is shown in solid line.

DownLoad: Full-Size Img PowerPoint

Information pertinent to the 2010 epidemic in Miyazaki obtained from the prefectural office showed that the first reported case of suspect FMD infection was on March 31 in a farm of swine and buffaloes. The first confirmed case, however, was reported 20 days later on April 20 ^[15]. Based on this, we set in our model the first confirmation of FMD symptom, $ t = 0 $ (days), as the April 20 report. It is known that clinical symptoms only appear around 2 days after infection ^[30]. This means that the first reported FMD infection on March 31 was exposed to the virus at least 22 days prior to the first confirmation of FMD symptom. Based on this, we started our simulation 22 days before the first confirmation of FMD symptom at $ t = -22 $. For the simulation, we set the number of cattle and swine farms at 11,030 and 655, based on the reported density of cattle and swine farms in Miyazaki prefecture in 2010 ^[17]. The initial conditions of the model were: $ S_c (t_0) = 11030 $, $ S_s (t_0) = 654 $, $ I_{1s} (t_0) = 1 $, and $ E_{c} (t_0) = I_{1c} (t_0) = I_{2c} (t_0) = E_{s} (t_0) = I_{2s}(t_0) = 0 $ where $ t_0 = -22 $. The depopulation capacity during the initial phase was set at 1 farm/day, and during the full-fledged depopulation phase at 7 farms/day as shown in Figure 3.

Figure 3.  The setting of depopulation capacity in our model. The duration between the first confirmation and the initiation of full-fledged depopulation was parameterized as $ d $. The depopulation capacity in our model is drawn by dashed line, whose value is 0 (undiscovered; $ \text{day} < 0 $), 1 (initial depopulation; $ 0 \le \text{day} < d $) and 7 (full-fledged depopulation; $ \text{day} \geq d $). The solid line means the number of completion of depopulation.

DownLoad: Full-Size Img PowerPoint

We parametrize the time gap between the detection of the first confirmation of FMD symptom and the initiation of a full-fledged depopulation as $ d $. We defined the depopulation factor $ \delta (t) $ as

We set the depopulation capacity at 1 farm/day after first confirmation of FMD symptom and time before $ d $, and at 7 farms/day any time after $ d $. Consistently, we initially set the $ d $ value at 21 days in the model to reflect the actual scenario during the 2010 FMD epidemic in Miyazaki.

The parameters used in our model are shown in Table 1. The durations of infection stages of the FMD virus serotype O for each species were reported by Mardones et al. ^[30]. From this, the transition parameters were determined (e.g. $ \lambda_c = 1/(\text{latent period of cattle}) $, $ \gamma_s = 1/(\text{subclinical period of swine}) $). The parameter $ \beta = \beta_{cc} $ is the transmission rate for indirect transmission among cattle. Although this was unknown, we obtained this value for the present study using maximum likelihood estimation.

Table 1.  Parameters of the model of O serotype of FMD virus spread. $ \lambda_c $, $ \lambda_s $, $ \gamma_c $ and $ \gamma_c $ are according to ^[30]. $ \beta_{cc} $ is estimated by maximum likelihood estimation. $ \beta_{cs} $, $ \beta_{sc} $ and $ \beta_{ss} $ are calculated by $ \beta_{cc} $ and ^[24].

Parameters	Definition	Value
$ \lambda_c $	Transition rate from $ E_c $ to $ I_{1c} $	0.279 [30]
$ \lambda_s $	Transition rate from $ E_s $ to $ I_{1s} $	0.326 [30]
$ \gamma_c $	Transition rate from $ I_{1c} $ to $ I_{2c} $	0.490 [30]
$ \gamma_s $	Transition rate from $ I_{1s} $ to $ I_{2s} $	0.441 [30]
$ \beta_{cc} $	Transmission coefficient from cattle to cattle	$ \beta = 1.057085 \times 10^{-5} $
$ \beta_{cs} $	Transmission coefficient from cattle to swine	$ \beta \times 0.77 $
$ \beta_{sc} $	Transmission coefficient from swine to cattle	$ \beta \times 2.45 $
$ \beta_{ss} $	Transmission coefficient from swine to swine	$ \beta \times 3.01 $

---

 | Show Table

DownLoad: CSV

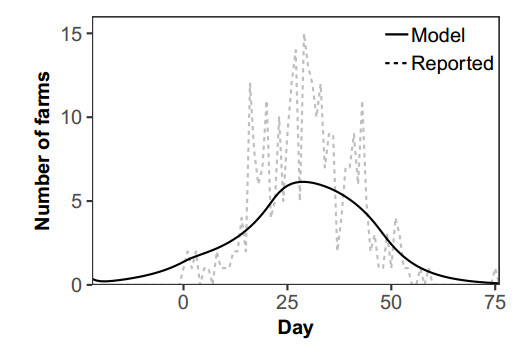
To estimate $ \beta $, we used the data of epicurve from $ t = 0 $ to $ t = 59 $ in Figure 2 and the relative ratio of transmission coefficient among cattle and swine ^[24]. We assumed that the number of newly infected farms followed the Poisson distribution and we defined the following likelihood function.

where $ k_t $ is the actual number of newly infected farms at day $ t $ and $ j_t $ is the number from our model at day $ t $. In the above-mentioned parameters and settings, we considered cumulative numbers of infected farms, which are represented by $ J_c $ and $ J_s $, and $ j_t $ is calculated by solving the ordinary differential equations of $ J_c $ and $ J_s $.

In the result of maximum likelihood estimation using the likelihood function (2.12), we obtain $ \beta = 1.057085 \times 10^{-5} $ and data fitting shown in Figure 4. Because the relative ratio of transmission coefficient among cattle and swine are known ^[24], we could obtain the other transmission coefficients $ \beta_{cs} $, $ \beta_{sc} $ and $ \beta_{ss} $ by multiplying the relative ratio by $ \beta ( = \beta_{cc}) $. We set the transmission force of clinical and subclinical animals equal for simplicity.

Figure 4.  Data fitting of maximum likelihood estimation whose likelihood is defined by (2.12). The solid line is the number of reported infectious farms calculated by our model for the estimate $ \beta = 1.057085 $, which corresponds to (2.16). The dashed line is number of actual reported infectious farms.

DownLoad: Full-Size Img PowerPoint

2.4.   Numerical calculation

We calculated the time evolution of the ordinary differential equations and final sizes for various settings numerically. Evolution of our model is calculated by the fourth-order Runge-Kutta method with time step 0.01. The final size was calculated by evolving our model from $ t = t_0 $ with the above mentioned initial conditions. We stopped the time evolution if the number of newly depopulated farms became less than $ 10^{-6} $. The time when the evolution stopped was referred to as $ T $. We regarded the final size as $ R_s (T) + R_c (T) $.

Simulated delays in the initiation of a full-fledged depopulation ($ d $) ranging from 0–60 days were evaluated using our model. Results from these simulations were summarized as a plot of the estimated the final size of the epidemic (reported as the number of farms) against the change in time $ d $ (reported in terms of days). Then, we analyzed the increasing rate of infected farms per day in relation to the maximum depopulation capacity (7 farms/day) to indicate the stage at which this capacity would be exceeded.

We varied the transmission rate ($ \beta $) by a factor ranging from 0.7 to 1.3 to evaluate the effect of different FMD-control strategies (i.e. vaccination, traffic restriction, and quarantine) on the the final size of the epidemic.

3.   Results

3.1.   Final size estimation

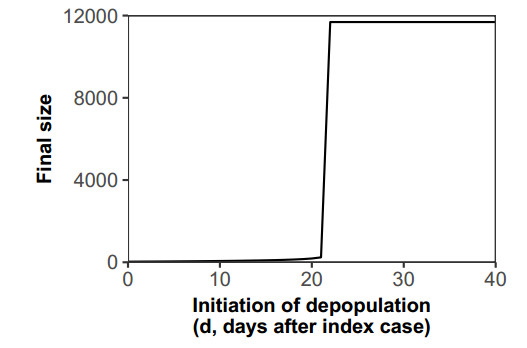
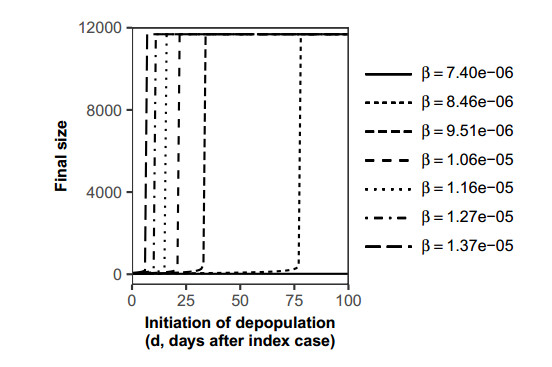
When we varied the commencement of the full-fledged depopulation ($ d = 0 $ to $ 60 $ days), the number of infected farms remained low when full-fledged depopulation was done any time until 21 days after detection of the first confirmation of FMD symptom (Figure 5). Full-fledged depopulation commenced at $ d = 21 $ days would have resulted in the infection of 238 farms. However, at $ d \ge 22 $, the number of infected farms abruptly increased to 11,685 farms—the total number of farms in Miyazaki at the time of the epidemic in 2010. Our model revealed a threshold between 21 and 22 days for the commencement of full-fledged depopulation. After which, the epidemic will reach a catastrophic situation wherein all farms would have been infected.

Figure 5.  The influence of $ d $ (the duration between the initiation of full-fledged depopulation and the first confirmation of FMD infection) on the cumulative number of infected farms. The final size is 238 farms when the full-fledged depopulation commenced at $ d = 21 $ days. The final sizes for $ d \ge 22 $ are 11,685 farms. The threshold phenomenon occurs between $ d = 21 $ and $ d = 22 $.

DownLoad: Full-Size Img PowerPoint

3.2.   Mathematical explanation of threshold phenomenon

To explain the threshold phenomenon shown in Figure 5, we evolved our model without full-fledged depopulation, that is, in the case, the depopulation capacity is 1 farm/day for $ t > 0 $. Then, we compared depopulation capacity and increasing rate of infected farms per day. We defined the increasing rate of infected farms $ r(t) $ (farms/day) as

which is equal to the derivative of the cumulative number of farms of subclinically infectious stage $ I_{1c} + I_{1s} $.

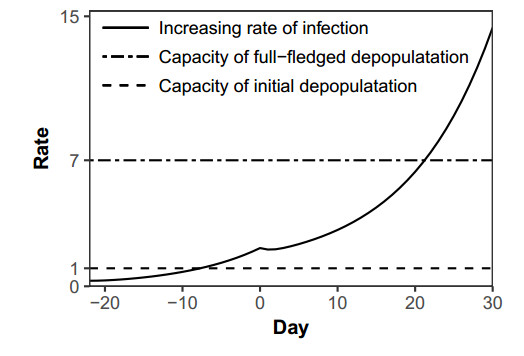
Figure 6 shows the time variation of $ r(t) $. The value of $ r(t) $ exceeded 1, that is the capacity of the initial depopulation, between $ t = -8 $ (14 days after the index case) and $ t = -7 $, which is before the initial depopulation starts at $ t = 0 $. After the beginning of the initial depopulation, $ r(t) $ exceeded 7 between $ t = 21 $ and $ t = 22 $. The timing when $ r(t) $ exceeded 7 equal to the threshold value of $ d $. This indicates that the excess of the increasing rate of infected farms over depopulation capacity causes the infection of all farms.

Figure 6.  Relationship between the increasing rate of infected farms ($ r(t) $) and depopulation capacities ($ \delta (t) $). The increasing rate of infected farms is shown in solid line. The depopulation capacity of initial and full-fledged depopulation for the analyses are shown in dashed line. The simulation of this analysis is calculated in the case that the full-fledged depopulation is not implemented, i.e., $ d = \infty $.

DownLoad: Full-Size Img PowerPoint

3.3.   Sensitivity analysis of $ \beta $

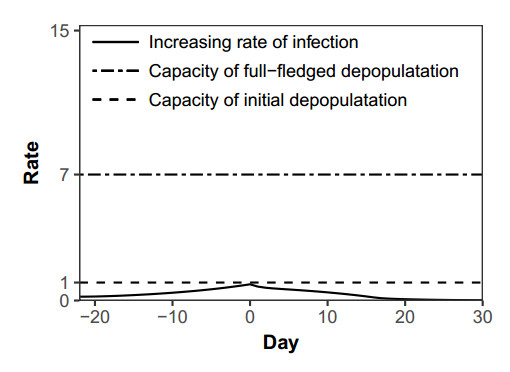
We have also varied the transmission rate; Figure 7 shows the result of final size estimation under different $ \beta $ values by a factor of 0.7 to 1.3 of its initial value. The dotted lines show resulting numbers of infected farms with different beta values relative to the delay in the initiation of a full-fledged depopulation ($ d $), and the threshold phenomena were evidently illustrated (Figure 7). Increasing the $ \beta $ value makes the threshold value for $ d $ earlier. When $ \beta $ reached a level 1.3 times higher than the initial value, the threshold for $ d $ occurred 6 days after the first confirmation of FMD symptom. But, at a lower $ \beta $ value of 0.7 times the initial estimate, there was no abrupt increase in the number of infected farms, in which case the increasing rate, $ r(t) $, had never exceeded the initial depopulation capacity (Figure 8).

Figure 7.  Final size estimation under different $ \beta $ values. The same analyses as Figure 5 were done under the different $ \beta $ values from 0.7 times the estimated $ \beta $ value to 1.3 times the estimated $ \beta $ value. The threshold phenomena occur for $ \beta $ values except for $ \beta = 7.4 \times 10^{-6} $.

DownLoad: Full-Size Img PowerPoint

Figure 8.  Relationship between the increasing rate of infected farms and initial depopulation capacity for $ \beta = 7.4 \times 10^{-6} $. The increasing rate of infected farms is shown in solid line. The depopulation capacities of initial and full-fledged depopulation are shown in dashed lines. In this case, because the increasing rate of infected farms is low and does not exceed the capacity of the initial depopulation, the threshold phenomenon does not occur.

DownLoad: Full-Size Img PowerPoint

4.   Discussion

The present study is aimed at revealing the qualitative features of outbreaks controlled by depopulation. Here, the simple deterministic model, the SEIIR model, was built to make a distinction between the asymptomatic and symptomatic stages of FMD infection. We simulated the two-phased depopulation pattern (i.e., initial and full-fledged depopulation phases) observed in the 2010 FMD epidemic in Miyazaki, Japan. Our numerical investigation clearly connected delays in the initiation of depopulation to the epidemic final size, and revealed the novel threshold phenomena, that is, the existence of a critical timing for the initiation of full-fledged depopulation.

The threshold phenomena, represented as the drastic increase of the final size, observed at 22 days occurred when the increasing rate of infected farms per day defined by (3.1) exceeded the depopulation capacity. This relationship between the depopulation capacity and the increasing rate of infection plays the most important role in the threshold phenomena and it determines the critical timing. Our numerical investigation indicates that decreasing the depopulation capacity would shift the critical timing earlier, while increasing the capacity would postpone it.

Decreasing the transmission coefficient of the disease may be achieved in practice by the implementation of other control strategies. We conducted simulations by varying the values for the disease transmission coefficient ($ \beta $) at $ \pm 30 $% the baseline value ($ 1.06 \times 10^{-5} $). It was shown that decreasing and increasing the transmission coefficient of the disease extended and shortened the critical period, respectively. Further, we found that by reducing the inter-farm transmission coefficient ($ \beta $) by 30%, infected farms would have been eliminated at the initial depopulation phase. Besides, if the initiation day of depopulation was fixed at 22 days after the first confirmed case and the range of $ \beta $ was set between $ 7.40 \times 10^{-6} $ and $ 8.46 \times 10^{-6} $, the epidemic final size would have been drastically reduced, which can be regarded as another threshold phenomenon.

The SEIIR model we have developed in this study has limitations. We did not factor in the model the stochasticity of infection, the geographic distribution or network structure of farms, the fluctuations of depopulation capacity, detailed estimation of transmission rate, nor any change in the FMD control strategy other than depopulation, even though the indirect transmission rate must have been reduced by several restrictions after the confirmation of FMD epidemic and other events could have likely influenced the model. Although it is known that clinical animals are more infectious ^[33], we assume that $ I_1 $ and $ I_2 $ have same transmission coefficients ($ \beta $) for simplicity and due to the difficulty of the parameter estimation. These limitations result in the imperfect prediction of the final size of an epidemic which was predicted as 237 farms but actually 292 farms. In fact, our model predicted the critical timing of the initiation of the full-fledged depopulation as 22 days after the index case, a discrepancy of 1 day from the actual (i.e., 21 days), which may implausible. Further, we only used the epidemic data from Miyazaki and the two-phase depopulation pattern unique to Miyazaki case. This information was sufficient for detecting the existence of a threshold in FMD treatment but not for predicting the critical timing in the actual FMD epidemic. Further development of this FMD model should incorporate factors like spatial features, to accurately predict the critical timing during the actual FMD epidemic.

Our formulation can be useful for models of other animal diseases concerning depopulation, although our model may have insufficient points as FMD modelling. Because the model is simple and the mechanism of the threshold phenomena is described by the relationship between the depopulation capacity and the increasing rate of infection, the same mechanism is expected to hold even if we consider models whose compartments are different, for example, SIR and SEIR.

5.   Conclusion

Using the SEIIR model we have developed, we hereby report the existence of the critical timing to initiate depopulation for FMD control—the threshold phenomenon. Surpassing the timing could lead to a catastrophic disease incursion in all farms in the area and even a possible spread outwards. Eventually, the epidemic would become an endemic. The existence of the critical timing appears to be a universal feature, at least in and SEIR-based model, and the timing can be influenced by the transmission rate and depopulation capacity. Further work has to be done on this phenomenon for a precise prediction of the critical timing for effective FMD control.

6.   Declarations

6.1.   Ethics approval and consent to participate

The analyzed data in this study is publicly available without identifying information. For this type of study, ethical approval is not required.

6.2.   Consent for publication

Not applicable.

6.3.   Availability of data and material

Data and simulation codes will be available from the corresponding author upon request.

6.4.   Authors' contributions

All the authors engaged in this study as group work in Summer boot camp of infectious disease modeling, 2017 ^*. Important data were gathered by JM, YN, TO, TS, and CZ. Construction of the mathematical model and simulation with the model were carried out equally by KI, FO, and TY. The manuscript was primarily written by KI with contributions from JM, YN, TO, and TY. All authors read and approved the manuscript.

^* Summer boot camp of infectious disease, 2017 was held at The Institute of Statistical Mathematics, Tachikawa, Tokyo, Japan; URL: https://sites.google.com/site/modelinfection/home/shortcourse4

Acknowledgements

We express sincere gratitude to all the staffs involved in Summer boot camp of infectious disease modeling, 2017. This work was partially supported by JSPS KAKENHI Grant Number JP19K19429.

Conflict of interest

The authors declare that they have no competing interests.