On the particle approximation to stationary solutions of the Boltzmann equation

1.   Introduction

As it is well known, the Boltzmann equation is a useful tool to understand the behaviour of a rarefied gas. From a mathematical side the study of the Boltzmann equation is mostly devoted to the initial value problem (see e.g., ^[8,27]). On the other hand in most of the physical applications the solutions of the Boltzmann equation are seen in a stationary non-equilibrium regime. Indeed after a short time dependent transient, the system has the tendency to stabilize in a non trivial stationary state which should describe transport phenomena. Here we are dealing with stationary solutions in presence of diffuse boundary conditions, namely the gas is thought to be in a vessel in contact with reservoirs localized at the boundary, possibly with a non constant temperature. For the existence problem of stationary solutions we address the reader to the recent reference ^[11] and references quoted therein.

Another interesting and largely open problem is the one of the validity of the Boltzmann equation. This means that we try to justify the use of the Boltzmann equation from mechanical particle systems by means of a suitable scaling limit, the so called Boltzmann-Grad (B-G) limit. Up to now we have only a short time result for general initial conditions ^[21] and a global result working only in a dispersive situation (hence not interesting from a thermodynamical view point) ^[15,16]. For recent progresses in the topic see e.g., ^{[3,4,5,12,23,24]}.

If one is interested in the validation problem for the stationary Boltzmann equation the validity for short time is useless. In addition even having a global result, it is probably true that the limit $t \to \infty$ and the B-G limit are not commutable so that we are far, for the moment, to be able in proving the validity of the stationary solutions which are known to exist. In this situation it may be interesting the study of simplified models to understand at least part of this difficult problem.

Some years ago in ^[9] a stochastic particle system in a container with diffusive boundary with varying temperature was proven to approximate the stationary solution of the corresponding Boltzmann equation (actually the Povzner equation which is a regularization of the true Boltzmann equation). The proof works only under severe assumptions on the Maxwellian at the boundary, namely it was assumed an unphysical cutoff on small and large velocities which we are going to remove in the present paper. The price we pay is the assumption of the presence of a non vanishing constant external field. In some sense we are approaching the Benard problem, even though we are working in a perturbative regime close to the free flow, so that quite far from the interesting features of the Benard effect.

We discuss our result more precisely. We consider, as in ^[9], a gas modelled by a stochastic particle system which is the non-homogeneous extension of the well known Kac's model (see ^[17,18]). The gas is localized between two vertical planes at different temperatures. We assume the existence of a non vanishing horizontal constant external field ${\bf F}$ and that the intensity of the collisions among the particles is sufficiently small. Then we have a unique solution of the stationary problem both for the particle system and the corresponding regularized Boltzmann equation. We prove that the one-particle distribution function of the stationary measure of the particle system converge to the solution of the Boltzmann equation, under a sort of local mean-field limit.

It is worth to say that our analysis is not merely academic. Indeed the particle models we are considering is the basis for the so called direct Montecarlo simulation method ^[2,8], which is widely used for the numerical simulations of real gases. Thus our result can be seen as a justification of the use of such algorithm assuming "true" the Boltzmann equation which however should be still derived from mechanical particle systems. We follow essentially the techniques of ^[9] and, as already mentioned, the presence of the external field is essential to remove the cutoff on small velocities. Indeed such a cutoff was assumed in ^[9] to avoid the particle to spend an unbounded amount of time to hit the boundary to thermalize, a feature which is the key ingredient to reach the stationary regime. Now we overcome this problem by the presence of an external field.

The central part of the main theorem in Section 4 follows essentially ^[9] but here we present a simplified version of the proof.

Section 3 is devoted to the study of the approach to the stationary regime for the Knudsen flow in presence of an external field.

2.   Notation and results

Consider

a parallelepiped in ${\mathbb R}^3$. Let $p = p(\bf x, \bf v; t)$ where ${\bf x} = (x, y, z) \in {\Lambda}$, ${\bf v} = (v_x, v_y, v_z) \in {\mathbb R}^3$ and $t \in {\mathbb R}^+$ be a positive function solving the following Boltzmann initial-boundary value problem in presence of a constant external field ${\bf F} = (F, 0, 0), F > 0$:

with initial condition

and periodic-diffusive boundary conditions

where:

and $C_{\pm}$ are constants chosen in such a way that

Moreover

are the incoming fluxes. Finally

is a regularized version of the Boltzmann collision operator where

is the usual elastic collision rule arising from the conservation of energy, momentum and angular momentum.

Here $\omega$ is the unit vector in the direction of the transferred momentum.

Furthermore

and we assume the collision kernel $B\geq 0$ to be bounded

The function $h_ \gamma$ is a symmetric regularizing spatial mollifier, bounded, vanishing for $|{\bf x}-{\bf y}| > \gamma$ and such that $\int h_ \gamma ({\bf x}, {\bf y}) d{\bf y} = 1$. Finally $\lambda$ is a positive constant modulating the intensity of the interaction.

The operator $Q$ differs from the usual Boltzmann collision operator for hard spheres because of the presence of the smearing function $h_ \gamma$ and the cutoff on large relative velocities. However this does not affect the usual conservation laws (mass, momentum and energy). Moreover, due to the normalization (2.5) which guarantees the mass conservation at the boundary, we have the mass conservation

From now on we shall assume that $m(t) = 1$.

The system we are dealing with describes a rarefied gas between two vertical plates $B_+$ and $B_-$ localized at $x = 0$ and $x = L$ i.e., $B_+ = \{{\bf x} = (x, y, z) \in \partial {\Lambda} | x = L\}$ and $B_- = \{{\bf x} = (x, y, z) \in \partial {\Lambda} | x = 0\}$. Such walls are at a thermal equilibrium with two different inverse temperatures $\beta_+$ and $\beta_-$ respectively. We assume periodicity in the $y$ and $z$ directions. When a particle hits one of the two walls it is instantaneously rejected with a probability distribution corresponding to its Maxwellian.

As already remarked the collision operator has been regularized so that it is Lipchitz continuous in $L^1 ({\bf x}, {\bf v})$. Therefore a global solution can be easily constructed by virtue of the positivity and mass conservation. Such a solution can be conveniently represented in a mild form :

where $S(t)$ is the Knudsen semigroup, that is the solution to the initial-boundary value problem

with same initial and boundary values as in Eqs. (2.2) and (2.3).

In this paper we are interested in the stationary equation

with boundary conditions (2.3) and normalization

To start with we note that a stationary solution $\bar g$ for the Knudsen flow i.e.,

can be explicitly constructed by means of the characteristics. Indeed denoting by ${\bf x}^F ({\bf x, } {\bf v}; t), {\bf v}^F ({\bf x, } {\bf v}; t)$ the solution of

with initial condition $({\bf x}, {\bf v})$, let $({\bf x}^F(-t), {\bf v}^F(-t)) = ({\bf x}^F({\bf x}, {\bf v}; -t), {\bf v}^F({\bf x}, {\bf v}; -t))$ be the backward characteristics leaving $({\bf x}, {\bf v})$ at time zero and $\tau$

the first impact time with the boundary, then

and

Note that, by symmetry, $\bar g({\bf x}, {\bf v}) = \bar g(x, {\bf v})$ and the flux $J$ is constant. Such a constant can be recovered by the normalization condition

We now establish a preliminary result which will be proven in the next section.

Theorem 2.1

For any $\eta > 0$ there exists $T(\eta)$ such that for $t \geq T(\eta)$ and any probability density $f$

Moreover if $\phi \in L^1 ({\bf x}, {\bf v})$ and $\int \phi d{\bf x} d{\bf v} = 0$ then

As we shall discuss in the next section the presence of a non-vanishing external field ${\bf F}$ is essential to obtain the independence of $T(\eta)$ from $f$ in (2.17) and hence (2.18) holds. This plays a fundamental role in establishing our main result as we shall discuss in the next section.

Theorem 2.2

If $\lambda$ is sufficiently small there exists a unique stationary solution $g = g({\bf x}, {\bf v})$ of the problem (2.10)

for all $t\geq 0$. Moreover if $p(t)$ solves problem (2.10) with $p_0$ as initial datum, then

where $C_1$ is a positive constant

The proof of Theorem 2.2 is standard and can be recovered in ^[9].

Next we introduce the $N$-particle process which gives the approximation, in the limit $N \to \infty$, to problem (2.9) or (2.10).

Let $Z_N = (\zeta_1, ..., \zeta_N), \, \, \zeta_i = ({\bf x}_i, {\bf v}_i), \, i = 1, ..., N,$ and set

We define the generator of the $N$-particle process, for any bounded continuous function $\Phi$ as

where

with the same boundary conditions (2.3) as for the Knudsen flow. Actually the semigroup generated by (2.21) is

where $S_{[i]}$ is the Knudsen semigroup associated to particle $i$. Note that the family $\{S_{[i]}(t) \}$ is commuting. The associated stochastic process consists in $N$ independent particles moving freely. The outgoing velocity of each particle after a collision with the boundary is distributed according to the probability density $|v_x| M_{\pm}({\bf v})$.

Moreover

where

The process described by $G_N$ consists of free motion (including the periodic-diffusive boundary conditions) of the $N$-particle system and random collisions. These collisions take place at random times, with random impact parameter $\omega$. The particles of the pair involved in the collision have mutual distance less than $\eta$, and their outgoing velocities after the interaction follow the deterministic elastic collision. This model, sometimes called soft balls model is a non-homogeneous variant of the well known Kac's model (see ^[17,18]). It was introduced by Cercignani in ^[10] and investigated from a quantitative point of view in ^[20,9]. The underlying idea is the same of the so-called direct simulation method ^[2], widely used in the applications (see ^[25,26]).

If the system is initially distributed according to a probability density $f_N(Z_N)$, its time evolution is given by $f_ N (t) = \exp (G_N t) f_N(0)$. In other words,

with the associated boundary conditions.

Next we consider the stationary version of (2.23), namely

with the same boundary conditions. We have

Theorem 2.3

For all $N > 0$ there exists a unique probability density $\tilde f_N = \tilde f_N(Z_N)$ which is invariant under the $N$-particle process.

Theorem 2.3 can be proven along the same arguments developed in ^[13] in a Hamiltonian context.

The main goal of this paper is to compare the stationary distribution $\tilde f_N$ with the one-particle stationary distribution $g$ constructed in Theorem 2.2.

Coming back to Eq. (2.23) we introduce the $k$-particle distribution functions of $f_k^ N (Z_N, t)$, marginals of $f_N$, for which we obtain the well-known BBGKY hierarchy of equations

with periodic boundary condition in the vertical directions and

if ${\bf x}_i = (L, y_i, z_i), ({\bf v} _i)_x > 0$ or ${\bf x}_i = (0, y_i z_i), (v_i)_x < 0$ respectively, $Z_k(i)$ is the configuration $Z_k$ deprived by $\zeta_i$,

and

Finally

The formal limit, for $N\to \infty$ of the hierarchy (2.25) is

which is satisfied by $f_k = p^{\otimes k}$ being $p$ the solution to (2.9). Therefore the term which is responsible of the correlations is $\frac {\lambda}N G^{jump} f^N_k (Z_k, t)$ which however is expected to be unimportant in the limit.

For the time depending problem the convergence for $N \to \infty$ can be proven. Before stating this well known result we introduce a useful notation. We denote by $P (t)$ the solution operator for the hierarchy (2.29), namely $(P(t) f_0)_k = f_k(t)$ where $f_0 = \{ (f_0)_k \} = \{p_0^{\otimes k} \}$ is the infinite sequence of the initial marginals. Analogously we denote by $(P^N(t) f_0)_k = f^N_k(t)$ the solution operator of the (finite) hierarchy for the particle system (2.25). Then

Theorem 2.4

Setting $a = 2 \sup_{z, z'} \int d\omega q(z, z', \omega)$ then for $\lambda t < \frac 1{8a}$

for some geometrical constant $c_1 = c_1(a)$.

For the proof see ^[9]. Indeed the presence of an external field does not change the proof that is based on the fact that the semigroup generated by $G^{free} + \frac {\lambda}N G_k^{jump}$ is isometric in $L^1$.

Note that the above result holds for a short time interval only, however since the time interval of validity does not depend on the initial condition, one can iterate the above result to reach arbitrary times. See ^[9] and references therein.

Coming back to the stationary problem for the particle system, the marginals $\{ \tilde f_k \}$ of the stationary measure do satisfy the following hierarchy

We now formulate the main result of the present paper

Theorem 2.5

There exists $\lambda_0 > 0$ such that for any $\lambda < \lambda_0$ and any integer $k$:

where $g_k = g^{\otimes k}$, being $g$ the solution of (2.19) and $c_2$ some positive computable constant.

3.   On the Knudsen flow

In this section we prove Theorem 2.1 and develop some considerations on the Knudsen flow (2.11). We first remark that the solution of (2.11) with initial datum $p_0$ can be given almost explicitly in terms of a series expansion. Indeed by (2.3) we have

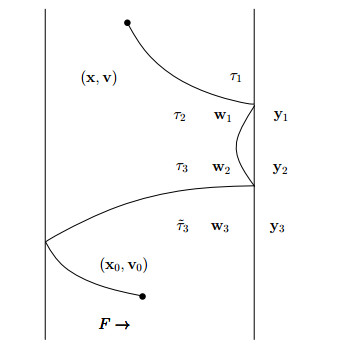
We explain the above formula. Given ${\bf x}^F(-s), {\bf v}^F(-s), s\in (0, t)$ the backward flow (2.14) starting at ${\bf x}, {\bf v}$ at time zero, let $\tau_1$ be the first hitting time in the time interval $(0, t)$ (if any). Let ${\bf y}_1 = {\bf x}^F(-\tau_1)$ and ${\bf w}^0 = {\bf v}^F(-\tau_1)$ be the corresponding trace on the boundary and the associate velocity respectively. Then we select randomly a velocity ${\bf w}^1$ according to $M_{\sigma_1} ({\bf w}^1)$, $\sigma_1 = \pm$ if ${\bf y}^1 \in S_{\pm}$ respectively and consider ${\bf x}^F(-t), {\bf v}^F(-t)$ the backward flow (2.14) starting at ${\bf y}, {\bf w}_1$ at time $\tau_1$ and so on. Therefore we have the sequences $\{ {\bf y}_j, {\bf w}_j, \tau_j, \sigma_j\}; j = 1, 2 \cdots$ of traces, incoming velocities, hitting times and sides of the boundary. Moreover $\chi_n$ is the indicator of the event

and $\tilde \tau_n = t- \sum_{k = 1}^n \tau_k$ is the residual time after the last ($n^{-th}$) collision with the boundary. See the figures below where we denote by $(x_0, v_0) = ({\bf y}^F_n (-\tilde \tau_n), {\bf w}^F_n (-\tilde \tau_n))$ the initial point.

Note that $\{ {\bf y}_j, {\bf w}_j, \tau_j, \sigma_j\}$ are random but ${\bf y}_1$, $\tau_1$ and $\sigma_1$ are fixed according to ${\bf x}, {\bf v}$.

Denoting by $t_m$ the maximal time for which the particle can pass from a side of the boundary to the other, by simple kinematic considerations we arrive to the conclusion that

then we fix $t = 3t_m$. Next we introduce the transition probability $P_t ({\bf x}, {\bf v} | {\bf x}_0, {\bf v}_0)$ of going from ${\bf x}_0, {\bf v}_0$ to ${\bf x}, {\bf v}$ in the time $t$. It is defined as

where $\delta_{{\bf x}_0, {\bf v}_0 }$ is the $\delta$-function centered in $({\bf x}_0, {\bf v}_0)$. By the same arguments in ^[9], Theorem 2.1 is a consequence of the following

Lemma

For $t = 3t_m$, there exists $\lambda > 0$ such that

Note that the statement of the above Lemma is not true whenever $F = 0$. Indeed a particle with an arbitrary small velocity needs an unbounded amount of time to reach the boundary to thermalize. Therefore $P_t ({\bf x}, {\bf v} | {\bf x}_0, {\bf v}_0)$ is not even absolutely continuous. The presence of the external field forces the particle to thermalize in a finite maximal time and this is enough to make working the arguments in ^[9]. This is a coupling argument, namely we consider two copies of the same process yielding the Knudsen flow, with initial states $f$ and $h$, both probability densities. Then as a consequence of the above Lemma, we have that

for two suitable constants $\alpha_1$ and $\alpha_2$. As a consequence we get both the exponential convergence to the equilibrium $\bar g$, as well as (2.17). (2.18) follows as a corollary.

For $F = 0$ we do not know how to proceed. We shall comment on this point later on.

Proof

We assume

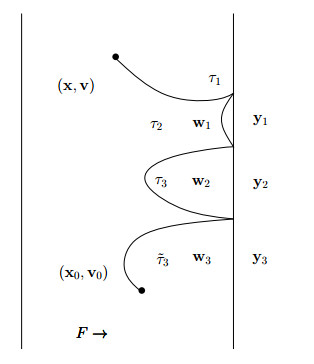
and, to evaluate $P_t ({\bf x}, {\bf v} | {\bf x}_0, {\bf v}_0)$ we consider only the contribution with $n = 3$. Then we have only two possible situations depicted in the following figures, namely either the first collision with the boundary of ${\bf x}^F(s), {\bf v}^F(s)$ for positive $s$ and initial state ${\bf x}_0, {\bf v}_0$ happens with $B_+$ or with $B_-$. This feature depends only on $({\bf x}_0, {\bf v}_0)$.

Note that the sequence of collisions left-right-left yields a positive final velocity so that it is excluded.

Clearly fixed $({\bf x}_0, {\bf v}_0)$ and $({\bf x}, {\bf v})$ there exists a trajectory connecting the two points in the time $t$. Indeed $\tau_1$ and $\tau_4$ are not random, as well as ${\bf y}_1$ ${\bf w}^0$ and ${\bf y}_3$ ${\bf w}^3$, and $t = 3t_m > \tau_1+\tau_4$.

Let us start to analyze the first possibility. We have

where $\chi_2 = \chi_2({\bf w}^{1}, {\bf w}^{2})$ is the indicator of the event : ${\bf y}_1$ and ${\bf y}_3$ are connected via two jumps in a time interval $t-\tau_1-\tau_4$. Setting ${\bf w}^2 = ((w^2)_x, {\bf w}^{\perp})$, we change variables,

and, computing the Jacobian of this transformation, setting ${\bf x}_0 = ((x_0)_x, {\bf x}_0^{\perp})$, ${\bf v}_0 = ((v_0)_x, {\bf v}_0^{\perp})$, we arrive to

where the set $B$ is formed by the pair ${\bf y_3}, \tilde \tau_3$ for which $\chi_2 = 1$. This yields an upper bound for ${\bf w}^{2}$ and a lower bound for $M_+ ({\bf w}^2)$. Moreover $C(F)$ denotes a positive constant, independent of ${\bf x}_0, {\bf v}_0$ and vanishing with $F$.

A similar estimate can be shown for the second possibility (see Figure 2).

Therefore integrating with respect to ${\bf x}$ and ${\bf v}$ we conclude.

The Lemma allows to prove (see ^[9]) the exponential convergence. For $F = 0$ $\lambda = 0$ and we do not have exponential convergence as it is shown in ^[1]. Actually we do not need, in principle, an exponential convergence to apply our method but we need that the convergence rate is independent of the initial datum and this is not the case when $F = 0$. For instance applying the methods of ^[1] where the approach to equilibrium is investigated in the particular case of a spherical domain with constant temperature in the boundary, we find (for special symmetric data) a rate of the form $\frac C t$ but, unfortunately, the constant $C$ depends on $\| f_0 \|_{L^\infty}$ and this estimate is useless in the present context. For more recent references on the problem see ^[14,19].

4.   Proof

Now we prove Theorem 2.5. We follow ^[9] however the present proof is slightly easier because it makes use of a simplifying cancellation not used in ^[9]. Moreover we do not try to optimize the constants and this makes the proof more transparent. As in ^[9] such a proof is based on a fundamental quantity, namely the kinetic error ${v_I}$, $I \subset {\mathbb N}$ which we are going to define.

Given two family of of symmetric functions $\Phi = \{ \Phi_I \}$ and $\Psi = \{ \Psi_I \}$ where $I \subset {\mathbb N}$ $\Phi_I$ and $\Psi_I$ are functions acting on $({\Lambda} \times {\mathbb R}^3)^{|I|}$, being $|I|$ the cardinality of $I$, we define the $*$-product as

where $Z_I = \{ \zeta_i \}_{i \in I}$,

The kinetic error $v_I$ is defined by

where we use the convention $(g)_{\emptyset} = (\tilde f^N) _{\emptyset} = (v)_{\emptyset} = 1$ and $\tilde f^N_k = 0$ for $k > N$.

The kinetic errors (also called $v$- functions in previous literature ^[6] and ^[7]) can be introduced also in the context of mechanical system (see ^[24]). For a recent result concerning a wide class of models including the one of the present paper, see ^[22].

Clearly

Then

where,

The first step is due to the time invariance of $\tilde f^N$.

Note that, setting $|I| = k > 0$, by Theorem 2.4

As regards the first term in (4.1) it is

by using the factorizing property of $P(t)$ and the invariance of $g$. The last step is due to the identity

In conclusion

For a given sequence $\phi = \{ \phi_j \}_{j = 1}^\infty$ we introduce, for $\alpha > 0$, the norm

Our goal is to show that

for suitable values of $t$ and $\lambda$. This concludes the proof because we fix $\alpha$ such that $e^ \alpha = 9$ so that, by Theorem 2.4

and hence by (4.3) and the above estimate we conclude that,

therefore Theorem 2.5 follows easily.

We evaluate $P (t) v^N$ in terms of a series expansion which is nothing else than the iteration of (2.29) in mild form (remind (2.27) and (2.8))

More precisely we can write the following formal series expansion

where

In the recent literature (see e.g., ^[24]) an expansion such that is called tree expansion because the sequence $i_1, i_2 \dots i_n = 1$ has a useful graphical representation in terms of a tree, more precisely a $(k-n)$ tree indicating that we have $k$ roots, namely the starting particles, and $n$ creations of new particles. Clearly a $(k-n)$ tree is identified with $k$ $(1-n_i)$ trees, where $i = 1 \cdots k$ and $\sum_i n_i = n$.

A more convenient way to write (4.6) is to use the factorizing property of $P(t)$, namely:

with the convention that $a_{1, n_i} (t)$ acts on the $i$-th variable $\zeta_i$ of $v^N_k$. Clearly the $a_{1, n_i} (t)$'s commute and if $v^N_{k+\sum_i n_i}$ would factorize also $(P(t) v^N)_k$ factorizes as well. Obviously this is not the case.

The difference between (4.6) and (4.8) is that in the latter we sum over all the trees associated to each particles while in the former we equivalently sum over all the $k-n$ trees.

The idea of the proof is the following. In the sequence $n_1 \cdots n_k$ we select the indices $i$ for which $n_i > 0$. In this case we gain at least $\lambda$ which is small. Actually we are working in a perturbative regime close to the free motion. On the other hand when $n_i = 0$ we gain $\eta$ by (2.18). Therefore we set $I = \{1, 2 \cdots k \}$ and denote by $L \subset I$ the set of indices $i$ for which $n_i = 0$. Denoting also by $S_L(t) = \prod_{[i]} S_{[i]}(t)$ the operator acting on functions of $|L|$ variables, where $S_{[i]}(t)$ is the Knudsen flow associated to the variable $i$, as matter of facts

We observe preliminary that $\int d \zeta _i v^N (\zeta_1 \cdots \zeta_j) = 0$ as follows from the definition, therefore

provided that $t \geq T(\eta)$.

To estimate the contribution due to $a(1, n_i)$ we realize that

and hence

Next we observe that

thus

Now we choose the parameters. First we fix $\eta = \frac 14$ and consequently $t = T(\eta)$. Finally $\lambda$ will be chosen so small that

and, by (4.12),

This implies (4.4) and concludes the proof of Theorem 2.5.

Acknowledgments

The author thanks R. Esposito and S. Simonella for fruitful conversations.

Conflict of interest

The author declares no conflict of interest.