Analyzing the control of dengue by releasing <em>Wolbachia</em>-infected male mosquitoes through a delay differential equation model

Bo Zheng; Lihong Chen; Qiwen Sun; Bo Zheng; Lihong Chen; Qiwen Sun

doi:10.3934/mbe.2019275

Mathematical Biosciences and Engineering

2019, Volume 16, Issue 5: 5531-5550. doi: 10.3934/mbe.2019275

Previous Article Next Article

Research article Special Issues

Analyzing the control of dengue by releasing Wolbachia-infected male mosquitoes through a delay differential equation model

1.
College of Mathematics and Information Sciences, Guangzhou University, Guangzhou, 510006, China
2.
Center for Applied Mathematics, Guangzhou University, Guangzhou, 510006, China

Received: 22 April 2019 Accepted: 12 June 2019 Published: 14 June 2019

To date, an innovative strategy to control dengue is to release Wolbachia-infected male mosquitoes into wild areas to sterilize wild female mosquito vectors by cytoplasmic incompatibility (CI). To investigate the efficacy of Wolbachia in blocking dengue virus transmission, we develop a deterministic mathematical model of human and mosquito populations in which one dengue serotype circulates. The delay differential equation model captures the respective extrinsic and intrinsic incubation periods (EIP and IIP) in the mosquito and human, as well as the maturation delay between mating and emergence of adult mosquitoes, which have received relatively little attention. We analyze the existence and stability of disease-free equilibria, and obtain a sufficient and necessary condition on the existence of the disease-endemic equilibrium. We also determine two threshold values of the release ratio

$\theta$ , denoted by

$\theta_1^*$ and

$\theta_2^*$ with

$\theta_1^*>\theta_2^*$ . When

$\theta>\theta_1^*$ , the mosquito population will be eradicated eventually. When

$\theta_2^* < \theta < \theta_1^*$ , a complete mosquito eradication becomes impossible, but virus eradication is ensured at the meantime. When

$\theta < \theta_2^*$ , the disease-endemic equilibrium emerges that allows dengue virus to circulate between humans and mosquitoes. We carry out sensitivity analysis of the threshold values in terms of the model parameters, and simulate several possible control strategies with different release ratios, which confirm the public awareness that reducing mosquito bites and killing adult mosquitoes are the most effective strategy to control the epidemic. Our model provides new insights on the effectiveness of Wolbachia in reducing dengue at a population level.

Keywords:

Citation: Bo Zheng, Lihong Chen, Qiwen Sun. Analyzing the control of dengue by releasing Wolbachia-infected male mosquitoes through a delay differential equation model[J]. Mathematical Biosciences and Engineering, 2019, 16(5): 5531-5550. doi: 10.3934/mbe.2019275

Related Papers:

[1]	K. M. S. Y. Konara, M. L. Kolhe, Arvind Sharma . Power dispatching techniques as a finite state machine for a standalone photovoltaic system with a hybrid energy storage. AIMS Energy, 2020, 8(2): 214-230. doi: 10.3934/energy.2020.2.214
[2]	Nagaraj C, K Manjunatha Sharma . Fuzzy PI controller for bidirectional power flow applications with harmonic current mitigation under unbalanced scenario. AIMS Energy, 2018, 6(5): 695-709. doi: 10.3934/energy.2018.5.695
[3]	Hari Charan Nannam, Atanu Banerjee . A novel control technique for a single-phase grid-tied inverter to extract peak power from PV-Based home energy systems. AIMS Energy, 2021, 9(3): 414-445. doi: 10.3934/energy.2021021
[4]	Aaron St. Leger . Demand response impacts on off-grid hybrid photovoltaic-diesel generator microgrids. AIMS Energy, 2015, 3(3): 360-376. doi: 10.3934/energy.2015.3.360
[5]	Mulualem T. Yeshalem, Baseem Khan . Design of an off-grid hybrid PV/wind power system for remote mobile base station: A case study. AIMS Energy, 2017, 5(1): 96-112. doi: 10.3934/energy.2017.1.96
[6]	Stefano Farnesi, Mario Marchesoni, Massimiliano Passalacqua, Luis Vaccaro . Soft-switching cells for Modular Multilevel Converters for efficient grid integration of renewable sources. AIMS Energy, 2019, 7(3): 246-263. doi: 10.3934/energy.2019.3.246
[7]	Rashid Al Badwawi, Mohammad Abusara, Tapas Mallick . Speed control of synchronous machine by changing duty cycle of DC/DC buck converter. AIMS Energy, 2015, 3(4): 728-739. doi: 10.3934/energy.2015.4.728
[8]	Yassine Charabi, Sabah Abdul-Wahab . The optimal sizing and performance assessment of a hybrid renewable energy system for a mini-gird in an exclave territory. AIMS Energy, 2020, 8(4): 669-685. doi: 10.3934/energy.2020.4.669
[9]	Lasanthika Dissawa, Nirmana Perera, Kapila Bandara, Prabath Binduhewa, Janaka Ekanayake . Thirteen-level inverter for photovoltaic applications. AIMS Energy, 2016, 4(2): 397-413. doi: 10.3934/energy.2016.2.397
[10]	Mohammad Aman YAQOBI, Hidehito Matayoshi, Natarajan Prabaharan, Hiroshi Takahashi, Ashraf M. Hemeida, Senjyu Tomonobu . Interconnected standalone DC microgrid fault protection based on Self-Adaptive DC fault current limiter with hybrid solid state circuit breaker. AIMS Energy, 2021, 9(5): 991-1008. doi: 10.3934/energy.2021045

Abstract

$\theta$ , denoted by

$\theta_1^*$ and

$\theta_2^*$ with

$\theta_1^*>\theta_2^*$ . When

$\theta>\theta_1^*$ , the mosquito population will be eradicated eventually. When

$\theta_2^* < \theta < \theta_1^*$ , a complete mosquito eradication becomes impossible, but virus eradication is ensured at the meantime. When

1. Introduction

Current worldwide trends in the field of electric power engineering are the reduction of carbon emissions and the decentralization of power generation, with the aim of improving environmental friendliness, reliability, and the quality of electricity supply to consumers ^[1]. One of the primary technologies that reflect and implement these trends is distributed generation, which refers to a low-power generating system that uses technologies of various types and produces electricity at the consumer's location ^[2].

One of the main reasons behind the development of distributed energy generation is the need to support the operation of a large number of consumers in regions without a centralized power supply system. The expansion of distributed energy use in these areas improves energy security, reduces electricity transmission losses, and enhances the security of the energy supply for consumers ^[3].

Currently, diesel generators are most commonly used to provide power to remote locations, as they have high reliability and relatively long service life ^[4]. However, they do have some disadvantages. Most existing diesel generators operate at a fixed (nominal) speed over the entire range of loads. This means that the internal combustion engine operates at a constant speed, even when the load on the generator changes. This results in suboptimal fuel efficiency, or reduced efficiency. Using a diesel generator with a variable speed drive engine, dependent on the load on the machine itself, can result in significant fuel savings of up to 20%.

It should be noted that the development and research of hybrid power systems based on diesel generators (DGs) with variable rotational speed constitute a relatively new technical direction in the field of small-scale power generation ^[5]. The main advantages of these plants include the stability of the power supply to consumers, the ability to maneuver, and the reduced negative impact on the environment ^[6]. It is most frequently proposed to combine DGs with power plants that use alternative energy sources ^[7].

A significant number of current global studies are devoted to the development and exploration of hybrid power systems. The primary focus of researchers is on incorporating renewable energy sources into existing conventional power generation facilities. A hybrid power system based on a diesel generator combined with solar and wind generation is discussed in detail in article ^[8]. During the modeling process, the authors investigated the operation of the power installation by gradually increasing the electrical load power (from 500 to 2,000 V∙A at a power factor of 0.9 and a frequency of 50 Hz). They also tested the operation of energy converters during this process. This research demonstrates the efficiency of a hybrid power system that combines a diesel generator with renewable energy sources, such as solar and wind power. The article ^[9] discusses the potential integration of renewable energy sources, such as wind and solar power, into a diesel-powered power plant that would serve oil and gas facilities. Options for implementing a wind farm or a solar panel farm were considered. However, the first option was chosen because solar panels are not effective in this region due to the low levels of sunlight. Additionally, the optimal configuration for the wind farm's equipment was determined. A hybrid power system for marine transportation is presented in ^[10]. This system consists of photovoltaic solar panels, a hydrogen fuel cell, and a diesel generator. According to the study, the system can reduce greenhouse gas emissions by 15% and produce 20% of its electricity from a fuel cell, which is powered by hydrogen. In ^[11], a three-channel power generation system is investigated, consisting of a wind turbine, a diesel generator, and a fuel cell. The wind turbine and the diesel generator are the main channels for producing electric energy, while the fuel cell serves as an auxiliary source. The management system for the installation is also considered.

There is also a lot of research into the development of hybrid power plants that operate only on renewable energy sources. These types of power plants are becoming especially popular due to the increasing number of renewable energy options available, because hybrid power plants can help to improve the reliability of the power supply for consumers. In the article ^[12], the authors developed a hybrid power generation system that combines a wind turbine, solar panels, and batteries Studies were conducted to evaluate the system's performance under different operating conditions. The results showed that the hybrid system achieved maximum efficiency during the summer months, with 78% of electricity generated from the wind turbine. In ^[13,14], the issue of integrating renewable energy sources into the electricity grid is discussed. The authors proposed using a direct current (DC) microgrid to simplify the control of electrical parameters and lower costs. The integration of large amounts of renewable energy systems necessitates the transformation of existing networks. As renewable energy facilities are gradually introduced, costs decrease thanks to the advancement of their production techniques, making it feasible to integrate new power stations into distribution networks at minimal cost.

Generating power from hydrogen fuel cells, with water as a reaction product, is becoming one of the most promising sources of energy today ^[15]. Key advantages of fuel cells are higher energy efficiency due to their reliability (absence of moving parts) and absences of intermediate stages of energy conversion (electrical efficiency up to 60%), polluting emissions, and noise ^[16]. Hydrogen fuel cells are already widely used in the transportation industry, space sector, etc. ^{[17,18,19,20,21]}. Meanwhile, fuel cells have some disadvantages, such as slow dynamic response, long starting time, and soft discharge characteristics ^[22]. These problems can be addressed by combining fuel cells with other energy sources in a hybrid power generation system. The articles ^[23,24] discuss technologies for integrating hydrogen energy into hybrid energy systems. They pay special attention to the generation of electricity using hydrogen fuel cells. They also consider the issues of energy storage systems, power flow management, and optimization algorithms and software for control systems. A method was proposed for optimizing the performance of hydrogen systems which allows for the numerical assessment of environmental, socio-environmental, and technical factors. The article ^[25] discusses the idea of incorporating fuel cells into a hybrid transportation system. A study on the economic viability of implementing a hydrogen fuel cell installation was conducted. As a result, a bus equipped with a serial hybrid system and lithium-ion batteries was designed.

Currently, a significant amount of research is devoted to optimizing hybrid power plants. In ^[26], the authors developed a hybrid power grid based on solar panels, wind turbines, batteries, and diesel generators. The optimization process revealed that the proposed network configuration offers optimal power generation with minimal investment and emissions. In ^[27], the researchers developed an algorithm for optimizing Raspberry Pi Pico controllers for solar panels. This algorithm achieves the maximum output power from solar panels, confirming its efficiency and highlighting the potential for placing solar panels as trees. The article ^[28] describes a modification to a high-voltage DC converter designed for use with renewable energy sources. Additionally, studies ^[29,30] analyzed various methods for optimizing hybrid energy systems based on renewable energy sources.

This work focuses on the development and simulation of a stand-alone dual-channel hybrid power system based on a variable-speed diesel generator and hydrogen fuel cell system. The main advantage of this proposed design is the utilization of a variable-speed diesel generator, which significantly decreases specific fuel consumption in comparison to conventional power plants with a constant-speed generator. This allows for optimal thermal conditions and reduces wear on the engine, leading to increased engine lifespan.

The aim of this study was to investigate the electromagnetic characteristics of a proposed power plant during operation with autonomous consumers with variable stepwise load profiles. The results allow us to establish the optimal configuration and specifications of electrical components for the subsequent implementation of a prototype dual-channel hybrid power system.

2. Stand-alone dual-channel hybrid power system structure

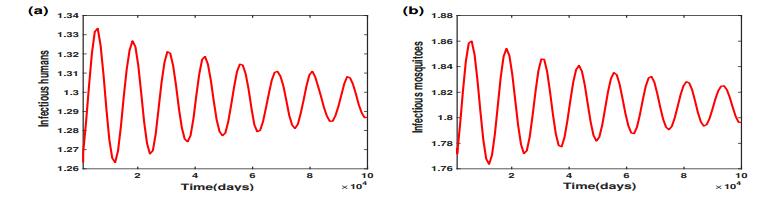
Figure 1 shows the structure of a stand-alone dual-channel hybrid power system developed by the authors. Due to the larger number of adjustable parameters, the dynamic requirements of the stabilization circuits can be reduced, and the output voltage can be maintained at a high-quality level.

Figure 1. Stand-alone dual-channel hybrid power system structure.

DownLoad: Full-Size Img PowerPoint

This system provides the consumer with electric power from two different energy sources. The primary source, which is a variable speed DG, stabilizes the output voltage and frequency. The DG consists of an internal combustion engine that rotates a three-phase synchronous generator. The load power at the diesel generator feeding is P = 3 kW with a nominal phase voltage of U_phase = 220 V and a frequency of f = 50 Hz.

When the main power generation channel is active, the switch K1 is closed, and K2 is open. The diesel engine (DE) drives a three-phase synchronous generator (SG). When the load power increases from zero to its nominal value, the rotation speed of the engine shaft and, consequently, the amplitude of the generator voltage will vary within a wide range. A controlled rectifier, connected to the generator via the impedance of an RL transmission line, stabilizes the output voltage at 250 V. This ensures that, despite changes in the speed of the diesel engine shaft, the required constant voltage is maintained at the DC link output.

From the output of the three-phase thyristor converter, a six-pulse rectified voltage is supplied to the first LC filter. Next, the smoothed voltage from the DC link (from the first filter) is supplied to a three-phase pulse width modulation (PWM) inverter. The PWM inverter output voltage is then supplied to the second LC filter. At the output of this filter, the smoothed sinusoidal voltage U_L-L is 220 V. The step-up three-phase transformer increases the voltage to the desired nominal value of 380 V.

The auxiliary power generation system with a lower power capacity (P_nom = 1 kW, U_L-L = 380 V) is powered by a hydrogen fuel cell system. The key component in the hydrogen fuel cell (HFC) structure is the hydrogen fuel cell stack, which significantly influences the efficiency and reliability of the power supply through this second channel. The model uses the parameters of the Horizon H-1000 X-Series hydrogen fuel cell to power a 1 kW load.

During operation of the second power generation channel, the switch K2 is closed, and the switch K1 is open. The voltage of 44 V from the hydrogen fuel cell is supplied to a step-up DC-DC converter. The output of the converter supplies a voltage of 250 V to a three-phase PWM converter, which then goes through an LC filter and a step-up transformer before reaching the load. When the load changes from 0 to its nominal state, the control system adjusts the output voltage of the step-up DC-DC converter to maintain it at the required 250 V level.

3. Materials and methods

During the design and development stages of energy complexes with complex structures, it is practical to use computer simulation modeling. Computer modeling allows one to research electromagnetic processes of the developed facility, determine the optimal control system structure, and solve the problem of electromagnetic compatibility of the power system major components, as well as load issues. Therefore, simulation modeling in a MATLAB Simulink environment was chosen as a research methodology.

3.1. Simulation model of a stand-alone dual-channel hybrid power system

The structure of the simulation model is based on an experimental power system prototype. The hybrid system model was developed using the MATLAB Simulink visual programming environment, which includes elements from the SimPowerSystems library for electrical devices. To solve the differential equations, the ode23tb solver was used. This solver employs the Runge-Kutta method for the initial part of the solution and a second-order implicit differentiation formula for the final part. This approach ensures high performance and accuracy in the model. The end time for the simulation is determined by the completion of transient processes that occur when the load changes.

Figure 2 shows a stand-alone dual-channel hybrid power system (SDHPS) simulation model developed using the MATLAB Simulink software package. The model consists of the following key components:

Figure 2. SDHPS simulation model.

DownLoad: Full-Size Img PowerPoint

● diesel engine,

● diesel engine control system,

● three-phase synchronous generator,

● three-phase bridge-circuit thyristor rectifier with smoothing exit filter,

● thyristor rectifier pulse-phase control system,

● autonomous voltage inverter with smoothing filter,

● PWM control system,

● step-up three-phase transformer,

● hydrogen fuel cell,

● hydrogen fuel cell control system,

● step-up pulse DC/DC-converter,

● DC/DC-converter control system,

● load,

● microprocessor-based control system of stand-alone dual-channel hybrid power system.

Table 1 shows the main parameters of the SDHPS simulation model blocks. The technical characteristics of the actual blocks of the hybrid power plant physical prototype have been used as parameters for the blocks in the simulation model. These values were obtained from publicly available catalogs (reference books) on electrical equipment and semiconductor components.

Table 1. The nominal parameters of the system units in MATLAB Simulink.

System unit	Parameter	Value
Diesel engine	Power, hp at crankshaft speed, rpm	4 3,000
Three-phase synchronous generator	Rated speed, rpm	3,000
	Rated power, kV∙A	3.5
	Rated voltage, kV	0.4
	Frequency, Hz	50
	Number of phases	3
Three-phase bridge-circuit thyristor rectifier	Rated mains voltage, kV	0.38
	Network frequency, Hz	50
	Rated load current, A	10
	Output voltage, V	0 ÷ 350
Autonomous voltage inverter	Input voltage, V	250
	Rated power, kW	3
	Rated load current, A	8
	Output voltage, V	220
Step-up three-phase transformer	Rated power, kV∙A	3.5
	Low voltage (line), V	150
	High voltage (line), V	380
	Windings connection	∆/Y
Hydrogen fuel cell	Rated power, W	1,000
	Efficiency, %	56
	Output voltage, V	44
	Fuel supply pressure, bar	0.6
	Operating temperature, ℃	65
	Maximum hydrogen consumption, l/min	34
Step-up pulse DC/DC-converter	Frequency, kHz	10
	Rated output voltage, V	250
	Rated load current, A	4
	Load power, kW	1
	Input voltage, V	44
Load	Rated line voltage, V	380
	Windings connection	Y
	Maximum power, kW	3

| Show Table

DownLoad: CSV

3.2. Diesel engine simulation model

As mentioned above, a synchronous generator is powered by a turbocharged internal combustion engine. The system of equations described below applies to this type of engine ^[31].

$\left. {\begin{array}{*{20}{c}} {\left( {{{\rm{T}}_{{\rm{ax}}}}{\rm{p + }}{{\rm{ \mathsf{ δ} }}_{{\rm{D \mathsf{ μ} }}}}} \right){{\rm{y}}_{\rm{0}}}{\rm{ = }}{{\rm{k}}_{\rm{1}}}{{\rm{y}}_{\rm{A}}}{\rm{ - }}{{\rm{ \mathsf{ μ} }}_{\rm{0}}}{\rm{;}}}\\ {\left( {{{\rm{T}}_{\rm{T}}}{\rm{p + }}{{\rm{ \mathsf{ δ} }}_{\rm{T}}}} \right){{\rm{y}}_{\rm{T}}}{\rm{ = }}{{\rm{k}}_{\rm{T}}}{{\rm{y}}_{\rm{0}}}{\rm{ - }}{{\rm{y}}_{\rm{A}}}{\rm{;}}}\\ {\left( {{{\rm{T}}_{\rm{K}}}{\rm{p + }}{{\rm{ \mathsf{ δ} }}_{\rm{M}}}} \right){{\rm{y}}_{\rm{A}}}{\rm{ = }}{{\rm{y}}_{\rm{T}}}{\rm{ - }}{{\rm{k}}_{\rm{K}}}{{\rm{y}}_{\rm{0}}}{\rm{;}}}\\ {\left( {{{\rm{T}}_{{\rm{ax}}}}{\rm{p + }}{{\rm{ \mathsf{ δ} }}_{\rm{D}}}} \right){{\rm{y}}_{\rm{0}}}{\rm{ = }}{{\rm{ \mathsf{ χ} }}_{\rm{0}}}{\rm{ - }}{{\rm{k}}_{\rm{D}}}{{\rm{y}}_{\rm{A}}}};\\ {\left( {{{\rm{T}}_{\rm{T}}}{\rm{p + }}{{\rm{ \mathsf{ δ} }}_{\rm{T}}}} \right){{\rm{y}}_{\rm{T}}}{\rm{ = }}{{\rm{k}}_{\rm{h}}}{{\rm{ \mathsf{ χ} }}_{\rm{0}}}{\rm{ + }}{{\rm{k}}_{\rm{T}}}{{\rm{y}}_{\rm{0}}}{\rm{ - }}{{\rm{y}}_{\rm{A}}}}\\ {{\rm{k}}_{\rm{g}}{\rm{g}}_{\rm{C}}{\rm{ = }}{{\rm{ \mathsf{ χ} }}_{\rm{0}}}{\rm{ + }}{{\rm{ \mathsf{ θ} }}_{\rm{\mathsf{ϕ}}}}{{\rm{y}}_{\rm{0}}}{\rm{;}}} \end{array}} \right\}$

(1)

Figure 3 shows the structure of the DE model, which is based on Eq 1.

Figure 3. Structural diagram of a diesel engine simulation model.

DownLoad: Full-Size Img PowerPoint

3.3. Synchronous generator simulation model

A synchronous generator model is an essential component of the SDHPS model. The model was developed based on Park-Gorev equations in a d-q coordinate system using per-unit notation ^[32].

When deriving the differential equations for a synchronous machine, several standard assumptions have been made:

● The positive directions of voltages and currents coincide with the positive d and q axes.

● The positive current directions of the excitation winding and damper winding also coincide with the d and q axes.

● The stator windings are assumed to be symmetrical, and there are no high spatial harmonics in the field.

● Iron losses and the dependence of resistances on temperature are neglected.

● The positive armature current direction is opposite to the d and q axes.

Considering the presented assumptions, the equations for the synchronous machine can be written as follows:

${{\rm{u}}_{\rm{d}}}{\rm{ = - }}{{\rm{r}}_{\rm{1}}}\cdot {{\rm{i}}_{\rm{d}}}{\rm{ + p \cdot }}{{\rm{\Psi }}_{\rm{d}}}\cdot \frac{{\rm{1}}}{{{{\rm{\Omega }}_{\rm{0}}}}}{\rm{ - }}{{\rm{\Psi }}_{\rm{q}}}{\rm{ \cdot \mathsf{ ω} ; }}$

(2)

${{\rm{u}}_{\rm{q}}}{\rm{ = - }}{{\rm{r}}_{\rm{1}}}\cdot {{\rm{i}}_{\rm{q}}}{\rm{ + p \cdot }}{{\rm{\Psi }}_{\rm{q}}}\cdot \frac{{\rm{1}}}{{{{\rm{\Omega }}_{\rm{0}}}}}{\rm{ + }}{{\rm{\Psi }}_{\rm{d}}}{\rm{ \cdot \mathsf{ ω} ; }}$

(3)

${{\rm{u}}_{\rm{f}}}{\rm{ = }}{{\rm{r}}_{\rm{f}}}\cdot {{\rm{i}}_{\rm{f}}}{\rm{ + p \cdot }}{{\rm{\Psi }}_{\rm{f}}}\cdot \frac{{\rm{1}}}{{{{\rm{\Omega }}_{\rm{0}}}}};$

(4)

${{\rm{u}}_{{\rm{kd}}}}{\rm{ = }}{{\rm{r}}_{{\rm{kd}}}}\cdot {{\rm{i}}_{{\rm{kd}}}}{\rm{ + p \cdot }}{{\rm{\Psi }}_{{\rm{kd}}}}\cdot \frac{{\rm{1}}}{{{{\rm{\Omega }}_{\rm{0}}}}}{\rm{ = 0; }}$

(5)

${{\rm{u}}_{{\rm{kq}}}}{\rm{ = }}{{\rm{r}}_{{\rm{kq}}}}\cdot {{\rm{i}}_{{\rm{kq}}}}{\rm{ + p \cdot }}{{\rm{\Psi }}_{{\rm{kq}}}}\cdot \frac{{\rm{1}}}{{{{\rm{\Omega }}_{\rm{0}}}}}{\rm{ = 0;}}$

(6)

$\Psi_{\mathrm{d}} = \mathrm{x}_{\mathrm{md}}\left(-\mathrm{i}_{\mathrm{d}}+\mathrm{i}_{\mathrm{f}}+\mathrm{i}_{\mathrm{kd}}\right)-\mathrm{x}_{\mathrm{as}} \cdot \mathrm{i}_{\mathrm{d}} ;$

(7)

$\Psi_{\mathrm{q}} = \mathrm{x}_{\mathrm{mq}}\left(-\mathrm{i}_{\mathrm{q}}+\mathrm{i}_{\mathrm{kq}}\right)+\mathrm{x}_{\mathrm{as}} \cdot \mathrm{i}_{\mathrm{q}} ;$

(8)

$\Psi_{\mathrm{f}} = \mathrm{x}_{\mathrm{md}}\left(-\mathrm{i}_{\mathrm{d}}+\mathrm{i}_{\mathrm{f}}+\mathrm{i}_{\mathrm{kd}}\right)+\mathrm{x}_{\mathrm{fs}} \cdot \mathrm{i}_{\mathrm{f}} ;$

(9)

$\Psi_{\mathrm{kd}} = \mathrm{x}_{\mathrm{md}}\left(-\mathrm{i}_{\mathrm{d}}+\mathrm{i}_{\mathrm{f}}+\mathrm{i}_{\mathrm{kd}}\right)+\mathrm{x}_{\mathrm{kds}} \cdot \mathrm{i}_{\mathrm{kd}} ;$

(10)

$\Psi_{\mathrm{kq}} = \mathrm{x}_{\mathrm{mq}}\left(-\mathrm{i}_{\mathrm{q}}+\mathrm{i}_{\mathrm{kq}}\right)+\mathrm{x}_{\mathrm{kqs}} \cdot \mathrm{i}_{\mathrm{kq}} ;$

(11)

${\rm{u}}_{\mathrm{a}}^2 = \mathrm{u}_{\mathrm{d}}^2+\mathrm{u}_{\mathrm{q}}^2 ;$

(12)

$\mathrm{i}_{\mathrm{a}}^2 = \mathrm{i}_{\mathrm{d}}^2+\mathrm{i}_{\mathrm{q}}^2;$

(13)

$\mathrm{P} = \mathrm{u}_{\mathrm{d}} \cdot \mathrm{i}_{\mathrm{d}}+\mathrm{u}_{\mathrm{q}} \cdot \mathrm{i}_{\mathrm{q}} ;$

(14)

$\mathrm{Q} = -\mathrm{u}_{\mathrm{d}} \cdot \mathrm{i}_{\mathrm{q}}+\mathrm{u}_{\mathrm{q}} \cdot \mathrm{i}_{\mathrm{d}} ;$

(15)

${\rm{\mathsf{μ}}} = \frac{\mathrm{J} \cdot \Omega_0}{\mathrm{M}_0} \cdot \frac{\mathrm{d} {\rm{\mathsf{ω}}}}{\mathrm{dt}}+\Psi_{\mathrm{q}} \cdot \mathrm{i}_{\mathrm{d}}-\Psi_{\mathrm{d}} \cdot \mathrm{i}_{\mathrm{q}} .$

(16)

Figure 4 shows a synchronous generator model, developed according to Eqs 2–16.

Figure 4. Synchronous generator simulation model.

DownLoad: Full-Size Img PowerPoint

3.4. Bridge-circuit thyristor rectifier simulation model

To regulate the output voltage of the DC link, the bridge-circuit thyristor rectifier is installed at the output of the synchronous generator. It is advisable to use a controlled rectifier to ensure electromagnetic compatibility during the parallel operation of the diesel generator set and the hydrogen fuel cell, in case of a wide change in load power.

It should be noted that the study of joint parallel operation is beyond the scope of this article. This paper considers the separate operation of two power generation channels.

The model was created using standard elements from the SimPowerSystems and Simulink libraries. The control system for the thyristor converter includes a proportional integral (PI) voltage controller. The controller generates control pulses for each of the six thyristors in the rectifier bridge.

3.5. PWM inverter simulation model

A SimPowerSystems Universal Bridge with insulated-gate bipolar transistor (IGBT) library contents block was used to create a three-phase inverter power circuit. Due to PWM, the voltage is regulated at the frequency converter output, and its form is approximated to the sinusoidal one. The autonomous voltage inverter (AVI) control system contains a PI voltage controller. An LC filter is used to smooth the PWM signal at the autonomous voltage inverter output.

The filter is primarily used to provide the desired AC total harmonic distortion (THD) in stationary mode. As soon as a three-phase inductive transformer is connected to AVI output, the filter calculation is approximate. Filter parameters' adjustment may be required further on, taking into consideration on-load non-linear voltage distortion coefficient. The filter parameters' calculated values for carrier frequency f_k = 2000 Hz are L_f ≥ 6.5 mH, С_f = 12 µF.

As shown in Figure 1, a step-up transformer is positioned after the filter, with load Z_l connected to the transformer output. The standard model of the three-phase transformer from the SimPowerSystems library is used.

3.6. Hydrogen fuel cell simulation model

For 1 kW hydrogen fuel cell modeling, the library cell Fuel Cell Stack of the Electric Drives/Extra Sources library with real stack parameters Horizon H-1000 series X was used.

Calculated current-voltage characteristics of the HFC model and its nominal parameters are shown in Figure 5 ^[33,34].

Figure 5. Hydrogen fuel cell model parameters.

DownLoad: Full-Size Img PowerPoint

The voltage from the hydrogen fuel cell is converted to a higher voltage using a pulse step-up DC-DC converter (Figures 1 and 2). These converters are more efficient than continuous voltage stabilizers and can also have good weight and size characteristics in some cases.

3.7. SDHPS experimental prototype

The SDHPS experimental prototype was developed to verify the simulation results. Figure 6 shows a photo of the prototype main blocks: (a) hydrogen fuel cell and (b) diesel generator set.

Figure 6. SDHPS experimental prototype blocks: (a) HFC, (b) DG.

DownLoad: Full-Size Img PowerPoint

The main characteristics of the physical models for HFC and DG are presented in Table 1.

4. Results

The results of the physical and simulation experiments are presented in terms of the time dependencies of the individual SDHPS units, with a stepwise change of the load (Figures 7 and 8).

Figure 7. Time dependencies: (a) load current, (b) internal combustion engine (ICE) speed variation, (c) bridge-circuit thyristor delay angle, (d) bridge-circuit rectifier output voltage.

DownLoad: Full-Size Img PowerPoint

Figure 8. The time dependence of the line voltage effective value on the load.

DownLoad: Full-Size Img PowerPoint

Figure 7 shows the dependencies of the load current I_load, the rotational speed of the synchronous generator shaft ω, the control angle of the thyristor rectifier α_y, and the voltage at the output of the rectifier U_d, with a stepwise changing load curve.

The following markings are used in Figures 7 and 8: The blue solid line represents the result of simulation modeling, the red dashed line represents the results of physical modeling.

Initially, the synchronous generator was operating with a load of 1.15 kW. The rotational speed of the generator shaft was 190 rad/s, and the load current was 1.75 A at this point. At times t = 15 s, 20 s, and 25 s, there were stepwise changes in the load. In the interval from 0 to 15 seconds, the load remained at 1.15 kW. Between 15 and 20 seconds, it increased to 2.05 kW. From 20 to 25 seconds, it reached 3 kW. Finally, between 25 and 30 seconds, the load returned to 2.05 kW.

At time t = 15 s, with a load of 900 W, the rotation speed of SG increased to 240 rad/s. When an additional 1 kW load was applied at time t = 20 s, the rotation speed of the SG shaft increased to 330 rad/s. As the load decreased at t = 25 s, the shaft speed decreased to 240 rad/s. The SDHPS control system adjusts the rotation speed of the generator's shaft based on changes in load, allowing for an efficient mode of operation for the diesel engine. This is described in the paper ^[31].

Depending on the load, the SDHPS control system adjusts the control angles of the bridge rectifier's thyristors. Figure 7(c) shows a graph of the corresponding change in angle α_y. At a load of P = 1.15 kW, the angle is 55 degrees, while at a load of 2.05 kW, it is 50 degrees, and at 3.05 kW, it drops to 40 degrees. Studies have shown that as the load changes from no load to full capacity, adjusting the control angle helps to stabilize the output voltage of the bridge rectifier at U_d = 250 V ± 5%. In this scenario, the load voltage remains within ΔU₁ = 380 V ± 2.5%, as shown in Figure 8. This demonstrates the proper operation of the SDHPS control system within the specified load range.

Spectral analysis of output voltage (on-load voltage) was carried out to assess voltage quality. Figure 9(a) shows spectral distribution and coefficient value of line voltage non-linear distortions after the filter, and Figure 9(b) shows this after the transformer or on-load at load power P = 1500 W.

Figure 9. Voltage spectral analysis: (a) after the filter, (b) after the transformer or on-load.

DownLoad: Full-Size Img PowerPoint

It can be observed that the non-linear distortion coefficient in the first case is THD = 4.18%, while in the second case THD = 3.82%. Higher harmonics amplitudes do not exceed 3% of the first harmonic. It can be concluded that, due to the transformer's inductance, the quality of the voltage delivered to the load has been slightly improved.

Figure 10 demonstrates the dependence between the nonlinear voltage distortion factor and the load level, ranging from 100 W to 3 kW, for the simulated (blue line) and physical (red dotted line) systems. In this case, the total harmonic distortion varies between 4.4% and 3.6% for the simulated model and between 4.6% and 3.75% for the physical prototype. Based on these findings, it can be concluded that the voltage quality supplied by the load across the entire power range meets the standards for 0.4 kV networks, with THD less than 8%.

Figure 10. The change in THD depends on the load power.

DownLoad: Full-Size Img PowerPoint

It should be noted that the difference between the simulation results and the data from the physical experiment for all the studied variables is no more than 3%. This indicates that the simulation model has an acceptable level of accuracy. The discrepancy can be explained by the simplifications made in the blocks of the simulation model.

As an example, Figure 11 shows the time dependencies of the output voltage, output current, IGBT current, and IGBT voltage of the step-up DC-DC converter, obtained as a result of simulation. The dependencies were calculated for a load of 1 kW and a carrier frequency of 10 kHz. Figure 11 demonstrates that the maximum collector current of the IGBT is 60 A, at a voltage of 250 V.

Figure 11. DC-DC converter time diagrams: (a) output voltage, (b) output current, (c) IGBT current, (d) voltage on IGBT.

DownLoad: Full-Size Img PowerPoint

The time dependences of the currents and voltages of the main components obtained as a result of simulation make it possible to select a component base for constructing the power section of a DC-DC converter.

5. Conclusions

A new stand-alone dual-channel hybrid power system, which uses a variable-speed diesel generator and hydrogen fuel cells, has been proposed. The diesel generator is the main source of electrical power generation. The hydrogen fuel cell acts as a backup power source. The dual-power system provides 3 kW of power when powered by the generator and 1 kW when powered by the fuel cell.

A unique feature of the proposed installation is the use of a developed variable-speed diesel generator. This system can reduce specific fuel consumption by up to 30% compared to conventional power plants that use constant-speed diesel generators. This allows for optimal thermal conditions and reduces wear on the engine, leading to increased engine lifespan.

An SDHPS simulation model was developed which consists of the following main components: diesel engine, synchronous generator, bridge-circuit thyristor rectifier, autonomous voltage inverter, step-up DC-DC converter, HFC, L-type filters, and transformer. Current, voltage, and capacity dependencies of SDHPS individual components were obtained as a result of computer modeling. Harmonic analysis of on-load voltages was carried out. It was found that at stepwise load demand change, THD non-linear distortion coefficient does not exceed 4.4%. At this, output voltage value fluctuation does not exceed 1%. Thus, on-load voltage quality meets standards' requirements.

The physical prototype of the SDHPS was described. The results of the computer simulation were compared to experimental data obtained from a physical prototype, showing high convergence.

The simulation results confirmed the operability and effectiveness of the proposed technical solutions. The introduction of the developed SDHPS into power systems for autonomous consumers will increase continuity, reliability, and environmental friendliness in their power supply.

Use of AI tools declaration

The authors state that they did not utilize artificial intelligence (AI) tools in crafting this article.

Acknowledgments

This research was funded by the Ministry of Science and Higher Education of the Russian Federation (state task No. FSWE-2022-0005).

Author contributions

Conceptualization, A.D. and A.K.; methodology, A.K.; software, Y.P.; validation, E.K. and A.K.; formal analysis, E.K.; investigation, A.K.; resources, A.D.; data curation, A.K.; writing—original draft preparation, Y.P. and A.K.; writing—review and editing, A.D. and E.K.; visualization, Y.P.; supervision, A.D. and E.K.; project administration, A.D. and E.K.; funding acquisition, E.K. All authors have read and agreed to the published version of the manuscript.

Conflict of interest

The authors assert that there are no competing interests in relation to the publication of this manuscript.

Appendix A

Table A1. List of symbols and nomenclature.

Symbol	Definition	Symbol	Definition
y₀, µ₀	shaft speed and engine load	ψ_f	excitation winding flux-linkage
y_A	forced air pressure	r_f, r₁	excitation winding and armature winding active resistance
y_T	turbine rotor speed	r_kd, r_kq	active resistance of the damper winding along the longitudinal and transverse axes
χ₀	fuel pump rack position	x_md, x_mq	stator winding inductive resistance projections on d and q axes
g_С	cyclical fuel delivery	x_kds, x_kqs	damper winding inductive resistance projections on d and q axes
T_аµ, T_T, T_аx, T_K	constants of diesel time in load action channel, turbocharger, intake manifold, diesel in regulatory action channel	x_fs, x_as	dissipation inductive resistance of excitation winding and armature winding
δ_Dµ, δ_D	diesel self-regulation in load action and regulatory action channels	M₀	load moment on SG shaft
δ_T, δ_M	intake manifold and turbocharger coefficients	Ω₀	synchronous angular frequency
k₁, k_D	diesel shaft torque dependency ratios to charging pressure and moment of resistance change on diesel shaft at load power change	J	rotating mass moment of inertia
k_T, k_K, k_h, k_g	air-flow rate through the diesel de-pendency ratios to its speed respectively, turbine torque dependency on its speed, turbine torque dependency on fuel pump rack position, diesel self-regulation	P	active power
ϴ_ɸ	diesel fuel-injection equipment gain ratio	Q	reactive power
u_d, u_q	armature voltage vector projection on d axis, q	ω	rotation speed
u_f	excitation voltage	µ	electromagnetic moment
i_f	excitation winding current	u_a	stator voltage
i_a	stator current	m	the number of rectification phases
i_d, i_q	armature current vector projection on d and q axes	U_line	line voltage
i_kd, i_kq	damper winding current projection on d and q axes	U_d	mean on-load voltage
ψ_d, ψ_q	d and q axes stator flux-linkage	ψ_kd, ψ_kq	damper circuit projection on d and q axes

| Show Table

DownLoad: CSV

Table A2. List of abbreviations.

Abbreviation	Meaning
AVI	autonomous voltage inverter
CC	coordinate converter
CS	current sensor
DE	diesel engine
DG	diesel generator
FC	frequency controller
FS	frequency sensor
FCU	fuel control unit
HFC	hydrogen fuel cell
ICE	internal combustion engine
LCS	load current sensor
PI	proportional integral controller
PWM	pulse width modulation
SDHPS	stand-alone dual-channel hybrid power system
SPG	synchronized 6-pulse generator
SG	three-phase synchronous generator
VR	voltage regulator

| Show Table

DownLoad: CSV

References

[1]	S. Bhatt, P. Gething, O. Brady, et al., The global distribution and burden of dengue, Nature, 496 (2013), 504–507.
[2]	Y. Wang, X. Liu, C. Li, et al., A survey of insecticide resistance in Aedes albopictus (Diptera: Culicidae) during a 2014 dengue fever outbreak in Guangzhou, China, J. Econ. Entomol., 110 (2017), 239–244.
[3]	F. Baldacchino, B. Caputo, F. Chandre, et al., Control methods against invasive Aedes mosquitoes in Europe: a review, Pest. Manag. Sci., 71 (2015), 1471–1485.
[4]	J. Werren, Biology of Wolbachia, Ann. Rev. Entomol., 42 (1997), 587–609.
[5]	G. Bian, D. Joshi, Y. Dong, et al., Wolbachia invades Anopheles stephensi populations and induces refractoriness to plasmodium infection, Science, 340 (2013), 748–751.
[6]	Z. Xi, C. Khoo and S. Dobson, Wolbachia establishment and invasion in an Aedes aegypti labora-tory population, Science, 310 (2005), 326–328.
[7]	E. Waltz, US reviews plan to infect mosquitoes with bacteria to stop disease, Nature, 89 (2016), 450–451.
[8]	M. Keeling, F. Jiggins and J. Read, The invasion and coexistence of competing Wolbachia strains, Heredity, 91 (2003), 382–388.
[9]	B. Zheng, M. Tang and J. Yu, Modeling Wolbachia spread in mosquitoes through delay differential equations, SIAM J. Appl. Math., 74 (2014), 743–770.
[10]	B. Zheng, M. Tang, J. Yu, et al., Wolbachia spreading dynamics in mosquitoes with imperfect maternal transmission, J. Math. Biol., 76 (2018), 235–263.
[11]	L. Cai, S. Ai and J. Li, Dynamics of mosquitoes populations with different strategies for releasing sterile mosquitoes, SIAM J. Appl. Math., 74 (2014), 1786–1809.
[12]	L. Cai, S. Ai and G. Fan, Dynamics of delayed mosquitoes populations models with two different strategies of releasing sterile mosquitoes, Math. Biosci. Eng., 15 (2018), 1181–1202.
[13]	M. Huang, J. Luo, L. Hu, et al., Assessing the efficiency of Wolbachia driven Aedes mosquito suppression by delay differential equations, J. Theor. Biol., 440 (2018), 1–11.
[14]	Y. Li and X. Liu, An impulsive model for Wolbachia infection control of mosquito-borne diseases with general birth and death rate functions, Nonlinear Anal: RWA, 37 (2017), 412–432.
[15]	L. Hu, M. Huang, M. Tang, et al., Wolbachia spread dynamics in stochastic environments, Theor. Popul. Biol., 106 (2015), 32–44.
[16]	M. Turelli and N. Barton, Deploying dengue-suppressing Wolbachia: Robust models predict slow but effective spatial spread in Aedes aegypti, Theor. Popul. Biol., 115 (2017), 45–60.
[17]	E. Newton and P. Reiter, A model of the transmission of dengue fever with an evaluation of the impact of ultra-low volume (ULV) insecticide applications on dengue epidemics, Am. J. Trop. Med. Hyg., 47 (1992), 709–720.
[18]	M. Atkinson, Z. Su, N. Alphey, et al., Analyzing the control of mosquito-borne diseases by a dominant lethal genetic system, Proc. Natl. Acad. Sci. USA, 104 (2007), 9540–9545.
[19]	S. Pinho, C. Ferreira, L. Esteva, et al., Modelling the dynamics of dengue real epidemics, Phil. Trans. R. Soc. A, 368 (2010), 5679–5693.
[20]	L. Xue, X. Fang and J. Hyman, Comparing the effectiveness of different strains of Wolbachia for controlling chikungunya, dengue fever, and zika, PLoS Neglect. Trop. D, 12 (2018), e0006666.
[21]	J. Zhang, C. Yang, Z. Jin, et al., Dynamics analysis of SIR epidemic model with correlation coef-ficients and clustering coefficient in networks, J. Theor. Biol., 449 (2018), 1–13.
[22]	L. Zou, J. Chen, X. Feng, et al., Analysis of a dengue model with vertical transmission and ap-plication to the 2014 dengue outbreak in Guangdong Province, China, B. Math. Biol., 80 (2018), 2633–2651.
[23]	C. Craig, The Etiology of Dengue Fever, J. Am. Med. Assoc., 75 (1920), 1171–1176.
[24]	C. Dye, Models for the population dynamics of the yellow fever mosquito, Aedes aegypti, J. Anim. Ecol., 53 (1984), 247–268.
[25]	F. Coutinhoa, M. Burattinia, L. Lopeza, et al., Threshold conditions for a non-autonomous epi-demic system describing the population dynamics of Dengue, Bull. Math. Biol., 68 (2006), 2263–2282.
[26]	M. Guzman and E. Harris, Dengue, Lancet, 385 (2015), 453–465.
[27]	M. Chan and M. Johansson, The incubation periods of dengue viruses, PLoS One, 7 (2012), e50972.
[28]	H. Smith, An Introduction to Delay Differential Equations with Applications to the Life Sciences, Volume 57, Springer, New York, 2011.
[29]	National Bureau of Statistics of China, National Data, Accessed 20 Jan 2019. Available from: http://data.stats.gov.cn/.
[30]	T. Scott, A. Morrison, L. Lorenz, et al., Longitudinal studies of Aedes aegypti (Diptera: Culicidae) in Thailand and Puerto Rico: population dynamics, J. Med. Entomol., 37 (2000), 77–88.
[31]	C. Paupy, B. Ollomo, B. Kamgang, et al., Comparative role of Aedes albopictus and Aedes ae-gypti in the emergence of Dengue and Chikungunya in central Africa, Vector-Borne and Zoonotic Diseases, 10 (2010), 259–266.
[32]	Y. Ye, S. Chenoweth, A. Carrasco, et al., Evolutionary potential of the extrinsic incubation period of dengue virus in Aedes aegypti, Evolution, 70 (2016), 2459–2469.
[33]	J. Yu, Modeling mosquitoes population suppression based on delay differential equations, SIAM J. Appl. Math., 78 (2018), 3168–3187.

This article has been cited by:

Surender Reddy Salkuti, Sustainable energy technologies for emerging renewable energy and electric vehicles, 2024, 12, 2333-8334, 1264, 10.3934/energy.2024057

Reader Comments

Your name:*

Email:*
© 2019 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

Mathematical Biosciences and Engineering

4.4

Metrics

Article views(5605) PDF downloads(803) Cited by(12)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(5) / Tables(2)

Mathematical Biosciences and Engineering

Analyzing the control of dengue by releasing Wolbachia-infected male mosquitoes through a delay differential equation model

Related Papers:

Abstract

1. Introduction

2. Stand-alone dual-channel hybrid power system structure

3. Materials and methods

3.1. Simulation model of a stand-alone dual-channel hybrid power system

3.2. Diesel engine simulation model

3.3. Synchronous generator simulation model

3.4. Bridge-circuit thyristor rectifier simulation model

3.5. PWM inverter simulation model

3.6. Hydrogen fuel cell simulation model

3.7. SDHPS experimental prototype

4. Results

5. Conclusions

Use of AI tools declaration

Acknowledgments

Author contributions

Conflict of interest

Appendix A

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

Mathematical Biosciences and Engineering

Analyzing the control of dengue by releasing Wolbachia-infected male mosquitoes through a delay differential equation model

Related Papers:

Abstract

1. Introduction

2. Stand-alone dual-channel hybrid power system structure

3. Materials and methods

3.1. Simulation model of a stand-alone dual-channel hybrid power system

3.2. Diesel engine simulation model

3.3. Synchronous generator simulation model

3.4. Bridge-circuit thyristor rectifier simulation model

3.5. PWM inverter simulation model

3.6. Hydrogen fuel cell simulation model

3.7. SDHPS experimental prototype

4. Results

5. Conclusions

Use of AI tools declaration

Acknowledgments

Author contributions

Conflict of interest

Appendix A

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog