Dynamics of an SLIR model with nonmonotone incidence rate and stochastic perturbation

1.   Introduction

The incidence of a disease is the number of individuals who become infected per unit of time and plays an important role in the study of mathematical epidemiology. Generally, incidence rate depends on both the susceptible and infective classes. In many epidemic models, the bilinear incidence rate is frequently used^[1]. However, in recent years, researchers have taken into account oscillations in incidence rates and proposed many nonlinear incidence rates. Let $S(t)$ be the number of susceptible individuals, $I(t)$ be the number of infective individuals, and $R(t)$ be the number of removed individuals at time $t$, respectively. After studying the cholera epidemic spread in Bari in 1973, Capasso and Serio ^[2] introduced the saturated incidence $g(I)S$ into epidemic models, where $g(I)$ is decreasing when $I$ is large enough, i.e.

This incidence rate seems more reasonable than the bilinear incidence rate because it includes the behavioral change and crowding effect of the infective individuals and prevents the unboundedness of the contact rate by choosing suitable parameters.

To incorporate the effect of the behavioral changes of the susceptible individuals, Liu et al.^[3] proposed the general incidence rate

where $p$ and $q$ are positive constants and $\alpha$ is a nonnegative constant. The special cases when $p, q$ and $k$ take different values have been used by many authors. For example, Ruan and Wang ^[4] studied the case when $p = 2, q = 2$ i.e. $g(I) = \frac{kI^2}{1+\alpha I^2}$ and got some complicated dynamics phenomenons, such as saddle-node bifurcation, Hopf bifurcation, Bogdanov-Takens bifurcation and the existence of none, one and two limit cycles. Derrick and van den Driessche^[5], Hethcote ^[6], Alexander and Moghadas^[7], etc. also used the general incidence rate.

If the function $g(I)$ is nonmonotone, that is, $g(I)$ is increasing when $I$ is small and decreasing when $I$ is large, it can be used to interpret the 'psychological' effect: for a very large number of infective individuals the infection force may decrease as the number of infective individuals increases, because in the presence of large number of infectives the population may tend to reduce the number of contacts per unit time^[8]. To model this phenomenon, Xiao and Ruan^[8] proposed a incidence rate

where $kI$ measures the infection force of the disease and $1/(1 + \alpha I^2)$ describes the psychological or inhibitory effect from the behavioral change of the susceptible individuals when the number of infective individuals is very large. This is important because the number of effective contacts between infective individuals and susceptible individuals decreases at high infective levels due to the crowding of infective individuals or due to the protection measures by the susceptible individuals. Notice that when $\alpha = 0$, the nonmonotone incidence rate (1.3) becomes the bilinear incidence rate^[8]. They used this incidence rate in an SIR model and got the result that this model does not exhibit complicated dynamics as other epidemic models with other types of incidence rates reported in. In this paper, we use this incidence rate in an SLIR model.

In fact, epidemic models are inevitably affected by environmental white noise which is an important component in realism, because it can provide an additional degree of realism in compared to their deterministic counterparts. Therefore, many stochastic models for the epidemic populations have been developed. In addition, both from a biological and from a mathematical perspective, there are different possible approaches to include random effects in the model. Here, we mainly mention three approaches. The first one is through time Markov chain model to consider environment noise in HIV epidemic (see, e.g., ^[9,10,11,12]). The second is with parameters perturbation. There is an intensive literature on this area, such as ^{[13,14,15,16,17,18,19]}. The last important issue to model stochastic epidemic system is to robust the positive equilibria of deterministic model. In this situation, it is mainly to investigate whether the stochastic system preserves the asymptotic stability properties of the positive equilibria of deterministic models, see ^[20,21,22]. Recently, Yang et.al^[19] discusses the stochastic SIR and SEIR epidemic models with saturated incidence rate $\beta S/(1+\alpha I)$. In this paper, we introduce randomness in the SLIR model with the second approaches as ^[13] and ^[15].

The rest of the paper is organized as follows: in Section 2, the deterministic SLIR mathematical model is formulated, boundedness of solutions and existence of a positively invariant and attracting set are shown. In Section 3, the basic reproductive number, the conditions to the existence of possible equilibria of the system and their stability are established. In section 4, we obtain the analytic results of dynamics of the SDE model. Finally, a brief discussion is given in Section 5.

2.   The deterministic model

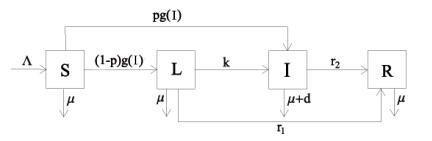
In this section, we formulate an SLIR model with incidence rate (1.3). Figure 1 shows the model diagram. The total population at time t, denoted by $N(t)$, is divided into four classes: susceptible ($S$), latent ($L$), infectious ($I$) and treatment ($R$).

All recruitment is into the susceptible class, and occurs at a constant rate $\Lambda$. We assume that an individual may be infected only through contacts with infectious individuals. The natural death rate is $\mu$. The infectious class has an additional death rate due to the disease with rate constant $d$. Thus individuals leave class $L$ for class $I$ at rate $k$. Latent and Infectious individuals are treated with rate constant $r_1$ and $r_2$, entering the treatment class, respectively. A fraction $p$ of newly infected individuals moves to the latent class ($L$), and the remaining fraction $1-p$, moves to the active class ($I$). The incidence rate is $g(I) = \frac{\beta I}{1+\alpha I^2}$. It is assumed that individuals in the latent class do not transmit infection. Combining all the aforementioned assumptions, the model is given by the following system of differential equations:

By adding all Eq (2.1), the dynamics of the total population $N(t)$ is given by:

Since $dN/dt < 0$ for $N > \Lambda/\mu$, then, without loss of generality, we can consider only solutions of (2.1) in the following positively subset of $R^4$:

With respect to model system (2.1), we have the following result:

Proposition 2.1. The compact set $\Omega_\varepsilon$ is a positively invariant and absorbing set that attracts all solutions of Eq (2.1) in $R^4$.

Proof. Define a Lyapunov function as $W(t) = S(t)+L(t)+I(t)+R(t)$, then we have:

Hence, that $\frac{dW}{dt}\leq 0$ for $W > \frac{\Lambda}{\mu}$. $\Omega_\varepsilon$ is a positively invariant set. On the other hand, solving the differential inequality Eq (2.3) yields:

$W(0)$ is the initial condition of $W(t)$. Thus, as $t\rightarrow \infty$, one has that $0\leq W(t)\leq \frac{\Lambda}{\mu}$.

To analysis the system (2.1), we notice that the variable $R$ does not participate in the first three equations. Thus we can consider only the equations for $S$, $L$ and $I$, i.e. the following system:

3.   Dynamics of the deterministic model

In this section, the model is analyzed in order to obtain the basic reproduction number, conditions for the existence and uniqueness of non-trivial equilibria and asymptotic stability of equilibria.

3.1.   Basic reproductive number

In this subsection, we define the basic reproduction number $R_0$ of system (2.4). $R_0$ is the average number of secondary infections that occur when one infective is introduced into a completely susceptible population^[23]. For many deterministic epidemiology models, an infection can get started in a fully susceptible population if and only if $R_0 > 1$. Thus the basic reproductive number $R_0$ is often considered as the threshold quantity that determines when an infection can invade and persist in a new host population^[1].

The disease-free equilibrium of system (2.4) is $X_0 = (S_0, 0, 0)$ with $S_0 = \Lambda/\mu$. In order to compute the basic reproduction number, it is important to distinguish new infections from all other class transitions in the population. The infected classes are $L$ and $I$. Following Van den Driessche and Watmough^[24], we can rewrite system (2.4) as

where $x = (L, I, S)$, $\mathscr{F}$ is the rate of appearance of new infections in each class, $\mathscr{V^+}$ is the rate of transfer into each class by all other means and $\mathscr{V^-}$ is the rate of transfer out of each class. Hence,

and

The jacobian matrices of $\mathscr{F}$ and $\mathscr{V}$ at the disease-free equilibrium $X_0 = (0, 0, \Lambda/\mu)$ can be partitioned as

where $F$ and $V$ correspond to the derivatives of $\mathscr{F}$ and $\mathscr{V}$ with respect to the infected classes:

The basic reproduction number is defined, following Van den Driessche and Watmough ^[24], as the spectral radius of the next generation matrix, $FV^{-1}$:

3.2.   Stability of the disease-free equilibrium

We have the following result about the global stability of the disease free equilibrium:

Theorem 3.1. When $R_0 > 1$, the disease free equilibrium $X_0$ is unstable.When $R_0\leq 1$, the disease free equilibrium $X_0$ is globally asymptotically stable in $\Omega_\varepsilon$; this implies the global asymptotic stability of the disease free equilibrium on the nonnegative orthant $R^3$. This means that the disease naturally dies out.

Proof. The Jacobian matrix of system (2.4) at $X_0$ is

and the characteristic equation is

From (3.1), we get the discriminant of $f(\lambda)$ is

Therefore, (3.1) has three real roots.

If $R_0 < 1$, we have

then

(3.1) has three negative real roots and hence $X_0$ is locally stable.

If $R_0 > 1$, (3.1) has at least one positive real root and hence $X_0$ is unstable.

When $R_0\leq1$, we can define the following Lyapunov-LaSalle function

Its time derivative along the trajectories of system (2.4) satisfies

Thus $R_0\leq 1$ implies that $\dot{V}\leq 0$. By LaSalle's invariance principle, the largest invariant set in $\Omega_\varepsilon$ contained in $\{(S, L, I, R)\in \Omega_\varepsilon, \dot{V} = 0\}$ is reduced to the disease-free equilibrium $X_0$. This proves the global asymptotic stability of the disease-free equilibrium on $\Omega_\varepsilon$ ^[25]. Since $\Omega_\varepsilon$ is absorbing, this proves the global asymptotic stability on the nonnegative octant for $R_0\leq 1$. It should be stressed that we need to consider a positively invariant compact set to establish the stability of $X_0$ since $V$ is not positive definite. Generally, the LaSalle's invariance principle only proves the attractivity of the equilibrium. Considering $\Omega_\varepsilon$ permits to conclude for the stability^[25,26,27]. This achieves the proof.

3.3.   Existence and uniqueness of endemic equilibrium

To find the positive equilibrium, let

which yields

We can see that

(ⅰ) there is one positive equilibrium if $R_0 > 1$;

(ⅱ) there is no positive equilibrium if $R_0\leq 1$.

Then we have the following result:

Theorem 3.2. When $R_0 > 1$, there exist an unique endemic equilibrium $X^* = (S^*, L^*, I^*)$ for the system (2.4) where $S^*, L^*$, and $I^*$ are defined as in (3.2) which is in the nonnegative octant $R^3_+$.

3.4.   Stability of endemic equilibrium

3.4.1.   Locally stability of endemic equilibrium

In this section, we denote $\mu+k+r_1 = A, \mu+d+r_2 = B$ for writing convenience.

Theorem 3.3. If $R_0 > 1$, the unique endemic equilibrium $X^*$ of system (2.4) is locally asymptotically stable.

Proof. The Jacobian matrix of system (2.4) at endemic equilibrium $X^* = (S^*, L^*, I^*)$ is

where

The characteristic equation of $J(X^*)$ is

where

According to direct calculation we have $a, c > 0$ and $ab > c$ when $R_0 > 1$. Therefore the endemic equilibrium $X^*$ is locally asymptotically stable in $\Omega_\varepsilon$ by Routh-Hurwitz criterion.

3.4.2.   Globally stability of endemic equilibrium

In this section, we briefly outline a general mathematical framework developed in ^[28] for proving global stability, which will be used to prove Theorem 3.10. Consider the autonomous dynamical system

where $f:D\rightarrow R^n$ open set and $f \in C ^1(D)$. Let $\bar{x}$ be an equilibrium of (3.3), i.e. $f(\bar{x}) = 0$. We recall that $\bar{x}$ is said to be globally stable in $D$ if it is locally stable and all trajectories in D converge to $\bar{x}$.

Assume that the following hypothesis hold:

(H1) $D$ is simply connected;

(H2) There exists a compact absorbing set $\Gamma\subset D$;

(H3) Eq (3.4) has a unique equilibrium $\bar{x}$ in $D$.

The Global Stability Problem arising in ^[28] is to find conditions under which the global stability of $\overline{x}$ with respect to $D$ is implied by its local stability. In ^[28], the main idea of this geometric approach to the global stability problem is as follows: Assume that (3.4) satisfies a condition in $D$, which precludes the existence of periodic solutions and suppose that this condition is robust, in the sense that it is also satisfied by ordinary differential equations that are $C^1$-close to (3.4); Then every nonwandering point of (3.4) is an equilibrium, as otherwise, by the $C^1$ closing lemma of Pugh ^[29,30], we can perturb (3.4) near such a nonequilibrium nonwandering point to get a periodic solution. As a special case, every omega limit point of (3.4) is an equilibrium. This implies that $\overline{x}$ attracts points in $D$. As a consequence, its global stability is implied by the local stability. For this purpose, we introduce the notion of robustness of a Bendixson criterion under local $C^1$ perturbations of $f$.

Definition 3.4. A point $x_0 \in D$ is wandering for (3.4) if there exists a neighborhood $U$ of $x_0$ and $t^* > 0$ such that $U \cap x(t, U)$ is empty for all $t > t^*$.

Thus, for example, any equilibrium, alpha limit point, or omega limit point is nonwandering.

Definition 3.5. A function $g \in C^1(D\rightarrow R^n)$ is called a $C^1$ local $\epsilon$-perturbation of $f$ at $x_0\in D$ if there exists an open neighborhood $U$ of $x_0$ in $D$ such that the support supp$(f-g) \subset U$ and $|f-g|_{C^1} < \epsilon$, where

and $| \cdot|$ denotes a vector norm on $R^n$ and the operator norm that it induces for linear mappings from $R^n$ to $R^n$.

Definition 3.6. A Bendixson Criterion for (3.4) is a condition satisfied by $f$, which precludes the existence of nonconstant periodic solutions to (3.4).

Definition 3.7. A Bendixson criterion is said to be robust under $C^1$ local perturbations of f at $x_0$ if, for each sufficiently small $\epsilon > 0$ and neighborhood $U$ of $x_0$, it is also satisfied by each $C^1$ local $\epsilon$-perturbations $g$ such that supp$(f-g)\subset U$.

The following is the local version of the global-stability principle proved by ^[28].

Theorem 3.8. Suppose that assumptions (H2) and (H3) hold and that (3.4) satisfies a Bendixson criterion that is robust under $C^1$ local perturbations of $f$ at all nonequilibrium nonwandering points for (3.4), then $\bar{x}$ is globally asymptotically stable with respect to $D$, provided it is stable.

The following is to introduce the quantity $\bar{q}_2$ given in ^[28]. Assume that (3.4) has a compact absorbing set $K \subset D$. Then every solution $x(t, x_0)$ of (3.4) exists for any $t > 0$. The quantity $\bar{q}_2$ is well defined:

where

and $x\mapsto P(x)$ is a $\Big(\begin{array}{c} n \\[-3pt] 2 \end{array} \Big)\times \Big(\begin{array}{l} n \\[-3pt] 2 \end{array} \Big)$ matrix-valued function, which is $C^1$ in $D$ and $A_f = (DP)(f)$ or, equivalently, $P_f$ is the matrix obtained by replacing each entry $a_{ij}$ in $P$ by its directional derivative in the direction of $f$, $\frac{\partial f}{\partial x}$^[2] is the second additive compound matrix of the Jacobian matrix $\frac{\partial f}{\partial x}$ of $f$. If $|\cdot|$ is a vector norm on $R^{\Big(\begin{array}{l} n \\[-4pt] 2 \end{array} \Big)}$, then $\rho(\mathcal{B})$ is the Lozinsk$\check{\mbox{i}}$ measure with respect to $|\cdot|$, which is defined by

Under assumptions (H1) and (H2), ^[28] proved that $\bar{q}_2 < 0$ is a Bendixson criterion for (3.3) and it is robust under $C^1$ local perturbations of $f$ at all nonequilibrium nonwandering points for (3.3) by means of the local version of $C^1$ closing lemma of Pugh ^[29,30]. Then we have the following theorem

Theorem 3.9. Under assumptions (H1), (H2), and (H3), the unique equilibrium $\bar{x}$ is globally asymptotically stable in $D$ if $\bar{q}_2 < 0$.

The criterion $\bar{q}_2 < 0$ provides the flexibility of a choice of $\Big(\begin{array}{l} n \\[-3pt] 2 \end{array} \Big)\times \Big(\begin{array}{l} n \\[-3pt] 2 \end{array} \Big)$ arbitrary function in addition to the choice of vector norms $|\cdot|$ in deriving suitable conditions. It has been remarked in ^[28] that, under the assumptions of Theorem 3.9, the classical result of Lyapunov, the classical Bendixson-Dulac condition, and the criterion in ^[31] are obtained as special cases ^[28]. In addition, it has also been stated in ^[28] that, under the assumptions of Theorem 3.9 the condition $\bar{q}_2 < 0$ also implies the local stability of the equilibrium $\bar{x}$, because, assuming the contrary, $\bar{x}$ is both the alpha and the omega limit point of a homoclinic orbit that is ruled out by the condition $\bar{q}_2 < 0$.

Global stability of endemic equilibrium.

We will focus on investigating the globally asymptotical stability of the unique endemic equilibrium $X^*(S^*, L^*, I^*)$. The main theorem of the method requires the use of Lozinsk$\check{\mbox{i}}$ Logarithmic norm.

Theorem 3.10. Assume that $R_0 > 1$. Then the unique endemic equilibrium $X^*$ is globally asymptotically stable in $R_3^+$.

Proof. We set $P$ as the following diagonal matrix:

Then $P$ is $C^1$ and nonsingular in $\overset{\circ}{\Omega}_\varepsilon$. Let $f$ denote the vector field of (2.4). Then

the second compound matrix $J$^[2] of the Jacobian matrix of system (2.4) can be calculated as follows

Then the matrix $\mathcal{B} = P_fP^{-1}+PJ$^[2]$P^{-1}$ in (3.6) can be written in matrix form

where

Let $(u, v, w)$ denote the vectors in $R^3$, we select a norm in $R^3$ as $|(u, v, w)| = \max\{|u|, |v|+|w|\}$ and let $\tilde{\mu}$ denote the Lozinsk$\check{\mbox{i}}$ measure with respect to this norm. Following the method in ^[32], we have the estimate $\tilde{\mu}(\mathcal{B})\leq \sup\{g_1, g_2\}$, where

$|\mathcal{B}_{12}|$ and $|\mathcal{B}_{21}|$ are matrix norms with respect to the $l_1$ vector norm and $\tilde{\mu}_1$ denotes the Lozinsk$\check{\mbox{i}}$ measure with respect to the $l_1$ norm. So

To calculate $\tilde{\mu}(\mathcal{B}_{22})$ we add the absolute value of the off-diagonal elements to the diagonal one in each column of $\mathcal{B}_{22}$, and then take the maximum of two sums, see ^[33]. We thus obtain,

Therefore

From (2.4) we have

The uniform persistence constant $c$ can be adjusted so that there exists $T > 0$ independent of $(S(0), L(0), I(0))\in K$, the compact absorbing set, such that

Substituting (3.9) into (3.7) and using (3.10), we obtain, for $t > T$,

Therefore $\tilde{\mu}(\mathcal{B})\leq \frac{L'}{L}+\frac{S'}{S}$ for $t > T$ by (3.8) and (3.11). Along each solution $(S(t), L(t), I(t))$ to (2.4) such that $(S(0), L(0), I(0))\in K$ and for $t > T$, we have

which implies $\bar{q}_2\leq 0$ from (3.5), proving Theorem 3.10.

In this section we proposed a nonmonotone and nonlinear incidence rate of the form $\beta IS/(1 + \alpha I^2)$, which is increasing when $I$ is small and decreasing when $I$ is large. It can be used to interpret the 'psychological' effect: the number of effective contacts between infective individuals and susceptible individuals decreases at high infective levels due to the quarantine of infective individuals or the protection measures by the susceptible individuals.

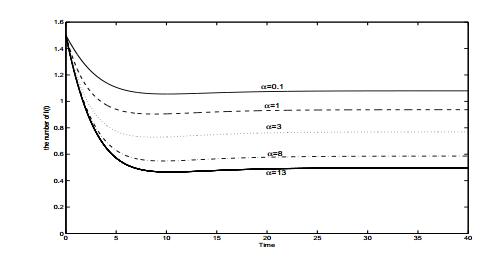
Recall that the parameter $\alpha$ describes the psychological effect of the general public toward the infectives. Though the basic reproduction number $R_0$ does not depend on $\alpha$ explicitly, numerical simulations indicate that when the disease is endemic, the steady state value $I^*$ of the infectives decreases as $\alpha$ increases (see Figure 2). From the steady state expression (3.2) we can see that $I^*$ approaches zero as $\alpha$ tends to infinity.

4.   Stochastic differential equation model

In this section we consider the stochastic model associated with the deterministic model in (2.1). We introduce randomness into the model (2.1) by replacing the parameters $\mu$ by $\mu\rightarrow \mu+\sigma_idB_i(t)(i = 1, 2, 3, 4)$ with the second approaches as ^[13] and ^[15], where $B_i(t)(i = 1, 2, 3, 4)$ are independent standard Brownian motions with $B_i(0) = 0$ and $\sigma_i^2(i = 1, 2, 3, 4)$ denote the intensities of the white noise. Then equation (2.1) becomes

Throughout this section, unless otherwise specified, let $(\Omega, \mathcal{F}, \mathbb{P})$ be a complete probability space with a filtration $\{\mathcal{F}_t\}_{t\geq 0}$. The Brown motions are defined on the complete probability space $(\Omega, \mathcal{F}, \mathbb{P})$. Denote

In general, consider $n$-dimensional stochastic differential equation^[35]:

with initial value $x(t_0) = x_0 \in R^n$. $B(t)$ denotes $n$-dimensional standard Brownian motions defined on the above probability space. Define the differential operator $\mathcal{L}$ associated with (4.2) by

If $\mathcal{L}$ acts on a function $V \in C^{2, 1}(S_h \times \bar{R}_+; \bar{R}_+)$, then

where

By Itô's formula,

4.1.   Existence and uniqueness of the positive solution of (4.1)

In this subsection we first show the solution of system (4.1) is global and positive. In order for a stochastic differential equation to have a unique global (i.e. no explosion in a finite time) solution for any given initial value, the coefficients of the equation are generally required to satisfy the linear growth condition and local Lipschitz condition ^[34,35]. However, the coefficients of system (4.1) do not satisfy the linear growth condition (as the incidence is nonlinear), so the solution of system (4.1) may explode at a finite time ^[34,35]. In this section, using Lyapunov analysis method (mentioned in ^[36]), we show the solution of system (4.1) is positive and global.

Theorem 4.1. There is a unique solution $(S(t), L(t), I(t), R(t))$ of system (4.1) on $t\geq 0$ for any intial value $(S(0), L(0), I(0), R(0))\in R_+^4$, and the solution will remain in $R_+^4$ with probability 1, namely, $(S(t), L(t), I(t), R(t))\in R_+^4$ for all $t > 0$ almost surely.

Proof. Since the coefficients of system (4.1) satisfy the local Lipschitz condition, then for any initial value $(S(0), L(0), I(0), R(0))\in R_+^4$, there is a unique local solution $(S(t), L(t), I(t), R(t))$ on $[0, \tau_e)$, where $\tau_e$ is the explosion time. To show this solution is global, we only need to prove that $\tau_e = \infty$ a.s. To this end, let $n_0 > 0$ be sufficiently large for every component of $S(0), L(0), I(0), R(0)$ lying within the interval $[\frac{1}{n_0}, n_0]\times[\frac{1}{n_0}, n_0]\times[\frac{1}{n_0}, n_0]\times[\frac{1}{n_0}, n_0]$. For each integer $n > n_0$, define the following stopping time

where throughout this paper, we set $\inf \emptyset = \infty$($\emptyset$ represents the empty set). Obviously, $\tau_n$ is increasing as $n \rightarrow \infty$. Let $\tau_\infty = \limsup\limits_{n\rightarrow \infty}\tau_n$, then $\tau_\infty \leq \tau_e$ a.s. In the following, we need to verify $\tau_\infty = \infty$ a.s. If this assertion is violated, there is a constant $K > 0$ and an $\varepsilon\in (0, 1)$ sucn that $P\{\tau_\infty \leq K\} > \varepsilon$. As a consequence, there exists an integer $n_1\geq n_0$ such that

Define a $C^2$-function $V: R_+^4\rightarrow R_+$ by

Applying the Itô's formula, we obtain

where

For $\forall I > 0, \frac{I}{1+\alpha I^2}\leq \frac{1}{2\sqrt{\alpha}}$. Hence there exists a suitable constant $M > 0$ independent of $S, L, I, T$ and $t$ such that $\mathcal{L}V\leq M$. The remainder of the proof is similar to Theorem 3.1 of ^[36] and hence is omitted. This completes the proof.

4.2.   Asymptotic behavior around the disease-free equilibrium of the deterministic model (2.1)

Obviously, $X_0 = (\frac{\Lambda}{\mu}, 0, 0, 0)$ is the solution of system (2.1), which is called the disease-free equilibrium. If $R_0 < 1$, then $X_0$ is globally asymptotically stable, which means the disease will vanish after some period of time. Therefore, it is interesting to study the disease-free equilibrium for controlling infectious disease. But, there is no disease-free equilibrium in system (4.1). It is natural to ask how we can consider the disease will extinct. In this subsection we mainly estimate the average of oscillation around $X_0$ in time to exhibit whether the disease will die out.

Theorem 4.2. Let $(S(t), L(t), I(t), R(t))$ be the solution of system (4.1) with initial value $(S(0), L(0), I(0), R(0))\in R_+^4$. If $R_0 = \frac{\beta \Lambda}{\mu}\frac{k(1-p)+(\mu+k+r_1)p}{(\mu+k+r_1)(\mu+d+r_2)}\leq 1$, and

then

Proof. Define $C^2$-function $V_1, V_2:R_+\rightarrow R_+$ and $V_3, V_4, V_5: R_+^2\rightarrow R_+$, respectively by

Along the trajectories of system (4.1), we have

Hence

From (4.3) and (4.4) we have

Considering positive definite $C^2$ function $V:R_+^4\rightarrow R_+$ such that

By computation,

Taking expectation above, (4.5) yields

Hence

This complete the proof.

4.3.   Asymptotic behavior around the endemic equilibrium of the deterministic model (2.4)

In this section, we will show there is a unique distribution for system (4.1) instead of asymptotically stable equilibrium(see ^[37]). We only consider the first three equation of system (4.1) because the variable $R$ does not participate in the first three equations. Before giving the main theorem, we first give a lemma (see ^[38]).

Let $X(t)$ be a regular temporally homogeneous Markov process in $E_l\subset R^l$ described by the stochastic differential equation:

and the diffusion matrix is defined as follows

Lemma 4.3. (see [38]) We assume that there exists a bounded domain $U\subset E_l$ with regular boundary, having the following properties:

● In the domain $U$ and some neighborhood thereof, the smallest eigenvalue of the diffusion matrix $A(x)$ is bounded away from zero.

● If $x\in E_l\backslash U$, the mean time $\tau$ at which a path issuing from $x$ reaches the set $U$ is finite, and $\sup_{x\in K}E_x\tau < \infty$ for every compact subsect $K\subset E_l$.

then, the Markov process $X(t)$ has a stationary distribution $\mu(\cdot)$ with density in $E_l$ such that for any Borel set $\mathcal{B}\subset E_l$,

and

for all $x\in E_l$ and $f(x)$ being a function integrable with respect to the measure $\breve{\mu}$.

Theorem 4.4. Let $(S(t), L(t), I(t))$ be the solution of system (4.1) with initial value $(S(0), L(0), I(0))\in R_+^3$. If $R_0 = \frac{\beta \Lambda}{\mu}\frac{k(1-p)+(\mu+k+r_1)p}{(\mu+k+r_1)(\mu+d+r_2)}\leq 1$, and the following conditions are satisfied:

(i)

(ii) $\delta < \min \{\rho_1 S^{*2}, \rho_2L^{*2}, \rho_3I^{*2}\}$, where $S^*, L^*, I^*$ are difined as in (3.2) and

then we have

Proof. As $R_0 > 1$, there is a unique endemic equilibrium $X^* = (S^*, L^*, I^*)$ such that

Define $C^2$ functions as follows:

By computation, we have

We discuss the follow prove in two cases: $(S-S^*)(I-I^*)\geq0$ or $(S-S^*)(I-I^*) < 0$.

1). If $(S-S^*)(I-I^*)\geq 0$, define

By computation, we have

2). If $(S-S^*)(I-I^*) < 0$, define

By computation, we have

Over all we have

where

If $\delta < \min \{\rho_1 S^{*2}, \rho_2L^{*2}, \rho_3I^{*2}\}$, then the ellipsoid

lies entirely $R_+^3$. We can take $U$ as any neighborhood of the ellipsoid such that $\overline{U}\in R_+^3$, where $\overline{U}$ is the closure of $U$. Thus, we have $LV < 0$ which implies the second condition in Lemma 4.3 is satisfied. Besides, there is $Q > 0$ such that

Applying Rayleigh's principle (see ^[39], p. 349), the first condition in Lemma 4.3 is satisfied. Therefore, the stochastic system (4.1) has a unique stationary distribution $\mu(\cdot)$ and it is ergodic.

4.4.   Exponential stability of system (4.1)

In this section, we investigate the exponential decay of the global solution of system (4.1) as the intensity of white noise is great. It can be shown below, even if the endemic equilibrium exists in the system (2.1), the stochastic effect may make washout more likely in system (4.1).

Theorem 4.5. Let $(S(t), L(t), I(t), R(t))$ be the solution of system (4.1) with any initial value $(S(0), L(0), I(0), R(0))\in R_+^4$. If $\frac{\Lambda \beta (\mu+k+r_1)}{\mu k} < (\frac{\sigma_3^2}{2}+\mu+d+r_2)\wedge (\frac{\sigma_2^2}{2})$ then,

where $\rightarrow ^\omega$ means the convergence in distribution and $\nu$ is a probability measure in $R_+^1$ such that $\int_0^\infty x\nu(dx) = \frac{\Lambda}{\mu}$. In particularly, $\nu$ has density $(A\sigma_1^2 x^2p(x))^{-1}$, where $A$ is a normal constant,

Proof. By comparison theorem, we see that $S(t)\leq X(t)$, where $X(t)$ is the global solution of the following stochastic system with initial value $X(0) = S(0)$:

Obviously, (4.8) is a diffusion process lying in $R_+^1$.

Firstly, we show (4.8) is stable in distribution and ergodic. Let $Y(t) = X(t)-\frac{\Lambda}{\mu}$, then $Y(t)$ satisfies

Theorem 2.1(a) in^[40] with $C = 1$ implies that the diffusion process $Y(t)$ is stable in distribution as $t\rightarrow \infty$, so does $X(t)$.

To prove the ergodicity of $X(t)$, we difine

and it is noted that for each integer $n\geq 1$, there exist positive constants $C_1(n), C_2(n)$ and $M(n)$ such that

Therefore, together with (4.10) we see

So $X(t)$ is ergodic (Theorem 1.16 in [41]), and with respect to the Lebesgue measure its invariant measure $\nu$ has density $(A\sigma_1^2 p(x)x^2)^{-1}$, where $A$ is a normal constant.

Now, we show that $f(t): = EX^p(t)$ is uniformly bounded for some $p > 1$ determined later. Applying It$\hat{\text{o}}$'s formula to $X^p$, we have

Taking expectation of equation above, and using the fact $a^{\frac{1}{p}}b^{\frac{p-1}{p}}\leq \frac{a}{p}+\frac{b(p-1)}{p}, a, b > 0$,

Choosing $\varepsilon > 0$ sufficiently small and $p > 1$ closely enough to 1 such that

Hence, $\sup_{t\geq 0}EX^p(t) = \sup_{t\geq 0}f(t) < \infty$, implying that $\int_0^\infty x^p\nu(dx) < \infty$. Together with its ergodicity we have

for all $x\in R_+^1$. On the other hand, Jensen's inequality yields

therefore, $\{ \frac{1}{T}\int_0^T X(t)dt, t\geq 0\}$ is uniformly integrable. Together with (4.11), we have

Taking expectation of (4.8), we have

Let $t\rightarrow \infty$, taking (4.12) into account, then we have $\int_0^\infty x\nu(dx) = \frac{\Lambda}{\mu}$.

We shall eventually show that $S(t)$ is stable in distribution. To do this, as in ^[15], we introduce a new stochastic process $S_\varepsilon (t)$ which is defined by initial condition $S_\varepsilon(0) = S(0)$ and the stochastic differential equation

We prove that

Therefore consider

The solution is given by

For almost $\omega\in\Omega, \exists T = T(\omega)$ such that $\varepsilon > \frac{\beta I(t)}{1+\alpha I^2(t)}, \ \ \forall t > T$.

Hence as the proof of Theorem 5.2 in ^[15] for almost $\omega\in \Omega$, for any $t > T$,

Therefore, $\liminf\limits_{t\rightarrow\infty}(S(t)-S_\varepsilon(t)\geq 0, \ a.e.$ Next, it is noted that

Taking the expectation of above equation, we see

where the last inequality is using the fact that $S_\varepsilon(t)\leq X(t)$. Hence we have

This implies that

Combining (4.13), (4.14) and the fact that $S(t)\leq X(t)$, we have

It has been shown that $X(t)$ converges weakly to distribution $\nu$, so does $S(t)$ as $t\rightarrow\infty$.

Secondly, using It$\hat{\text{o}}$'s formula to $\log[L+\frac{\mu+k+r_1}{k}I]$ and the fact that $S(t)\leq X(t)$ show

Integrating the above inequality from 0 to $t$, together with (4.11) and the fact that $\lim_{t\rightarrow \infty}\frac{|B_i(t)|}{t} = 0, i = 2, 3$^[35], yields

To help with the proof we introduce another diffusion process $\widetilde{R}(t)$ which is defined by the initial condition $\widetilde{R}(0) = R(0)$ and the stochastic differential equation

Then consider

The solution is given by

By (4.15) and the fact that $\lim\limits_{t\rightarrow \infty}\frac{|B_4(t)|}{t} = 0,$ it has been shown that, for any $\tilde{\varepsilon} > 0$ and almost $\omega\in \Omega, \exists T = T(\omega)$ such that

where $\zeta$ is defined in (4.15). Hence for all $\omega\in \Omega$, if $t > T(\omega)$, then

Therefore,

Let $\tilde{\varepsilon}\rightarrow 0$, we get $\limsup\limits_{t\rightarrow \infty }\frac{1}{t}\log|R(t)-\widetilde{R}(t)|\leq (r_1 \vee r_2)\cdot \{[-(\mu+\frac{\sigma_4^2}{2})]\vee \zeta\},$ a.e. On the other hand,

and hence, $\limsup\limits_{t\rightarrow \infty }\frac{1}{t}\log\widetilde{R}(t) = -(\mu+\frac{\sigma_4^2}{2})$, Therefore

5.   Discussion

Based on the model proposed in Xiao and Ruan^[8], we proposed an SLIR model with a nonmonotone and nonlinear incidence rate of the form $\beta IS/(1 + \alpha I^2)$ which is increasing when $I$ is small and decreasing when $I$ is large. It can be used to interpret the 'psychological' effect: the number of effective contacts between infective individuals and susceptible individuals decreases at high infective levels due to the quarantine of infective individuals or the protection measures by the susceptible individuals.

We have provided a complete description of the asymptotic behaviour of the solutions of the deterministic model (2.1) and (2.4). Interestingly, this model does not exhibit complicated dynamics as other epidemic models with other types of incidence rates reported in ^{[1,3,4,5,6,8]}. In terms of the basic reproduction number $R_0 = \frac{\beta \Lambda}{\mu}\frac{k(1-p)+(\mu+k+r_1)p}{(\mu+k+r_1)(\mu+d+r_2)}$, our main results indicate that when $R_0 < 1$, the disease-free equilibrium is globally attractive. When $R_0 > 1$, the endemic equilibrium exists and is globally stable.

A stochastic differential equation (SDE) is formulated for describing the disease in this case. We prove the existence and uniqueness of the solution of this SDE. We proved the positivity of the solutions. Then, we investigate the stability of the model. We illustrated the dynamical behavior of the SLIR model according to $R_0 < 1$. We proved that the infective tends asymptotically to zero exponentially almost surely as $R_0 < 1$. We also proved that the SLIR model has the ergodic property as the fluctuation is small, where the positive solution converges weakly to the unique stationary distribution.

Acknowledgments

This work is supported by the National Natural Science Foundation of China No:11601542 and 11771407, the Postdoctoral Research Grant in Henan Province No:001803011.

Conflict of interest

The authors declare no conflict of interest.