1. Introduction
Rotational grazing has been used in agriculture for many years and has been accepted as a more efficient and sustainable alternative to continuous grazing. Agricultural publications explain that rotational grazing provides grasses with more sunlight, water, and nutrients as well as more time to regrow and deepen roots, which leads to a higher quality and quantity of forage and expedited browsing on the cattle's behalf [12,23,27]. Thus it is conducive that for the same amount of grass in both situations, rotational grazing can support more cattle and is thus more productive. However, there exists no quantified method published that concretely describes this improvement [10,24].
Moreover, rotational grazing as a whole requires many parameters, such as the number of paddocks, rotational period, and proper factor which is a percentage of the total forage that should be consumed. Farmers have experimented with these; some use thirty paddocks and rotate every day while others use three and rotate every two weeks. Thus most claim that rotational grazing varies by farms and offer the following equations as a numerical guidance [17]:
|
Number of Paddocks=Days of RestDays of Grazing+1,
|
(1.1)
|
and
|
Number of Days=v⋅a⋅pw⋅i⋅H,
|
(1.2)
|
where v,a,p,w,i,H denote the total amount of forage, the number of acres, the proper factor, the weight of an individual head of cattle, the amount of forage consumed as a percentage of weight, and the number of cattle, respectively. Such variables are difficult to approximate and do not take into account the rate of consumption by the cattle and the growth rate of the forage. Equation (1.1) is designed for a single-paddock grazing system, meaning that only one paddock is grazed at a time, which does not consider the efficiency of simultaneous multi-paddock use.
In this paper we use a dynamical differential equation model by Noy-Meir and May to describe the continuous grazing system [18,19] and study the effect of rotational grazing in a multi-paddock setting. The general ordinary differential equation model for a renewable natural resource exploited by natural or human causes in [18,19] is
|
V′(t)=G(V(t))−H⋅c(V(t)),
|
(1.3)
|
where V(t) is the quantity of the resource, G(V) is the growth rate of the resource, c(V) is the rate that the resource is consumed, and the parameter H is the strength of the consumption. Typically the growth rate function G(V) is of the logistic type or Ricker type, and the harvesting rate c(V) is a Holling type functional response; thus, multiple stable equilibria can coexist in certain parameter ranges for a continuous grazing system [13]. The notion of alternative stable states in ecosystems was revived in the early twenty-first century with increasing concerns in the environmental problems around the world [25,26]. As levels of resources have fluctuated, people now turn to examining the various relationships among predators and prey. In the case of grazing, the notion of a predator-prey system has become an herbivore-plant system, where the cattle are the predator while the forage is the prey [19]. Studies of this topic in particular may have an impact on intensive grazing management, a field which, as described above, generally lacks quantitative measures. Moreover, previous work evaluating grazing mathematically do not incorporate rotational grazing in detail, nor do they attempt to use practical values of variables; instead, most perform a graphical analysis focusing on multiple equilibria.
This paper aims to examine and optimize rotational grazing as well as to compare it to continuous grazing through mathematical models. For some realistic standards, the proper factor is recommended to be 50% [28]. A cow-calf pair requires a minimum of 2.5 acres; since a calf is considered half of a cow, the land needed is 5/3 acres for one head of cattle, or 0.6 heads per acre [3,16]. The average rotational period is 3 to 7 days, while the rest period ranges from 21 to 42 days, depending on the time of year and plant type [6]. More specifically, we seek to complete the following objectives using parameters similar to those mentioned above.
1.Find the ideal proper factor that maximizes the number of cattle in a continuous system.
2.Compare the productivity of rotational and continuous grazing, and conclude that rotational grazing is more productive.
3.Describe the optimal grazing configuration that maximizes, or at least obtains a balance between, the number of cattle and the amount of stockpiled forage based on the number of total paddocks, the number of paddocks grazed at any time, and the length of the grazing and rest periods.
4.Compare this model to standards in reality.
A mathematical model of rotational grazing based on Noy-Meir's base model was first considered in Noy-Meir [20]. In his scheme, the land is divided into n paddocks, and only 1 paddock is grazed by the cattle in a single rotational period. Our model allows for m≥1 paddocks to be grazed simultaneously, and our results show that when m≥2, the system can support a larger number of cattle than m=1. Furthermore, his scheme incorporated a separate ungrazeable residual plant biomass in the grass growth function that is similar to the concept of the proper factor. However, in our study the proper factor is seen as part of V(t) itself and has a prominent role in determining the sustainability of a rotational grazing configuration. Noy-Meir also evaluated productivity on the basis of maximizing the consumption per head of cattle instead of maximizing the number of cattle and stockpiled forage. Lastly, while his scheme tested different values for the initial amount of grass, this paper focuses on keeping most parameters constant for more consistency in the comparisons of productivity between rotational and continuous grazing. Another mathematical model was recently proposed in [11], but their focus is quite different from ours. The model introduced here intends to provide an explanation of the benefits of rotational grazing in a general quantitative way. The optimal harvesting of a renewable natural resource distributed spatially has also been considered in [8,7] recently, but their focus is quite different from ours. Our model does not explicitly contain a spatial variable, and the harvesting function which we use here is more complicated. An age-structured fish harvesting model was recently considered in [9] (see also [4,5] for earlier work), and a first order linear partial differential equation was used to described the fish population distribution and dynamical behavior. The model concluded that the time-average maximal extraction of the resource is provided by time-constant extraction rate. In our current setting, this conclusion means that any rotational (in space, thus time-periodic for any particulate paddock) strategy yields no better average forage consumption (in the long run) than the best continuous strategy. However, our model uses a nonlinear (logistic) growth rate and also a nonlinear harvesting function, and our results show that the nonlinear model gives a different answer.
We organize the remaining parts of the paper in the following way. In Section 2 we introduce our differential equation model, and in Section 3 we make some concluding remarks.
2. Model and results
2.1. Continuous grazing
We use a commonly used grazing system (1.3) as our base model for the growth of grass in a single paddock. In (1.3), the time t is measured by days, and the amount of forage V(t) is measured by pounds per acre. To be more specific, we use a logistic function to represent the grass growth, and we use the Holling type II functional response to model the grass consumption by the cattle [17,19]. The logistic function has the explicit form
|
G(V)=gmaxV(1−VVmax).
|
(2.1)
|
Here V is the amount of forage, gmax is the maximum growth rate per capita, and Vmax is the carrying capacity of forage. The parameter Vmax is approximately 2400 pounds per acre in dry mass since the forage generally weighs 200 pounds per acre per inch and the average grass height is 12 inches [21], while gmax is 1352400=0.05625 per acre per day because the maximum growth rate of grass is 148 kilograms dry mass per hectare per day, or 135 pounds dry mass per acre per day [14].
The grass consumption rate has the explicit form
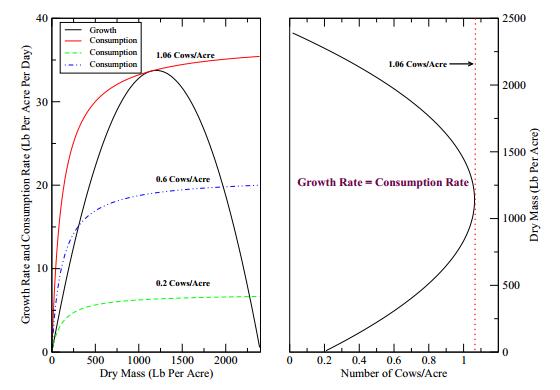
Here H⋅c(V) is the total dry mass grass consumption by the cattle per acre per day in pounds, where H is the number of cattle per acre. The parameter cmax is the maximum consumption rate per head of cattle, while K is the half-saturation value for the Holling type II functional response. In our study cmax is approximately 35 pounds dry mass per acre per day because cattle consume at most 2.5% of their body weight, which, for an average head of beef cattle, is at most 1400 pounds [1,2]. K is chosen to be 120 here. This choice is not supported by any literature but it is chosen to be significantly smaller than the carrying capacity so the grazing function c(V) is closer to a step function. The graphs of growth rate function g(V) and the consumption rate function H⋅c(V) with those chosen parameter values are plotted in Figure 1 left panel. We remark that the choices of parameter values here are based on the agriculture literature cited for a generic type of grass and cattle. Different types of grass and cattle may have different parameter values but the model still exhibits similar qualitative behavior.
Summarizing the above description, we have the following continuous grass-grazing model in a single paddock:
|
V′(t)=gmaxV(t)(1−V(t)Vmax)−H⋅cmaxV(t)V(t)+K.
|
(2.3)
|
The dynamics of (2.3) are governed by the number of nonnegative equilibria. V=0 is a trivial equilibrium, and two possible additional positive equilibria can be solved by a quadratic equation:
|
gmaxcmax(1−VVmax)(V+K)=H.
|
(2.4)
|
Define
|
H0=gmaxKcmax,Hmax=gmax(Vmax+K)24cmaxVmax.
|
(2.5)
|
Then when 0≤H≤H0 or H=Hmax, (2.3) has one positive equilibrium V+; when H0<H<Hmax, (2.3) has two positive equilibria V+ and V−, where
|
V±=Vmax−K±√(Vmax+K)2−4H12,H1=HcmaxVmaxgmax,
|
(2.6)
|
and when H>Hmax, there is no positive equilibrium; thus, the grassland collapses due to overconsumption by cattle. From elementary stability analysis, it is well-known that the trivial equilibrium V=0 is locally asymptotically stable when H>H0 and unstable when 0≤H<H0; the large positive equilibrium V+ is locally asymptotically stable, and the small positive equilibrium V− is unstable. Thus the maximum sustainable number of cows is achieved at H=Hmax. Figure 1 right panel shows the bifurcation diagram of positive equilibria versus the parameter H.
Using the parameter values we mentioned above, we find that H0≈0.1928 heads of cattle per acre, Hmax≈1.0631 heads of cattle per acre, and when H=Hmax, the equilibrium forage is V∗=(Vmax−K)/2=1140 pounds of dry matter per acre remaining out of the original 2400 pounds. These values are achieved when the proper factor p=V∗/Vmax=47.5%, which is set as a baseline for rotational grazing.
2.2. Rotational grazing model
For the rotational grazing, we divide the entire grassland into n equal size paddocks where n is an integer at least 2, and we define Vj(t) to be the grass biomass in the j-th paddock. Using the base model (2.3), the dynamic model for rotational grazing is
|
V′j(t)=gmaxVj(t)(1−nVj(t)Vmax)−Hj(t)⋅cmaxVj(t)Vj(t)+K,1≤j≤n.
|
(2.7)
|
Here all parameters gmax,Vmax,cmax and K are the same as in (2.3) so that the grassland is homogenous. In each paddock the carrying capacity is Vmax/n. The function Hj(t) is the number of cattle per acre put in the j-th paddock at time t. Table 1 summarizes all the variables and parameters used in our study.
Table 1. Table of variables and parameters in the equations.
| Variable |
Meaning |
Units |
|
|
| t |
time |
days |
|
|
| Vj(t) |
grass biomass in paddock j |
pounds/acre |
|
|
| Parameter |
Meaning |
Units |
Value |
Reference |
| Vmax |
grass carrying capacity |
pounds/acre |
2400 |
[21] |
| gmax |
maximum growth rate per capita rate per capita |
day−1 |
0.05625 |
[14] |
| cmax |
maximum consumption rate per head of cattle |
pounds/(acre⋅day) |
35 |
[1,2] |
| K |
half-saturation value |
pounds/acre |
120 |
|
| Hj |
number of cattle per acre in paddock j |
cattle/acre |
|
|
In a rotational grazing strategy, we choose a rotational period T, and Hj(t) are some properly chosen time-periodic functions with period nT. We also choose an integer m≥1, which is the number of paddocks grazed at once. Then the rotational strategy is defined by
|
Hj(t)={H/m,knT+jT≤t<knT+(j+m)T,0,knT+(j+m)T≤t<(k+1)nT+jT,
|
(2.8)
|
where k is any integer and H is the total number of cattle per acre. In this strategy, in a whole rotational cycle nT, each paddock is grazed by a total of H/m cows over a time period mT, and in the other period of length (n−m)T the paddock is not grazed. This rotational strategy is a cyclic one. For example, if n=7 and m=3, let Pi=paddock i (1≤i≤7). Then the grazed paddocks for each rotational period are
|
Period 1 :P5,P6,P7; Period 2 :P6,P7,P1; Period 3:P7,P1,P2; Period 4 :P1,P2,P3; Period 5 :P2,P3,P4; Period 6:P3,P4,P5; Period 7 :P4,P5,P6; then Period 8 will start another cycle.
|
Note that a noncyclic rotation scheme can also be designed. For example,
|
Period 1 :P1,P2,P3; Period 2 :P4,P5,P6; Period 3:P1,P2,P7; Period 4 :P3,P4,P5; Period 5 :P1,P6,P7; Period 6:P2,P3,P4; Period 7 :P5,P6,P7; then Period 8 will start another cycle.
|
In this paper we only consider the cyclic rotational strategy, so we will not compare the effectiveness of noncyclic rotational strategy.
2.3. Results
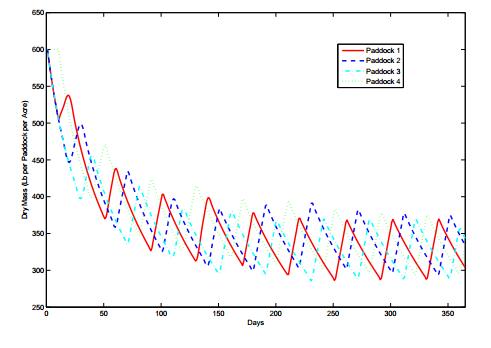
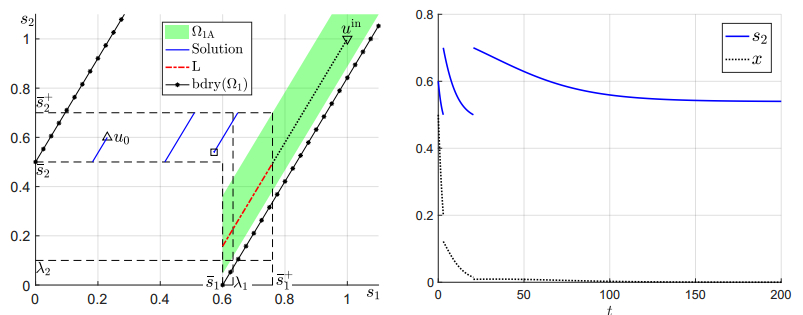
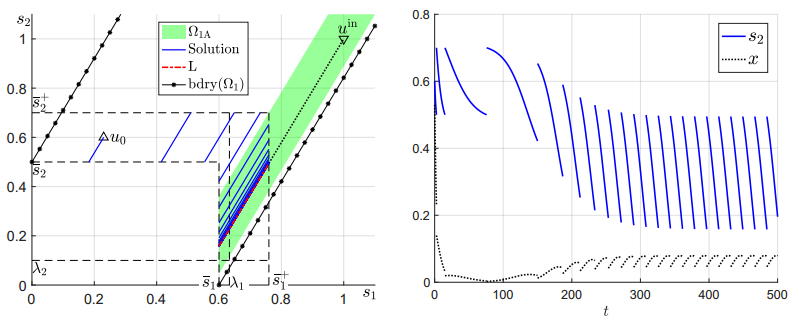
The model (2.7) with cyclic rotational grazing (2.8) is numerically integrated with Matlab using the ode45 solver. In the simulation we choose the number of paddocks n, the number of paddocks grazed at once m, and the rotational period T. For the total time of integration, we use Ttotal=365 days (1 year, as the rotational period T is much smaller (typically less than 20 days)). The initial value is chosen to be the carrying capacity, that is Vj(0)=Vmax/n. Figure 3 shows a solution trajectory with (n,m,T)=(4,3,10) for 0≤t≤365. For a solution trajectory, we can also calculate the amount of stockpiled forage; that is, the average value of n∑j=1Vj(t) over the time span.
For a fixed H value (the total number of cattle per acre), the model (2.7) can be integrated as above. We set a criterion to find a maximum sustainable cattle number HRmax. If the proper factor Vj(t)/Vj(0)=nVj(t)/Vmax in one of the paddocks is below the base proper factor from the continuous grazing situation, then the H value is not sustainable. Hence the maximum sustainable cattle number HRmax is defined as the supremum of all H values such that the proper factor in each paddock is no less than than the base proper factor in the continuous grazing model for all t>0. Numerically we calculate HRmax(Ttotal) which is not for all t>0 but only for t∈(0,Ttotal), the time period of integration. Clearly HRmax≤HRmax(T1)≤HRmax(T2) for 0<T2<T1 but when Ttotal is large, the value of HRmax(Ttotal) is close to that of HRmax. In the following we use Ttotal=365 days. We have also experimented with Ttotal=3650 days, and the results for the two cases are very close. We remark that the way of defining HRmax is not unique. For example one can define HR,∗max to be the supremum of all H values such that the solution Vj(t)>0 for all t>0 and all 1≤j≤n, or equivalently the supremum of all H values such that a positive equilibrium exists. Such a definition gives a larger value as it is clear that HR,∗max≥HRmax. But we consider the base proper factor in the continuous grazing model to be an indicator of healthiness of each individual paddock, so we believe it is more reasonable to use that as the criterion of sustainability. Moreover we will later show that HRmax(Ttotal)>Hmax (the maximum sustainable cattle number for continuous grazing case) for some choices of (n,m,T), which implies that
|
HR,∗max≥HRmax≥HRmax(Ttotal)>Hmax,
|
Hence the rotational grazing is more effective regardless of definitions of the maximum sustainable cattle number.
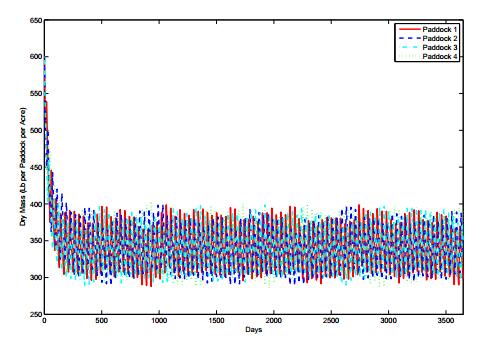
For example, if we set (n,m,T)=(4,3,10) as in Figure 3, then we find HRmax(365)=1.30 head of cattle per acre under the restriction that Vi(t)≥2400n×p=24004×0.475=285 pounds per acre for 0≤t≤365, and the stockpiled forage is VS(365)=1455.38 pounds per acre. If we keep (n,m,T)=(4,3,10), but integrate (2.7) for 0≤t≤3650 (10 years), then we find HRmax(3650)=1.28 head of cattle per acre with VS(3650)=1373.78. For Ttotal=36500, we find HRmax(36500)=1.25 head of cattle per acre with VS(36500)=1414.77.
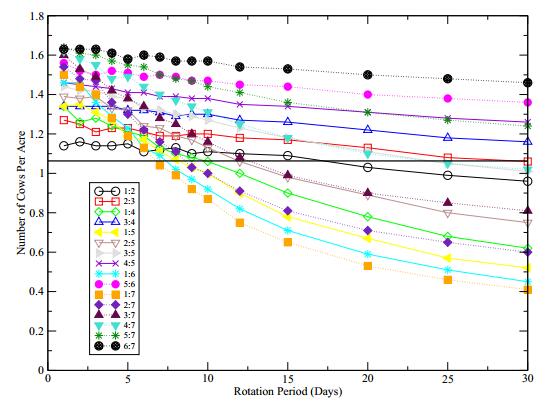
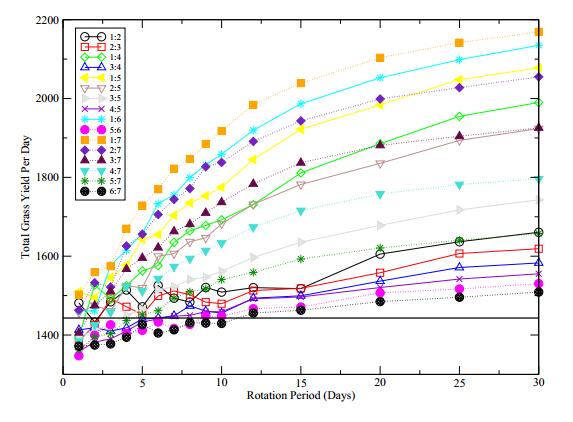
Figure 5 shows the maximum sustainable number of cattle per acre depending on the rotation period and paddock scheme, shown by m:n in the figure legend, and the bold black line shows the values in a continuous grazing system. Let HRmax(n,m,T) be the maximum sustainable number of cattle when the rotational scheme (n,m,T) is used. Then it is evident from Figure 5 that
1.HRmax(n,m,T) is decreasing in T, so a longer rotational period decreases the maximum sustainable number of cattle.
2.For the same n, HRmax(n,m,T) is larger for larger m.
As the rotation period increases, the grass is not able to sustain as much cattle as the continuous grazing case, especially in configurations with less paddocks grazed than resting, such as schemes 1:7 and 1:6. All rotational schemes in Figure 5 perform better than the continuous grazing scheme when the rotational period T is smaller than 5 days. In general, results in Figure 5 show that rotational grazing can support a larger number of cattle per acre if the rotational scheme (n,m,T) is chosen carefully.
Figure 6 similarly describes the amount of stockpiled forage for all the rotational schemes used in Figure 5. Let VRS(n,m,T) be the stockpiled forage when the maximum sustainable number of cattle is achieved and the rotational scheme (n,m,T) is used. Then we can observe that
1.VRS(n,m,T) is increasing in T, so a longer rotational period increases the stockpiled forage.
2.For the same n, VRS(n,m,T) is smaller for larger m.
As the rotation period increases, more stockpiled forage is available, mainly for the configurations mentioned above that minimize the number of cattle. Nevertheless, most grazing schemes show better yields and productivity than the continuous grazing system.
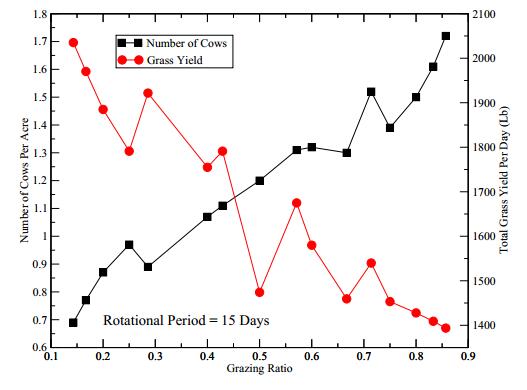
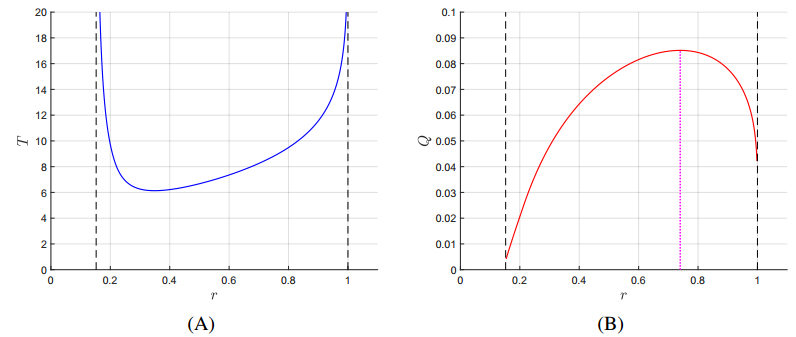
Comparing Figure 5 and Figure 6, one can see that usually a larger maximum number of cattle HRmax(n,m,T) is accompanied by a smaller amount of stockpiled forage VRS(n,m,T). This is also shown in Figure 7 where the rotational period is fixed at 15 days and the rotational schemes are represented by their grazing ratios m:n. If the goal is to maximize both the number of cattle and stockpiled forage, we can find a point that balances the number of cattle and amount of forage based on the grazing ratio. Figure 7 shows that a grazing ratio of roughly 0.45 will balance both, and that is an optimal configuration when both the number of cattle and forage amount are in consideration.
With our results, we discuss the observations made in Noy-Meir [20]. Aside from the differences in the general approaches as noted earlier, his scheme used very different values for n, T, and H. The values of n and T in [20] are much larger, ranging from 1 to 25 (with m=1) and from 10 to 80 days, respectively. The parameter H is set at a standard value of approximately 12 head of cattle per acre and serves as a fixed parameter instead of a varied parameter. Nevertheless, such a large H is possible since Vmax is set as 4460 pounds per acre and cmax is only 6.6 pounds, resulting in different ranges of solutions to the growth and consumption functions. For rotational grazing, Noy-Meir's simulations indicated that a few paddocks (n=2 or 3) and a rotation period less than 10−20 days produce yields similar to those of continuous grazing. From Figure 5, this holds true in our model as well. In addition, with a Vmax greater than roughly 1338 pounds per acre, his study revealed that a longer T and a larger n decrease average production. We confirm that such a configuration correlates with a low H, although Noy-Meir did not utilize stockpiled forage, which would increase in this situation, in evaluating productivity. However, his paper also considered a low Vmax less than 1338 pounds per acre, for which a longer T and a larger n, coupled with the availability of residual plant biomass, would improve productivity; we do not consider this scenario.
3. Conclusion
This paper mathematically compares rotational and continuous grazing and evaluates several schemes of rotational grazing through use of a differential equation model. With parameters found in agriculture literature, in continuous grazing, the proper factor 47.5% yields the maximum number of cattle 1.06 heads per acre. In rotational grazing, maximizing both the number of cattle and the amount of stockpiled forage frequently conflicts. Grazing many paddocks at once and having shorter rotation periods sustains more cattle but less stockpiled forage. On the contrary, grazing one or two paddocks at once and having longer rotation periods sustains less cattle but more stockpiled forage. Thus, depending on which variable has higher priority, one can employ a near-optimal grazing configuration as described above. In addition, a balance between the two dependent variables was achieved at a grazing ratio of approximately 0.45 for a 15 day rotational period, showing that grazing can be optimized. In almost all situations for rotational grazing, the figures exceeded those of continuous grazing, confirming that rotational grazing is more productive. Compared to agricultural publications, the ideal proper factor 47.5% and the recommended 50% have little difference in applications, and a conventional grazing period of 3−7 days seeks to maximize the number of cattle. However, an ensuing rest period of 21−42 days indicates that few paddocks are grazed at once by standard, and even 1.06 heads per acre exceeds the conventional amount of approximately 0.6 heads per acre [6]. Therefore, it is clearly possible for ranching operations to become more efficient through simultaneous multi-paddock grazing and more intensive management in general. On the other hand, our study also show that long rotation period could decrease the number of cattle supported for some rotational schemes (Figure 5), while short rotation period could reduce total grass yield for certain rotational schemes (Figure 6), so rotational grazing is not always a better strategy than the continuous one.
This study brings to attention many possible future ideas. Firstly in our model, the economical factors of implementing rotational grazing are ignored for simplicity. In reality, the fencing cost of dividing the grassland into paddocks and the labor cost of rotating cattle can be significant. Note that our results indicate that either a shorter rotational period T or a higher grazing ratio m/n lead to a larger maximum number of cattle. Adding economical factors in the cost-benefit analysis could make the result more delicate. Secondly, we use a Holling type II grazing function in the differential equation model. For some types of grasses or cattle, other kinds of grazing functions, such as the Holling type III functional response or other sigmoid functions, can be used. Moreover, a time delay can be incorporated into the model as the grass growth is not instant. Thirdly, the growth of grass strongly depends on the weather and temperature. It is known that both cool and warm season grasses decrease in quantity during winter months. It was suggested in [15] that the constant growth rate gmax in (2.3) can be replaced by a seasonal varying function
|
gmax(t)=A[(sin2π(t−24)365)2⋅e−t730+cos2(π(t−200)365)]+B.
|
(3.1)
|
These modifications can lead to possibly more accurate predictions, but we expect that the qualitative behavior of a more sophisticated model is not much different from the one we consider here. We also remark that in our study we cite several different agriculture papers for parameter values as there is no any prior agricultural study providing all parameters which we need here. In the future, it would be nice to better estimate these parameters for a single biological system to test the model which we propose here.
In general, the prediction based on our model favors rotational grazing over conventional continuous grazing. This leads to a more advanced mathematical question in optimization. Our model suggests several control mechanisms which can be optimized, and other optimization approaches have also been taken [22]. One is the control parameter trio (n,m,T), which is the total number of paddocks, the number of paddocks grazed at any time, and the rotational period. Our results have partially shed some insight regarding this optimization, but economical consideration can complicate the optimization problem. A second line of optimization is the rotational schemes. We only use the cyclic rotation scheme in this study, but apparently other rotational schemes are possible as mentioned in subsection 2.2. Exploring other rotational schemes may greatly improve the maximum number of cattle supported by the farm. A third optimization thought is on the geometric configuration of dividing the land into paddocks. Indeed, some practical ways have been implemented by farmers [21]. Usually the paddocks are in a pizza-shaped configuration with gates opened or a water fountain at the center of the circle, which can reduce the cost of rotating the cattle. Minimizing the length of fencing is another geometric consideration. Our hope is that the study given here can motivate more qualitative and quantitative modeling of rotational grazing, which has great potential of increasing the amount of agricultural product with limited resource.
Acknowledgments
We thank the anonymous reviewers and the editor for very helpful comments which improved the manuscript.









 DownLoad:
DownLoad: