1. Introduction
The amorphous alloys, such as Si-C, Si-Ge and Ge-C are very important materials in current technologies and have stimulated a growing interest due to their electrical, optical and structural properties and their low cost compared with that of the crystalline form [1,2] making them suitable for different applications. They can be prepared by several techniques: materials with composition, and hence properties, varying in a wide range are obtained changing the preparation method, the deposition conditions and/or the precursors [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,
29,30,31].
In our laboratory, hydrogenated germanium carbides have been produced by X-ray activated - Chemical Vapor Deposition from germane/hydrocarbons systems [32,33,34,35,36,37,38,39,40,41,42] which is an innovative method to obtain materials from decomposition of gaseous reactants. Our previous results indicate that, by changing the hydrocarbon species mixed with germane or the hydrocarbon/germane molar ratio in the mixture, materials in a wide range of composition with different characteristics can be obtained. For GeH4/alkane mixtures, the percentage of carbon atoms in the solid increases with the number of carbon atoms in the reactant hydrocarbon molecule but it remains low even when an high hydrocarbon molar fraction in the irradiated mixture is employed. Moreover, an increase of hydrocarbon percentage in the mixture causes a decrease of the solid yield [32,33,34,35].
When irradiation of germane takes place in the presence of unsaturated hydrocarbons, the carbon incorporation in the solid during the polymerization reactions sharply increases [36,37,38,39,40,41,42] proportionally to the unsaturation degree of the hydrocarbon. Moreover, the bonding and the properties of the materials obtained by radiolysis of mixtures with hydrocarbons having a double bond [36,37] are different from those of the solids obtained using alkynes [38,39,40,41,42].
The solids yield increases if unsaturated hydrocarbons are employed. However, results obtained in previous works using ethene or ethyne [36,37,38,39,40,41,42] show that the composition—and hence the properties —of materials are closely affected by irradiation time. The composition of deposited material changes quickly during irradiation making difficult to obtain uniform films.
Here we report the results of studies performed with the aim to obtain materials with constant composition and properties with respect to the irradiation time. Characterization of materials obtained at room temperature by X-ray activation of germane/allene mixtures with different hydrocarbon percentage and increasing irradiation dose is presented.
2. Materials and Method
The samples were obtained by X-ray activated Chemical Vapor Deposition technique, using a CPXT-320 tube by Gilardoni SpA, with a maximum output of 320 keV, as X-ray source. The absorbed dose rate of reactant species was about 5 × 103 Gy/h. The germane/allene mixtures were irradiated at room temperature in 365 mL Pyrex vessels, at a total pressure of 700 Torr, varying the total irradiation time between 1 and 5 hours. GeH4/C3H4 mixtures with 5, 10, 20, 30, 50 and 70% of allene have been irridiated.
Allene (97% purity) and GeH4 monogermane were supplied by S.I.A.D. (Società Italiana Acetilene e Derivati) S.p.A.
In the synthesis procedure, the vial bottom (with KBr pellets and quartz substrate discs) was positioned on the primary beam trajectory, so that both gaseous molecules and growing solids were activated by the main X-ray beam.
The solid products were collected, weighted and their composition was determined by means of a Thermo Electron Corporation CHNS-O analyzer for Htotal and C content while the Ge content was calculated as the difference.
The products were examined by IR spectroscopy (KBr pellets) with a FTIR Bruker Equinox 55 instrument equipped with a deconvolution program of overlapped peaks. The resolution was 2 cm−1. All spectra were recorded at room temperature.
The UV-VIS spectra were obtained with a Perkin-Elmer Lambda 15 spectrophotometer from the material deposited on the quartz disk, using a clean quartz disk irradiated at the same dose as a reference. To avoid any possible oxidation by oxygen in the air all the analyses on solids were performed immediately after opening the vials.
3. Results and Discussion
GexC1-x:H alloys have been prepared by X-Ray Chemical Vapor Deposition (X-Ray CVD) from mixtures of GeH4 with allene. The effects of the C3H4 molar fraction in the irradiating mixture on the solid chemical composition and bonding configuration have been investigated. Samples obtained from radiolysis of mixtures containing 10, 30, 50 and 70% of allene were analyzed. Moreover, since the most evident changes of solids composition are observed if allene percentage lower than 30% is employed, materials obtained after 5 hours irradiation of mixtures with 5 and 20 allene percentage have also been investigated. The irradiation dose effect on the composition, the characteristics and the properties of the deposited solids, has also been verified performing experiments varying the irradiation time from 1 to 5 hours each step.
From the irradiation of germane/allene mixtures, solid products were obtained, which deposited on the bottom of irradiated ampoules. Films were obtained when mixtures with 30% of allene were irradiated. Moreover, films were obtained from mixtures with lower or higher allene percentage for irradiation times higher than 1 hour, independently from the allene percentage, with the exception of the 5% allene mixture which leads to powders deposition after 5 hours irradiation.
It is noteworthy to remind that previously performed experiments on germane alone [43,44] produced a black powder of an amorphous cross-linked polymer whereas at the doses used here, no solid product is formed from irradiation of allene alone. Moreover, a considerably lower quantity of solid is obtained when germane is irradiated alone even if the irradiation time is higher. The experimental results indicate that reactions between GeH4 and C3H4 are greatly favored with respect the self-condensations of the two precursors and indicate that the solids collected are not simple mixture of co-precipitated hydrogenated C-C or Ge-Ge polymers, but instead a network containing Ge-C bonds. At room temperature the solids are stable to the air and insoluble in the common organic solvents. The solids composition has been determined by elemental CHNS-O analysis for H and C content while the Ge content was calculated as the difference.
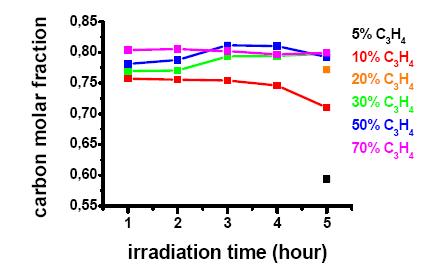
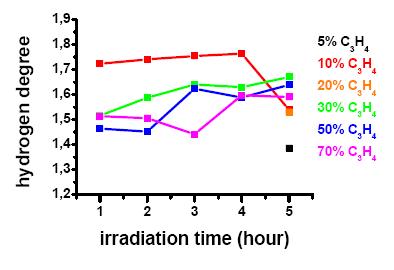
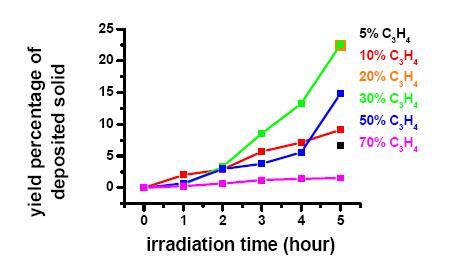
In Figure 1, the yield percentage (calculated with respect the total precursors mass) of the solid phases obtained from irradiation of the different GeH4/C3H4 mixtures and after different irradiation time are reported. C and H contents are shown in Figures 2 and 3 as carbon molar fraction (defined as C/C+Ge) and hydrogenation degree (defined as the atomic ratio H/C+Ge), respectively.
The solid yields increases with irradiation time (as expected) and little variation of the carbon content is observed for materials obtained from mixtures with the same allene percentage and irradiated for increasing time. Only, the solids obtained from 30% allene mixture exhibit a C/C+Ge ratio increasing up to 5 hours. Moreover, it is interesting to note that the carbon molar fraction varies, for each mixture, in a narrow range with respect to those observed for solids deposited from X-Ray CVD of GeH4/C2H2 systems and irradiated for the same time. For example, C/C+Ge ratio values from 0.79 to 0.86 are found for materials from mixtures with 30% of ethyne irradiated for 1 and 2 hours, respectively [40], whereas from the analogous mixture with allene, solids with about the same C/C+Ge ratio are obtained.
IR spectroscopy was used to investigate the structures and the hydrogen bonding configurations of the a-GeC:H materials obtained; these are interesting features because hydrogen can terminate the dangling bonds thus affecting the optical and electrical properties of the materials. In fact, it is known [9,45] that passivation promotes formation of sp3 hybridized C atoms over the sp2 ones thus influencing the material disorder degree.
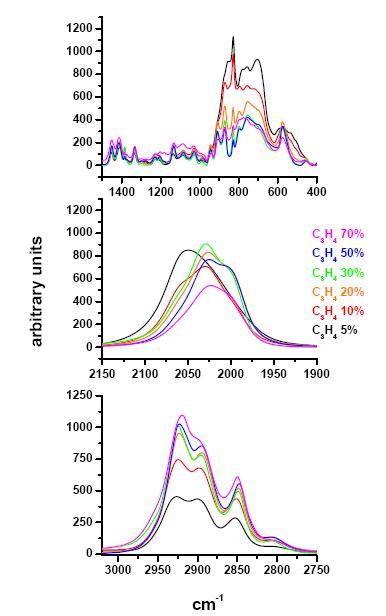
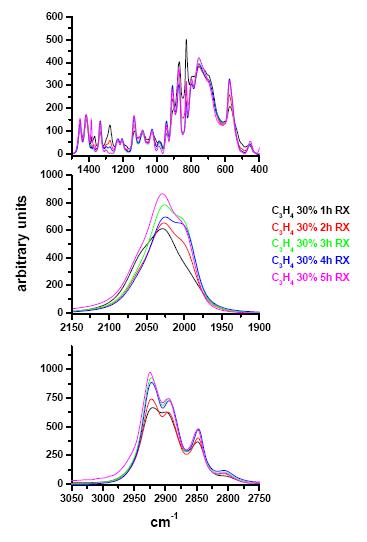
Figure 4 shows the IR spectra of the solids obtained from 5 hours irradiation of mixtures with C3H4 percentage ranging from 5 to 70% while, in Figure 5, the IR spectra of the solids obtained from mixtures with 30% of C3H4 and increasing irradiation time (1-5 hours) are reported as an example. The spectra have been superimposed and divided in three regions: from 3050 to 2750 cm−1, from 2150 to 1900 cm−1 and from 1500 to 400 cm−1.
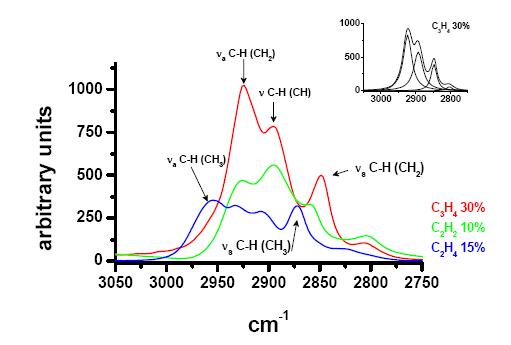
The partially overlapped bands in the 3050-2750 cm−1 range can be assigned to the C-H bonds stretching signals (νC-H). The deconvolution of νC-H peaks gives signals around 2925, 2896 and 2851 cm−1 as evidenced in the insert of Figure 6. In Figure 6 the IR absorption spectrum of the solid deposited from irradiation of mixtures with 30% of allene, irradiated for 5 hours is compared with those of solids obtained, in previous works [37,39], from mixtures with 10% of ethyne and 15% of ethene.
It is interesting to note that, as observed for samples deposited from ethyne, the signals around 2953 and 2872 cm−1, attributable to stretching modes of the C-H bond in the CH3 group, are absent, whereas they are clearly identifiable in IR spectra of solids obtained from radiolysis of germane/ethene mixtures.
Therefore, the materials obtained from radiolysis of allene mixtures only contain mono- and di-hydrocarbon groups and the bands at 2851 and 2925 cm−1 can be attributed to the symmetrical and asymmetrical stretching vibrations of hydrogen atoms in the CH2 group, respectively, while the signal around 2896 cm−1 to the C-H stretching mode in monohydrocarbon group[3,6,9,17,46,47,48,49,50,51]. The signal around 2800 cm−1 is also present, but it has not been attributed yet.
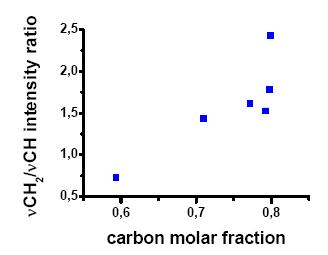
Moreover, while in the solid obtained from ethyne, the integrated absorption of deconvoluted CH stretching signal (∫νCH), is always higher than those attributed to the CH2 stretching mode (∫νCH2), in the solids from allene, ∫νCH2˃∫νCH (see Figures 4, 5 and 6). This is in agreement with the H/C ratio calculable as a difference considering the hydrogenation degree of a-Ge:H obtained from 5 hours radiolysis (H/Ge = 1.12) [44]. In fact H/C values are between 1.65 and 1.80, for 5 hours radiolysis, when allene content ranges from 10 to 70%. Therefore it can be hypothesized that H atoms are incorporated in the solid network mainly as -CH2 groups promoting the C-sp3 atoms hybridization, a polymeric-like character of the network and affecting the resulting structural order [45,52,53].
The absence of CH3 bonding configuration is a remarkable feature and it is in agreement with the above mentioned stability to the air. In fact CH3 groups favor oxidation leading to less dense materials with inner surfaces or voids [48] which allow the oxygen penetration into the sample.
Another feature in this spectrum zone is the absence of signals, at wavenumber higher than 3000 cm−1, attributable to C-H stretching modes of grouping with unsaturated carbon, even if in the carbon precursor two unsaturations are present.
The above considerations, the elemental analysis results and the absence of allene autocondensation reactions (as above reported) indicate that polymerization reactions leading to mixed species, containing Ge-C bonds, are favored.
In the 2150-1900 cm−1 wave number region the samples exhibit a signal resulting from partially overlapped peaks (Figures 5 and 6). Three deconvoluted bands are obtained around 1990, 2020 and 2050 cm−1, attributable to Ge-H bond stretching in the GeHn (n = 1-3) groups [40,43] but a univocal attribution is not possible. In fact in Ge-C:H alloys, a different number of neighbouring carbon atoms can be bound to Ge and the Ge-Hn stretching mode can be shifted as a consequence of the higher carbon electronegativity [37,45,54]. Therefore, as reported in a previous work [39], the band around 2050 cm−1 can be attributed to GeH3, C2GeH2 or C3GeH; the band around 2020 cm−1 to GeC2GeH or GeCGeH2 and the band around 1990 cm−1 can be assigned to Ge2CGeH or Ge2GeH2: each deconvoluted band is a sum of contributions of different groups.
In agreement with the above considerations the integrated absorption of deconvoluted signals does not exhibit a regular trend with increasing carbon content in the solids. Moreover, as it is evident in Figure 4, a shift of the Ge-Hn stretching band to lower wave numbers is observed with increasing allene percentage. These findings indicate a variation of the contribution of the different groups to each signal. In fact, it must be considered that the Ge-C bonds formation is promoted by an higher hydrocarbon percentage; moreover, a change of the Ge atoms hydrogenation degree is expected considering the increase of both CHn (n = 1, 2) stretching band intensities, (Figure 4) and the ∫νCH2/∫νCH ratio, shown in Figure 7. Therefore, less hydrogenated GexCyHz (x, y, z = 1-3) groups and with more C neighbouring atoms are favored.
In the 1500-400 cm−1 range the interpretation of IR spectra is difficult due to the presence of many broad and partially overlapped bands (Figures 4 and 5).
However, the GeCHn (n = 1, 2) and GeH2 bending modes [3,27,29], besides Ge-C stretching and Ge-H wagging modes, are generally found in the wave number region between 500 and 900 cm−1. Moreover, rocking vibrational modes of various skeletal group systems, such as Ge-H, Ge-C, and (CHm)n-C/Ge, are expected at 1200-400 cm−1 [3,6,40,49,55]. In particular, the sharp band at 570 cm−1 can be attributed to the superimposed signals of Ge-C stretching and GeH wagging modes. The finding that the signal intensity increases with the solid carbon content, while a decreasing of Ge atoms hydrogenation degree is expected, as above reported, confirms the signal attribution and indicates an increase of Ge-C bonds.
Optical properties
One of the most important characteristics of these materials is the optical bandgap value (Eopt), i.e. the gap between the extended state in the valence and in the conduction band. The absorption spectrum in the ultraviolet-visible range is commonly used to obtain the Eopt value.
For this reason, absorption measurements have been made at photon energies between 0.5 and 7 eV for all the solids. The optical gap values have been obtained using the common procedure of Tauc [56,57] from intercept with the x axis of the extrapolated linear part of the curve obtained by plotting (ahn)1/2 against the photon energy according to:
(ahn)1/2 = B1/2(hn-Eopt)
where a is the absorption coefficient from spectrophotometric measurements, h the Planck's constant, nthe photon frequency and Eopt is the optical band gap.
These measurements also allow to obtain the B1/2 value (so-called Tauc slope) which is considered to be a measure of the randomness of the network. Large B1/2 values correspond to high order and imply the existence of wider tails of localized states in energy band structures [58,59].
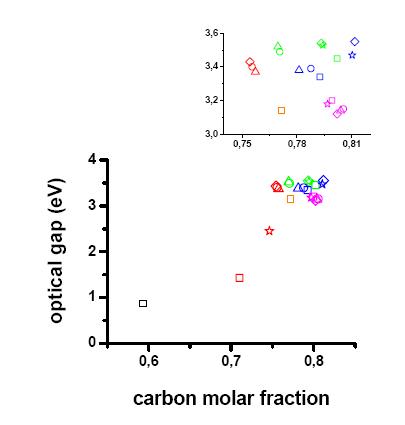
In Figure 8 the Eopt value of the solids obtained from 1 to 5 hours irradiation of GeH4/C3H4 mixtures with different percentage of C3H4 is reported as a function of carbon molar fraction.
The trend of gap values, increasing for carbon molar fraction between 0.59 and 0.75, is consistent with C sp3-bonding configuration, in agreement with the compositional and infrared spectroscopy results above reported and evidencing high hydrogen content and absence of any C-H stretching modes of grouping with unsaturated carbon. In fact, in a-GeC:H sp3 bonded alloys, the Ge-Ge bonds can be replaced by stronger Ge-C bonds or even stronger C-C bonds [60,61], leading to high Eopt values which increase with C content. For C/(C+Ge) values higher than 0.75, the Eopt is less influenced by the carbon molar fraction increase and values varying in a narrow range centered around 3.5 eV found. This is probably because for carbon molar fraction values higher than 0.75, the carbon incorporation affects the Ge-C and particularly the C-C bonds formation not so much as for lower values. This hypothesis is supported by IR results: in fact, the raise of Ge-C bond stretching signal (around 570 cm−1) observed if solids obtained with lower allene percentage (having lower C/(Ge+C) values) are compared, is sharper with respect to that observed when comparing materials from allene percentage higher than 20%.
Moreover, it is interesting to note that Eopt values around 3.5 eV are found also starting from mixtures with very different allene percentage, thus indicating that the a-GeC:H obtained not only have close composition but also show very similar structural and optical properties.
It is interesting to compare the results obtained from 1 to 5 hours irradiation of GeH4/C3H4 mixtures with 10 and 30% of C3H4 (mixtures with 50 and 70% of C3H4 show similar trend to 30%).
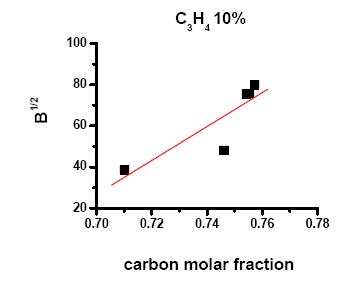
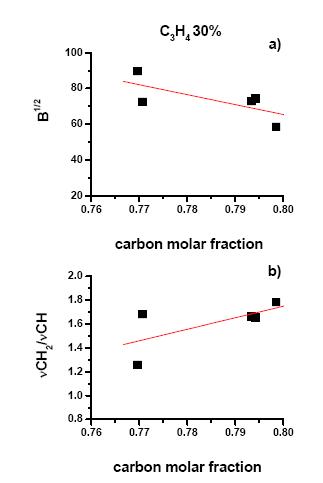
In Figures 9 and 10 the B1/2 value of solids, obtained from 1 to 5 hours irradiation of GeH4/C3H4 mixtures with 10 and 30 % of C3H4, are reported as a function of carbon molar fraction, respectively. Figure 10 also reports the ∫νCH2/∫νCH ratio as a function of carbon molar fraction.
To explain the different trend of B1/2 with carbon molar fraction, the very different nature of the material obtained from 10 and 30 allene percentage must be considered. In fact, the B1/2 value can be affected by composition, atoms distribution in the material and hydrogenation degree of carbon atoms. At low C3H4 percentage, the deposition probability of Ge-rich materials is higher and increases with irradiation time, as confirmed by composition results showing a reduction of carbon molar fraction (see Figure 2). As a consequence, amorphous germanium zones (a-Ge) can be formed in the solid matrix leading to lower Eopt and more disordered material and hence, lower B1/2 value. A calculation of Ge-rich and C-rich zones percentage in the materials is not possible, but Raman results show, for solids obtained with lower C3H4 percentage, a weak signal due to amorphous germanium clusters, while the absence of sp2 C signals confirm the polymeric character of the material.
For higher allene percentage the a-Ge zone are sharply reduced and the B1/2value mainly depends on hydrogen distribution. The ∫νCH2/∫νCH ratio increases with carbon content (figure 10) increasing the polymeric character of the material and the disorder degree [62] leading to lower B1/2 values.
4. Conclusion
GexC1-x:H alloys have been obtained by X-Ray Chemical Vapor Deposition from mixtures of GeH4 with C3H4. They can be considered a randomly bound network of carbon and germanium atoms with hydrogen atoms terminating all the dangling bonds. Moreover, the IR spectra indicate that the materials obtained from radiolysis only contain mono and dihydrocarbon groups while unsaturated hydrogenated carbon moieties are absent. This finding, the elemental analysis results and the absence of allene autocondensation reactions products indicate that polymerization reactions leading to mixed species, containing Ge-C bonds, are favored.
It is remarkable that (except for allene lower than 20%) the solids exhibit composition and Eopt value varying in a narrow range even starting from mixtures with allene content ranging from 20 to 70%. The high gap value can be attributed to C sp3-bonding configuration also favored by the high hydrogen solid content. The B1/2 value, related to the order degree, was found to be dependent on solid composition, atoms distribution in the material and hydrogenation degree of carbon atoms.
Acknowledgments
The authors thank the University of Turin for financial support.
Conflict of Interest
The authors report no conflict of interests in this research.









 DownLoad:
DownLoad: