1. Introduction

Chalcogenide based semiconductors are a broad class of materials which display a wide variety of useful electronic properties. For example, copper indium gallium selenides and cadmium tellurides are widely used in photovoltaics for power generation, [1] and bismuth tellurides are widely used for thermoelectric devices [2]. Additionally, while not as common as III-V semiconductor lasers such as gallium arsenide, zinc selenides have been used for lasing applications [3]. Moreover, cadmium tellurides, selenides, and sulfides are widely used for tunable fluorescent dyes (quantum dots) for medical research and diagnostics [4].

In the interest of extending the library of chalcogenide materials available for electronic applications, we have investigated the band structure and the partial density of states for three lanthanide sulfide systems. The lanthanide sulfides (Ln_xS_y) are a class of chalcogenides composed of a lanthanide cation (⁵⁷La-⁷¹Lu) and the anion sulfur. Sulfur is, by convention, considered as the simplest chalcogen anion due to its similarities with selenium and tellurium and dissimilarity with oxygen. Although lanthanide cations tend to prefer to take a 3+ oxidation state, several lanthanides are known to additionally take a 2+ oxidation state, for instance, as in monosulfide (LnS) or mixed valence (Ln₃S₄) structures. Generally, La through Sm can most easily take the Ln₃S₄ mixed valence structure, while Gd through Dy are capable of taking this structure with S and Se, but not with Te [5]. It is important to note that although the Ln₃S₄ structure is nominally mixed valency, each Ln atom is crystallographically equivalent in this structure. More exotic is the lanthanide monosulfide (LnS) structure, in which the rare earth cations are entirely in the 2+ state. Of the lanthanide monosulfides, samarium monosulfide (SmS) has received by far the most attention. SmS was discovered as far back as 1956 [6], and is notable for the presence of a semiconducting low pressure phase and a metallic high pressure phase [7]. More recently, lanthanum monosulfide (LaS) has received increased attention due to its metallic properties and low work function, potentially making it suitable for use as a cold cathode material [8]. However, difficulty in preparing high quality lanthanide sulfide samples with controlled stoichiometry and high crystallinity have limited the understanding and electronic applications of this class of chalcogenides. Consequently, several authors have recommended using high quality band structure calculations to enable a better understanding of the electronic structures of lanthanide sulfides [9].

In order to rectify the lack of high quality data on the lanthanide sulfides, we have applied density functional theory (DFT) to predict the electronic structures of two specific crystal systems with varying sulfide content: the LnS structure and the Ln₃S₄ structure. Additionally, calculations with the lanthanide sulfides are very time-consuming to calculate, because of the need to take into account the effect of the f-shell electrons in these many atom unit cells. Thus, we have limited our study to three lanthanide group elements: lanthanum, samarium, and gadolinium.

2. Materials and Method

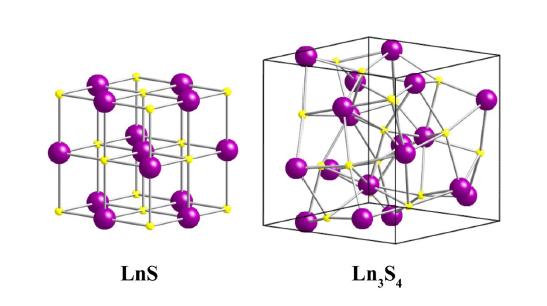
We applied density functional theory implemented in the CASTEP code [10] to calculate the band diagram and density of states of two lattice structures of lanthanide sulfides (LnS and Ln₃S₄) for three lanthanides (Ln = La, Sm and Gd). Spin-polarization was considered in the computation because both Sm and Gd have unpaired spins in these structures. The unit cell of ideal LnS adopts the NaCl structure with space group Fm-3m (#225) symmetry. The lattice parameters for LaS, SmS and GdS were obtained from the International Centre for Diffraction Data (ICDD) and are a = 5.854 Å, a = 5.970 Å, and a = 5.562 Å, respectively. The unit cell of ideal Ln₃S₄ adopts the cubic symmetry with space group I-43d (#220). The lattice parameters for Ln₃S₄ were also obtained from the ICDD, and are: La₃S₄ (a = 8.73 Å), Sm₃S₄ (a = 8.556 Å), and Gd₃S₄ (a = 8.378 Å). Both crystal structures are illustrated in Figure 1. The LnS structure is a simple rock salt cubic structure. The Ln₃S₄ structure is considerably more complex, while still remaining cubic. This structure, prototyped by Th₃P₄, is a non-centrosymmetric body centered cubic system with the space group I-43d. In this structure, there are 18 lanthanide cations in each unit cell, with two located in each face along a diagonal glide plane, and the remaining 6 making up a distorted octahedron contained within the unit cell [11]. In spite of its complex appearance, the entire structure is composed of a single unique cation Wyckoff site and a single unique anion site.

Figure 1. Unit cells of two lanthanide sulfides: (left) LnS and (right) Ln₃S₄ (Ln = La, Sm and Gd).

DownLoad: Full-Size ImgPowerPoint

The plane wave basis set was utilized together with the generalized gradient approximation (GGA), and Perdew-Burke-Ernzerhof (PBE) exchange and correlation functional [12]. An energy cutoff of 380 eV was applied to the planewave basis set and ultra-soft pseudopotentials were employed with the valence electron configurations as 5s²5p⁶5d¹6s², 4f⁷5s²5p⁶5d¹6s², and 4f⁶5s²5p⁶6s² for La, Gd, and Sm atoms, respectively. Brillouin zone integrations were performed with a Monkhorst-pack of 7 × 7 × 7 k points for the LnS structures, while 5 × 5 × 5 k points were used for the Ln₃S₄ structures. A Gaussian broadening was applied with a smearing width of 0.1 eV. The DFT+U method was used for the corrections of on-site coulomb interactions with U = 6 eV [13, 14] for the f-electrons of Sm and Gd. Moreover, the ensemble density functional theory (EDFT) [15, 16] scheme programmed in CASTEP was used to overcome the convergence problem inherent in f-electron systems.

3. Results and Discussions

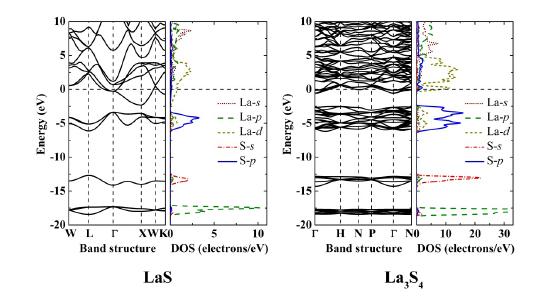
As the simplest lanthanide element, lanthanum serves as a natural place to start the discussion of the lanthanide sulfides, even though the electronic structure of LaS does exist in the literature [17]. Lanthanum takes a unique spot in the lanthanide series because it contains no f-shell electrons in its electronic structure of [Xe]5d¹6s² [18], which greatly simplifies the electronic structure calculations for lanthanide sulfides. Additionally, the electronic structure of La₃S₄ generated considerable interest in the past due to its conducting to superconducting transition temperature at 7.2 K [19]. As shown in Figure 2, both LaS and La₃S₄ are expected to behave as a metal due to occupied bands overlapping the Fermi level (shown as 0 eV in our figures). More specifically, LaS is predicted to be a semimetal due to lower occupancy at the Fermi level with large density of states above and below. This indeed is consistent with the experimentally determined properties of LaS [8, 20] and with previous calculations which made use of a full-potential linear muffin-tin orbital (LMTO) method for computing the band structure [17]. Similarly, La₃S₄ is predicted to be a metal. Although again there is a gap in energy bands less than 1 eV below the Fermi level, the calculated band structure of La₃S₄ has a high occupancy of d-orbitals at the Fermi level visible in the partial density of states (pDOS) (Figure 2). This is consistent with previously published experimental and computation results [19].

Figure 2. Band diagram and density of states of lanthanum sulfides: (left) LaS and (right) La₃S₄. The Fermi level is indicated by the dashed lines.

DownLoad: Full-Size ImgPowerPoint

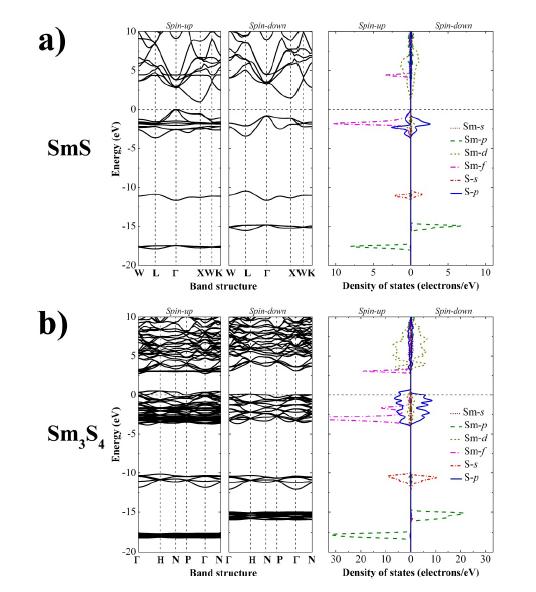
Samarium is typically believed to take the electronic structure [Xe]4f⁶6s² [18]. Unlike LaS, SmS is reported to be a narrow band gap semiconductor at atmospheric pressure and ambient temperature, but with a unique ability to switch to a metallic state at a moderately low pressure of 6.5 kbar [7]. Just as in the case of LaS, older LMTO methods were applied to simulate the band structure of SmS [21]. Our results, as shown in Figure 3, indicate SmS to be a narrow indirect band gap semiconductor with a gap of about 1 eV. This result corroborates with the observed semiconductor behavior of SmS, although it does differ from the experimental band gap of 0.15 eV [7]. Still, our calculation is an improvement from previous simulation results. Earlier work using a LMTO method predicted metallic behavior for SmS, and was forced to change the unit cell to 1.05 times the experimental values in order to introduce semiconductor behavior [21]. However, we have no reasons to doubt previous findings that a decrease in unit cell parameters (such as from high pressure) would force a narrowing of the band gap and reintroduce metallic character to the system.

Figure 3. Band diagram and density of states of samarium sulfides: (a) SmS and (b) Sm₃S₄. The Fermi level is indicated by the dashed lines.

DownLoad: Full-Size ImgPowerPoint

The electronic structure for Sm₃S₄, as shown in Figure 3, is in many ways the most surprising result of our calculations. Unlike the other systems, Sm₃S₄ has a large 2.1 eV band gap above the Fermi level. However, unlike in a well-behaved semiconductor, the Fermi level is not located inside the band gap. Instead, the Fermi level is 0.6 eV below the edge of the bottom bands, suggesting that technically Sm₃S₄ is a metal, but the large band gap’s presence gives Sm₃S₄ character similar to that of an extremely degenerate semiconductor. Surprisingly, this result is consistent with the observed properties of experimental Sm₃S₄ samples. It was found that Sm₃S₄’s extinction coefficient trails off rapidly for photon energies below 2 eV (similar to a semiconductor with a 2 eV band gap) but remains appreciable all the way down to 0 eV (similar to a metal) [22]. Additionally, this is similar to the behavior of other samarium sulfides such as alpha phase Sm₂S₃ [23].

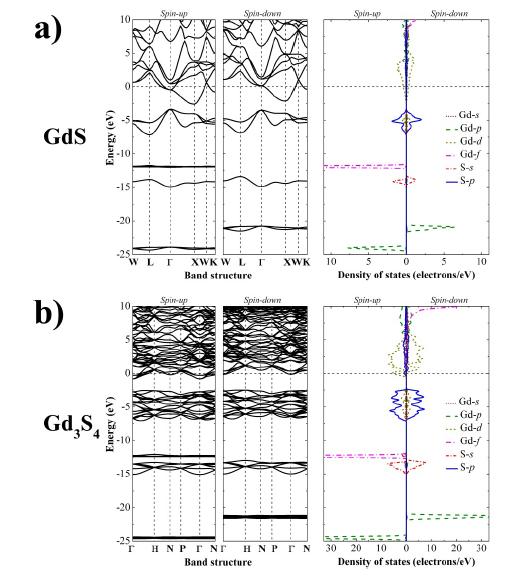
Unlike the simple case for lanthanum, gadolinium is expected to take the electronic structure of [Xe]4f⁷5d¹6s² [18]. However, similar to LaS, our calculation predicted gadolinium monosulfide (GdS) to be a semimetal with occupied d-orbitals present at the Fermi level (Figure 4).

Figure 4. Band diagrams and density of states of gadolinium sulfides: (a) GdS and (b) Gd₃S₄. The Fermi level is indicated by the dashed lines.

DownLoad: Full-Size ImgPowerPoint

Additionally, just as in the case of La₃S₄, Gd₃S₄ is a semimetal with a wide gap in energy states extending from less than 1 eV below the Fermi level to several eVs below. The partial density of states for the gadolinium sulfides provides some clues for this similarity in electronic structure with those of the lanthanide sulfides: their occupied f-orbitals are at considerably lower energy levels than in the case of samarium (~ −12 eV for both gadolinium sulfides). This is likely a consequence of Gd containing a completely half-filled f-shell, which lowers the energy levels of these orbitals. These results are in excellent agreement with the theoretical band structure of GdS and Gd₃S₄ conjectured from electron energy loss and photoemission spectroscopy experiments [24].

4. Conclusion

Band structures and partial density of states have been calculated for LaS, La₃S₄, SmS, Sm₃S₄, GdS, and Gd₃S₄ using a DFT+U approach. To the best of our knowledge, this is the first time that this approach has been applied to most of these studied systems. Additionally, our calculation results have good correlation with existing experimental measurements for these systems. LaS, La₃S₄, GdS, and Gd₃S₄ are predicted to be semimetals. While SmS is predicted to be an indirect gap semiconductor, Sm₃S₄ is expected to behave similarly to a heavily degenerate semiconductor. To improve the predictions of our computation method for other lanthanide systems where reliable f-orbital electronic contributions must be considered, further experimental measurement are needed to obtain a better estimation of the correction factor, U, for the on-site coulomb interactions.

Acknowledgements

We are grateful to the funding supports in part from Nebraska Center for Energy Sciences, NSF-EPSCoR (EPS-1010674), and Department of Energy (DE-EE0003174). We thank the University of Nebraska Holland Computing Center for providing computations resources.

Conflict of Interests

The authors report no conflict of interests in this research.