Theoretical study of Ni doping SrTiO₃ using a density functional theory

1.   Introduction

Photocatalytic water splitting using semiconductor materials provides a way to produce clean hydrogen fuel ^[1,2,3,4]. A photocatalytic water splitting has to be proper band positions, i.e., the valence band maximum V_BM should be more positive than the water oxidation potential and the conduction band minimum C_BM must be more negative than the hydrogen reduction potential, the SrTiO₃ has benne a most stability and an abundance of raw materials, and thus it is a promising photocatalyst for producing hydrogen from water using solar energy ^[5,6]. SrTiO₃ is a cubic perovskite structure material ^[7]. However, SrTiO₃ use at range of applications in many fields such as, photocatalysis ^[8,9,10], energy storage ^[11,12], sensing ^[13], micro wave devices^[14], anode material for lithium-ion batteries ^[15], H₂S solar cells ^[16], and random access memories^[17]. Can be synthesize SrTiO₃ by several methods such as sol-gel ^[18], treatment hydrothermal ^{[8,10,13,19,20]}, solid state reaction ^[15], polymeric precursor method ^[9], pulsed laser decomposition ^[21,22], co-precipitation/solvo-thermal ^[15], and electro-spinning ^[23]. And many studies have been done about metal-doped SrTiO₃, such as Fe, La and Mn ^[24,25,26].

In this work, the structural and electronic properties of both SrTiO₃ and SrNi_0.125Ti_0.875O₃ were calculated by using the full potential augmented plane wave plus local orbital (FP-(APW + lo)) method based on density functional theory (DFT) ^[27]. This is implemented in wien2k code to solve Kohn Sham equation within Full Potential Linearized Augmented Plane Wave (FP-LAPW) method. This method is one of the best methods for appropriate computation of electronic states of various crystalline solids. For structural optimization and the electronic properties the exchange correlation approximation is treated with Perdew-Burke-Ernzerhof Generalized Gradient Approximation (PBE-GGA) Trans-Blaha modified Becke-Johnson (TB-mBJ) potential is employed ^{[28,29,30,31]}.

The outline of this paper is as follows: in section computational details, we give the computation details. The results and discussion are presented in section results and discussion. Finally section conclusions concludes the paper.

2.   Computational details

All calculations were performed in the framework of the density function theory (DFT) ^[27] using the WIEN2k package ^[32], the full-potential Linearized augmented plane-wave method (FP-LAPW) ^[27] and the generalized-gradient approximation PBE-GGA with the exchange-correlation functional suggested by Perdew, Burke, and Ernzerhof (PBE) ^[27].

In these computations, and in order to investigate the structural and electronic properties of SrTiO₃ and SrNi_0.125Ti_0.875O₃, the unit cell is separated in two regions, an interstitial region and non-overlapping atomic spheres. In each of these regions, Kohn-Sham wave functions and charge densities as well as electronic potentials are calculated in a different way inside the unit cell. Inside the atomic sphere, they are defined usually by the RMT (radius of muffin tin) around the position of each atom, a spherical harmonic expansion is used, whereas in the interstitial space of the unit cell a plane wave basis set is taken into account. RMT values were chosen as 1.65 a.u. for O, 1.75 a.u. for Ti, 1.8 a.u. for Ni and 2.2 a.u. for Sr. Charge density was Fourier expanded up to G_max = 12 au⁻¹. The plane wave cut-off K_max × R_MT radius was taken such that R_MT × K_max = 9. For convergence of energy we used a 7 × 7 × 7 k-points grid in the special irreducible Brillouin zone. The self-consistent convergence criteria of total energy calculations of the system were achieved when the total energy stabilized within 10⁻⁴ Ry.

3.   Results and discussion

3.1.   Structural analysis

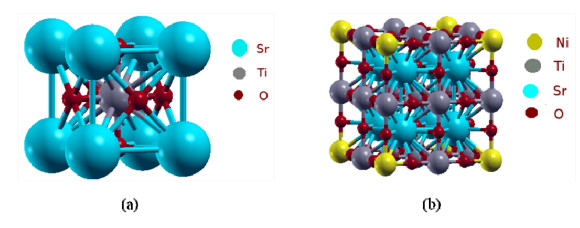
For the calculion of structural and electronic properties of Ni doped SrTiO₃, we adopt for the SrTiO₃ compound—a cubic structure (space group). Pm3m where atomic positions in the elementary cell as presented in Figure 1a are Sr: (0, 0, 0); O: (0, 1/2, 1/2), (1/2, 1/2, 0), (1/2, 0, 1/2); and Ti: (1/2, 1/2, 1/2) When, for the Ni-doped compound SrNi_0.125Ti_0.875O₃, we build a cubic super-cell having twice the cell parameter of the parent SrTiO₃ compound Figure 1b whose atomic positions are listed in Table 1.

Figure 1.  (a) SrTiO₃ perovskite structure, and (b) supercell of SrNi_0.125Ti_0.875O₃ structure.

DownLoad: Full-Size Img PowerPoint

Table 1.  Atomic positions for cubic supercell SrNi_0.125Ti_0.875O₃.

Atom	Positions
Sr	(0.75, 0.75, 0.75)(0.25, 0.25, 0.25)(0.25, 0.75, 0.75)(0.75, 0.25, 0.25)(0.25, 0.25, 0.75)(0.75, 0.75, 0.25)(0.75, 0.25, 0.75)(0.25, 0.75, 0.25)
Ni	(0, 0, 0)
Ti	(0.5, 0.0, 0.0)(0.0, 0.5, 0.0)(0.0, 0.0, 0.5)(0.0, 0.5, 0.5)(0.5, 0.0, 0.5)(0.5, 0.5, 0.0)(0.5, 0.5, 0.5)
O	(0.0, 0.0, 0.75)(0.0, 0.0, 0.25)(0.75, 0.0, 0.0)(0.25, 0.0, 0.0)(0.0, 0.75, 0.0)(0.0, 0.25, 0.0)(0.5, 0.0, 0.75)

---

 | Show Table

DownLoad: CSV

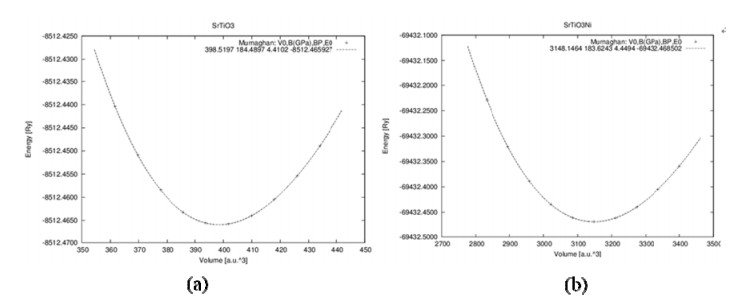
All calculations were performed for a 40 atom (5 × 8) super-cell (with a₀ = 7.81 Å) (Figure 1b). The optimization of the lattice constants for SrTiO₃ and SrNi_0.125Ti_0.875O₃ is made by minimization of the total energy. The calculate lattice parameters, bulk moduli, pressure derivatives B' for SrTiO₃ and SrNi_0.125Ti_0.875O₃ were calculated by fitting the total energy E versus volume V data to the non-linear Murnagham equation of state ^[27]. We present the E (V) relationship of both SrTiO₃ and SrNi_0.125Ti_0.875O₃ in Figure 2a, b respectively.

Figure 2.  Calculated total energy curves as a function of cell volume for (a) SrTiO₃ and (b) SrNi_0.125Ti_0.875O₃.

DownLoad: Full-Size Img PowerPoint

Table 2 presents the calculate lattice parameters, bulk moduli, their pressure derivatives B' together with available experimental data and other theoretical data for both SrTiO₃ and SrNi_0.125Ti_0.875O₃. The value of our calculated lattice constants for both SrTiO₃ (3.894 Å) and SrNi_0.125Ti_0.875O₃ (3.877 Å). This is in good agreement with the experiment results ^[7] that the lattice constant of SrNi_0.125Ti_0.875O₃ films increase after doping. From the values of bulk moduli, we can conclude that the SrNi_0.125Ti_0.875O₃ is slightly less stable than SrTiO₃.

Table 2.  Calculated lattice constants, bulk moduli B, pressure derivatives B' and compared to experimental data and other available works for SrTiO₃ and SrNi_0.125Ti_0.875O₃.

Compounds	Method	Approximation	Lattice constant (Å)	B (GPa)	B'	Refs.
SrTiO3	FP-LAPW	PBE-GGA	3.894	184.489	4.41	Present
	Experimental	Experimental	3.905	/	/	[7]
	FP-LAPW	GGA-96	3.905	184	/	[33]
			3.87	194	/	[34]
SrNi0.125Ti0.875O3	FP-LAPW	PBE-GGA	3.877	183.62	4.44	Present

---

 | Show Table

DownLoad: CSV

3.2.   Electronic properties

3.2.1.   Density of states

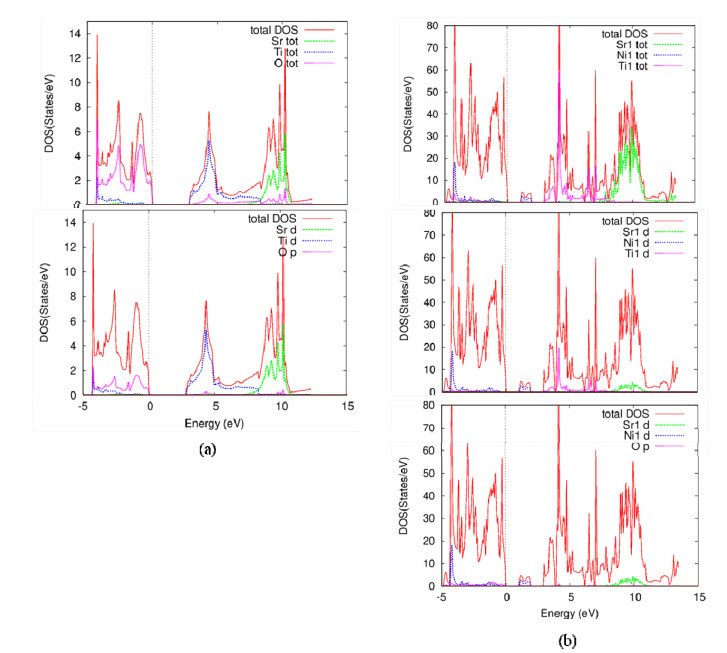
In this section, the electronic structures for both SrTiO₃ and SrNi_0.125Ti_0.875O₃ will be studied and compared to each other. Several indicators will be used to detect the effects of Ni doping on the SrTiO₃ electronic composition, which is total DOS and states partial density (PDOS). From these tools, some aspects of structural features can be demonstrated. The total DOS and PDOS for SrTiO₃ are first calculated for comparison and the results are shown in Figure 3a. For clarity, only the Ti 3d, O 2p and Sr 5p PDOS are shown and this will be evident in the following figures. The top of the valence bands (VBs) mainly consists of O 2p states and the most important vacancy power bands in the lower conduction bands (CBs) mainly consist of Ti 3d states. There is no interference between PDOS between Sr atoms and O atoms, meaning that the Sr-O bonds have a high ion city. Furthermore, the band gap in SrTiO₃ is about 2.857 eV, which is less than the experimental value (of about 3.2 eV) ^[32]. This is naturally underestimated by the DFT ^[35,36] and by cause the strong self-interaction of the Ti 3d states ^[37] (Figure 3).The total DOS and PDOS for SrNi_0.125Ti_0.875O₃ are shown in (Figure 3).Where we see the control of both the Ti 3d, Ni 3d, O 2p and Sr 5p PDOS are shown and this will be evident in the following figures. The top of the valence bands (VBs) mainly consists of Ni 3d and O 2p states and the most important vacancy power bands in the lower conduction bands (CBs) mainly consist of Ti 3d states. We also notice no overlap between PDOS Sr atoms and O atoms, meaning that the Sr-O bonds have a high ion. Furthermore, the band gap in SrNi_0.125Ti_0.875O₃ is about 1.078 eV. From all this we conclude that Ni atoms reduce the band gap and improve the effectiveness of SrTiO₃.

Figure 3.  The calculated total and partial density of states for (a) SrTiO₃ and (b) SrNi_0.125Ti_0.875O₃.

DownLoad: Full-Size Img PowerPoint

3.2.2.   Band structure

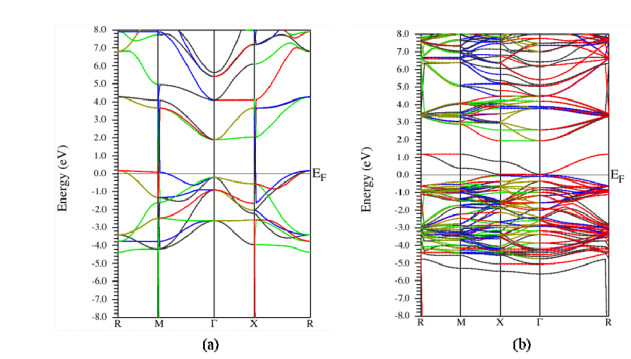
We calculated the band structures of SrTiO₃ (Figure 4), and the effect for all doping by nickel metal atoms on the electronic properties of SrTiO₃. We found that the SrTiO₃ has an indirect gap Γ-M point of Brillouin zone, and our calculated value of this gap (about 2.857 eV) is lower than the experimental value (around 3.2 eV). The largely, due to the well-known shortcoming of exchange-correction functionals in describing, excited states using the PBE-GGA approximation ^[38,39]. However, the characters of band structures and the relative variation of band gap are reasonable and reliable, so a scissors worker (1.3 eV) was performed to correct the underestimation of the band gaps of doped SrTiO₃ ^{[35,36,37,38,39,40]}. Figure 4 shows the calculated band structures SrNi_0.125Ti_0.875O₃ and SrTiO₃ around band gap states. Because 1.078 eV, which is an indirect gap (Γ-M point of Brillouin zone). Two isolated defect bands crossing the Brillouin zone make a great decrease to the band gap, thus the optical absorption edge towards the visible light region is largely expanded. The defect bands are close to the valence band, which indicates that Ni dopant atoms are the acceptor impurities, leading to the increase of whole concentration ^[39].

Figure 4.  Electronic band structure of (a) SrTiO₃ and (b) SrNi_0.125Ti_0.875O₃.

DownLoad: Full-Size Img PowerPoint

3.2.3.   Charge density

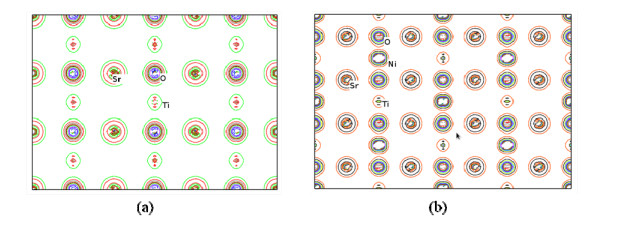
Figure 5 represents the charge density of SrNi_0.125Ti_0.875O₃ and SrTiO₃. The Sr, Ti, and Ni atoms contain more basic electrons, resulting in a higher overall density of charge near the nucleus position, while oxygen atoms are larger with a large number of valence electrons. In the compounds SrTiO₃ and SrNi_0.125Ti_0.875O₃, we note a difference in ionic bonds between Ni-O and Ti-O. This is due to the electronic distribution of Ni and Ti atoms.

Figure 5.  Charge density on the (111) plane for (a) SrTiO₃ and (b) SrNi_0.125Ti_0.875O₃.

DownLoad: Full-Size Img PowerPoint

4.   Conclusion

We investigated the structural and electronic properties of Ni-doped SrTiO₃ by a first-principles calculation of FP-LAPW method based on DFT. The calculated results the structure of SrNi_0.125Ti_0.875O₃ is less stable than that of pure SrTiO₃. The Ni fully acts as an electron donor in SrNi_0.125Ti_0.875O₃ and the Fermi level shifts into the CBs after Ni doping. The DOS of the SrNi_0.125Ti_0.875O₃ system shift toward low energies and the band gap of SrTiO₃ is 2.857 eV and reduced by about 1.779 eV for SrNi_0.125Ti_0.875O₃.

Conflict of interests

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.