Insights into cell motility provided by the iterative use of mathematical modeling and experimentation

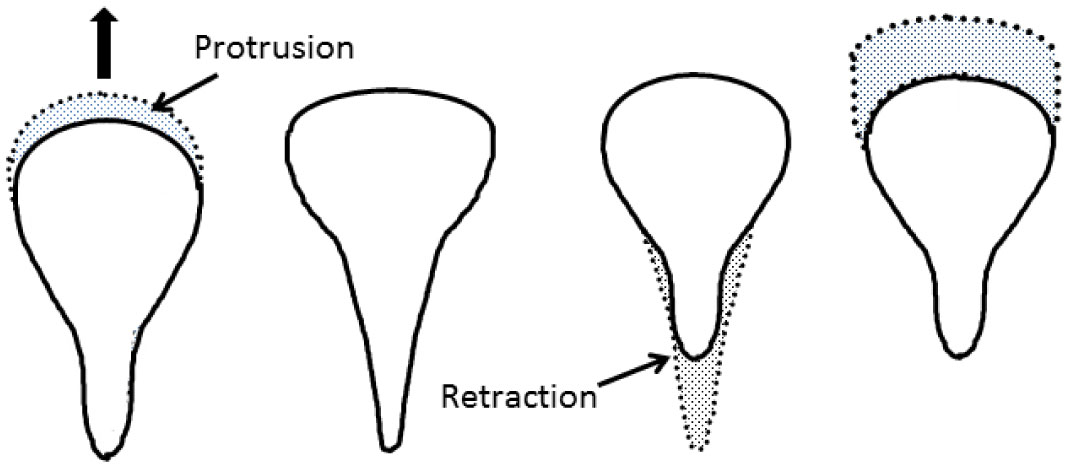
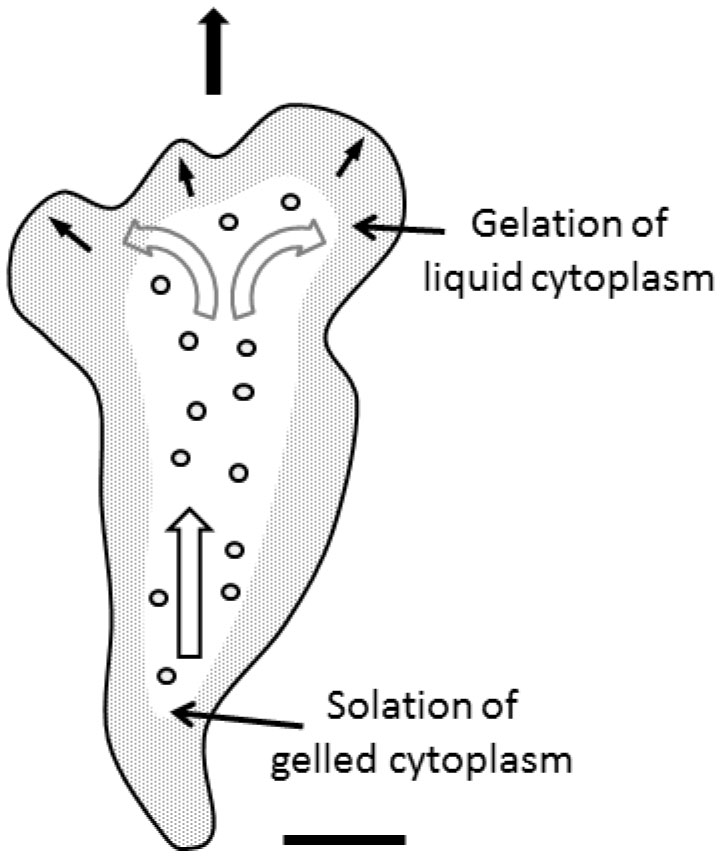
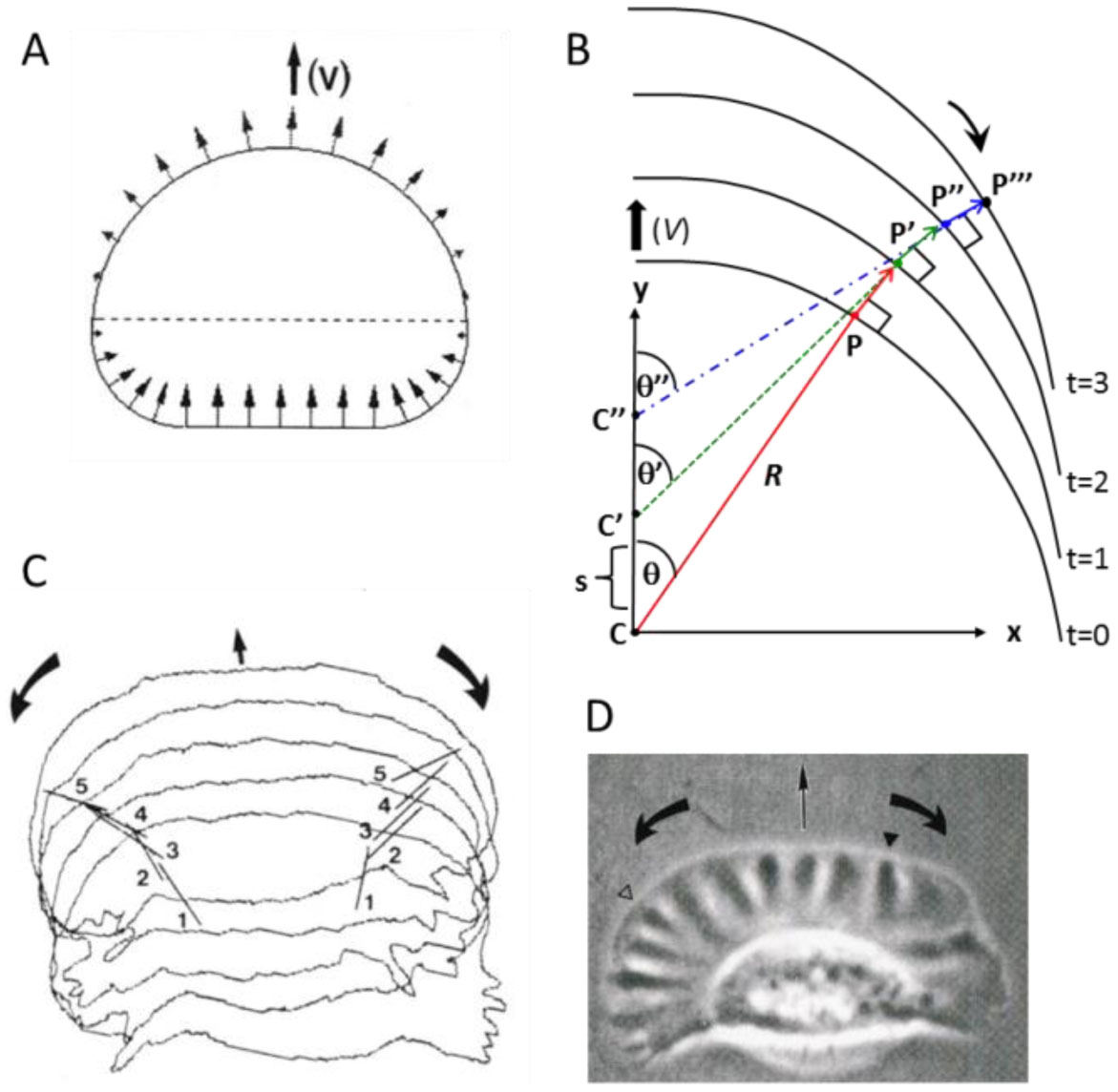
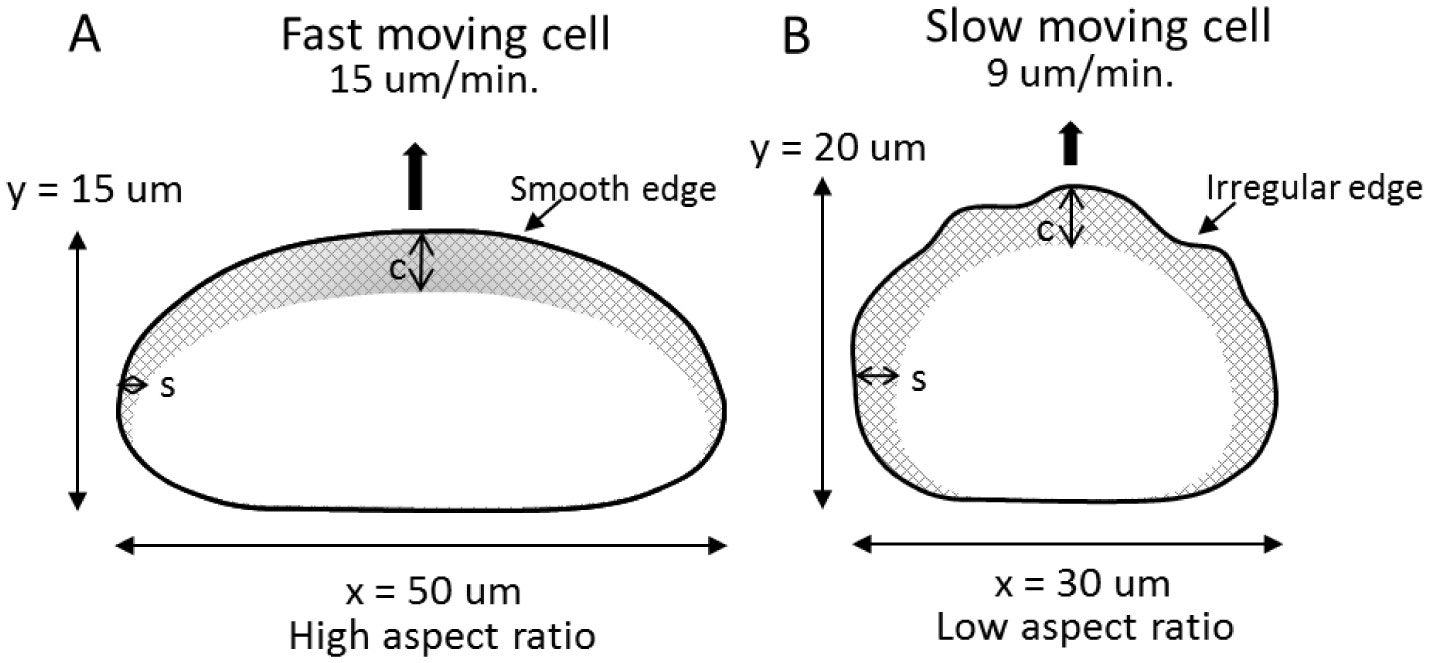
Cell movement is a complex phenomenon that is fundamental to many physiological and disease processes. It has been the subject of study for more than 200 years, and yet we still do not fully understand this process. Cell movement consists of four steps; protrusion and adhesion formation at the front followed by contractile force generation and detachment at the rear. Much is known about the molecular mechanisms underlying these steps however, it is not clear how they are integrated at the cellular level. Part of the problem is the incorporation of a vast amount of molecular and biophysical data into a basic working model of motility. A promising solution to this problem is the combined approach of mathematical modeling and experimentation, using the fish epithelial keratocyte as a model system. The goal of this review is to illustrate, using examples, how the reciprocity between experimentation and modeling can provide new insights into the mechanism of cell motility. Several modeling approaches are described including: conceptual models, “bottom-up” models based on molecular dynamics, and “top-down” models that consider cell shape and movement. The Graded Radial Extension (GRE) model forms the basis of a several mathematical models, from a simpler 1D model that links actin filament dynamics to cell shape, to more complex 2D and 3D simulations of keratocyte movement. Together these models suggest that cell movement emerges from the mechanical interaction between different sub-processes of motility, namely, the treadmilling actin meshwork, the plasma membrane, adhesion turnover and contractile force generation. In addition, the feedback regulation between these sub-processes is important for the robust, self-organizing nature of movement.