1. Introduction
In a
short period of time metal halide perovskite (MHP) materials, with the general
formula ABX3, have revealed outstanding optoelectronic properties
that make them uniquely suited for photovoltaic applications [1,2,3,4]. Along
with their rapid development from liquid junction to solid state cells
[5,6,7], the power conversion efficiency (PCE) was promoted from the initial 3.8% to recent
values over 22% [8], thus standing close to nowadays inorganic thin film technologies [9]. A
better control on the perovskite film morphology and composition through a
large variety of solution processed techniques, together with an optimization
of the device structure and interfaces, have allowed to a large extend such
meteoric rise in efficiency [10,11,12,13,14,15,16,17,18,19]. However, there
are still open questions regarding the role of the different interfaces present
in the cell on the related charge processes that need to be further clarified.
MHP
solar cells in planar configuration are strongly demanded at the forefront of a
future next generation of printable photovoltaics [20]. In such
case, the perovskite layer is sandwiched in between two charge transporting
interlayers resulting in n-i-p or p-i-n like architectures [15]. Although
they resemble in a way the configurations adopted by polymer solar cells (PSCs), the intrinsic characteristics of the perovskite layer are the ones governing
the most the charge carrier lifetime and diffusion lengths [21,22,23,24]. On
the other hand, electron and hole selective layers (ESLs and HSLs, respectively)
are expected to fulfil the requirements to facilitate charge transport and to assist
charge collection towards the respective electrodes, thus being essential in
determining the final device performance [14,15]. Despite
the mesoscopic TiO2 n-i-p architectures have yielded the highest
efficiencies reported so far [8,25,26], different
metal oxide ESLs deposited as thin films have been proposed to simplify the device
fabrication process. Among them, SnO2 has recently demonstrated to
be a promising choice due to its high electron mobility, wide band gap and long
stability under UV illumination [27,28]. Also, ensembles
based on a double ESL have been suggested to allow a more suitable energy band
alignment with the conduction band of the perovskite material
[29,30].
Similarly, although a great effort has been done on searching efficient HSL
alternatives, small molecule type compounds, typically 2, 2', 7, 7'-tetrakis(N, N-di-p-methoxyphenylamine)-9, 9'-spirobifluorene
(spiro-OMeTAD), have dominated the superior overall performances until now. However, their intrinsically low conductivity and the associated instability issues
derived from the use of chemical dopants, which are added to increase the
conductivity in presence of O2, may compromise somehow the
reproducibility and long term stability of the
devices [31,32,33,34,35,36]. Besides, when the n-i-p architecture is considered, the HSL is sought to protect the quite
sensitive absorber layer against the external humidity conditions by acting as
a functional barrier [37,38,39]. Indeed, a variety of approaches
has been also explored with the aim of hindering the moisture ingress through the
top HSL
[40,41,42,43].
Herein
we evaluate and analyse the behaviour of different conjugated polymers when
employed as the HSLs in planar perovskite solar cells designed with a typical
n-i-p architecture. Such semiconducting polymers have been widely used in a
variety of soft electronics, including PSCs, due to both their good film
forming ability when processed through solution techniques and their unique and
tuneable optical and electrical properties [44,45,46,47]. In
spite of the high charge mobility they can exhibit in their pristine form, the
parasitic absorption displayed over the visible range has restricted to a large
extent their use in the context of perovskite solar cells [15]. However, several studies have already demonstrated that the morphology and crystallinity
of such polymeric compounds can play a crucial role on the efficacy of charge
extraction and recombination and, therefore, on the final performance of the
device
[48,49,50,51,52,53].
In addition to an efficient charge generation and collection, raised open circuit voltage (Voc) values
are also desired. Those will be mainly determined by the energy differences
between the Fermi levels of the ESL and the HSL. For this reason, apart from revealing
suitable hole mobility and chemical compatibility with the perovskite layer, another prerequisite to be accomplished by the HSL is that of a proper energy
band alignment with the active layer. On the basis of such requirement, poly-3-hexylthiophene
(P3HT) and poly([2, 6'-4, 8-di(5-ethylhexylthienyl)benzo[1, 2-b; 3, 3-b]dithiophene] {3-fluoro-2[(2-ethylhexyl)carbonyl]thieno[3, 4-b]thiophenediyl})
(PTB7-Th) are chosen herein as the hole transporting materials for planar perovskite
solar cells. Those have demonstrated to give rise to optimal device performance
when employed in bulk heterojunction PSCs [54,55]. Moreover, although P3HT has been explored in other research works within the field of
perovskite solar cells, chemical dopants or more sophisticated approaches to
tune its electrical properties have usually been employed to reach the best efficiency
values
[56,57,58].
In the present study, we pay attention to establish a possible correlation
between the corresponding photovoltaic features and the dissimilar HSL
properties for optimized devices yielding overall performances over 14%. Also, general aspects regarding the cell stability and the barrier protection
provided by the different polymeric compounds will be discussed. To the best of
our knowledge, no previous studies on the stability of the multilayer stacks or
the complete devices have been carried out before when incorporating such kind
of conducting polymers, free of additives, and under ambient conditions.
2. Materials
and Methods
All
commercially available chemicals were employed without any further
purification. A 40 nm transparent film made of TiO2 was first deposited
by spin coating on top of the previously cleaned conductive fluorine tin oxide
(FTO) substrates (8 Ω·cm−2, Pilkington®). To do
so, a 0.25 M solution of titanium (Ⅳ) isopropoxide (TTIP 97%, Sigma Aldrich) in
anhydrous ethanol (99.5%, Sharlau) was prepared by slowly adding the titanate
precursor onto the alcoholic solvent while stirring. A final concentration of
0.02
M
in hydrochloric acid (HCl 37%, Sigma Aldrich) was adjusted to avoid the
precipitation of slurries during the preparation of the solution. A rotation speed
of 3000 rpm was held during 40 seconds to give rise to the required thickness, the substrates being afterwards thermally annealed at 150 ℃ during 20 minutes
and, subsequently, at 500 ℃ for 30 minutes. After cooling down, they were
transferred to a N2 glovebox for next fabrication steps. Similarly
to the recipe reported by Lee at al. [7], the
MHP precursor was prepared by dissolving methylammonium iodide (CH3NH3I
99.5%, 1-Material) and lead(Ⅱ) chloride (PbCl2 98%, Sigma-Aldrich) in
dimethylformamide (DMF 99.8%, Sigma-Aldrich) with a 3:1 molar ratio and a 32 wt% concentration.
The perovskite solution was spin-coated on top of the ESL at 1500 rpm and the
resulting films were annealed for 2 hours at 90 ℃ and 20 minutes at 125 ℃. For
the HSL precursors, P3HT (4002-E, Rieke) and PTB7:Th (1-Material) solutions
with a concentration of 15 mg/ml and
10
mg/ml, respectively, were prepared in anhydrous chlorobenzene (CB 99.8%, Sigma
Aldrich) and kept under stirring overnight at 60 ℃ before using. They were
also deposited by spin coating the respective solutions at a rotation speed of
2000 rpm during 45 seconds. Finally, an 80 nm thick gold top contact layer was
evaporated in a high vacuum chamber (Lesker). The deposition rate was adjusted
to 0.6 Å/s and a metal mask was place to define an active area of 0.096 cm2.
The
optical transmission of the different samples was measured over the wavelength
range of interest using a UV-vis-NIR spectrometer (Lambda 950, PerkinElmer).
Both the surface morphology and the cross section of the samples were evaluated
by field emission scanning electron microscopy (FEG-SEM, FEI Inspect F50-EBL).
The X-ray diffraction (XRD) patterns were recorded with a Bruker D8 Advance
diffractometer (Bruker, Cu-Kα source). Film thickness values were checked
employing a surface profilometer (KLA-Tencor Alpha-Step IQ Surface Profiler).
The photovoltaic performance of the fabricated solar cells was determined using
an AM 1.5G solar simulator (Sun 3000, Abet Technologies). The illumination
intensity corresponding to 100 mW·cm−2 was adjusted with a monocrystalline
silicon reference cell (Hamamatsu) calibrated at the Fraunhofer Institute for
Solar Energy Systems. The current density-voltage characteristics (JV) curves
were then recorded by scanning voltages from negative to positive (forward) and
from positive to negative (reverse) using a Keithley 2400 SourceMeter. EQE
analysis was performed using a quantum efficiency measurement system (QEX10, PV
Measurements). In this case, the devices were illuminated using a monochromatic
light coming from a Xenon lamp. The spectral response of the
calibrated silicon cell was used as a reference. All set of devices were tested
under ambient conditions and without encapsulation.
3. Results
and Discussion
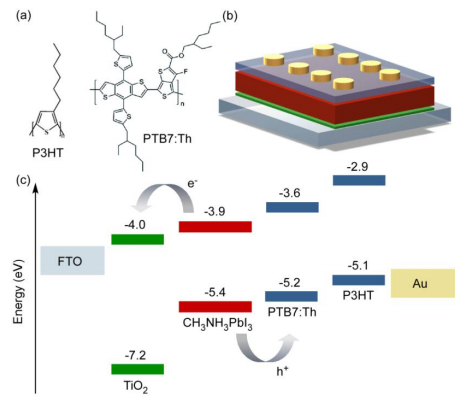
The
simplified molecular structures corresponding to the P3HT and PTB7:Th polymers to
be used as HSLs can be found in Figure 1a. A scheme of the planar n-i-p device
configuration proposed and the energy level diagram of the studied materials
are also illustrated in Figures 1b–c.
As
clearly seen, the MHP is sandwiched in between a thin and compact layer of TiO2
and the HSL. FTO substrates and gold layers are used as the respective bottom
and top contacts. The same colour code for both the scheme and the diagram was
used to identify each one of the layers composing the device. The energy levels
for the different materials were extracted from the literature. From them, a
proper alignment between the conduction bands of the ESL (TiO2) and
the perovskite is observed. Similarly, the highest occupied molecular orbitals
(HOMO) energies suitably matched that of the perovskite valence band.
An
optical characterization of both the perovskite and the HSL constituents was performed
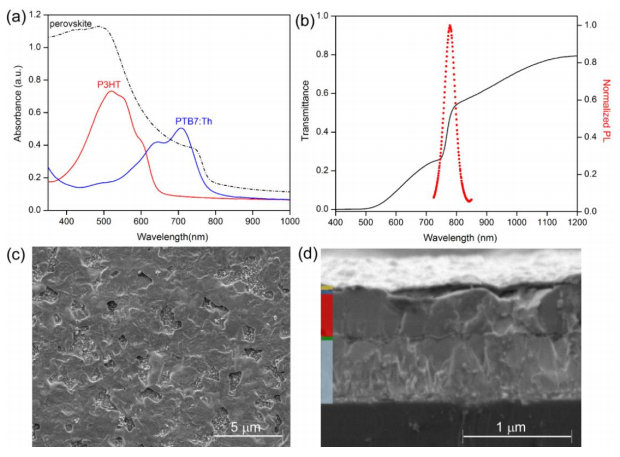
prior to the evaluation of the device performance. Figure 2a displays the
absorbance measured for perovskite and polymeric films when deposited onto
common glass substrates following the general procedure described in the
Materials and methods section. While the MHP exhibits an absorption that is extended
over the whole visible range, ranging from 350 to 760 nm, the conjugated
polymers present narrower absorption bands centred at 530 nm and 700 nm for the
P3HT and PTB7:Th, respectively. In principle, parasitic losses may be affecting
the most in the case of PTB7:Th since its corresponding absorption takes place
at a wavelength range in which the one resulting from the perovskite starts to
decrease. However, by conventional optical spectroscopy, it is difficult to
evaluate separately the contribution of useful and parasitic absorption in the
polymeric compound since photoexcitation can generate charge carriers in both
the perovskite and the HSLs. As shown in Figure 2b, the steady state photoluminescence
measured when the perovskite film was excited with a 532 nm continuous wave
laser coincides with the onset of absorption detected in the transmittance
spectrum.
Figures
2c–d show SEM images taken from the top view of a perovskite layer and from the
cross section of a complete cell in which P3HT was employed as the HSL. A long
range interconnected and multi-faceted crystallites were observed from the top
view image. Also, in spite of the special care taken during the crystallization
process, large void spaces were formed into the films as a consequence of the
removal of excess material during the thermal annealing step, as suggested
elsewhere
[11].
On the other hand, the continuous perovskite layer can be clearly appreciated
from the cross section image, the thicknesses of the different layers being
about 40 nm, 350 nm, 75 nm and 80 nm for the ESL, MHP, HSL and Au, respectively. Those were also double checked by using a surface profilometer.
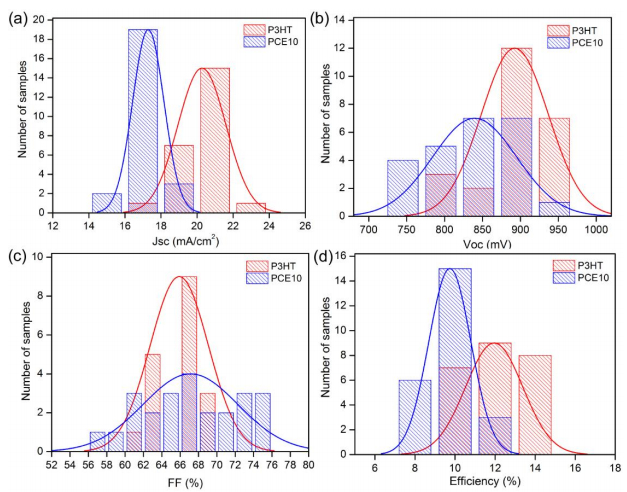
The
photovoltaic parameters extracted from the corresponding JV curves of complete
devices integrating P3HT and PTB7:Th are compared in Figures 3a–d.
Histogram
plots are used to check the frequency distribution of each single variable
dataset: the short circuit photocurrent density (Jsc), the open circuit
photovoltage (Voc), the fill factor (FF) and the overall efficiency. For the
analysis, a total of 24 samples were considered and the voltage scans were
carried out from open circuit to short circuit conditions. As displayed in
these graphs, higher Jsc and Voc were obtained for the case of devices based on
P3HT as the HSL. Given that the FF values were similar in both cases, although with
a narrower distribution for P3HT devices, the best device performances were still
attained for perovskite solar cells integrating P3HT polymer. An average
efficiency of about 12% was observed for P3HT based solar cells, which means an
improvement of above 20% with respect to the average values achieved for the
PTB7:Th ones. These preliminary results suggest that, to sufficiently translate
the deeper HOMO levels of conjugated polymers into higher Voc values, strategies
for further improving and designing solution-processed interfacial materials
should be taken into consideration.
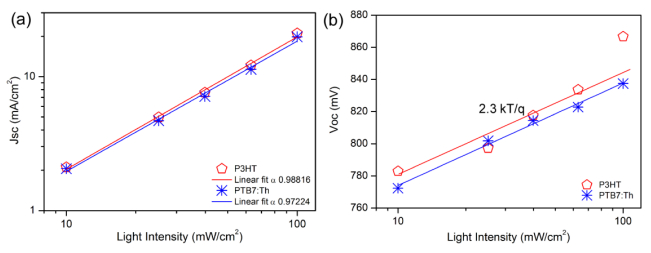
Since
the loss of photogenerated charge carriers can be associated to different recombination
processes taking place within the device, a deeper insight into the possible
factors or mechanisms determining the resulting photovoltaic characteristics is
required. To probe the kinetics of charge carrier recombination, the JV curves
were measured while the complete devices were illuminated over a range of light
intensities going from 10 to 100 mW/cm2. Representative perovskite
solar cells displaying photovoltaic parameters over the average range were
selected to carry out this study. In Figures 4a–b, the Jsc and Voc data are
plotted on a log-log and linear-log scale, respectively. The Jsc-light
intensity curves show a similar dependence for both the P3HT and PTB7:Th based
devices. In this case, the curves were fitted according to the relation Jsc ∝ Фα, where Ф corresponds to the light intensity and α to the exponent of the
dependence. The factor α was calculated to be close to 1 in both cases, which implies
that photocurrent is determined by the generation rate of electron–hole pairs
due to photon absorption. The deviation from α = 1 is
typically attributed to bimolecular recombination or unbalanced charge
transport of electrons and holes [59]. On the other
hand, the light intensity dependence of Voc reveals the dominant recombination
mechanism in the device as no external current is extracted under such
conditions and all of the photogenerated charge carriers recombine. Slopes of
kT/q and 2kT/q will indicate dominant bimolecular and trap-assisted
recombination, respectively [60,61]. In here, a
similar behaviour is also attained for both kinds of devices, a slope of ~2.3
kT/q being calculated. That means that trap assisted recombination is still the
main recombination mechanism in perovskite solar cells. However, due to
significant changes in the charge collection probability, which seems also to
be dependent on the light intensity at a given applied voltage, bimolecular
recombination cannot be completely disregarded. Although recombination channels
can be present at the grain boundaries of the perovskite and at the interfaces, the latter has been conferred as the dominant loss mechanism
[62,63,64].
Nonetheless, perovskite morphologies prepared under certain preparation methods
might be more sensitive to the sign of traps, thus playing a crucial role on
the final device performance and affecting the hysteretic behaviour of the
cell.
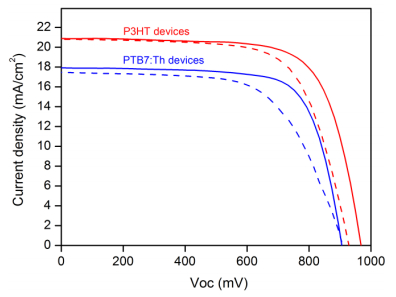
In
order to investigate the hysteresis of the fabricated devices, the JV characteristics
curves were sweeping from both forward and reverse directions. The results
corresponding to the best performing cells are presented in Figure 5 and
summarized in Table 1. All experimental data were collected without applying
any preconditioning voltage to the cells. A slight hysteretic behaviour can be
deduced from the graph, which affected mainly to the FF value of the devices
while the Jsc and Voc were kept almost unaltered. This behaviour is more
frequently shown in planar perovskite solar cells as a consequence of either
the reduced contact area between the perovskite layer and the respective charge
selective layers or the ineffective charge extraction of the latter. Although
some studies have tried to correlate the density of traps and mobile ionic defects
with the hysteretic behaviour [64], it is quite
challenging yet the extrapolation to the large variety of perovskite
morphologies, compositions and device configurations reported up to date.
Table 1. Summary of the photovoltaic parameters extracted from the Ⅳ curves presented
in Figure 5 and measured for perovskite solar cells using P3HT and PTB7:Th under
standard one sun illumination condition (100 mW/cm2).
| Device configuration |
Jsc (mA/cm2) |
Voc (mV) |
FF (%) |
PCE (%) |
| FTO/TiO2/MHP/P3HT/Au from OC to SC |
20.9 |
968 |
71.4 |
14.4 |
| FTO/TiO2/MHP/P3HT/Au from SC to OC |
20.8 |
929 |
68.2 |
13.2 |
| FTO/TiO2/MHP/PTB7:Th/Au from OC to SC |
17.9 |
906 |
73.1 |
11.8 |
| FTO/TiO2/MHP/PTB7:Th/Au from SC to OC |
17.5 |
906 |
63 |
10 |
As it can be clearly observed in Table 1, the perovskite solar cell based on P3HT displays PCE values of 14.4% and 13.2%
when scanned in forward and reverse directions, respectively. In a similar way, that incorporating PTB7:Th as the HSL exhibits PCE values of 11.8% and 10% in
the forward and reverse scans. As commented before, almost no changes in the
Jsc and Voc were observed, while the reduction in the FF value was around 4.5%
and 14% for the case of perovskite solar cells incorporating P3HT and PTB7:Th. It
means that around 92% and 85% of the efficiency values measured under reverse
scan were maintained for the forward sweep in both kinds of devices.
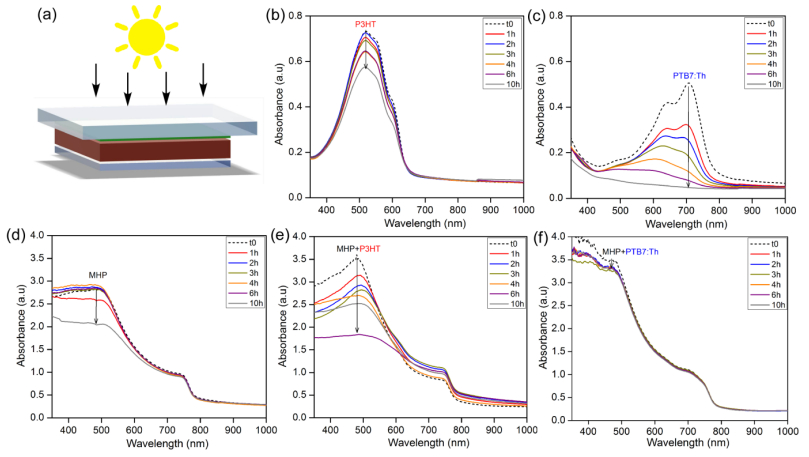
Finally, in order to address the stability issue of perovskite solar cells, a
preliminary study of the barrier properties offered by the two conjugated
polymers was carried out by means of optical measurements. Although no evidence
of degradation after prolonged time exposures was noticed during the
photovoltaic characterization of the complete devices (Figure S1 in the Supplementary
section), such test could be employed as a quick tool to evaluate the stability
of individual and stacked layers under stressed conditions (light, temperature
and H2O). To do so, the samples were kept under continuous
illumination at 1 sun while the corresponding optical properties were check at
certain time intervals (every 1 hour in this experiment). Since the final goal
was to identify any degradation signal over the visible spectral range, those
were constructed onto common glass substrates following the proposed n-i-p
architecture and without depositing the top metallic layer. A schematic drawing
of the samples under 1 sun illumination is depicted in Figure 6a, and the
results extracted from this analysis are presented in Figures 6b–f.
No UV
filters were employed during the illumination of samples and the humidity in
the laboratory was around 40%. Those are key parameters that can determine the
kinetics of deterioration in polymeric and perovskite materials. Figures 6b–c
show the clear degradation of the different polymeric compounds under simulated
sunlight illumination conditions. Whereas P3HT still preserved its optical
features after 10 hours of continuous illumination, PTB7:Th became almost
transparent over the visible, with no apparent absorbance after this time.
However, when the perovskite layer was considered, the sample covered by
PTB7:Th surprisingly kept (Figure 6f) the same response after the 10 hour
illumination time. It might be explained due to the synergy of both the
perovskite and the PTB7:Th films, the former blocking the UV radiation to reach
the polymeric material and the latter behaving as an effective barrier
protection to avoid the ingress of moisture. On the other hand, the most
significant change detected in the bare and P3HT coated perovskite films was
located at the spectral range comprised between 350 nm and 600 nm, as shown in
Figures 6d–e.
4. Conclusions
The
results presented in this work show the potential that different conjugated
polymers can have when performing as HSLs in perovskite solar cells. P3HT and PTB7:Th
based devices were herein evaluated to establish a possible correlation between
the photovoltaic performance and the respective optical and electrical
properties conferred by the polymeric material. Although parasitic losses seem
to be affecting the most in the case of perovskite solar cells integrating
PTB7:Th as the HSL, recombination kinetics extracted from the light intensity
dependence of Voc reveal the same behaviour in both types of devices, with a
trap assisted recombination being the main loss mechanism. Even though, performances of around 14% and 12% in reverse voltage scans, or 13% and 10% in
forward scans, were reached for pristine P3HT and PTB7:Th based solar cells, respectively. Since chemical additive free polymers are desired for long term
stability cells, this study opens the door for a conscious and rational optimization
of the electrical and optical properties of polymeric compounds to yield perovskite
solar cells with an optimal compromise between efficiency and stability.
Acknowledgments
This
research was carried out at ICFO with financial support from the Spanish MINECO
(Severo Ochoa program, grant No.: SEV-2015-0522), the MINECO and the Fondo
Europeo de Desarrollo Regional FEDER (grant No.: MAT2014-52985-R), the Fundació
Privada Cellex, and from the EC FP7 Program (ICT-2011.35) under grant agreement
n NMP3-SL-2013-604506. The author thanks the collaboration of Dr. Miguel Montes-Bajo
for his assistance with the structural characterization of the samples
presented in this paper.
Conflict of
Interest
The
author declares no conflicts of interest in this paper.









 DownLoad:
DownLoad: