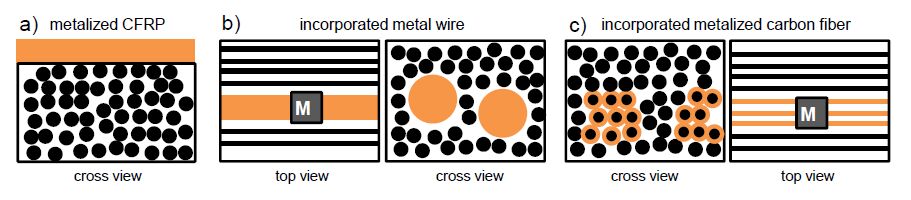
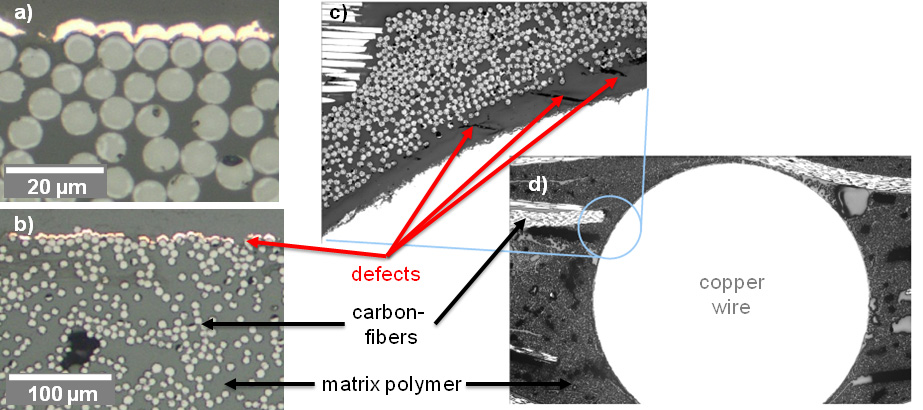
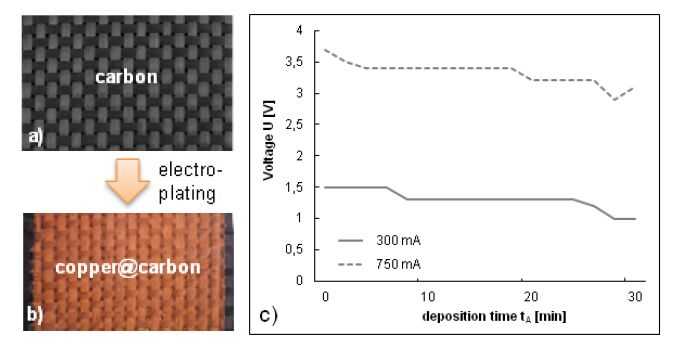
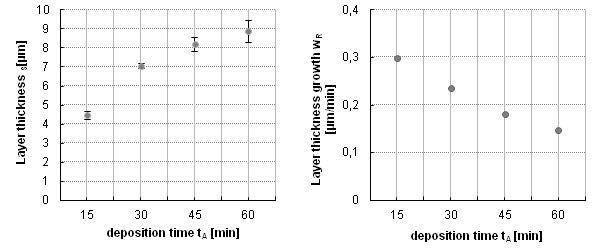
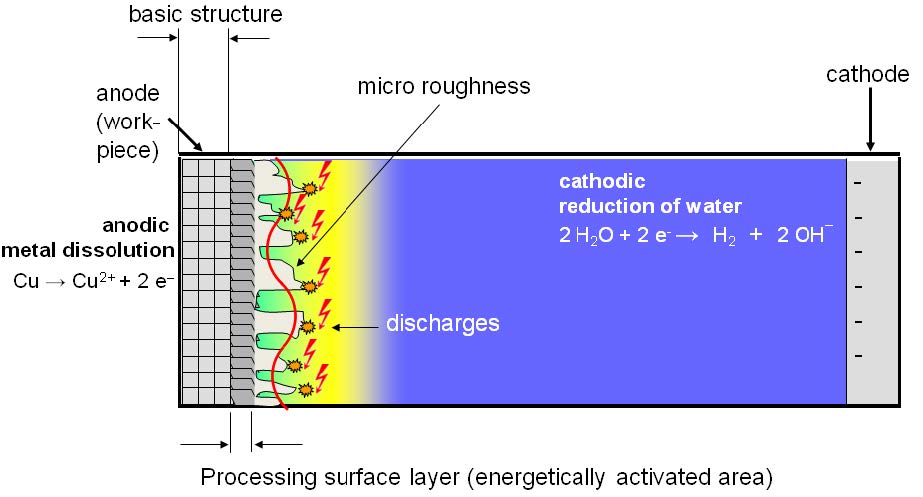
Efficient lightweight structures require intelligent materials that meet versatile functions. Especially, carbon-fiber-reinforced polymers (CFRPs) are gaining relevance. Their increasing use aims at reducing energy consumption in many applications. CFRPs are generally very light in weight, while at the same time being extremely stiff and strong (specific strength: CFRPs: 1.3 Nm kg–1, steel: 0.27 Nm kg–1; specific stiffness: CFRPs: 100 Nm kg–1, steel: 25 Nm kg–1). To increase performance and especially functionality of CFRPs, the integration of microelectronic components into CFRP parts is aspired. The functionalization by sensors, actuators and electronics can enable a high lightweight factor and a new level of failure-safety. The integration of microelectronic components for this purpose requires a working procedure to provide electrical contacts for a reliable connection to energy supply and data interfaces. To overcome this challenge, metalized carbon fibers are used. Metalized fibers are, similar to the usual reinforcing fibers, able to be soldered and therefore easy to incorporate into CFRPs. Unfortunately, metalized fibers have to be pre-treated by flux-agents. Until now, there is no flux which is suitable for mass production without destroying the polymer of the CFRP. The process of plasma electrolytic polishing (PeP) could be an option, but is so far not available for copper. Thus, in this study, plasma electrolytic polishing is transferred to copper and its alloys. To achieve this, electrolytic parameters as well as the electrical setup are adapted. It can be observed that the gloss and roughness can be adjusted by means of this procedure. Finally, plasma electrolytic polishing is used to treat thin copper layers on carbon fibers.
1.
Introduction
The communication between neurons is commonly mediated by endogenous messengers called neurotransmitters. These chemical mediators influence our physical and mental health. For instance, monoamine neurotransmitters regulate our mood, sleep, social behavior and stress response [1,2,3,4,5]. These neurotransmitters are synthesized in the brain monoaminergic system; in other words, the brain neural circuitry including serotonergic, dopaminergic, and noradrenergic neurons is responsible for the synthesis of serotonin, dopamine and norepinephrine, respectively [1,2,3,4,5]. Major depressive disorder (MDD), usually known simply as depression, has been consistently associated with an impaired monoaminergic neurotransmission [1,2,3,4,5]. Also, oscillations in the levels of the monoamine neurotransmitters have been hypothesized to cause mood disorders in depressed patients [1,2,3,4,5]. In fact, most depressed individuals report mood swings [6,7,8]. Here, it is shown that mood fluctuations can be a consequence of the interaction of these three neurotransmitters.
There are mathematical models about the interplay among CRH (corticotropin releasing hormone), ACTH (adrenocorticotropic hormone) and cortisol [9,10]. Dysregulation of the neuroendocrine system controlling these three hormones has also been associated with MDD [10]. However, up to now, there is no approved medication acting on these hormones for treating MDD symptoms [11]. In fact, the available drugs usually target the monoaminergic system [1,4]. Mathematical models about the dynamics of dopamine [12], serotonin [13] and norepinephrine [14] can be found in the literature, but no model was found about the mutual influence of serotonin, dopamine, and norepinephrine.
Prior to the current COVID-19 pandemic, MDD affected about 5% of the population worldwide [15]. Unfortunately, due to the pandemic, this prevalence has increased [16]. Different aspects of MDD have been studied by using distinct mathematical approaches, such as artificial intelligence techniques [17], complexity measures [18], game theory [19], population dynamics [20], regression algorithms [21], signal analysis [22], statistical analysis [23]. In this work, the role of monoamine neurotransmitters in mood regulation is investigated from a dynamical systems theory perspective [24,25].
Bifurcation analyses have been carried out in theoretical works about neurodynamics [26,27]. In these works, Hopf bifurcation can occur and it is usually related to the emergence of periodic spiking. Here, a bifurcation analysis is carried out in a model about monoamine neurotransmission. This analysis shows that Hopf bifurcation can occur and it can be related to the emergence of mood oscillations. The proposed model can undergo a Hopf bifurcation by varying the value of a parameter that can be altered by taking antidepressants.
This manuscript is organized as follows. In Section 2, a mathematical model about the neurotransmitter dynamics is proposed. In Section 3, the long-term behavior of this model is analyzed. In Section 4, numerical simulations are performed by taking values of the model parameters in order to obtain plausible numbers for the neurotransmitter concentrations. In Section 5, the possible relevance of this work is stressed.
2.
The mathematical model
Let the levels of serotonin, dopamine, and norepinephrine in the blood plasma at the time $ t $ be respectively denoted by the variables $ S(t) $, $ D(t) $ and $ N(t) $. The proposed model is written as the following set of nonlinear ordinary differential equations:
In this model, $ \alpha $ and $ \beta $ are the constant influxes of serotonin and dopamine, respectively; $ a $, $ e $ and $ g $ are the rate constants related to degradation/reuptake of serotonin, dopamine and norepinephrine, respectively; $ b $ is the rate constant related to the excitatory effect of dopamine on serotonergic neurons [28]; $ c $ is the rate constant related to the excitatory effect of norepinephrine on serotonergic neurons [29]; $ f $ is the rate constant related to the inhibitory effect of serotonin on dopaminergic neurons [28]; and $ h $ is the rate constant related to the conversion of dopamine into norepinephrine [30]. The nine model parameters ($ \alpha $, $ \beta $, $ a $, $ b $, $ c $, $ e $, $ f $, $ g $ and $ h $) and the three variables ($ S(t) $, $ D(t) $ and $ N(t) $) are positive real numbers. In the next section, this model is analyzed by using methods from dynamical systems theory [24,25].
3.
Analytical results
In the state space $ S \times D \times N $, an equilibrium point $ (S^*, D^*, N^*) $ corresponds to a stationary solution obtained from $ F_1(S^*, D^*, N^*) = 0 $, $ F_2(S^*, D^*, N^*) = 0 $ and $ F_3(S^*, D^*, N^*) = 0 $, in which $ S^* $, $ D^* $ and $ N^* $ are constants. This model presents a single positive equilibrium point with coordinates:
in which $ x = afg $, $ y = aeg-\alpha fg - \beta (bg + ch) $ and $ z = -\alpha eg $. This equilibrium point exists for any set of positive parameter values. Notice that $ N^* $ is written in terms of $ D^* $, which depends on $ S^* $ (which depends only on the model parameters).
The local stability of this equilibrium point can be determined from the eigenvalues $ \lambda $ of the Jacobian matrix J computed at this point [24,25]. The matrix J expresses the linearization of the original dynamical system around such a point. Recall that the eigenvalues $ \lambda $ of J are computed from $ \det ({\bf{J}}- \lambda \bf{I}) = 0 $, in which $ \bf{I} $ is the identity matrix. According to the Hartman-Grobman theorem, $ (S^*, D^*, N^*) $ is locally asymptotically stable if all eigenvalues have negative real part [24,25]. In this case, the matrix J is given by:
The eigenvalues $ \lambda_1 $, $ \lambda_2 $ and $ \lambda_3 $ of $ {\bf{J}}(S^*, D^*, N^*) $ are the roots of:
According to the Routh-Hurwitz stability criterion [31], the roots of this polynomial have negative real part if $ \theta_1 > 0 $, $ \theta_2 > 0 $, $ \theta_3 > 0 $, and $ \theta_1 \theta_2 - \theta_3 > 0 $. In this case:
Obviously, the conditions $ \theta_1 > 0 $, $ \theta_2 > 0 $, and $ \theta_3 > 0 $ are satisfied; therefore, the asymptotical stability of $ (S^*, D^*, N^*) $ depends on the sign of $ \Delta \equiv \theta_1 \theta_2 - \theta_3 $. For $ \Delta > 0 $, this steady state is locally asymptotically stable.
Serotonin has a predominant role in mood fluctuations in depressed patients [32]. Hence, several commonly prescribed antidepressants alter the value of $ a $, that is, the reuptake of this monoamine [4,11]. In this study, $ a $ is considered the bifurcation parameter.
Let the three eigenvalues of J be written as $ \lambda_1(a) = \rho(a) + i \omega(a) $, $ \lambda_2(a) = \rho(a) - i \omega(a) $, and $ \lambda_3(a) = - \sigma(a) $, with $ i = \sqrt{-1} $. Hopf bifurcation occurs if there is a critical value of $ a $, called $ a_c $, such that $ \rho(a_c) = 0 $, $ \omega(a_c) \neq 0 $, $ d \rho(a)/da|_{a = a_c} \neq 0 $, and $ \sigma(a_c) > 0 $ [24,25].
For the third-order polynomial given by Eq (3.3), there is a Hopf bifurcation if $ \Delta(a) = 0 $ and $ \partial \Delta(a)/\partial a \neq 0 $ for $ a = a_c $. These conditions, which were already found (for instance) in ecological [33] and electronic systems [34], are derived by inserting $ \lambda_1 = \rho + i \omega $ into Eq (3.3) and by separating the real part from the imaginary part. Thus, the following expressions are obtained:
For $ \omega \neq 0 $, an expression for $ \omega^2 $ is obtained from Eq (3.8) and it can be used to rewrite Eq (3.7) as [33]:
If $ \Delta = 0 $ for $ a = a_c $, then $ \rho = 0 $ is the only real root of Eq (3.9). Also, by differentiating $ Q = Q(\rho(a), a) $ with respect to $ a $ by taking into account the Implicit Function Theorem [24,25], then:
As $ \theta_1 > 0 $ and $ \theta_2 > 0 $, then $ d \rho/da|_{a = a_c} \neq 0 $ if $ \partial \Delta/\partial a|_{a = a_c} \neq 0 $.
In short, the point equilibrium with coordinates given by Eq (3.1) experiences a Hopf bifurcation for $ a = a_c $ if $ \Delta(a_c) = 0 $ and $ \partial \Delta/\partial a|_{a = a_c} \neq 0 $. In this case, Eq (3.3) is written as $ \lambda^3+\sigma \lambda^2+ \omega^2 \lambda + \sigma \omega^2 = 0 $. In fact, for $ a = a_c $, then $ \lambda_{1, 2} $ are imaginary numbers (because $ \rho(a_c) = 0 $ and $ \omega(a_c) = \sqrt{\theta_2(a_c)} $) and $ \lambda_3 $ is a negative real number (because $ \sigma(a_c) = \theta_1(a_c) > 0 $). For $ \Delta(a) < 0 $, an asymptotically stable limit cycle appears. Recall that a limit cycle is a closed and isolated trajectory in the state space, which corresponds to a solution that varies periodically in time [24,25]. Here, limit cycle implies oscillatory neurotransmitter levels, which can be associated with mood fluctuations. Hence, mood fluctuations can be caused via Hopf bifurcation of the nonlinear system ruling the neurotransmitter interplay.
4.
Numerical results
Computer simulations were performed in order to illustrate the analytical results derived above. Here, the value of $ a $ is varied and the other eight parameters are kept fixed. In these simulations, $ b = 0.001 $, $ c = 0.04 $, $ e = 3 $, $ f = 0.1 $, $ g = 2 $, $ h = 80 $, $ \alpha = 50 $ and $ \beta = 200 $. These parameter values were chosen in order to obtain realistic numbers for $ S^* $, $ N^* $ and $ D^* $.
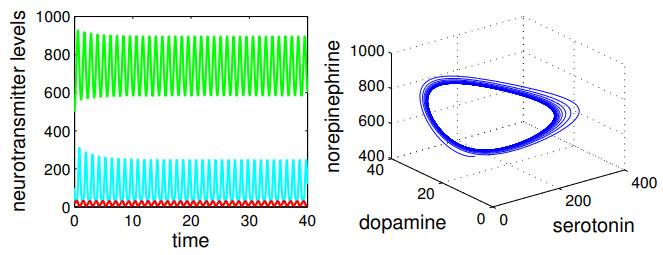
Figure 1 shows the time evolutions of $ S(t) $ (cyan line), $ D(t) $ (red line) and $ N(t) $ (green line) for $ a = 20 $. In this case, $ S(t) \to S^* \simeq 133 $, $ D(t) \to D^* \simeq 12 $, and $ N(t) \to N^* \simeq 490 $, which are the coordinates of the equilibrium point found from Eq (3.1). Since $ \Delta \simeq 207 > 0 $, this point is asymptotically stable, as observed in the numerical simulation. Figure 2 shows $ S(t) $, $ D(t) $ and $ N(t) $ for $ a = 30 $. In this case, $ \Delta \simeq -70 < 0 $; therefore, the equilibrium point is unstable and the trajectory converges to a limit cycle.
The computer simulations revealed that, for the parameter values used in Figures 1 and 2, there are two critical values of $ a $, denoted by $ a_{c1} $ and $ a_{c2} $, so that for $ a < a_{c1} \simeq 25.9 $ and $ a > a_{c2} \simeq 68.8 $, the system converges to a stationary solution; for $ a_{c1} < a < a_{c2} $, the system converges to an oscillatory solution. In fact, for $ a > 25.9 $, an attracting limit cycle emerges; however, this cycle disappears for $ a > 68.8 $. For instance, for $ a = 75 $, then $ \Delta \simeq 65 > 0 $ and $ S(t) \to S^* \simeq 15 $, $ D(t) \to D^* \simeq 45 $, and $ N(t) \to N^* \simeq 1789 $.
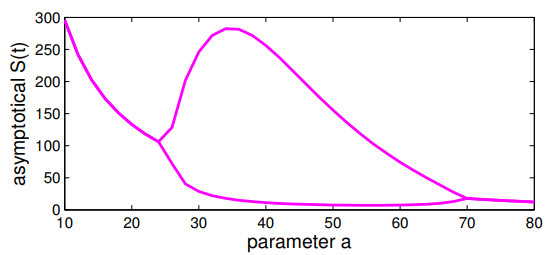
Figure 3 presents the asymptotical behavior of $ S(t) $ in function of $ a $: for $ a < a_{c1} $ and $ a > a_{c2} $, the plot shows the coordinate $ S^* $ of the attracting equilibrium point; for $ a_{c1} < a < a_{c2} $, the plot shows the minimum and the maximum of the attracting oscillatory behavior of $ S(t) $. Thus, Hopf bifurcations occur for $ a = a_{c1} $ and $ a = a_{c2} $.
5.
Discussion and conclusions
The normal ranges of $ S(t) $, $ D(t) $ and $ N(t) $ in human blood plasma are 50–200 ng/mL, 0–30 pg/mL and 200–1700 pg/mL, respectively [35]. Notice that the coordinates of the asymptotically stable steady-state shown in Figure 1 correspond to an individual with normal levels of these three neurotransmitters.
Figures 2 and 3 show that the long-term behavior of $ S(t) $, $ D(t) $ and $ N(t) $ can be oscillatory. Such an oscillation can be suppressed, for instance, by increasing $ \alpha $. For instance, for $ \alpha = 100 $ and $ a = 30 $, the convergence is to the steady state given by $ S^* \simeq 81 $, $ D^* \simeq 18 $ and $ N^* \simeq 719 $, which are numbers that belong to the normal ranges of the three neurotransmitters [35].
Most available antidepressants are monoamine reuptake inhibitors; that is, they inhibit the reuptake of a monoamine neurotransmitter, which increases its extracellular level [4,11]. In the model, taking a serotonin reuptake inhibitor corresponds to decreasing the value of $ a $. Notice that for $ a = 20 $ (which can represent either a non-depressed individual or an individual being treated with antidepressants), the neurotransmitter levels tend to a steady state, which is in contrast to the oscillatory behavior observed for $ a = 30 $ (which can represent an untreated depressed individual).
In short, the neurotransmitter interactions considered in the proposed model can be at least partially the underlying biochemical basis of mood swings experienced by depressed individuals. This conclusion leads to the following conjecture: the intrinsic mechanism of mood shifts observed, for instance, in people with anxiety syndromes [36] and bipolar disorders [37] can also be a type-Hopf bifurcation. The predictions of the proposed model can be tested by using experimentally obtained parameter values.
Acknowledgments
RL thanks to Instituto Presbiteriano Mackenzie for the scholarship. LHAM is partially supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) under the grant #304081/2018-3. This study was also supported by Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) (finance code 001).
Conflict of interest
The authors declare that they have no conflict of interest.










 DownLoad:
DownLoad: