1.
Introduction
The notion of extriangulated categories, whose extriangulated structures are given by E-triangles with some axioms, was introduced by Nakaoka and Palu in [1] as a simultaneous generalization of exact categories and triangulated categories. They gave a bijective correspondence between Hovey twin cotorsion pairs and admissible model structures which unified the work of Hovey, Gillespie and Yang (see [2,3,4]). Exact categories and triangulated categories are extriangulated categories, while there exist some other examples of extriangulated categories which are neither exact nor triangulated, see [1,5,6].
Motivated by the ideas of projective covers and injective envelopes, Auslander and Buchweitz analyzed the framework in which the theory of maximal Cohen-Macaulay approximation can be developed. They systematically established their theory in abelian categories, which is known as Auslander-Buchweitz approximation theory. Up to now, Auslander-Buchweitz approximation theory has many important applications, see for example [7,8,9,10]. In particular, Becerril and coauthers [7] have revisited Auslander-Buchweitz approximation theory. From the notions of relative generators and cogenerators in approximation theory, they introduced the concept of left Frobenius pairs in an abelian category, established a bijective correspondence between left Frobenius pairs and relative cotorsion pairs, and showed how to construct an exact model structure from a strong left Frobenius pair, as a result of Hovey-Gillespie correspondence applied to two complete cotorsion pairs on an exact category (see [2,3]).
The aim of this paper is to introduce the concept of left Frobenius pairs in an extriangulated category and give a method to construct more admissible model structures from strong left Frobenius pairs. For this purpose, we need to establish a bijective correspondence between left Frobenius pairs and cotorsion pairs in an extriangulated category under certain conditions.
The paper is organized as follows. In Section 2, we recall the definition of an extriangulated category and outline some basic properties that will be used later. In Section 3, we first introduce the concept of left Frobenius pairs (see Definition 3.4), and then study relative resolution dimension and thick subcategories with respect to a given left Frobenius pair. As a result, we give a bijective correspondence between left Frobenius pairs and cotorsion pairs in an extriangulated category under certain conditions (see Theorem 3.12). In Section 4, we give a method to construct the admissible model structure from a strong left Frobenius pair under certain conditions (see Theorem 4.4), which generalizes a main result of Hu et al. in [5]. This is based on the bijective correspondence established in Section 3.
2.
Preliminaries
Throughout this paper, C denotes an additive category. By the term "subcategory" we always mean a full additive subcategory of an additive category closed under isomorphisms and direct summands. We denote by C(A,B) the set of morphisms from A to B in C.
Let X and Y be two subcategories of C, a morphism f:X→C in C is said to be an X-precover of C if X∈X and C(X′,f):C(X′,X)→C(X′,C) is surjective for all X′∈X. If any C∈Y admits an X-precover, then X is called a precovering class in Y. By dualizing the definitions above, we get notions of an X-preenvelope of C and a preenveloping class in Y. For more details, we refer to [23].
Let us briefly recall some definitions and basic properties of extriangulated categories from [1]. We omit some details here, but the reader can find them in [1].
Assume that E:Cop×C→Ab is an additive bifunctor, where C is an additive category and Ab is the category of abelian groups. For any objects A,C∈C, an element δ∈E(C,A) is called an E-extension. Let s be a correspondence which associates an equivalence class 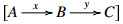 to any E-extension δ∈E(C,A). This s is called a realization of E, if it makes the diagram in [1,Definition 2.9] commutative. A triplet (C,E,s) is called an extriangulated category if it satisfies the following conditions.
to any E-extension δ∈E(C,A). This s is called a realization of E, if it makes the diagram in [1,Definition 2.9] commutative. A triplet (C,E,s) is called an extriangulated category if it satisfies the following conditions.
1. E:Cop×C→Ab is an additive bifunctor.
2. s is an additive realization of E.
3. E and s satisfy certain axioms in [1,Definition 2.12].
In particular, we recall the following axioms which will be used later:
(ET4) Let δ∈E(D,A) and δ′∈E(F,B) be E-extensions realized by
respectively. Then there exists an object E∈C, a commutative diagram
in C, and an E-extension δ″∈E(E,A) realized by 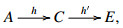 which satisfy the following compatibilities.
which satisfy the following compatibilities.
(i) 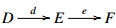 realizes E(F,f′)(δ′),
realizes E(F,f′)(δ′),
(ii) E(d,A)(δ″)=δ,
(iii) E(E,f)(δ″)=E(e,B)(δ′).
(ET4)op Dual of (ET4).
Remark 2.1. Note that both exact categories and triangulated categories are extriangulated categories (see [1,Example 2.13]) and extension closed subcategories of extriangulated categories are again extriangulated (see [1,Remark 2.18]). Moreover, there exist extriangulated categories which are neither exact categories nor triangulated categories (see [1,Proposition 3.30], [6,Example 4.14] and [5,Remark 3.3]).
Lemma 2.2. [1,Corollary 3.12] Let (C,E,s) be an extriangulated category and
an E-triangle. Then we have the following long exact sequences:
where natural transformations δ♯ and δ♯ are induced by E-extension δ∈E(C,A) via Yoneda's lemma.
Let C,E be as above, we use the following notation:
∙ A sequence 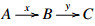 is called a conflation if it realizes some E-extension δ∈E(C,A). In this case, x is called an inflation, y is called a deflation, and we write it as
is called a conflation if it realizes some E-extension δ∈E(C,A). In this case, x is called an inflation, y is called a deflation, and we write it as
We usually do not write this "δ" if it is not used in the argument.
∙ Given an E-triangle 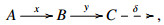 we call A the CoCone of y:B→C and C the Cone of x:A→B.
we call A the CoCone of y:B→C and C the Cone of x:A→B.
∙ An E-triangle sequence in C [11] is displayed as a sequence
over C such that for any n, there are E-triangles 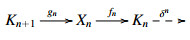 and the differential dn=gn−1fn.
and the differential dn=gn−1fn.
∙ An object P∈C is called projective if for any E-triangle 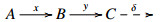 and any morphism c∈C(P,C), there exists b∈C(P,B) satisfying y∘b=c. Injective objects are defined dually. We denote the subcategory consisting of projective (resp., injective) objects in C by Proj(C) (resp., Inj(C)).
and any morphism c∈C(P,C), there exists b∈C(P,B) satisfying y∘b=c. Injective objects are defined dually. We denote the subcategory consisting of projective (resp., injective) objects in C by Proj(C) (resp., Inj(C)).
∙ We say C has enough projectives (resp., enough injectives) if for any object C∈C (resp., A∈C), there exists an E-triangle 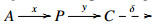 (resp.,
(resp., 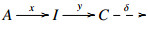 satisfying P∈Proj(C) (resp.,I∈Inj(C)).
satisfying P∈Proj(C) (resp.,I∈Inj(C)).
Remark 2.3. (1) If (C,E,s) is an exact category, then the definitions of having enough projectives and having enough injectives agree with the usual definitions.
(2) If (C,E,s) is a triangulated category, then Proj(C) and Inj(C) consist of zero objects.
Definition 2.4. [1,Definition 4.2] Let X, Y be two subcategories of C. Define full subcategories Cone(X,Y) and CoCone(X,Y) of C as follows.
(1) C belongs to Cone(X,Y) if and only if it admits a conflation X→Y→C satisfying X∈X and Y∈Y;
(2) C belongs to CoCone(X,Y) if and only if it admits a conflation C→X→Y satisfying X∈X and Y∈Y. $
Suppose that (C,E,s) is an extriangulated categories with enough projectives and injectives. For a subcategory B⊆C, put Ω0B=B, and for i>0, we define ΩiB inductively by
We call ΩiB the i-th syzygy of B (see [12,Section 5]). Dually we define the i-th cosyzygy ΣiB by Σ0B=B and ΣiB=Cone(Σi−1B,Inj(C)) for i>0.
Let X be any object in C. It admits an E-triangle
where I0∈Inj(C) (resp., P0∈Proj(C)). In [12] the authors defined higher extension groups in an extriangulated category having enough projectives and injectives as Ei+1(X,Y)≅E(X,ΣiY)≅E(ΩiX,Y) for i≥0, and they showed the following result:
Lemma 2.5. [12,Proposition 5.2] Let 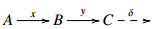 be an E-triangle. For any object X∈B, there are long exact sequences
be an E-triangle. For any object X∈B, there are long exact sequences
From now on to the end of the paper, we always suppose that (C,E,s) is an extriangulated categories with enough projectives and injectives.
3.
Frobenius pairs and cotorsion pairs
In this section, we introduce the concept of Frobenius pairs and show that it has very nice homological properties, which are necessary to construct cotorsion pairs from Frobenius pairs. At first, we need introduce the following definitions.
Definition 3.1. Let X be a subcategory of C.
1. For any non-negative integer n, we denote by ˇXn (resp., ^Xn) the class of objects C∈C such that there exists an E-triangle sequence
with each Xi∈X. Moreover, we set ˇX=∞⋃n=0ˇXn, ˆX=∞⋃n=0^Xn.
2. For any C∈C, the X-resolution dimension of C is defined as
If C∉^Xn for any n∈N, then resdimX(C)=∞.
For a subcategory X of C, define X⊥={Y∈C|Ei(X,Y)=0foralli≥1,andallX∈X}. Similarly, we can define ⊥X.
Definition 3.2. Let X and W be two subcategories of C. We say that
(1) W is a cogenerator for X, if W⊆X and for each object X∈X, there exists an E-triangle 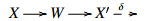 with W∈W and X′∈X. The notion of a generator is defined dually.
with W∈W and X′∈X. The notion of a generator is defined dually.
(2) W is X-injective if W⊆X⊥. The notion of an X-projective subcategory is defined dually.
(3) W is an X-injective cogenerator for X if W is a cogenerator for X and W⊆X⊥. The notion of an X-projective generator for X is defined dually.
(4) X is a thick subcategory if it is closed under direct summand and for any E-triangle
in C and two of A,B,C are in C, then so is the third.
The following theorem unifies some results of [13] and [9]. It shows that any object in ˆX admits two E-triangles: one giving rise to an X-precover and the other to a ˆW-preenvelope.
Theorem 3.3. Let X and W be two subcategories of C. Suppose X is closed under extensions and W is a cogenerator for X. Consider the following conditions:
(1) C is in ^Xn.
(2) There exists an E-triangle 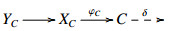 with XC∈X and YC∈^Wn−1.
with XC∈X and YC∈^Wn−1.
(3) There exists an E-triangle 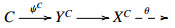 with XC∈X and YC∈^Wn.
with XC∈X and YC∈^Wn.
Then, (1)⇔(2)⇒(3). If X is also closed under CoCone of deflations, then (3)⇒(2), and hence all three conditions are equivalent. If W is X-injective, then φC is an X-precover of C and ψC is a ˆW-preenvelope of C.
Proof. The proof is dual to that of [14,Proposition 3.6].
Definition 3.4. A pair (X,W) is called a left Frobenius pair in C if the following holds:
(1) X is closed under extensions and CoCone of deflations,
(2) W is an X-injective cogenerator for X.
If in addition W is also an X-projective generator for X, then we say (X,W) is a strong left Frobenius pair.
Example 3.5. (1) Assume that C=R-Mod is the category of left R-modules for a ring R. A left R-module N is called Gorenstein projective [23,24] if there is an exact sequence of projective left R-modules
with N=Ker(P0→P0) such that HomR(P,Q) is exact for any projective left R-module Q. Let GP(R) be the full subcategory of R-Mod consisting of all Gorenstein projective modules and P(R) the subcategory of R-Mod consisting of all projective modules. Then (GP(R),P(R)) is a strong left Frobenius pair.
(2) Let C be a triangulated category with a proper class ξ of triangles. Asadollahi and Salarian [15] introduced and studied ξ-Gprojective and ξ-Ginjective objects, and developed a relative homological algebra in C. Let GP(ξ) denotes the full subcategory of ξ-Gprojective objects and P(ξ) denotes the full subcategory of ξ-projective objects. Then (GP(ξ),P(ξ)) is a strong left Frobenius pair.
(3) Let T be a triangulated category, and let M be a silting subcategory of T with M=addM, where addM is the smallest full subcategory of T which contains M and which is closed under taking isomorphisms, finite direct sums, and direct summands. Then (T≥0,M) is a left Frobenius pair by [14,Corollary 3.7] and [16,Proposition 2.7], where T≥0:=⋃n≥0M[−n]∗⋯M[−1]∗M.
(4) In [17], the authors showed that if (X,Y) is a complete and hereditary cotorsion pair in an abelian category A and Y is closed under kernels of epimorphisms, then (G(X)⋂Y,X⋂Y) is a strong left Frobenius pair, where G(X) is the class of objects M in A satisfying that there exists an exact sequence
with each term in X such that M≅Ker(X0→X1) and HomA(X,Q) is exact for any object Q in X⋂Y.
Lemma 3.6. Let (X,W) be a left Frobenius pair in C.Given an E-triangle 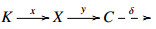 with X∈X, then C∈ˆX if and only if K∈ˆX.
with X∈X, then C∈ˆX if and only if K∈ˆX.
Proof. The proof is dual to that of [14,Lemma 3.8].
Proposition 3.7. Let (X,W) be a left Frobenius pair in C. The following statements are equivalent for any C∈ˆX and non-negative integer n.
(1) resdimX(C)≤n.
(2) If U→Xn−1→⋯→X0→C is an E-triangle sequence with Xi∈X for 0≤i≤n−1, then U∈X.
Proof. (2)⇒(1) is trivial.
(1)⇒(2). Let C be in ˆX. Then by Theorem 3.3, we have an E-triangle sequence Wn→⋯→W1→X→C with X∈X and Wi∈W for 1≤i≤n. Since W⊆X⊥, it is easy to see that ˆW⊆X⊥. Thus we have En+i(C,Y)≅Ei(Wn,Y)=0 for all i≥1 and Y∈ˆW. If U→Xn−1→⋯→X0→C is an E-triangle sequence with Xi∈X for 0≤i≤n−1, then we have Ei(U,Y)≅En+i(C,Y)=0 for all i≥1 and Y∈ˆW. Note that U∈ˆX by Lemma 3.6. Hence there exists an E-triangle 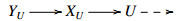 with XU∈X and YU∈ˆW by Theorem 3.3. It follows that the above E-triangle splits. Hence U∈X.
with XU∈X and YU∈ˆW by Theorem 3.3. It follows that the above E-triangle splits. Hence U∈X.
If X is a subcategory of C, then we denote by Thick(X) the smallest thick subcategory that contains X. The following result shows that for a left Frobenius pair (X,W) in C, ˆX is an extriangulated category. In particular, if C is a triangulated category, then ˆX is the smallest triangulated subcategory of C containing X and is closed under direct summands and isomorphisms.
Proposition 3.8. Let (X,W) be a left Frobenius pair in C. Then Thick(X)=ˆX.
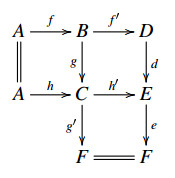
Proof. For any E-triangle 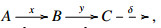 we need to check that if any two of A,B and C are in ˆX, then the third one is in ˆX. Since ˆX is closed under extensions by the dual of [14,Corollary 3.7], it suffices to show that if B∈ˆX, then A∈ˆX if and only if C∈ˆX. We first show that if A and B are in ˆX, then C∈ˆX. Since B∈ˆX, we have an E-triangle
we need to check that if any two of A,B and C are in ˆX, then the third one is in ˆX. Since ˆX is closed under extensions by the dual of [14,Corollary 3.7], it suffices to show that if B∈ˆX, then A∈ˆX if and only if C∈ˆX. We first show that if A and B are in ˆX, then C∈ˆX. Since B∈ˆX, we have an E-triangle  with XB∈X,YB∈ˆW. By (ET4)op, we obtain a commutative diagram
with XB∈X,YB∈ˆW. By (ET4)op, we obtain a commutative diagram
It follows that L∈ˆX as A and YB are in ˆX. Therefore C∈ˆX.
Suppose now B and C are in ˆX. It follows from Lemma 3.6 that L∈ˆX. Applying the just established result to the E-triangle  one has that A∈ˆX.
one has that A∈ˆX.
Suppose C1⊕C2∈ˆX. We proceed by induction on n=resdimX(C1⊕C2). If n=0, then C1 and C2 are in X.
Suppose n>0. There is an E-triangle 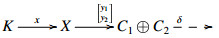 with X∈X and resdimX(K)=n−1. By (ET4)op, we obtain the following commutative diagrams:
with X∈X and resdimX(K)=n−1. By (ET4)op, we obtain the following commutative diagrams:
Hence there is an E-triangle
By Lemma 3.6, L1⊕L2∈ˆX, and Proposition 3.7 shows that resdimX(L1⊕L2)≤n−1. By the induction hypothesis, L1 and L2 are in ˆX. It follows that C1 and C2 are in ˆX. Hence ˆX is closed under direct summands. Thus Thick(X)=ˆX.
Definition 3.9. [1,Definition 4.1] Let U, V ⊆ C be a pair of full additive subcategories, closed under isomorphisms and direct summands. The pair (U, V) is called a cotorsion pair on C if it satisfies the following conditions:
(1) E(U,V)=0;
(2) For any C∈C, there exists a conflation VC→UC→C satisfying UC∈U and VC∈V;
(3) For any C∈C, there exists a conflation C→VC→UC satisfying UC∈U and VC∈V. $
Lemma 3.10. Let X and W be two subcategories of C such that W is X-injecive. Then the following statements hold.
(1) If W is a cogenerator for X, then W=X⋂X⊥=X⋂ˆW.
(2) If W is a cogenerator for X, then ˆW=ˆX⋂X⊥.
Proof. The proof is dual to that of [14,Proposition 4.2].
The following result gives a method to construct cotorsion pairs on extriangulated categories.
Proposition 3.11. Let (X,W) be a left Frobenius pair in C. Then (X,ˆW) is a cotorsion pair on the extriangulated category Thick(X).
Proof. Note that Thick(X) is an extriangulated category by [1,Remark 2.18]. It suffices to show that ˆW is closed under direct summands by Theorem 3.3. Note that ˆW=ˆX⋂X⊥ by Proposition 3.10. Since Thick(X) = ˆX is closed under direct summands by Proposition 3.8, so is ˆW. This completes the proof.
Now we are in a position to state and prove the main result of this section.
Theorem 3.12. Let C be an extriangulated category. The assignments
give mutually inverse bijections between the following classes:
(1) Left Frobenius pairs (X,W) in C.
(2) Cotorsion pairs (U,V) on the extriangulated category Thick(U) with V⊆U⊥.
Proof. Let (X,W) be a left Frobenius pair. Then (X,ˆW) is a cotorsion pair on the extriangulated category ˆX by Proposition 3.11. Note that Thick(X)=ˆX and ˆW⊆X⊥. Then (X,ˆW) is a cotorsion pair on the extriangulated category Thick(X) with ˆW⊆X⊥.
Assume (U,V) is a cotorsion pair on the extriangulated category Thick(U) with V⊆U⊥. For U∈U, we have an E-triangle 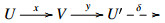 with V∈V and U′∈U. Thus V∈Thick(U) as Thick(U) is a thick subcategory. Since (U,V) is a cotorsion pair on the extriangulated category Thick(U), it follows from [1,Remark 4.6] that U is closed under extensions in Thick(U). It implies that V∈U. Thus V∈U⋂V. Note that V⊆U⊥. It follows that U⋂V is an U-injective cogenerator. Let
with V∈V and U′∈U. Thus V∈Thick(U) as Thick(U) is a thick subcategory. Since (U,V) is a cotorsion pair on the extriangulated category Thick(U), it follows from [1,Remark 4.6] that U is closed under extensions in Thick(U). It implies that V∈U. Thus V∈U⋂V. Note that V⊆U⊥. It follows that U⋂V is an U-injective cogenerator. Let 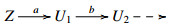 be an E-triangle with U1,U2∈U. Then we have an exact sequence E(U1,V)⟶E(Z,V)⟶E2(U2,V) for any V∈V. Since V⊆U⊥, E(Z,V)=0. Note that Z∈Thick(U) as Thick(U) is a thick subcategory. Thus there exists an E-triangle $
be an E-triangle with U1,U2∈U. Then we have an exact sequence E(U1,V)⟶E(Z,V)⟶E2(U2,V) for any V∈V. Since V⊆U⊥, E(Z,V)=0. Note that Z∈Thick(U) as Thick(U) is a thick subcategory. Thus there exists an E-triangle $ 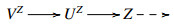 with UZ∈U and VZ∈V as (U,V) is a cotorsion pair on the extriangulated category Thick(U). Therefore the above E-triangle splits by E(Z,V)=0. Hence Z∈U. So U is closed under CoCone of deflations. Note that U is closed under extensions in Thick(U). It follows that U is closed under extensions in C. Thus (U,U⋂V) is a left Frobenius pair in C.
with UZ∈U and VZ∈V as (U,V) is a cotorsion pair on the extriangulated category Thick(U). Therefore the above E-triangle splits by E(Z,V)=0. Hence Z∈U. So U is closed under CoCone of deflations. Note that U is closed under extensions in Thick(U). It follows that U is closed under extensions in C. Thus (U,U⋂V) is a left Frobenius pair in C.
Based on the above argument, it is enough to check that the compositions
are identities. Since U⋂V is an U-injective cogenerator for U, ^U⋂V=ˆU⋂U⊥=Thick(U)⋂U⊥ where the first equality is due to Proposition 3.10 and the second equality is due to Proposition 3.8. It follows from [1,Remark 4.4] that Thick(U)⋂U⊥=V. Thus ^U⋂V=V. This completes the proof.
As a consequence of Theorem 3.12 and Remark Remark 2.3, we have the following result.
Corollary 3.13. [7,Throrem 5.4] Let A be an abelian category with enough projectives and injectives. The assignments
give mutually inverse bijections between the following classes:
(1) Left Frobenius pairs (X,W) in A.
(2) Cotorsion pairs (U,V) on the exact category Thick(U) with V⊆U⊥.
As an application, we have the following result in [10].
Corollary 3.14. [10,Theorem 3.11] Let C be a triangulated category. The assignments
give mutually inverse bijections between the following classes:
(1) Left Frobenius pairs (X,W) in C.
(2) Co-t-structures (U,V) on the triangulated category Thick(U).
Proof. Note that any triangulated category can be viewed as an extriangulated category, and its projective objects and injective objects consist of zero objects by Remark Remark 2.3.
Let (X,W) be a left Frobenius pair. By Theorem 3.12, (X,ˆW) is a cotorsion pair on the triangulated category Thick(X). Since X is closed under CoCone of deflations and extensions, it is easy to see that X[−1]⊆X. Hence (X,ˆW) is a co-t-structure on the triangulated category Thick(X).
Assume (U,V) is a co-t-structure on the triangulated category Thick(U). It is easy to see that (U,V) is a cotorsion pair on Thick(U) with V⊆U⊥. Hence the corollary follows from Theorem 3.12.
Definition 3.15. [18,Definition 2.1] Let R and S be rings. An (S-R)-bimodule C=SCR is semidualizing if:
(1) SC admits a degreewise finite S-projective resolution.
(2) CR admits a degreewise finite R-projective resolution.
(3) The homothety map SSSSγ→HomR(C,C) is an isomorphism.
(4) The homothety map RRRγR→HomS(C,C) is an isomorphism.
(5) Ext≥1S(C,C)=0=Ext≥1R(C,C).
Definition 3.16. [18,Definition 3.1] A semidualizing bimodule C=SCR is faithfully semidualizing if it satisfies the following conditions for all modules SN and MR.
(1) If HomS(C,N)=0, then N=0.
(2) If HomR(C,M)=0, then M=0.
Definition 3.17. [18,Definition 4.1] The Bass class BC(S) with respect to C consists of all S-modules N satisfying
(1) Ext≥1S(C,N)=0=TorR≥1(C,HomS(C,N))=0.
(2) The natural evaluation homomorphism νN:C⊗RHomS(C,N)→N is an isomorphism.
Remark 3.18. Let C=SCR be a faithfully semidualizing module. Then Bass class BC(S) is an exact category by [18,Theorem 6.2] and BC(S) has enough projectives and injectives by [20,Remark 3.13].
By [18], the class of C-projective left S-modules, denoted by PC(S) the collection of the left S-modules of the form C⊗RP for some projective left R-module P. Recall from [20] that a left S-module M is called C-Gorenstein projective if there is an exact sequence of left S-modules
with each term in PC(S) such that N≅Ker(W0→W0) and both HomR(W,Q) and HomR(Q,W) are exact for any object Q in PC(S). It should be noted that C-Gorenstein projectives defined here are different from those defined in [19] when S=R is a commutative Noetherian ring (see [20,Proposition 3.6]).
For convenience, we write GC-Proj(S) for the classes of C-Gorenstein projective left S-modules. By [20,Proposition 3.5], one has that GC-Proj(S) ⊆BC(S). As a consequence of Theorem 3.12, we have the following result.
Corollary 3.19. Let C=SCR be a faithfully semidualizing module. Then
(1) (GC-Proj(S),PC(S)) is a strong left Frobenius pair in BC(S).
(2) (GC-Proj(S),^PC(S)) is a cotorsion pair on ^GC−Proj(S).
Proof. Since PC(S) is projectively resolving and PC(S)⊆PC(S)⊥ by [18,Corollary 6.4] and [18,Theorem 6.4], GC-Proj(S) is closed under kernels of epimorphisms and direct summand by [21,Theorem 4.12] and [21,Proposition 4.11]. Hence (GC-Proj(S),PC(S)) is a strong left Frobenius pair in BC(S). (2) follows from Theorem 3.12.
4.
Admissible model structures associated with Frobenius pairs
In this section, we shall use our results in Section 3 to construct more admissible model structures in extriangulated categories. At first, we need to recall the following definition.
Definition 4.1. [1,Definition 5.1] Let (S, T) and (U, V) be cotorsion pairs on C. Then P=((S, T), (U, V)) is called a twin cotorsion pair if it satisfies E(S,V)=0. Moreover, P is called a Hovey twin cotorsion pair if it satisfies Cone(V,S) = CoCone(V,S). $
In [1] Nakaoka and Palu gave a correspondence between admissible model structures and Hovey twin cotorsion pairs on C. Essentially, an admissible model structure on C is a Hovey twin cotorsion pair P=((S, T), (U, V)) on C. For more details, we refer to [1,Section 5]. By a slight abuse of language we often refer to a Hovey twin cotorsion pair as an admissible model structure.
Lemma 4.2. Let (X,W) be a strong left Frobenius pair in C. Then (W,ˆX) is a cotorsion pair on the extriangulated category Thick(X).
Proof. Since W⊆⊥X, one has E(W,ˆX)=0. For any C∈ˆX, there exists an E-triangle
with XC∈X and YC∈ˆW by Theorem 3.3. Since W is a generator for X, we have an E-triangle 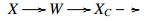 with W∈W and X∈X. By (ET4)op, we obtain a commutative diagram
with W∈W and X∈X. By (ET4)op, we obtain a commutative diagram
It follows that Z∈ˆX as X and YC are in ˆX. Note that Thick(X)=ˆX. The second column and E(W,ˆX)=0 show that (W,ˆX) is a cotorsion pair on Thick(X).
Proposition 4.3. Let (X,W) be a strong left Frobenius pair in C. Then P=((W,ˆX),(X,ˆW)) is an admissible model structure on the extriangulated category Thick(X)
Proof. By Theorem 3.12 and Lemma 4.2, we only need to check that Cone(ˆW,W)=CoCone(ˆW,W). It is obvious that Cone(ˆW,W)=ˆW⊆CoCone(ˆW,W). Let C∈CoCone(ˆW,W). Then we have an E-triangle 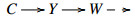 with Y∈ˆW and W∈W. By Theorem 3.3, one has that C∈ˆX. Since E(W,ˆX)=0, it follows that C is a direct summand of Y. Note that ˆW is closed under direct summand by Proposition 3.11. Thus C∈ˆW. Hence the equality Cone(ˆW,W)=CoCone(ˆW,W) holds.
with Y∈ˆW and W∈W. By Theorem 3.3, one has that C∈ˆX. Since E(W,ˆX)=0, it follows that C is a direct summand of Y. Note that ˆW is closed under direct summand by Proposition 3.11. Thus C∈ˆW. Hence the equality Cone(ˆW,W)=CoCone(ˆW,W) holds.
Theorem 4.4. Let (X,W) be a strong left Frobenius pair in C. If n is a non-negative integer, then the following statements are equivalent:
(1) ^Xn=C.
(2) P=((W,C),(X,^Wn)) is an admissible model structure on C.
Proof. (1)⇒(2). If ^Xn=C, then (W,C) is a cotorsion pair on C by Lemma 4.2 and (X,ˆW) is a cotorsion pair on C by Theorem 3.12. To prove (2), we only need to check that ^Wn=ˆW. Note that ^Wn⊆ˆW is obvious. Let C∈ˆW. Then there is an E-triangle 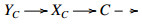 with XC∈X and YC∈^Wn−1 by Theorem 3.3. Since ˆW is closed under extensions, XC∈X⋂ˆW=W. Hence C∈^Wn implies ^Wn=ˆW.
with XC∈X and YC∈^Wn−1 by Theorem 3.3. Since ˆW is closed under extensions, XC∈X⋂ˆW=W. Hence C∈^Wn implies ^Wn=ˆW.
(2)⇒(1). Since (X,^Wn) is a cotorsion pair on C, one has that C=^Xn by Theorem 33.
As an application, we have the following result in [3].
Corollary 4.5. [3,Theorem 8.6] Suppose R is a Gorenstein ring. Let GP(R) be the subcategory of R-Mod consisting of Gorenstein projective modules and P(R) the subcategory of R-Mod consisting of projective modules. Then ((P(R),R-Mod),(GP(R),^P(R)) is an admissible model structure on R-Mod.
Proof. It follows from Example 3.5 and Proposition 4.3.
Let n be a non-negative integer. In the following, we denote by GC−Proj(S)≤n (resp., PC(S)≤n) the class of modules with C-Gorenstein projective (resp., C-projective) dimension at most n
Corollary 4.6. Let C=SCR be a faithfully semidualizing module. Then the following statements are equivalent:
(1) GC−Proj(S)≤n=BC(S).
(2) P=((PC(S),BC(S)),(GC−Proj(S),PC(S)≤n) is an admissible model structure on BC(S).
Proof. It follows from Corollary 3.19 and Theorem 4.4.
Let (C,E,s) be an extriangulated category and ξ a proper class of E-triangles. By [5], an object P∈C is called ξ-projective if for any E-triangle
in ξ, the induced sequence of abelian groups $ 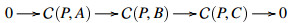 is exact. We denote P(ξ) the class of ξ-projective objects of C. Recall from [5] that an object M∈C is called ξ-Gprojective if there exists a diagram
is exact. We denote P(ξ) the class of ξ-projective objects of C. Recall from [5] that an object M∈C is called ξ-Gprojective if there exists a diagram
in C satisfying that: (1) Pn is ξ-projective for each integer n; (2) there is a C(−,P(ξ))-exact E-triangle 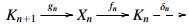 in ξ and dn=gn−1fn for each integer n such that M≅Kn for some n∈Z. We denote by GP(ξ) the class of ξ-Gprojective objects in C. Specializing Theorem 4.4 to the case X=GP(ξ), we have the following result in [5].
in ξ and dn=gn−1fn for each integer n such that M≅Kn for some n∈Z. We denote by GP(ξ) the class of ξ-Gprojective objects in C. Specializing Theorem 4.4 to the case X=GP(ξ), we have the following result in [5].
Corollary 4.7. [5,Theorem 5.9] Let (C,E,s) be an extriangulated category satisfying Condition (WIC) (see [1,Condition 5.8]). Assume that ξ is a proper class in C.Set Eξ:=E|ξ, that is,
for any A,C∈C, and sξ:=s|Eξ.If n is a non-negative integer, then the following conditions are equivalent:
(1) sup{ξ-GpdA|A∈C}⩽n.
(2) P=((P(ξ),C),(GP(ξ),P⩽n(ξ))) is an admissible model structure on (C,Eξ,sξ), where P⩽n(ξ)={A∈C|ξ-pdA⩽n}.
Proof. It is easy to check that (GP(ξ),P(ξ)) is a strong left Frobenius pair in (C,Eξ,sξ). Thus the corollary follows from Theorem 4.4.
Acknowledgments
The authors are grateful to the referees for reading the paper carefully and for many suggestions on mathematics and English expressions. Yajun Ma was supported by NSFC (Grant No. 12171230). Haiyu Liu and Yuxian Geng were supported by the NSFC (Grants Nos. 12171206 and 12126424) and the Natural Science Foundation of Jiangsu Province (Grant No. BK20211358).
Conflict of interest
The authors declare there is no conflicts of interest.









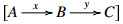 to any
to any 
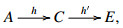 which satisfy the following compatibilities.
which satisfy the following compatibilities.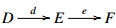 realizes
realizes 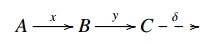

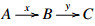 is called a conflation if it realizes some
is called a conflation if it realizes some 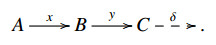
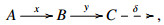 we call
we call 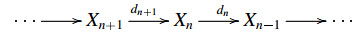
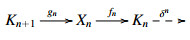 and the differential
and the differential 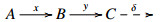 and any morphism
and any morphism 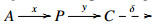 (resp.,
(resp., 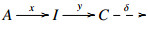 satisfying
satisfying 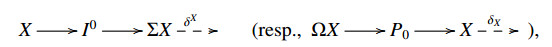
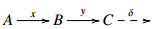 be an
be an 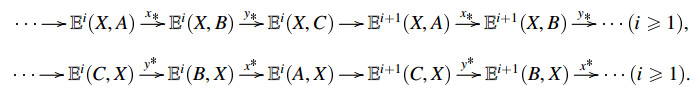
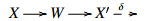 with
with 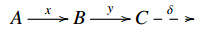
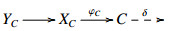 with
with 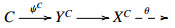 with
with 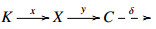 with
with  with
with 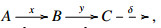 we need to check that if any two of
we need to check that if any two of  with
with 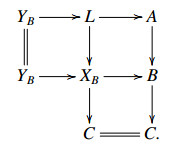
 one has that
one has that 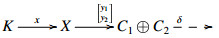 with
with 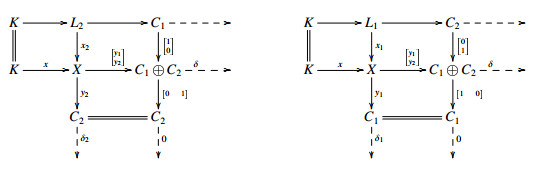
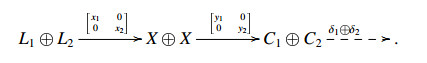
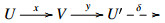 with
with 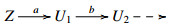 be an
be an 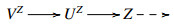 with
with 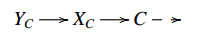
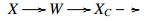 with
with 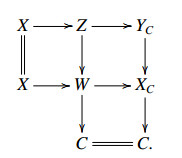
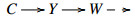 with
with 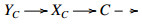 with
with 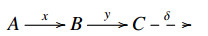
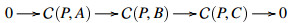 is exact. We denote
is exact. We denote 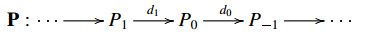
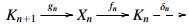 in
in 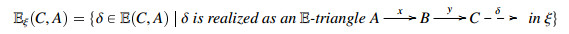








 DownLoad:
DownLoad: