1.
Introduction
The role of teachers in addressing student welfare, particularly in responding to underperforming students in academics (known as "students at risk"), is increasingly crucial [1]. According to Alyahyan and Düştegör [2], there are various factors that can impact a student's academic performance, such as their prior academic achievements, demographics, and online learning behaviors. If these factors can be identified earlier, educators can use the data to identify students at risk at an earlier stage.
The advancement of information and communication technology has changed the way students acquire knowledge, particularly for generations surrounded by technology from a young age. The increased use of learning management systems (LMS) has generated substantial educational data, leading to the emergence of learning analytics [3]. As a result, learning analytics is increasingly being utilized in identifying students at risk and providing them with timely assistance [4]. Instructors can monitor student behavior in real-time and intervene promptly to support students who are at risk, which ultimately helps to reduce failure rates [5].
Learning analytics refers to the process of identifying a problem, applying statistical models using data, and predicting future trends to obtain actionable insights [6]. The Signals project conducted at Purdue University is one of the most well-known learning analytics initiatives. Under the project, students are given signals in the form of red, yellow, or green on their Blackboard site. Lecturers can monitor students who receive yellow and red signals at an early stage and provide necessary interventions to help them [7]. Previous studies have demonstrated that it is possible to predict the academic performance of students in mathematics [8]. However, it is crucial to develop and validate prediction models for different courses [9], such as actuarial science, which involves different mathematics subjects from other courses.
A complete learning analytics process involves five steps: data collection, data reporting, prediction, intervention, and reassessment [10]. However, most research works have primarily focused on the first three steps and paid less attention to the last two steps [4]. Although the Signals project did provide support for students at risk, it did not specify the learning support for mathematics subjects. As pointed out in the study [8], most learning analytics relevant studies have relied on quantitative methods and emphasized that future studies can explore the use of mixed methods to support learning analytics applications in mathematics. Therefore, there is a need to bridge this gap for a comprehensive learning analytics process.
This study aimed to develop a prediction model for locating students at risk in an actuarial science course and suggest intervention strategies for them. A quantitative method was applied on the predictive model, while a qualitative method was used to gather insight on the intervention strategy. We concluded the study by assessing the effectiveness of both the predictive model and intervention strategy.
2.
Literature review
2.1. Predictive model
Different classification techniques are necessary to classify students as "at risk" or "not at risk", such as discriminant analysis, logistic regression, and neural networks [11]. Statistical modelling has a high prediction accuracy of 84% [12] and possibly even 86% [13] for students at risk. Therefore, it is becoming more and more popular for classifying students at risk and predicting academic performance. One popular technique for classification and dimensionality reduction that allows for non-linear data separation is quadratic discriminant analysis (QDA) [14].
QDA is a supervised learning technique that models the probability distribution of each class using a quadratic function [15]. It is assumed that each class's predictor variables have a multivariate normal distribution. QDA uses the predictor variables of a class to estimate the likelihood that an observation will belong to that class. Using training data, the quadratic function's means and covariance matrices are estimated for each class [15]. Using the Bayes theorem to compute the posterior probability of each class's observation, a new observation is classified using QDA by being assigned to the class with the highest probability [16].
QDA can identify more complex patterns in the data than linear methods. Because of this, it can be used in situations where predictor variables and classes have a non-linear relationship, allowing for more flexible decision boundaries [16]. Thus, QDA provides the benefit of more flexibility with respect to the features of the covariance matrix for various classes and fewer restrictive assumptions [14].
2.2. Learning behavior affecting students' academic performance
An overview of the learning behaviors influencing academic performance is given in Table 1. Lakkaraju et al. [17] found that past academic achievement, as determined by the cumulative grade point average (CGPA), is a predictor of academic performance. On the other hand, Choi et al. [4] found a relationship between exam scores in pre-requisite courses and overall academic success. Mueen et al. [13] and Yang et al. [18] stressed the significance of consistent exercise grades and homework performance, and highlighted their impact on academic achievement. The importance of Blackboard clicks in measuring engagement was highlighted by Shah and Barkas' [19] investigation of student interactions within the Blackboard learning management system.
Furthermore, Yang et al. [18] highlighted a relationship between the number of video views and academic achievement, while Mubarak et al. [12] investigated the possible impact of the total amount of time spent watching videos. Besides, six studies [4, 13, 17, 19‒21] supported the significance of attendance as a factor impacting academic performance. Finally, studies by Choi et al. and Yang et al. [4,18] show a connection between assessment performance and academic success. To summarize, the results in Table 1 show that a number of variables, including past academic performance, various forms of engagement, attendance, and assessment performance, have been studied and found to be associated with academic success.
2.3. Intervention strategy
It is the duty of educational institutions to provide students at risk with intervention activities in order to lower dropout rates. For higher education, the Peer Assisted Learning Program (PALP) is regarded as a significant intervention strategy [22]. In addition to helping students transition to university life and develop better study habits, PALP has proven to be helpful by offering a secure and friendly environment for discussion with mentors [22]. Besides, according to Cheng and Walters [23], attending PALS in mathematics raises the chance that students will pass the course and complete the program.
3.
Methodology
3.1. Participants
This study targeted full-time actuarial science undergraduate students from a private university in Selangor. A convenience sampling was applied to select the samples, where the students were selected because of the convenient accessibility of the study. Two datasets were collected for this research. The first dataset was utilized for developing the prediction model, while the second dataset was used to predict students who were at risk. Both datasets were collected from different groups of students in two semesters. The first dataset consisted of a total of 61 students, while the second dataset had a total of 69 students. All of them were enrolled in a Year 2 actuarial science course. The demographic information of the students is presented in Table 2.
3.2. Research procedures
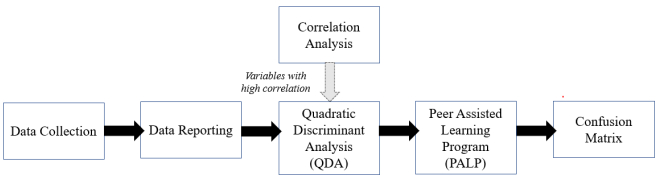
In this study, we have conducted five steps of learning analytics as presented in Figure 1. The details for each step will be elaborated further in the following sections.
3.2.1. Data collection and data reporting
The data presented in Table 3 was collected to assess the impact of different variables on students' academic performance. The primary data collected were Blackboard data, attendance, CGPA, pre-requisite subject marks, final marks of the Year 2 course, and gender. Five types of Blackboard data were collected: Blackboard clicks, videos views, total minutes spent in videos, homework marks, and assessment marks. Blackboard is one of the teaching and learning tools which has been widely used in that private university and students are required to use it from their first year of study. Attendance was collected through the university attendance system. Students' marks in pre-requisite subjects, their current CGPA, gender, and final marks were also collected from the Enterprise Manager Database Express (EMX), i.e., a system to key in and to view students' data upon their registration to join the university.
As stated in section 3.1, two datasets were collected for this research. Despite having the same variables for both datasets, their descriptive statistics differed. For this paper, we will only be discussing the first dataset, which is presented in Table 4. Table 4 shows the mean, standard deviation, and minimum and maximum values for each variable. It has shown that female students have a higher mean value in all variables, including final marks, CGPA, pre-requisite marks, and assessment marks. These findings align with Hyde et al.'s study [24], where females performed slightly better than males in mathematics. However, a study [25] claimed that although males and females differ very little in mathematics performance, males tend to have positive attitudes toward the subject. Additionally, a more recent study [26] found that males outperformed females in mathematics under time-pressure settings.
In terms of range, male students tended to have a wider range on each variable, except for video views and total minutes spent on videos. Therefore, in general, female students tended to perform more consistently across various variables as compared to male students. This finding is consistent with the results obtained in McSporran and Young's study [27], where female students were found to be more motivated, possess better online engagement, and manage their learning schedules more effectively than male students.
3.2.2. Correlation analysis
Correlation is a statistical technique used to assess the degree of relationship between two variables [28]. The correlation coefficient (r or R) is used to measure the degree of association of two variables. The sign of the correlation coefficient describes the direction of the correlation. A positive sign means that the two variables are moving in the same direction, i.e., when one variable increases, the other does as well. A correlation coefficient of 1 indicates a perfect relationship, 0.7 and above indicates a strong relationship, whereas a value of 0.4 to 0.6 indicates a moderate relationship, a value 0.3 and below is considered a weak relationship, and lastly 0 indicates no relationship between the variables [29].
3.2.3. Quadratic discriminant analysis (QDA)
To ensure the reliability of QDA, we will assess the underlying assumptions of QDA. The variance inflation factor (VIF) will be used to verify whether the samples are independent of each other. VIF provides a measure of multicollinearity among the independent variables, revealing correlations between multiple independent variables. A VIF less than 5 suggests a low correlation of the variable with another variable, while a value between 5 and 10 indicates a moderate correlation. VIF values exceeding 10 indicate a high, intolerable correlation among model variables. On the other hand, we have performed Shapiro-Wilk's test to check if the assumption of multivariate normality held. The null hypothesis for this test was that the sample came from a normal distribution, where a 95% significance level was used. We also tested the equality of covariance matrices, another assumption for QDA, using Box's M test. Using the strong correlated variables identified through correlation analysis, we partitioned the dataset into 70% training data and 30% testing data to assess the model's accuracy. Finally, the prediction model was applied to identify students at risk. To determine whether a student was "at risk" or "not at risk", the final marks from the Year 2 course were considered. If a student scored below 50, they were considered "at risk", otherwise they were considered "not at risk".
3.2.4. Peer Assisted Learning Program (PALP)
The Peer Assisted Learning Program (PALP) is offered to all students who enroll in the actuarial science course. Four PALP classes were conducted throughout the semester by a senior, i.e., peer mentor. Each session was 1.5 hours and was conducted physically in the classroom. During the last class of the PALP, a survey was carried out to understand the effectiveness of the PALP using descriptive analysis and open-ended questions analysis.
3.2.5. Confusion matrix
The metrics that are commonly used in literature to measure the classification performance of a model are based on the true positive (TP), true negative (TN), false positive (FP), and false negative (FN) values from the confusion matrix, as shown in Table 5 [4]. With that, the effectiveness of the prediction model can be evaluated. Based on the values collected in Table 5, we applied the formula given in Table 6 [30] to calculate the classification performance of the prediction model in identifying students at risk and students not at risk. The prediction model can be considered a good model if it has high values for each metric [31].
4.
Results and discussion
4.1. Correlation analysis
We applied correlation analysis to understand the variables that influenced the final marks of the Year 2 course. The results in Table 7 indicate that the final marks of the course were rather strongly correlated (r > 0.7) with the CGPA, prerequisite subject marks, and assessment marks. This confirms the significance of these factors in determining the overall academic success of the students. The other variables, on the other hand, show either a moderate or weak relationship with the final marks. The variables with a strong correlation will be included in the QDA to predict students at risk on the second data set.
4.2. Quadratic discriminant analysis to predict students at risk
Based on Table 8, it can be concluded that the three variables are independent of each other and there is no multicollinearity issue, as the VIF of each variable is less than 5. Furthermore, the observed covariance matrices for the variables are equal across groups since the p-value of Box's M test (0.062) is above 0.05. However, the null hypothesis for multivariate normality is rejected as the p-value is below 0.05 under the Shapiro-Wilk test (0.0000). The normality assumption is violated in this study due to the dichotomous nature of the robust dependent variable, meaning that this method can tolerate some deviation from the normality. Despite that the normality assumption is not met, the analysis can still be useful, according to Tabachnick and Fidell [32]. In fact, Lachenbruch [33] reviewed several studies that used discriminant analysis and found that the discriminant function performs fairly well even with non-normal data. After verifying the QDA assumptions, the prediction of students at risk using QDA proceeded with the three variables identified under correlation analysis, to form the prediction model. Upon performing the QDA with the second dataset, 54 students were identified as "not at risk" and 15 students identified as "at risk".
4.3. Survey results for the Peer Assisted Learning Program
A total of 40 students attended the PALP, which included one student who was identified as a student at risk through QDA. The students responded to the survey, which consisted of two parts. The first part had six open-ended questions with 5-point Likert scale questions ranging from 1 (poor) to 5 (superior). The results of the first part are presented in Table 9, which reports the mean and standard deviation of each close-ended question. The second part of the survey included the open-ended question, where students could provide further elaboration about the PALP.
From Table 9, item 1 had the highest mean of 4.52, where students were asked whether the peer mentor "demonstrated good knowledge of the subject matter". On the other hand, item 6 had the lowest mean of 4.23, where students were asked about "the suitability of dates and times arranged". To understand the reasons behind the low score for item 6, some of the open-ended responses provided by students are shown below:
"Classes are too late (not able to concentrate, too tired)."
"The frequency of the PALP classes should be increased, especially when the final exam is near. Only one class was spent doing final exam questions."
"The session should be 2 hours long."
In short, students wished to have a longer PALP session, to conduct the PALP earlier, and have more PALP classes to help them prepare better for their final exam. The open-ended questions also revealed some significant keywords about the PALP, such as "good", "online", "better", "give", "questions", "answers", and "session". To support this, some selected comments given by students are presented below:
"It'll be easier for the discussion if the questions can be shared before the session."
"It's better if some answers are provided."
"Prefer an online session (could watch recording, clearer view of the screen)."
"All good. Thanks for the effort."
"Give more questions with answers."
To summarize the results of the open-ended comments, it appears that students preferred online PALP than a physical one. They also expressed a desire for more practice questions and for the answers to those questions to be provided. Additionally, they preferred to receive the questions before the class. Overall, the students were satisfied with the way the PALP was conducted, as long as the mentor had a good knowledge of the subject matter and was able to effectively explain the topic and address students' questions.
4.4. Assess the effectiveness of the Peer Assisted Learning Program and quadratic discriminant analysis
At the end of the semester, we compared the list of students who were correctly and incorrectly predicted as "at risk" and "not at risk" using QDA, as summarized in Table 10. Out of 15 students who were predicted as "at risk", only one attended the PALP but with poor attendance (as shown in Table 11). Therefore, they may not have benefited from it and hence failed the course. Of the remaining 14 students, who did not attend the PALP, only five managed to pass the course. On the other hand, out of the 54 students who were predicted as "not at risk", 39 of them attended the PALP and passed the course. Of the remaining 15 students who did not attend the PALP, 14 managed to pass the course, and only one did not.
Based on the analysis of the academic performance of students who attended the PALP, it was found that 97.5% of them passed the course as per Table 11. Additionally, it was noticed that students who scored at least 60 in the final marks had better attendance than those who scored below 60. However, we cannot conclude whether the PALP was an effective intervention strategy for students at risk because a majority of them failed to attend. The results are deemed to be normal since assisting students at risk requires a long-term effort and may not result in an immediate reduction in the failure rate [1]. Nonetheless, it was observed that students who attended the PALP had a higher probability of passing the course. This result is consistent with the study conducted by Cheng and Walters [23], which showed that attending the PALP for mathematics increased the likelihood of students passing the subject and completing the program.
Table 10 shows that, out of 69 students, only six students were predicted for the wrong categories, which are students no. 6, 8, 10, 12, 21, and 23, provided in the appendix. We also observed that all 10 students who failed the course (i.e., actual "at risk") were males. This is consistent with our previous observation that female students tend to perform better than male students in this course.
Using the confusion matrix formula given in Table 5, we calculated the values of accuracy, precision, sensitivity, and specificity of the prediction model. The accuracy of the model was found to be 91%, while the precision, sensitivity, and specificity were 98%, 91%, and 91%, respectively. Based on these results, we can conclude that QDA is a good prediction model for identifying students at risk for the actuarial science course. The accuracy obtained from this study (91%) is better that those reported in previous studies by Mubarak et al. (84%) and Mueen et al. (86%) [12,13].
5.
Conclusions
To summarize, we successfully developed a QDA prediction model to identify students at risk for an actuarial science course with high levels of accuracy, precision, sensitivity, and specificity. Our prediction model relied solely on students' learning behaviors related to academic performance, i.e., CGPA, pre-requisite subject marks, and assessment marks. While we cannot conclude that the PALP is an effective intervention strategy for students at risk, our results shows that students who attended had a significantly higher chance of passing the course. Moving forward, our focus will be on finding ways to encourage more students at risk to attend the PALP. In addition, we will consider the feedback we have received from students to improve the program.
In this study, we observed that all 10 students who failed the course were male. This finding can be investigated further since previous studies have suggested that male students tend to perform better than female students in mathematics. To validate these results, we need a larger sample size. Additionally, this raises questions about whether we should pay extra attention to male students or create a customized intervention program for them. These are areas that require further investigation in future studies.
Use of AI tools declaration
The authors would like to disclose that an AI tool was utilized in the development of this paper. The primary AI tool used was Grammarly, which was used to assist in improving writing, providing suggestions, and enhancing the overall quality of the written paper.
Acknowledgments
The authors would like to thank the reviewers for their constructive feedback.
Conflict of interest
The authors declare that there are no conflicts of interest in this paper.
Ethics declaration
The authors declare that the ethics committee approval was waived for the study.









 DownLoad:
DownLoad: