Conceptual analogy between mass density and probability density – An almost non-technical note

1.   Introduction

Integration can be used to derive the mass of non-homogeneous objects if the structure is not too complex. Such an exercise, however, is not only useful in engineering, but can also be a very illustrative, tangible way of introducing multivariate probability theory with continuous variables. It seems logical to start with the three-dimensional case, since this is what we encounter every day, and thus what we can easily relate to.

2.   Mass of a physical object

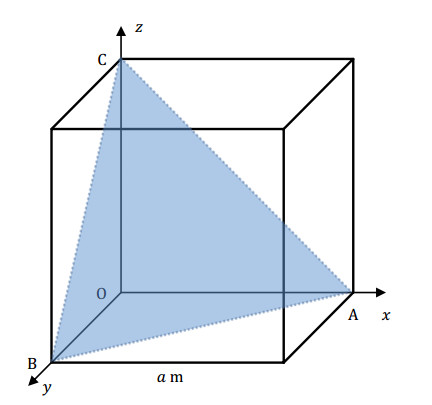
Take a non-homogeneous cube with an edge of $a$ meters. Suppose that its density ($\rho$) depends on the sum of the shortest distances from the three faces meeting at a given vertex. Thus, placing the cube into a Cartesian coordinate system where the origin is that particular vertex (Figure 1), the density can be expressed as the sum of the spatial coordinates, ¹

It follows that the density of the large cube is a spectrum between $0\;\mathrm{k}\mathrm{g}/{\mathrm{m}}^{3}$ and $3a\;\mathrm{k}\mathrm{g}/{\mathrm{m}}^{3}$. Since the equation $x+y+z = j\in {\mathbb{R}}^{+}\;\mathrm{m}$ defines a hyperplane, the cube consists of a continuum of parallel cross-sections (slices). Practically speaking, each slice is a set of points for which the sums of the coordinates are equal (Figure 2).

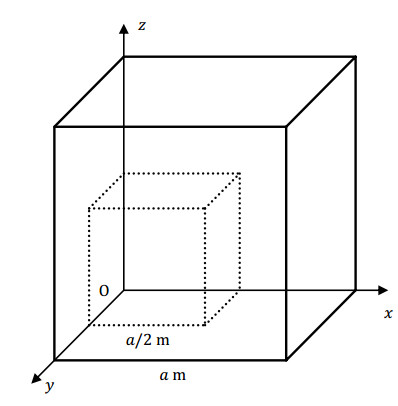
Question 1: What is the mass of the small cube with an edge of $a/2$ meters and its relation to the mass of the large cube?

If the material were homogeneous, the answer would be straightforward. The volume of the small cube is ${a}^{3}/8\;{\mathrm{m}}^{3}$, which should be multiplied by the density of the material to get the mass. In our case, however, the density is in not a constant but a linear function of $x, y, z$. Triple integration comes to our rescue.

In this process, the object is scanned properly along each dimension. Since we are dealing with cubes that have three edges on the axes of the coordinate system, we have an easy job: The limits of integration, i.e. the lower and upper bounds of the scan are simply the origin and the edge length in each dimension. That is, the mass of the small cube is (substituting Equation 1)²

The mass is calculated in the same way for the large cube:

Table 1 summarises our answer to Question 1.

Of a homogeneous object and its non-homogenous lookalike, the one with the lower average density is the lighter. Since the density of the homogeneous is assumed to be equal to the spectral maximum of the non-homogeneous, it is obvious why the homogeneous is the heavier.

Overall, for complex structures, it is usually necessary to go beyond simple geometric formulae and use integration to calculate the mass. Depending on the shape of the surface and also the density structure, other coordinate systems may be more useful. For example, in the spherical coordinate system, the three coordinates of a point $P$ are the radial distance (i.e., the length of the line segment $OP$), the azimuthal angle (measured between the x-axis and $OP$'s projected line segment on the xy-plane) and the zenith angle (measured between the z-axis and $OP$). With a concrete example, the point $\left(a, a, a\right)$ in our Cartesian coordinate system would be the point $\left(a\sqrt{3}, \pi /4, \pi /4\right)$ in a spherical coordinate system assuming identical axes, where the two 45° angles are in radians. Without going into the details, this alone suggests that for a non-homogeneous sphere, the radial and angular scans under the spherical coordinate system (with more obvious limits of integration) may be more appropriate than the scans along the axes under the Cartesian coordinate system.

3.   From mass density through occurrence density to …

The above concept can be readily applied to probability calculations. Let us suppose that a source emits sinusoidal pulses for which all their characteristics (amplitude, wavelength, speed) are random variables. Assume that each variable can take a value between 0 and $a$ in their own unit of measurement, and that a pulse is more likely to occur if the value of any of its properties is greater.³ Assuming direct proportionality with proportionality constant 1 for each variable and, for simplicity, taking the values without the units of measurement, it means

where $x$, $y$ and $z$ are the values for amplitude, wavelength and speed, respectively.⁴ Thus, we know the ranges (0 to $a$ for each), we know the occurrence density of the triplets (defined by function $f$), and so we know the set of all possible outcomes of our random experiment, i.e., the sample space ($S$).⁵ This abstract space can be imagined as if it were a real space. That is, $x$, $y$, and $z$ can be thought of as "spatial" coordinates and the function $f$ as the descriptor of "mass" density.

Question 2: What is the probability that the next pulse emitted will have amplitude and wavelength of $a/2$ meters or less and speed of $a/2$ $m/s$ or less?

Actually, we have already solved this puzzle. The set of outcomes defined in Question 2 is a so-called event ($E$), therefore the probability in question is (recall Table 1)

where $Pr$ is a function called probability measure that maps all events to a real number between 0 and 1, i.e., $Pr:Event\to \left[\mathrm{0, 1}\right]$. That is, the domain of this function is a collection of sets.

For example, let us take two events whose union gives the sample space: The one that we have already defined ($E$), and its complement set (${E}^{C}$), where all three variables are greater than $a/2$ (in their own unit of measurement). Then, the domain consists of these two disjoint events which the probability measure maps to $1/16$ and $15/16$ (recall Equation 5), plus the trivial events, the empty set ($\mathrm{\varnothing }$) and the sample space ($S$), which it maps to 0 and 1.⁶ Note that non-trivial events are not necessarily defined as disjoints. The point is that all outcomes should be covered, i.e., the union of non-trivial events should be the sample space. Empty set can be, for example, an elementary event, meaning an event having only a single outcome (e.g., "Each variable equals $a$/2"). By geometric analogy, a point has no extent and hence no mass, i.e. the numerator in Equation 5 and so the probability will be zero ($Pr:\mathrm{\varnothing }\to 0$).

4.   … probability density

Recall that the "mass" of the large cube is $3{a}^{4}/2$. Thus, with $a:=\sqrt[4]{2/3}$, our non-homogenous structure of the large cube represents not only an occurrence density, but also a probability density: It integrates to 1 just like the probability density function (PDF) of a normal (Gaussian) or any other absolutely continuous probability distribution.⁷ Practically, as the "mass" of the sample space is 1, it means that the "mass" of an event is also the probability of the event (e.g., $\mathrm{Pr}\left(E\right)="Mass"\;of\;small\;cube/1$).

Thus, in this case, Equation 4 is a three-variable joint PDF. A three-variable PDF has three marginal PDFs. The marginal PDF shows the probability distribution of a variable considering all related value pairs of the remaining two variables. For example, it shows the probability distribution of amplitude considering all related pairs of wavelength and speed. Formally, the marginal PDF of amplitude is (using the expression ${a}^{2}x+{a}^{3}$ obtained in Equation 3 after the integration with respect to $z$ and $y$, and substituting $a = \sqrt[4]{2/3}$)

Question 3: What is the probability that the next pulse emitted will have amplitude of a/2 meters or less?

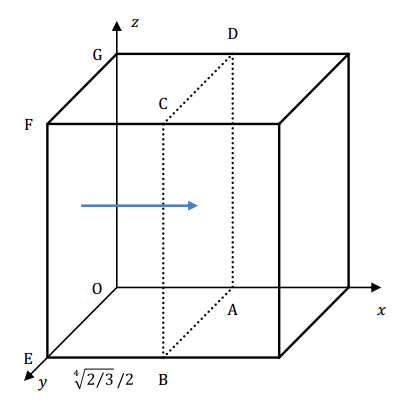
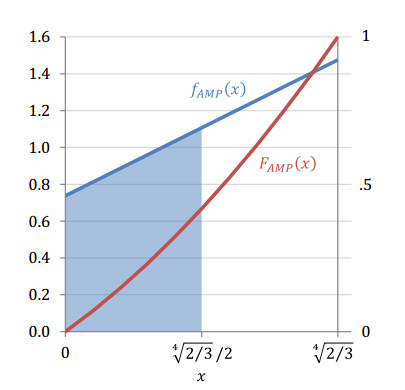
To answer this question, we need to integrate ${f}_{AMP}\left(x\right)$ from 0 to $\sqrt[4]{2/3}/2$ (i.e., halfway). Visually, the integration of this function can be also thought of as an underlying cross-section scan of the large cube along the desired segment of the $x$-axis. That is, the "mass" of the ABCDEFGO cuboid in Figure 3 and the size of the shaded area in Figure 4 are exactly the same, namely the probability we want to find.

The cumulative distribution function (CDF) simply shows the integrated "mass" of the PDF from the minimum value of the random variable to a specific value of the random variable, i.e., the probability that the random variable is smaller than the specific value. As for amplitude, the event is $amplitude\le x$, and so the related probability is $Pr\left(amplitude\le x\right)$. It logically follows that the CDF goes from 0 to 1 as $x$ increases from its minimum value. Formally, the marginal CDF of amplitude is (using Equation 6)

where the expressions after sign $\equiv$ recalls the underlying content highlighted in Figure 3. The specific value from Question 3 is $x = \sqrt[4]{2/3}/2$, so substituting this into Equation 7 gives the probability sought.

To conclude this section, let us invoke our old acquaintance, the small cube. The probability of the event it represents (here: "All variables are $\sqrt[4]{2/3}/2$ or less in their own unit of measurement") is, of course, already known. Notice, however, that since it is located at the origin (i.e., at the minimum values of the variables), the probability can be expressed by the joint CDF,

5.   Towards generalisation with a bit of formalism

Let us return to the general concept of "small cube / large cube" with $a > 0$. The concept can be easily generalized to higher (or lower) dimensions. For example, if the duration of a pulse varies, this new dimension can be added to our sample space. Assuming a range of 0 to $a$ seconds, the sample space becomes a tesseract, i.e., a 4-dimensional hypercube.

Let $w$, $x$, $y$, and $z$ denote the values (without the units of measurement) for duration, amplitude, wavelength and speed, respectively. Suppose that, in the occurrence density function, the duration also has the same proportionality as the other addends. Thus, the sample space is (denoting dimension in parenthesis)

whereas the occurrence density function is ${f}^{\left(4\right)}\left(w, x, y, z\right) = w+x+y+z$. Using the result of Equation 3, the "mass" of such an object is

The event in which the duration is $a/2$ seconds or less, in addition to the other three analogous conditions, is

and so its "mass", using the result of Equation 2, is

and so the probability of such an event is

6.   Dimensionality and shape issues

Notice that the probability of our 4-dimensional event (see Equation 13) is only half of the probability of our 3-dimensional event (see Equation 5). It is easy to see that the probabilities of events defined along similar patterns dwarf as the dimension increases. Assuming an occurrence density of 1, for simplicity, the limit is

where $n\in \mathbb{N}$ denotes the dimension and $k > 1$ is a constant.

Note that, in this context, the shape of the sample space and the event is not irrelevant. Think of a homogeneous spherical sample space and a cubical event with radius ($r$) and edge ($l$) of $a$ "metres" and identical center of symmetry. It follows that ${E}_{cube(l = a)}^{\left(3\right)}\subset {S}_{sphere(r = a)}^{\left(3\right)}$ as the body diagonal of the cube is smaller than the diameter of the sphere ($a\sqrt{3} < 2a$). As $n$ goes to infinity, however, their ratio also goes to infinity,

where $\mathrm{\Gamma }$ denotes the gamma function.⁸ That is, beyond a certain point, ${E}_{cube(l = a)}^{\left(n\right)}\not\subset {S}_{sphere(r = a)}^{\left(n\right)}$ is inevitable, which relation makes no sense.

7.   Conclusions

I proposed an approach for those who prefer visualisation to abstraction when they first encounter a more complex subject such as multivariate probability theory with continuous variables. Once the link is established through a three-dimensional physical example, one could easily move towards abstraction. In fact, geometry as a complement can help to understand several algebraic concepts. Adventurous readers with a deeper interest in geometric probability should delve into the books of, for example, Solomon ^[3], Klain and Rota ^[4], or Mathai ^[5].

Use of AI tools declaration

The author declares that he did not use Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The author thanks the anonymous reviewers for their helpful comments.

Conflict of interest

The author declares that there is no conflict of interest to disclose.

Ethics declaration

The author declares that there was no human participation in this article and therefore ethics approval and informed consent were not required.

¹ Note that the unit of measurement of the variables is meter, and so $\mathrm{m} \cdot \mathrm{k}\mathrm{g}/{\mathrm{m}}^{4} = \mathrm{k}\mathrm{g}/{\mathrm{m}}^{3}$.

² Only power rule is applied: $\int {x}^{n}dx = {x}^{n+1}/\left(n+1\right)+c$. Note that the constant cancels out for a definite integral. For simplicity, the units of measurement were omitted during the integration. However, notice that, at the end, the meters would be to the fourth power, which together with the factor $\;\mathrm{k}\mathrm{g}/{\mathrm{m}}^{4}$ of the density function is ${\mathrm{m}}^{4} \cdot \mathrm{k}\mathrm{g}/{\mathrm{m}}^{4} = \mathrm{k}\mathrm{g}$.

³ This is just an arbitrary example with no underlying physical content.

⁴ If the function were defined for the values with units of measurement, it would be $f\left(x, y, z\right) = x/\mathrm{m}+y/\mathrm{m}+z \cdot \mathrm{s}/\mathrm{m}$ similar to Equation 1.

⁵ Note that, in a continuous space, a single point (triplet) has no mass and hence no density, but the very small environment around it has mass and hence density.

⁶ This collection $\left\{\mathrm{\varnothing }, E, {E}^{C}, S\right\}$ is a so-called $\sigma$-algebra on $S$. The trio of sample space, $\sigma$-algebra, and probability measure is called the probability space.

⁷ The Cantor distribution is a notable example of a continuous (but not absolutely continuous) distribution without a PDF. For a geometric discussion of this interesting distribution, see Presnell ^[1].

⁸ For an in-depth discussion of the interesting properties of n-sphere's volume (e.g., besides its asymptotic nullity, its non-monotonicity to n), see Smith and Vamanamurthy ^[2].