The purpose of fins or extended surfaces is to increase the dissipation of heat from hot sources into their surroundings. Fins like annular fins, longitudinal fins, porous fins, and radial fins are used on the surface of equipments to enhance the rate of heat transfer. There are many applications of fins, including superheaters, refrigeration, automobile parts, combustion engines, electrical equipment, solar panels, and computer CPUs. Based on a wide range of applications, the effects of stretching/shrinking on a fully wet trapezoidal fin with internal heat generation is investigated. The shooting approach is used to calculate the trapezoidal fin's thermal profile, tip temperature, and efficiency. It is observed that with an increase in the shrinking and wet parameter, the temperature distribution decreases and efficiency increases. On the other hand, when stretching increases, the temperature distribution increases and efficiency diminishes. Using the computed results, it is concluded that shrinking trapezoidal fins improves the effectiveness and performance of the system.
Citation: Sharif Ullah, Obaid J. Algahtani, Zia Ud Din, Amir Ali. Numerical analysis of stretching/shrinking fully wet trapezoidal fin[J]. Networks and Heterogeneous Media, 2024, 19(2): 682-699. doi: 10.3934/nhm.2024030
| [1] | Jie Gu, Lijuan Nong, Qian Yi, An Chen . Two high-order compact difference schemes with temporal graded meshes for time-fractional Black-Scholes equation. Networks and Heterogeneous Media, 2023, 18(4): 1692-1712. doi: 10.3934/nhm.2023074 |
| [2] | Liping Yu, Hans Kleppe, Terje Kaarstad, Svein M. Skjaeveland, Steinar Evje, Ingebret Fjelde . Modelling of wettability alteration processes in carbonate oil reservoirs. Networks and Heterogeneous Media, 2008, 3(1): 149-183. doi: 10.3934/nhm.2008.3.149 |
| [3] | Li-Bin Liu, Yige Liao, Guangqing Long . Error estimate of BDF2 scheme on a Bakhvalov-type mesh for a singularly perturbed Volterra integro-differential equation. Networks and Heterogeneous Media, 2023, 18(2): 547-561. doi: 10.3934/nhm.2023023 |
| [4] | Steinar Evje, Aksel Hiorth . A mathematical model for dynamic wettability alteration controlled by water-rock chemistry. Networks and Heterogeneous Media, 2010, 5(2): 217-256. doi: 10.3934/nhm.2010.5.217 |
| [5] | Bendong Lou . Self-similar solutions in a sector for a quasilinear parabolic equation. Networks and Heterogeneous Media, 2012, 7(4): 857-879. doi: 10.3934/nhm.2012.7.857 |
| [6] | Stefan Berres, Ricardo Ruiz-Baier, Hartmut Schwandt, Elmer M. Tory . An adaptive finite-volume method for a model of two-phase pedestrian flow. Networks and Heterogeneous Media, 2011, 6(3): 401-423. doi: 10.3934/nhm.2011.6.401 |
| [7] | Alessandra Pluda . Evolution of spoon-shaped networks. Networks and Heterogeneous Media, 2016, 11(3): 509-526. doi: 10.3934/nhm.2016007 |
| [8] | Liuchao Xiao, Wenbo Li, Leilei Wei, Xindong Zhang . A fully discrete local discontinuous Galerkin method for variable-order fourth-order equation with Caputo-Fabrizio derivative based on generalized numerical fluxes. Networks and Heterogeneous Media, 2023, 18(2): 532-546. doi: 10.3934/nhm.2023022 |
| [9] | Huanhuan Li, Meiling Ding, Xianbing Luo, Shuwen Xiang . Convergence analysis of finite element approximations for a nonlinear second order hyperbolic optimal control problems. Networks and Heterogeneous Media, 2024, 19(2): 842-866. doi: 10.3934/nhm.2024038 |
| [10] | Massimiliano Zanin, Ernestina Menasalvas, Pedro A. C. Sousa, Stefano Boccaletti . Preprocessing and analyzing genetic data with complex networks: An application to Obstructive Nephropathy. Networks and Heterogeneous Media, 2012, 7(3): 473-481. doi: 10.3934/nhm.2012.7.473 |
The purpose of fins or extended surfaces is to increase the dissipation of heat from hot sources into their surroundings. Fins like annular fins, longitudinal fins, porous fins, and radial fins are used on the surface of equipments to enhance the rate of heat transfer. There are many applications of fins, including superheaters, refrigeration, automobile parts, combustion engines, electrical equipment, solar panels, and computer CPUs. Based on a wide range of applications, the effects of stretching/shrinking on a fully wet trapezoidal fin with internal heat generation is investigated. The shooting approach is used to calculate the trapezoidal fin's thermal profile, tip temperature, and efficiency. It is observed that with an increase in the shrinking and wet parameter, the temperature distribution decreases and efficiency increases. On the other hand, when stretching increases, the temperature distribution increases and efficiency diminishes. Using the computed results, it is concluded that shrinking trapezoidal fins improves the effectiveness and performance of the system.
Abbreviations: Nr: Dimensionless radiation parameter; qh: Dimensional heat generation(W/m3); t0: Fin's base thickness (m); σ: Stefane-Boltzmann constant (W/m2K4); Ts: Dimensional surface temperature (K); η: Fin efficiency; x: axial distance (m); p1: constant; kf: Thermal conductivity number (W/mK); Uf: Speed of moving fin (m/s); Cp: Specific heat coefficient (J/kgK) ; Wf: Fin's width (m); θb: Dimensional base temperature (K); F(x): Trapezoidal fin's thickness (m); ρf: Density of material (kg/m3); Tb: Fin base temperature (K); ε: Surface emissivity; Lf: Fins length (m); hc: Convective heat coefficient (W/m2K); θ(0): Dimensionless Fin's tip temperature; S∗t: Rate of stretching/shrinking (m); δ: Fin's tip Semi-fin thickness (m); T∞: Dimensional ambient temperature (K); Af: Area of fin's surface (m2); θ(X): Non-dimensional temperature; Nc: Dimensionless convection parameter; Qh: Non-dimensional internal heat generation; T: Fin temperature (K); St: Dimensionless Stretching/shrinking parameter; θa: Non-dimensional ambient temperature; hm: Mass transfer coefficient; ih: Latent heat of evaporation (J/kg); ˜w: Humidity ratio for the saturated air (g/m3); ˜wa: Humidity ratio for the ambient air (g/m3); H(x): Fin's structure area; qm: Exponential index of h; p2: Dimensionless wet parameter; p0: Constant
Besides nanofluids and cooling fluids, extended surfaces, known as fins, of different geometric shapes have been extensively used to improve heat transfer mechanisms in various engineering processes. The use of fins allows a heated source to transfer heat more efficiently to a colder liquid by increasing the surface area. In superheaters, microprocessors, electrical equipment, gas turbines, refrigeration, aircraft engines, car radiators, and vehicles, fins are used to transfer heat. Among the most interesting studies in this field has been the improvement of heat transfer rate. It is essential to develop more efficient, reliable, and lightweight models to reach this goal. The majority of fins are formed from metals or alloys that are highly thermally conductive. Typically, fins are used in electric transformers, space vehicles, photovoltaic panels, microelectronic components, and combustion engines. In response to these applications, several researchers explored heat transfer through various shapes of fins, including rectangular, exponential, trapezoidal, and radial. In a wide range of technological systems and machines, fins play a prominent role. These include air conditioning, refrigeration, aviation engineering, automobile industries, home electronic systems, power plants, microelectronics, and cryogenic processing [1,2,3,4].
There have been several studies that have examined various fin profiles to increase thermal transmission and enhance the efficiency of engineering appliances. An analysis of the heat exchange efficiency of rectangular radiating fins has shown that neglecting the thermal radiation effect reduces the fin's heat dissipation capacity and efficiency [5]. Copper and aluminium fins are particularly affected by this influence. Analyses were performed numerically on trapezoidal and exponential fins with multiple nonlinearities. It has been shown that exponential fins are more productive and transfer more heat than trapezoidal fins [6,7]. Numerous methods have been developed to estimate the thermal dissipation from radiative fins based on the radiative parameters. There have been several studies using Differential Transform Method (DTM) [8,9]. For studying radiative parameters, variational iteration and least squares have been used [10,11]. A rectangular-shaped fin considering linear and exponential temperature-dependent thermal conductivity is studied to determine the temperature distribution [12]. It is observed that the temperature field increases with increasing thermal conductivity while diminishing with increasing thermo-geometric parameters. In [13], an investigation of the heat distribution and efficiency of a rectangular-shaped longitudinal fin is conducted with a magnetic field applied. It was found that as thermal conductivity increases, the longitudinal fin temperature profile improves, but for Hartmann number and thermometric parameters decline.
In addition to convection, radiative heat loss from fin surfaces cannot be ignored if it is comparable to that from natural convection. Due to this, it is necessary to take both heat losses into account at the same time when assessing the thermal performance of conductive, convective and radiative fins, regardless of whether the device has a low convection or radiation heat transfer coefficient. An experimental and numerical study of the temperature along a fin cooled by convection and radiation as well as superficial electromagnetic flow has been investigated in [14,15,16]. This analysis shows that heat transmission through radiation is nearly 15–20% of the whole. The results elaborate that heat is transmitted through radiation between 15–20% of the whole. As a result of [17] experiments on cylindrical fins with 0.99 surface emissivity, one-third of the heat is transmitted through radiation. The effectiveness of the radiative-rectangular fin was examined through the decomposition method by [18]. Also, the same procedure was implied for determining the performance of the convective rectangular fin along with the convective-radiative longitudinal fin and observing the fin's thermal field. By introducing all nonlinearities, [19] analytically presented the convective-radiative straight fin's thermal performance along with various profiles. Through the same analytical technique, [20] also analyzes the radiation effect on the constructional T-shaped fin's performance. According to [21], a trapezoidal fin can be optimized to dissipate more heat when mutual irradiation is considered. The geometrical optimization technique for a convective-radiative longitudinal fin was applied by [22]. [23] examined thermal performance for optimum exponential fin profiles in response to temperature jump. Temperature jump has a negative impact on fin efficiency because it lowers the efficiency of the fins. While exponential fins of growing shapes have higher efficiency than rectangular or decaying ones, exponential fins of rectangular shapes have low efficiency. As a result, exponential fins that can withstand a certain temperature jump are useful for technological cooling. In [24] a wavy fin is examined for its heat transfer under the combined influence of radiation and convection. In both wavy and rectangular fins, the thermal distribution decreased when the convection-conduction and radiation-conduction variables increased.
According to [25], a wetted straight fin's efficiency can be evaluated analytically using a relationship between fin temperature and humidity ratios. It was found that the efficiency of the fins was directly proportional to atmospheric pressure. [26] examined porous semi-spherical fins under totally wet conditions using the modified fin parameter. A least squares method was applied, and numerical calculations were used to validate the results. According to the results, mass transfer must be limited to achieve high fin efficiency. A numerical study by [27] investigated the radial fin problem under wet and porous conditions using spectral collocation, and found that a full wet fin improves heat transfer. The heat transfer of a radiative-convective, wetted and wavy fin is computed in [28]. They observed a decrease in the temperature profile with rising wet and convective-conductive parameters. The temperature distribution within a conductive-radiative rectangular profiled annular fin with the influence of internal heat generation is analyzed in [29]. In the report, the large increase in heat generation parameters leads to an increase in temperature distribution, but the temperature distribution decreases as thermogeometric and radiative-conductive parameters increase.
The thermal behavior and effectiveness of conventionally stretching and shrinking moving rectangular fins have been investigated in [30]. It has been shown that stretching reduces fin efficiency while shrinking increases it, indicating significant benefits for fin design. The numerical simulation of the stretching and contraction mechanism in an exponential-shaped fin was discussed by [31]. The shrinking mechanism significantly enhances the cooling effect of the fin, particularly when it is in motion. Researchers examined the stretching and shrinkage phenomenon for moving fins with different profiles [32]. The Differential Transform Method was used to analyze and validate numerical and analytical results for a convective-radiative rectangular fin that is stretching and shrinking in [33]. By shrinking and moving the fin, they could see that the temperature distribution in the fin is lowered. It is observed that setting a shrinking mechanism on the fin surface can reduce the negative effects of internal heat generation and motion on the fin heat transfer rate.
Based on the homotopy analysis technique, [34] accurately determined the trapezoidal fin's thermal performance The two-dimensional heat transfer investigation through trapezoidal fins was discussed by changing the fin's base thickness in [35]. The results show that heat loss decreases linearly with an increase in the fin's shape factor. In [36], the temperature profile study of a trapezoidal fin was conducted. This analysis also demonstrated that fin size along with the thermal conductivity coefficient enormously influences temperature transmission versus other variables. The thermal behavior of moving trapezoidal extended surfaces was also examined [37]. According to [38], variation in the mass flow rate intensifies the thermal transmission efficiency of trapezoidal fins. The thermal performance of a wet porous convective-radiative trapezoidal fin was scrutinized in [39] and found that porosity as well as wet nature enhances the fin's cooling.
Using The finite difference method (FDM), several innovative methods were used to calculate the numerical behavior of a fully wet porous trapezoidal fin under motion and periodic heating circumstances [40]. It is observed that periodic heat transfer causes the fin thermal profile to have a wavy pattern against time. This analysis is useful when designing fin structures for applications such as solar collectors, airborne applications, and refrigeration systems. In the current study, we aim to numerically examine the impact of the stretching/shrinking mechanism along with heat generation on the thermal transmission characteristics of a moving trapezoidal profiled longitudinal fin. By introducing dimensionless parameters into the equation, the governing equation is non-dimensionalized, and the numerical solution is derived by using the shooting technique to examine the effect of various parameters on stretching/shrinking and moving trapezoidal fins. By using graphical representations of the thermal profile of the fin and the efficiency of the fin, the study conforms with the physical interpretations. In comparison to longitudinal fins that are not stretched, stretching reduces their performance. The present work highlights the role shrinking plays in assisting the fin's function and emphasises the need for further research in this area.
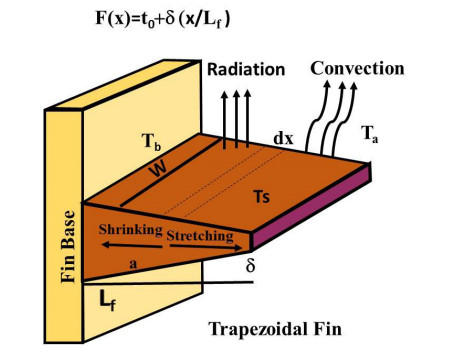
Here, the thermal transfer problem of a stretching/shrinking, convective-radiative and fully wet trapezoidal fin with fin's structure area H(x) varies with the fin's thickness tf(x) involving internal heat generation is considered and is shown in Figure 1. Considering that the fin is completely wet, convection and radiation will lose heat to the surrounding. Let the fin's base thickness, base temperature, width, convective coefficient, thickness, surface temperature, density, thermal conductivity, taper ratio, Stefan-Boltmann constant, emissivity, thermal profile, and ambient temperature be indicated by τ0,Tb,Wf,h,F(x),Ts,ρf,kc,δ,σ,ε,T, and Ta, respectively. The stretching/shrinking and moving mechanism in horizontal direction is considered in fin with a speed Uf(1+S∗tx). Here, x is the traveled distance from the base, Uf shows the local speed, and S∗t indicates the fin's stretching/shrinking rate.
The energy equation under aforementioned considerations for trapezoidal fin as [23,31,37]
| qx−q(x+dx)=hcPf(T−Ta)−ρfH(x)CpUf(1+S∗tx)dTdx−2hmih(˜w−˜wa)−2ϵPfσ(T4−T4s)−qhH(x) | (2.1) |
After simplification, Eq (2.1) becomes
| −dqdx−2hcPf(T−Ta)+ρfH(x)CpUf(1+S∗tx)dTdx−2hmih(˜w−˜wa)−2ϵPfσ(T4−T4s)+qhH(x)=0. | (2.2) |
For conduction, Fourier's law proposed that [41]
| qx=−k(H(x))dTdx. | (2.3) |
and considering the fin fully wet, we have [31]
| ˜w−˜wa=bw(T−Ta). | (2.4) |
Putting Eqs (2.3) and (2.4) in Eq (2.2), we get
| ddx(keffH(x)dTdx)−2hPf(T−Ta)+ρfH(x)CpUf(1+S∗tx)dTdx−2hmih(˜w−˜wa)−2ϵPfσ(T4−T4s)+qhH(x)=0. | (2.5) |
Here, the fin's perimeter, cross-section area H(x), and heat transfer coefficient h are given by [26]
| Pf=Wfdx,H(x)=WfF(x). | (2.6) |
| h=hc[T−TaTb−Ta]qm. | (2.7) |
where, F(x) is trapezoidal fin's thickness and is given as
| F(x)=t0−δ(xLf). | (2.8) |
By putting Eqs (2.6)–(2.8) in Eq (2.5), we obtain
| keffddx[Wf(t0−δ(xLf))dTdx]−2hchmihLfe23cpWfdx[T−TaTb−Ta]qm(T−Ta)+qhWf(t0−δ(xLf))+ρf(t0−δWf(xLf))CpUf(1+S∗tx)dTdx−2hcWfdx[T−TaTb−Ta]qm(T−Ta)−ϵWfdxσ(T4−T4s)=0. | (2.9) |
Introducing the boundary conditions
| Atx=Lf,T=Tb,andx=0,dTdx=0, | (2.10) |
and proposing the non-dimensional parameters
| θs=TsTb,X=xLf,θ=TTb,Qh=qhL2fkefft0,θa=TaTb,Nc=hρfL2fkefft0,p1=2hchmihbwL2fkefft0Lfe23cpp0=2hcL2fkefft0,p2=p0+p1,Nr=ϵσL2fT3bkefft0,Pe=UfρfCpLfkeff,St=S∗tLf,Cf=δt0. |
Using the boundary conditions (2.10) and the above non-dimensional terms, Eq (2.9) can be written in the form
| d2θdx2−CfdθdX−Cfxd2θdx2+Pe(1+Stx)(1−Cfx)dθdx−N2c[θ(x)−θa]−p2(θ−θa)(qm+1)(1−θa)qm−Nr[θ(x)4−θ4s]+Qh(1−Cfx)=0, | (2.11) |
with boundary conditions
| x=1,θ(x)=1,x=0,dθ(x)dx=0. | (2.12) |
where θa is the temperature ratio, Nr is the surface radiation parameter, Pe indicates the Peclet number, p2 denotes the wet parameter, Nc is the convection-conduction parameter, and St denotes the stretching/shrinking parameter in Eq (2.11) together with conditions (2.12).
A fin's efficiency is determined by the decrease in temperature potential between the fin and its surroundings. The fin's efficiency η is computed from the ratio of total thermal transport and maximum thermal transport of the fin.
The thermal transmission through the fin is given by the following equation
| qf=∫Lf0[hcWf(T−Ta)+ϵWfσ(T4−T4s)] | (2.13) |
The thermal transmission through the ideal fin is given by
| qI=LfhcWf(T−Ta)+ϵLfWfσ(T4−T4s) | (2.14) |
The fin's efficiency can be computed from (2.13)-(2.14) as
| η=qfqI. | (2.15) |
Eq (2.15) for the considered trapezoidal fin in the non-dimensional form can be obtained in the form
| η=∫10[Nr[θ4(X)−θ4s]+N2c[θ(X)−θa]]Nr[1−θ4s]+N2c[1−θa]. | (2.16) |
Equations (2.11) and (2.16) anticipated that the fin's thermal profile θ(X) and the fin's efficiency η depends on parameters involved, namely the radiative parameter Nr, wet parameter p2, heat generation Qh, stretching/shrinking parameter St, power index qm, convection parameter Nc, taper ratio Cf, and Peclet number Pe.
In the shooting method, boundary value problem are converted into initial value problems in order to solve them numerically. In general, multiple paths are described until we identify the best boundary value; the process is repeated. It is useful when boundary conditions (BCs) are defined on both ends of an interval but the solution behavior between them is unknown.
To begin, determine the Dirichlet boundary value of a linear differential equation.
| d2Hdz2=N(z)dHdz+R(z)H+G(z)subject toH(u)=χ,H(v)=ε, | (3.1) |
on the interval [u,v]. The terms, N(z) and R(z) represent the arbitrary functions, and G(z) indicates the source term.
The BVP (3.1) can be typically solved as a linear combination of the functions ξ(z) and ψ(z)
| H(w)=ξ(w)+γ−ξ(v)φ(v)⋅φ(w). | (3.2) |
Eq (3.2) forms initial value problems
| d2ξdw2=s(w)dξdw+p(w)ξ+t(w),subject toξ(u)=χ,dξ(u)dw=0, | (3.3) |
| d2ψdw2=s(w)dψdw+p(w)ψ+t(w),subject toψ(u)=χ,dψ(u)dw=0, | (3.4) |
where ξ(w) and ψ(w) are the solutions of initial value problems (3.3) and (3.4) respectively.
Here, we analyzed the temperature field, the temperature of the fin's tip θ(0) and the fin's efficiency η considering stretching/shrinking, fully wet and radiative trapezoidal fins involving convection. The temperature field θ(x) behavior of nine physical parameters is illustrated in Figures 2–6.
Figure 2a illustrates that The thermal profile begins to decline as shrinking increases because particles become closer together; consequently, convection heat transfer increases, and hence the thermal profile decreases by approximately 1% when shrinking rises from 0.1 to 0.2. Contrary to that, when stretching is increased from 0.1 to 0.2, the particles move away from each other, so convection heat transfer decreases and the thermal profile rises by 1%. The thermal profile decays of about 1% with the rising convective parameter Nc from 0.1 to 0.3 as shown in Figure 2b. Because by enlarging convection, the heat transport is enhanced at the fin's surface. So the temperature profile declines.
Figure 3a shows that the temperature profile steps down of about 6% when the radiative parameter Nr is boosted from 0.1 to 0.3. Physically, elevating the value of Nr causes the enhancement of heat loss from the fin's surface to the outside field. Hence, a lower temperature resulted.
Figures 3b and 4a illustrate the effects of enhancing θs and θa on the behavior of the thermal profile. The thermal profile upgrading occurs when the value of θa and θs increases from 0.1 to 0.3 because thermal exchange via convection from the trapezoidal fin's surface decreases, and as a result, the thermal profile is augmented by 8% and 9% respectively. Figure 4b depicts that incrementing the Peclet number Pe causes the enhancement of the heat distribution. In fact, the fin's speed increases with the increase in Peclet numbers. Thus, the interaction time between the surroundings and the surface is decreased. So, the temperature enhances of about 5% when the Peclet number enhances from 0.1 to 0.3.
Figure 5a displays that the temperature field is augmented when the internal heat generation Qh value is incremented. Because the heat rate absorbed by the fin's structure increases with an increase in Qh, cooling is observed by lowering the value of Qh. Thus, increasing Qh from 0.1 to 0.3 upgrade the temperature field by 6%. While enhancing the fin's taper ratio, the Cf value causes the thermal profile to decline, as exhibited in Figure 5b. Therefore, increasing Cf from 0.1 to 0.3 reduces the temperature field by 3%.
Figure 6a captures the influence of the wet parameter p2 on a fully wet trapezoidal fin. As wet parameter p2 increases, the thermal profile is reduced, and hence fin cooling is enhanced, as the fin surface temperature decreases. Due to the wetness surrounding the fin, more heat is absorbed by the surrounding fluid, contributing to the loss of heat via convection.
The significance of the exponential index qm for the energy attribute of the stretching/shrinking trapezoidal fin can be seen in Figure 6b. A higher value of qm increases the temperature field in the fin. Here, heat transfer coefficient h becomes more sensitive to fin temperature as qm increases. In this way, qm negatively affects the convectional heat loss, raising the fin surface temperature.
Further, the trapezoidal fin's tip temperature θ(0) along the dimensionless stretching/shrinking parameter is illustrated in Figures 7–9. These figures display the repercussions of the stretching/shrinking phenomena, that by increasing the shrinking parameter, the trapezoidal fin's tip temperature rises. However, the enhancement of stretching results in the opposite result. Figures 7a, b demonstrates the exceeding of trapezoidal fin's tip temperature θ(0) by the role of amplifying Pe and Qh from 0.4 to 0.8. Also, Figure 8a shows that fin's tip temperature decrements when Nr upgrade from 0.4 to 0.8 while the outcome is contrast for intensifying θa from 0.4 to 0.8 as captured in Figure 8b. Figure 9a anticipate the cause of amplifying Nc from 0.4 to 0.8, that is reducing the trapezoidal fin's tip temperature. In comparison, the outcome is contrasted for ameliorating the fin's taper ratio Cf from 0.4 to 0.8 as portrayed in Figure 9b.
The efficiency of a fully wet trapezoidal fin along with the stretching/shrinking parameter with considered parameters is visualized in Figures 10–13. According to these figures, the fin's efficiency η will rise with shrinking, but decay with stretching. Furthermore, increasing the values of Nr, Nc, Cf from 0.4 to 0.8 and p2 from 0.1 to 0.3 causes the acceleration of the fin's efficiency η as presented in Figures 10a, b, Figure 11b, and Figure 13a. While Figure 11a, Figures 12a, b, and Figure 13b depict the decrementing of the efficiency η, that is caused continuously by increasing Qh, θs, θa from 0.4 to 0.8 and qm from 1 to 3.
Finally, it is observed that qm is the dominant factor which affect the heat transfer positively, means that when qm is enhanced, it increase heat transfer more than the others factors. While, θs is the affect that the heat transfer negatively more than the other negative factors. The aforesaid behavior of a stretching/shrinking fully wet trapezoidal fin with radiation showed that the trapezoidal fin shrinking effect yields higher thermal exchange efficiency and preferable economic results as compared to stretching trapezoidal fin.
In this analysis, the thermal behavior of the stretching/shrinking, moving, fully wet, and radiative trapezoidal fin accompanied by internal heat generation and convection effects is addressed. The thermal profile, tip temperature, and efficiency of the trapezoidal fin model are analyzed through numerical methods, and the effects of the included parameters are shown graphically. The computed results depict that the temperature profile augments when stretching, surface temperature, power index, internal heat generation, Peclet number, and ambient temperature elevate from 0.1 to 0.3. In contrast, the temperature profile diminishes when increasing the fin's taper ratio, wet parameter, radiative parameter, shrinking parameter, and convective parameter from 0.1 to 0.3. The trapezoidal fin's tip temperature, along with stretching/shrinking elevates by escalating stretching, Peclet number, internal heat generation, ambient temperature, and surface temperature. However, fin's tip temperature degrades with increasing fin's taper ratio, convective parameter, shrinking, and radiative parameters from 0.1 to 0.3. The fin's efficiency of a trapezoidal fin improves when the effect of shrinking increases from 0.1 to 0.2 and decreases with increase stretching from 0.1 to 0.2. Furthermore, efficiency increases with the increase in fin's taper ratio, wet parameter, convective parameter, and radiative parameter from 0.1 to 0.3 but decays when the values of Peclet number, surface temperature, power index, internal heat generation, and ambient temperature grow from 0.1 to 0.3. The study concludes that stretching, surface temperature, power index, internal heat generation, Peclet number, and ambient temperature negatively impact the efficiency and heat transfer of fins, while the fin's taper ratio, wet parameter, radiative parameter, shrinking parameter, and convective parameter positively affect heat transfer and efficiency. When the shrinking effect is incorporated into a moving radiative trapezoidal fin, the effectiveness and thermal behavior of the shrinking fin become preferable as compared to a stretching trapezoidal fin and significantly applicable in economic appliances. This work highlights the role that shrinking and wet parameters play in assisting fin function and emphasises the necessity for further research into this field.
It is also declared that all the authors have equal contribution in the manuscript. Further, the authors have checked and approved the final version of the manuscript.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Researchers Supporting Project number (RSP2024R447), King Saud University, Riyadh, Saudi Arabia.
It is declared that all authors have no conflict of interest regarding this manuscript.
Here, we include the Mathematica code used for the numerical solution to calculate the effect of different parameters as discussed in the results and discussion Section 4.
| St=0.3;θs=0.5;θa=0.1;Pe=0.7;Nc=0.3;Qh=0.2;Cf=0.3;Nr=0.3;qm=1;tickFunc=Charting‘ScaledTicks[{Identity, Identity},TicksLength→{.03,.018}][##]&;ODE1=D[θ[x],x,2]−Cf∗D[θ[x],x]−Cf∗x∗D[θ[x],x,2]−N2c∗(θ[x]−θa)+Pe∗(1−Cf∗x)∗(1+St∗x)∗D[θ[x],x]−p2∗(θ[x]−θa)(qm+1)/(1−θa)−Nr∗(θ[x]4−θ4s)+Qh∗(1−Cf∗x)=0;sol1=ParametricNDSolveValue[{ODE1,θ[1]=1,θ′[0]=0},θ[x],{x,0,1},{p2},Method→{“Shooting”,“StartingInitialConditions”→{θ′[0]=−0.668826(Sqrt[p2])}}];data=Plot[{sol1[0.1],sol1[0.2],sol1[0.3]},x,0,1,PlotStyle→{Red,Green,Blue,Purple,Magenta,Cyan},PlotRange→All,Frame→True,FrameTicks→{{tickFunc,tickFunc},{tickFunc,False}},FrameStyle→Directive[Black,AbsoluteThickness[2]],FrameTicksStyle→Directive[Black,12],LabelStyle→Directive[Bold,12],FrameLabel→X,θ[X]] |
| [1] |
A. D. Kraus, A. Aziz, J. Welty, D. P. Sekulic, Extended surface heat transfer, Appl. Mech. Rev., 54 (2001), B92. https://doi.org/10.1115/1.1399680 doi: 10.1115/1.1399680

|
| [2] | S. Kalpakjian, Manufacturing Engineering and Technology, Chennai: Pearson Education (India), 2001. |
| [3] |
Y. Shi, Q. Lan, X. Lan, J. Wu, T. Yang, B. Wang, Robust optimization design of a flying wing using adjoint and uncertainty-based aerodynamic optimization approach, Struct Multidisc Optim, 66 (2023), 110. https://doi.org/10.1007/s00158-023-03559-z doi: 10.1007/s00158-023-03559-z

|
| [4] |
Y. Shi, C. Song, Y. Chen, H. Rao, T. Yang, Complex standard eigenvalue problem derivative computation for laminar-turbulent transition prediction, AIAA J., 61 (2023), 3404–3418. https://doi.org/10.2514/1.J062212 doi: 10.2514/1.J062212

|
| [5] | T. S. Mogaji, F. D. Owoseni, Numerical analysis of radiation effect on heat flow through fin of rectangular profile, Am. J. Eng. Res., 6 (2017), 36–46. |
| [6] |
M. Turkyilmazoglu, Heat transfer from moving exponential fins exposed to heat generation, Int. J. Heat Mass Tran., 116 (2018), 346–351. https://doi.org/10.1016/j.ijheatmasstransfer.2017.08.091 doi: 10.1016/j.ijheatmasstransfer.2017.08.091

|
| [7] |
Z. U. Din, A. Ali, Z. A. Khan, G. Zaman, Investigation of moving trapezoidal and exponential fins with multiple nonlinearities, Ain Shams Eng. J., 14 (2023), 101959. https://doi.org/10.1016/j.asej.2022.101959 doi: 10.1016/j.asej.2022.101959

|
| [8] |
M. Torabi, H. Yaghoobi, A. Aziz, Analytical solution for convective-radiative continuously moving fin with temperature-dependent thermal conductivity, Int. J. Thermophys., 33 (2012), 924–941. https://doi.org/10.1007/s10765-012-1179-z doi: 10.1007/s10765-012-1179-z

|
| [9] |
S. Mosayebidorcheh, T. Mosayebidorcheh, Series solution of convective radiative conduction equation of the nonlinearfin with temperature dependent thermal conductivity, Int. J. Heat Mass Tran., 55 (2012), 6589–6594. https://doi.org/10.1016/j.ijheatmasstransfer.2012.06.066 doi: 10.1016/j.ijheatmasstransfer.2012.06.066

|
| [10] |
M. Miansari, D. D. Ganji, M. Miansari, Application of He's variational iteration method to nonlinear heat transfer equations, Phys. Lett. A, 372 (2008), 779–785. https://doi.org/10.1016/j.physleta.2007.08.065 doi: 10.1016/j.physleta.2007.08.065

|
| [11] |
A. R. Shateri, B. Salahshour, Comprehensive thermal performance of convection radiation longitudinal porousfins with various profiles and multiple nonlinearities, Int. J. Mech. Sci., 136 (2018), 252–263. https://doi.org/10.1016/j.ijmecsci.2017.12.030 doi: 10.1016/j.ijmecsci.2017.12.030

|
| [12] |
R. S. V. Kumar, R. N. Kumar, G. Sowmya, B. C. Prasannakumara, I. E. Sarris, Exploration of temperature distribution through a longitudinal rectangular fin with linear and exponential temperature-dependent thermal conductivity using DTM-Pade approximant, Symmetry, 14 (2022), 690. https://doi.org/10.3390/sym14040690 doi: 10.3390/sym14040690

|
| [13] |
G. Sowmya, R. S. V. Kumar, Y. Banu, Thermal performance of a longitudinal fin under the influence of magnetic field using Sumudu transform method with pade approximant (STM‐PA), Z. Angew. Math. Mech., 103 (2023), e202100526. https://doi.org/10.1002/zamm.202100526 doi: 10.1002/zamm.202100526

|
| [14] |
D. W. Mueller Jr, H. I. Abu-Mulaweh, Prediction of the temperature in a fin cooled by natural convection and radiation, Appl. Therm. Eng., 26 (2006), 1662–1668. https://doi.org/10.1016/j.applthermaleng.2005.11.014 doi: 10.1016/j.applthermaleng.2005.11.014

|
| [15] |
Z.Wang, S. Wang, X. Wang, X. Luo, Underwater moving object detection using superficial electromagnetic flow velometer array based artificial lateral line system, IEEE Sens. J., 24 (2024), 12104–12121. https://doi.org/10.1109/JSEN.2024.3370259 doi: 10.1109/JSEN.2024.3370259

|
| [16] |
Z. Wang, S. Wang, X. Wang, X. Luo, Permanent magnet-based superficial flow velometer with ultralow output drift, IEEE Trans. Instrum. Meas., 72 (2023). https://doi.org/10.1109/TIM.2023.3304692 doi: 10.1109/TIM.2023.3304692

|
| [17] | J. A. Edwards, J. B. Chaddock, An experimental investigation of the radiation and free convection heat transfer from a cylindrical disk extended surface, Trans. Am. Soc. Heat, Refrigerating, Air-Conditioning Eng., 69 (1963), 313–322. |
| [18] |
C. Arslanturk, Optimum design of space radiators with temperature-dependent thermal conductivity, Appl. Therm. Eng., 26 (2006), 1149–1157. https://doi.org/10.1016/j.applthermaleng.2005.10.038 doi: 10.1016/j.applthermaleng.2005.10.038

|
| [19] |
M. Torabi, Q. Zhang, Analytical solution for evaluating the thermal performance and efficiency of convective–radiative straight fins with various profiles and considering all non-linearities, Energy Convers. Manage., 66 (2013), 199–210. https://doi.org/10.1016/j.enconman.2012.10.015 doi: 10.1016/j.enconman.2012.10.015

|
| [20] |
D. Bhanja, B. Kundu, Radiation effect on optimum design analysis of a constructal T-shaped fin with variable thermal conductivity, Heat Mass Transfer, 48 (2012), 109-122. https://doi.org/10.1007/s00231-011-0845-1 doi: 10.1007/s00231-011-0845-1

|
| [21] |
B. V. Karlekar, B. T. Chao, Mass minimization of radiating trapezoidal fins with negligible base cylinder interaction, Int. J. Heat Mass Tran., 6 (1963), 33–48. https://doi.org/10.1016/0017-9310(63)90027-9 doi: 10.1016/0017-9310(63)90027-9

|
| [22] |
H. Azarkish, S. M. H. Sarvari, A. Behzadmehr, Optimum geometry design of a longitudinal fin with volumetric heat generation under the influences of natural convection and radiation, Energy Convers. Manage., 51 (2010), 1938–1946. https://doi.org/10.1016/j.enconman.2010.02.026 doi: 10.1016/j.enconman.2010.02.026

|
| [23] |
M. Turkyilmazoglu, Thermal performance of optimum exponential fin profiles subjected to a temperature jump, Int. J. Numer. Method. H., 32 (2022), 1002–1011. https://doi.org/10.1108/HFF-02-2021-0132 doi: 10.1108/HFF-02-2021-0132

|
| [24] |
S. B. Prakash, K. Chandan, K. Karthik, S. Devanathan, R. S. V. Kumar, K. V. Nagaraja, et al., Investigation of the thermal analysis of a wavy fin with radiation impact: an application of extreme learning machine, Phys. Scr., 99 (2023), 015225. https://doi.org/10.1088/1402-4896/ad131f doi: 10.1088/1402-4896/ad131f

|
| [25] |
M. H. Sharqawy, S. M. Zubair, Efficiency and optimization of straight fins with combined heat and mass transfer–-An analytical solution, Appl. Therm. Eng., 28 (2008), 2279–2288. https://doi.org/10.1016/j.applthermaleng.2008.01.003 doi: 10.1016/j.applthermaleng.2008.01.003

|
| [26] |
M. Hatami, G. R. M. Ahangar, D. D. Ganji, K. Boubaker, Refrigeration efficiency analysis for fully wet semi-spherical porous fins, Energy Convers. Manage., 84 (2014), 533–540. https://doi.org/10.1016/j.enconman.2014.05.007 doi: 10.1016/j.enconman.2014.05.007

|
| [27] |
F. khani, M. T. Darvishi, R. S. R. Gorla, B. J. Gireesha, Thermal analysis of a fully wet porous radial fin with natural convection and radiation using the spectral collocation method, Int. J. Appl. Mech. Eng., 21 (2016), 377–392. https://doi.org/10.1515/ijame-2016-0023 doi: 10.1515/ijame-2016-0023

|
| [28] |
B. S. Poornima, I. E. Sarris, K. Chandan, K. V. Nagaraja, R. V. Kumar, S. B. Ahmed, Evolutionary computing for the radiative–-convective heat transfer of a wetted wavy fin using a genetic algorithm-based neural network, Biomimetics, 8 (2023), 574. https://doi.org/10.3390/biomimetics8080574 doi: 10.3390/biomimetics8080574

|
| [29] |
R. S. V. Kumar, I. E. Sarris, G. Sowmya, A. Abdulrahman, Iterative solutions for the nonlinear heat transfer equation of a convective-radiative annular fin with power law temperature-dependent thermal properties, Symmetry, 15 (2023), 1204. https://doi.org/10.3390/sym15061204 doi: 10.3390/sym15061204

|
| [30] |
M. Turkyilmazoglu, Stretching/shrinking longitudinal fins of rectangular profile and heat transfer, Energy Convers. Manage., 91 (2015), 199–203. https://doi.org/10.1016/j.enconman.2014.12.007 doi: 10.1016/j.enconman.2014.12.007

|
| [31] |
B. J. Gireesha, M. L. Keerthi, G. Sowmya, Effects of stretching/shrinking on the thermal performance of a fully wetted convective-radiative longitudinal fin of exponential profile, Appl. Math. Mech.-Engl. Ed., 43 (2022), 389–402. https://doi.org/10.1007/s10483-022-2836-6 doi: 10.1007/s10483-022-2836-6

|
| [32] |
M. Mosavat, R. Moradi, M. R. Takami, M. B. Gerdroodbary, D. D. Ganji, Heat transfer study of mechanical face seal and fin by analytical method, Eng. Sci. Technol. Int. J., 21 (2018), 380–388. https://doi.org/10.1016/j.jestch.2018.05.001 doi: 10.1016/j.jestch.2018.05.001

|
| [33] |
Z. U. Din, A. Ali, S. Ullah, G. Zaman, K. Shah, N. Mlaiki, Investigation of heat transfer from convective and radiative stretching/shrinking rectangular fins, Math. Probl. Eng. 2022 (2022), 1026698. https://doi.org/10.1155/2022/1026698 doi: 10.1155/2022/1026698

|
| [34] |
F. Khani, A. Aziz, Thermal analysis of a longitudinal trapezoidal fin with temperature-dependent thermal conductivity and heat transfer coefficient, Commun. Nonlinear Sci., 15 (2010), 590–601. https://doi.org/10.1016/j.cnsns.2009.04.028 doi: 10.1016/j.cnsns.2009.04.028

|
| [35] |
H. S. Kang, Analysis of reversed trapezoidal fins using a 2-D analytical method, Univ. J. Mech. Eng., 3 (2015), 202–207. https://doi.org/10.13189/ujme.2015.030505 doi: 10.13189/ujme.2015.030505

|
| [36] |
R. Das, Estimation of feasible materials and thermal conditions in a trapezoidal fin using genetic algorithm, Proc Inst Mech Eng G J Aerosp Eng, 230 (2016), 2356–2368. https://doi.org/10.1177/0954410015623975 doi: 10.1177/0954410015623975

|
| [37] |
M. Turkyilmazoglu, Efficiency of the longitudinal fins of trapezoidal profile in motion, J. Heat Transfer, 139 (2017), 094501. https://doi.org/10.1115/1.4036328 doi: 10.1115/1.4036328

|
| [38] | T. O. Onah, A. M. Nwankwo, F. L. Tor, Design and development of a trapezoidal plate fin heat exchanger for the prediction of heat exchanger effectiveness, Eur J Mech Eng Res, 6 (2019), 21–36. |
| [39] | B. J. Gireesha, M. L. Keerthi, D. O. Soumya, Study on efficiency of fully wet porous trapezoidal fin structures in the presence of convection and radiation, J Eng Manage, 5 (2021), 66–72. |
| [40] |
B. J. Gireesha, M. L. Keerthi, Effect of periodic heat transfer on the transient thermal behavior of a convective-radiative fully wet porous moving trapezoidal fin, Appl. Math. Mech.-Engl. Ed., 44 (2023), 653–668. https://doi.org/10.1007/s10483-023-2974-6 doi: 10.1007/s10483-023-2974-6

|
| [41] |
W. Waseem, M. Sulaiman, S. Islam, P. Kumam, R. Nawaz, M. A. Z. Raja, et al., A study of changes in temperature profile of porous fin model using cuckoo search algorithm, Alex. Eng. J., 59 (2020), 11–24. https://doi.org/10.1016/j.aej.2019.12.001 doi: 10.1016/j.aej.2019.12.001

|
| 1. | S. Lalith Kumar, H. G. Nagaraja, B. J. Gireesha, Thermal Analysis of a Functionally Graded Conical Fin by Wavelets and Spectral Method, 2025, 2688-4534, 10.1002/htj.23389 |