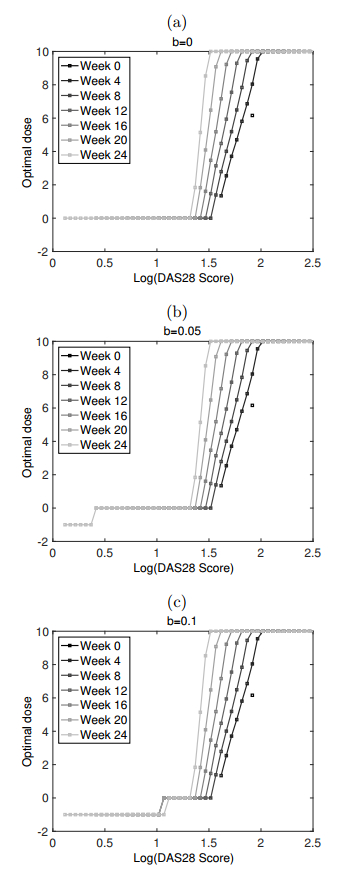
Optimal policy of tocilizumab dosing for rheumatoid arthritis. The cost functions are
In response-guided dosing (RGD), the goal is to make optimal dosing decisions based on the stochastic evolution of a patient's disease condition. Typically, RGD is formulated as a finite-horizon problem with decision-making occurring over a predetermined time frame. In this paper we relax the latter assumption to allow for the possibility of ending treatment early. This could occur due to remission of the disease or a finding of futility in treatment of the disease. Our framework is formulated as a stochastic dynamic program (DP) where a stop/do-not-stop decision is made in discrete sessions, and if stopping is not chosen, an optimal dose is determined for that session. Numerical simulations for rheumatoid arthritis are presented, and monotonicity of the stop/do-not-stop threshold with respect to time is proven.
Citation: Jakob Kotas. Optimal stopping for response-guided dosing[J]. Networks and Heterogeneous Media, 2019, 14(1): 43-52. doi: 10.3934/nhm.2019003
| [1] | Jakob Kotas . Optimal stopping for response-guided dosing. Networks and Heterogeneous Media, 2019, 14(1): 43-52. doi: 10.3934/nhm.2019003 |
| [2] | Vincent Renault, Michèle Thieullen, Emmanuel Trélat . Optimal control of infinite-dimensional piecewise deterministic Markov processes and application to the control of neuronal dynamics via Optogenetics. Networks and Heterogeneous Media, 2017, 12(3): 417-459. doi: 10.3934/nhm.2017019 |
| [3] | Urszula Ledzewicz, Heinz Schättler, Shuo Wang . On the role of tumor heterogeneity for optimal cancer chemotherapy. Networks and Heterogeneous Media, 2019, 14(1): 131-147. doi: 10.3934/nhm.2019007 |
| [4] | Maya Briani, Rosanna Manzo, Benedetto Piccoli, Luigi Rarità . Estimation of NO$ _{x} $ and O$ _{3} $ reduction by dissipating traffic waves. Networks and Heterogeneous Media, 2024, 19(2): 822-841. doi: 10.3934/nhm.2024037 |
| [5] | Mary Luz Mouronte, Rosa María Benito . Structural properties of urban bus and subway networks of Madrid. Networks and Heterogeneous Media, 2012, 7(3): 415-428. doi: 10.3934/nhm.2012.7.415 |
| [6] | Mary Luz Mouronte, Rosa María Benito . Structural analysis and traffic flow in the transport networks of Madrid. Networks and Heterogeneous Media, 2015, 10(1): 127-148. doi: 10.3934/nhm.2015.10.127 |
| [7] | Michiel Bertsch, Masayasu Mimura, Tohru Wakasa . Modeling contact inhibition of growth: Traveling waves. Networks and Heterogeneous Media, 2013, 8(1): 131-147. doi: 10.3934/nhm.2013.8.131 |
| [8] | Alberto Bressan, Khai T. Nguyen . Optima and equilibria for traffic flow on networks with backward propagating queues. Networks and Heterogeneous Media, 2015, 10(4): 717-748. doi: 10.3934/nhm.2015.10.717 |
| [9] | Amaury Hayat, Benedetto Piccoli, Shengquan Xiang . Stability of multi-population traffic flows. Networks and Heterogeneous Media, 2023, 18(2): 877-905. doi: 10.3934/nhm.2023038 |
| [10] | Prateek Kunwar, Oleksandr Markovichenko, Monique Chyba, Yuriy Mileyko, Alice Koniges, Thomas Lee . A study of computational and conceptual complexities of compartment and agent based models. Networks and Heterogeneous Media, 2022, 17(3): 359-384. doi: 10.3934/nhm.2022011 |
In response-guided dosing (RGD), the goal is to make optimal dosing decisions based on the stochastic evolution of a patient's disease condition. Typically, RGD is formulated as a finite-horizon problem with decision-making occurring over a predetermined time frame. In this paper we relax the latter assumption to allow for the possibility of ending treatment early. This could occur due to remission of the disease or a finding of futility in treatment of the disease. Our framework is formulated as a stochastic dynamic program (DP) where a stop/do-not-stop decision is made in discrete sessions, and if stopping is not chosen, an optimal dose is determined for that session. Numerical simulations for rheumatoid arthritis are presented, and monotonicity of the stop/do-not-stop threshold with respect to time is proven.
Optimal stopping of stochastic dynamic programs (DPs) (also known as Markov decision processes) has been an area of interest in operations research for decades [14,5,16]. This paper attempts to apply the theory of optimal stopping to the problem of response-guided dosing, where patients receive dosing specific to their individual disease progression over time.
Treatment paradigms for various diseases allow for stopping due to adverse events, and in some cases guidelines have been constructed for when to stop treatment. For some diseases, a recommendation to stop treatment is made typically at the end of a gradual tapering-down of dose for patients who respond well to treatment and are considered to be in remission. For others, patients are given a standard dose and the treatment decision at each time step is of the stop/do-not-stop type. In addition, stopping treatment may occur for patients in poor disease states due to a finding of futility or a desire to switch to a different drug or type of treatment.
Discontinuation of pharmacological therapy has been studied in a number of diseases. For rheumatoid arthritis (RA), a protocol for discontinuing the biologic agent infliximab has been developed by Maas et al.: patients whose 28-joint disease activity score (DAS28) is below 3.2, and have received stable dose for at least 6 months, have their doses tapered down by 25% of the original dose every 8-12 weeks until discontinuation of treatment is achieved or the patient experiences a flare-up [23]. Another study on adapting dose of the biologic agent infliximab based on patient response ended up stopping treatment for 7 of 76 patients due to adverse events [4]. One meta-analysis compared gradual lowering of dose (also called "down-titration") and discontinuation versus continuation of the drugs adalimumab and etanercept in RA patients with low DAS28 scores with mixed results, finding that stopping treatment produces benefits in some, but not all patients [24].
Infliximab is also used to treat other inflammatory bowel diseases (IBD) including Crohn's disease and ulcerative colitis (UC). Other studies have focused mainly on patient outcomes after the decision to stop infliximab treatment. Several studies have been conducted on the risk of IBD disease relapse after a decision to interrupt treatment of infliximab [11,12,19]. A prevalence study found that an "important proportion" of RA patients in remission were directed to down-titrate or discontinue treatment the drug, indicating that the stopping decision is not uncommon in practice, though a patient-specific numerical framework does not exist [10]. One study found that 62% of patients who stopped a second-line drug in combination therapy for RA did not experience a flare within one year; yet patients who continued the second-line drug had a lower chance of flare [22]. A meta-analysis of flare rates for RA patients with low DAS28 scores or in remission found that "more than one-third of patients" may down-titrate or stop disease-modifying anti-rheumatic drugs (DMARD) without risk of a flare for one year [9].
Some clinical trials for hepatitis have included the possibility of stopping treatment within a response-guided framework. A response-guided clinical trial using telaprevir for hepatitis C directed patients with an HCV RNA level greater than 1000 IU per mL at week 4, or who had virologic failure at week 12 or between weeks 24 and 36 of the study, to stop treatment [15]. Jacobson et al. developed stopping rules for patients destined to fail boceprevir-based combination therapy for hepatitis C based on phase 3 trial databases; the rules were then applied retroactively to determine how many patients could have stopped treatment early to minimize drug toxicity, resistance, and costs [6]. Along the same vein, Davis, et al. performed a retrospective analysis of patients taking pegylated interferon alfa-2b and ribavirin for hepatitis C to identify a rule that would have stopped treatment early for some patients; they found that patients who did not achieve an early virologic response of at least 2 logs in the first 12 weeks compared with baseline was predictive of ultimate futility of the therapy, and thus could have been stopped early [3]. Response-guided dosing of peginterferon in hepatitis B studies have established a rule to stop treatment if there is no decline of serum HBsAg levels from baseline to weeks 12 or 24 [20,21].
While these studies have considered the decision of when to stop treatment, the rules developed are ad hoc, specific to individual drugs and diseases. Stopping treatment is typically considered only at one of a few pre-specified time-points during treatment, and is not considered as an alternative to dosing in each individual session. In addition, stopping is generally considered only for cases of drug futility and not disease remission. Furthermore, the stopping criteria that have been developed for specific drugs and diseases have not been built using a mathematically rigorous optimal stopping approach.
In the operations research literature, several authors have considered optimal stopping rules for clinical trials by creating a stochastic dynamic programming approach. Papers by Berry and Müller et al. considered Bayesian approaches to phase Ⅱ clinical trials [1,13]. Their work, like ours, considers a sequential decision problem where patients in the trial are dosed over discrete sessions. At each time point, three arms are considered: continuation of pharmaceutical treatment; stopping for futility; or stopping for efficacy, with direction to enroll in a phase Ⅲ clinical trial. Along the way, dose-response parameters are learned. Our work differs from theirs in that we do not consider dosing in the context of a clinical trial; rather, we look at drugs that have already been brought to market and thus information about the dose-response parameter is assumed to be known.
In this paper, we extend the previous stochastic DP model of Kotas and Ghate [7] to allow for stopping treatment as an alternative to administering dose in any session. That paper modeled the disease progression of an individual patient as a finite-horizon, fixed-length Markov decision process. The optimal solution balances improving the patient's disease state as much as possible at the end of treatment with the costs incurred due to adverse effects in each treatment session. This paper's additional contribution is to allow stopping, which in essence adds an additional option to the decision-space, so that in any session a dose may still be administered, or a decision to stop may be made. If the decision-maker stops treatment, then no dose may be administered in future sessions, and as a result no future per-session costs are incurred.
Our model with stopping is an extension of the stochastic DP model for RGD by Kotas and Ghate [7]. For completeness, we give an overview of that model here.
Let
For
|
$ xt+1=xt+f(dt;θ), for xt,xt+1∈X, and dt∈D, $
|
(1) |
where
Aversion to dose is modeled using a continuous cost function
Let
|
$ Jt(xt)=mindt∈D(c(dt)+k∑j=1Jt+1(xt+f(dt;vj))pj), with JT+1(xT+1)=h(xT+1). $
|
(2) |
Problem (2) involves optimizing a continuous function over the nonempty compact set
Bellman's equations (2) can be solved approximately easily using backward induction through discretization of
The aforementioned model took the number of equally-spaced treatment sessions
If treatment is terminated when the state is
|
$ xt+1=xt+f(dt;θ), $
|
(3) |
as in the model without stopping described in section 3. The Bellman's equations then become:
|
$ Jt(xt)=min{mindt∈D(c(dt)+k∑j=1Jt+1(xt+f(dt;vj))pj),h(xt)}, with JT+1(xT+1)=h(xT+1). $
|
(4) |
where the outer minimization problem chooses the more optimal of continuing treatment or stopping now. The Bellman's equations can be solved numerically using backward induction with discretization of the state-action space.
We reconsider the rheumatoid arthritis problem based on OPTION trial data which was discussed in the Kotas and Ghate model [7,18]. We begin by reviewing that model.
We seek to determine an optimal dose of the drug tocilizumab in combination therapy with a fixed dose of methotrexate for rheumatoid arthritis. The patient state
|
$ xt+1=xt+lnκ2−ln(κ1+κ2+dt)+θ $
|
(5) |
where
The terminal state cost function is taken to be exponential:
For our stopping variation, all parameters were set to the same values as [7], except we consider a slightly different cost function
Bellman's equations (2) were solved approximately using backward induction with a discretization of
Results of numerical simulation are given in Figure 1. Three subfigures are shown corresponding to the values
The value of the parameter
In Figure 1, we make the following observations. With
We also note that when
In our numerical experiments, we have observed that if stopping is ever optimal, it is optimal below a threshold state. Let us define this threshold state in session
A zoom-in of Subfigure 1c is given in Figure 2, centered on
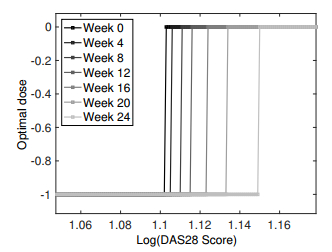
Optimal policy with the cost function
This result is not only numerically observed, but provable. In fact a proof for a general DP problem with stopping is found in section 4.4, volume 1 of [2]. For convenience we provide a counterpart of this proof using our notation.
By the Bellman's equations (4), it is optimal to stop at time
|
$ Tt={xt|h(xt)≤mindt∈Dc(dt)+k∑j=1Jt+1(xt+f(dt;vj))pj} $
|
(6) |
Equation (4) along with the boundary condition of the DP,
|
$ JT−1(x)≤JT(x) ∀x $
|
(7) |
Using equation 4 along with the stationarity property of our problem and the monotonicity property of DP, we obtain via induction
|
$ Jt(x)≤Jt+1(x) ∀x,t. $
|
(8) |
Using this fact, we see
|
$ T1⊂T2⊂…⊂TN−1. $
|
(9) |
In our numerical simulations we have observed that
We have presented an extension of the stochastic DP model of [7] where the decision-maker can decide to stop treatment at any treatment session. If a decision to stop is made in the current period, all future per-session costs are avoided, and the patient's final disease state is taken to be the current state. Intuitively, we expect the decision to stop will be optimal, if ever, at low disease states. At these states, the future per-session cost outweighs the benefit of lowering the disease state through treatment. In some cases, we may also find the existence of a wait-and-see region, where zero dose is given in a particular session, but the decision to stop is not made– this can incur a per-session cost, but the possibility of giving a dose later to lower the disease state outweighs that per-session cost, so we continue. At the highest disease states, positive doses are given as the benefit of reducing disease state wins out over the per-session costs.
We reconsidered the rheumatoid arthritis example of [7] again, but this time allowing for stopping. For the original problem, stopping was never optimal over the states considered. However, by adding a fixed per-session cost
In the literature, stopping is mentioned not only for patients in very low disease states (remission,) but also sometimes for very high disease states, as this indicates a failure of the drug to have an effect on the patient. In practice, this would often indicate the need to switch to a different drug or treatment scheme. As we were only considering the dose of a single drug in our framework, this situation did not arise for us, but could be another interesting direction for future work.
Optimal policy of tocilizumab dosing for rheumatoid arthritis. The cost functions are
Optimal policy with the cost function