Ticagrelor is more effective than clopidogrel in carrier of nonfunctional CYP2C19 allele who has diabetes and acute coronary syndrome - case report and literature review

1.   Introduction

In the past few decades, more and more diffusion processes have been shown to not satisfy Fickian laws, such as signal transduction in biological cells, foraging behavior of animals, viscoelastic and viscoplastic flow, and solute migration in groundwater. However, fractional partial differential equations (FPDEs) play a very important role in describing anomalous diffusion Ref. ^[1,2,3], so in recent years, FPDEs have attracted extensive attention. In this paper, we study one type of time-fractional diffusion equation (TFDE), which can be obtained from the standard diffusion equation by replacing the first-order time derivative with a fractional derivative of order $\alpha$, $0 < \alpha < 1$.

Where $u_0(x)$ is a smooth function and $D^{\alpha}_t u(x, t)$ is the Caputo fractional derivative defined by Definition 2.1.

The exact solutions of most fractional differential equations are difficult to obtain analytically, and even if they can be obtained, most of them contain special functions that are difficult to calculate. In recent years, many numerical methods have been proposed. For example, Ref. ^[4,5] used finite difference to solve the fractional diffusion equation. Yang et al. ^[6] used the finite volume method to solve the nonlinear fractional diffusion equation. Jin et al. studied the finite element method for solving the homogeneous fractional diffusion equation in ^[7]. Some scholars have developed meshless methods ^[8,9,10,11] and spectral methods ^{[12,13,14,15]} to solve fractional diffusion equations.

The reproducing kernel space and its related theories are the ideal spatial framework for function approximation ^[16,17]. The function approximation in this space has uniform convergence, while the Caputo-type fractional derivative of the approximate function still has uniform convergence. Therefore, the reproducing kernel space is also the ideal spatial framework for the numerical processing of Caputo-type fractional derivatives. Numerical solutions to differential equations based on orthogonal polynomials are commonly used. For example, quartic splines and cubic splines are used, respectively, to solve numerical solutions of differential equations in Ref. ^[18,19,20]. In Ref. ^[21,22,23], based on the idea of wavelet, a multi-scale orthonormal basis is constructed in the reproducing kernel space by using piecewise polynomials, and ${\varepsilon}$-approximate solutions of integer-order differential equations are obtained.

For TFDE, most methods use the finite difference method to deal with time variables. Due to the non-singularity of fractional differentiation, the difference scheme at the initial time needs to be further transformed. And the results are not ideal; when the step size reaches $0.001$, the error is only $10^{-5}$ in Ref. ^[10]. So, the main motivation of this paper is to obtain the ${\varepsilon}$-approximation solution of TFDE. By constructing a multiscale orthonormal basis in the multiple reproducing kernel space, a numerical algorithm is designed to obtain the approximate solution of TFDE. In order to avoid the influence of fractional non-singularity, this paper constructs the orthonormal basis by using Legendre polynomials, which can be operated by the property of fractional differentiation. In addition, the method in this paper has a good convergence order.

The paper is organized as follows: In Section 2, the fundamental definitions are provided, and Legendre polynomials and related spaces are introduced. In Section 3, the ${\varepsilon}$-approximation solutions are given. In Section 4, convergence analysis and time complexity are presented for the proposed method. In Section 5, numerical solutions for several fractional diffusion equations are presented. The paper concludes by stating the advantages of the method.

2.   Caputo fractional derivative and related space

In this section, the Caputo fractional derivative and its properties are introduced. Legendre polynomials and their associated spaces are also discussed. This knowledge will be used when constructing the basis.

2.1.   Caputo fractional derivative

Definition 2.1. The Caputo fractional derivative is defined as follows ^[24]:

For ease of calculation, a property of the Caputo differential needs to be given here.

Property 2.1.

Proof. According to the definition of Caputo differentiation, the conclusion can be obtained using integration by parts. □

2.2.   Legendre polynomials and the related spaces

Legendre polynomials are known to be orthogonal on $L^2[-1, 1]$. Since the variables being analyzed are often defined in different intervals, it is necessary to transform Legendre polynomials on $[0, b]$. Legendre polynomials defined on [0, b] are shown below

Clearly, $\{l_j(x)\}_{j = 0}^{\infty}$ is orthogonal on $L^2[0, b]$, and

Let $p_j(x) = \sqrt{\frac{2j+1}{b}}l_j(x)$, $\{p_j(x)\}_{j = 0}^{\infty}$ is an orthonormal basis on $L^2[0, b]$.

Consider Eq (1.1); this section gives the following reproducing kernel space. For convenience, the absolutely continuous function is denoted as AC.

Definition 2.2. $W_1[0, T] = \{u(t)\mid u(0) = 0, \; u \; is\; AC, u^{\prime}\in L^2[0, T]\}$, and

If $b = T$ and $T_j(t) = p_j(t)$, note that $T_j(t) = \sum\limits_{k = 0}^{j}c_kt^k$. Let

Theorem 2.1. $\{J_0T_j(t)\}_{j = 0}^{\infty}$ is an orthonormal basis on $W_1[0, T]$.

Definition 2.3. $W_2[0, b] = \{u(x)\mid u(0) = u(b) = 0, \; u \; is\; AC, u^{\prime\prime}\in L^2[0, b]\}$, and

Similarly, denote $p_j(x) = \sum\limits_{k = 0}^{j}d_kx^k$. Integrating $p_j(x)$ twice yields $J^2_0p_j(x)$, if $J^2_0p_j(x)\in W_2[0, b]$, then

Obviously, $\{J^2_0p_j(x)\}_{j = 0}^{\infty}$ is an orthonormal basis on $W_2[0, b]$.

2.3.   Introduction of $W(\Omega)$

Put $\Omega = [0, b]\times [0, T]$, and let's define the space $W(\Omega)$.

Definition 2.4. $W(\Omega) = \{u(x, t)\mid u(x, 0) = 0, u(0, t) = u(b, t) = 0, \; \frac{\partial u}{\partial x}$ is continuous functions, $\frac{\partial^3 u}{\partial t\partial x^2}\in L^2(\Omega)\}$.

Clearly, $W(\Omega)$ is an inner product space, and

Theorem 2.2. If $u(x, t), v(x, t)\in W(\Omega)$, and $v(x, t) = v_1(x)v_2(t)$, then

Proof. Clearly,

Similarly, $\langle u, v\rangle_{W(\Omega)} = \langle \langle u, v_1\rangle_{W_2}, v_2\rangle_{W_1}$. □

Note

Theorem 2.3. $\{\phi_{ij}(x, t)\}_{i, j = 0}^{\infty}$ is an orthonormal basis on $W(\Omega)$.

Proof. First of all, orthogonality. For $\forall \phi_{ij}(x, t), \phi_{mn}(x, t) \in W(\Omega)$, according to Theorem 2.2,

Second, completeness. $\forall u \in W(\Omega)$, if $\langle u, \phi_{ij}\rangle_{W(\Omega)} = 0$ means $u\equiv 0$. In fact, by Theorem 2.4,

Since $\{J^2_0p_i(x)\}_{i = 0}^{\infty}$ and $\{J_0T_j(t)\}_{j = 0}^{\infty}$ are complete systems of $W_2[0, b]$ and $W_1[0, T]$, respectively, $\langle u, J^2_0p_{i}(x)\rangle_{W_2} = 0$ and $\langle u, J_0T_{j}(t)\rangle_{W_1} = 0$. So $u\equiv 0$. □

3.   Numerical algorithms

Let $L:W(\Omega)\to L^2(\Omega)$,

Then Eq (1.1) is

Theorem 3.1. Operator $L$ is a bounded and linear operator.

Proof. Clearly, $L$ is linear, and one only needs to prove boundedness. According to Cauchy Schwartz's inequality, we derive that

Put $K(x, t, y, s) = r(x, y)q(t, s)$ be the RK function in $W(\Omega)$, then

Similarly

By Eq (3.2), there exists positive constants $M_1$ such that

where $M_1 = \|\frac{\partial^2r(x, y)}{\partial x^2}q(t, s)\|^2_{W(\Omega)} S_{\Omega}$, $S_{\Omega}$ represents the area of the region $\Omega$.

By Eq (3.3), there exist positive constants $M_2, M_3$, such that

and

From Eqs (3.4) and (3.5), we can get

where $M = \sqrt{M_1}+\sqrt{M_3}$. □

Definition 3.1. $u^{{\varepsilon}}$ is named the ${\varepsilon}$-approximate solution for Eq (3.1), $\forall {\varepsilon} > 0$, if

Ref. ^[21,22] proved the existence of ${\varepsilon}-$approximate solutions to boundary value problems of linear ordinary differential equations. Using the same method, we can prove that the ${\varepsilon}$-approximate solution of Eq (3.1) exists.

Theorem 3.2. $\forall\; {\varepsilon} > 0$, $\exists\; N_1, N_2 > 0$, when $n_1 > N_1, n_2 > N_2$,

is the ${\varepsilon}$-approximate solution of Eq (3.1), where $c_{ij}^*$ satisfies

Proof. Let $u(x, t)$ be the solution of Eq (3.1),

where $c_{ij} = \langle u, \phi_{ij}\rangle_{W(\Omega)}$, and $u_{n_1n_2}(x, t) = \sum_{i = 0}^{n_1}\sum_{j = 0}^{n_2} c_{ij}\phi_{ij}(x, t)$.

Because $L$ is a bounded operator, $\forall\; {\varepsilon} > 0$, $\exists\; N_1, N_2 > 0$, when $n_1 > N_1, n_2 > N_2$,

so

□

From Theorem 3.2, note

$J$ is a quadratic form about $c = (c_{ij})_{i, j = 0}^{n_1, n_2}$, and $c^* = (c_{ij}^*)_{i, j = 0}^{n_1, n_2}$ is the minimum value of $J$. To find $c^*$, just need $\frac{\partial J}{\partial c_{ij}} = 0$. That is

so

Put $N = (n_1+1)\times (n_2+1)$, and the $N$-order matrix $\textbf{A}$ and the $N$-order vector $\textbf{b}$,

so Eq (3.6) is

From Property 2.1,

From Ref. ^[21], if $L$ is reversible, then Eq (3.7) exists and is unique.

4.   Convergence analysis and complexity analysis

4.1.   Convergence analysis

Let $u(x, t)$ be the exact solution to Eq (3.1), and

Fourier truncation of $u(x, t)$ is $u_{N_1, N_2}(x, t)$, and

In Ref. ^[25], if $u^{(m)}(x)\in L^2[0, b]$, then

Theorem 4.1. Assume $\frac{\partial^{m+n}u(x, t)}{\partial t^m \partial x^n}\in L^2(\Omega)$, then

where $C_1, C_2$ are constants.

Proof. Recalling the definition of $W(\Omega)$, we get

According to Eq (4.1), it follows that

so

where $C_0 = {\int}_a^b C^2(x)\left(\sum\limits_{k = \min\{m, N_1+1\}}^m \|u^{(k+1)}_{xx}\|_{L^2[0, T]}^2\right) dx$. Assume $C_1 = \sqrt{C_0}$; that is

Similarly,

□

Theorem 4.2. Assume $\frac{\partial^{m+n}w(x, t)}{\partial t^m \partial x^n}\in L^2(\Omega)$, $u_{N_1N_2}^{{\varepsilon}}(x, t)$ is the approximate solution of Eq (3.1), then

where $C = 2M_2\max\{C_1, C_2\}$, $N = \min\{N_1, N_2\}$, and $\gamma = \min\{m, n\}$.

Proof. We know

where $M_2 = \|L^{-1}\|\|L\|$. Moreover,

So

□

So, the proposed method is $\gamma$-order convergence, and the convergence rate depends on $N$.

4.2.   Complexity analysis

The proposal of an algorithm requires not only a reliable theory but also the feasibility of calculation. The huge calculation process is costly. Next, the time complexity of the algorithm will be analyzed.

According to the analysis in Section 3, the complexity of the algorithm depends on Eqs (3.6) and (3.7). Next, the algorithm can be illustrated in four steps, as follows:

(1) $\textbf{A}$ of Eq (3.7). We know $\textbf{A} = \left(\langle L\phi_{ij}, L\phi_{kl}\rangle_{L^2}\right)_{N\times N}$, and

Set the number of multiplications required to compute $\langle L\phi_{ij}, L\phi_{kl}\rangle_{L^2}$ as $C_1$, where $C_1$ is constant. Clearly, the computing time needed for $\textbf{A}$ is $Num_1 = C_1N^2.$

(2) $\textbf{b}$ of Eq (3.7). We know $\textbf{b} = \left(\langle L\phi_{ij}, f\rangle_{L^2}\right)_{N\times N}$, and

Set the number of multiplications required to compute $\langle L\phi_{ij}, f\rangle_{L^2}$ as $C_2$, where $C_1$ is constant. Clearly, the computing time needed for $\textbf{b}$ is $Num_2 = C_2N.$

(3) We use the Gaussian elimination method to solve Eq (3.7). From my mathematical knowledge, Gaussian elimination requires operations

(4) To the ${\varepsilon}-$approximation solution $u_N^{{\varepsilon}}(x, t)$, the number of computations is $N$.

In summary, the multiplication times of this algorithm in the execution process are

5.   Numerical examples

This section discusses three numerical examples to reveal the accuracy of the proposed algorithm. Compared with Ref. ^{[26,27,28,29]}, the results demonstrate that our method is remarkably effective. All the results are calculated using the mathematical software Mathematica 13.0.

In this paper, $N = N_1\times N_2$ is the number of bases, and $e_N(x) = |u(x)-u_N(x)|$ is the absolute error. $ME_N$ denotes the maximum absolute error when the number of bases is $N$. The convergence order can be calculated as follows:

Example 5.1. Consider the test problem suggested in ^[26,27]

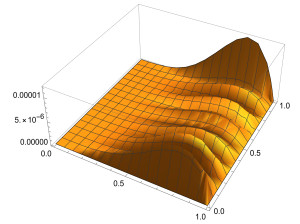
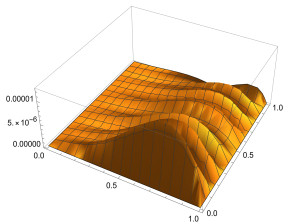
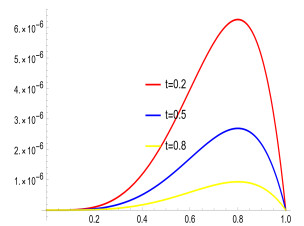
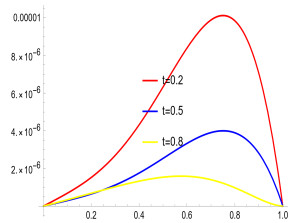
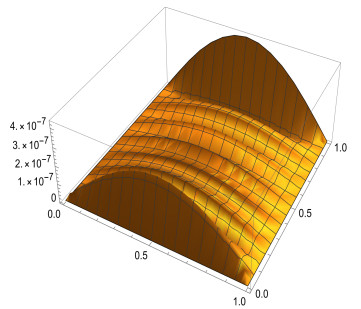
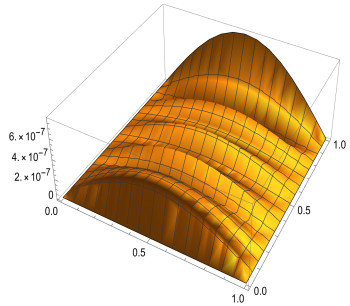
where $f(x) = \frac{3\sqrt{\pi}}{4\Gamma(2.5-\alpha)}x^4(x-1)t^{1.5-\alpha}-(20x^3-12x^2)t^{1.5}$, and the analytical solution is given by $u(x, t) = x^4(x-1)t^{1.5}$. The numerical results are shown in Tables 1 and 2. Table 1 shows that when $\alpha$ is 0.5 or 0.8, respectively, our results are better than those in Ref. ^[26,27]. Meanwhile, we also show the results when $\alpha = 0.01$ and $\alpha = 0.99$ in Table 1 and find that the results are not much different from those when a = 0.5 and a = 0.8, demonstrating the robustness of our method. Table 2 indicates that the absolute error gets better as the number of bases increases. Figures 1 and 2 shows the absolute errors when $\alpha = 0.01$ and $\alpha = 0.99$, respectively. Figures 3 and 4 show the absolute errors at different times when $\alpha = 0.01$ and $\alpha = 0.99$.

Example 5.2. We consider the same FDEs as that in ^[28]

With $f(x, t) = \frac{2}{\Gamma(3-\alpha)}t^{2-\alpha}\sin(2\pi x)+4\pi^2t^2\sin(2\pi x)$, the exact solution of the problem is given by $u(x, t) = t^2\sin(2\pi x)$. Tables 3–5, respectively, show the comparison of absolute error and convergence order with Ref. ^[28] when $\alpha$ is 0.2, 0.5, or 0.8. Obviously, the proposed method is superior to Ref. ^[28]. $N\times L$ denotes the number of bases in Ref.^[28].

Example 5.3. Considering the following problem with $f(x, t) = \frac{\Gamma(4+\alpha)}{6}\sin(\pi x)+\pi^2t^{3+\alpha}\sin(\pi x)+\pi t^{3+\alpha}\cos(\pi x)$ ^[29]:

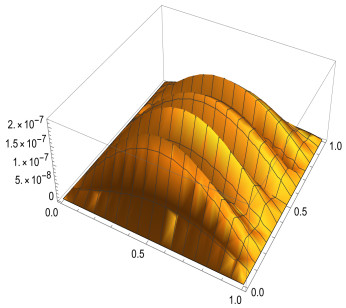
The exact solution of the problem is given by $u(x, t) = t^{3+\alpha}\sin(\pi x)$. Table 6 shows the comparison of absolute error and convergence order with Ref. ^[29] when $\alpha$ is 0.1. Obviously, the proposed method is superior to Ref. ^[29]. Figures 5–7 show the absolute errors when $\alpha = 0.1$, $\alpha = 0.01$ and $\alpha = 0.99$ respectively.

6.   Conclusions

In this paper, an effective numerical algorithm based on Legendre polynomials is proposed for TFDE. Based on Legendre polynomials, an orthonormal basis is constructed in the reproducing kernel spaces $W_1[0, 1]$ and $W_2[0, b]$. Then we define the multiple reproducing kernel space and develop the orthonormal basis in this space. The ${\varepsilon}$-approximate solution of TFDE is obtained. From the above analysis and the numerical examples, it is clear that the presented method is successfully employed for solving TFDE. The numerical results show that our method is much more accurate than other algorithms. In this paper, because the orthonormal basis constructed in the binary reproducing kernel space contains power terms, the properties of fractional differentiation can be used to calculate fractional differentiation, so as to eliminate the influence of the non-singularity of fractional differentiation. However, the method presented in this paper is suitable for the case where the initial boundary value condition is 0, and for the non-zero case, it needs to be further simplified to the cases where the initial boundary value condition is 0. We are also trying to design methods for cases where initial boundary values are non-zero.

Author contributions

Yingchao Zhang: Conceived of the study, designed the study, and proved the convergence of the algorithm; Yingzhen Lin: Reviewed the full text. All authors were involved in writing the manuscript. All authors read and approved the final manuscript.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This study was supported by the Characteristic Innovative Scientific Research Project of Guangdong Province (2023KTSCX181, 2023KTSCX183) and Basic and Applied Basic Research Project Zhuhai City (2320004002520)

Conflict of interest

The authors have no conflicts of interest to declare.