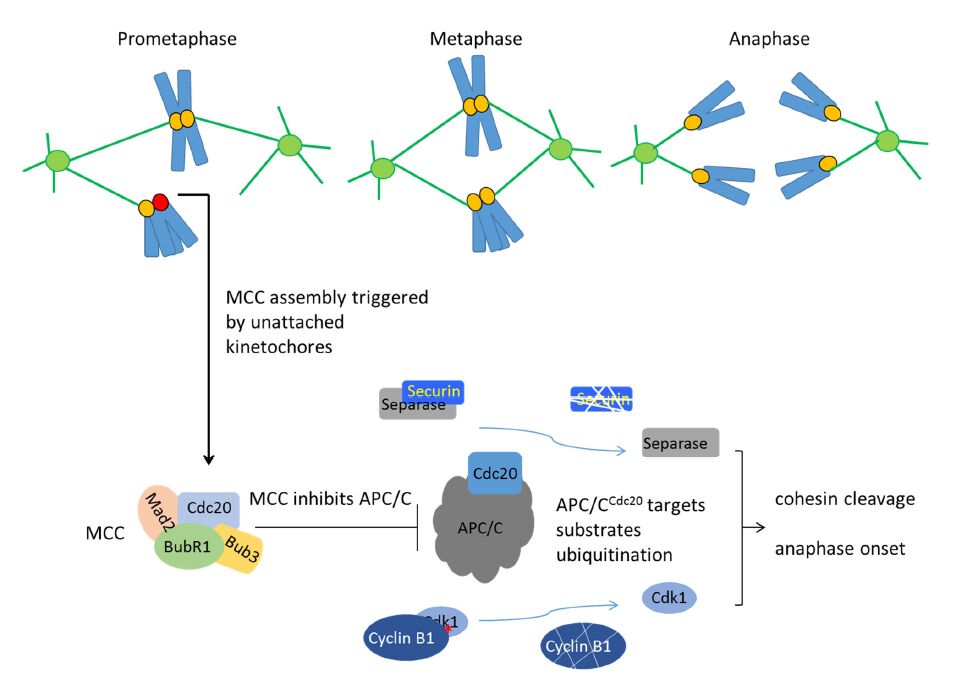
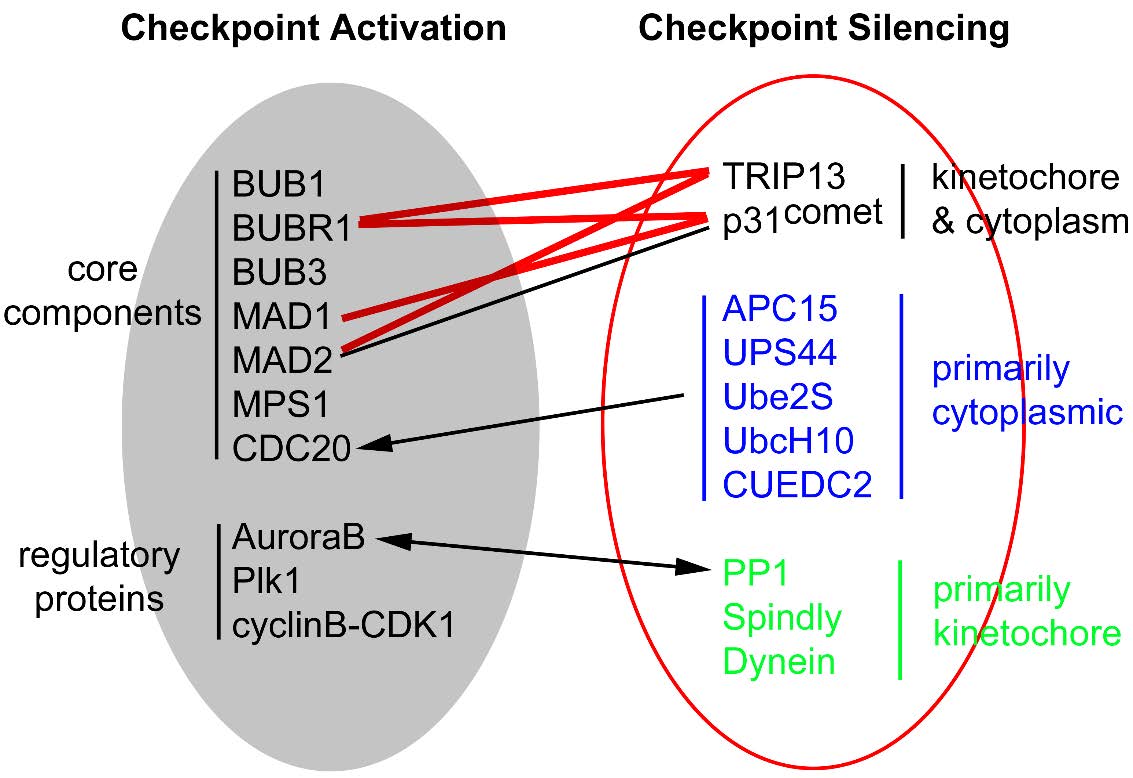
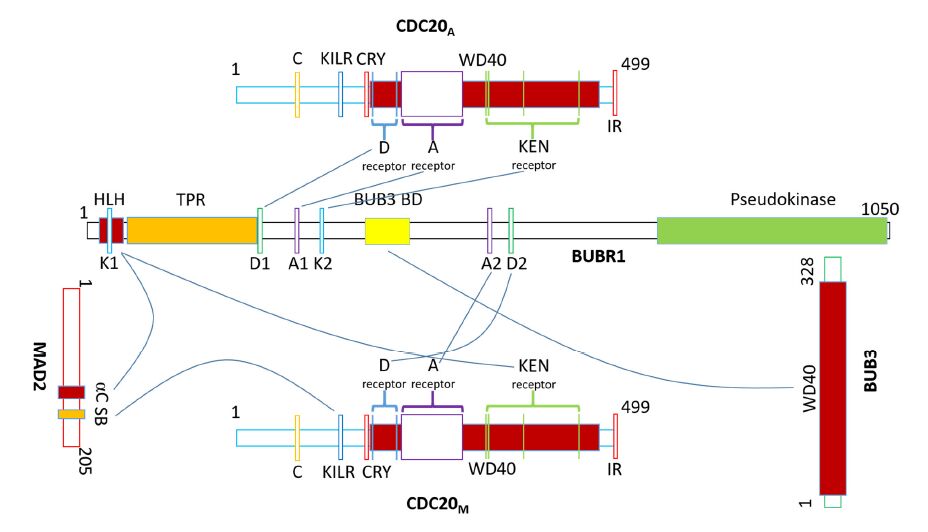
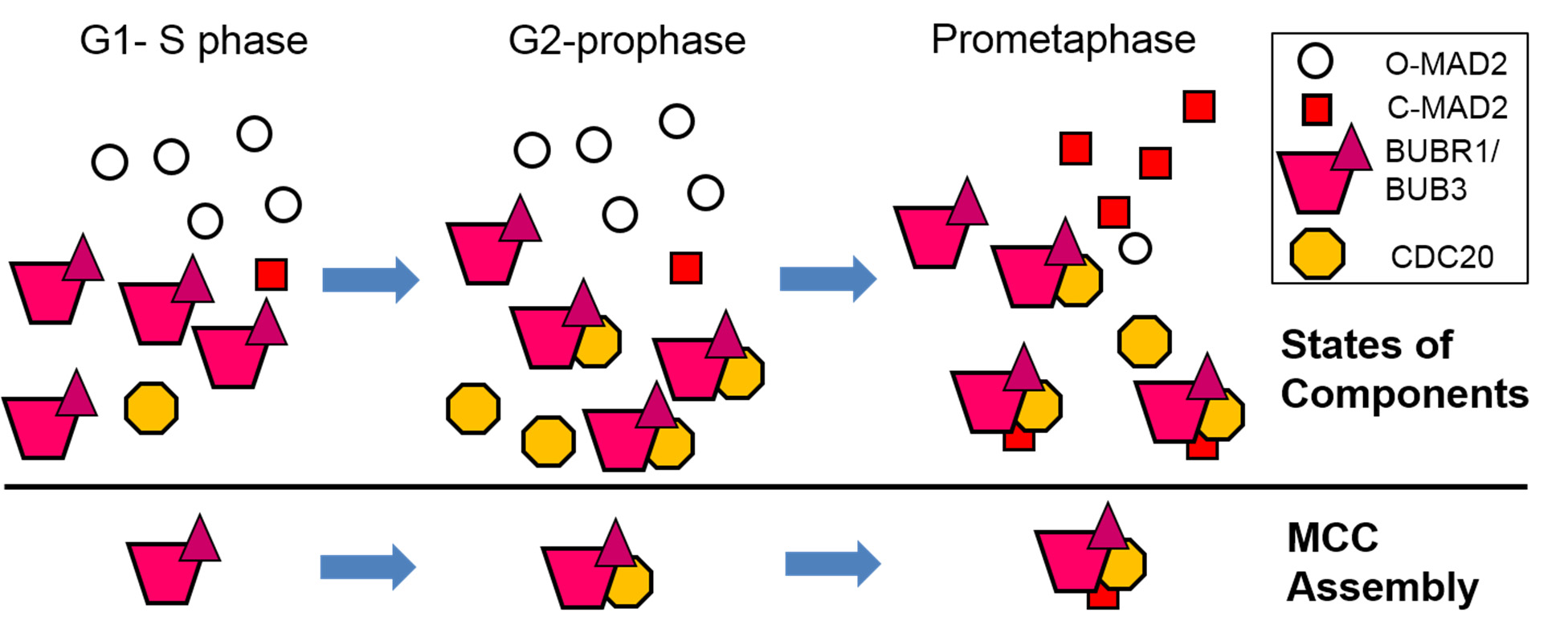
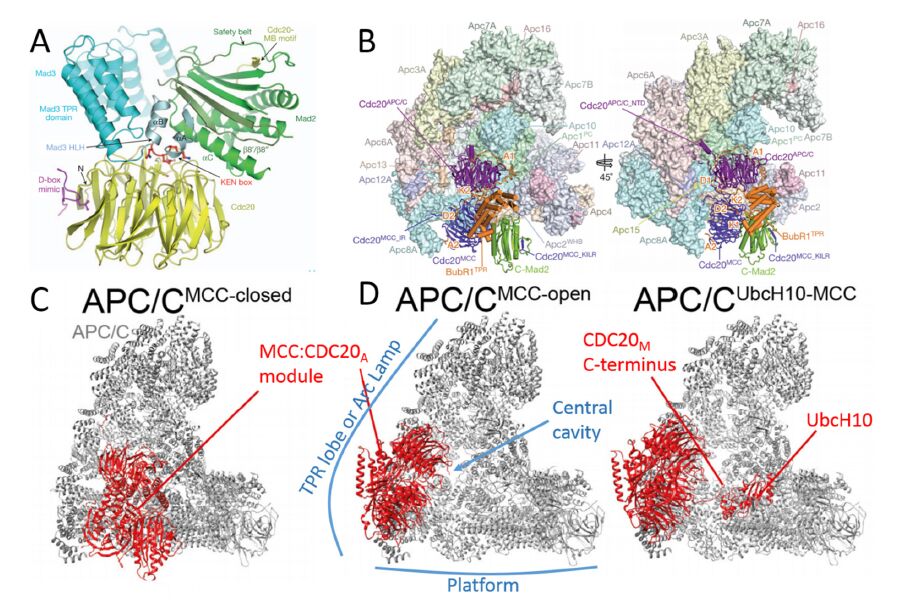
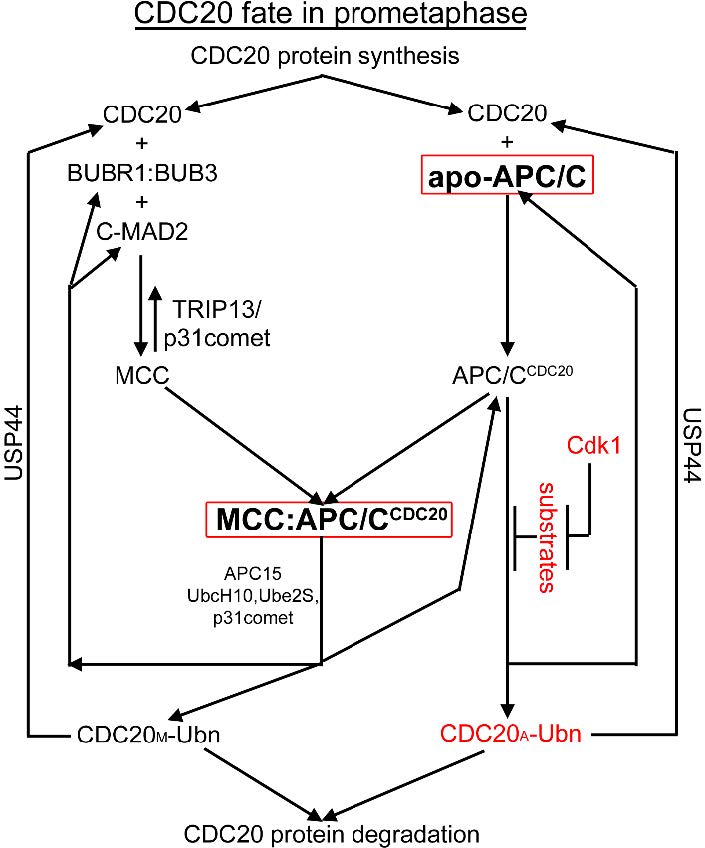
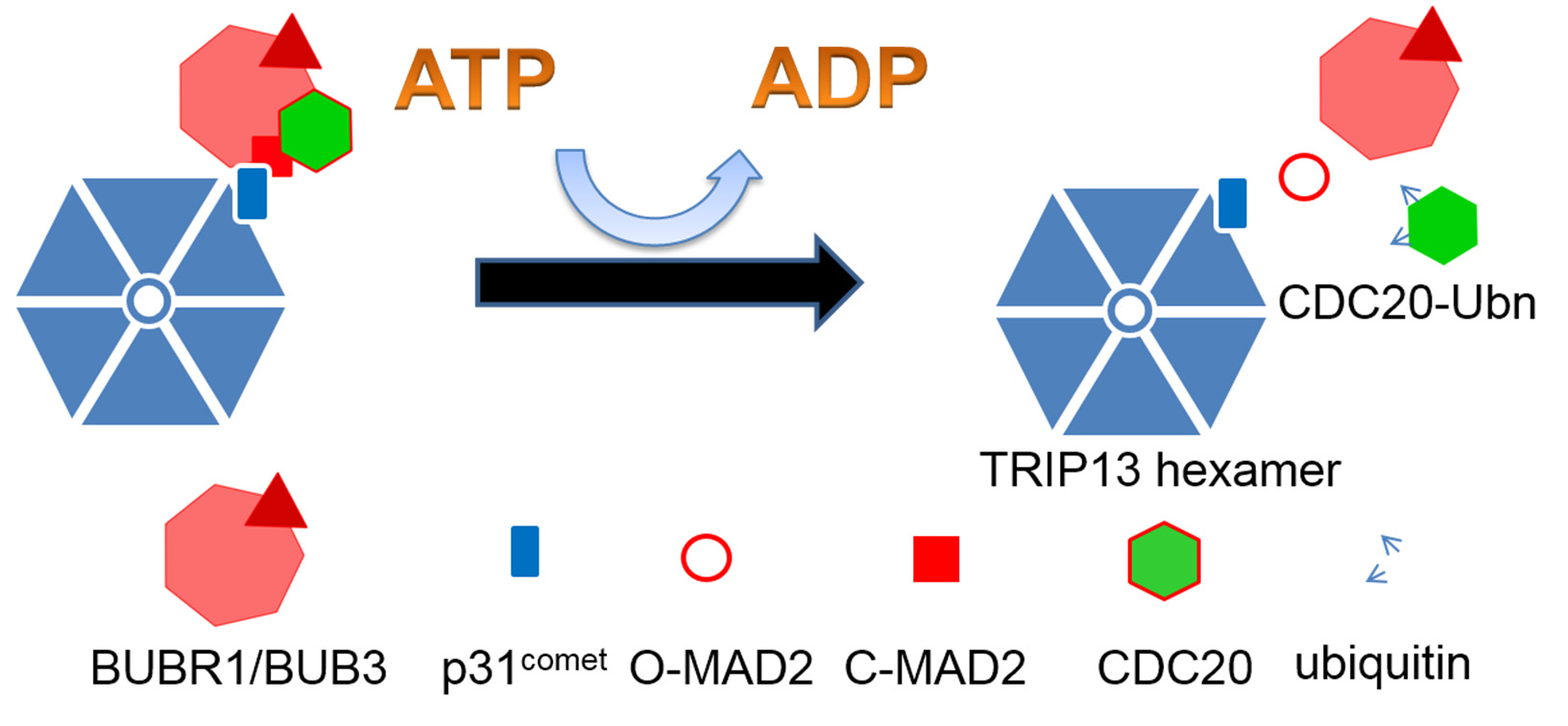
The mitotic checkpoint complex (MCC): looking back and forth after 15 years

1.   Introduction

1.1.   Motivation and literature review

In December 2019, Wuhan city in China—home to 11 million people—first came to the global spotlight with the reports of a pneumonia-like disease. Initially it was suspected that certain animals such as bats were its origin. Later on, however, with an unexpected surge of the corona cases all over the world, it was declared as a serious infectious pandemic which spread from one infected person to another through direct or indirect contact. This severe acute respiratory syndrome, later called COVID-19, is actually caused by a novel Coronavirus SARS-CoV-2.

Besides, SARS-CoV-2, there have also been identified at least six other kinds of coronavirus that originate from animals. Most of them cause common cold which, in certain cases, can prove a potential threat to human health. Each infected person is estimated to pass the phenomenon on to three other people. It lasts approximately between 1–14 days. The common symptoms include: sore throat, fever, general weakness, shortness of breath, cough, pain etc. There are particular groups of people among whom the risk factor becomes too higher. They include old men and women, obese guys, chain smokers, those fighting hypertension and cancer patients. Prevention seems to be the only sure cure out there.

When it initiated in China nearly two years ago, the COVID-19 was limited only to the city of Wuhan. With the progress of time, however, it first spread in the whole country and then within months reached almost every corner of the world. It happened largely due to the careless of the masses. As a result, most government were forced to impose such strict regulations as lockdown. Maintaining social distancing too could be a very viral step to curb the spread of the virus which is generally reliant upon other people to reach the healthy segment of the society.

The second wave of this contagious coronavirus was another reminder that it's over. As we learn through media, the death rate was once again on the rise. In Pakistan and Azad Kashmir (just like the rest of the world), all educational institutions were closed for two or more months. The reason was simple. People didn't take the threat seriously and, as a result, its spread couldn't be stopped. Nations globally need to learn their lessons quickly. Without taking all the precautionary measures, we won't be able to fight COVID-19. On the other hand, as compared to second wave, the third and forth waves of coronavirus were not so serious and rate of new cases controlled.

Various vaccines are continuously being tested throughout the world. Most of them have reportedly proven successful too. This, however, seems to be time consuming task. It isn't simple to first agree on a single vaccine and then make it simultaneously available across all the continents. Therefore, we, the people, are left with no other option than taking care of ourselves and near and dear ones. Kids, being less immune, are particularly prone to catch most ailments. If there's a strict parental control, it will not just keep their own families safe, but the whole society at large will also be in a better position to defy this looming health danger.

In the meanwhile, many chemists, biologists, doctors and mathematicians are trying to study the behavior of coronavirus. On the mathematical side, there are few models already discovered, to study it's behavior. Some of them are: SIR (Susceptible, Infected and Recovered) model, SIQR (Susceptible, Infectious, Quarantined and Recovered) model, SEIR (Susceptible, Exposed, Infected and Recovered) model, and SIRS (Susceptible, Infected and Recovered, Susceptible) model. For instance, Zou et al. ^[1] suggested the following epidemic model (SuEIR), which is alternative to the SEIR model by considering the unreported COVID-19 cases and instructed by machine learning algorithms based on the reported historical data, for forecasting the propagation of COVID-19 comprising a lot of authentic and casualty cases at national levels in the United States:

where $\beta$ is the exposure rate between the susceptible and infected people, $\sigma$ expresses the ratio of cases in the revealed sections that are either confirmed as infectious or dead/recovered without authentication, $\mu$ is the rate of realization of the infected cases, and $\gamma$ represents the alteration rate between the sections $I$ and $R$. Ray et al. ^[2] estimated the real-time application of an open, collective ensemble to predict deaths attributable to COVID-19 in the United States. Shea et al. ^[3] explored multiple COVID-19 mathematical models to comprehend the sources of widespread COVID-19 disease. Nadim et al. ^[4] studied the stability analysis of the following compartmental epidemic model of COVID-19 to forecast and control the upsurge:

where $\Pi$ is recuitment rate, $\beta$ is transmission rate. $r_Q$, $r_A$ and $r_J$ are modification factors for quarantined, asymptomatic and isolated respectively. $\gamma_1$ is the rate at which the exposed individuals are diminished by quarantine, and $\gamma_2$ is the rate at which the symptomatic individuals are diminished by isolation. $k_1$ and $k_2$ are rates at which exposed become infected, quarantined individuals are isolated, respectively. $p$ is the proportion of asymptomatic individuals. $\sigma_1$, $\sigma_2$, $\sigma_3$, $\sigma_4$ are respectively the recovery rates from quarantined, asymptomatic, symptomatic and isolated individuals. $\delta$ and $\mu$ are the diseases induced mortality rate and natural death rate, respectively. Li et al. ^[5] developed a SEIQR COVID-19 model, described by the system of difference equation:

where human host incubation period is $\frac{1}{\delta}$ days. Infectious cases at the rate $m$ revert to confirmed cases, and recovered rate is $\gamma$. Susceptible humans acquire COVID-19 through direct contact with exposed cases and infected cases at rates $\frac{\beta S_tE_t}{N_t}$ and $\frac{\beta_1S_tI_t}{N_t}$, respectively. Tian et al. ^[6] investigated the spread and control of COVID-19 using a data set that included case reports, human movement, and public health interventions. Sun et al. ^[7] presented the following model to show the propagation of COVID-19 in Wuhan:

where $N$, $S$, $E$, $I$, $Q$, $R$ are total, susceptible, exposed, infected, confirmed and removed populations, respectively. $\beta_1^{'}$ and $\beta_2^{'}$ are infection coefficients under lockdown, and $m_1$ is confirmation rate depends on the rickness of medical resources. $\delta$ is transform rate from the exposed population to infected population, and $\gamma$ is transform rate from the confirmed population to the removed population. In 2021, Tesfaya et al. ^[8] suggested the following continuous-time stochastic COVID-19 epidemic model with jump-diffusion derived by both Gaussian and non-Gaussian noises:

where $S, \ I$ and $R$ respectively denote susceptible, infected and recovered populations, whereas joining rate of people to susceptible class through migration or birth is $\Lambda$, $\beta$ is the rate at which susceptible class tends to infected one, $\nu$ is due to coronavirus death, recovery rate is $\gamma$, and $\sigma$ is the rate of deteriorate in health.

1.2.   Statement of the problem

Motivated from the aforementioned studies, the purpose of this study is to investigate the dynamical characteristics of COVID-19 epidemic model, which is discrete analogue of continuous-time stochastic COVID-19 epidemic model (1.5), by Euler-forward formula. It is noted here that by applying Euler-forward formula the continuous-time stochastic COVID-19 epidemic model (1.5) takes the following form:

After simplification, model (1.6) takes the following form:

with $h$ is step size and $t$ is denoted by $n$. It is also important to note that in the proposed work we study dynamical characteristics of discrete-time COVID-19 epidemic model (1.7), which is counter part of epidemic model (1.5), because discrete model gives more efficient computational results as compared to continuous once.

1.3.   Structure of the paper

In the subsequent Section existence of equilibrium solutions of discrete COVID-19 epidemic model (1.7) is explored. In Section 3 we have constructed linearized form of discrete COVID-19 epidemic model (1.7) whereas Section 4 is about the exploration of local behavior of COVID-19 epidemic model (1.7) at equilibrium solutions. In Section 5 periodic points with period-$n$ of COVID-19 epidemic model (1.7) is investigated. The convergence rate for COVID-19 epidemic model (1.7) is studied in Section 6. In detailed bifurcation analysis about equilibrium solutions of discrete COVID-19 epidemic model (1.7) is given in Section 7. Section 8 is about the study of chaos control of COVID-19 epidemic model (1.7). Numerical verifications of theoretical results are given in Section 9. The concluding remarks are given in Section 10.

2.   Existence of equilibrium solutions of discrete COVID-19 epidemic model (1.7)

In $\mathbb{R}_+^3$, existence of equilibrium solutions of COVID-19 epidemic model (1.7) is studied in this Section, as follows:

Lemma 2.1. For existence results regarding equilibrium solutions of discrete COVID-19 epidemic model (1.7), following statements hold:

${\rm{(i)}}$ $\forall \ h, \ \beta, \ \Lambda, \ \nu, \ \sigma, \ \gamma > 0$, discrete COVID-19 epidemic model (1.7) has boundary equilibrium solution: $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$;

$({\rm{ii}})$ If $\beta > \frac{\nu \left(\nu+\gamma\right)}{\Lambda}$ then discrete COVID-19 epidemic model (1.7) has interior equilibrium solution:

Proof. If equilibrium solution of COVID-19 epidemic model (1.7) is $E_{SIR}(S, I, R)$ then

It is noted that for $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$ algebraic system (2.1) satisfied identically. Thus one can obtain that the boundary solution of discrete COVID-19 epidemic model (1.7) is $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$. For the interior equilibrium solution of discrete COVID-19 epidemic model (1.7), one need to solve following algebraic system simultaneously:

$2^{nd}$ equation of (2.2) yields

Using Eq (2.3) in $1^{st}$ equation of (2.2) one has

From $3^{rd}$ equation of (2.2) one has

From Eqs (2.4) and (2.5) one has

Using Eq (2.6) in Eq (2.5) one has

Finally, from Eqs (2.3), (2.6) and (2.7) it can be concluded that if $\beta > \frac{\nu (\nu+\gamma)}{\Lambda}$ then interior equilibrium solution of discrete COVID-19 epidemic model (1.7) is $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)$. Moreover it is important here to mention that if $\beta > \frac{\nu (\nu+\gamma)}{\Lambda}$, i.e., $\frac{\beta \Lambda}{\nu (\nu+\gamma)} > 1$ then discrete COVID-19 epidemic model (1.7) has interior equilibrium solution, and hence basic reproductive number is $R_0 = \frac{\beta \Lambda}{\nu (\nu+\gamma)}$.

3.   Linearized form of model (1.7)

In the present Section, linearized form of discrete COVID-19 epidemic model (1.7) about equilibrium solution $E_{SIR}(S, I, R)$ is explored. The linearized form of discrete COVID-19 epidemic model (1.7) about equilibrium solution $E_{SIR}(S, I, R)$ under the map

is

where

and

4.   Local behavior of discrete COVID-19 epidemic model (1.7) about equilibrium solutions

Local dynamic behavior of COVID-19 epidemic model (1.7) about equilibrium solutions: $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$ and $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)$ is explored in this section.

4.1.   Local dynamic behavior of COVID-19 epidemic model (1.7) about $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$

About $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$, Eq (3.3) becomes

with characteristic roots are

From Eq (4.2) and by stability theory ^[9,10,11,12], one can conclude local dynamic behavior of discrete COVID-19 epidemic model (1.7) about $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$ as follows.

Lemma 4.1. For local dynamic behavior of COVID-19 epidemic model (1.7) about $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$, following statements hold:

$({\rm{i}})$ $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$ of discrete COVID-19 model (1.7) is a sink if

with

$({\rm{ii}})$ $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$ of discrete COVID-19 model (1.7) is a source if (4.4) holds and additionally

$({\rm{iii}})$ $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$ of discrete COVID-19 model (1.7) is a saddle if (4.4) hold and additionally

or

or

or

$({\rm{iv}})$ $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$ of discrete COVID-19 model (1.7) is non-hyperbolic if

or

or

Proof. $(i)$ By stability theory $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$ of discrete COVID-19 model (1.7) is a sink if eigenvalues of $J|_{E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)}$ which are depicted in (4.2) satisfying $|\lambda_{1, 2, 3}| < 1$. So if $|\lambda_1| = \left|1-\nu h\right| < 1$, $|\lambda_2| = \left|1-\nu h-\gamma h+\frac{\beta \Lambda h}{\nu}\right| < 1$ and $|\lambda_3| = \left|1-\nu h-\sigma h\right| < 1$ then straightforward manipulation implies that $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$ of discrete COVID-19 model (1.7) is a sink if $0 < \nu < \min\left\{\frac{2}{h}, \frac{2}{h}-\sigma\right\}$, $\frac{\nu (\nu h+\gamma h-2)}{h \Lambda} < \beta < \frac{\nu (\nu+\gamma)}{\Lambda}$ with $\sigma < \frac{2}{h}$ and $\nu > \frac{2}{h}-\gamma$. In similarly way one can prove conclusions $(ii)$-$(iv)$.

4.2.   Local dynamic behavior of discrete COVID-19 epidemic model (1.7) about interior equilibrium solution: $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)$

In order to find local dynamic behavior of discrete COVID-19 epidemic model (1.7) about interior equilibrium solution: $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)$ following theorem is utilized which shows the fact that all roots of the characteristic equation of $J|_{E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{(\nu+\sigma) (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}, \frac{\gamma (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}\right)}$ whose absolute value less than one (^[13], Theorem 1.2.3).

Theorem 4.2. The necessary and sufficient conditions for roots of following third-degree polynomial

satisfying $\left|\lambda_{1, 2, 3}\right| < 1$ are

Lemma 4.3. $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)$ of discrete COVID-19 epidemic model (1.7) is a stable if

where

Proof. About $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)$, Eq (3.3) becomes

The characteristic polynomial of $J|_{E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)}$ about interior equilibrium solution $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)$ of discrete COVID-19 epidemic model (1.7) is

where $\mathcal{H}_1, \mathcal{H}_2$ and $\mathcal{H}_3$ are depicted in Eq (4.16). Now Theorem 4.2 implies that interior equilibrium solution $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)$ of discrete COVID-19 epidemic model (1.7) is a sink if $\left|\mathcal{H}_1 + \mathcal{H}_3\right| < 1+\mathcal{H}_2, \ \left|\mathcal{H}_1-3\mathcal{H}_3\right| < 3-\mathcal{H}_2$ and $\mathcal{H}_3^2 + \mathcal{H}_2 - \mathcal{H}_3\mathcal{H}_1 < 1$.

5.   Periodic points with period-$n$ of discrete COVID-19 epidemic model (1.7)

Motivated from existing study ^[14], in this section it is explored that equilibrium solutions: $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$ and $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)$ of discrete COVID-19 epidemic model (1.7) are periodic points with period-$n$.

Theorem 5.1. $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$ and $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)$ of discrete COVID-19 epidemic model (1.7) are periodic points of prime period-$1$.

Proof. From model (1.7) one denotes

where $f(S, I, R), \ g(S, I, R)$ and $h(S, I, R)$ are depicted in Eq (3.4). From Eq (5.1) the computation yields

Therefore Eq (5.2) implies that $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$ and $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)$ of discrete COVID-19 epidemic model (1.7) are periodic points of prime period-$1$.

Theorem 5.2. Equilibrium solution: $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$ of discrete COVID-19 epidemic model (1.7) is a periodic point of period-$n$.

Proof. From Eq (5.1) we have

Equation (5.3) implies that equilibrium solution:$E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$ of discrete COVID-19 epidemic model (1.7) is a periodic point of period-$n$.

Theorem 5.3. Equilibrium solution: $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{(\nu+\sigma) (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}, \frac{\gamma (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}\right)$ of discrete COVID-19 epidemic model (1.7) is a periodic point of period-$n$.

Proof. From Eq (5.3) the following computation yields the required statement:

6.   Convergence rate of discrete COVID-19 epidemic model (1.7)

Convergence rate of discrete COVID-19 epidemic model (1.7) is studied for the completeness of this Section.

Theorem 6.1. If $\{(S_n, I_n, R_n)\}$ is a positive solution of discrete COVID-19 epidemic model (1.7) such that $\lim\limits_{n\to\infty}\{(S_n, I_n, R_n)\} = E_{SIR}(S, I, R)$ then

satisfying the following mathematical relation:

Proof. It is recalled that if $\{(S_n, I_n, R_n)\}$ is a positive solution of COVID-19 epidemic model (1.7) such that $\lim\limits_{n\to\infty}\{(S_n, I_n, R_n)\} = E_{SIR}(S, I, R)$, then in order for error terms one has

Set

In view of Eq (6.4), Eq (6.3) becomes:

where

From Eq (6.6), one has

that is

where $\sigma_{11}, \sigma_{12}, \sigma_{13}, \sigma_{21}, \sigma_{22}, \sigma_{32}, \sigma_{33}\rightarrow0$ as $n\rightarrow \infty$. In view of existing literature ^[15], one has the following error system:

where $A = J|_{E_{SIR}(S, I, R)}$ and $B_n = \left(\begin{array}{ccc} \sigma_{11} & \sigma_{12} & \sigma_{13}\\ \sigma_{21} & \sigma_{22} & 0\\ 0 & \sigma_{32} & \sigma_{33} \end{array} \right)$. Therefore one has the following limiting system of error terms

which is same as linearized system of discrete COVID-19 epidemic model (1.7) about $E_{SIR}(S, I, R)$. Particularly Eq (6.10) implies that

and

which are same as respective linearized system obtained at equilibrium solution $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$ and $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{(\nu+\sigma) (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}, \frac{\gamma (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}\right)$ of the discrete COVID-19 epidemic model (1.7).

7.   Bifurcations of discrete COVID-19 epidemic model (1.7)

The bifurcation analysis about $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$ and $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{(\nu+\sigma) (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}, \frac{\gamma (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}\right)$ of the discrete COVID-19 epidemic model (1.7) are explored deeply in the section by bifurcation theory ^[16,17].

7.1.   Bifurcation analysis about $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$

From (4.2) the computation yields $\lambda_1|_{(4.10)} = -1$ but $\lambda_{2, 3} = -1-\gamma h+\frac{\beta \Lambda h^2}{2}, -1-\sigma h\ne 1$ or $-1$, which implies that discrete COVID-19 epidemic model (1.7) may undergo flip bifurcation if $(\Lambda, \beta, \gamma, \nu, \sigma, h)$ located in the set:

The following Theorem guarantees the fact that if $(\Lambda, \beta, \gamma, \nu, \sigma, h)\in \mathcal{F}|_{E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)}$ then discrete COVID-19 epidemic model (1.7) does not undergo flip bifurcation.

Theorem 7.1. If $(\Lambda, \beta, \gamma, \nu, \sigma, h)\in \mathcal{F}|_{E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)}$ then discrete COVID-19 epidemic model (1.7) does not undergo flip bifurcation.

Proof. Since discrete COVID-19 epidemic model (1.7) is invariant with respect to $I = R = 0$. Therefore in order to determine bifurcation, discrete COVID-19 epidemic model (1.7) is restricted on $I = R = 0$, where it becomes

From Eq (7.2) one denotes the map

Now if $\nu = \nu^{\ast} = \frac{2}{h}$ and $S = S^\ast = \frac{\Lambda}{\nu}$ then from Eq (7.3) one gets

and

It is noted that the condition obtained in Eq (7.6) violates the non-degenerate condition for the existence of flip bifurcation and hence one can say that discrete COVID-19 epidemic model (1.7) does not undergo flip bifurcation if $(\Lambda, \beta, \gamma, \nu, \sigma, h)\in \mathcal{F}|_{E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)}$.

7.2.   Bifurcation analysis about $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{(\nu+\sigma) (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}, \frac{\gamma (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}\right)$

By utilizing explicit criterion (without finding eigenvalues), we will explore hopf and flip bifurcations by choosing $h$ as a bifurcation parameter about $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{(\nu+\sigma) (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}, \frac{\gamma (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}\right)$ of discrete COVID-19 epidemic model (1.7) in this section.

7.2.1.   Hopf bifurcation about $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{(\nu+\sigma) (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}, \frac{\gamma (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}\right)$

By using following explicit criterion^[18], hopf bifurcation for the discrete COVID-19 epidemic model (1.7) about $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{(\nu+\sigma) (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}, \frac{\gamma (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}\right)$ is explored.

Lemma 7.2. Consider the following $n$-dimensional discrete dynamical system:

where $h\in \mathbb{R}$ is considered as a bifurcation parameter. Moreover characteristic polynomial of $J|_X$ about $X$ of $n$-dimensional discrete dynamical system, which is depicted in system (7.7), is

Now considering the determinants: $\Delta_0^\pm(h) = 1$, $\Delta_1^\pm(h), \cdots, \Delta_n^\pm(h)$, which can be expressed as

where $j = 1, \cdots, n$. Furthermore, hopf bifurcation occurs at critical value $h = h_0$ if following parametric conditions hold:

$\Gamma_1:$ Eigenvalue assignment: $P_{h_0}(1) > 0, \ (-1)^nP_{h_0}(-1) > 0, \ \Delta_{n-1}^-(h_0) = 0, \ \Delta_{n-1}^+(h_0) > 0, \ \Delta_j^\pm(h_0) > 0$ where $j = n-3, n-5, \cdots, 1$ (or 2), when $n$ is even (or odd, respectively).

$\Gamma_2:$ Transversality condition: $\frac{d}{dh}\Delta_{n-1}^-(h_0)\neq0$.

$\Gamma_3:$ Nonresonance condition: $\cos(\frac{2\pi}{l})\neq1-0.5P_h(1)\frac{\Delta_{n-3}^-(h_0)}{\Delta_{n-2}^+(h_0)}$ or resonance condition $\cos\left(\frac{2\pi}{l}\right) = 1-0.5P_h(1)\frac{\Delta_{n-3}^-(h_0)}{\Delta_{n-2}^+(h_0)}$, where $l = 3, 4, \cdots$.

Theorem 7.3. If

then about $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{(\nu+\sigma) (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}, \frac{\gamma (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}\right)$ discrete COVID-19 epidemic model (1.7) undergoes a hopf bifurcation at a critical value $h_0$ where $\mathcal{H}_1, \mathcal{H}_2, \mathcal{H}_3$ are depicted in Eq (4.16) and $h_0$ is the real root of $1 -\mathcal{H}_2(h) +\mathcal{H}_3(h)(\mathcal{H}_1(h) -\mathcal{H}_3(h)) = 0$.

Proof. By utilizing Lemma 7.2 for $n = 3$, one gets:

Finally

7.2.2.   Flip bifurcation about $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{(\nu+\sigma) (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}, \frac{\gamma (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}\right)$

By using following explicit criterion ^[18,19], flip bifurcation for the discrete COVID-19 epidemic model (1.7) about $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{(\nu+\sigma) (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}, \frac{\gamma (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}\right)$ by choosing $h$ as a bifurcation parameter is explored.

Lemma 7.4. Consider the system (7.7) with $h\in \mathbb{R}$ is a bifurcation parameter. Moreover, characteristic polynomial of $J|_X$ about $X$ of system (7.7) is of the form, which is depicted in Eq (7.8). Now considering the determinants: $\Delta_0^\pm(h) = 1$, $\Delta_1^\pm(h), \cdots, \Delta_n^\pm(h)$, which are depicted in Eq (7.9) and $j = 1, \cdots, n$. Furthermore flip bifurcation occurs at critical value $h = h_0$ if following parametric conditions hold:

$\Gamma_1:$ Eigenvalue assignment: $P_{h_0}(-1) = 0, \ P_{h_0}(1) > 0, \ \Delta_{n-1}^{\pm}(h_0) > 0, \ \Delta_j^\pm(h_0) > 0$ where $j = n-3, n-5, \cdots, 1$ (or 2), when $n$ is even (or odd, respectively).

$\Gamma_2:$ Transversality condition: $\frac{\sum\limits_{i = 1}^{n}(-1)^{n-i}\mathcal{H}_i^{'}}{\sum\limits_{i = 1}^{n}(-1)^{n-i}(n-i+1)\mathcal{H}_{i-1}}\neq 0$ where $\mathcal{H}_i^{'}$ represents the derivative w.r.t $h$ at $h = h_0$.

Theorem 7.5. If

then about $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{(\nu+\sigma) (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}, \frac{\gamma (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}\right)$ discrete COVID-19 epidemic model (1.7) undergoes a flip bifurcation at a critical value $h_0$, where $h_0$ is the real root of $1 - \mathcal{H}_1(h) + \mathcal{H}_2 (h)- \mathcal{H}_3(h) = 0$.

Proof. By utilizing Lemma 7.4 for $n = 3$, one gets:

8.   Chaos control

In this Section, feedback control strategy is utilized in order to study chaos in discrete COVID-19 epidemic model (1.7) about interior equilibrium solution: $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)$. By utilizing feedback control strategy, discrete COVID-19 epidemic model (1.7) takes the form

with $\delta$ is chosen as the control parameter. The $J^C|_{E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)}$ about interior equilibrium solution $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)$ of controlled discrete COVID-19 epidemic model (8.1) is

the characteristic polynomial of $J^C|_{E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)}$ about interior equilibrium solution $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)$ is

where

Based on linear stability theory the local dynamics of controlled discrete COVID-19 epidemic model (8.1) about $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{(\nu+\sigma) (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}, \frac{\gamma (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}\right)$ can be stated as following Lemma:

Lemma 8.1. $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{(\nu+\sigma) (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}, \frac{\gamma (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}\right)$ of controlled discrete COVID-19 epidemic model (8.1) is a sink if

where $\mathcal{H}_1^{*}, \mathcal{H}_2^{*}$ and $\mathcal{H}_3^{*}$ are depicted in Eq (8.4).

Proof. Since $J^C|_{E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)}$ about interior equilibrium solution $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)$ of controlled discrete COVID-19 epidemic model (8.1) has characteristics polynomial which is depicted in model (8.3). By Theorem 4.2 $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)$ of controlled discrete COVID-19 epidemic model (8.1) is a sink if $|\mathcal{H}_1^{*}+\mathcal{H}_3^{*}| < 1+\mathcal{H}_2^{*}$, $|\mathcal{H}_1^{*}-3\mathcal{H}_3^{*}| < 3-\mathcal{H}_2^{*}$ and ${\mathcal{H}_3^{*}}^2+\mathcal{H}_2^{*}-\mathcal{H}_3^{*}\mathcal{H}_1^{*} < 1$ where $\mathcal{H}_1^{*}$, $\mathcal{H}_2^{*}$ and $\mathcal{H}_3^{*}$ are depicted in Eq (8.4).

9.   Numerical simulations

Theoretical results are illustrated numerically in this section. In this regard, following cases are presented to discuss the correctness of obtained theoretical results about equilibrium solutions for discrete COVID-19 epidemic model (1.7) :

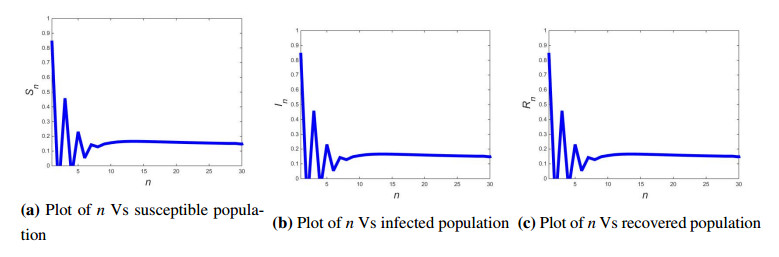
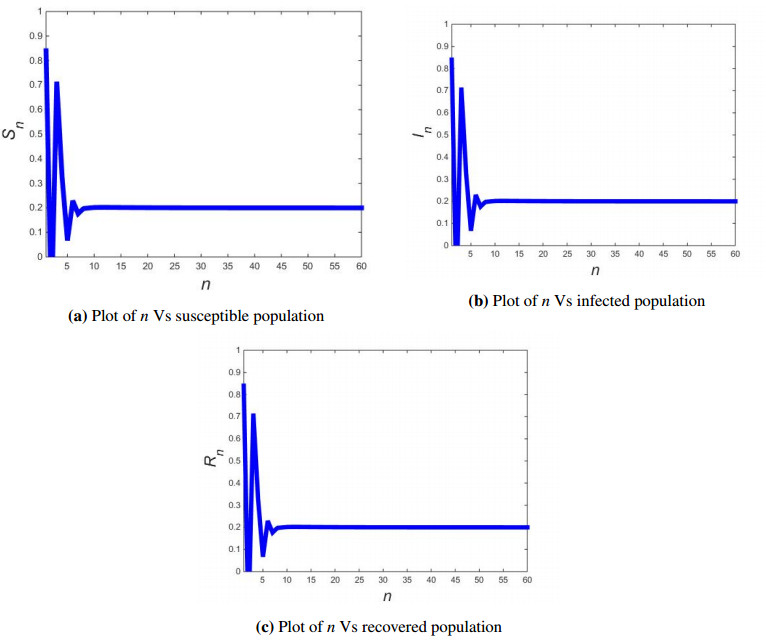
Case Ⅰ: If $h = 0.565, \ \beta = 3, \ \Lambda = 0.4, \ \nu = 0.2, \ \sigma = 2, \ \gamma = 0.4$ then from Eq (4.13) computation yields $\left|\mathcal{H}_1 + \mathcal{H}_3\right| = 0.0791966397692303 < 1+\mathcal{H}_2 = 0.3493437692307695$, $\left|\mathcal{H}_1-3\mathcal{H}_3\right| = 3.512871619153845 < 3-\mathcal{H}_2 = 3.6506562307692305$ and $\mathcal{H}_3^2 + \mathcal{H}_2 - \mathcal{H}_3\mathcal{H}_1 = 0.8910931323439 < 1$, which implies that equilibrium solution $E^+_{SIR}\left(0.2, 1.5230769230769232, 0.27692307692307694\right)$ of discrete COVID-19 epidemic model (1.7) is a sink. In this case plots for discrete COVID-19 epidemic model (1.7) with initial values $(S_0, I_0, R_0) = (0.84, 0.84, 0.0082)$ are drawn in Figure 1 which show that interior equilibrium solution $E^+_{SIR}\left(0.2, 1.5230769230769232, 0.27692307692307694\right)$ is a sink.

Case Ⅱ: Now in this case it is proved that at $h = 0.9645432692307686$, discrete COVID-19 epidemic model (1.7) undergoes a hopf bifurcation if $\beta = 3, \ \Lambda = 0.4, \ \nu = 0.2, \ \sigma = 0.42, \ \gamma = 4.5$ and $h\in[0.1, 1.9]$ with initial values $(S_0, I_0, R_0) = (0.94, 0.00084, 0.000782)$. If $\beta = 3, \ \Lambda = 0.4, \ \nu = 0.2, \ \sigma = 0.42, \ \gamma = 4.5$ and $h = 0.9645432692307686$ then from Eq (4.18) one gets:

whose roots are $\lambda_{1, 2} = 0.625071481557993\pm0.7805675133791408\iota, \lambda_3 = 0.8070913461538463$ where $|\lambda_{1, 2}| = |0.625071481557993\pm0.7805675133791408\iota| = 1$. This implies that for said parametric values the eigenvalues criterion for the existence of hopf bifurcation holds, and hence discrete COVID-19 epidemic model (1.7) may undergo hopf bifurcation. In the rest of simulation, it is proved that discrete COVID-19 epidemic model (1.7) must undergo hopf bifurcation. For instance, if $\beta = 3, \ \Lambda = 0.4, \ \nu = 0.2, \ \sigma = 0.42, \ \gamma = 4.5$ and $h = 0.9645432692307686$ then from Eq (7.10) the computation yields

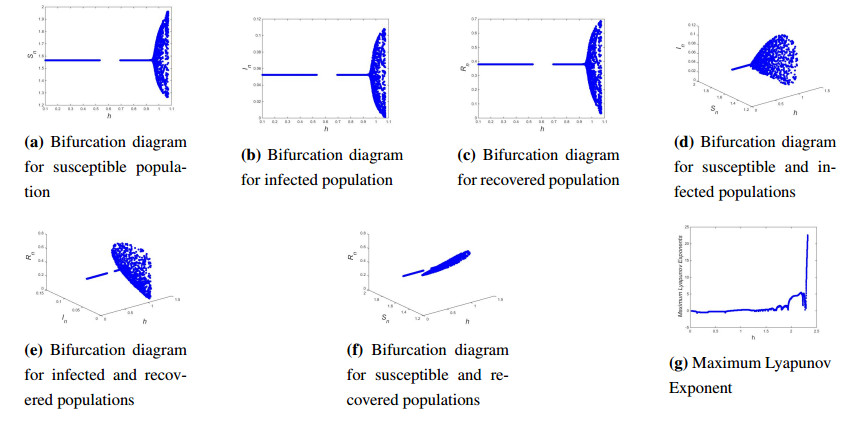
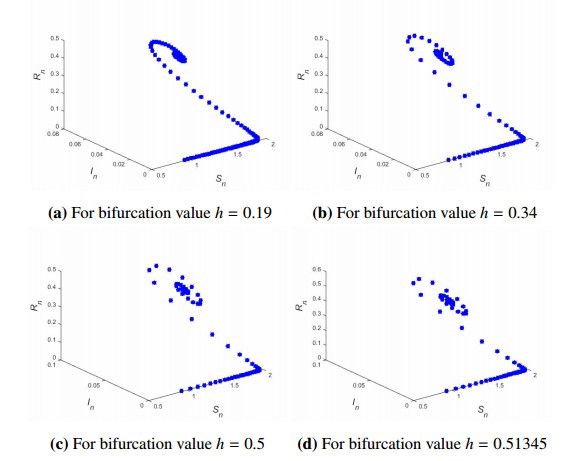
Moreover $\cos\frac{2\pi}{l} = 0.6250714815579933$ implies $l = \pm7.0158253519640486$. Thus from Eq (9.2) all conditions of Theorem 7.3 hold and hence it can be concluded that discrete COVID-19 epidemic model (1.7) undergoes hopf bifurcation. So hopf bifurcation diagram and maximum lypunov exponents are drawn in Figure 2. Finally some phase portraits for discrete COVID-19 epidemic model (1.7) are also plotted for certain values of $h$ with initial values $(S_0, I_0, R_0) = (0.94, 0.00084, 0.000782)$ in Figure 3.

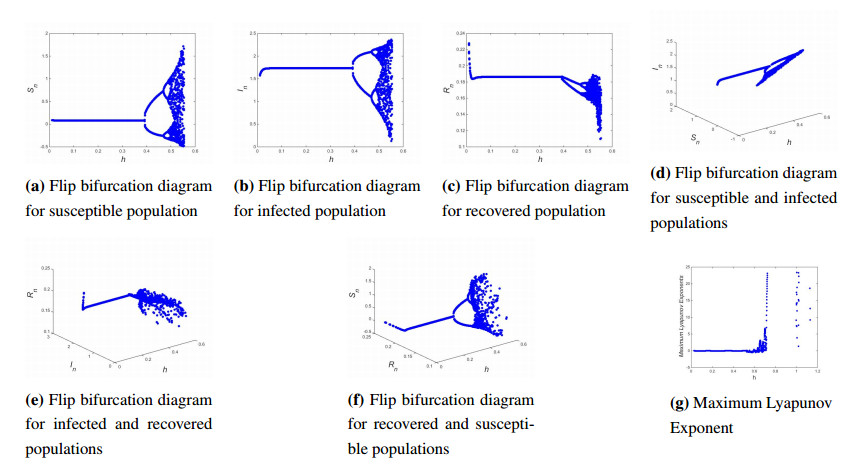
Case Ⅲ: Now in this case it is proved that at $h = 0.3882629532979648$, discrete COVID-19 epidemic model (1.7) undergoes a flip bifurcation if $\beta = 3, \ \Lambda = 0.4, \ \nu = 0.2, \ \sigma = 0.2, \ \gamma = 0.043$ and $h\in[0.01, 1.5]$ with initial values $(S_0, I_0, R_0) = (0.4, 0.6, 0.7)$. If $\beta = 3, \ \Lambda = 0.4, \ \nu = 0.2, \ \sigma = 0.2, \ \gamma = 0.043$ and $h = 0.3882629532979648$, then from Eq (4.18) one gets:

whose roots are $\lambda_{1} = -1$ but $\lambda_{2, 3} = 0.8264286135915285, 0.922347409340407\not = 1\ \mathrm{or} \ -1$. This implies that for said parametric values the eigenvalues criterion for the existence of flip bifurcation holds, and hence discrete COVID-19 epidemic model (1.7) may undergo flip bifurcation. In the rest of simulation it is proved that discrete COVID-19 epidemic model (1.7) must undergo flip bifurcation. For instance if $\beta = 3, \ \Lambda = 0.4, \ \nu = 0.2, \ \sigma = 0.2, \ \gamma = 0.043$ and $h = 0.3882629532979648$, then from Eq (7.12) the computation yields

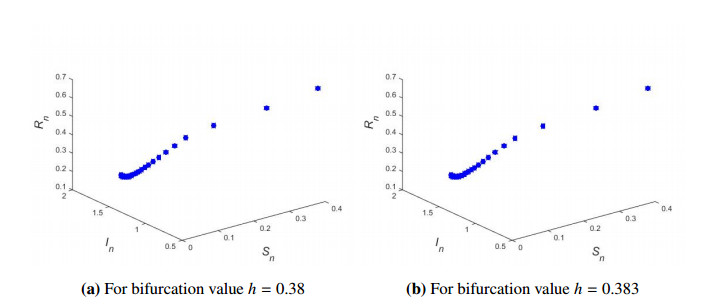
Thus from Eq (9.4) all conditions of Theorem 7.5 hold and hence it can be concluded that discrete COVID-19 epidemic model (1.7) undergoes flip bifurcation. So flip bifurcation diagrams and maximum lypunov exponents are drawn in Figure 4. Finally, phase portraits for discrete COVID-19 epidemic model (1.7) are also plotted for $h = 0.38, 0.383$ with initial values $(S_0, I_0, R_0) = (0.4, 0.6, 0.7)$ in Figure 5.

Case Ⅳ: The numerical simulation will be provided in order to verify result of Lemma 8.1 for controlled discrete COVID-19 epidemic model (8.1). If $h = 0.5643, \ \beta = 3, \ \Lambda = 0.22, \ \nu = 0.2, \ \sigma = 2, \ \gamma = 0.43, \delta = 0.22$ then from Eq (8.5) computation yields $|\mathcal{H}_1^{*}+\mathcal{H}_3^{*}| = 1.9887516175217854 < 1+\mathcal{H}_2^{*} = 2.062885326736867, |\mathcal{H}_1^{*}-3\mathcal{H}_3^{*}| = 1.4779003281575345 < 3-\mathcal{H}_2^{*} = 1.937114673263$ and ${\mathcal{H}_3^{*}}^2+\mathcal{H}_2^{*}-\mathcal{H}_3^{*}\mathcal{H}_1^{*} = 0.8415173747084458 < 1$ which implies that interior equilibrium solution of controlled discrete COVID-19 epidemic model (8.1) is a sink. In this case plots for discrete COVID-19 epidemic model (1.7) with initial values $(S_0, I_0, R_0) = (0.84, 0.84, 0.0082)$ are drawn in Figure 6, which show that interior equilibrium solution is a sink.

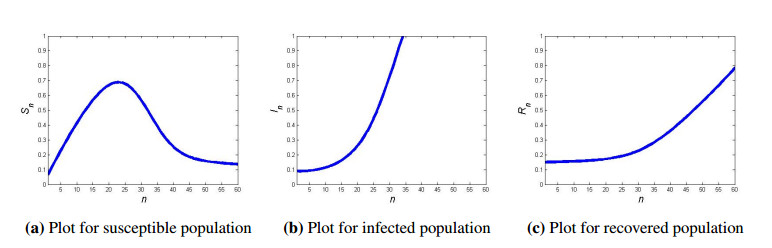
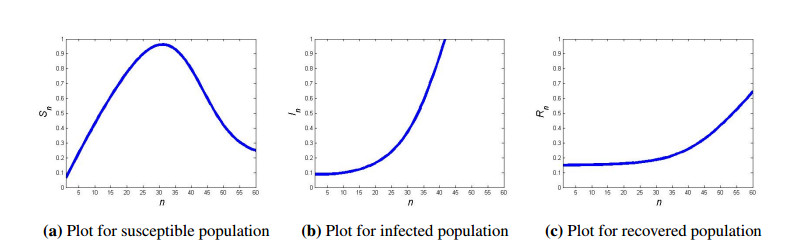
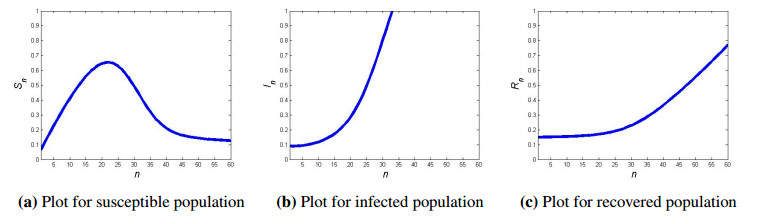
Case Ⅴ: Finally, we will fit real data, obtained from published materials for three different countries France, Italy and United Kingdom, to our under consideration discrete epidemic model (1.7) in order for the effectiveness of our mathematical analysis regarding stability. The collected real data is depicted in Table 1 whereas corresponding dynamical analysis of discrete epidemic model (1.7) of France, Italy and the United Kingdom are respectively given in Figures 7–9. In Figure 7(a) the plot of susceptible population show a curve that represent the number of susceptible individuals increase rapidly with the passage of time. After peak, the number of susceptible individuals decrease and attain a steady state whereas Figure 7(b) shows a curve that represent the infection rate is sharply increase with the passage of time and reach to its maximum level. Finally, Figure 7(c) represent that curve goes upward slowly which means that the number of recovered individuals were small initially due to less medical care and facilities but with the passage of time the recovery rate increases due to proper medication and vaccination. Similar results can be interpreted for real data plotted in Figures 8 and 9 for Italy and United Kingdom, respectively.

10.   Conclusions

Beginning from the COVID-19, different mathematicians have proposed mathematical models to predict the cause of COVID-19 pandemic starting from Wuhan city of China in December 2019. For instance, few newly proposed mathematical models regarding COVID-19 pandemic are quoted in references ^{[1,2,3,4,5,6,7]}. In the references ^{[1,2,3,4,5,6,7]} and more study indicates that different authors predict the case of this disease by mathematical models representing systems of differential or difference equations, and moreover based on date analysis and mathematical analysis authors have explored the effect of lockdown and medical resources on the COVID-19 transformation in Wuhan city of China. So motivation from aforementioned studies, in this paper we have explored local dynamical properties, bifurcation and control in a discrete-time COVID-19 epidemic model in $\mathbb{R}_+^3$. Algebraically, it is proved that discrete COVID-19 epidemic model (1.7) has boundary equilibrium solution: $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right) \ \forall \ h, \ \beta, \ \Lambda, \ \nu, \ \sigma, \ \gamma > 0$ but it has has interior equilibrium solution: $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)$ if $\beta > \frac{\nu \left(\nu+\gamma\right)}{\Lambda}$. Further local dynamical characteristics with topological classifications about equilibrium solutions $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$ and $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)$ of discrete COVID-19 epidemic model (1.7) are explored. It is investigated that $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$ of discrete COVID-19 epidemic model (1.7) is a sink if $0 < \nu < \min\left\{\frac{2}{h}, \frac{2}{h}-\sigma\right\} \ \ \mathrm{and} \ \ \frac{\nu (\nu h+\gamma h-2)}{h \Lambda} < \beta < \frac{\nu (\nu+\gamma)}{\Lambda}$ with $\sigma < \frac{2}{h}\ \ \mathrm{and}\ \ \nu > \frac{2}{h}-\gamma$; source if (4.4) holds and additionally $\nu > \max\left\{\frac{2}{h}, \frac{2}{h}-\sigma\right\} \ \ \mathrm{and} \ \beta < \frac{\nu (\nu h+\gamma h-2)}{h \Lambda}$; saddle if (4.4) holds and additionally $\nu > \max\left\{\frac{2}{h}, \frac{2}{h}-\sigma\right\} \ \ \mathrm{and} \ \frac{\nu (\nu h+\gamma h-2)}{h \Lambda} < \beta < \frac{\nu (\nu+\gamma)}{\Lambda},$ or $\frac{2}{h}-\sigma < \nu < \frac{2}{h}\ \mathrm{and} \ \ \frac{\nu (\nu h+\gamma h-2)}{h \Lambda} < \beta < \frac{\nu (\nu+\gamma)}{\Lambda},$ or $0 < \nu < \min\left\{\frac{2}{h}, \frac{2}{h}-\sigma\right\}\ \ \mathrm{and} \ \beta < \frac{\nu (\nu h+\gamma h-2)}{h \Lambda},$ or $\frac{2}{h}-\sigma < \nu < \frac{2}{h}\ \mathrm{and} \ \ \beta < \frac{\nu (\nu h+\gamma h-2)}{h \Lambda}$; non-hyperbolic if $\nu = \frac{2}{h},$ or $\beta = \frac{\nu (\nu h+\gamma h-2)}{h \Lambda},$ or $\nu = \frac{2}{h}-\sigma$, and moreover interior equilibrium solution $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)$ of discrete COVID-19 epidemic model (1.7) is a sink if $\left|\mathcal{H}_1 + \mathcal{H}_3\right| < 1+\mathcal{H}_2, \ \ \left|\mathcal{H}_1-3\mathcal{H}_3\right| < 3-\mathcal{H}_2, \ \ \mathcal{H}_3^2 + \mathcal{H}_2 - \mathcal{H}_3\mathcal{H}_1 < 1$ where $\mathcal{H}_1, \mathcal{H}_2$ and $\mathcal{H}_3$ are depicted in Eq (4.16). It is shown that $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$ and $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)$ of discrete COVID-19 epidemic model (1.7) are periodic points of period-$n$. We have also studied convergence rate for discrete COVID-19 epidemic model (1.7). Further, in order to understand dynamics of discrete COVID-19 epidemic model (1.7) deeply, we have studied the possible bifurcation scenarios. It is proved that about $E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)$ there exist no flip bifurcation if $(\Lambda, \beta, \gamma, \nu, \sigma, h)\in \mathcal{F}|_{E_{S00}\left(\frac{\Lambda}{\nu}, 0, 0\right)} = \left\{(\Lambda, \beta, \gamma, \nu, \sigma, h):\nu = \frac{2}{h}\right\}$, but discrete COVID-19 epidemic model (1.7) undergoes both hopf and flip bifurcations about $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)$ by choosing $h$ as bifurcation parameter. We have studied hopf and flip bifurcations about $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)$ of discrete COVID-19 epidemic model (1.7) by utilizing explicit criterion. By feedback control strategy, chaos in discrete COVID-19 epidemic model (1.7) about $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{\left(\nu+\sigma\right) \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}, \frac{\gamma \left(\beta \Lambda-{\nu}^2-\nu \gamma\right)}{\beta \left({\nu}^2+\left(\sigma+\gamma\right) \nu\right)}\right)$ is also explored. For controlled system (8.1) it is proved that $E^+_{SIR}\left(\frac{\nu+\gamma}{\beta}, \frac{(\nu+\sigma) (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}, \frac{\gamma (\beta \Lambda-{\nu}^2-\nu \gamma)}{\beta ({\nu}^2+(\sigma+\gamma) \nu)}\right)$ is a sink if $|\mathcal{H}_1^{*}+\mathcal{H}_3^{*}| < 1+\mathcal{H}_2^{*}, \ |\mathcal{H}_1^{*}-3\mathcal{H}_3^{*}| < 3-\mathcal{H}_2^{*}$ and ${\mathcal{H}_3^{*}}^2+\mathcal{H}_2^{*}-\mathcal{H}_3^{*}\mathcal{H}_1^{*} < 1$, where $\mathcal{H}_1^{*}, \mathcal{H}_2^{*}$ and $\mathcal{H}_3^{*}$ are depicted in Eq (8.4). Finally numerically verified theoretical results.

Acknowledgments

This research is partially supported by the Higher Education Commission of Pakistan.

Conflict of interest

The authors declare that they have no conflicts of interest regarding the publication of this paper.