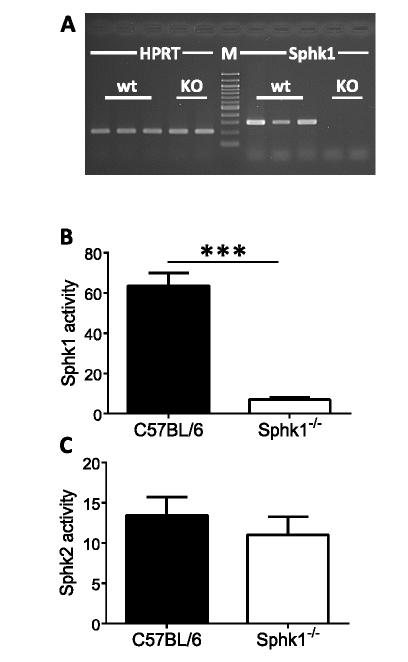
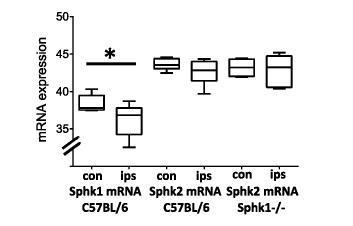
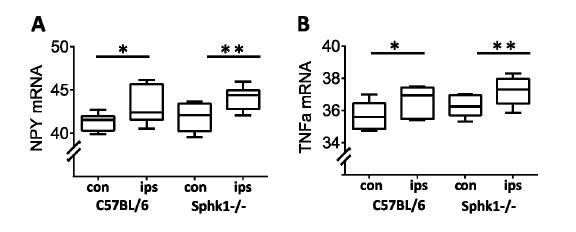
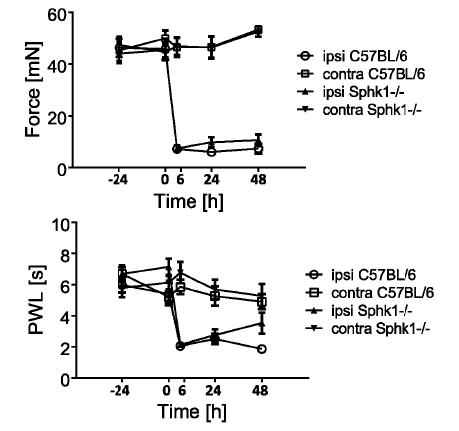
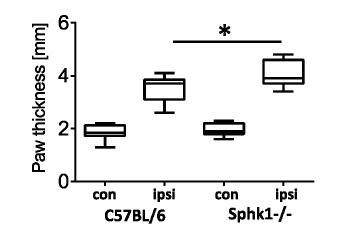
The bioactive sphingolipid, sphingosine 1-phosphate (S1P), is a multifunctional mediator that regulates a multitude of processes such as proliferation and differentiation, immune responses, airway constriction and nociception. S1P is synthesized by two sphingosine kinase isoforms, Sphk1 and Sphk2, which are expressed ubiquitously, but exhibit differential tissue expression patterns among organs. S1P has been shown to be involved in sensory neuron nociceptive signalling. However, the presence and regulation of Sphk expression in sensory neurons under conditions of persistent inflammatory pain are currently unknown. We therefore assessed the expression levels of Sphk in murine dorsal root ganglion (DRG) neurons, explored the localisation of Sphk mRNA using In-Situ-Hybridization and used mice with a global null mutation for Sphk1 to investigate the response of sensory neurons in a model of persistent inflammation. Here we showed the expression of both Sphk isoforms in mouse primary sensory neurons. The relative mRNA expression levels for markers of inflammation and nociceptive activity, TNFα and NPY, increased whereas mRNA expression levels for Sphk1 but not Sphk2 decreased in ipsilateral DRG in response to peripheral inflammation. Mice with a global deletion of Sphk1 showed a substantial reduction in Sphk1- but not Sphk2-activity in spinal cord but responded to CFA inflammation in a similar way to control mice, with increased sensitivity to mechanical and thermal stimuli, although the degree of inflammation-induced paw swelling was slightly increased in the Sphk1-/- mice. In summary, Sphk1 mRNA was expressed in virtually all sensory DRG neurons and its expression changed in response to peripheral inflammation. However, deficiency of Sphk1did not impact on the inflammation-dependent changes in the expression of pro-inflammatory markers in DRGs, nor did it significantly change nocifensive behaviour.
1.
Introduction
Functionally graded materials (FGM) are an advanced composite material class whose vary gradually and continuously in the composition of microstructure constituents through the dimension of the material [1,2,3]. The behavior composition of FGM reduce the structural weight with increasing its coefficient modulus of stiffness and strength [4,5,6,7,8]. The properties of all constituents can be employed, for example, the toughness of a metal can be mated with the refractoriness of a ceramic, without any compromise in the toughness of the metal side or the refractoriness of the ceramic side [9,10,11,12,13,14]. The simple rule of mixture (Voigt law) is used to obtain the effective micromechanics material properties in the commencement of research papers. But to assess the effect of the micromechanical models on the structural responses of FG plates several micromechanical models of FGMs have been studied in [14,15,16]. Gasik has studied different micromechanical models to obtain the effective material properties of FGMs with power-law, Sigmoid, and exponential function distributions of volume fraction across the thickness of the static, buckling, free and forced vibration analyses for simply-supported FG plates resting on an elastic foundation [17]. Akbarzadeh et al. [18] have investigated about the influences of different forms of micromechanical models on FGM pressurized hollow cylinders. They have used the numerical results via finite element method (FEM) analyses for detailed and homogenized models of functionally graded (FG) carbon nanotube reinforced composite (CNTRC) beams. The effect of the imposed temperature field on the response of the FGM plate composed of Metal and Ceramic with the Mori–Tanaka micromechanical method is discussed [19,20].
Shen et al. [21] have studied the small and large amplitude frequency of vibrations are presented for a functionally graded rectangular plate resting on a two-parameter elastic foundation with two kinds of micromechanics models, namely, Voigt model and Mori–Tanaka model. The comparison studies reveal that the difference between these two models is much less compared to the difference caused by different solution methodologies and plate theories. In literature there is no available work treating the impact of the homogenization models on the sandwich FGM plate. In this paper we have studied the impact of (Reuss, LRVE, Tamura) homogenization or micromechanical models on the axial and shear stress of sandwich functionally graded materials plate subjected to linear and nonlinear thermal loads. The static and elastic behavior of the simply supported is considered. Using an integral higher shear deformation theory (HSDT), the governing partial differential equations are solved in the Cartesian coordinate via Navier solution method. Those Numerous micromechanical models have been examined to attain the effective material properties of the two-phase FGM plate (Metal and ceramic). The numerical results are compared with those given by other model existing in the literature to confirm the accuracy of the (HSDT). The present results are in good agreement with all models studied of homogenization for all values of the material index and all geometry configurations of the FG-sandwich plates.
2.
Materials and methods
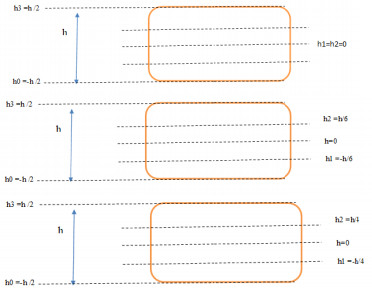
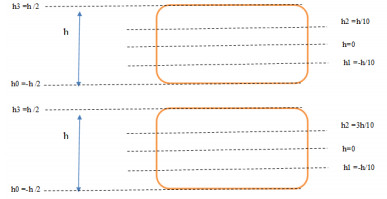
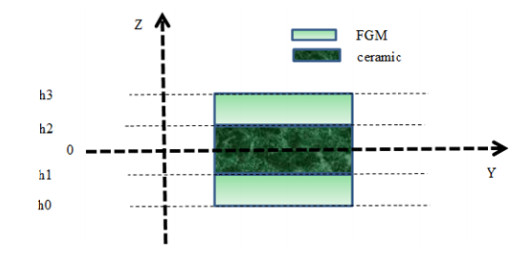
The geometry domain is assumed as a uniform rectangular plate with thickness "h", length "a", and width "b" as shown in Figure 1. The plate has three layers. The FG-face sheets are made by two materials metal and ceramic.
2.1. Materials characteristics
The mechanical and thermal proprieties of Metal (Titanium) are Young modulus $E\left(z \right)$ is 66.2 GPa, thermal expansion coefficients $\alpha $ is 10.3 (10−6/K). The mechanical and thermal proprieties of Ceramic (Zirconia) are Young modulus $E\left(z \right)$ is 117 GPa, thermal expansion coefficients $\alpha $ is 7.11 (10−6/K). The Poison coefficient is supposed the same in the metal and the ceramic ($\nu $ is 1/3). In the following.
Several types of geometries configurations are exanimated depending the thickness of each layer as shown in Table 1.
The volumes fraction of the FG- faces sheet are assumed varies as following functions (Eq 1).
Where K is the material index.
A number of micromechanics models have been proposed for the determination of effective properties of FGMs. K is the material index.
(1) Voigt model
The Voigt model is relatively simple; this model is frequently used in most FGM analyses estimates properties of FGMs as:
(2) Reuss model
Reuss assumed the stress uniformity through the material and obtained the effective properties as:
(3) Tamura model
The Tamura model uses actually a linear rule of mixtures, introducing one empirical fitting parameter known as "stress-to-strain transfer". For q = 0 correspond to Reuss rule and with$q = \pm \infty $to the Voigt rule, being invariant to the consideration of with phase is matrix and which is particulate. The effective property is found as:
(4) Description by a representative volume element (LRVE)
The LRVE is developed based on the assumption that the microstructure of the heterogeneous material is known. The input for the LRVE for the deterministic micromechanical framework is usually volume average or ensemble average of the descriptors of the microstructures.
The effective property is expressed as follows by the LRVE method:
2.2. Displacement base field
Based on the same assumptions of the conventional HSDT (with fives variables or more). The displacement field of the proposed HSDT is only with four unknowns variables and can be written in a simpler form as:
Where ${u_0}\left({x, y} \right)$, ${v_0}\left({x, y} \right)$, ${w_0}\left({x, y} \right)$, and $\theta \left({x, y} \right)$ are the four-unknown displacement functions of middle surface of the FG-sandwich plate. $f\left(z \right)$ is the warping function and (${k_1}$ and ${k_2}$) are constants.
In the current research work the proposed combined (exponential/hyperbolic) warping function ensures the nullity condition of the free surfaces of the FG-sandwich plate (zero transverse shear stresses at top and the Bottom of the FG-sandwich plate). The present exponential/hyperbolic warping function $f\left(z \right)$ is expressed as:
The stresses/strains linear relation of the PFG-sandwich plate can be expressed as:
Where
The variation of the temperature field across the thicness is assumed to be:
Where
The principle of virtual works of the considered PFG-sandwich plates is expressed as $\delta {\text{ }}U + \delta {\text{ }}V = 0$ where $ \delta U $is the variation of strain energy; and $ \delta V $ is the variation of the virtual work done by external load applied to the plate. The governing equations can be obtained as follows:
Based on the Navier method, the following expansions of displacements are
where ($U$, $V$, $W$, $X$) are unknown functions to be determined and $ \alpha = \pi /a $ and $\beta = \pi /b$.
In the present work, the transverse temperature loads T1, T2, and T3 in double sinus series form as:
The closed-form solution can be written as following matrix form:
Where
And
Where and $ ({L^T}, {}^a{L^T}, {R^T}) $ are coefficients calculated by integral summation formulations, in which $ \bar z = z/h, \bar f(z) = f(z)/h{\text{ and }}\bar \psi (z) = \psi (z)/h $.
3.
Results and discussion
In the following three sections, the results have been presented.
3.1. Comparisons and validation
A comparison has been done to verify the accuracy of the present theory of different models of homogenization (Reuss, Tamura and LRVE). Results are compared with the mixture model (Voigt) using by Zankour and Algamidi [22].
The dimensionless transverse and normal stress are expressed as:
with ${E_0} = 1{\kern 1pt} {\kern 1pt} GPa$ and ${\alpha _0} = {10^6}{\kern 1pt} {\kern 1pt} K$.
Table 2 presents the variation of dimensionless axial stress "${\bar \sigma _x}$" of the square FG-sandwich plate subjected to linearly thermal load "${T_3} = 0$" versus volumes fractions (material index "$k$") for different values of layer thickness ratio. It is remarkable that there is a proportional relationship between the index "$k$" the dimensionless normal stress "${\bar \sigma _x}$".
The Table 3 presents the variation of the dimensionless shear stress "${\bar \tau _{xz}}$" of the square FG-sandwich plate subjected to nonlinearly thermal load "${T_3} = - 100$" versus volumes fractions (material index "$k$") for different values of layer thickness ratio.from the Table 3 the shear stress "${\bar \tau _{xz}}$" and the index $k$ have direct relation. We can see from the Tables 2 and 3 that the present results are in good agreement with all models studied of homogenization (Voigt Zenkour et al. [22], Reuss, LRVE and Tamura) for all values of the material index "$k$" and all configurations of the FG-sandwich plate (1-0-1, 1-1-1, 1-2-1, 2-1-2 and 2-2-1).
3.2. Parametric study
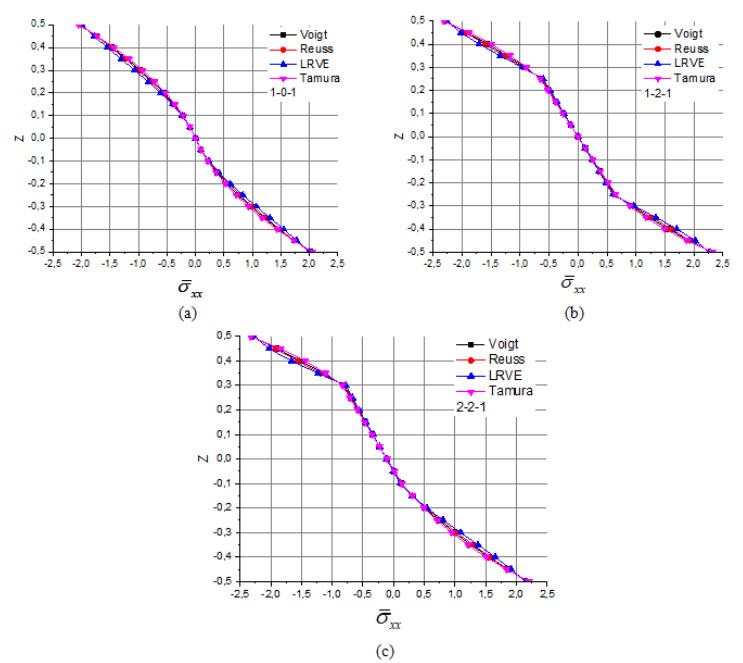
In this section, the parametric studies are presented in the explicit graphs form. Figure 2 plots the variation of the axial stress "${\bar \sigma _x}$" across the total thickness "$h$" of FG-sandwich plate ($k = 1$) under linear thermal loads "${T_3} = 0$" with different micromechanical models. From the plotted graphs, it is clear that the compressive stresses are obtained at the top of the plate. We can see that the present results are in good agreement with different models Voigt, Reuss, LRVE and Tamura for configurations of the FG-sandwich plate (1-0-1, 1-2-1 and 2-2-1) and the material index $k = 1$ (Figure 2a–c).
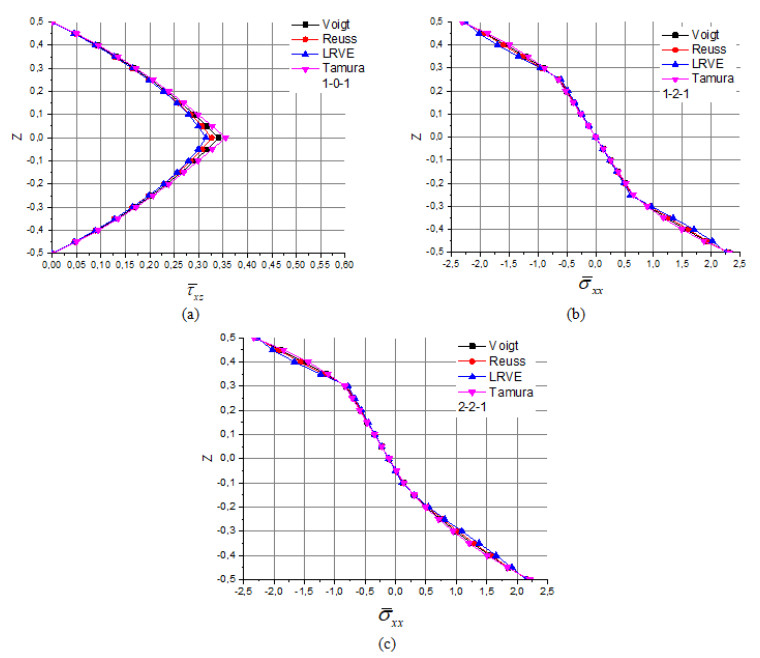
Figure 3 illustrates the variation of the "${\bar \tau _{xz}}$" through the total thickness of the 1-0-1, 1-2-1 and 2-2-1 FG-sandwich plate under linear thermal loads "${T_3} = 0$". It is noted that the shear stress "${\bar \tau _{xz}}$" is parabolically varied through the total thickness of the FG-sandwich plate. We can see that the present results are in good agreement with different models Voigt, Reuss, LRVE and Tamura for configurations of the FG-sandwich plate (1-0-1, 1-2-1 and 2-2-1) and the material index $k = 1$(Figure 3a–c).
3.3. Effect of the thermal loads on the normal and shear stress
In the present section three types of the temperature distribution across the thickness are considered. The first one, the temperature is linearly distributed through the thickness $T = z{\kern 1pt} {\kern 1pt} {T_2}$, in the second type the temperatures vary nonlinearly across $h$ ($T = z{\kern 1pt} {\kern 1pt} {T_2} + \psi (z){\kern 1pt} {\kern 1pt} {\kern 1pt} {T_3}$) and the third type is reserved for a combination of linear and nonlinear distributions $ T(z) = {T_1} + (z/h){T_2} + (\Psi (z)/h){T_3} $.
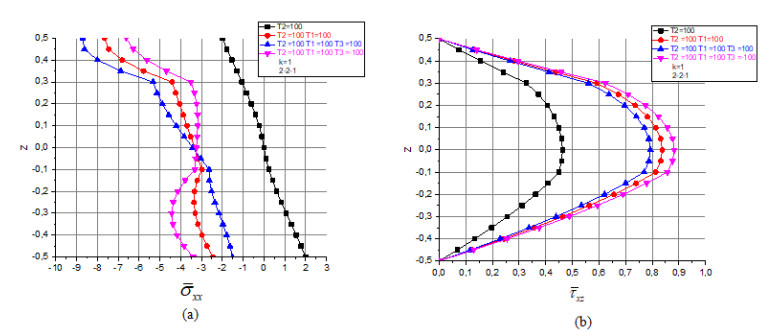
Figure 4a shows the distributions of the axial stress "${\bar \sigma _x}$" through the total thickness of the simply supported 2-2-1 FG-sandwich plate for various values of the thermal load ($ {T_1} = 100 $), $ {T_2} = 100 $ and $ {T_3} = 100 $ with ($k = 1$). From the plotted curves, it can be observed that the axial stress "${\bar \sigma _x}$" is c influenced by the values of the thermal load.
Figure 4b plot the variation of the shear stress "${\bar \tau _{xz}}$" through the thickness $h$ of the 2-2-1 square FG-sandwich plate ($k = 1$). For different values of the thermal load ($ {T_1} = 100 $), $ {T_2} = 100 $ and $ {T_3} = 100 $. It can be noted from the graphs that the shear stress "${\bar \tau _{xz}}$" has a parabolic variation through the thickness. The maximal values of the shear stress "${\bar \tau _{xz}}$" are obtained at the mid-plane axis "$\overline z = 0$". And it is clearly influenced by the values of the thermal load.
4.
Conclusions
In this investigation, the impact of (Reuss, LRVE, Tamura) homogenization or micromechanical models on the axial and shear stress of sandwich functionally graded materials plate subjected to linear and nonlinear thermal loads have studied. The static and elastic behavior of the simply supported is considered. Using an integral higher shear deformation theory (HSDT), the governing partial differential equations are solved in the Cartesian coordinate via Navier solution method. Those Numerous micromechanical models have been examined to attain the effective material properties of the two-phase FGM plate (Metal and ceramic). The numerical results are compared with those given by other model existing in the literature to confirm the accuracy of the (HSDT). The present results are in good agreement with all models studied of homogenization for all values of the material index and all geometry configurations of the FG-sandwich plates.
Acknowledgments
The authors gratefully acknowledge the support provided by University of Sidi Bel Abbes, Algeria while the preparation of the doctorate thesis.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: