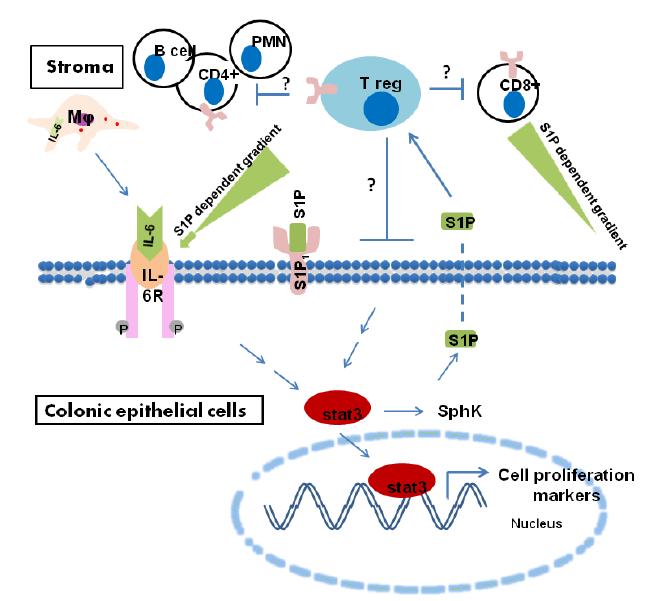
|
[1]
|
Curotto de Lafaille MA, Lafaille JJ (2009) Natural and adaptive foxp3+ regulatory T cells: more of the same or a division of labor? Immunity 30: 626-635. doi: 10.1016/j.immuni.2009.05.002

|
|
[2]
|
Sakaguchi S (2005) Naturally arising Foxp3-expressing CD25+CD4+ regulatory T cells in immunological tolerance to self and non-self. Nat Immunol 6: 345-352.
|
|
[3]
|
Maggi E, Cosmi L, Liotta F, et al. (2005) Thymic regulatory T cells. Autoimmun Rev 4: 579-586. doi: 10.1016/j.autrev.2005.04.010

|
|
[4]
|
Mougiakakos D, Choudhury A, Lladser A, et al. (2010) Regulatory T cells in cancer. Adv Cancer Res 107: 57-117. doi: 10.1016/S0065-230X(10)07003-X

|
|
[5]
|
Jonuleit H, Schmitt E (2003) The regulatory T cell family: distinct subsets and their interrelations. J Immunol 171: 6323-6327. doi: 10.4049/jimmunol.171.12.6323

|
|
[6]
|
Mucida D, Kutchukhidze N, Erazo A, et al. (2005) Oral tolerance in the absence of naturally occurring Tregs. J Clini Invest 115: 1923-1933. doi: 10.1172/JCI24487

|
|
[7]
|
Sakaguchi S, Sakaguchi N, Asano M, et al. (1995) Immunologic self-tolerance maintained by activated T cells expressing IL-2 receptor alpha-chains (CD25). Breakdown of a single mechanism of self-tolerance causes various autoimmune diseases. J Immunol 155: 1151-1164.
|
|
[8]
|
Roncarolo MG, Gregori S, Battaglia M, et al. (2006) Interleukin-10-secreting type 1 regulatory T cells in rodents and humans. Immunol Rev 212: 28-50. doi: 10.1111/j.0105-2896.2006.00420.x

|
|
[9]
|
Setoguchi R, Hori S, Takahashi T, et al. (2005) Homeostatic maintenance of natural Foxp3(+) CD25(+) CD4(+) regulatory T cells by interleukin (IL)-2 and induction of autoimmune disease by IL-2 neutralization. J Exp Med 201: 723-735. doi: 10.1084/jem.20041982

|
|
[10]
|
Barron L, Dooms H, Hoyer KK, et al. (2010) Cutting edge: mechanisms of IL-2-dependent maintenance of functional regulatory T cells. J Immunol 185: 6426-6430. doi: 10.4049/jimmunol.0903940

|
|
[11]
|
Read S, Mauze S, Asseman C, et al. (1998) CD38+ CD45RB(low) CD4+ T cells: a population of T cells with immune regulatory activities in vitro. Eur J Immunol 28: 3435-3447. doi: 10.1002/(SICI)1521-4141(199811)28:11<3435::AID-IMMU3435>3.0.CO;2-P

|
|
[12]
|
Fu S, Yopp AC, Mao X, et al. (2004) CD4+ CD25+ CD62+ T-regulatory cell subset has optimal suppressive and proliferative potential. Am J Transplant 4: 65-78. doi: 10.1046/j.1600-6143.2003.00293.x

|
|
[13]
|
Allakhverdi Z, Fitzpatrick D, Boisvert A, et al. (2006) Expression of CD103 identifies human regulatory T-cell subsets. J Allergy Clin Immunol 118: 1342-1349. doi: 10.1016/j.jaci.2006.07.034

|
|
[14]
|
Brunkow ME, Jeffery EW, Hjerrild KA, et al. (2001) Disruption of a new forkhead/winged-helix protein, scurfin, results in the fatal lymphoproliferative disorder of the scurfy mouse. Nat Genet 27: 68-73.
|
|
[15]
|
Chatila TA, Blaeser F, Ho N, et al. (2000) JM2, encoding a fork head-related protein, is mutated in X-linked autoimmunity-allergic disregulation syndrome. J Clini Invest 106: R75-81. doi: 10.1172/JCI11679

|
|
[16]
|
Bennett CL, Christie J, Ramsdell F, et al. (2001) The immune dysregulation, polyendocrinopathy, enteropathy, X-linked syndrome (IPEX) is caused by mutations of FOXP3. Nat Genet 27: 20-21. doi: 10.1038/83713

|
|
[17]
|
Allan SE, Passerini L, Bacchetta R, et al. (2005) The role of 2 FOXP3 isoforms in the generation of human CD4+ Tregs. J Clini Invest 115: 3276-3284. doi: 10.1172/JCI24685

|
|
[18]
|
Tang Q, Bluestone JA (2008) The Foxp3+ regulatory T cell: a jack of all trades, master of regulation. Nat Immunol 9: 239-244. doi: 10.1038/ni1572

|
|
[19]
|
LeGuern C (2003) Regulation of T-cell functions by MHC class II self-presentation. Trends Immunol 24: 633-638. doi: 10.1016/j.it.2003.10.010

|
|
[20]
|
Coutinho A, Caramalho I, Seixas E, et al. (2005) Thymic commitment of regulatory T cells is a pathway of TCR-dependent selection that isolates repertoires undergoing positive or negative selection. Curr Top Microbiol 293: 43-71.
|
|
[21]
|
Burchill MA, Yang J, Vang KB, et al. (2008) Linked T cell receptor and cytokine signaling govern the development of the regulatory T cell repertoire. Immunity 28: 112-121. doi: 10.1016/j.immuni.2007.11.022

|
|
[22]
|
Liston A, Nutsch KM, Farr AG, et al. (2008) Differentiation of regulatory Foxp3+ T cells in the thymic cortex. P Natl Acad Sci USA 105: 11903-11908. doi: 10.1073/pnas.0801506105

|
|
[23]
|
Gershon RK, Kondo K (1970) Cell interactions in the induction of tolerance: the role of thymic lymphocytes. Immunology 18: 723-737.
|
|
[24]
|
Lopes JE, Torgerson TR, Schubert LA, et al. (2006) Analysis of FOXP3 reveals multiple domains required for its function as a transcriptional repressor. J Immunol 177: 3133-3142. doi: 10.4049/jimmunol.177.5.3133

|
|
[25]
|
Wu Y, Borde M, Heissmeyer V, et al. (2006) FOXP3 controls regulatory T cell function through cooperation with NFAT. Cell 126: 375-387. doi: 10.1016/j.cell.2006.05.042

|
|
[26]
|
Shimizu J, Yamazaki S, Takahashi T, et al. (2002) Stimulation of CD25(+)CD4(+) regulatory T cells through GITR breaks immunological self-tolerance. Nat Immunol 3: 135-142. doi: 10.1038/ni759

|
|
[27]
|
Sakaguchi S (2004) Naturally arising CD4+ regulatory t cells for immunologic self-tolerance and negative control of immune responses. Annu Rev Immunol 22: 531-562. doi: 10.1146/annurev.immunol.21.120601.141122

|
|
[28]
|
Krummel MF, Allison JP (1995) CD28 and CTLA-4 have opposing effects on the response of T cells to stimulation. J Exp Med 182: 459-465. doi: 10.1084/jem.182.2.459

|
|
[29]
|
Walunas TL, Lenschow DJ, Bakker CY, et al. (1994) CTLA-4 can function as a negative regulator of T cell activation. Immunity 1: 405-413. doi: 10.1016/1074-7613(94)90071-X

|
|
[30]
|
Onishi Y, Fehervari Z, Yamaguchi T, et al. (2008) Foxp3+ natural regulatory T cells preferentially form aggregates on dendritic cells in vitro and actively inhibit their maturation. P Natl Acad Sci USA 105: 10113-10118. doi: 10.1073/pnas.0711106105

|
|
[31]
|
Belladonna ML, Puccetti P, Orabona C, et al. (2007) Immunosuppression via tryptophan catabolism: the role of kynurenine pathway enzymes. Transplantation 84: S17-20.
|
|
[32]
|
Horwitz DA, Zheng SG, Gray JD (2008) Natural and TGF-beta-induced Foxp3(+)CD4(+) CD25(+) regulatory T cells are not mirror images of each other. Trends Immunol 29: 429-435. doi: 10.1016/j.it.2008.06.005

|
|
[33]
|
Apostolou I, von Boehmer H (2004) In vivo instruction of suppressor commitment in naive T cells. J Exp Med 199: 1401-1408. doi: 10.1084/jem.20040249

|
|
[34]
|
Kretschmer K, Apostolou I, Hawiger D, et al. (2005) Inducing and expanding regulatory T cell populations by foreign antigen. Nat Immunol 6: 1219-1227. doi: 10.1038/ni1265

|
|
[35]
|
Coombes JL, Siddiqui KR, Arancibia-Carcamo CV, et al. (2007) A functionally specialized population of mucosal CD103+ DCs induces Foxp3+ regulatory T cells via a TGF-beta and retinoic acid-dependent mechanism. J Exp Med 204: 1757-1764. doi: 10.1084/jem.20070590

|
|
[36]
|
Selvaraj RK, Geiger TL (2007) A kinetic and dynamic analysis of Foxp3 induced in T cells by TGF-beta. J Iimmunol 178: 7667-7677. doi: 10.4049/jimmunol.178.12.7667

|
|
[37]
|
Faria AM, Weiner HL (2006) Oral tolerance and TGF-beta-producing cells. Inflamm Allergy Drug Targets 5: 179-190. doi: 10.2174/187152806778256034

|
|
[38]
|
Weiner HL (2001) Induction and mechanism of action of transforming growth factor-beta-secreting Th3 regulatory cells. Immunol Rev 182: 207-214. doi: 10.1034/j.1600-065X.2001.1820117.x

|
|
[39]
|
Carrier Y, Yuan J, Kuchroo VK, et al. (2007) Th3 cells in peripheral tolerance. II. TGF-beta-transgenic Th3 cells rescue IL-2-deficient mice from autoimmunity. J Immunol 178: 172-178.
|
|
[40]
|
Walker MR, Carson BD, Nepom GT, et al. (2005) De novo generation of antigen-specific CD4+CD25+ regulatory T cells from human CD4+CD25- cells. P Natl Acad Sci USA 102: 4103-4108. doi: 10.1073/pnas.0407691102

|
|
[41]
|
Wilczynski JR, Radwan M, Kalinka J (2008) The characterization and role of regulatory T cells in immune reactions. Front Biosci 13: 2266-2274. doi: 10.2741/2840

|
|
[42]
|
Mazza G, Sabatos-Peyton CA, Protheroe RE, et al. (2010) Isolation and characterization of human interleukin-10-secreting T cells from peripheral blood. Hum Immunol 71: 225-234. doi: 10.1016/j.humimm.2009.12.003

|
|
[43]
|
Pinchuk IV, Beswick EJ, Saada JI, et al. (2011) Human colonic myofibroblasts promote expansion of CD4+ CD25high Foxp3+ regulatory T cells. Gastroenterology 140: 2019-2030. doi: 10.1053/j.gastro.2011.02.059

|
|
[44]
|
Wingo PA, Ries LA, Parker SL, et al. (1998) Long-term cancer patient survival in the United States. Cancer Epidemiol Biomarkers Prev 7: 271-282.
|
|
[45]
|
Cannon-Albright LA, Skolnick MH, Bishop DT, et al. (1988) Common inheritance of susceptibility to colonic adenomatous polyps and associated colorectal cancers. N Engl J Med 319: 533-537. doi: 10.1056/NEJM198809013190902

|
|
[46]
|
Peltomaki P, de la Chapelle A (1997) Mutations predisposing to hereditary nonpolyposis colorectal cancer. Adv Cancer Res 71: 93-119. doi: 10.1016/S0065-230X(08)60097-4

|
|
[47]
|
Hawkins NJ, Ward RL (2001) Sporadic colorectal cancers with microsatellite instability and their possible origin in hyperplastic polyps and serrated adenomas. J Natl Cancer I 93: 1307-1313. doi: 10.1093/jnci/93.17.1307

|
|
[48]
|
Fishel R, Lescoe MK, Rao MR, et al. (1993) The human mutator gene homolog MSH2 and its association with hereditary nonpolyposis colon cancer. Cell 75: 1027-1038. doi: 10.1016/0092-8674(93)90546-3

|
|
[49]
|
Al-Tassan N, Chmiel NH, Maynard J, et al. (2002) Inherited variants of MYH associated with somatic G:C-->T:A mutations in colorectal tumors. Nat Genet 30: 227-232. doi: 10.1038/ng828

|
|
[50]
|
Grady WM, Carethers JM (2008) Genomic and epigenetic instability in colorectal cancer pathogenesis. Gastroenterology 135: 1079-1099. doi: 10.1053/j.gastro.2008.07.076

|
|
[51]
|
Kinzler KW, Vogelstein B (1996) Lessons from hereditary colorectal cancer. Cell 87: 159-170. doi: 10.1016/S0092-8674(00)81333-1

|
|
[52]
|
MacPhee M, Chepenik KP, Liddell RA, et al. (1995) The secretory phospholipase A2 gene is a candidate for the Mom1 locus, a major modifier of ApcMin-induced intestinal neoplasia. Cell 81: 957-966. doi: 10.1016/0092-8674(95)90015-2

|
|
[53]
|
Shoemaker AR, Gould KA, Luongo C, et al. (1997) Studies of neoplasia in the Min mouse. Biochimica et biophysica acta 1332: F25-48.
|
|
[54]
|
de Miranda NF, Hes FJ, van Wezel T, et al. (2012) Role of the microenvironment in the tumourigenesis of microsatellite unstable and MUTYH-associated polyposis colorectal cancers. Mutagenesis 27: 247-253. doi: 10.1093/mutage/ger077

|
|
[55]
|
Salama P, Phillips M, Grieu F, et al. (2009) Tumor-infiltrating FOXP3+ T regulatory cells show strong prognostic significance in colorectal cancer. J Clin Oncol 27: 186-192. doi: 10.1200/JCO.2008.18.7229

|
|
[56]
|
Ladoire S, Martin F, Ghiringhelli F (2011) Prognostic role of FOXP3+ regulatory T cells infiltrating human carcinomas: the paradox of colorectal cancer. Cancer Immunol Immunother 60: 909-918. doi: 10.1007/s00262-011-1046-y

|
|
[57]
|
Boland CR (2010) Chronic inflammation, colorectal cancer and gene polymorphisms. Digestive diseases 28: 590-595. doi: 10.1159/000320053

|
|
[58]
|
Danese S, Mantovani A Inflammatory bowel disease and intestinal cancer: a paradigm of the Yin-Yang interplay between inflammation and cancer. Oncogene 29: 3313-3323.
|
|
[59]
|
Chaput N, Louafi S, Bardier A, et al. (2009) Identification of CD8+CD25+Foxp3+ suppressive T cells in colorectal cancer tissue. Gut 58: 520-529. doi: 10.1136/gut.2008.158824

|
|
[60]
|
Brudvik KW, Henjum K, Aandahl EM, et al. (2012) Regulatory T-cell-mediated inhibition of antitumor immune responses is associated with clinical outcome in patients with liver metastasis from colorectal cancer. Cancer Immunol Immunother 61: 1045-1053. doi: 10.1007/s00262-011-1174-4

|
|
[61]
|
Zeng JC, Zhang Z, Li TY, et al. (2013) Assessing the role of IL-35 in colorectal cancer progression and prognosis. Int J Clin Exp Pathol 6: 1806-1816.
|
|
[62]
|
Bates GJ, Fox SB, Han C, et al. (2006) Quantification of regulatory T cells enables the identification of high-risk breast cancer patients and those at risk of late relapse. J Clin Oncol 24: 5373-5380. doi: 10.1200/JCO.2006.05.9584

|
|
[63]
|
Fu J, Xu D, Liu Z, et al. (2007) Increased regulatory T cells correlate with CD8 T-cell impairment and poor survival in hepatocellular carcinoma patients. Gastroenterology 132: 2328-2339. doi: 10.1053/j.gastro.2007.03.102

|
|
[64]
|
Betts G, Jones E, Junaid S, et al. (2012) Suppression of tumour-specific CD4(+) T cells by regulatory T cells is associated with progression of human colorectal cancer. Gut 61: 1163-1171. doi: 10.1136/gutjnl-2011-300970

|
|
[65]
|
Bacic D, Uravic M, Bacic R, et al. (2011) Augmentation of regulatory T cells (CD4+CD25+Foxp3+) correlates with tumor stage in patients with colorectal cancer. Coll Antropol 35 Suppl 2: 65-68.
|
|
[66]
|
Mempel TR, Pittet MJ, Khazaie K, et al. (2006) Regulatory T cells reversibly suppress cytotoxic T cell function independent of effector differentiation. Immunity 25: 129-141. doi: 10.1016/j.immuni.2006.04.015

|
|
[67]
|
Slaney CY, Rautela J, Parker BS (2013) The emerging role of immunosurveillance in dictating metastatic spread in breast cancer. Cancer Res 73: 5852-5857. doi: 10.1158/0008-5472.CAN-13-1642

|
|
[68]
|
Koebel CM, Vermi W, Swann JB, et al. (2007) Adaptive immunity maintains occult cancer in an equilibrium state. Nature 450: 903-907. doi: 10.1038/nature06309

|
|
[69]
|
Bonertz A, Weitz J, Pietsch DH, et al. (2009) Antigen-specific Tregs control T cell responses against a limited repertoire of tumor antigens in patients with colorectal carcinoma. J Clini Invest 119: 3311-3321.
|
|
[70]
|
Duchmann R, May E, Heike M, et al. (1999) T cell specificity and cross reactivity towards enterobacteria, bacteroides, bifidobacterium, and antigens from resident intestinal flora in humans. Gut 44: 812-818. doi: 10.1136/gut.44.6.812

|
|
[71]
|
Naito Y, Saito K, Shiiba K, et al. (1998) CD8+ T cells infiltrated within cancer cell nests as a prognostic factor in human colorectal cancer. Cancer Res 58: 3491-3494.
|
|
[72]
|
Golby SJ, Chinyama C, Spencer J (2002) Proliferation of T-cell subsets that contact tumour cells in colorectal cancer. Clin Exp Immunol 127: 85-91. doi: 10.1046/j.1365-2249.2002.01730.x

|
|
[73]
|
Le Gouvello S, Bastuji-Garin S, Aloulou N, et al. (2008) High prevalence of Foxp3 and IL17 in MMR-proficient colorectal carcinomas. Gut 57: 772-779. doi: 10.1136/gut.2007.123794

|
|
[74]
|
Nosho K, Baba Y, Tanaka N, et al. (2010) Tumour-infiltrating T-cell subsets, molecular changes in colorectal cancer, and prognosis: cohort study and literature review. J Pathol 222: 350-366. doi: 10.1002/path.2774

|
|
[75]
|
Gooden MJ, de Bock GH, Leffers N, et al. (2011) The prognostic influence of tumour-infiltrating lymphocytes in cancer: a systematic review with meta-analysis. Brit J Cancer 105: 93-103. doi: 10.1038/bjc.2011.189

|
|
[76]
|
Sinicrope FA, Rego RL, Ansell SM, et al. (2009) Intraepithelial effector (CD3+)/regulatory (FoxP3+) T-cell ratio predicts a clinical outcome of human colon carcinoma. Gastroenterology 137: 1270-1279. doi: 10.1053/j.gastro.2009.06.053

|
|
[77]
|
Katz SC, Bamboat ZM, Maker AV, et al. (2013) Regulatory T cell infiltration predicts outcome following resection of colorectal cancer liver metastases. Ann Surg Oncol 20: 946-955. doi: 10.1245/s10434-012-2668-9

|
|
[78]
|
Blatner NR, Mulcahy MF, Dennis KL, et al. (2012) Expression of RORgammat marks a pathogenic regulatory T cell subset in human colon cancer. Sci Transl Med 4: 164ra159.
|
|
[79]
|
Awasthi A, Kuchroo VK (2009) Th17 cells: from precursors to players in inflammation and infection. Int Immunol 21: 489-498. doi: 10.1093/intimm/dxp021

|
|
[80]
|
Liu Z, Huang Q, Liu G, et al. (2014) Presence of FOXP3(+)Treg cells is correlated with colorectal cancer progression. Int J Clin Exp Med 7: 1781-1785.
|
|
[81]
|
Sojka DK, Huang YH, Fowell DJ (2008) Mechanisms of regulatory T-cell suppression - a diverse arsenal for a moving target. Immunology 124: 13-22. doi: 10.1111/j.1365-2567.2008.02813.x

|
|
[82]
|
Ishimaru N, Nitta T, Arakaki R, et al. (2010) In situ patrolling of regulatory T cells is essential for protecting autoimmune exocrinopathy. PloS One 5: e8588. doi: 10.1371/journal.pone.0008588

|
|
[83]
|
Akeus P, Langenes V, von Mentzer A, et al. (2014) Altered chemokine production and accumulation of regulatory T cells in intestinal adenomas of APC(Min/+) mice. Cancer Immunol Immunother 63: 807-819. doi: 10.1007/s00262-014-1555-6

|
|
[84]
|
Michaud J, Im DS, Hla T (2010) Inhibitory role of sphingosine 1-phosphate receptor 2 in macrophage recruitment during inflammation. J Immunol 184: 1475-1483. doi: 10.4049/jimmunol.0901586

|
|
[85]
|
Ishimaru N, Yamada A, Nitta T, et al. (2012) CCR7 with S1P1 signaling through AP-1 for migration of Foxp3+ regulatory T-cells controls autoimmune exocrinopathy. Am J Pathol 180: 199-208. doi: 10.1016/j.ajpath.2011.09.027

|
|
[86]
|
Goetzl EJ, Liao JJ, Huang MC (2008) Regulation of the roles of sphingosine 1-phosphate and its type 1 G protein-coupled receptor in T cell immunity and autoimmunity. Biochimica et biophysica acta 1781: 503-507. doi: 10.1016/j.bbalip.2008.03.001

|
|
[87]
|
Wang W, Graeler MH, Goetzl EJ (2004) Physiological sphingosine 1-phosphate requirement for optimal activity of mouse CD4+ regulatory T Cells. FASEB J 18: 1043-1045.
|
|
[88]
|
Rosen H, Goetzl EJ (2005) Sphingosine 1-phosphate and its receptors: an autocrine and paracrine network. Nat Rev Immunol 5: 560-570. doi: 10.1038/nri1650

|
|
[89]
|
Pyne S, Pyne NJ (2011) Translational aspects of sphingosine 1-phosphate biology. Trends Mol Med 17: 463-472. doi: 10.1016/j.molmed.2011.03.002

|
|
[90]
|
Kohama T, Olivera A, Edsall L, et al. (1998) Molecular cloning and functional characterization of murine sphingosine kinase. J Biol Chem 273: 23722-23728. doi: 10.1074/jbc.273.37.23722

|
|
[91]
|
Liu H, Chakravarty D, Maceyka M, et al. (2002) Sphingosine kinases: a novel family of lipid kinases. Prog Nucleic Acid Res Mol Biol 71: 493-511. doi: 10.1016/S0079-6603(02)71049-0

|
|
[92]
|
Wang W, Huang MC, Goetzl EJ (2007) Type 1 sphingosine 1-phosphate G protein-coupled receptor (S1P1) mediation of enhanced IL-4 generation by CD4 T cells from S1P1 transgenic mice. J Immunol 178: 4885-4890. doi: 10.4049/jimmunol.178.8.4885

|
|
[93]
|
Sawicka E, Dubois G, Jarai G, et al. (2005) The sphingosine 1-phosphate receptor agonist FTY720 differentially affects the sequestration of CD4+/CD25+ T-regulatory cells and enhances their functional activity. J Immunol 175: 7973-7980. doi: 10.4049/jimmunol.175.12.7973

|
|
[94]
|
Liu G, Yang K, Burns S, et al. (2010) The S1P(1)-mTOR axis directs the reciprocal differentiation of T(H)1 and T(reg) cells. Nat Immunol 11: 1047-1056. doi: 10.1038/ni.1939

|
|
[95]
|
Snider AJ, Orr Gandy KA, Obeid LM (2010) Sphingosine kinase: Role in regulation of bioactive sphingolipid mediators in inflammation. Biochimie 92: 707-715. doi: 10.1016/j.biochi.2010.02.008

|
|
[96]
|
Spiegel S, Milstien S (2011) The outs and the ins of sphingosine-1-phosphate in immunity. Nat Rev Immunol 11: 403-415. doi: 10.1038/nri2974

|
|
[97]
|
Maceyka M, Harikumar KB, Milstien S, et al. (2012) Sphingosine-1-phosphate signaling and its role in disease. Trends Cell Biol 22: 50-60. doi: 10.1016/j.tcb.2011.09.003

|
|
[98]
|
Schwalm S, Pfeilschifter J, Huwiler A (2013) Sphingosine-1-phosphate: a Janus-faced mediator of fibrotic diseases. Biochim Biophys Acta 1831: 239-250. doi: 10.1016/j.bbalip.2012.07.022

|
|
[99]
|
Nguyen AV, Wu YY, Liu Q, et al. (2013) STAT3 in Epithelial Cells Regulates Inflammation and Tumor Progression to Malignant State in Colon. Neoplasia 15: 998-1008. doi: 10.1593/neo.13952

|
|
[100]
|
Liang J, Nagahashi M, Kim EY, et al. (2013) Sphingosine-1-phosphate links persistent STAT3 activation, chronic intestinal inflammation, and development of colitis-associated cancer. Cancer Cell 23: 107-120. doi: 10.1016/j.ccr.2012.11.013

|
|
[101]
|
Lee H, Herrmann A, Deng JH, et al. (2009) Persistently activated Stat3 maintains constitutive NF-kappaB activity in tumors. Cancer Cell 15: 283-293. doi: 10.1016/j.ccr.2009.02.015

|
|
[102]
|
Nagahashi M, Hait NC, Maceyka M, et al. (2014) Sphingosine-1-phosphate in chronic intestinal inflammation and cancer. Adv Biol Regul 54: 112-120. doi: 10.1016/j.jbior.2013.10.001

|
|
[103]
|
Daniel C, Sartory N, Zahn N, et al. (2007) FTY720 ameliorates Th1-mediated colitis in mice by directly affecting the functional activity of CD4+CD25+ regulatory T cells. J Immunol 178: 2458-2468. doi: 10.4049/jimmunol.178.4.2458

|
|
[104]
|
Bos PD, Rudensky AY (2012) Treg cells in cancer: a case of multiple personality disorder. Sci Transl Med 4: 164fs144.
|
|
[105]
|
Liao X, Lochhead P, Nishihara R, et al. Aspirin use, tumor PIK3CA mutation, and colorectal-cancer survival. N Engl J Med 367: 1596-1606.
|
|
[106]
|
Nguyen AV, Wu YY, Lin EY (2014) STAT3 and sphingosine-1-phosphate in inflammation-associated colorectal cancer. World J Gastroenterol 20: 10279-10287. doi: 10.3748/wjg.v20.i30.10279

|
|
[107]
|
Khan S, Burt DJ, Ralph C, et al. (2011) Tremelimumab (anti-CTLA4) mediates immune responses mainly by direct activation of T effector cells rather than by affecting T regulatory cells. Clin Immunol 138: 85-96. doi: 10.1016/j.clim.2010.09.011

|
|
[108]
|
Saha A, Chatterjee SK (2010) Combination of CTL-associated antigen-4 blockade and depletion of CD25 regulatory T cells enhance tumour immunity of dendritic cell-based vaccine in a mouse model of colon cancer. Scand J Immunol 71: 70-82. doi: 10.1111/j.1365-3083.2009.02355.x

|
|
[109]
|
Yano H, Thakur A, Tomaszewski EN, et al. (2014) Ipilimumab augments antitumor activity of bispecific antibody-armed T cells. J Transl Med 12: 191. doi: 10.1186/1479-5876-12-191

|
|
[110]
|
Liu H, Hu B, Xu D, et al. (2003) CD4+CD25+ regulatory T cells cure murine colitis: the role of IL-10, TGF-beta, and CTLA4. J Immunol 171: 5012-5017. doi: 10.4049/jimmunol.171.10.5012

|
|
[111]
|
von Boehmer H, Daniel C (2013) Therapeutic opportunities for manipulating T(Reg) cells in autoimmunity and cancer. Nat Rev Drug Discov 12: 51-63.
|
|
[112]
|
Rech AJ, Mick R, Martin S, et al. (2012) CD25 blockade depletes and selectively reprograms regulatory T cells in concert with immunotherapy in cancer patients. Sci Transl Med 4: 134ra162.
|









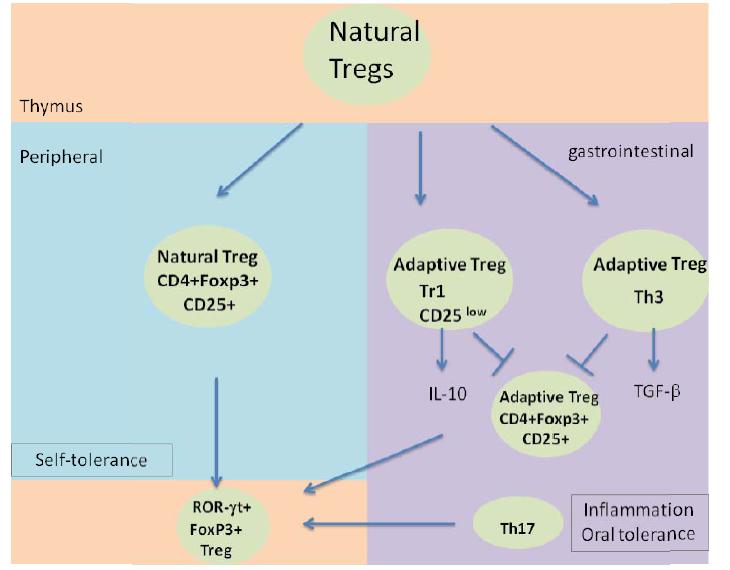
 DownLoad:
DownLoad: