The impact of a <i>Saccharomyces cerevisiae</i> bio-protective strain during cold static clarification on Catarratto wine

Enrico Viola; Vincenzo Naselli; Rosario Prestianni; Antonino Pirrone; Antonella Porrello; Filippo Amato; Riccardo Savastano; Antonella Maggio; Micaela Carusi; Venera Seminerio; Valentina Craparo; Azzurra Vella; Davide Alongi; Luca Settanni; Giuseppe Notarbartolo; Nicola Francesca; Antonio Alfonzo; Enrico Viola; Vincenzo Naselli; Rosario Prestianni; Antonino Pirrone; Antonella Porrello; Filippo Amato; Riccardo Savastano; Antonella Maggio; Micaela Carusi; Venera Seminerio; Valentina Craparo; Azzurra Vella; Davide Alongi; Luca Settanni; Giuseppe Notarbartolo; Nicola Francesca; Antonio Alfonzo

doi:10.3934/microbiol.2025003

AIMS Microbiology

2025, Volume 11, Issue 1: 40-58. doi: 10.3934/microbiol.2025003

Previous Article Next Article

Research article

The impact of a Saccharomyces cerevisiae bio-protective strain during cold static clarification on Catarratto wine

1.
Department of Agricultural, Food and Forest Sciences (SAAF), University of Palermo, Viale delle Scienze, Bldg. 5, 90128, Palermo, Italy
2.
Department of Biological, Chemical and Pharmaceutical Sciences and Technologies (STEBICEF), University of Palermo, Viale delle Scienze, Bldg. 16, 90128, Palermo, Italy
3.
Az. Agr. G. Milazzo - Terre Della Baronia S.r.l., S.S. 123 km. 12+70, 92023, Campobello di Licata, Italy

Received: 17 June 2024 Revised: 13 December 2024 Accepted: 23 December 2024 Published: 09 January 2025

The study aimed to evaluate the impact of the early addition of a Saccharomyces cerevisiae HD A54 strain before pressing during winemaking. This approach aimed to reduce the dissolved oxygen in the grape must, thus preserving the wine characteristics. Two different treatments were settled: Trial A, where sulphite or other substances were not added during pressing; and Trial B, where a S. cerevisiae strain was added at the pressing stage. The chemical parameters were determined through an enzymatic analyzer, which indicated a faster fructose consumption compared to the glucose in Trial A. The plate counts were measured to monitor the microbial groups during vinification. Both treatments showed regular trends with respect to the Saccharomyces population. Trial B exhibited a higher oxygen consumption compared to the control trial, especially in the early stages of winemaking. This was determined through a dissolved O₂ analysis. Furthermore, Trial B had lower absorbance values at the post-pressing and pre-clarification stages. Both the dissolved oxygen and the absorbance analyses underscored the positive impact of the S. cerevisiae HD A54 strain in protecting against oxidative processes in the grape musts at the pre-fermentative stage. The analysis of volatile organic compounds detected 30 different compounds, including alcohols and esters. Trial B had higher alcohol levels, particularly hydroxyethylbenzene (135.31 mg/L vs. 44.23 mg/L in Trial A). Trial A had almost a four times higher ethyl acetate concentration than Trial B, which is an indicator of oxidation. Interestingly, Trial B showed higher concentrations of 3-methyl-butyl acetate and 2-phenylethyl acetate, which are molecules that correspond to fruity (banana) and floreal (rose) aromas, respectively. Regarding the sensory analysis, Trial B received better scores for the fruity and floral attributes, as well as the overall wine quality.

Keywords:

Citation: Enrico Viola, Vincenzo Naselli, Rosario Prestianni, Antonino Pirrone, Antonella Porrello, Filippo Amato, Riccardo Savastano, Antonella Maggio, Micaela Carusi, Venera Seminerio, Valentina Craparo, Azzurra Vella, Davide Alongi, Luca Settanni, Giuseppe Notarbartolo, Nicola Francesca, Antonio Alfonzo. The impact of a Saccharomyces cerevisiae bio-protective strain during cold static clarification on Catarratto wine[J]. AIMS Microbiology, 2025, 11(1): 40-58. doi: 10.3934/microbiol.2025003

Related Papers:

[1]	Yizheng Li, Dingguo Wang . Lie algebras with differential operators of any weights. Electronic Research Archive, 2023, 31(3): 1195-1211. doi: 10.3934/era.2023061
[2]	Qiang Li, Lili Ma . 1-parameter formal deformations and abelian extensions of Lie color triple systems. Electronic Research Archive, 2022, 30(7): 2524-2539. doi: 10.3934/era.2022129
[3]	Wen Teng, Xiansheng Dai . Nonabelian embedding tensors on 3-Lie algebras and 3-Leibniz-Lie algebras. Electronic Research Archive, 2025, 33(3): 1367-1383. doi: 10.3934/era.2025063
[4]	Xueru Wu, Yao Ma, Liangyun Chen . Abelian extensions of Lie triple systems with derivations. Electronic Research Archive, 2022, 30(3): 1087-1103. doi: 10.3934/era.2022058
[5]	Baoling Guan, Xinxin Tian, Lijun Tian . Induced 3-Hom-Lie superalgebras. Electronic Research Archive, 2023, 31(8): 4637-4651. doi: 10.3934/era.2023237
[6]	Bing Sun, Liangyun Chen, Yan Cao . On the universal $ \alpha $-central extensions of the semi-direct product of Hom-preLie algebras. Electronic Research Archive, 2021, 29(4): 2619-2636. doi: 10.3934/era.2021004
[7]	Kailash C. Misra, Sutida Patlertsin, Suchada Pongprasert, Thitarie Rungratgasame . On derivations of Leibniz algebras. Electronic Research Archive, 2024, 32(7): 4715-4722. doi: 10.3934/era.2024214
[8]	Margarida Camarinha . A natural 4th-order generalization of the geodesic problem. Electronic Research Archive, 2024, 32(5): 3396-3412. doi: 10.3934/era.2024157
[9]	Hongliang Chang, Yin Chen, Runxuan Zhang . A generalization on derivations of Lie algebras. Electronic Research Archive, 2021, 29(3): 2457-2473. doi: 10.3934/era.2020124
[10]	Ying Hou, Liangyun Chen, Keli Zheng . Super-bimodules and $ \mathcal{O} $-operators of Bihom-Jordan superalgebras. Electronic Research Archive, 2024, 32(10): 5717-5737. doi: 10.3934/era.2024264

Abstract

1. Introduction

The notion of a pre-Lie algebra has been introduced independently by M. Gerstenhaber in deformation theory of rings and algebras ^[1] and by Vinberg, under the name of left-symmetric algebra, in his theory of homogeneous convex cones ^[2]. Its defining identity is weaker than associativity and lead also to a Lie algebra using commutators. This algebraic structure describes some properties of cochain spaces in Hochschild cohomology of an associative algebra, rooted trees and vector fields on affine spaces. Moreover, it is playing an increasing role in algebra, geometry and physics due to their applications in nonassociative algebras, combinatorics, numerical analysis and quantum field theory, see ^[3,4,5,6].

Hom-type algebras appeared naturally when studying $q$ -deformations of some algebras of vector fields, like Witt and Virasoro algebras. It turns out that the Jacobi identity is no longer satisfied, these new structures involving a bracket and a linear map satisfy a twisted version of the Jacobi identity and define a so called Hom-Lie algebras which form a wider class, see ^[7,8]. Hom-pre-Lie algebras were introduced in ^[9] as a class of Hom-Lie admissible algebras, and play important roles in the study of Hom-Lie bialgebras and Hom-Lie 2-algebras ^[10,11,12]. Recently Hom-pre-Lie algebras were studied from several aspects. Cohomologies of Hom-pre-Lie algebras were studied in ^[13]; The geometrization of Hom-pre-Lie algebras was studied in ^[14]; Universal $\alpha$ -central extensions of Hom-pre-Lie algebras were studied in ^[15]; Hom-pre-Lie bialgebras were studied in ^[16,17]. Furthermore, connections between (Hom-)pre-Lie algebras and various algebraic structures have been established and discussed; like with Rota-Baxter operators, $\mathcal{O}$ -operators, (Hom-)dendriform algebras, (Hom-)associative algebras and Yang-Baxter equation, see ^{[5,18,19,20,21,22]}.

The cohomology of pre-Lie algebras was defined in ^[23] and generalized in a straightforward way to Hom-pre-Lie algebras in ^[13]. Note that the cohomology given there has some restrictions: the second cohomology group can only control deformations of the multiplication, and it can not be applied to study simultaneous deformations of both the multiplication and the homomorphism in a Hom-pre-Lie algebra. The main purpose of this paper is to define a new type of cohomology of Hom-pre-Lie algebras which is richer than the previous one. The obtained cohomology is called the full cohomology and allows to control simultaneous deformations of both the multiplication and the homomorphism in a Hom-pre-Lie algebra. This type of cohomology was established for Hom-associative algebras and Hom-Lie algebras in ^[24,25], and called respectively $\alpha$ -type Hochschild cohomology and $\alpha$ -type Chevalley-Eilenberg cohomology. See ^[26,27,28] for more studies on deformations and extensions of Hom-Lie algebras.

The paper is organized as follows. In Section 2, first we recall some basics of Hom-Lie algebras, Hom-pre-Lie algebras and representations, and then provide our main result defining the full cohomology of a Hom-pre-Lie algebra with coefficients in a given representation. In Section 3, we study one parameter formal deformations of a Hom-pre-Lie algebra, where both the defining multiplication and homomorphism are deformed, using formal power series. We show that the full cohomology of Hom-pre-Lie algebras controls these simultaneous deformations. Moreover, a relationship between deformations of a Hom-pre-Lie algebra and deformations of its sub-adjacent Lie algebra is established. Section 4 deals with abelian extensions of Hom-pre-Lie algebras. We show that the full cohomology fits perfectly and its second cohomology group classifies abelian extensions of a Hom-pre-Lie algebra by a given representation. The proof of the key Lemma to show that the four operators define a cochain complex is lengthy and it is given in the Appendix.

2. The full cohomology of Hom-pre-Lie algebras

In this section, first we recall some basic facts about Hom-Lie algebras and Hom-pre-Lie algebras. Then we introduce the full cohomology of Hom-pre-Lie algebras, which will be used to classify infinitesimal deformations and abelian extensions of Hom-pre-Lie algebras.

Definition 2.1. (see ^[7]) A Hom-Lie algebra is a triple $(\mathfrak g, [\cdot, \cdot]_{ \mathfrak g}, \phi_{ \mathfrak g})$ consisting of a vector space $\mathfrak g$ , a skew-symmetric bilinear map $[\cdot, \cdot]_{ \mathfrak g}:\wedge^2 \mathfrak g\longrightarrow \mathfrak g$ and a homomorphism $\phi_{ \mathfrak g}: \mathfrak g\longrightarrow \mathfrak g$ , satisfying $\phi_{ \mathfrak g}[x, y] = [\phi_{ \mathfrak g}(x), \phi_{ \mathfrak g}(y)]$ and

$\begin{equation} [\phi_{ \mathfrak g}(x), [y, z]_{ \mathfrak g}]_{ \mathfrak g}+[\phi_{ \mathfrak g}(y), [z, x]_{ \mathfrak g}]_{ \mathfrak g}+[\phi_{ \mathfrak g}(z), [x, y]_{ \mathfrak g}]_{ \mathfrak g} = 0, \quad \forall\; x, y, z\in \mathfrak g. \end{equation}$

(2.1)

A Hom-Lie algebra $(\mathfrak g, [\cdot, \cdot]_{ \mathfrak g}, \phi_{ \mathfrak g})$ is said to be regular if $\phi_{ \mathfrak g}$ is invertible.

Definition 2.2. (see ^[29]) A representation of a Hom-Lie algebra $(\mathfrak g, [\cdot, \cdot]_{ \mathfrak g}, \phi_{ \mathfrak g})$ on a vector space $V$ with respect to $\beta\in \mathfrak {gl}(V)$ is a linear map $\rho: \mathfrak g\longrightarrow \mathfrak {gl}(V)$ , such that for all $x, y\in \mathfrak g$ , the following equalities are satisfied:

$\begin{eqnarray} \rho(\phi_{ \mathfrak g}(x))\circ \beta& = &\beta\circ \rho(x), \end{eqnarray}$

(2.2)

$\begin{eqnarray} \rho([x, y]_{ \mathfrak g})\circ \beta& = &\rho(\phi_{ \mathfrak g}(x))\circ\rho(y)-\rho(\phi_{ \mathfrak g}(y))\circ\rho(x). \end{eqnarray}$

(2.3)

We denote a representation of a Hom-Lie algebra $(\mathfrak g, [\cdot, \cdot]_{ \mathfrak g}, \phi_{ \mathfrak g})$ by a triple $(V, \beta, \rho)$ .

Definition 2.3. (see ^[9]) A Hom-pre-Lie algebra $(A, \cdot, \alpha)$ is a vector space $A$ equipped with a bilinear product $\cdot:A\otimes A\longrightarrow A$ , and $\alpha\in \mathfrak {gl}(A)$ , such that for all $x, y, z\in A$ , $\alpha(x \cdot y) = \alpha(x)\cdot \alpha(y)$ and the following equality is satisfied:

$\begin{eqnarray} (x\cdot y)\cdot \alpha(z)-\alpha(x)\cdot (y\cdot z) = (y\cdot x)\cdot \alpha(z)-\alpha(y)\cdot (x\cdot z). \end{eqnarray}$

(2.4)

A Hom-pre-Lie algebra $(A, \cdot, \alpha)$ is said to be regular if $\alpha$ is invertible.

Let $(A, \cdot, \alpha)$ be a Hom-pre-Lie algebra. The commutator $[x, y]_C = x\cdot y-y\cdot x$ defines a Hom-Lie algebra $(A, [\cdot, \cdot]_C, \alpha)$ , which is denoted by $A^C$ and called the sub-adjacent Hom-Lie algebra of $(A, \cdot, \alpha)$ .

Definition 2.4. (see ^[13]) A morphism from a Hom-pre-Lie algebra $(A, \cdot, \alpha)$ to a Hom-pre-Lie algebra $(A', \cdot', \alpha')$ is a linear map $f:A\longrightarrow A'$ such that for all $x, y\in A$ , the following equalities are satisfied:

$\begin{eqnarray} f(x\cdot y)& = &f(x)\cdot' f(y), \quad \forall x, y\in A, \end{eqnarray}$

(2.5)

$\begin{eqnarray} f\circ \alpha& = &\alpha'\circ f. \end{eqnarray}$

(2.6)

Definition 2.5. (see ^[17]) A representation of a Hom-pre-Lie algebra $(A, \cdot, \alpha)$ on a vector space $V$ with respect to $\beta\in \mathfrak {gl}(V)$ consists of a pair $(\rho, \mu)$ , where $\rho:A\longrightarrow \mathfrak {gl}(V)$ is a representation of the sub-adjacent Hom-Lie algebra $A^C$ on $V$ with respect to $\beta\in \mathfrak {gl}(V)$ , and $\mu:A\longrightarrow \mathfrak {gl}(V)$ is a linear map, satisfying, for all $x, y\in A$ :

$\begin{eqnarray} \beta\circ \mu(x)& = &\mu(\alpha(x))\circ \beta, \end{eqnarray}$

(2.7)

$\begin{eqnarray} \mu(\alpha(y))\circ\mu(x)-\mu(x\cdot y)\circ \beta& = &\mu(\alpha(y))\circ\rho(x)-\rho(\alpha(x))\circ\mu(y). \end{eqnarray}$

(2.8)

We denote a representation of a Hom-pre-Lie algebra $(A, \cdot, \alpha)$ by a quadruple $(V, \beta, \rho, \mu)$ . Furthermore, Let $L, R:A\longrightarrow \mathfrak {gl}(A)$ be linear maps, where $L_xy = x\cdot y, R_xy = y\cdot x$ . Then $(A, \alpha, L, R)$ is also a representation, which we call the regular representation.

Let $(A, \cdot, \alpha)$ be a Hom-pre-Lie algebra. In the sequel, we will also denote the Hom-pre-Lie algebra multiplication $\cdot$ by $\omega$ .

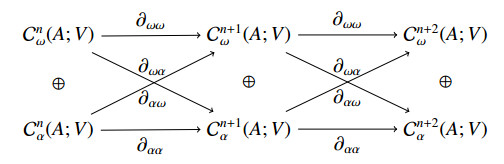
Let $(V, \beta, \rho, \mu)$ be a representation of a Hom-pre-Lie algebra $(A, \omega, \alpha)$ . We define ${\mathcal{C}}^n_\omega(A; V)$ and ${\mathcal{C}}^n_\alpha(A; V)$ respectively by

${\mathcal{C}}^n_\omega(A;V) = \mathrm{Hom}(\wedge^{n-1} A\otimes A, V), \quad {\mathcal{C}}^n_\alpha(A;V) = \mathrm{Hom}(\wedge^{n-2} A\otimes A, V), \quad \forall n\geq 2.$

Define the set of cochains $\tilde{ {\mathcal{C}}}^n(A; V)$ by

$\begin{equation} \left\{\begin{array}{ll} & \tilde{ {\mathcal{C}}}^n(A;V) = {\mathcal{C}}^n_\omega(A;V)\oplus {\mathcal{C}}^n_\alpha(A;V), \quad \forall n\geq 2, \\ & \tilde{ {\mathcal{C}}}^1(A;V) = \mathrm{Hom}(A, V). \end{array}\right. \end{equation}$

(2.9)

For all $(\varphi, \psi) \in \tilde{ {\mathcal{C}}}^n(A; V), x_1, \dots, x_{n+1}\in A$ , we define $\partial_{\omega\omega}: {\mathcal{C}}^n_\omega(A; V)\longrightarrow {\mathcal{C}}^{n+1}_\omega(A; V)$ by

$\begin{eqnarray*} &&(\partial_{\omega\omega}\varphi)(x_1, \dots, x_{n+1})\\ && = \sum\limits_{i = 1}^n(-1)^{i+1}\rho(\alpha^{n-1}(x_i))\varphi(x_1, \dots, \widehat{x_i}, \dots, x_{n+1})\\ &&+\sum\limits_{i = 1}^n(-1)^{i+1}\mu(\alpha^{n-1}(x_{n+1}))\varphi(x_1, \dots, \widehat{x_i}, \dots, x_n, x_i)\\ &&-\sum\limits_{i = 1}^n(-1)^{i+1} \varphi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}\dots, \alpha(x_n), x_i\cdot x_{n+1})\\ &&+\sum\limits_{1\leq i < j\leq n}(-1)^{i+j} \varphi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1})), \end{eqnarray*}$

where the hat corresponds to deleting the element, define $\partial_{\alpha\alpha}: {\mathcal{C}}^n_\alpha(A; V)\longrightarrow {\mathcal{C}}^{n+1}_\alpha(A; V)$ by

$\begin{eqnarray*} &&(\partial_{\alpha\alpha} \psi)(x_1, \dots, x_n)\\ && = \sum\limits_{i = 1}^{n-1}(-1)^i\rho(\alpha^{n-1}(x_i))\psi(x_1, \dots, \widehat{x_i}, \dots, x_n)\\ &&+\sum\limits_{i = 1}^{n-1}(-1)^i\mu(\alpha^{n-1}(x_n))\psi(x_1, \dots, \widehat{x_i}, \dots, x_{n-1}, x_i)\\ &&-\sum\limits_{i = 1}^{n-1}(-1)^i \psi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \alpha(x_{n-1}), x_i\cdot x_n)\\ &&+\sum\limits_{1\leq i < j\leq n-1}(-1)^{i+j-1} \psi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_n)), \end{eqnarray*}$

define $\partial_{\omega\alpha}: {\mathcal{C}}^n_\omega(A; V)\longrightarrow {\mathcal{C}}^{n+1}_\alpha(A; V)$ by

$\begin{eqnarray*} (\partial_{\omega\alpha} \varphi)(x_1, \dots, x_n) = \beta\varphi(x_1, \dots, x_n)-\varphi(\alpha(x_1), \dots, \alpha(x_n)), \end{eqnarray*}$

and define $\partial_{\alpha\omega}: {\mathcal{C}}^n_\alpha(A; V)\longrightarrow {\mathcal{C}}^{n+1}_\omega(A; V)$ by

$\begin{eqnarray*} &&(\partial_{\alpha\omega} \psi)(x_1, \dots, x_{n+1})\\ && = \sum\limits_{1\leq i < j\leq n}(-1)^{i+j}\rho([\alpha^{n-2}(x_i), \alpha^{n-2}(x_j)]_C) \psi(x_1, \dots, \hat{x_i}, \dots, \hat{x_j}, \dots, x_{n+1})\\ &&+\sum\limits_{1\leq i < j\leq n}(-1)^{i+j}\mu(\alpha^{n-2}(x_i)\cdot\alpha^{n-2}(x_{n+1}))\psi(x_1, \dots, \hat{x_i}, \dots, \hat{x_j}, \dots, x_n, x_j)\\ &&-\sum\limits_{1\leq i < j\leq n}(-1)^{i+j}\mu(\alpha^{n-2}(x_j)\cdot\alpha^{n-2}(x_{n+1}))\psi(x_1, \dots, \hat{x_i}, \dots, \hat{x_j}, \dots, x_n, x_i). \end{eqnarray*}$

Define the operator $\tilde{\partial}:\tilde{ {\mathcal{C}}}^n(A; V)\longrightarrow \tilde{ {\mathcal{C}}}^{n+1}(A; V)$ by

$\begin{eqnarray} \tilde{\partial}(\varphi, \psi)& = &(\partial_{\omega\omega}\varphi+\partial_{\alpha\omega}\psi, \partial_{\omega\alpha}\varphi+\partial_{\alpha\alpha}\psi), \quad \forall \varphi \in {\mathcal{C}}^n_\omega(A;V), \psi \in {\mathcal{C}}^n_\alpha(A;V), n\geq 2, \end{eqnarray}$

(2.10)

$\begin{eqnarray} \tilde{\partial}(\varphi)& = &(\partial_{\omega\omega}\varphi, \partial_{\omega\alpha}\varphi), \quad \forall \varphi \in \mathrm{Hom}(A, V). \end{eqnarray}$

(2.11)

The following diagram will explain the above operators:

Lemma 2.6. With the above notations, we have

$\begin{eqnarray} \partial_{\omega\omega}\circ \partial_{\omega\omega}+\partial_{\alpha\omega}\circ \partial_{\omega\alpha}& = &0, \end{eqnarray}$

(2.12)

$\begin{eqnarray} \partial_{\omega\omega}\circ \partial_{\alpha\omega}+\partial_{\alpha\omega}\circ \partial_{\alpha\alpha}& = &0, \end{eqnarray}$

(2.13)

$\begin{eqnarray} \partial_{\omega\alpha}\circ \partial_{\omega\omega}+\partial_{\alpha\alpha}\circ \partial_{\omega\alpha}& = &0, \end{eqnarray}$

(2.14)

$\begin{eqnarray} \partial_{\omega\alpha}\circ \partial_{\alpha\omega}+\partial_{\alpha\alpha}\circ \partial_{\alpha\alpha}& = &0. \end{eqnarray}$

(2.15)

Proof. The proof is given in the Appendix.

Theorem 2.7. The operator $\tilde{\partial}:\tilde{C}^n(A; V)\longrightarrow \tilde{C}^{n+1}(A; V)$ defined as above satisfies $\tilde{\partial}\circ\tilde{\partial} = 0$ .

Proof. When $n\geq 2$ , for all $(\varphi, \psi)\in \tilde{ {\mathcal{C}}}^n(A; V)$ , by (2.10) and Lemma 2.6, we have

$\begin{eqnarray*} \tilde{\partial}\circ\tilde{\partial}(\varphi, \psi) & = &\tilde{\partial}(\partial_{\omega\omega}\varphi+\partial_{\alpha\omega}\psi, \partial_{\omega\alpha}\varphi+\partial_{\alpha\alpha}\psi)\\ & = &(\partial_{\omega\omega}\partial_{\omega\omega}\varphi+\partial_{\omega\omega}\partial_{\alpha\omega}\psi+\partial_{\alpha\omega}\partial_{\omega\alpha}\varphi+\partial_{\alpha\omega}\partial_{\alpha\alpha}\psi, \\ &&\partial_{\omega\alpha}\partial_{\omega\omega}\varphi+\partial_{\omega\alpha}\partial_{\alpha\omega}\psi+\partial_{\alpha\alpha}\partial_{\omega\alpha}\varphi+\partial_{\alpha\alpha}\partial_{\alpha\alpha}\psi)\\ & = &0. \end{eqnarray*}$

When $n = 1$ , for all $\varphi \in \mathrm{Hom}(A, V)$ , by (2.11) and Lemma 2.6, we have

$\begin{eqnarray*} \tilde{\partial}\circ\tilde{\partial}(\varphi) & = &\tilde{\partial}(\partial_{\omega\omega}\varphi, \partial_{\omega\alpha}\varphi)\\ & = &(\partial_{\omega\omega}\partial_{\omega\omega}\varphi+\partial_{\alpha\omega}\partial_{\omega\alpha}\varphi, \partial_{\omega\alpha}\partial_{\omega\omega}\varphi+\partial_{\alpha\alpha}\partial_{\omega\alpha}\varphi)\\ & = &0. \end{eqnarray*}$

This finishes the proof.

We denote the set of closed $n$ -cochains by $\tilde{Z}^n(A; V)$ and the set of exact $n$ -cochains by $\tilde{B}^n(A; V)$ . We denote by $\tilde{H}^n(A; V) = \tilde{Z}^n(A; V)/\tilde{B}^n(A; V)$ the corresponding cohomology groups.

Definition 2.8. Let $(V, \beta, \rho, \mu)$ be a representation of a Hom-pre-Lie algebra $(A, \cdot, \alpha)$ . The cohomology of the cochain complex $(\oplus_{n = 1}^\infty\tilde{C}^n(A; V), \partial)$ is called the full cohomology of the Hom-pre-Lie algebra $(A, \cdot, \alpha)$ with coefficients in the representation $(V, \beta, \rho, \mu)$ .

We use $\tilde{\partial}_{ \mathrm{reg}}$ to denote the coboundary operator of the Hom-pre-Lie algebra $(A, \cdot, \alpha)$ with coefficients in the regular representation. The corresponding cohomology group will be denoted by $\tilde{H}^n(A; A)$ .

Remark 2.9. Compared with the cohomology theory of Hom-pre-Lie algebras studied in ^[13], the above full cohomology contains more informations. In the next section, we will see that the second cohomology group can control simultaneous deformations of the multiplication and the homomorphism in a Hom-pre-Lie algebra.

3. Formal deformations of Hom-pre-Lie algebras

In this section, we study formal deformations of Hom-pre-Lie algebras using the cohomology theory established in the last section. We show that the infinitesimal of a formal deformation is a 2-cocycle and depends only on its cohomology class. Moreover, if the cohomology group $\tilde{H}^2(A; A)$ is trivial, then the Hom-pre-Lie algebra is rigid.

Definition 3.1. Let $(A, \omega, \alpha)$ be a Hom-pre-Lie algebra, $\omega_t = \omega+\sum_{i = 1}^{+\infty} \omega_it^i:A[[t]]\otimes A[[t]]\longrightarrow A[[t]]$ be a $\mathbb K[[t]]$ -bilinear map and $\alpha_t = \alpha+\sum_{i = 1}^{+\infty} \alpha_it^i:A[[t]]\longrightarrow A[[t]]$ be a $\mathbb K[[t]]$ -linear map, where $\omega_i:A\otimes A\longrightarrow A$ and $\alpha_i:A\longrightarrow A$ are linear maps. If $(A[[t]], \omega_t, \alpha_t)$ is still a Hom-pre-Lie algebra, we say that $\{\omega_i, \alpha_i\}_{i\geq1}$ generates a $1$ -parameter formal deformation of a Hom-pre-Lie algebra $(A, \omega, \alpha)$ .

If $\{\omega_i, \alpha_i\}_{i\geq1}$ generates a $1$ -parameter formal deformation of a Hom-pre-Lie algebra $(A, \omega, \alpha)$ , for all $x, y, z\in A$ and $n = 1, 2, \dots$ , we then have

$\begin{equation} \sum\limits_{i+j+k = n\atop i, j, k\geq 0}\omega_i(\omega_j(x, y), \alpha_k(z))-\omega_i(\alpha_j(x), \omega_k(y, z))-\omega_i(\omega_j(y, x), \alpha_k(z))+\omega_i(\alpha_j(y), \omega_k(x, z)) = 0. \end{equation}$

(3.1)

Moreover, we have

$\begin{eqnarray} &&\sum\limits_{i+j+k = n\atop 0 < i, j, k\leq n-1 }\omega_i(\omega_j(x, y), \alpha_k(z))-\omega_i(\alpha_j(x), \omega_k(y, z))-\omega_i(\omega_j(y, x), \alpha_k(z))+\omega_i(\alpha_j(y), \omega_k(x, z))\\ & = &(\partial_{\omega\omega}\omega_n+\partial_{\alpha\omega}\alpha_n)(x, y, z). \end{eqnarray}$

(3.2)

For all $x, y\in A$ and $n = 1, 2, \dots$ , we have

$\begin{equation} \sum\limits_{i+j+k = n\atop i, j, k\geq 0}\omega_i(\alpha_j(x), \alpha_k(y))-\sum\limits_{i+j = n\atop i, j\geq 0}\alpha_i(\omega_j(x, y)) = 0. \end{equation}$

(3.3)

Moreover, we have

$\begin{equation} \sum\limits_{i+j+k = n\atop 0 < i, j, k\leq n-1}\omega_i(\alpha_j(x), \alpha_k(y))-\sum\limits_{i+j = n\atop i, j > 0}\alpha_i(\omega_j(x, y)) = (\partial_{\omega\alpha}\omega_n+\partial_{\alpha\alpha}\alpha_n)(x, y). \end{equation}$

(3.4)

Proposition 3.2. Let $(\omega_t = \omega+\sum_{i = 1}^{+\infty} \omega_it^i, \alpha_t = \alpha+\sum_{i = 1}^{+\infty} \alpha_it^i)$ be a $1$ -parameter formal deformation of a Hom-pre-Lie algebra $(A, \omega, \alpha)$ . Then $(\omega_1, \alpha_1)$ is a $2$ -cocycle of the Hom-pre-Lie algebra $(A, \omega, \alpha)$ with coefficients in the regular representation.

Proof. When $n = 1$ , by (3.1), we have

$\begin{eqnarray*} \nonumber 0& = &(x\cdot y)\cdot\alpha_1(z)+\omega_1(x, y)\cdot\alpha(z)+\omega_1(x\cdot y, \alpha(z))-\alpha(x)\cdot\omega_1(y, z)\\ \nonumber &&-\alpha_1(x)\cdot (y\cdot z)-\omega_1(\alpha(x), y\cdot z)-(y\cdot x)\cdot\alpha_1(z)-\omega_1(y, x)\cdot\alpha(z)\\ \nonumber &&-\omega_1(y\cdot x, \alpha(z))+\alpha(y)\cdot\omega_1(x, z)+\alpha_1(y)\cdot(x\cdot z)+\omega_1(\alpha(y), x\cdot z)\\ & = &-(\partial_{\omega\omega}\omega_1+\partial_{\alpha\omega}\alpha_1)(x, y, z), \end{eqnarray*}$

and by (3.3), we have

$\begin{eqnarray*} \nonumber 0& = &\omega_1(\alpha(x), \alpha(y))+\alpha_1(x)\cdot \alpha(y)+\alpha(x)\cdot \alpha_1(y)-\alpha(\omega_1(x, y))-\alpha_1(x\cdot y)\\ & = &-(\partial_{\omega\alpha}\omega_1+\partial_{\alpha\alpha}\alpha_1)(x, y), \end{eqnarray*}$

which implies that $\tilde{\partial}_{ \mathrm{reg}}(\omega_1, \alpha_1) = 0$ . Thus, $(\omega_1, \alpha_1)$ is a $2$ -cocycle of the Hom-pre-Lie algebra $(A, \omega, \alpha)$ .

Definition 3.3. The $2$ -cocycle $(\omega_1, \alpha_1)$ is called the infinitesimal of the $1$ -parameter formal deformation $(A[[t]], \omega_t, \alpha_t)$ of the Hom-pre-Lie algebra $(A, \omega, \alpha)$ .

Definition 3.4. Let $(\omega_t' = \omega+\sum_{i = 1}^{+\infty} \omega_i't^i, \alpha_t' = \alpha+\sum_{i = 1}^{+\infty} \alpha_i't^i)$ and $(\omega_t = \omega+\sum_{i = 1}^{+\infty} \omega_it^i, \alpha_t = \alpha+\sum_{i = 1}^{+\infty} \alpha_it^i)$ be two $1$ -parameter formal deformations of a Hom-pre-Lie algebra $(A, \omega, \alpha)$ . A formal isomorphism from $(A[[t]], \omega_t', \alpha_t')$ to $(A[[t]], \omega_t, \alpha_t)$ is a power series $\Phi_t = \sum_{i = 0}^{+\infty} \varphi_it^i$ , where $\varphi_i:A\longrightarrow A$ are linear maps with $\varphi_0 = { {\rm{Id}}}$ , such that

$\begin{eqnarray} \Phi_t\circ \omega_t'& = &\omega_t \circ(\Phi_t\times \Phi_t), \end{eqnarray}$

(3.5)

$\begin{eqnarray} \alpha_t\circ \Phi_t& = &\Phi_t\circ \alpha_t'. \end{eqnarray}$

(3.6)

Two $1$ -parameter formal deformations $(A[[t]], \omega_t', \alpha_t')$ and $(A[[t]], \omega_t, \alpha_t)$ are said to be equivalent if there exists a formal isomorphism $\Phi_t = \sum_{i = 0}^{+\infty} \varphi_it^i$ from $(A[[t]], \omega_t', \alpha_t')$ to $(A[[t]], \omega_t, \alpha_t)$ .

Theorem 3.5. Let $(A, \omega, \alpha)$ be a Hom-pre-Lie algebra.If two $1$ -parameter formal deformations $(\omega_t' = \omega+\sum_{i = 1}^{+\infty} \omega_i't^i, \alpha_t' = \alpha+\sum_{i = 1}^{+\infty} \alpha_i't^i)$ and $(\omega_t = \omega+\sum_{i = 1}^{+\infty} \omega_it^i, \alpha_t = \alpha+\sum_{i = 1}^{+\infty} \alpha_it^i)$ are equivalent, then there infinitesimals $(\omega_1', \alpha_1')$ and $(\omega_1, \alpha_1)$ are in the same cohomology class of $\tilde{H}^2(A; A)$ .

Proof. Let $(\omega_t', \alpha_t')$ and $(\omega_t, \alpha_t)$ be two $1$ -parameter formal deformations. By Proposition 3.2, we have $(\omega_1', \alpha_1')$ and $(\omega_1, \alpha_1) \in \tilde{Z}^2(A; A)$ . Let $\Phi_t = \sum_{i = 0}^{+\infty} \varphi_it^i$ be the formal isomorphism. Then for all $x, y\in A$ , we have

$\begin{eqnarray*} \omega_t'(x, y) & = &\Phi_t^{-1}\circ\omega_t(\Phi_t(x), \Phi_t(y))\\ & = &({ {\rm{Id}}}-\varphi_1 t+\dots)\omega_t\big(x+\varphi_1(x)t+\dots, y+\varphi_1(y)t+\dots\big)\\ & = &({ {\rm{Id}}}-\varphi_1 t+\dots)\Big(x\cdot y+\big(x\cdot\varphi_1(y)+\varphi_1(x)\cdot y+\omega_1(x, y)\big)t+\dots\Big)\\ & = &x\cdot y+\Big(x\cdot\varphi_1(y)+\varphi_1(x)\cdot y+\omega_1(x, y)-\varphi_1(x\cdot y)\Big)t+\dots. \end{eqnarray*}$

Thus, we have

$\begin{eqnarray*} \omega_1'(x, y)-\omega_1(x, y)& = &x\cdot\varphi_1(y)+\varphi_1(x)\cdot y-\varphi_1(x\cdot y)\\ & = &\partial_{\omega\omega}\varphi_1(x, y), \end{eqnarray*}$

which implies that $\omega_1'-\omega_1 = \partial_{\omega\omega}\varphi_1.$

For all $x\in A$ , we have

$\begin{eqnarray*} \alpha_t'(x) & = &\Phi_t^{-1}\circ\alpha_t(\Phi_t(x))\\ & = &({ {\rm{Id}}}-\varphi_1 t+\dots)\alpha_t\big(x+\varphi_1(x)t+\dots\big)\\ & = &({ {\rm{Id}}}-\varphi_1 t+\dots)\Big(\alpha(x)+\big(\alpha(\varphi_1(x))+\alpha_1(x))t+\dots\Big)\\ & = &\alpha(x)+\Big(\alpha(\varphi_1(x))+\alpha_1(x)-\varphi_1(\alpha(x))\Big)t+\dots. \end{eqnarray*}$

Thus, we have

$\begin{equation} \nonumber\alpha_1'(x)-\alpha_1(x) = \alpha(\varphi_1(x))-\varphi_1(\alpha(x)) = \partial_{\omega\alpha}\varphi_1(x), \end{equation}$

which implies that $\alpha_1'-\alpha_1 = \partial_{\omega\alpha}\varphi_1.$

Thus, we have $(\omega_1'-\omega_1, \alpha_1'-\alpha_1)\in \tilde{B}^2(A; A)$ . This finishes the proof.

Definition 3.6. A $1$ -parameter formal deformation $(A[[t]], \omega_t, \alpha_t)$ of a Hom-pre-Lie algebra $(A, \omega, \alpha)$ is said to be trivial if it is equivalent to $(A, \omega, \alpha)$ , i.e. there exists $\Phi_t = \sum_{i = 0}^{+\infty} \varphi_it^i$ , where $\varphi_i:A\longrightarrow A$ are linear maps with $\varphi_0 = { {\rm{Id}}}$ , such that

$\begin{eqnarray} \Phi_t\circ \omega_t& = &\omega \circ(\Phi_t\times \Phi_t), \end{eqnarray}$

(3.7)

$\begin{eqnarray} \alpha \circ\Phi_t& = &\Phi_t\circ\alpha_t. \end{eqnarray}$

(3.8)

Definition 3.7. Let $(A, \omega, \alpha)$ be a Hom-pre-Lie algebra. If all $1$ -parameter formal deformations are trivial, we say that $(A, \omega, \alpha)$ is rigid.

Theorem 3.8. Let $(A, \omega, \alpha)$ be a Hom-pre-Lie algebra. If $\tilde{H}^2(A; A) = 0$ , then $(A, \omega, \alpha)$ is rigid.

Proof. Let $(\omega_t = \omega+\sum_{i = 1}^{+\infty} \omega_it^i, \alpha_t = \alpha+\sum_{i = 1}^{+\infty} \alpha_it^i)$ be a $1$ -parameter formal deformation and assume that $n\geq1$ is the minimal number such that at least one of $\omega_n$ and $\alpha_n$ is not zero. By (3.2), (3.4) and $\tilde{H}^2(A; A) = 0$ , we have $(\omega_n, \alpha_n)\in \tilde{B}^2(A; A)$ . Thus, there exists $\varphi_n \in \tilde{ {\mathcal{C}}}^1(A; A)$ such that $\omega_n = \partial_{\omega\omega}(-\varphi_n)$ and $\alpha_n = \partial_{\omega\alpha}(-\varphi_n)$ . Let $\Phi_t = { {\rm{Id}}}+\varphi_nt^n$ and define a new formal deformation $(\omega_t', \alpha_t')$ by $\omega_t'(x, y) = \Phi_t^{-1}\circ\omega_t(\Phi_t(x), \Phi_t(y))$ and $\alpha_t'(x) = \Phi_t^{-1}\circ\alpha_t(\Phi_t(x))$ . Then $(\omega_t', \alpha_t')$ and $(\omega_t, \alpha_t)$ are equivalent. By a straightforward computation, for all $x, y\in A$ , we have

$\begin{eqnarray*} \omega_t'(x, y) & = &\Phi_t^{-1}\circ\omega_t(\Phi_t(x), \Phi_t(y))\\ & = &({ {\rm{Id}}}-\varphi_n t^n+\dots)\omega_t\big(x+\varphi_n(x)t^n, y+\varphi_n(y)t^n\big)\\ & = &({ {\rm{Id}}}-\varphi_n t^n+\dots)\Big(x\cdot y+\big(x\cdot\varphi_n(y)+\varphi_n(x)\cdot y+\omega_n(x, y)\big)t^n+\dots\Big)\\ & = &x\cdot y+\Big(x\cdot\varphi_n(y)+\varphi_n(x)\cdot y+\omega_n(x, y)-\varphi_n(x\cdot y)\Big)t^n+\dots. \end{eqnarray*}$

Thus, we have $\omega_1' = \omega_2' = \dots = \omega_{n-1}' = 0$ . Moreover, we obtain

$\begin{eqnarray*} \omega_n'(x, y)& = &\varphi_n(x)\cdot y+x\cdot \varphi_n(y)+\omega_n(x, y)-\varphi_n(x\cdot y)\\ & = &\partial_{\omega\omega}\varphi_n(x, y)+\omega_n(x, y)\\ & = &0. \end{eqnarray*}$

For all $x\in A$ , we get

$\begin{eqnarray*} \alpha_t'(x) & = &\Phi_t^{-1}\circ\alpha_t(\Phi_t(x))\\ & = &({ {\rm{Id}}}-\varphi_n t^n+\dots)\alpha_t\big(x+\varphi_n(x)t^n\big)\\ & = &({ {\rm{Id}}}-\varphi_1 t^n+\dots)\Big(\alpha(x)+\big(\alpha(\varphi_n(x))+\alpha_n(x))t^n+\dots\Big)\\ & = &\alpha(x)+\Big(\alpha(\varphi_n(x))+\alpha_n(x)-\varphi_n(\alpha(x))\Big)t^n+\dots. \end{eqnarray*}$

Thus, $\alpha_1' = \alpha_2' = \dots = \alpha_{n-1}' = 0$ , and

$\begin{eqnarray*} \alpha_n'(x, y)& = &\alpha(\varphi_n(x))+\alpha_n(x)-\varphi_n(\alpha(x))\\ & = &\partial_{\omega\alpha}\varphi_n(x)+\alpha_n(x)\\ & = &0. \end{eqnarray*}$

By repeating this process, we obtain that $(A[[t]], \omega_t, \alpha_t)$ is equivalent to $(A, \omega, \alpha)$ . The proof is finished.

At the end of this section, we recall $1$ -parameter formal deformations of Hom-Lie algebras, and establish the relation between $1$ -parameter formal deformations of Hom-pre-Lie algebras and $1$ -parameter formal deformations of Hom-Lie algebras.

Definition 3.9. (see ^[25]) Let $(\mathfrak g, [\cdot, \cdot]_{ \mathfrak g}, \phi_{ \mathfrak g})$ be a Hom-Lie algebra, $[\cdot, \cdot]_t = [\cdot, \cdot]_{ \mathfrak g}+\sum_{i = 1}^{+\infty} \bar{\omega}_it^i: \mathfrak g[[t]]\wedge \mathfrak g[[t]]\longrightarrow \mathfrak g[[t]]$ be a $\mathbb K[[t]]$ -bilinear map and $\phi_t = \phi_{ \mathfrak g}+\sum_{i = 1}^{+\infty} \phi_it^i: \mathfrak g[[t]]\longrightarrow \mathfrak g[[t]]$ be a $\mathbb K[[t]]$ -linear map, where $\bar{\omega}_i: \mathfrak g\otimes \mathfrak g\longrightarrow \mathfrak g$ and $\phi_i: \mathfrak g\longrightarrow \mathfrak g$ are linear maps. If $(\mathfrak g[[t]], [\cdot, \cdot]_t, \phi_t)$ is still a Hom-Lie algebra, we say that $\{\bar{\omega}_i, \phi_i\}_{i\geq1}$ generates a $1$ -parameter formal deformation of a Hom-Lie algebra $(\mathfrak g, [\cdot, \cdot]_{ \mathfrak g}, \phi_{ \mathfrak g})$ .

Proposition 3.10. Let $(\omega_t = \omega+\sum_{i = 1}^{+\infty} \omega_it^i, \alpha_t = \alpha+\sum_{i = 1}^{+\infty} \alpha_it^i)$ be a $1$ -parameter formal deformation of a Hom-pre-Lie algebra $(A, \omega, \alpha)$ , then

$\{\omega_i-\omega_i\circ \sigma, \alpha_i\}_{i\geq1}$

generates a $1$ -parameter formal deformation of the sub-adjacent Hom-Lie algebra $A^C$ , where $\sigma:A\otimes A\longrightarrow A\otimes A$ is the flip operator defined by $\sigma(x\otimes y) = y\otimes x$ for all $x, y\in A$ .

Proof. Let $(A[[t]], \omega_t, \alpha_t)$ be a $1$ -parameter formal deformation of a Hom-pre-Lie algebra $(A, \omega, \alpha)$ . For all $x, y\in A$ , we have

$\begin{eqnarray*} \omega_t(x, y)-\omega_t(y, x)& = &\omega(x, y)-\omega(y, x)+\sum\limits_{i = 1}^{+\infty} \omega_i(x, y)t^i-\sum\limits_{i = 1}^{+\infty} \omega_i(y, x)t^i\\ & = &[x, y]_C+\sum\limits_{i = 1}^{+\infty}(\omega_i-\omega_i\circ \sigma)(x, y)t^i, \end{eqnarray*}$

and

$\begin{equation} \nonumber\alpha_t\circ(\omega_t(x, y)-\omega_t(y, x)) = \omega_t(\alpha_t(x), \alpha_t(y))-\omega_t(\alpha_t(y), \alpha_t(x)). \end{equation}$

Therefore, $\{\omega_i-\omega_i\circ \sigma, \alpha_i\}_{i\geq1}$ generates a $1$ -parameter formal deformation of the sub-adjacent Hom-Lie algebra $A^C$ .

4. Abelian extensions of Hom-pre-Lie algebras

In this section, we study abelian extensions of Hom-pre-Lie algebras using the cohomological approach. We show that abelian extensions are classified by the cohomology group $\tilde{H}^2(A; V)$ .

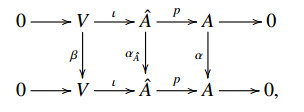
Definition 4.1. Let $(A, \cdot, \alpha)$ and $(V, \cdot_V, \beta)$ be two Hom-pre-Lie algebras. An extension of $(A, \cdot, \alpha)$ by $(V, \cdot_V, \beta)$ is a short exact sequence of Hom-pre-Lie algebra morphisms:

where $(\hat{A}, \cdot_{\hat{A}}, \alpha_{\hat{A}})$ is a Hom-pre-Lie algebra.

It is called an abelian extension if $(V, \cdot_V, \beta)$ is an abelian Hom-pre-Lie algebra, i.e. for all $u, v\in V, u\cdot_V v = 0$ .

Definition 4.2. A section of an extension $(\hat{A}, \cdot_{\hat{A}}, \alpha_{\hat{A}})$ of a Hom-pre-Lie algebra $(A, \cdot, \alpha)$ by $(V, \cdot_V, \beta)$ is a linear map $s:A\longrightarrow \hat{A}$ such that $p\circ s = {\rm{Id}}_A$ .

Let $(\hat{A}, \cdot_{\hat{A}}, \alpha_{\hat{A}})$ be an abelian extension of a Hom-pre-Lie algebra $(A, \cdot, \alpha)$ by $(V, \beta)$ and $s:A\longrightarrow \hat{A}$ a section. For all $x, y\in A$ , define linear maps $\theta:A\otimes A\longrightarrow V$ and $\xi:A\longrightarrow V$ respectively by

$\begin{eqnarray} \theta(x, y)& = &s(x)\cdot_{\hat{A}}s(y)-s(x\cdot y), \end{eqnarray}$

(4.1)

$\begin{eqnarray} \xi(x)& = &\alpha_{\hat{A}}(s(x))-s(\alpha(x)). \end{eqnarray}$

(4.2)

And for all $x, y\in A, u\in V$ , define $\rho, \mu:A\longrightarrow \mathfrak {gl}(V)$ respectively by

$\begin{eqnarray} \rho(x)(u)& = &s(x)\cdot_{\hat{A}} u, \end{eqnarray}$

(4.3)

$\begin{eqnarray} \mu(x)(u)& = &u\cdot_{\hat{A}} s(x). \end{eqnarray}$

(4.4)

Obviously, $\hat{A}$ is isomorphic to $A\oplus V$ as vector spaces. Transfer the Hom-pre-Lie algebra structure on $\hat{A}$ to that on $A\oplus V$ , we obtain a Hom-pre-Lie algebra $(A\oplus V, \diamond, \phi)$ , where $\diamond$ and $\phi$ are given by

$\begin{eqnarray} (x+u)\diamond (y+v)& = &x\cdot y+\theta(x, y)+\rho(x)(v)+\mu(y)(u), \quad \forall \; x, y\in A, u, v\in V, \end{eqnarray}$

(4.5)

$\begin{eqnarray} \phi(x+u)& = &\alpha(x)+\xi(x)+\beta(u), \quad \forall \; x\in A, u\in V. \end{eqnarray}$

(4.6)

Theorem 4.3. With the above notations, we have

${\rm{(i) }}$ $(V, \beta, \rho, \mu)$ is a representation of the Hom-pre-Lie algebra $(A, \cdot, \alpha)$ ,

${\rm{(ii)}}$ $(\theta, \xi)$ is a $2$ -cocycle of the Hom-pre-Lie algebra $(A, \cdot, \alpha)$ with coefficients in the representation $(V, \beta, \rho, \mu)$ .

Proof. For all $x\in A$ , $v\in V$ , by the definition of a Hom-pre-Lie algebra, we have

$\begin{equation} \nonumber\phi(x\diamond v)-\phi(x)\diamond \phi(v) = \beta(\rho(x)(v))-\rho(\alpha(x))\beta(v) = 0, \end{equation}$

which implies that

$\begin{equation} \beta\circ \rho(x) = \rho(\alpha(x))\circ\beta. \end{equation}$

(4.7)

Similarly, we have

$\begin{equation} \beta\circ \mu(x) = \mu(\alpha(x))\circ\beta. \end{equation}$

(4.8)

For all $x, y\in A$ , $v\in V$ , by the definition of a Hom-pre-Lie algebra, we have

$\begin{eqnarray} &&(x\diamond y)\diamond\phi(v)-\phi(x)\diamond (y\diamond v)-(y\diamond x)\diamond\phi(v)+\phi(y)\diamond (x\diamond v)\\ & = &(x\cdot y+\theta(x, y))\diamond \beta(v)-(\alpha(x)+\xi(x))\diamond\rho(y)(v)\\ &&-(y\cdot x+\theta(y, x))\diamond \beta(v)+(\alpha(y)+\xi(y))\diamond\rho(x)(v)\\ & = &\rho(x\cdot y)\beta(v)-\rho(\alpha(x))\rho(y)(v)-\rho(y\cdot x)\beta(v)+\rho(\alpha(y))\rho(x)(v)\\ & = &\rho([x, y]_C)\beta(v)-\rho(\alpha(x))\rho(y)(v)+\rho(\alpha(y))\rho(x)(v)\\ & = &0, \end{eqnarray}$

which implies that

$\begin{equation} \rho([x, y]_C)\circ\beta = \rho(\alpha(x))\circ\rho(y)-\rho(\alpha(y))\circ\rho(x). \end{equation}$

(4.9)

Similarly, we have

$\begin{equation} \mu(\alpha(y))\circ\mu(x)-\mu(x\cdot y)\circ \beta = \mu(\alpha(y))\circ\rho(x)-\rho(\alpha(x))\circ\mu(y). \end{equation}$

(4.10)

By (4.7), (4.8), (4.9), (4.10), we obtain that $(V, \beta, \rho, \mu)$ is a representation.

For all $x, y\in A$ , by the definition of a Hom-pre-Lie algebra, we have

$\begin{eqnarray} &&\phi(x\diamond y)-\phi(x)\diamond \phi(y)\\ & = &\phi\big(x\cdot y+\theta(x, y)\big)-\alpha(x)\cdot \alpha(y)-\theta(\alpha(x), \alpha(y))-\rho(\alpha(x))\xi(y)-\mu(\alpha(y))\xi(x)\\ & = &\xi(x\cdot y)+\beta(\theta(x, y))-\theta(\alpha(x), \alpha(y))-\rho(\alpha(x))\xi(y)-\mu(\alpha(y))\xi(x)\\ & = &\partial_{\omega\alpha}\theta(x, y)+\partial_{\alpha\alpha}\xi(x, y)\\ & = &0, \end{eqnarray}$

which implies that

$\begin{equation} \partial_{\omega\alpha}\theta+\partial_{\alpha\alpha}\xi = 0. \end{equation}$

(4.11)

For all $x, y, z\in A$ , by the definition of a Hom-pre-Lie algebra, we have

$\begin{eqnarray} &&(x\diamond y)\diamond\phi(z)-\phi(x)\diamond (y\diamond z)-(y\diamond x)\diamond\phi(z)+\phi(y)\diamond (x\diamond z)\\ & = &\big(x\cdot y+\theta(x, y)\big)\diamond(\alpha(z)+\xi(z))-(\alpha(x)+\xi(x))\diamond\big(y\cdot z +\theta(y, z)\big)\\ &&-\big(y\cdot x+\theta(y, x)\big)\diamond(\alpha(z)+\xi(z))+(\alpha(y)+\xi(y))\diamond\big(x\cdot z +\theta(x, z)\big)\\ & = &\theta(x\cdot y, \alpha(z))+\mu(\alpha(z))\theta(x, y)-\theta(\alpha(x), y\cdot z)-\rho(\alpha(x))\theta(y, z)\\ &&-\theta(y\cdot x, \alpha(z))-\mu(\alpha(z))\theta(y, x)+\theta(\alpha(y), x\cdot z)+\rho(\alpha(y))\theta(x, z)\\ &&+\rho(x\cdot y)\xi(z)-\mu(y\cdot z)\xi(x)-\rho(y\cdot x)\xi(z)+\mu(x\cdot z)\xi(y)\\ & = &-\partial_{\omega\omega}\theta(x, y, z)-\partial_{\alpha\omega}\xi(x, y, z)\\ & = &0, \end{eqnarray}$

which implies that

$\begin{equation} \partial_{\omega\omega}\theta+\partial_{\alpha\omega}\xi = 0. \end{equation}$

(4.12)

By Eqs (4.11) and (4.12), we obtain that $\tilde{\partial}(\theta, \xi) = 0$ , which implies that $(\theta, \xi)$ is a $2$ -cocycle of the Hom-pre-Lie algebra $(A, \cdot, \alpha)$ . The proof is finished.

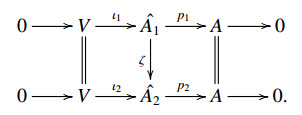
Definition 4.4. Let $(\hat{A_1}, \cdot_{\hat{A_1}}, \alpha_{\hat{A_1}})$ and $(\hat{A_2}, \cdot_{\hat{A_2}}, \alpha_{\hat{A_2}})$ be two abelian extensions of a Hom-pre-Lie algebra $(A, \cdot, \alpha)$ by $(V, \beta)$ . They are said to be isomorphic if there exists a Hom-pre-Lie algebra isomorphism $\zeta:(\hat{A_1}, \cdot_{\hat{A_1}}, \alpha_{\hat{A_1}})\longrightarrow (\hat{A_2}, \cdot_{\hat{A_2}}, \alpha_{\hat{A_2}})$ such that the following diagram is commutative:

Proposition 4.5. With the above notations, we have

${\rm(i)}$ Two different sections of an abelian extension of a Hom-pre-Lie algebra $(A, \cdot, \alpha)$ by $(V, \beta)$ give rise to the same representation of $(A, \cdot, \alpha)$ ,

${\rm(ii)}$ Isomorphic abelian extensions give rise to the same representation of $(A, \cdot, \alpha)$ .

Proof. ${\rm(i)}$ Let $(\hat{A}, \cdot_{\hat{A}}, \alpha_{\hat{A}})$ be an abelian extension of a Hom-pre-Lie algebra $(A, \cdot, \alpha)$ by $(V, \beta)$ . Choosing two different sections $s_1, s_2:A\longrightarrow \hat{A}$ , by equations (4.3), (4.4) and Theorem 4.3, we obtain two representations $(V, \beta, \rho_1, \mu_1)$ and $(V, \beta, \rho_2, \mu_2)$ . Define $\varphi:A\longrightarrow V$ by $\varphi(x) = s_1(x)-s_2(x)$ . Then for all $x\in A$ , we have

$\begin{eqnarray*} \rho_1(x)(u)-\rho_2(x)(u)& = &s_1(x)\cdot_{\hat{A}} u-s_2(x)\cdot_{\hat{A}} u\\ & = &(\varphi(x)+s_2(x))\cdot_{\hat{A}} u-s_2(x)\cdot_{\hat{A}} u\\ & = &\varphi(x)\cdot_{\hat{A}} u\\ & = &0, \end{eqnarray*}$

which implies that $\rho_1 = \rho_2$ . Similarly, we have $\mu_1 = \mu_2$ . This finishes the proof.

${\rm(ii)}$ Let $(\hat{A_1}, \cdot_{\hat{A_1}}, \alpha_{\hat{A_1}})$ and $(\hat{A_2}, \cdot_{\hat{A_2}}, \alpha_{\hat{A_2}})$ are two isomorphic abelian extensions of a Hom-pre-Lie algebra $(A, \cdot, \alpha)$ by $(V, \beta)$ . Let $s_1:A_1\longrightarrow \hat{A_1}$ and $s_2:A_2\longrightarrow \hat{A_2}$ be two sections of $(\hat{A_1}, \cdot_{\hat{A_1}}, \alpha_{\hat{A_1}})$ and $(\hat{A_2}, \cdot_{\hat{A_2}}, \alpha_{\hat{A_2}})$ respectively. By equations (4.3), (4.4) and Theorem 4.3, we obtain that $(V, \beta, \rho_1, \mu_1)$ and $(V, \beta, \rho_2, \mu_2)$ are their representations respectively. Define $s'_1:A_1\longrightarrow \hat{A_1}$ by $s'_1 = \zeta^{-1}\circ s_2$ . Since $\zeta:(\hat{A_1}, \cdot_{\hat{A_1}}, \alpha_{\hat{A_1}})\longrightarrow (\hat{A_2}, \cdot_{\hat{A_2}}, \alpha_{\hat{A_2}})$ is a Hom-pre-Lie algebra isomorphism satisfying the commutative diagram in Definition 4.4, by $p_2\circ \zeta = p_1$ , we have

$\begin{equation} p_1\circ s'_1 = p_2\circ \zeta \circ \zeta^{-1}\circ s_2 = {\rm{Id}}_A. \end{equation}$

(4.13)

Thus, we obtain that $s'_1$ is a section of $(\hat{A_1}, \cdot_{\hat{A_1}}, \alpha_{\hat{A_1}})$ . For all $x\in A, u\in V$ , we have

$\begin{eqnarray*} \rho_1(x)(u)& = &s'_1(x) \cdot_{\hat{A_1}} u\\ & = &(\zeta^{-1}\circ s_2)(x)\cdot_{\hat{A_1}} u\\ & = &\zeta^{-1}(s_2(x) \cdot_{\hat{A_2}} u)\\ & = &\rho_2(x)(u), \end{eqnarray*}$

which implies that $\rho_1 = \rho_2$ . Similarly, we have $\mu_1 = \mu_2$ . This finishes the proof.

So in the sequel, we fix a representation $(V, \beta, \rho, \mu)$ of a Hom-pre-Lie algebra $(A, \cdot, \alpha)$ and consider abelian extensions that induce the given representation.

Theorem 4.6. Abelian extensions of a Hom-pre-Lie algebra $(A, \cdot, \alpha)$ by $(V, \beta)$ are classified by $\tilde{H}^2(A; V)$ .

Proof. Let $(\hat{A}, \cdot_{\hat{A}}, \alpha_{\hat{A}})$ be an abelian extension of a Hom-pre-Lie algebra $(A, \cdot, \alpha)$ by $(V, \beta)$ . Choosing a section $s:A\longrightarrow \hat{A}$ , by Theorem 4.3, we obtain that $(\theta, \xi)\in \tilde{Z}^2(A; V)$ . Now we show that the cohomological class of $(\theta, \xi)$ does not depend on the choice of sections. In fact, let $s_1$ and $s_2$ be two different sections. Define $\varphi:A\longrightarrow V$ by $\varphi(x) = s_1(x)-s_2(x)$ . Then for all $x, y\in A$ , we have

$\begin{eqnarray*} \theta_1(x, y)& = &s_1(x)\cdot_{\hat{A}} s_1(y)-s_1(x\cdot y)\\ & = &\big(s_2(x)+\varphi(x)\big)\cdot_{\hat{A}} \big(s_2(y)+\varphi(y)\big)-s_2(x\cdot y)-\varphi(x\cdot y)\\ & = &s_2(x)\cdot_{\hat{A}} s_2(y)+\rho(x)\varphi(y)+\mu(y)\varphi(x)-s_2(x\cdot y)-\varphi(x\cdot y)\\ & = &\theta_2(x, y)+\partial_{\omega\omega}\varphi(x, y), \end{eqnarray*}$

which implies that $\theta_1-\theta_2 = \partial_{\omega\omega}\varphi$ .

For all $x\in A$ , we have

$\begin{eqnarray*} \xi_1(x)& = &\alpha_{\hat{A}}(s_1(x))-s_1(\alpha(x))\\ & = &\alpha_{\hat{A}}(\varphi(x)+s_2(x))-\varphi(\alpha(x))-s_2(\alpha(x))\\ & = &\alpha_{\hat{A}}(\varphi(x))+\alpha_{\hat{A}}(s_2(x))-\varphi(\alpha(x))-s_2(\alpha(x))\\ & = &\xi_2(x)+\beta(\varphi(x))-\varphi(\alpha(x)), \end{eqnarray*}$

which implies that $\xi_1-\xi_2 = \partial_{\omega\alpha}\varphi$ .

Therefore, we obtain that $(\theta_1-\theta_2, \xi_1-\xi_2)\in \tilde{B}^2(A; V)$ , $(\theta_1, \xi_1)$ and $(\theta_2, \xi_2)$ are in the same cohomological class.

Now we prove that isomorphic abelian extensions give rise to the same element in $\tilde{H}^2(A; V)$ . Assume that $(\hat{A_1}, \cdot_{\hat{A_1}}, \alpha_{\hat{A_1}})$ and $(\hat{A_2}, \cdot_{\hat{A_2}}, \alpha_{\hat{A_2}})$ are two isomorphic abelian extensions of a Hom-pre-Lie algebra $(A, \cdot, \alpha)$ by $(V, \beta)$ , and $\zeta:(\hat{A_1}, \cdot_{\hat{A_1}}, \alpha_{\hat{A_1}})\longrightarrow (\hat{A_2}, \cdot_{\hat{A_2}}, \alpha_{\hat{A_2}})$ is a Hom-pre-Lie algebra isomorphism satisfying the commutative diagram in Definition 4.4. Assume that $s_1:A\longrightarrow \hat{A_1}$ is a section of $\hat{A_1}$ . By $p_2\circ \zeta = p_1$ , we have

$\begin{equation} p_2\circ (\zeta\circ s_1) = p_1\circ s_1 = {\rm{Id}}_A. \end{equation}$

(4.14)

Thus, we obtain that $\zeta\circ s_1$ is a section of $\hat{A_2}$ . Define $s_2 = \zeta\circ s_1$ . Since $\zeta$ is an isomorphism of Hom-pre-Lie algebras and $\zeta\mid_V = {\rm{Id}}_V$ , for all $x, y\in A$ , we have

$\begin{eqnarray*} \theta_2(x, y)& = &s_2(x)\cdot_{\hat{A_2}} s_2(y)-s_2(x\cdot y)\\ & = &(\zeta\circ s_1)(x)\cdot_{\hat{A_2}}(\zeta\circ s_1)(y)-(\zeta\circ s_1)(x\cdot y)\\ & = &\zeta\big(s_1(x)\cdot_{\hat{A_1}} s_1(y)-s_1(x\cdot y)\big)\\ & = &\theta_1(x, y), \end{eqnarray*}$

and

$\begin{eqnarray*} \xi_2(x)& = &\alpha_{\hat{A_2}}(s_2(x))-s_2(\alpha(x))\\ & = &\alpha_{\hat{A_2}}(\zeta(s_1(x)))-\zeta(s_1(\alpha(x)))\\ & = &\zeta(\alpha_{\hat{A_1}}(s_1(x))-s_1(\alpha(x)))\\ & = &\xi_1(x). \end{eqnarray*}$

Thus, isomorphic abelian extensions gives rise to the same element in $\tilde{H}^2(A; V)$ .

Conversely, given two 2-cocycles $(\theta_1, \xi_1)$ and $(\theta_2, \xi_2)$ , by Eqs (4.5) and (4.6), we can construct two abelian extensions $(A\oplus V, \diamond_1, \phi_1)$ and $(A\oplus V, \diamond_2, \phi_2)$ . If $(\theta_1, \xi_1), (\theta_2, \xi_2)\in \tilde{H}^2(A; V)$ , then there exists $\varphi:A\longrightarrow V$ , such that $\theta_1 = \theta_2+\partial_{\omega\omega}\varphi$ and $\xi_1 = \xi_2+\partial_{\omega\alpha}\varphi$ . We define $\zeta:A\oplus V\longrightarrow A\oplus V$ by

$\begin{equation} \zeta(x+u) = x+u+\varphi(x), \quad \forall \; x\in A, u\in V. \end{equation}$

(4.15)

For all $x, y\in A, u, v\in V$ , by $\theta_1 = \theta_2+\partial_{\omega\omega}\varphi$ , we have

$\begin{eqnarray} &&\zeta\big((x+u)\diamond_1(y+v)\big)- \zeta(x+u)\diamond_2\zeta(y+v)\\ & = &\zeta\big(x\cdot y+\theta_1(x, y)+\rho(x)(v)+\mu(y)(u)\big)-\big(x+u+\varphi(x)\big)\diamond_2 \big(y+v+\varphi(y)\big)\\ & = &\theta_1(x, y)+\varphi(x\cdot y)-\theta_2(x, y)-\rho(x)\varphi(y)-\mu(y)\varphi(x)\\ & = &\theta_1(x, y)-\theta_2(x, y)-\partial_{\omega\omega}\varphi(x, y)\\ & = &0, \end{eqnarray}$

(4.16)

and for all $x\in A, u\in V$ , by $\xi_1 = \xi_2+\partial_{\omega\alpha}\varphi$ , we have

$\begin{eqnarray} &&\zeta \circ\phi_1(x+u)-\phi_1\circ \zeta(x+u)\\ & = &\zeta\big(\alpha(x)+\xi_1(x)+\beta(u)\big)-\phi_2\big(x+u+\varphi(x)\big)\\ & = &\xi_1(x)+\varphi(\alpha(x))-\xi_2(x)-\beta(\varphi(x))\\ & = &\xi_1(x)-\xi_2(x)-\partial_{\omega\alpha}\varphi(x)\\ & = &0, \end{eqnarray}$

(4.17)

which implies that $\zeta$ is a Hom-pre-Lie algebra isomorphism from $(A\oplus V, \diamond_1, \phi_1)$ to $(A\oplus V, \diamond_2, \phi_2)$ . Moreover, it is obvious that the diagram in Definition 4.4 is commutative. This finishes the proof.

Appendix: The proof of Lemma 2.6

By straightforward computations, for all $x_1, \dots, x_{n+2}\in A$ , we have

$\begin{eqnarray} &&\partial_{\omega\omega}(\partial_{\omega\omega}\varphi)(x_1, \dots, x_{n+2})\\ & = &\sum\limits_{i = 1}^{n+1}(-1)^{i+1}\rho(\alpha^n(x_i))(\partial_{\omega\omega}\varphi)(x_1, \dots, \widehat{x_i}, \dots, x_{n+2})\\ &&+\sum\limits_{i = 1}^{n+1}(-1)^{i+1}\mu(\alpha^n(x_{n+2}))(\partial_{\omega\omega}\varphi)(x_1, \dots, \widehat{x_i}, \dots, x_{n+1}, x_i)\\ &&-\sum\limits_{i = 1}^{n+1}(-1)^{i+1} (\partial_{\omega\omega}\varphi)(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \alpha(x_{n+1}), x_i\cdot x_{n+2})\\ &&+\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+j} (\partial_{\omega\omega}\varphi)([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+2}))\\ & = &\sum\limits_{1\leq j < i\leq n+1}(-1)^{i+1}(-1)^{j+1}\rho(\alpha^n(x_i))\rho(\alpha^{n-1}(x_j))\varphi(x_1, \dots, \widehat{x_j}, \dots, \widehat{x_i}, \dots, x_{n+2}) \end{eqnarray}$

(4.18)

$\begin{eqnarray} &&+\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+1}(-1)^j\rho(\alpha^n(x_i))\rho(\alpha^{n-1}(x_j))\varphi(x_1, \dots, \widehat{x_i}, \dots, \widehat{x_j}, \dots, x_{n+2}) \end{eqnarray}$

(4.19)

$\begin{eqnarray} &&+\sum\limits_{1\leq j < i\leq n+1}(-1)^{i+1}(-1)^{j+1}\rho(\alpha^n(x_i))\mu(\alpha^{n-1}(x_{n+2}))\varphi(x_1, \dots, \widehat{x_j}, \dots, \widehat{x_i}, \dots, x_{n+1}, x_j) \end{eqnarray}$

(4.20)

$\begin{eqnarray} &&+\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+1}(-1)^j\rho(\alpha^n(x_i))\mu(\alpha^{n-1}(x_{n+2}))\varphi(x_1, \dots, \widehat{x_i}, \dots, \widehat{x_j}, \dots, x_{n+1}, x_j) \end{eqnarray}$

(4.21)

$\begin{eqnarray} &&-\sum\limits_{1\leq j < i\leq n+1}(-1)^{i+1}(-1)^{j+1}\rho(\alpha^n(x_i))\varphi(\alpha(x_1), \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_i)}, \dots, \alpha(x_{n+1}), x_j\cdot x_{n+2}) \end{eqnarray}$

(4.22)

$\begin{eqnarray} &&-\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+1}(-1)^j\rho(\alpha^n(x_i))\varphi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), x_j\cdot x_{n+2}) \end{eqnarray}$

(4.23)

$+\sum\limits_{1\leq j < k < i\leq n+1}(-1)^{i+1}(-1)^{j+k}\rho(\alpha^n(x_i))\varphi([x_j, x_k]_C, \alpha(x_1), \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_i)}, \dots, \alpha(x_{n+2}))$

(4.24)

$\begin{eqnarray} &&+\sum\limits_{1\leq j < i < k\leq n+1}(-1)^{i+1}(-1)^{j+k-1}\rho(\alpha^n(x_i))\varphi([x_j, x_k]_C, \alpha(x_1), \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_k)}, \dots, \alpha(x_{n+2})) \end{eqnarray}$

(4.25)

$\begin{eqnarray} &&+\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+1}(-1)^{j+k}\rho(\alpha^n(x_i))\varphi([x_j, x_k]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_k)}, \dots, \alpha(x_{n+2})) \end{eqnarray}$

(4.26)

$\begin{eqnarray} &&+\sum\limits_{1\leq j < i\leq n+1}(-1)^{i+1}(-1)^{j+1}\mu(\alpha^n(x_{n+2}))\rho(\alpha^{n-1}(x_j))\varphi(x_1, \dots, \widehat{x_j}, \dots, \widehat{x_i}, \dots, x_{n+1}, x_i) \end{eqnarray}$

(4.27)

$\begin{eqnarray} &&+\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+1}(-1)^j\mu(\alpha^n(x_{n+2}))\rho(\alpha^{n-1}(x_j))\varphi(x_1, \dots, \widehat{x_i}, \dots, \widehat{x_j}, \dots, x_{n+1}, x_i) \end{eqnarray}$

(4.28)

$\begin{eqnarray} &&+\sum\limits_{1\leq j < i\leq n+1}(-1)^{i+1}(-1)^{j+1}\mu(\alpha^n(x_{n+2}))\mu(\alpha^{n-1}(x_i))\varphi(x_1, \dots, \widehat{x_j}, \dots, \widehat{x_i}, \dots, x_{n+1}, x_j) \end{eqnarray}$

(4.29)

$\begin{eqnarray} &&+\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+1}(-1)^j\mu(\alpha^n(x_{n+2}))\mu(\alpha^{n-1}(x_i))\varphi(x_1, \dots, \widehat{x_i}, \dots, \widehat{x_j}, \dots, x_{n+1}, x_j) \end{eqnarray}$

(4.30)

$\begin{eqnarray} &&-\sum\limits_{1\leq j < i\leq n+1}(-1)^{i+1}(-1)^{j+1}\mu(\alpha^n(x_{n+2}))\varphi(\alpha(x_1), \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_i)}, \dots, \alpha(x_{n+1}), x_j\cdot x_i) \end{eqnarray}$

(4.31)

$\begin{eqnarray} &&-\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+1}(-1)^j\mu(\alpha^n(x_{n+2}))\varphi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), x_j\cdot x_i) \end{eqnarray}$

(4.32)

$\begin{eqnarray} &&+\sum\limits_{1\leq j < k < i\leq n+1}(-1)^{i+1}(-1)^{j+k}\mu(\alpha^n(x_{n+2}))\varphi([x_j, x_k]_C, \alpha(x_1), \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_k)}, \end{eqnarray}$

(4.33)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_i)}, \dots, \alpha(x_{n+1}), \alpha(x_i))\\ &&+\sum\limits_{1\leq j < i < k\leq n+1}(-1)^{i+1}(-1)^{j+k-1}\mu(\alpha^n(x_{n+2}))\varphi([x_j, x_k]_C, \alpha(x_1), \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_i)}, \end{eqnarray}$

(4.34)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_k)}, \dots, \alpha(x_{n+1}), \alpha(x_i))\\ &&+\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+1}(-1)^{j+k}\mu(\alpha^n(x_{n+2}))\varphi([x_j, x_k]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \end{eqnarray}$

(4.35)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_k)}, \dots, \alpha(x_{n+1}), \alpha(x_i))\\ &&-\sum\limits_{1\leq j < i\leq n+1}(-1)^{i+1}(-1)^{j+1}\rho(\alpha^n(x_j))\varphi(\alpha(x_1), \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_i)}, \dots, \alpha(x_{n+1}), x_i\cdot x_{n+2}) \end{eqnarray}$

(4.36)

$\begin{eqnarray} &&-\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+1}(-1)^j\rho(\alpha^n(x_j))\varphi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), x_i\cdot x_{n+2}) \end{eqnarray}$

(4.37)

$\begin{eqnarray} &&-\sum\limits_{1\leq j < i\leq n+1}(-1)^{i+1}(-1)^{j+1}\mu(\alpha^{n-1}(x_i \cdot x_{n+2}))\varphi(\alpha(x_1), \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_i)}, \dots, \alpha(x_{n+1}), \alpha(x_j)) \end{eqnarray}$

(4.38)

$\begin{eqnarray} &&-\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+1}(-1)^j\mu(\alpha^{n-1}(x_i \cdot x_{n+2}))\varphi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), \alpha(x_j)) \end{eqnarray}$

(4.39)

$\begin{eqnarray} &&+\sum\limits_{1\leq j < i\leq n+1}(-1)^{i+1}(-1)^{j+1}\varphi(\alpha^2(x_1), \dots, \widehat{\alpha^2(x_j)}, \dots, \widehat{\alpha^2(x_i)}, \dots, \alpha^2(x_{n+1}), \alpha(x_j)\cdot(x_i\cdot x_{n+2})) \end{eqnarray}$

(4.40)

$\begin{eqnarray} &&+\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+1}(-1)^j\varphi(\alpha^2(x_1), \dots, \widehat{\alpha^2(x_i)}, \dots, \widehat{\alpha^2(x_j)}, \dots, \alpha^2(x_{n+1}), \alpha(x_j)\cdot(x_i\cdot x_{n+2})) \end{eqnarray}$

(4.41)

$\begin{eqnarray} &&-\sum\limits_{1\leq j < k < i\leq n+1}(-1)^{i+1}(-1)^{j+k}\varphi([\alpha(x_j), \alpha(x_k)]_C, \alpha^2(x_1), \dots, \widehat{\alpha^2(x_j)}, \dots, \widehat{\alpha^2(x_k)}, \dots, \end{eqnarray}$

(4.42)

$\begin{eqnarray} &&\widehat{\alpha^2(x_i)}, \dots, \alpha^2(x_{n+1}), \alpha(x_i \cdot x_{n+2}))\\ &&-\sum\limits_{1\leq j < i < k\leq n+1}(-1)^{i+1}(-1)^{j+k-1}\varphi([\alpha(x_j), \alpha(x_k)]_C, \alpha^2(x_1), \dots, \widehat{\alpha^2(x_j)}, \dots, \widehat{\alpha^2(x_i)}, \dots, \end{eqnarray}$

(4.43)

$\begin{eqnarray} &&\widehat{\alpha^2(x_k)}, \dots, \alpha^2(x_{n+1}), \alpha(x_i \cdot x_{n+2}))\\ &&-\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+1}(-1)^{j+k}\varphi([\alpha(x_j), \alpha(x_k)]_C, \alpha^2(x_1), \dots, \widehat{\alpha^2(x_i)}, \dots, \widehat{\alpha^2(x_j)}, \dots, \end{eqnarray}$

(4.44)

$\begin{eqnarray} &&\widehat{\alpha^2(x_k)}, \dots, \alpha^2(x_{n+1}), \alpha(x_i \cdot x_{n+2}))\\ &&+\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+j}\rho(\alpha^{n-1}[x_i, x_j]_C)\varphi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+2})) \end{eqnarray}$

(4.45)

$\begin{eqnarray} &&+\sum\limits_{1\leq k < i < j\leq n+1}(-1)^{i+j}(-1)^k\rho(\alpha^n(x_k)))\varphi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+2})) \end{eqnarray}$

(4.46)

$\begin{eqnarray} &&+\sum\limits_{1\leq i < k < j\leq n+1}(-1)^{i+j}(-1)^{k+1}\rho(\alpha^n(x_k)))\varphi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+2})) \end{eqnarray}$

(4.47)

$\begin{eqnarray} &&+\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+j}(-1)^k\rho(\alpha^n(x_k)))\varphi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_k)}, \dots, \alpha(x_{n+2})) \end{eqnarray}$

(4.48)

$\begin{eqnarray} &&+\sum\limits_{1\leq k < i < j\leq n+1}(-1)^{i+j}(-1)^k\mu(\alpha^n(x_{n+2})))\varphi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_i)}, \dots, \end{eqnarray}$

(4.49)

$\begin{eqnarray} &&\widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), \alpha(x_k))\\ &&+\sum\limits_{1\leq i < k < j\leq n+1}(-1)^{i+j}(-1)^{k+1}\mu(\alpha^n(x_{n+2})))\varphi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_k)}, \dots, \end{eqnarray}$

(4.50)

$\begin{eqnarray} &&\widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), \alpha(x_k))\\ &&+\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+j}(-1)^k\mu(\alpha^n(x_{n+2})))\varphi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \end{eqnarray}$

(4.51)

$\begin{eqnarray} &&\widehat{\alpha(x_k)}, \dots, \alpha(x_{n+1}), \alpha(x_k))\\ &&+\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+j}\mu(\alpha^n(x_{n+2}))\varphi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), [x_i, x_j]_C) \end{eqnarray}$

(4.52)

$\begin{eqnarray} &&-\sum\limits_{1\leq k < i < j\leq n+1}(-1)^{i+j}(-1)^k\varphi(\alpha[x_i, x_j]_C, \alpha^2(x_1), \dots, \widehat{\alpha^2(x_k)}, \dots, \widehat{\alpha^2(x_i)}, \dots, \widehat{\alpha^2(x_j)}, \end{eqnarray}$

(4.53)

$\begin{eqnarray} &&\dots, \alpha^2(x_{n+1}), \alpha(x_k) \cdot \alpha(x_{n+2}))\\ &&-\sum\limits_{1\leq i < k < j\leq n+1}(-1)^{i+j}(-1)^{k+1}\varphi(\alpha[x_i, x_j]_C, \alpha^2(x_1), \dots, \widehat{\alpha^2(x_i)}, \dots, \widehat{\alpha^2(x_k)}, \dots, \widehat{\alpha^2(x_j)}, \end{eqnarray}$

(4.54)

$\begin{eqnarray} &&\dots, \alpha^2(x_{n+1}), \alpha(x_k) \cdot \alpha(x_{n+2}))\\ &&-\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+j}(-1)^k\varphi(\alpha[x_i, x_j]_C, \alpha^2(x_1), \dots, \widehat{\alpha^2(x_i)}, \dots, \widehat{\alpha^2(x_j)}, \dots, \widehat{\alpha^2(x_k)}, \end{eqnarray}$

(4.55)

$\begin{eqnarray} &&\dots, \alpha^2(x_{n+1}), \alpha(x_k) \cdot \alpha(x_{n+2}))\\ &&-\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+j}\varphi(\alpha^2(x_1), \dots, \widehat{\alpha^2(x_i)}, \dots, \widehat{\alpha^2(x_j)}, \dots, \alpha^2(x_{n+1}), [x_i, x_j]_C \cdot \alpha(x_{n+2})) \end{eqnarray}$

(4.56)

$\begin{eqnarray} &&+\sum\limits_{1\leq k < l < i < j\leq n+1}(-1)^{i+j}(-1)^{k+l}\varphi([\alpha(x_k), \alpha(x_l)]_C, \alpha[x_i, x_j]_C, \alpha^2(x_1), \dots, \widehat{\alpha^2(x_k)}, \dots, \end{eqnarray}$

(4.57)

$\begin{eqnarray} &&\widehat{\alpha^2(x_l)}, \dots, \widehat{\alpha^2(x_i)}, \dots, \widehat{\alpha^2(x_j)}, \dots, \alpha^2(x_{n+2}))\\ &&+\sum\limits_{1\leq k < i < l < j\leq n+1}(-1)^{i+j}(-1)^{k+l+1}\varphi([\alpha(x_k), \alpha(x_l)]_C, \alpha[x_i, x_j]_C, \alpha^2(x_1), \dots, \widehat{\alpha^2(x_k)}, \dots, \end{eqnarray}$

(4.58)

$\begin{eqnarray} &&\widehat{\alpha^2(x_i)}, \dots, \widehat{\alpha^2(x_l)}, \dots, \widehat{\alpha^2(x_j)}, \dots, \alpha^2(x_{n+2}))\\ &&+\sum\limits_{1\leq i < k < l < j\leq n+1}(-1)^{i+j}(-1)^{k+l}\varphi([\alpha(x_k), \alpha(x_l)]_C, \alpha[x_i, x_j]_C, \alpha^2(x_1), \dots, \widehat{\alpha^2(x_i)}, \dots, \end{eqnarray}$

(4.59)

$\begin{eqnarray} &&\widehat{\alpha^2(x_k)}, \dots, \widehat{\alpha^2(x_l)}, \dots, \widehat{\alpha^2(x_j)}, \dots, \alpha^2(x_{n+2}))\\ &&+\sum\limits_{1\leq i < j < k < l\leq n+1}(-1)^{i+j}(-1)^{k+l}\varphi([\alpha(x_k), \alpha(x_l)]_C, \alpha[x_i, x_j]_C, \alpha^2(x_1), \dots, \widehat{\alpha^2(x_i)}, \dots, \end{eqnarray}$

(4.60)

$\begin{eqnarray} &&\widehat{\alpha^2(x_j)}, \dots, \widehat{\alpha^2(x_k)}, \dots, \widehat{\alpha^2(x_l)}, \dots, \alpha^2(x_{n+2}))\\ &&+\sum\limits_{1\leq i < k < j < l\leq n+1}(-1)^{i+j}(-1)^{k+l+1}\varphi([\alpha(x_k), \alpha(x_l)]_C, \alpha[x_i, x_j]_C, \alpha^2(x_1), \dots, \widehat{\alpha^2(x_i)}, \dots, \end{eqnarray}$

(4.61)

$\begin{eqnarray} &&\widehat{\alpha^2(x_k)}, \dots, \widehat{\alpha^2(x_j)}, \dots, \widehat{\alpha^2(x_l)}, \dots, \alpha^2(x_{n+2}))\\ &&+\sum\limits_{1\leq k < i < j < l\leq n+1}(-1)^{i+j}(-1)^{k+l}\varphi([\alpha(x_k), \alpha(x_l)]_C, \alpha[x_i, x_j]_C, \alpha^2(x_1), \dots, \widehat{\alpha^2(x_k)}, \dots, \end{eqnarray}$

(4.62)

$\begin{eqnarray} &&\widehat{\alpha^2(x_i)}, \dots, \widehat{\alpha^2(x_j)}, \dots, \widehat{\alpha^2(x_l)}, \dots, \alpha^2(x_{n+2}))\\ &&+\sum\limits_{1\leq k < i < j\leq n+1}(-1)^{i+j}(-1)^k\varphi([[x_i, x_j]_C, \alpha(x_k)]_C, \alpha^2(x_1), \dots, \widehat{\alpha^2(x_k)}, \dots, \widehat{\alpha^2(x_i)}, \dots, \widehat{\alpha^2(x_j)}, \dots, \alpha^2(x_{n+2})) \end{eqnarray}$

(4.63)

$\begin{eqnarray} &&+\sum\limits_{1\leq i < k < j\leq n+1}(-1)^{i+j}(-1)^{k+1}\varphi([[x_i, x_j]_C, \alpha(x_k)]_C, \alpha^2(x_1), \dots, \widehat{\alpha^2(x_i)}, \dots, \widehat{\alpha^2(x_k)}, \dots, \widehat{\alpha^2(x_j)}, \dots, \alpha^2(x_{n+2})) \end{eqnarray}$

(4.64)

$\begin{eqnarray} &&+\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+j}(-1)^k\varphi([[x_i, x_j]_C, \alpha(x_k)]_C, \alpha^2(x_1), \dots, \widehat{\alpha^2(x_i)}, \dots, \widehat{\alpha^2(x_j)}, \dots, \widehat{\alpha^2(x_k)}, \dots, \alpha^2(x_{n+2})). \end{eqnarray}$

(4.65)

The terms (4.22) and (4.37), (4.23) and (4.36), (4.24) and (4.48), (4.25) and (4.47), (4.26) and (4.46), (4.33) and (4.51), (4.34) and (4.50), (4.35) and (4.49) cancel each other. By the definition of the sub-adjacent Hom-Lie algebra, the sum of (4.63), (4.64) and (4.65) is zero. By the antisymmetry condition, the term (4.57) and (4.60), (4.58) and (4.61), (4.59) and (4.62) cancel each other. By the definition of the sub-adjacent Lie bracket, the sum of (4.31), (4.32) and (4.52) is zero. By the definition of Hom-pre-Lie algebras, the sum of (4.40), (4.41) and (4.56) is zero. Since $\alpha$ is an algebra morphism, the term (4.42) and (4.55), (4.43) and (4.54), (4.44) and (4.53) cancel each other.

Since $(V, \beta, \rho, \mu)$ is a representation of the Hom-pre-Lie algebra $(A, \cdot, \alpha)$ , the sum of (4.18) and (4.19) can be written as

$\begin{equation} \sum\limits_{1\leq i < j\leq n+1}(-1)^{i+j+1}\rho([\alpha^{n-1}(x_i), \alpha^{n-1}(x_j)]_C)\beta\varphi(x_1, \dots, \widehat{x_i}, \dots, \widehat{x_j}, \dots, x_{n+2}), \end{equation}$

(4.66)

the sum of (4.20), (4.28) and (4.29) can be written as

$\begin{equation} -\sum\limits_{1\leq j < i\leq n+1}(-1)^{i+j+1}\mu(\alpha^{n-1}(x_i) \cdot\alpha^{n-1}(x_{n+2}))\beta\varphi(x_1, \dots, \widehat{x_j}, \dots, \widehat{x_i}, \dots, x_{n+1}, x_j), \end{equation}$

(4.67)

and the sum of (4.21), (4.27) and (4.30) can be written as

$\begin{equation} \sum\limits_{1\leq i < j\leq n+1}(-1)^{i+j+1}\mu(\alpha^{n-1}(x_i) \cdot\alpha^{n-1}(x_{n+2}))\beta\varphi(x_1, \dots, \widehat{x_i}, \dots, \widehat{x_j}, \dots, x_{n+1}, x_j). \end{equation}$

(4.68)

Thus, we have

$\begin{eqnarray*} \nonumber&&\partial_{\omega\omega}(\partial_{\omega\omega}\varphi)(x_1, \dots, x_{n+2})\\ & = &\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+j+1}\rho([\alpha^{n-1}(x_i), \alpha^{n-1}(x_j)]_C)\beta\varphi(x_1, \dots, \widehat{x_i}, \dots, \widehat{x_j}, \dots, x_{n+2}), \\ &&+\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+j+1}\mu(\alpha^{n-1}(x_i) \cdot\alpha^{n-1}(x_{n+2}))\beta\varphi(x_1, \dots, \widehat{x_i}, \dots, \widehat{x_j}, \dots, x_{n+1}, x_j)\\ &&-\sum\limits_{1\leq j < i\leq n+1}(-1)^{i+j+1}\mu(\alpha^{n-1}(x_i) \cdot\alpha^{n-1}(x_{n+2}))\beta\varphi(x_1, \dots, \widehat{x_j}, \dots, \widehat{x_i}, \dots, x_{n+1}, x_j)\\ &&-\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+j+1}\rho(\alpha^{n-1}[x_i, x_j]_C)\varphi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+2}))\\ &&-\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+j+1}\mu(\alpha^{n-1}(x_i \cdot x_{n+2}))\varphi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), \alpha(x_j))\\ &&+\sum\limits_{1\leq j < i\leq n+1}(-1)^{i+j+1}\mu(\alpha^{n-1}(x_i \cdot x_{n+2}))\varphi(\alpha(x_1), \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_i)}, \dots, \alpha(x_{n+1}), \alpha(x_j)). \end{eqnarray*}$

For all $x_1, \dots, x_{n+2}\in A$ , we have

$\begin{eqnarray*} &&\partial_{\alpha\omega}(\partial_{\omega\alpha}\varphi)(x_1, \dots, x_{n+2})\\ & = &\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+j}\rho([\alpha^{n-1}(x_i), \alpha^{n-1}(x_j)]_C) (\partial_{\omega\alpha}\varphi)(x_1, \dots, \hat{x_i}, \dots, \hat{x_j}, \dots, x_{n+2})\\ &&+\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+j}\mu(\alpha^{n-1}(x_i)\cdot\alpha^{n-1}(x_{n+2}))(\partial_{\omega\alpha}\varphi)(x_1, \dots, \hat{x_i}, \dots, \hat{x_j}, \dots, x_{n+1}, x_j)\\ &&-\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+j}\mu(\alpha^{n-1}(x_j)\cdot\alpha^{n-1}(x_{n+2}))(\partial_{\omega\alpha}\varphi)(x_1, \dots, \hat{x_i}, \dots, \hat{x_j}, \dots, x_{n+1}, x_i)\\ & = &\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+j}\rho([\alpha^{n-1}(x_i), \alpha^{n-1}(x_j)]_C)\beta\varphi(x_1, \dots, \widehat{x_i}, \dots, \widehat{x_j}, \dots, x_{n+2}), \\ &&-\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+j}\rho([\alpha^{n-1}(x_i), \alpha^{n-1}(x_j)]_C)\varphi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+2}))\\ &&+\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+j}\mu(\alpha^{n-1}(x_i) \cdot\alpha^{n-1}(x_{n+2}))\beta\varphi(x_1, \dots, \widehat{x_i}, \dots, \widehat{x_j}, \dots, x_{n+1}, x_j)\\ &&-\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+j}\mu(\alpha^{n-1}(x_i) \cdot\alpha^{n-1}(x_{n+2}))\varphi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), \alpha(x_j))\\ &&-\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+j}\mu(\alpha^{n-1}(x_j) \cdot\alpha^{n-1}(x_{n+2}))\beta\varphi(x_1, \dots, \widehat{x_i}, \dots, \widehat{x_j}, \dots, x_{n+1}, x_i)\\ &&+\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+j}\mu(\alpha^{n-1}(x_j) \cdot\alpha^{n-1}(x_{n+2}))\varphi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), \alpha(x_i)).\\ \end{eqnarray*}$

Since $\alpha$ is an algebra morphism, we obtain that $\partial_{\omega\omega}\circ \partial_{\omega\omega}+\partial_{\alpha\omega}\circ \partial_{\omega\alpha}$ = 0.

For all $x_1, \dots, x_{n+2}\in A$ , we have

$\begin{eqnarray} &&\partial_{\omega\omega}(\partial_{\alpha\omega}\psi)(x_1, \dots, x_{n+2})\\ & = &\sum\limits_{i = 1}^{n+1}(-1)^{i+1}\rho(\alpha^n(x_i))(\partial_{\alpha\omega}\psi)(x_1, \dots, \widehat{x_i}, \dots, x_{n+2})\\ &&+\sum\limits_{i = 1}^{n+1}(-1)^{i+1}\mu(\alpha^n(x_{n+2}))(\partial_{\alpha\omega}\psi)(x_1, \dots, \widehat{x_i}, \dots, x_{n+1}, x_i)\\ &&-\sum\limits_{i = 1}^{n+1}(-1)^{i+1}(\partial_{\alpha\omega}\psi)(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \alpha(x_{n+1}), x_i\cdot x_{n+2})\\ &&+\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+j} (\partial_{\alpha\omega}\psi)([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+2}))\\ & = &\sum\limits_{1\leq j < k < i\leq n+1}(-1)^{i+1}(-1)^{j+k}\rho(\alpha^n(x_i))\rho([\alpha^{n-2}(x_j), \alpha^{n-2}(x_k)]_C)\psi(x_1, \dots, \hat{x_j}, \dots, \hat{x_k} \dots, \hat{x_i}, \dots, x_{n+2}) \end{eqnarray}$

(4.69)

$\begin{eqnarray} &&+\sum\limits_{1\leq j < i < k\leq n+1}(-1)^{i+1}(-1)^{j+k-1}\rho(\alpha^n(x_i))\rho([\alpha^{n-2}(x_j), \alpha^{n-2}(x_k)]_C)\psi(x_1, \dots, \hat{x_j}, \dots, \hat{x_i} \dots, \hat{x_k}, \dots, x_{n+2}) \end{eqnarray}$

(4.70)

$\begin{eqnarray} &&+\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+1}(-1)^{j+k}\rho(\alpha^n(x_i))\rho([\alpha^{n-2}(x_j), \alpha^{n-2}(x_k)]_C)\psi(x_1, \dots, \hat{x_i}, \dots, \hat{x_j} \dots, \hat{x_k}, \dots, x_{n+2}) \end{eqnarray}$

(4.71)

$\begin{eqnarray} &&+\sum\limits_{1\leq j < k < i\leq n+1}(-1)^{i+1}(-1)^{j+k}\rho(\alpha^n(x_i))\mu(\alpha^{n-2}(x_j)\cdot\alpha^{n-2}(x_{n+2}))\psi(x_1, \dots, \hat{x_j}, \dots, \hat{x_k} \dots, \hat{x_i}, \dots, x_{n+1}, x_k) \end{eqnarray}$

(4.72)

$\begin{eqnarray} &&+\sum\limits_{1\leq j < i < k\leq n+1}(-1)^{i+1}(-1)^{j+k-1}\rho(\alpha^n(x_i))\mu(\alpha^{n-2}(x_j)\cdot\alpha^{n-2}(x_{n+2}))\psi(x_1, \dots, \hat{x_j}, \dots, \hat{x_i} \dots, \hat{x_k}, \dots, x_{n+1}, x_k) \end{eqnarray}$

(4.73)

$\begin{eqnarray} &&+\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+1}(-1)^{j+k}\rho(\alpha^n(x_i))\mu(\alpha^{n-2}(x_j)\cdot\alpha^{n-2}(x_{n+2}))\psi(x_1, \dots, \hat{x_i}, \dots, \hat{x_j} \dots, \hat{x_k}, \dots, x_{n+1}, x_k) \end{eqnarray}$

(4.74)

$\begin{eqnarray} &&-\sum\limits_{1\leq j < k < i\leq n+1}(-1)^{i+1}(-1)^{j+k}\rho(\alpha^n(x_i))\mu(\alpha^{n-2}(x_k)\cdot\alpha^{n-2}(x_{n+2}))\psi(x_1, \dots, \hat{x_j}, \dots, \hat{x_k} \dots, \hat{x_i}, \dots, x_{n+1}, x_j) \end{eqnarray}$

(4.75)

$\begin{eqnarray} &&-\sum\limits_{1\leq j < i < k\leq n+1}(-1)^{i+1}(-1)^{j+k-1}\rho(\alpha^n(x_i))\mu(\alpha^{n-2}(x_k)\cdot\alpha^{n-2}(x_{n+2}))\psi(x_1, \dots, \hat{x_j}, \dots, \hat{x_i} \dots, \hat{x_k}, \dots, x_{n+1}, x_j) \end{eqnarray}$

(4.76)

$\begin{eqnarray} &&-\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+1}(-1)^{j+k}\rho(\alpha^n(x_i))\mu(\alpha^{n-2}(x_k)\cdot\alpha^{n-2}(x_{n+2}))\psi(x_1, \dots, \hat{x_i}, \dots, \hat{x_j} \dots, \hat{x_k}, \dots, x_{n+1}, x_j) \end{eqnarray}$

(4.77)

$\begin{eqnarray} &&+\sum\limits_{1\leq j < k < i\leq n+1}(-1)^{i+1}(-1)^{j+k}\mu(\alpha^n(x_{n+2}))\rho([\alpha^{n-2}(x_j), \alpha^{n-2}(x_k)]_C)\psi(x_1, \dots, \hat{x_j}, \dots, \hat{x_k} \dots, \hat{x_i}, \dots, x_{n+1}, x_i) \end{eqnarray}$

(4.78)

$\begin{eqnarray} &&+\sum\limits_{1\leq j < i < k\leq n+1}(-1)^{i+1}(-1)^{j+k-1}\mu(\alpha^n(x_{n+2}))\rho([\alpha^{n-2}(x_j), \alpha^{n-2}(x_k)]_C)\psi(x_1, \dots, \hat{x_j}, \dots, \hat{x_i} \dots, \hat{x_k}, \dots, x_{n+1}, x_i) \end{eqnarray}$

(4.79)

$\begin{eqnarray} &&+\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+1}(-1)^{j+k}\mu(\alpha^n(x_{n+2}))\rho([\alpha^{n-2}(x_j), \alpha^{n-2}(x_k)]_C)\psi(x_1, \dots, \hat{x_i}, \dots, \hat{x_j} \dots, \hat{x_k}, \dots, x_{n+1}, x_i) \end{eqnarray}$

(4.80)

$\begin{eqnarray} &&+\sum\limits_{1\leq j < k < i\leq n+1}(-1)^{i+1}(-1)^{j+k}\mu(\alpha^n(x_{n+2}))\mu(\alpha^{n-2}(x_j)\cdot\alpha^{n-2}(x_i))\psi(x_1, \dots, \hat{x_j}, \dots, \hat{x_k} \dots, \hat{x_i}, \dots, x_{n+1}, x_k) \end{eqnarray}$

(4.81)

$\begin{eqnarray} &&+\sum\limits_{1\leq j < i < k\leq n+1}(-1)^{i+1}(-1)^{j+k-1}\mu(\alpha^n(x_{n+2}))\mu(\alpha^{n-2}(x_j)\cdot\alpha^{n-2}(x_i))\psi(x_1, \dots, \hat{x_j}, \dots, \hat{x_i} \dots, \hat{x_k}, \dots, x_{n+1}, x_k) \end{eqnarray}$

(4.82)

$\begin{eqnarray} &&+\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+1}(-1)^{j+k}\mu(\alpha^n(x_{n+2}))\mu(\alpha^{n-2}(x_j)\cdot\alpha^{n-2}(x_i))\psi(x_1, \dots, \hat{x_i}, \dots, \hat{x_j} \dots, \hat{x_k}, \dots, x_{n+1}, x_k) \end{eqnarray}$

(4.83)

$\begin{eqnarray} &&-\sum\limits_{1\leq j < k < i\leq n+1}(-1)^{i+1}(-1)^{j+k}\mu(\alpha^n(x_{n+2}))\mu(\alpha^{n-2}(x_k)\cdot\alpha^{n-2}(x_i))\psi(x_1, \dots, \hat{x_j}, \dots, \hat{x_k} \dots, \hat{x_i}, \dots, x_{n+1}, x_j) \end{eqnarray}$

(4.84)

$\begin{eqnarray} &&-\sum\limits_{1\leq j < i < k\leq n+1}(-1)^{i+1}(-1)^{j+k-1}\mu(\alpha^n(x_{n+2}))\mu(\alpha^{n-2}(x_k)\cdot\alpha^{n-2}(x_i))\psi(x_1, \dots, \hat{x_j}, \dots, \hat{x_i} \dots, \hat{x_k}, \dots, x_{n+1}, x_j) \end{eqnarray}$

(4.85)

$\begin{eqnarray} &&-\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+1}(-1)^{j+k}\mu(\alpha^n(x_{n+2}))\mu(\alpha^{n-2}(x_k)\cdot\alpha^{n-2}(x_i))\psi(x_1, \dots, \hat{x_i}, \dots, \hat{x_j} \dots, \hat{x_k}, \dots, x_{n+1}, x_j) \end{eqnarray}$

(4.86)

$\begin{eqnarray} &&-\sum\limits_{1\leq j < k < i\leq n+1}(-1)^{i+1}(-1)^{j+k}\rho([\alpha^{n-1}(x_j), \alpha^{n-1}(x_k)]_C)\psi(\alpha(x_1), \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_k)}, \end{eqnarray}$

(4.87)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_i)}, \dots, \alpha(x_{n+1}), x_i\cdot x_{n+2})\\ &&-\sum\limits_{1\leq j < i < k\leq n+1}(-1)^{i+1}(-1)^{j+k-1}\rho([\alpha^{n-1}(x_j), \alpha^{n-1}(x_k)]_C)\psi(\alpha(x_1), \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_i)}, \end{eqnarray}$

(4.88)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_k)}, \dots, \alpha(x_{n+1}), x_i\cdot x_{n+2})\\ &&-\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+1}(-1)^{j+k}\rho([\alpha^{n-1}(x_j), \alpha^{n-1}(x_k)]_C)\psi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \end{eqnarray}$

(4.89)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_k)}, \dots, \alpha(x_{n+1}), x_i\cdot x_{n+2})\\ &&-\sum\limits_{1\leq j < k < i\leq n+1}(-1)^{i+1}(-1)^{j+k}\mu(\alpha^{n-1}(x_j)\cdot\alpha^{n-2}(x_i\cdot x_{n+2}))\psi(\alpha(x_1), \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_k)}, \end{eqnarray}$

(4.90)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_i)}, \dots, \alpha(x_{n+1}), \alpha(x_k))\\ &&-\sum\limits_{1\leq j < i < k\leq n+1}(-1)^{i+1}(-1)^{j+k-1}\mu(\alpha^{n-1}(x_j)\cdot\alpha^{n-2}(x_i\cdot x_{n+2}))\psi(\alpha(x_1), \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_i)}, \end{eqnarray}$

(4.91)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_k)}, \dots, \alpha(x_{n+1}), \alpha(x_k))\\ &&-\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+1}(-1)^{j+k}\mu(\alpha^{n-1}(x_j)\cdot\alpha^{n-2}(x_i\cdot x_{n+2}))\psi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \end{eqnarray}$

(4.92)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_k)}, \dots, \alpha(x_{n+1}), \alpha(x_k))\\ &&+\sum\limits_{1\leq j < k < i\leq n+1}(-1)^{i+1}(-1)^{j+k}\mu(\alpha^{n-1}(x_k)\cdot\alpha^{n-2}(x_i\cdot x_{n+2}))\psi(\alpha(x_1), \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_k)}, \end{eqnarray}$

(4.93)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_i)}, \dots, \alpha(x_{n+1}), \alpha(x_j))\\ &&+\sum\limits_{1\leq j < i < k\leq n+1}(-1)^{i+1}(-1)^{j+k-1}\mu(\alpha^{n-1}(x_k)\cdot\alpha^{n-2}(x_i\cdot x_{n+2}))\psi(\alpha(x_1), \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_i)}, \end{eqnarray}$

(4.94)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_k)}, \dots, \alpha(x_{n+1}), \alpha(x_j))\\ &&+\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+1}(-1)^{j+k}\mu(\alpha^{n-1}(x_k)\cdot\alpha^{n-2}(x_i\cdot x_{n+2}))\psi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \end{eqnarray}$

(4.95)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_k)}, \dots, \alpha(x_{n+1}), \alpha(x_j))\\ &&+\sum\limits_{1\leq k < l < i < j\leq n+1}(-1)^{i+j}(-1)^{k+l}\rho([\alpha^{n-1}(x_k), \alpha^{n-1}(x_l)]_C)\psi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_k)}, \dots, \end{eqnarray}$

(4.96)

$\begin{eqnarray} &&\widehat{\alpha(x_l)}, \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+2}))\\ &&+\sum\limits_{1\leq k < i < l < j\leq n+1}(-1)^{i+j}(-1)^{k+l-1}\rho([\alpha^{n-1}(x_k), \alpha^{n-1}(x_l)]_C)\psi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_k)}, \dots, \end{eqnarray}$

(4.97)

$\begin{eqnarray} &&\widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_l)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+2}))\\ &&+\sum\limits_{1\leq k < i < j < l\leq n+1}(-1)^{i+j}(-1)^{k+l}\rho([\alpha^{n-1}(x_k), \alpha^{n-1}(x_l)]_C)\psi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_k)}, \dots, \end{eqnarray}$

(4.98)

$\begin{eqnarray} &&\widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_l)}, \dots, \alpha(x_{n+2}))\\ &&+\sum\limits_{1\leq i < k < l < j\leq n+1}(-1)^{i+j}(-1)^{k+l}\rho([\alpha^{n-1}(x_k), \alpha^{n-1}(x_l)]_C)\psi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \end{eqnarray}$

(4.99)

$\begin{eqnarray} &&\widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_l)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+2}))\\ &&+\sum\limits_{1\leq i < k < j < l\leq n+1}(-1)^{i+j}(-1)^{k+l-1}\rho([\alpha^{n-1}(x_k), \alpha^{n-1}(x_l)]_C)\psi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \end{eqnarray}$

(4.100)

$\begin{eqnarray} &&\widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_l)}, \dots, \alpha(x_{n+2}))\\ &&+\sum\limits_{1\leq i < j < k < l\leq n+1}(-1)^{i+j}(-1)^{k+l}\rho([\alpha^{n-1}(x_k), \alpha^{n-1}(x_l)]_C)\psi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \end{eqnarray}$

(4.101)

$\begin{eqnarray} &&\widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_l)}, \dots, \alpha(x_{n+2}))\\ &&+\sum\limits_{1\leq k < i < j\leq n+1}(-1)^{i+j}(-1)^k\rho([\alpha^{n-2}[x_i, x_j]_C, \alpha^{n-1}(x_k)]_C)\psi(\alpha(x_1), \dots, \widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_i)}, \end{eqnarray}$

(4.102)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+2}))\\ &&+\sum\limits_{1\leq i < k < j\leq n+1}(-1)^{i+j}(-1)^{k+1}\rho([\alpha^{n-2}[x_i, x_j]_C, \alpha^{n-1}(x_k)]_C)\psi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_k)}, \end{eqnarray}$

(4.103)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+2}))\\ &&+\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+j}(-1)^k\rho([\alpha^{n-2}[x_i, x_j]_C, \alpha^{n-1}(x_k)]_C)\psi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \end{eqnarray}$

(4.104)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_k)}, \dots, \alpha(x_{n+2}))\\ &&+\sum\limits_{1\leq k < l < i < j\leq n+1}(-1)^{i+j}(-1)^{k+l}\mu(\alpha^{n-1}(x_k)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_k)}, \dots, \end{eqnarray}$

(4.105)

$\begin{eqnarray} &&\widehat{\alpha(x_l)}, \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), \alpha(x_l))\\ &&+\sum\limits_{1\leq k < i < l < j\leq n+1}(-1)^{i+j}(-1)^{k+l-1}\mu(\alpha^{n-1}(x_k)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_k)}, \dots, \end{eqnarray}$

(4.106)

$\begin{eqnarray} &&\widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_l)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), \alpha(x_l))\\ &&+\sum\limits_{1\leq k < i < j < l\leq n+1}(-1)^{i+j}(-1)^{k+l}\mu(\alpha^{n-1}(x_k)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_k)}, \dots, \end{eqnarray}$

(4.107)

$\begin{eqnarray} &&\widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_l)}, \dots, \alpha(x_{n+1}), \alpha(x_l))\\ &&+\sum\limits_{1\leq i < k < l < j\leq n+1}(-1)^{i+j}(-1)^{k+l}\mu(\alpha^{n-1}(x_k)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \end{eqnarray}$

(4.108)

$\begin{eqnarray} &&\widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_l)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), \alpha(x_l))\\ &&+\sum\limits_{1\leq i < k < j < l\leq n+1}(-1)^{i+j}(-1)^{k+l-1}\mu(\alpha^{n-1}(x_k)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \end{eqnarray}$

(4.109)

$\begin{eqnarray} &&\widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_l)}, \dots, \alpha(x_{n+1}), \alpha(x_l))\\ &&+\sum\limits_{1\leq i < j < k < l\leq n+1}(-1)^{i+j}(-1)^{k+l}\mu(\alpha^{n-1}(x_k)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \end{eqnarray}$

(4.110)

$\begin{eqnarray} &&\widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_l)}, \dots, \alpha(x_{n+1}), \alpha(x_l))\\ &&-\sum\limits_{1\leq k < l < i < j\leq n+1}(-1)^{i+j}(-1)^{k+l}\mu(\alpha^{n-1}(x_l)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_k)}, \dots, \end{eqnarray}$

(4.111)

$\begin{eqnarray} &&\widehat{\alpha(x_l)}, \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), \alpha(x_k))\\ &&-\sum\limits_{1\leq k < i < l < j\leq n+1}(-1)^{i+j}(-1)^{k+l-1}\mu(\alpha^{n-1}(x_l)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_k)}, \dots, \end{eqnarray}$

(4.112)

$\begin{eqnarray} &&\widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_l)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), \alpha(x_k))\\ &&-\sum\limits_{1\leq k < i < j < l\leq n+1}(-1)^{i+j}(-1)^{k+l}\mu(\alpha^{n-1}(x_l)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_k)}, \dots, \end{eqnarray}$

(4.113)

$\begin{eqnarray} &&\widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_l)}, \dots, \alpha(x_{n+1}), \alpha(x_k))\\ &&-\sum\limits_{1\leq i < k < l < j\leq n+1}(-1)^{i+j}(-1)^{k+l}\mu(\alpha^{n-1}(x_l)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \end{eqnarray}$

(4.114)

$\begin{eqnarray} &&\widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_l)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), \alpha(x_k))\\ &&-\sum\limits_{1\leq i < k < j < l\leq n+1}(-1)^{i+j}(-1)^{k+l-1}\mu(\alpha^{n-1}(x_l)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \end{eqnarray}$

(4.115)

$\begin{eqnarray} &&\widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_l)}, \dots, \alpha(x_{n+1}), \alpha(x_k))\\ &&-\sum\limits_{1\leq i < j < k < l\leq n+1}(-1)^{i+j}(-1)^{k+l}\mu(\alpha^{n-1}(x_l)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_i, x_j]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \end{eqnarray}$

(4.116)

$\begin{eqnarray} &&\widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_l)}, \dots, \alpha(x_{n+1}), \alpha(x_k))\\ &&+\sum\limits_{1\leq k < i < j\leq n+1}(-1)^{i+j}(-1)^k\mu(\alpha^{n-2}[x_i, x_j]_C\cdot\alpha^{n-1}(x_{n+2}))\psi(\alpha(x_1), \dots, \widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_i)}, \end{eqnarray}$

(4.117)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), \alpha(x_k))\\ &&+\sum\limits_{1\leq i < k < j\leq n+1}(-1)^{i+j}(-1)^{k+1}\mu(\alpha^{n-2}[x_i, x_j]_C\cdot\alpha^{n-1}(x_{n+2}))\psi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_k)}, \end{eqnarray}$

(4.118)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), \alpha(x_k))\\ &&+\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+j}(-1)^k\mu(\alpha^{n-2}[x_i, x_j]_C\cdot\alpha^{n-1}(x_{n+2}))\psi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \end{eqnarray}$

(4.119)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_k)}, \dots, \alpha(x_{n+1}), \alpha(x_k))\\ &&-\sum\limits_{1\leq k < i < j\leq n+1}(-1)^{i+j}(-1)^k\mu(\alpha^{n-1}(x_k)\cdot\alpha^{n-1}(x_{n+2}))\psi(\alpha(x_1), \dots, \widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_i)}, \end{eqnarray}$

(4.120)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), [x_i, x_j]_C)\\ &&-\sum\limits_{1\leq i < k < j\leq n+1}(-1)^{i+j}(-1)^{k+1}\mu(\alpha^{n-1}(x_k)\cdot\alpha^{n-1}(x_{n+2}))\psi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_k)}, \end{eqnarray}$

(4.121)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), [x_i, x_j]_C)\\ &&-\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+j}(-1)^k\mu(\alpha^{n-1}(x_k)\cdot\alpha^{n-1}(x_{n+2}))\psi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \\ \nonumber&&\dots, \widehat{\alpha(x_k)}, \dots, \alpha(x_{n+1}), [x_i, x_j]_C), \end{eqnarray}$

(4.122)

and

$\begin{eqnarray} &&\partial_{\alpha\omega}(\partial_{\alpha\alpha} \psi)(x_1, \dots, x_{n+2})\\ & = &\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+j}\rho([\alpha^{n-1}(x_i), \alpha^{n-1}(x_j)]_C)(\partial_{\alpha\alpha} \psi)(x_1, \dots, \hat{x_i}, \dots, \hat{x_j}, \dots, x_{n+2})\\ &&+\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+j}\mu(\alpha^{n-1}(x_i)\cdot\alpha^{n-1}(x_{n+2}))(\partial_{\alpha\alpha} \psi)(x_1, \dots, \hat{x_i}, \dots, \hat{x_j}, \dots, x_{n+1}, x_j)\\ &&-\sum\limits_{1\leq i < j\leq n+1}(-1)^{i+j}\mu(\alpha^{n-1}(x_j)\cdot\alpha^{n-1}(x_{n+2}))(\partial_{\alpha\alpha} \psi)(x_1, \dots, \hat{x_i}, \dots, \hat{x_j}, \dots, x_{n+1}, x_i)\\ & = &\sum\limits_{1\leq k < i < j\leq n+1}(-1)^{i+j}(-1)^k\rho([\alpha^{n-1}(x_i), \alpha^{n-1}(x_j)]_C)\rho(\alpha^{n-1}(x_k))\psi(x_1, \dots, \hat{x_k}, \dots, \hat{x_i}, \dots, \hat{x_j}\dots, x_{n+2}) \end{eqnarray}$

(4.123)

$\begin{eqnarray} &&+\sum\limits_{1\leq i < k < j\leq n+1}(-1)^{i+j}(-1)^{k+1}\rho([\alpha^{n-1}(x_i), \alpha^{n-1}(x_j)]_C)\rho(\alpha^{n-1}(x_k))\psi(x_1, \dots, \hat{x_i}, \dots, \hat{x_k}, \dots, \hat{x_j}\dots, x_{n+2}) \end{eqnarray}$

(4.124)

$\begin{eqnarray} &&+\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+j}(-1)^k\rho([\alpha^{n-1}(x_i), \alpha^{n-1}(x_j)]_C)\rho(\alpha^{n-1}(x_k))\psi(x_1, \dots, \hat{x_i}, \dots, \hat{x_j}, \dots, \hat{x_k}, \dots, x_{n+2}) \end{eqnarray}$

(4.125)

$\begin{eqnarray} &&+\sum\limits_{1\leq k < i < j\leq n+1}(-1)^{i+j}(-1)^k\rho([\alpha^{n-1}(x_i), \alpha^{n-1}(x_j)]_C)\mu(\alpha^{n-1}(x_{n+2}))\psi(x_1, \dots, \hat{x_k}, \dots, \hat{x_i}, \dots, \hat{x_j}\dots, x_{n+1}, x_k) \end{eqnarray}$

(4.126)

$\begin{eqnarray} &&+\sum\limits_{1\leq i < k < j\leq n+1}(-1)^{i+j}(-1)^{k+1}\rho([\alpha^{n-1}(x_i), \alpha^{n-1}(x_j)]_C)\mu(\alpha^{n-1}(x_{n+2}))\psi(x_1, \dots, \hat{x_i}, \dots, \hat{x_k}, \dots, \hat{x_j}\dots, x_{n+1}, x_k) \end{eqnarray}$

(4.127)

$\begin{eqnarray} &&+\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+j}(-1)^k\rho([\alpha^{n-1}(x_i), \alpha^{n-1}(x_j)]_C)\mu(\alpha^{n-1}(x_{n+2}))\psi(x_1, \dots, \hat{x_i}, \dots, \hat{x_j}, \dots, \hat{x_k}\dots, x_{n+1}, x_k) \end{eqnarray}$

(4.128)

$\begin{eqnarray} &&-\sum\limits_{1\leq k < i < j\leq n+1}(-1)^{i+j}(-1)^k\rho([\alpha^{n-1}(x_i), \alpha^{n-1}(x_j)]_C)\psi(\alpha(x_1), \dots, \widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_i)}, \end{eqnarray}$

(4.129)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), x_k\cdot x_{n+2})\\ &&-\sum\limits_{1\leq i < k < j\leq n+1}(-1)^{i+j}(-1)^{k+1}\rho([\alpha^{n-1}(x_i), \alpha^{n-1}(x_j)]_C)\psi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_k)}, \end{eqnarray}$

(4.130)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), x_k\cdot x_{n+2})\\ &&-\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+j}(-1)^k\rho([\alpha^{n-1}(x_i), \alpha^{n-1}(x_j)]_C)\psi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \end{eqnarray}$

(4.131)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_k)}, \dots, \alpha(x_{n+1}), x_k\cdot x_{n+2})\\ &&+\sum\limits_{1\leq k < l < i < j\leq n+1}(-1)^{i+j}(-1)^{k+l-1}\rho([\alpha^{n-1}(x_i), \alpha^{n-1}(x_j)]_C)\psi([x_k, x_l]_C, \alpha(x_1), \dots, \widehat{\alpha(x_k)}, \end{eqnarray}$

(4.132)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_l)}, \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+2}))\\ &&+\sum\limits_{1\leq k < i < l < j\leq n+1}(-1)^{i+j}(-1)^{k+l}\rho([\alpha^{n-1}(x_i), \alpha^{n-1}(x_j)]_C)\psi([x_k, x_l]_C, \alpha(x_1), \dots, \widehat{\alpha(x_k)}, \end{eqnarray}$

(4.133)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_l)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+2}))\\ &&+\sum\limits_{1\leq k < i < j < l\leq n+1}(-1)^{i+j}(-1)^{k+l-1}\rho([\alpha^{n-1}(x_i), \alpha^{n-1}(x_j)]_C)\psi([x_k, x_l]_C, \alpha(x_1), \dots, \widehat{\alpha(x_k)}, \end{eqnarray}$

(4.134)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_l)}, \dots, \alpha(x_{n+2}))\\ &&+\sum\limits_{1\leq i < k < l < j\leq n+1}(-1)^{i+j}(-1)^{k+l-1}\rho([\alpha^{n-1}(x_i), \alpha^{n-1}(x_j)]_C)\psi([x_k, x_l]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \end{eqnarray}$

(4.135)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_l)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+2}))\\ &&+\sum\limits_{1\leq i < k < j < l\leq n+1}(-1)^{i+j}(-1)^{k+l}\rho([\alpha^{n-1}(x_i), \alpha^{n-1}(x_j)]_C)\psi([x_k, x_l]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \end{eqnarray}$

(4.136)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_l)}, \dots, \alpha(x_{n+2}))\\ &&+\sum\limits_{1\leq i < j < k < l\leq n+1}(-1)^{i+j}(-1)^{k+l-1}\rho([\alpha^{n-1}(x_i), \alpha^{n-1}(x_j)]_C)\psi([x_k, x_l]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \end{eqnarray}$

(4.137)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_l)}, \dots, \alpha(x_{n+2}))\\ &&+\sum\limits_{1\leq k < i < j\leq n+1}(-1)^{i+j}(-1)^k\mu(\alpha^{n-1}(x_i)\cdot\alpha^{n-1}(x_{n+2}))\rho(\alpha^{n-1}(x_k))\psi(x_1, \dots, \hat{x_k}, \dots, \hat{x_i}, \dots, \hat{x_j}\dots, x_{n+1}, x_j) \end{eqnarray}$

(4.138)

$\begin{eqnarray} &&+\sum\limits_{1\leq i < k < j\leq n+1}(-1)^{i+j}(-1)^{k+1}\mu(\alpha^{n-1}(x_i)\cdot\alpha^{n-1}(x_{n+2}))\rho(\alpha^{n-1}(x_k))\psi(x_1, \dots, \hat{x_i}, \dots, \hat{x_k}, \dots, \hat{x_j}\dots, x_{n+1}, x_j) \end{eqnarray}$

(4.139)

$\begin{eqnarray} &&+\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+j}(-1)^k\mu(\alpha^{n-1}(x_i)\cdot\alpha^{n-1}(x_{n+2}))\rho(\alpha^{n-1}(x_k))\psi(x_1, \dots, \hat{x_i}, \dots, \hat{x_j}, \dots, \hat{x_k}\dots, x_{n+1}, x_j) \end{eqnarray}$

(4.140)

$\begin{eqnarray} &&+\sum\limits_{1\leq k < i < j\leq n+1}(-1)^{i+j}(-1)^k\mu(\alpha^{n-1}(x_i)\cdot\alpha^{n-1}(x_{n+2}))\mu(\alpha^{n-1}(x_j))\psi(x_1, \dots, \hat{x_k}, \dots, \hat{x_i}, \dots, \hat{x_j}\dots, x_{n+1}, x_k) \end{eqnarray}$

(4.141)

$\begin{eqnarray} &&+\sum\limits_{1\leq i < k < j\leq n+1}(-1)^{i+j}(-1)^{k+1}\mu(\alpha^{n-1}(x_i)\cdot\alpha^{n-1}(x_{n+2}))\mu(\alpha^{n-1}(x_j))\psi(x_1, \dots, \hat{x_i}, \dots, \hat{x_k}, \dots, \hat{x_j}\dots, x_{n+1}, x_k) \end{eqnarray}$

(4.142)

$\begin{eqnarray} &&+\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+j}(-1)^k\mu(\alpha^{n-1}(x_i)\cdot\alpha^{n-1}(x_{n+2}))\mu(\alpha^{n-1}(x_j))\psi(x_1, \dots, \hat{x_i}, \dots, \hat{x_j}, \dots, \hat{x_k}\dots, x_{n+1}, x_k) \end{eqnarray}$

(4.143)

$\begin{eqnarray} &&-\sum\limits_{1\leq k < i < j\leq n+1}(-1)^{i+j}(-1)^k\mu(\alpha^{n-1}(x_i)\cdot\alpha^{n-1}(x_{n+2}))\psi(\alpha(x_1), \dots, \widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_i)}, \end{eqnarray}$

(4.144)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), x_k\cdot x_j)\\ &&-\sum\limits_{1\leq i < k < j\leq n+1}(-1)^{i+j}(-1)^{k+1}\mu(\alpha^{n-1}(x_i)\cdot\alpha^{n-1}(x_{n+2}))\psi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_k)}, \end{eqnarray}$

(4.145)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), x_k\cdot x_j)\\ &&-\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+j}(-1)^k\mu(\alpha^{n-1}(x_i)\cdot\alpha^{n-1}(x_{n+2}))\psi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \end{eqnarray}$

(4.146)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_k)}, \dots, \alpha(x_{n+1}), x_k\cdot x_j)\\ &&+\sum\limits_{1\leq k < l < i < j\leq n+1}(-1)^{i+j}(-1)^{k+l-1}\mu(\alpha^{n-1}(x_i)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_k, x_l]_C, \alpha(x_1), \dots, \widehat{\alpha(x_k)}, \end{eqnarray}$

(4.147)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_l)}, \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), \alpha(x_j))\\ &&+\sum\limits_{1\leq k < i < l < j\leq n+1}(-1)^{i+j}(-1)^{k+l}\mu(\alpha^{n-1}(x_i)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_k, x_l]_C, \alpha(x_1), \dots, \widehat{\alpha(x_k)}, \end{eqnarray}$

(4.148)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_l)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), \alpha(x_j))\\ &&+\sum\limits_{1\leq k < i < j < l\leq n+1}(-1)^{i+j}(-1)^{k+l-1}\mu(\alpha^{n-1}(x_i)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_k, x_l]_C, \alpha(x_1), \dots, \widehat{\alpha(x_k)}, \end{eqnarray}$

(4.149)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_l)}, \dots, \alpha(x_{n+1}), \alpha(x_j))\\ &&+\sum\limits_{1\leq i < k < l < j\leq n+1}(-1)^{i+j}(-1)^{k+l-1}\mu(\alpha^{n-1}(x_i)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_k, x_l]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \end{eqnarray}$

(4.150)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_l)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), \alpha(x_j))\\ &&+\sum\limits_{1\leq i < k < j < l\leq n+1}(-1)^{i+j}(-1)^{k+l}\mu(\alpha^{n-1}(x_i)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_k, x_l]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \end{eqnarray}$

(4.151)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_l)}, \dots, \alpha(x_{n+1}), \alpha(x_j))\\ &&+\sum\limits_{1\leq i < j < k < l\leq n+1}(-1)^{i+j}(-1)^{k+l-1}\mu(\alpha^{n-1}(x_i)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_k, x_l]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \end{eqnarray}$

(4.152)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_l)}, \dots, \alpha(x_{n+1}), \alpha(x_j))\\ &&-\sum\limits_{1\leq k < i < j\leq n+1}(-1)^{i+j}(-1)^k\mu(\alpha^{n-1}(x_j)\cdot\alpha^{n-1}(x_{n+2}))\rho(\alpha^{n-1}(x_k))\psi(x_1, \dots, \hat{x_k}, \dots, \hat{x_i}, \dots, \hat{x_j}\dots, x_{n+1}, x_i) \end{eqnarray}$

(4.153)

$\begin{eqnarray} &&-\sum\limits_{1\leq i < k < j\leq n+1}(-1)^{i+j}(-1)^{k+1}\mu(\alpha^{n-1}(x_j)\cdot\alpha^{n-1}(x_{n+2}))\rho(\alpha^{n-1}(x_k))\psi(x_1, \dots, \hat{x_i}, \dots, \hat{x_k}, \dots, \hat{x_j}\dots, x_{n+1}, x_i) \end{eqnarray}$

(4.154)

$\begin{eqnarray} &&-\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+j}(-1)^k\mu(\alpha^{n-1}(x_j)\cdot\alpha^{n-1}(x_{n+2}))\rho(\alpha^{n-1}(x_k))\psi(x_1, \dots, \hat{x_i}, \dots, \hat{x_j}, \dots, \hat{x_k}\dots, x_{n+1}, x_i) \end{eqnarray}$

(4.155)

$\begin{eqnarray} &&-\sum\limits_{1\leq k < i < j\leq n+1}(-1)^{i+j}(-1)^k\mu(\alpha^{n-1}(x_j)\cdot\alpha^{n-1}(x_{n+2}))\mu(\alpha^{n-1}(x_i))\psi(x_1, \dots, \hat{x_k}, \dots, \hat{x_i}, \dots, \hat{x_j}\dots, x_{n+1}, x_k) \end{eqnarray}$

(4.156)

$\begin{eqnarray} &&-\sum\limits_{1\leq i < k < j\leq n+1}(-1)^{i+j}(-1)^{k+1}\mu(\alpha^{n-1}(x_j)\cdot\alpha^{n-1}(x_{n+2}))\mu(\alpha^{n-1}(x_i))\psi(x_1, \dots, \hat{x_i}, \dots, \hat{x_k}, \dots, \hat{x_j}\dots, x_{n+1}, x_k) \end{eqnarray}$

(4.157)

$\begin{eqnarray} &&-\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+j}(-1)^k\mu(\alpha^{n-1}(x_j)\cdot\alpha^{n-1}(x_{n+2}))\mu(\alpha^{n-1}(x_i))\psi(x_1, \dots, \hat{x_i}, \dots, \hat{x_j}, \dots, \hat{x_k}\dots, x_{n+1}, x_k) \end{eqnarray}$

(4.158)

$\begin{eqnarray} &&+\sum\limits_{1\leq k < i < j\leq n+1}(-1)^{i+j}(-1)^k\mu(\alpha^{n-1}(x_j)\cdot\alpha^{n-1}(x_{n+2}))\psi(\alpha(x_1), \dots, \widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_i)}, \end{eqnarray}$

(4.159)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), x_k\cdot x_i)\\ &&+\sum\limits_{1\leq i < k < j\leq n+1}(-1)^{i+j}(-1)^{k+1}\mu(\alpha^{n-1}(x_j)\cdot\alpha^{n-1}(x_{n+2}))\psi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_k)}, \end{eqnarray}$

(4.160)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), x_k\cdot x_i)\\ &&+\sum\limits_{1\leq i < j < k\leq n+1}(-1)^{i+j}(-1)^k\mu(\alpha^{n-1}(x_j)\cdot\alpha^{n-1}(x_{n+2}))\psi(\alpha(x_1), \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \end{eqnarray}$

(4.161)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_k)}, \dots, \alpha(x_{n+1}), x_k\cdot x_i)\\ &&-\sum\limits_{1\leq k < l < i < j\leq n+1}(-1)^{i+j}(-1)^{k+l-1}\mu(\alpha^{n-1}(x_j)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_k, x_l]_C, \alpha(x_1), \dots, \widehat{\alpha(x_k)}, \end{eqnarray}$

(4.162)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_l)}, \dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), \alpha(x_i))\\ &&-\sum\limits_{1\leq k < i < l < j\leq n+1}(-1)^{i+j}(-1)^{k+l}\mu(\alpha^{n-1}(x_j)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_k, x_l]_C, \alpha(x_1), \dots, \widehat{\alpha(x_k)}, \end{eqnarray}$

(4.163)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_l)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), \alpha(x_i))\\ &&-\sum\limits_{1\leq k < i < j < l\leq n+1}(-1)^{i+j}(-1)^{k+l-1}\mu(\alpha^{n-1}(x_j)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_k, x_l]_C, \alpha(x_1), \dots, \widehat{\alpha(x_k)}, \end{eqnarray}$

(4.164)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_i)}, \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_l)}, \dots, \alpha(x_{n+1}), \alpha(x_i))\\ &&-\sum\limits_{1\leq i < k < l < j\leq n+1}(-1)^{i+j}(-1)^{k+l-1}\mu(\alpha^{n-1}(x_j)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_k, x_l]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \end{eqnarray}$

(4.165)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_l)}, \dots, \widehat{\alpha(x_j)}, \dots, \alpha(x_{n+1}), \alpha(x_i))\\ &&-\sum\limits_{1\leq i < k < j < l\leq n+1}(-1)^{i+j}(-1)^{k+l}\mu(\alpha^{n-1}(x_j)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_k, x_l]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \end{eqnarray}$

(4.166)

$\begin{eqnarray} &&\dots, \widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_l)}, \dots, \alpha(x_{n+1}), \alpha(x_i))\\ &&-\sum\limits_{1\leq i < j < k < l\leq n+1}(-1)^{i+j}(-1)^{k+l-1}\mu(\alpha^{n-1}(x_j)\cdot\alpha^{n-1}(x_{n+2}))\psi([x_k, x_l]_C, \alpha(x_1), \dots, \widehat{\alpha(x_i)}, \\ \nonumber&&\dots, \widehat{\alpha(x_j)}, \dots, \widehat{\alpha(x_k)}, \dots, \widehat{\alpha(x_l)}, \dots, \alpha(x_{n+1}), \alpha(x_i)). \end{eqnarray}$

(4.167)

By the definition of the sub-adjacent Hom-Lie algebra, the sum of (4.102), (4.103) and (4.104) is zero. By the definition of Hom-pre-Lie algebras, the sum of (4.90), (4.95) and (4.118) is zero, the sum of (4.91), (4.92) and (4.119) is zero, the sum of (4.93), (4.94) and (4.117) is zero. Obviously, the sum of (4.96) and (4.137) is zero, the sum of (4.97) and (4.136) is zero, the sum of (4.98) and (4.135) is zero, the sum of (4.99) and (4.134) is zero, the sum of (4.100) and (4.133) is zero, the sum of (4.101) and (4.132) is zero, the sum of (4.87) and (4.131) is zero, the sum of (4.88) and (4.130) is zero, the sum of (4.89) and (4.129) is zero, the sum of (4.105) and (4.152) is zero, the sum of (4.106) and (4.151) is zero, the sum of (4.107) and (4.150) is zero, the sum of (4.108) and (4.149) is zero, the sum of (4.109) and (4.148) is zero, the sum of (4.110) and (4.147) is zero, the sum of (4.111) and (4.167) is zero, the sum of (4.112) and (4.166) is zero, the sum of (4.113) and (4.165) is zero, the sum of (4.114) and (4.164) is zero, the sum of (4.115) and (4.163) is zero, the sum of (4.116) and (4.162) is zero. By the definition of the sub-adjacent Lie bracket, the sum of (4.120), (4.145) and (4.146) is zero, the sum of (4.121), (4.144) and (4.161) is zero, the sum of (4.122), (4.159) and (4.160) is zero. Since $(V, \beta, \rho)$ is a representation of the sub-adjacent Hom-Lie algebra $A^C$ , the sum of (4.69), (4.70), (4.71), (4.123), (4.124) and (4.125) is zero. Since $(V, \beta, \rho, \mu)$ is a representation of the Hom-pre-Lie algebra $(A, \cdot, \alpha)$ , the sum of (4.73), (4.74), (4.78), (4.82), (4.83), (4.128), (4.138), (4.139), (4.143) and (4.158) is zero, the sum of (4.72), (4.77), (4.79), (4.81), (4.86), (4.127), (4.140), (4.142), (4.153) and (4.157) is zero, the sum of (4.75), (4.76), (4.80), (4.84), (4.85), (4.126), (4.141), (4.154), (4.155) and (4.156) is zero. Thus, we have $\partial_{\omega\omega}\circ \partial_{\alpha\omega}+\partial_{\alpha\omega}\circ \partial_{\alpha\alpha} = 0$ .

Similarly, we have $\partial_{\omega\alpha}\circ \partial_{\omega\omega}+\partial_{\alpha\alpha}\circ \partial_{\omega\alpha} = 0$ and $\partial_{\omega\alpha}\circ \partial_{\alpha\omega}+\partial_{\alpha\alpha}\circ \partial_{\alpha\alpha} = 0$ . This finishes the proof.

Acknowledgments

We give warmest thanks to Yunhe Sheng for helpful comments that improve the paper. This work is supported by National Natural Science Foundation of China (Grant No. 12001226).

Conflict of interest

The authors declare there is no conflicts of interest.

Acknowledgments

The support for this research was provided through different funding that were used to support and develop different and separate parts of total research. There was no overlap in the use of funds for the same activity. The funding sources were: (i) PSR-Rural Development Program Sicily 2014/2022-Sub-measure 16.01 “Support for the establishment and management of operational groups of the EIP on agricultural productivity and sustainability”-DDG. no. 5428 of 29/12/2021, project title: “Aromaticity and Longevity of Catarratto: Innovation in Field and Cellar based on Biodiversity, Subproducts and High Sustainability Bio-technologies”. Grant number: 24250128113; (ii) Project PRIMA MEDIET4ALL−“Transnational Movement to Support the Sustainable Transition towards a Healthy and Eco-friendly Agri-Food System through the Promotion of MEDIET and its Lifestyle in Modern Society.”−Transnational call PRIMA Partnership for Reaserch and Innovative in the Mediterranean Area-Call 2022, Tematic Area 3-Food value chain: Topic 2.3.1-2022 (RIA) Enabling the transition to healthy and sustainable dietary behaviour. Grant number: B73C23000060001; (iii) Supply Chain and District Contracts (5th call) project “White Wine Identity: new horizons for an integrated and sustainable development of the Italian white wine supply chain”, which was funded by the Ministry of Agriculture, Food Sovereignty and Forests. Grant number: PRI-1058; (iv) Convenzione di ricerca: “Biotecnologie Sostenibili per il Miglioramento della Qualità Tecnologia e Sensoriale dei Vini” tra Dipartimento di Scienze Agrarie, Alimentari e Forestali (SAAF) e HTS Enologia di Luigi Scavone; prot. 5574 04/10/2021; CON 0404.

Conflict of interest

The authors declare no conflict of interest.

Author contributions

Conceptualization, N.F., G.M. and A.A.; methodology, A.M. and A.Po.; software, R.P. and V.N.; validation, N.F., A.A. and G.M.; formal analysis, V.C., E.V., D.A., A.V., V.S. and A.Pi.; investigation, V.C., R.P., F.A. and G.N.; resources, N.F., F.A. and G.N.; data curation, E.V., V.C., M.C., R.P. and A.A.; writing—original draft preparation, E.V., R.P., A.A. and L.S.; writing—review and editing, N.F., A.A., G.M. and L.S.; visualization, A.A. and N.F.; supervision, A.A., N.F. and G.M.; project administration, N.F.; funding acquisition, N.F. All authors have read and agreed to the published version of the manuscript.

References

[1]	Ferrer-Gallego R, Puxeu M, Nart E, et al. (2017) Evaluation of Tempranillo and Albariño SO₂-free wines produced by different chemical alternatives and winemaking procedures. Food Res Int 102: 647-657. https://doi.org/10.1016/j.foodres.2017.09.046
[2]	Guerrero RF, Cantos-Villar E (2015) Demonstrating the efficiency of sulphur dioxide replacements in wine: A parameter review. Trends Food Sci Technol 42: 27-43. https://doi.org/10.1016/j.tifs.2014.11.004
[3]	Christofi S, Malliaris D, Katsaros G, et al. (2020) Limit SO₂ content of wines by applying High Hydrostatic Pressure. Innov Food Sci Emerg Technol 62: 102342. https://doi.org/10.1016/j.ifset.2020.102342
[4]	Santos MC, Nunes C, Cappelle J, et al. (2013) Effect of high pressure treatments on the physicochemical properties of a sulphur dioxide-free red wine. Food Chem 141: 2558-2566. https://doi.org/10.1016/j.foodchem.2013.05.022
[5]	Roullier-Gall C, Hemmler D, Gonsior M, et al. (2017) Sulfites and the wine metabolome. Food Chem 237: 106-113. https://doi.org/10.1016/j.foodchem.2017.05.039
[6]	Di Gianvito P, Englezos V, Rantsiou K, et al. (2022) Bioprotection strategies in winemaking. Int J Food Microbiol 364: 109532. https://doi.org/10.1016/j.ijfoodmicro.2022.109532
[7]	Ferraz P, Cassio F, Lucas C (2019) Potential of yeasts as biocontrol agents of the phytopathogen causing cacao witches' broom disease: Is microbial warfare a solution?. Front Microbiol 10: 1766. https://doi.org/10.3389/fmicb.2019.01766
[8]	Keswani C, Singh HB, Hermosa R, et al. (2019) Antimicrobial secondary metabolites from agriculturally important fungi as next biocontrol agents. Appl Microbiol Biotechnol 103: 9287-9303. https://doi.org/10.1007/s00253-019-10209-2103
[9]	OIV (International Organisation of Vine and Wine)Recueil des methodes internationales d'analyses des vins et des moûts (2010). Avaible from: https://www.oiv.int/fr/normes-et-documents-techniques/methodes-danalyse/recueil-des-methodes-internationales-danalyse-des-vins-et-des-mouts-2-vol
[10]	Directive 2003/89/EC of the European parliament and of the council amending directive 2000/13/EC as regards indication of the ingredients present in foodstuffs. Avaible from: http://data.europa.eu/eli/dir/2003/89/oj
[11]	Lisanti MT, Blaiotta G, Nioi C, et al. (2019) Alternative methods to SO₂ for microbiological stabilization of wine. Compr Rev Food Sci Food Saf 18: 455-479. https://doi.org/10.1111/1541-4337.12422
[12]	Silva M, Gama J, Pinto N, et al. (2019) Sulfite concentration and the occurrence of headache in young adults: A prospective study. Eur J Clin Nutr 73: 1316-1322. https://doi.org/10.1038/s41430-019-0420-2
[13]	Santos MC, Nunes C, Rocha MAM, et al. (2015) High pressure treatments accelerate changes in volatile composition of sulphur dioxide-free wine during bottle storage. Food Chem 188: 406-414. https://doi.org/10.1016/j.foodchem.2015.05.002
[14]	Fredericks IN, du Toit M, Krügel M (2011) Efficacy of ultraviolet radiation as an alternative technology to inactivate microorganisms in grape juices and wines. Food Microbiol 28: 510-517. https://doi.org/10.1016/j.fm.2010.10.018
[15]	Pandin C, Le Coq D, Canette A, et al. (2017) Should the biofilm mode of life be taken into consideration for microbial biocontrol agents?. Microb Biotechnol 10: 719-734. https://doi.org/10.1111/1751-7915.12693
[16]	Bauer MA, Kainz K, Carmona-Gutierrez D, et al. (2018) Microbial wars: Competition in ecological niches and within the microbiome. Microb Cell 5: 215. https://doi.org/10.15698/mic2018.05.628
[17]	Parijs I, Steenackers HP (2018) Competitive inter-species interactions underlie the increased antimicrobial tolerance in multispecies brewery biofilms. ISME J 12: 2061-2075. https://doi.org/10.1038/s41396-018-0146-5
[18]	Ghoul M, Mitri S (2016) The ecology and evolution of microbial competition. Trends Microbiol 24: 833-845. https://doi.org/10.1016/j.tim.2016.06.011
[19]	Curiel JA, Morales P, Gonzalez R, et al. (2017) Different non-Saccharomyces yeast species stimulate nutrient consumption in Saccharomyces cerevisiae mixed cultures. Front Microbiol 8: 2121. https://doi.org/10.3389/fmicb.2017.02121
[20]	Petitgonnet C, Klein GL, Roullier-Gall C, et al. (2019) Influence of cell-cell contact between L. thermotolerans and S. cerevisiae on yeast interactions and the exo-metabolome. Food Microbiol 83: 122-133. https://doi.org/10.1016/j.fm.2019.05.005
[21]	Prior KJ, Bauer FF, Divol B (2019) The utilisation of nitrogenous compound by commercial non-Saccharomyces yeasts associated with wine. Food Microbiol 79: 75-84. https://doi.org/10.1016/j.fm.2018.12.002
[22]	Siedler S, Balti R, Neves AR (2019) Bioprotective mechanisms of lactic acid bacteria against fungal spoilage of food. Curr Opin Biotechnol 56: 138-146. https://doi.org/10.1016/j.copbio.2018.11.015
[23]	Pallmann CL, Brown JA, Olineka TL, et al. (2001) Use of WL medium to profile native flora fermentations. Am J Enol Vitic 52: 198-203. http://dx.doi.org/10.5344/ajev.2001.52.3.198
[24]	Couto MB, Reizinho RG, Duarte FL (2005) Partial 26S rDNA restriction analysis as a tool to characterise non-Saccharomyces yeasts present during red wine fermentations. Int J Food Microbiol 102: 49-56. https://doi.org/10.1016/j.ijfoodmicro.2005.01.005
[25]	ISO 15214Microbiology of food and animal feeding stuffs–Horizontal method for the enumeration of mesophilic lactic acid bacteria–Colony-count technique at 30 °C (1998).
[26]	OIV (International Organisation of Vine and Wine)Compendium of international methods of wine and must analysis (2020). Available from: https://www.oiv.int/en/technical-standards-and-documents/methods-of-analysis/compendium-of-international-methods-of-analysis-of-wines-and-musts-2-vol
[27]	OIV (International Organisation of Vine and Wine)Compendium of international methods of wine and must analysis (2020). Available from: https://www.oiv.int/en/technical-standards-and-documents/methods-of-analysis/compendium-of-international-methods-of-analysis-of-wines-and-musts-2-vol
[28]	Matraxia M, Alfonzo A, Prestianni R, et al. (2021) Non-conventional yeasts from fermented honey by-products: Focus on Hanseniaspora uvarum strains for craft beer production. Food Microbiol 99: 103806. https://doi.org/10.1016/j.fm.2021.103806
[29]	Chawafambira A (2021) The effect of incorporating herbal (Lippia javanica) infusion on the phenolic, physicochemical, and sensorial properties of fruit wine. Food Sci Nutr 9: 4539-4549. https://doi.org/10.1002/fsn3.2432
[30]	Francesca N, Naselli V, Prestianni R, et al. (2024) Impact of two new non-conventional yeasts, Candida oleophila and Starmerella lactis-condensi, isolated from sugar-rich substrates, on Frappato wine aroma. Food Biosci 57: 103500. https://doi.org/10.1016/j.fbio.2023.103500
[31]	Jackson RS (2016) Wine Tasting: A Professional Handbook. Boston: Academic Press.
[32]	Issa-Issa H, Guclu G, Noguera-Artiaga L, et al. (2020) Aroma-active compounds, sensory profile, and phenolic composition of Fondillón. Food Chem 316: 126353. https://doi.org/10.1016/j.foodchem.2020.126353
[33]	Cochran WG, Cox GM (1957) Experimental designs. New York: John Wiley & Sons.
[34]	Di Maro E, Ercolini D, Coppola S (2007) Yeast dynamics during spontaneous wine fermentation of the Catalanesca grape. Int J Food Microbiol 117: 201-210. https://doi.org/10.1016/j.ijfoodmicro.2007.04.007
[35]	Varela C, Sengler F, Solomon M, et al. (2016) Volatile flavour profile of reduced alcohol wines fermented with the non-conventional yeast species Metschnikowia pulcherrima and Saccharomyces uvarum. Food Chem 209: 57-64. https://doi.org/10.1016/j.foodchem.2016.04.024
[36]	González SS, Barrio E, Querol A (2007) Molecular identification and characterization of wine yeasts isolated from Tenerife (Canary Island, Spain). J Appl Microbiol 102: 1018-1025. https://doi.org/10.1111/j.1365-2672.2006.03150.x
[37]	Sannino C, Francesca N, Corona O, et al. (2013) Effect of the natural winemaking process applied at industrial level on the microbiological and chemical characteristics of wine. J Biosci Bioeng 116: 347-356. https://doi.org/10.1016/j.jbiosc.2013.03.005
[38]	Minebois R, Pérez-Torrado R, Querol A (2020) A time course metabolism comparison among Saccharomyces cerevisiae, S. uvarum and S. kudriavzevii species in wine fermentation. Food Microbiol 90: 103484. https://doi.org/10.1016/j.fm.2020.103484
[39]	Morgan SC, Haggerty JJ, Johnston B, et al. (2019) Response to sulfur dioxide addition by two commercial Saccharomyces cerevisiae strains. Fermentation 5: 69. https://doi.org/10.3390/fermentation5030069
[40]	Csoma H, Kállai Z, Czentye K, et al. (2023) Starmerella lactis-condensi, a yeast that has adapted to the conditions in the oenological environment. Int J Food Microbiol 401: 110282. https://doi.org/10.1016/j.ijfoodmicro.2023.110282
[41]	Alfonzo A, Prestianni R, Gaglio R, et al. (2021) Effects of different yeast strains, nutrients and glutathione-rich inactivated yeast addition on the aroma characteristics of Catarratto wines. Int J Food Microbiol 360: 109325. https://doi.org/10.1016/j.ijfoodmicro.2021.109325
[42]	Windholtz S, Nioi C, Coulon J, et al. (2023) Bioprotection by non-Saccharomyces yeasts in oenology: Evaluation of O₂ consumption and impact on acetic acid bacteria. Int J Food Microbiol 405: 110338. https://doi.org/10.1016/j.ijfoodmicro.2023.110338
[43]	Catarino A, Alves S, Mira H (2014) Influence of technological operations in the dissolved oxygen content of wines. J Chem Chem Eng 8: 390-394. https://doi.org/10.17265/1934-7375%2F2014.04.010
[44]	Darias-Martı́n J, Dı́az-González D, Dı́az-Romero C (2004) Influence of two pressing processes on the quality of must in white wine production. J Food Eng 63: 335-340. https://doi.org/10.1016/j.jfoodeng.2003.08.005
[45]	Villano D, Fernández-Pachón MS, Troncoso AM, et al. (2006) Influence of enological practices on the antioxidant activity of wines. Food Chem 95: 394-404. https://doi.org/10.1016/j.foodchem.2005.01.005
[46]	Selli S, Cabaroglu T, Canbas A, et al. (2004) Volatile composition of red wine from cv. Kalecik Karasι grown in central Anatolia. Food Chem 85: 207-213. https://doi.org/10.1016/j.foodchem.2003.06.008
[47]	Cañas PI, Romero EG, Alonso SG, et al. (2008) Changes in the aromatic composition of Tempranillo wines during spontaneous malolactic fermentation. J Food Compos Anal 21: 724-730. https://doi.org/10.1016/j.jfca.2007.12.005
[48]	Fariña L, Villar V, Ares G, et al. (2015) Volatile composition and aroma profile of Uruguayan Tannat wines. Food Res Int 69: 244-255. https://doi.org/10.1016/j.foodres.2014.12.029
[49]	De Lerma NL, Bellincontro A, Mencarelli F, et al. (2012) Use of electronic nose, validated by GC–MS, to establish the optimum off-vine dehydration time of wine grapes. Food Chem 130: 447-452. https://doi.org/10.1016/j.foodchem.2011.07.058
[50]	Li H (2006) Wine Tasting. Beijing: China Science Press 29-106.
[51]	Li H, Tao YS, Wang H, et al. (2008) Impact odorants of Chardonnay dry white wine from Changli County (China). Eur Food Res Technol 227: 287-292. https://doi.org/10.1007/s00217-007-0722-9
[52]	Ferreira V, López R, Cacho JF (2000) Quantitative determination of the odorants of young red wines from different grape varieties. J Sci Food Agric 80: 1659-1667. https://doi.org/10.1002/1097-0010(20000901)80:11%3C1659::AID-JSFA693%3E3.0.CO;2-6
[53]	Gómez-Míguez MJ, Cacho JF, Ferreira V, et al. (2007) Volatile components of Zalema white wines. Food Chem 100: 1464-1473. https://doi.org/10.1016/j.foodchem.2005.11.045
[54]	Guth H (1997) Quantitation and sensory studies of character impact odorants of different white wine varieties. J Agric Food Chem 45: 3027-3032. https://doi.org/10.1021/jf970280a
[55]	Rocha SM, Rodrigues F, Coutinho P, et al. (2004) Volatile composition of Baga red wine: Assessment of the identification of the would-be impact odourants. Anal Chim Acta 513: 257-262. https://doi.org/10.1016/j.aca.2003.10.009
[56]	Lloret A, Boido E, Lorenzo D, et al. (2002) Aroma variation in Tannat wines: Effect of malolactic fermentation on ethyl lactate level and its enantiomeric distribution. Ital J Food Sci 14: 175-180. http://hdl.handle.net/10449/18119
[57]	Delgado JA, Sánchez-Palomo E, Alises MO, et al. (2022) Chemical and sensory aroma typicity of La Mancha Petit Verdot wines. LWT 162: 113418. https://doi.org/10.1016/j.lwt.2022.113418
[58]	Yao M, Wang F, Arpentin G (2023) Bioprotection as a tool to produce natural wine: Impact on physicochemical and sensory analysis. BIO Web Conf 56: 02019. https://doi.org/10.1051/bioconf/20235602019
[59]	Bayram M, Kayalar M (2018) White wines from Narince grapes: Impact of two different grape provenances on phenolic and volatile composition. OENO One 52: 81-92. https://doi.org/10.20870/oeno-one.2018.52.2.2114
[60]	Zoecklein BW, Fugelsang KC, Gump BH, et al. (1995) Volatile acidity. Wine Analysis and Production . New York: Springer 192-198. https://doi.org/10.1007/978-1-4757-6978-4_11
[61]	Canonico L, Comitini F, Ciani M (2019) Metschnikowia pulcherrima selected strain for ethanol reduction in wine: Influence of cell immobilization and aeration condition. Foods 8: 378. https://doi.org/10.3390%2Ffoods8090378
[62]	Laguna L, Sarkar A, Bryant MG, et al. (2017) Exploring mouthfeel in model wines: Sensory-to-instrumental approaches. Food Res Int 102: 478-486. https://doi.org/10.1016/j.foodres.2017.09.009

This article has been cited by:

Shuangjian Guo, Ripan Saha, On α-type (equivariant) cohomology of Hom-pre-Lie algebras, 2023, 0092-7872, 1, 10.1080/00927872.2023.2243514

Reader Comments

Your name:*

Email:*
© 2025 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)