1. Introduction
Since 1976, about 25 outbreaks of EVD have been declared including the latest one in Western Africa (2014-2015) which was the most devastating one among human populations [18,56]. There are five known Ebola virus strains: ZEBOV, SEBOV, ICEBOV, BDBV, REBOV [18]. Of these, the first four have highly threatened both human and nonhuman primates, causing viral hemorrhagic fever with case fatality rates of up to 90% [18,50]. For instance, the most recent and deadliest Ebola outbreak in Western Africa was caused by the ZEBOV virus strain.
No approved treatments and homologated vaccines are currently available. However, dedicated research efforts have led to the first therapeutic trial with ZMapp [28]. Furthermore, the VSV-ZEBOV vaccine has been found and is still in its third experimental phase [28]. These two remarkable efforts have helped to curtain the recent Western Africa outbreak, even though the latter effort was less decisive (due to its late trial at the end of the West African outbreak) than the former.
Other control efforts (including rehydration, isolation, education of populations at risk, avoidance of consumption of bush meat, practicing of safe burials) have been implemented to stop past Ebola outbreaks. In addition to the threat EVD poses to human health, the negative impact of EVD infection on already threatened animal populations in Africa has come to light and led to a resurgence of efforts to understand the complex life ecology of Ebola virus in nature [26,51]. However, despite considerable efforts, it remains unclear how the EVD is maintained and transmitted in nature, and how the index case (first patient) is infected. Since EVD is a zoonotic-borne disease (transmitted accidentally by direct contact with infected living or dead animals), human epidemics were concomitant with epizootic in great apes [37,38]. Moreover, due to the fact that recent works have provided new evidence that fruit bats might play an important role as a reservoir species of EVD, some intricate and pending questions which are biologically relevant have been raised:
1. Where and how does the index case (first patient) acquire the infection?
2. Do direct transmissions from bats to humans and/or nonhuman primates occur?
3. Which human behaviors expose humans to the risk of contracting EVD from non-human sources?
4. Are fruit bats the only reservoir hosts for Ebola viruses?
5. What are the environmental factors contributing to Ebola virus transmission to human beings and non-human primates from the reservoir species?
6. Can mathematical modeling help to understand and predict the of EVD outbreaks in the future?
This paper focuses on the last question. We address it, with the ultimate aim to answer the other five questions. Before moving to the modeling section, there is a need to support and motivate these questions. Since the 1976 Sudan outbreak where there was evidence that the index case was a worker in a cotton factory with evidence of bats at site, many other index cases (from 1994-2001) showed evident contacts with bats and/or consumption of butchered great apes and/or other wildlife meat. The synoptic Table 1 summarizes the sources for contamination of the first patient during EVD outbreaks and highlights his/her contact with bats, dead or butchered wildlife bush meat. The table also talks to the transmission from bat to human, from non-human primate to human, and it illustrates how human behaviors can drive the contamination of EVD. The issue of fruit bats being reservoir for Ebola viruses is supported by the work [37] which has demonstrated that fruit bats bear Ebola viruses and are not affected by the disease. Furthermore, the first four questions are biologically investigated in [26,37,51] where the known, the probable/suspected and the hypothetical direct transmission mechanisms (routes) of EVD are addressed. Regarding the fifth question, the works in [9,10,46,53,60] highlight the indirect environmental contamination route of EVD.
Table 1. Routes of transmission for index case in some known Ebola virus outbreaks.
| Year | Country | Species | Starting date | Source of infection |
| 1976 |
DRC |
Zaire |
September |
Unknown. Index case was a mission school teacher. |
| 1976 |
Sudan |
Sudan |
June |
Worker in a cotton factory. |
|
|
|
|
Evidence of bats at site. |
| 1977 |
DRC |
Zaire |
June |
Unknown (retrospective). |
| 1979 |
Sudan |
Sudan |
July |
Worker in cotton factory. |
|
|
|
|
Evidence of bats at site. |
| 1994 |
Gabon |
Zaire |
December |
Gold-mining camps. |
|
|
|
|
Evidence of bats at site. |
| 1994 |
Ivory Coast |
Ivory Coast |
November |
Scientist performing autopsy on a dead wild chimpanzee. |
| 1995 |
Liberia |
Ivory Coast |
December |
Unknown. Refugee from civil war. |
| 1995 |
DRC |
Zaire |
January |
Index case worked in a forest adjoining the city. |
| 1996 |
Gabon |
Zaire |
January |
People involved in the butchering of a dead chimpanzee. |
| 1996-1997 |
Gabon |
Zaire |
July |
Index case was a hunter living in a forest camp. |
| 2000-2001 |
Uganda |
Sudan |
September |
Unknown. |
| 2001-2002 |
Gabon |
Zaire |
October |
Contact with dead or butchered apes or other wildlife. |
| 2001-2002 |
DRC |
Zaire |
October |
Contact with dead or butchered apes or other wildlife. |
| 2002-2003 |
DRC |
Zaire |
December |
Contact with dead or butchered apes or other wildlife. |
| 2003 |
DRC |
Zaire |
November |
Contact with dead or butchered apes or other wildlife. |
| 2004 |
Sudan |
Sudan |
May |
Unknown. |
| 2005 |
DRC |
Zaire |
April |
unknown. |
| 2007 |
DRC |
Zaire |
December |
Contact with dead or butchered apes or other wildlife. |
| 2007 |
Uganda |
Bundibugyo |
December |
Unknown. |
| 2008 |
DRC |
Zaire |
December |
Index case was a village chief and a hunter. |
| 2012 |
Uganda |
Bundibugyo |
June |
Index case was a secondary school teacher in Ibanda district. |
| 2012 |
DRC |
Zaire |
June |
Index case was a hunter living in a forest camp. |
| 2013-2015 |
Guinea |
Zaire |
December |
Contact with bats or fruits contaminated by bat droppings. |
| 2014-2015 |
Liberia |
Zaire |
April |
Index case was transported from Guinea. |
| 2014-2015 |
Sierra Leone |
Zaire |
April |
A traditional healer, treating Ebola patients from Guinea. |
| 2014 |
DRC |
Zaire |
August |
Pregnant women who butchered a bush animal. |
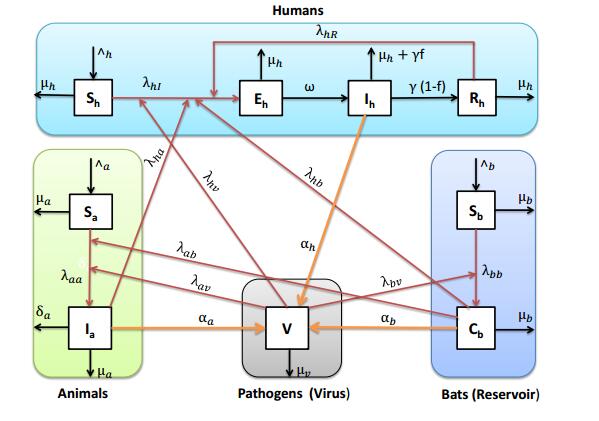
The complexity of the questions raised above is captured in [26,51] for the EVD mechanisms of transmission in a complex Ebola virus life ecology as depicted in Fig. 1 of the disease transmission diagram. This will be reflected in the construction of our model by: (a) Taking into account the well known, the probable/suspected, the hypothetical and the environmental transmission pathways; (b) Involving the interplay between the epizootic phase (during which the disease circulates periodically amongst non-human primate populations and decimates them), the enzootic phase (during which the disease always remains in fruit bat populations) and the epidemic phase (during which the EVD threatens and decimates human populations) of the disease under consideration.
The complexity of the Ebola virus life ecology is clear from the biological studies carried out in [26,51] (see also Ebola virus ecology and transmission therein). From the mathematical point of view, the complexity and challenges we are confronted with and have addressed range from the modeling of the forces of infection, the computation of the reproduction number (see Eq. (8) and Remark1), the computation of the endemic equilibrium, to the use of less standard tools (e.g. decomposition techniques [54]) to investigate the dynamics of EVD.
Note that the recent and former EVD outbreaks have highlighted the importance of human behavior in the transmission process [11,21,41]. For instance, there were evidence of behavioral reaction and self-protection measures: people were scared, they panicked and left care centers, etc... As this important feature calls for a different modeling approach based on "Behavioral Epidemiology" developed in [41], we are busy investigating it in another work, where self-protection measures driven by human behavior is incorporated.
The rest of the paper is organized as follows. In Section 2 we derive the model. The mathematical analysis starts in Section 3 with the basic properties of the model, followed by the computation of the reproduction number $\mathcal R_0$ and the establishment of the global asymptotic stability of the disease-free equilibrium. It ends with the investigation of the endemic equilibrium. Section 4 deals with the model without the environmental contamination, while the sensitivity analysis is shown in Section 5. In Section 6, we provide numerical simulations to support the theory and assess the impact of the environmental contamination. Finally Section 8 summarizes our findings and highlights possible extensions.
2. Model formulation
To avoid confusion, bat will not be called "animal". The term animal is reserved for any non-human primate and/or any other wild animal that may be responsible for the transmission of EVD. Note that our model formulation is focused essentially on non-human primates (great apes) as animal species.
Motivated by the biological papers [25,26,37,51] regarding the transmission mechanisms and the recent mathematical works [9,53], our model is based on the zoonotic-borne disease setting and takes into account both direct and indirect transmission routes. We distinguish three host populations: humans and animals as end hosts and fruit bats as intermediate reservoir hosts [5,32,37,45,47]. Since the model incorporates the indirect environmental transmission, we add the dynamics of the concentration of free living Ebola viruses in the environment [53,56,60]. The latter compartment should not be considered as an epidemiological class; it is regarded as a pool of Ebola viruses. This pool is supplied by infected humans, infected animals and infected fruit bats with:
(ⅰ) The presence of carcasses of infected and dead animals in the forest on which some animals can feed [56].
(ⅱ) The manipulation of infected fruit bats and animals hunted by humans for food.
(ⅲ) The contaminated fruits harvested for food by humans and primates in the forest [25,26,37].
(ⅳ) The contaminated syringes re-used in health care centers [50,55,58].
(ⅴ) The bed linen contaminated by infected human's stool, urine, vomits or sweat in health care centers or in family homes of infected individuals [50,55].
(ⅵ) The bush fruits contaminated by bats droppings [38].
2.1. The variables
As mentioned earlier, the variables include the human, the animal, the bat (reservoir of Ebola viruses) populations and the concentration of free living Ebola viruses in the environment. More precisely, at time $t$, $S_h(t)$, $S_a(t)$ and $S_b(t)$ denote the susceptible human, animal and bat compartments, respectively. The symbols $I_h(t)$, $I_a(t)$ and $I_b(t)$ denote the infected human, animal and bat compartments, respectively. Since there is an intrinsic incubation period of approximately 2-21 days (on average 8-10 days) of EVD in humans [7,50,55], we introduce $E_h(t)$, the exposed (or infected in latent stage) human individuals class. There is a recovered class $R_h(t)$ for humans only, because fruit bats are the reservoir of Ebola viruses and nobody cares for infected animals (once infected, they ultimately die). The total human, animal and bat populations at time $t$ are, $N_h(t) = S_h(t)+E_h(t)+I_h(t)+R_h(t)$, $N_a(t)=S_a(t)+I_a(t)$ and $N_b(t)=S_b(t)+I_b(t)$, respectively. The concentration of Ebola viruses in the environment at time $t$, is denoted by $V(t)$.
2.2. Main assumptions
The model derivation is based on the following main assumptions:
${\bf(A_1)}$ Infected humans always deposit Ebola viruses in the environment through the routes indicated above, with which susceptible individuals can come into contact.
${\bf(A_2)}$ Human-animal and human-bat contact rates are very low. This assumption is motivated by the fact that the literature does not indicate clearly how the human beings come into contact with either living animals, or the living fruit bats.
${\bf(A_3)}$ Contacts between animals and fruit bats are frequent, occurring during competition for food in the dry seasons where food (specially fruits) is scarce.
${\bf(A_4)}$ Infected fruit bats always contribute to the Ebola virus shedding in the environment. Actually, as reported in [25,26,37,38], the scarcity of food during the dry season, compels bats to deliver allowing their placenta and blood to contaminate fruits and leaves on which some animals (apes, duikers) feed.
${\bf(A_5)}$ The sharing of contaminated food (fruits) by animals (monkeys, duikers) and fruit bats is possible allowing adequate contacts between these two wildlife species.
${\bf(A_6)}$ There are not Ebola-deceased fruit bats since they are a natural reservoir of Ebola viruses.
${\bf(A_7)}$ Ebola-deceased humans can still infect during unsafe funeral practices, where their corpses are manipulated (e.g. washing, autopsy, dressing-up) as it is the case in many places in Africa [50].
${\bf(A_8)}$ Ebola-deceased animals can still infect humans, e.g., during manipulation of bats for food [50].
${\bf(A_9)}$ Clinically Ebola-recovered men (resp. women) still transmit the disease probably through sexual intercourse (resp. breast-feeding) [50].
${\bf(A_{10})}$ Ebola-infected animals do not recover since nobody cares about them.
2.3. The equations
The works in [26,51] amongst others on the complex Ebola virus life ecology lead to the dynamics flowchart in Fig. 1 which in turn gives the following system of nonlinear ordinary differential equations:
|
$
\dfrac{dS_h}{dt} = \Lambda_h - (\lambda_h+ \mu_h)S_h,
$
|
(1a)
|
|
$
\dfrac{dE_h}{dt} = \lambda_hS_h - \left(\mu_h + \omega\right)E_h,
$
|
(1b)
|
|
$
\dfrac{dI_h}{dt} = \omega E_h - \left( \mu_h+\gamma \right)I_h,
$
|
(1c)
|
|
$
\dfrac{dR_h}{dt} = \gamma(1-f)I_h - \mu_hR_h,
$
|
(1d)
|
|
$
\dfrac{dV}{dt} = \alpha_h I_h + \alpha_a I_a + \alpha_b I_b - \mu_v V,
$
|
(1e)
|
|
$
\dfrac{dS_a}{dt} = \Lambda_a - (\lambda_a+ \mu_a) S_a,
$
|
(1f)
|
|
$
\dfrac{dI_a}{dt} = \lambda_aS_a - (\mu_a +\delta_a ) I_a,
$
|
(1g)
|
|
$
\dfrac{dS_b}{dt} = \Lambda_b - (\lambda_b + \mu_b)S_b,
$
|
(1h)
|
|
$
\dfrac{dI_b}{dt} = \lambda_bS_b -\mu_b I_b.
$
|
(1i)
|
The force of infection acting on humans is,
|
$
\lambda_h=\dfrac{\beta_{hh}\left(I_h+\xi_h\nu_h\gamma f I_h + \theta_h\gamma(1-f) I_h\right)}{N_h} + \dfrac{\beta_{ha}\left(1+\xi_a\nu_a\delta_a\right)I_a}{N_h}+ \dfrac{\beta_{hb}I_b}{N_h} + \dfrac{\beta_{hv}V}{K+V}.
$
|
(2)
|
It is the sum of the contributions below:
● The human-to-human force of infection
|
$
\lambda_{hh} = \dfrac{\beta_{hh}}{N_h}\left(1+\xi_h\nu_h\gamma f + \theta_h\gamma(1-f)\right)I_h,
$
|
which gathers the three contamination processes by:
-infected, i.e. $\frac{\beta_{hh}}{N_h}I_h$;
-Ebola-deceased, i.e. $\frac{\beta_{hh}}{N_h}\left(\xi_h\nu_h\gamma f \right)I_h$ and
-clinically recovered individuals i.e. $\frac{\beta_{hh}}{N_h}\left(\theta_h\gamma(1-f)\right)I_h$.
● The animal-to-human force of infection
|
$
\lambda_{ha} = \dfrac{\beta_{ha}(1 + \xi_a\nu_a\delta_a)I_a}{N_h}, \;\;\;\;\text{where} \;\;\;\; \xi_a = \dfrac{1}{\tau_a}.
$
|
● The bat-to-human force of infection
|
$
\lambda_{hb}= \dfrac{\beta_{hb}I_b}{N_b}.
$
|
● The environment-to-human force of infection
|
$
\lambda_{hv}= \dfrac{\beta_{hv}V}{K+V}.
$
|
Similarly, the force of infection within the animal population
|
$
\lambda_a= \dfrac{\beta_{aa} (1 + \xi_a\nu_a\delta_a)I_a}{N_a} + \dfrac{\beta_{ab}I_b}{N_a} + \dfrac{\beta_{av}V}{K+V},
$
|
(3)
|
involves the following three contributions:
● The animal-to-animal force of infection
|
$
\lambda_{aa}= \dfrac{\beta_{aa} (1+\xi_a\nu_a\delta_a)I_a}{N_a};
$
|
● The bat-to-animal force of infection
|
$
\lambda_{ab}= \dfrac{\beta_{ab}I_b}{N_a}.
$
|
● The environment-to-animal force of infection
|
$
\lambda_{av}= \dfrac{\beta_{av}V}{K+V}.
$
|
Finally, the force of infection in bat's population is modeled by
|
$
\lambda_b = \beta_{bb}I_b + \dfrac{\beta_{bv}V}{K+V}
$
|
(4)
|
and consists of two contributions from:
-Within bat adequate contacts
|
$
\lambda_{bb} = \beta_{bb}I_b.
$
|
-The contact with the environment
|
$
\lambda_{bv} = \dfrac{\beta_{bv}V}{K+V}.
$
|
Note that we have considered the infection through contact with environmental free Ebola viruses. As it is the case for most models involving free-living pathogens in the environment [3,4,8,12,17,49,53,59], the environmental-related forces of infection, $\lambda_{hv}$, $\lambda_{av}$ and $\lambda_{bv}$ are modeled using Michealis-Menten or Holling type Ⅱ functional responses. The constant $K$ represents the minimum amount of viruses in the environment capable of ensuring 50% chance of contracting the disease. Moreover, for the sake of simplicity, the contribution of dead animals and humans to environment is modeled by relating them to infective individuals. This simplification avoids the need to add compartments counting number of deceased humans and animal carcasses in the environment.
Finally, the last equation of system (1) describes the dynamics of Ebola viruses with shedding from humans, animals and bats. The parameters used for system (1) and their biological interpretations are giving in Table 2. For notational simplifications let,
Table 2. Model constant parameters and their biological interpretation.
| Symbols | Biological interpretations |
|
$\Lambda_{h}, \Lambda_a, \Lambda_b$
|
Recruitment rate of susceptible humans, animals and bats, respectively. |
|
$\mu_{h}, \mu_{a}, \mu_{b}$
|
Natural mortality rate of humans, animals and bats, respectively. |
|
$\nu_h$
|
Virulence of Ebola virus in the corpse of the dead humans. |
|
$\tau_h$
|
Mean duration of time that elapse after death before a human cadaver is completely buried. |
|
$\xi_{h}= 1/\tau_h$
|
Modification parameter of infectiousness due to dead human individuals. |
|
$\tau_a$
|
Mean duration of time that elapse after death before an animal's cadaver is completely cleared out. |
|
$\xi_{a} =1/\tau_a$
|
Modification parameter of infectiousness due to dead animals individuals. |
|
$\nu_a$
|
Virulence of Ebola virus in the corpse of dead animals. |
|
$\omega $
|
Incubation rate of human individuals. |
|
$\gamma$
|
Removal rate from infectious compartment due to either to disease induced death, or by recovery. |
|
$\delta_a$
|
Death rate of infected animals. |
|
$\alpha_h, \alpha_a, \alpha_b$
|
Shedding rates of Ebola virus in the environment by humans, animals and bats, respectively. |
|
$r_h$
|
Mean duration of time that elapse before the complete clearance of Ebola virus in humans. |
|
$\theta_h = 1/r_h$
|
Modification parameter of contact rate of recovered humans (sexual activity of recovered). |
|
in the semen/breast milk of a recovered man/woman. |
|
$f$
|
Proortion of removed human individuals who die due EVD (i.e. case fatality rate). |
|
$K$
|
Virus 50 % infectious dose, sufficient to cause EVD. |
|
$\beta_{hh}$
|
Contact rate between susceptible humans and infected humans. |
|
$\beta_{hb}$
|
Contact rate between susceptible humans and bats. |
|
$\beta_{hv}$
|
Contact rate between susceptible humans and Ebola viruses. |
|
$\beta_{ha}$
|
Contact rate between susceptible humans and infected animals. |
|
$\beta_{bb}$
|
Contact rate between susceptible bats and infectious bats. |
|
$\beta_{ab}$
|
Contact rate between susceptible animals and infectious bats. |
|
$\beta_{bv}$
|
Contact rate between susceptible bats and and Ebola viruses. |
|
$\beta_{aa}$
|
Contact rate between susceptible and infected animals. |
|
$\beta_{av}$
|
Contact rate between susceptible animals and Ebola viruses. |
|
$
\Phi_h = 1+\xi_h\nu_h\gamma f + \theta_h\gamma(1-f) \;\;\;\; \text{and} \;\;\;\; \Phi_a = 1+\xi_a\nu_a\delta_a.
$
|
With this notation it is easy to check that system (1) interconnects the following sub-models:
● The human population sub-model
|
$
\left\{dShdt=Λh−βhhΦhShIhNh−βhaΦaShIaNh−βhbShIbNh−βhvShVK+V−μhSh,dEhdt=βhhΦhShIhNh+βhaΦaShIaNh+βhbShIbNh+βhvShVK+V−(μh+ω)Eh,dIhdt=ωEh−(μh+γ)Ih,dRhdt=γ(1−f)Ih−μhRh.\right.
$
|
(5)
|
● The animal population sub-model
|
$
\left\{dSadt=Λa−βaaΦaSaIaNa−βabSaIbNa−βavSaVK+V−μaSa,dIadt=βaaΦaSaIaNa+βabSaIbNa+βavSaVK+V−(μa+δa)Ia.\right.
$
|
(6)
|
● The bat population sub-model
|
$
\left\{dSbdt=Λb−βbbSbIb−βbvSbVK+V−μbSb,dIbdt=βbbSbIb+βbvSbVK+V−μbIb.\right.
$
|
(7)
|
It should be emphasized that not much is known about the bat-to-bat EVD transmission. However, knowing that fruit bats settle or congregate for rest or sleep (they live in colony), it is acceptable to assume that direct bat-to-bat contact is the main route of transmission and can be modeled by mass action incidence.
● The evolution of free-living Ebola viruses in the environment which is modeled by Eq. (1e).
The model presented her is a new in many respects. It extends the existing works [1,9,16,24,35,36,44,53] in the sense that it considers the three phases of disease: the epizootic cycle in animals, the enzootic phase in fruit bats and the epidemic phase in humans. In particular, the novelty of our model is clear from the most recent work [9], where direct human-to-human transmission was considered and all other sources (e.g. consumption of bush meat, manipulation of fruit bats, indirect environmental contamination) were encompassed in a constant recruitment of Ebola viruses in the environment. The model developed here enriches the latter by modeling this recruitment through consideration of the complex Ebola virus life ecology, where animals and bats are explicitly involved in the EVD transmission cycle. It is therefore understandable why throughout this paper, we refer to system (1) as the full model.
3. Theoretical analysis of the full model
3.1. Basic properties
3.1.1. Positivity and boundedness of solutions
For the EVD transmission model (1) to be epidemiological meaningful, it is important to prove that all state variables are non-negative at all time. That is, solutions of the system (1) with non-negative initial data will remain non-negative for all time $t>0$.
Theorem 3.1. Let the initial data $S_h(0), E_h(0), I_h(0), R_h(0), S_a(0), I_a(0), S_b(0)$, $ I_b(0), V(0)$ be non-negative. Then a solution $S_h(t), E_h(t), I_h(t), R_h(t), S_a(t), I_a(t)$, $ S_b(t), I_b(t), V(t))$ of the model (1) are non-negative for all $t > 0$, when it exists.
Furthermore, if we set $\Lambda_v = \dfrac{\alpha_h\Lambda_h}{\mu_h} + \dfrac{\alpha_a\Lambda_a}{\mu_a} + \dfrac{\alpha_b\Lambda_b}{\mu_b}$, then for any initial condition such that
|
$N_h(0)\leq \dfrac{\Lambda_h}{\mu_h},\;\; N_a(0)\leq \dfrac{\Lambda_a}{\mu_a}, \;\;N_b(0)\leq \dfrac{\Lambda_b}{\mu_b}
, \;\;V(0)\leq \dfrac{\Lambda_v}{\mu_v}, $
|
we have
|
$ N_h(t)\leq \dfrac{\Lambda_h}{\mu_h}, \;\; N_a(t)\leq \dfrac{\Lambda_a}{\mu_a},\;\; N_b(t)\leq \dfrac{\Lambda_b}{\mu_b}
,\;\; V(t)\leq \dfrac{\Lambda_v}{\mu_v}, \; \forall t\geq 0. $
|
Proof. Suppose $S_h(0)\geq 0$. The first equation of system (1) is equivalent to
|
$\dfrac{d}{dt}\left\{S_h(t)\rho(t)\right\} = \Lambda_h\rho(t), $
|
where $\rho(t) = \exp{\left(\int^t_0 (\lambda_h(p)+\mu_h)dp\right)} >0$ is the integrating factor. Hence, integrating this last relation with respect to $t$, we have
|
$ S_h(t)\rho(t) - S_h(0) = \int^{t}_0 \Lambda_h \rho(t)dt, $
|
so that the division of both side by $\rho(t)$ yields
|
$ S_h(t) = \left[S_h(0) + \int^{t}_0 \Lambda_h \rho(t)dt \right]\times \rho(t)^{-1} >0. $
|
The same arguments can be used to prove that $S_a(t)>0$, $S_b(t)>0$ and
$E_h(t), I_h(t), R_h(t), I_a(t), I_b(t), V(t)\geq 0$ for all $t>0$.
Furthermore, $(d N_h)/dt = \Lambda_h- \mu_h N_h - \gamma f I_h \leq \Lambda_h- \mu_h N_h $. Thus, by Gronwall inequality, we have
$ N_h(t)\leq N_h(0)e^{-\mu_h t} + \dfrac{\Lambda_h}{\mu_h}\left( 1- e^{-\mu_h t}\right) \:$ and then $\:\; N_h(t)\leq \dfrac{\Lambda_h}{\mu_h}, \: \forall t\geq 0 $ whenever $ N_h(0)\leq \dfrac{\Lambda_h}{\mu_h}.$ Similarly, $N_a(t)\leq \dfrac{\Lambda_a}{\mu_a}, \: \forall t\geq 0 $, whenever $N_a(0)\leq \dfrac{\Lambda_a}{\mu_a}$, $ N_b(t)\leq \dfrac{\Lambda_b}{\mu_b}$ $N_b(0)\leq \dfrac{\Lambda_b}{\mu_b}.$
Finally, using the fact that $I_h \leq N_h, I_a\leq N_a, I_b\leq N_b$ and Gronwall inequality, one has $V(t)\leq \dfrac{\Lambda_v}{\mu_v}, \: \forall t\geq 0$ if $ V(0)\leq \dfrac{\Lambda_v}{\mu_v}$. This completes the proof.
Combining Theorem 3.1 with the trivial existence and uniqueness of a local solution for the model (1), we have established the following theorem which ensures the mathematical and biological well-posedness of system (1) (see [9], Theorem 3.3).
Theorem 3.2. The dynamics of model (1) is a dynamical system in the biological feasible compact set
|
$
\Gamma = \left\{(S_h, E_h, I_h, R_h, S_a, I_a, S_b, I_b, V) \in \mathbb R^9_+: N_h\leq \frac{\Lambda_h}{\mu_h}, N_a\leq \frac{\Lambda_a}{\mu_a}, N_b\leq \frac{\Lambda_b}{\mu_b}, V\leq \frac{\Lambda_v}{\mu_v} \right\}
$
|
3.1.2. Basic reproduction number
The disease free equilibrium (DFE) of the model is obviously
|
$P_0 = \left( S^0_h, 0, 0, 0, S^0_a, 0, S^0_b, 0, 0\right),\;\; \text{where} \;\; S^0_h = \dfrac{\Lambda_h}{\mu_h},\;\; S^0_a = \dfrac{\Lambda_a}{\mu_a},\;\; S^0_b = \dfrac{\Lambda_b}{\mu_b}.$
|
To compute the basic reproduction number of the model, we use the standard method of the next generation matrix developed in [2,8,19,20]. We separate the infected states $\left( E_h, I_h, R_h, I_a, I_b, V\right)$ form the uninfected states $\left(S_h, S_a, S_b, \right)$. Let $\mathcal F $ and $\mathcal W $ be the vectors representing the new and transported cases into the infected states, respectively. Thus
|
$ \mathcal F=
\left(λhSh00λaSaλbSb0\right)
\;\; \text{and}\;\; \mathcal W = \left((μh+ω)Eh−ωEh+(μh+γ)Ih−γ(1−f)Ih+μhRh(μa+δa)IaμbIb−αhIh−αaIa−αbIb+μvV\right). $
|
The Jacobian matrices $F$ of $ \mathcal F$ and $W$ of $ \mathcal W$ evaluated at the DFE are
|
$ F= \left(0βhhΦh0βhaΦaβhbβhvΛhμhK000000000000000βaaΦaβabβavΛaμaK0000βbbΛbμbβbvΛbμbK000000\right) $
|
and
|
$ W= \left((μh+ω)00000−ω(μh+γ)00000−γ(1−f)μh000000μa+δa000000μb00−αh0−αa−αbμv\right), \text{respectively}.$
|
$W$ is a lower triangular and invertible matrix. Thus, thanks to [8], $\mathcal R_0$ is obtained as the maximum eigenvalue of the positive matrix $FW^{-1}$, where
|
$ FW^{-1} = (Rhhv0Rhhv200Rahv0Rbhv0βhvΛhKμhμv000000000000Rhav0βavαhΛaKμaμv(μh+γ)0Raav0Rbav0βavΛaKμaμvRhbv0βbvαhωKμbμv(μh+γ)0Rabv0Rbbv0βbvΛbKμbμv000000)$
|
and
|
$ Rhhv0=βhhΦhω(μh+ω)(μh+γ)+αhβhvΛhωKμhμv(μh+ω)(μh+γ),Rbav0=βavΛaαbKμaμbμv+βabμb,Rahv0=βhaΦaμa+δa+βhvαaΛhKμhμv(μa+δa),Rbhv0=βhbμb+βhvαbΛhKμhμbμv,Raav0=βaaΦaμa+δa+βavΛaαaKμaμv(μa+δa),Rabv0=βbvΛbαaKμbμv(μa+δa),Rhav0=βavαhΛaωKμaμv(μh+ω)(μh+γ),Rhbv0=βbvαhΛbωKμbμv(μh+ω)(μh+γ),Rbbv0=βbbΛbμ2b+βbvΛbαbKμ2bμv,Rhhv20=βhhΦhμh+γ+βhvαhΛhKμh(μh+γ).
$
|
Since zero is an eigenvalue for $FW^{-1}$ of multiplicity 3, simple algebraic matrix properties show that its non vanishing eigenvalues are those of the $(3\times3)$ matrix
|
$
\mathcal G = \left(Rhhv0Rahv0Rbhv0Rhav0Raav0Rbav0Rhbv0Rabv0Rbbv0\right),
$
|
(8)
|
Therefore,
|
$\mathcal R_0= \rho{(\mathcal G)}, $
|
where for a square matrix $M$, $\rho{(M)}$ denotes its the spectral radius.
Based on some of the realistic assumptions stated in subsection 2.2, the remark below gives the explicit formula of the basic reproduction number $\mathcal R_0$ in special cases.
Remark 1. In some cases, the explicit formula for $\mathcal R_0$ are straightforward as thrived below.
1. In the sub-model with only human population dynamics and environmental transmission [53], the basic reproduction number denoted by $\mathcal R_{0, hv}$ is
|
$
\mathcal R_{0, hv} = \mathcal R^{hhv}_0 = \dfrac{\beta_{hh}\Phi_h\omega}{(\mu_h+\omega)(\mu_h+\gamma)} + \dfrac{\alpha_h\beta_{hv}\Lambda_h\omega}{K\mu_h\mu_v(\mu_h+\omega)(\mu_h+\gamma)}.
$
|
(9)
|
If in addition, the indirect transmission is neglected (i.e. $\beta_{hv}=0$), then the basic reproduction number reduces to
|
$
\mathcal R_{0, h} = \dfrac{\beta_{hh}\Phi_h\omega}{(\mu_h+\omega)(\mu_h+\gamma)}.
$
|
(10)
|
We emphasize that the basic reproduction number giving by (10) is suitable for comparison with the basic reproduction numbers for some existing EDV models. For instance, looking at the expression $\Phi_h$, (10) is the sum of three contributions:
(ⅰ) The contribution from infected human individuals, i.e. $\frac{\beta_{hh}\omega}{(\mu_h+\omega)(\mu_h+\gamma)}$.
(ⅱ) The contribution from the clinically recovered individuals, i.e.$\frac{\beta_{hh}\theta_h\omega}{(\mu_h+\omega)(\mu_h+\gamma)}$, where $\theta_h = \frac{\gamma(1-f)}{r_h}$ (see [53] for more details in such comparisons).
(ⅲ) The contribution from Ebola-deceased individuals, i.e. $\frac{\beta_{hh}\xi_h\nu_h\gamma f\omega}{(\mu_h+\omega)(\mu_h+\gamma)}$.
With the above decomposition of $\mathcal R_{0, h}$, it is straightforward that the environmental contamination increases its range, such that $\mathcal R_{0, h}$ is always larger than the basic reproduction numbers for the few existing SEIR classical models with standard incidence forces of infection.
2. In the sub-model without animal's population dynamics, the basic reproduction number denoted by $\mathcal R_{0, hbv}$ is
|
$
\mathcal R_{0, hbv}= \dfrac{\mathcal R^{hhv}_0+\mathcal R^{bbv}_0+ \sqrt{\left(\mathcal R^{hhv}_0-\mathcal R^{bbv}_0\right)^2+4\mathcal R^{hbv}_0\mathcal R^{bhv}_0}}{2}.
$
|
(11)
|
3. In the sub-model without bat's population dynamics, the basic reproduction number denoted by $\mathcal R_{0, hav}$ is
|
$
\mathcal R_{0, hav}=\dfrac{\mathcal R^{hhv}_0+\mathcal R^{aav}_0+ \sqrt{\left(\mathcal R^{hhv}_0-\mathcal R^{aav}_0\right)^2+4\mathcal R^{hav}_0\mathcal R^{ahv}_0}}{2}.
$
|
(12)
|
4. Suppose $ \beta_{bv}=0$, then $\mathcal R^{hbv}_0 = \mathcal R^{abv}_0 =0$ and the basic reproduction number is
|
$
\mathcal R_0 = \max\left\{\mathcal R_{0, b} \; ;\; \dfrac{\mathcal R^{hhv}_0+\mathcal R^{aav}_0 + \sqrt{\left(\mathcal R^{hhv}_0-\mathcal R^{aav}_0\right)^2+4\mathcal R^{hav}_0\mathcal R^{bhv}_0}}{2}\right\}.
$
|
(13)
|
5. If $ \beta_{bv}=\beta_{av}=0$, then $ \mathcal R_0 $ simply becomes
|
$
\mathcal R_0 = \max\left\{ \mathcal R_{0, hv}\; ; \; \mathcal R_{0, a} \; ;\; \mathcal R_{0, b} \right\}
$
|
(14)
|
where $\mathcal R_{0, hv}$ is given in (9) and
|
$
\mathcal R_{0, a} = \dfrac{\beta_{aa}\Phi_a}{\delta_a +\mu_a} \;, \; \mathcal R_{0, b} = \dfrac{\beta_{bb}\Lambda_b}{\mu^2_b}
$
|
(15)
|
are the intra-specific basic reproduction numbers of the animal's population and bat's population without the environmental transmission, respectively and $ \mathcal R_{0, hv}$ is the intra-specific basic reproduction number in the human population with the environmental transmission.
3.2. Stability of the disease-free equilibrium
Using Theorem 2 in [20], the following result is established:
Lemma 3.3. The DFE of system (1) is LAS whenever $\mathcal R_0 <1$, and unstable whenever $\mathcal R_0>1$.
The epidemiological implication of Lemma 3.3 is that EVD can be eliminated from the community when $\mathcal R_0 < 1$ and the initial sizes of the sub-populations in the model are in the basin of attraction of the DFE $P_0$. But, for the disease to be eliminated independently of the initial sizes of sub-populations, the global asymptotic (GAS) stability of the DFE must be established when $\mathcal R_0 <1$. This is the substance of the following theorem.
Theorem 3.4. The DFE $P_0$ of system (1) is GAS if $\mathcal R_0 < 1$ in $\Gamma$.
Proof. Let $x= \left( E_h, I_h, R_h, I_a, I_b, V\right)$ and $y=\left(S_h, S_a, S_b\right)$ be the disease compartments (infected) and uninfected states, respectively. Then system (1) can be re-written in the form
|
$
\left\{dxdt=(F−W)x−f(x,y),dydt=g(x,y), \right.
$
|
(16)
|
where $F$ and $W$ are giving above,
|
$f(x,y)=((Nh−Sh)[βhhΦhIh+βhaΦaIaNh+βhbIb]+βhvV(ΛhμhK−ShK+V)00(Na−Sa)[βaaΦaIa+βabIbNa]+βavV(ΛaμaK−SaK+V)βbbIb(Λbμb−Sb)+βbvV(ΛbμbK−SbK+V)0),$
|
and
|
$
g(x, y) = (Λh−λhSh−μhShΛa−λaSa−μaSaΛb−λbSb−μbSb). $
|
It is straightforward that $f(x, y)\geq 0$ for all $(x, y) \in \Gamma $. Therefore $(dx)/dt \leq \left(F-W\right)x $. We then consider the following auxiliary linear subsystem from (16):
|
$
\dfrac{d\widehat{x}}{dt} = \left(F-W\right)\widehat{x}.
$
|
(17)
|
From Theorem 2 in [20], we have $\mathcal R_0 < 1 \Longleftrightarrow\sigma(F-W) <0$, where, for a square matrix $M$, $\sigma(M) $ denotes its stability modulus. So, when $\mathcal R_0 < 1$, the eigenvalues of $F-W$ all have negative real parts. Therefore, non-negative solutions of (17) are such that $\lim_{t\to+\infty}
\widehat{x} = 0$, or equivalently $\lim_{t\to+\infty} \widehat{E_h} = \lim_{t\to+\infty} \widehat{I_h} = \lim_{t\to+\infty} \widehat{I_a} = \lim_{t\to+\infty}
\widehat{I_b} = \lim_{t\to+\infty} \widehat{V} = 0$. By the standard comparison principle [33,48] and the non-negativity of $x$, non-negative solutions of (1) satisfy $\lim_{t\to+\infty} E_h = \lim_{t\to+\infty} I_h = \lim_{t\to+\infty} I_a = \lim_{t\to+\infty} I_b = \lim_{t\to+\infty} V = 0$. Therefore, since $\lim_{t\to+\infty} x = 0$, system (1) is an asymptotically autonomous system [14] (Theorem 2.5) with the limit system:
|
$
\left\{d¯Shdt=Λh−μh¯Sh,d¯Sadt=Λa−μa¯Sa,d¯Sbdt=Λb−μb¯Sb. \right.
$
|
(18)
|
It is straightforward that the linear system (18) has a unique equilibrium given by $(S^0_h, S^0_a, S^0_b)$ which is globally asymptotically stable. This completes the proof.
Remark 2. To extend this global result in the case when $\mathcal R_0 =1$ (which we do not address here), the construction of a suitable Lyapunov function and the use of LaSalle' Invariance Principle are necessary.
3.3. Existence of endemic equilibrium of model (1)
In this section, we investigate the existence of equilibrium points other than the disease free equilibrium, namely possible boundary equilibrium points and interior equilibria. First of all, let us give some useful remarks.
Assume that an equilibrium is such that $I_b=0$, then from Eqs. (1h) and (1i), $V=0$, and $I_a =0$. Using these statements in Eqs. (1b), (1c) and (1d) gives $I_h=E_h=R_h=0$. Thus, the said equilibrium point is disease free.
Similarly, if an equilibrium of (1) is such that $I_a=0$, then from Eq. (1e), $I_a=V=0$ and from Eq. (1i), one has $I_h=0$. Replacing these values in Eqs. (1b), (1c) and (1d) yields $I_h=E_h=R_h=0$ and the said equilibrium point is disease free as well.
Obviously, if an equilibrium of (1) is such that $V=0$, then from Eq. (1i), $I_h=I_a=I_b=0$. Introducing these in Eqs.(1b), (1c) and (1d) leads to the $E_h=R_h=0$, and once more, the corresponding equilibrium is disease free. All in all, the only boundary equilibrium point for system (1) where the disease absent in the human population is the disease free equilibrium.
Conversely, assume the human population is disease free, then the free virus concentration $V=0$, and from Eq.(1i), we have $I_a=I_b=0$. Thus, the full system is disease free. Note that, the non existence of boundary equilibria is due to the fact the disease transmission "one way" (that is, from animals and bats to humans and not the other way round).
As a consequence, we have proven the following result:
Lemma 3.5. System (1) has no other boundary equilibrium than the disease-free equilibrium.
This lemma is very important as it excludes the possibility for the full model (1) to exhibit non trivial boundary equilibrium points. This suggests that the full model could have exactly one interior (endemic) equilibrium with the disease being present in all the populations under consideration. This, together with the existence and uniqueness of interior equilibrium for some system (1)-related sub-models [9], motivates the following conjecture that we make.
Conjecture 1. Assume that $\mathcal R_0 > 1 $ for system (1). Then there exists a unique interior (endemic) equilibrium.
The stability of the endemic equilibrium will be shown numerically at a later stage.
Remark 3. Actually, Conjecture 1 could be addressed in a separate work, by reducing the finding of equilibria to a fixed-point problem and apply a suitable fixed-point theorem for a multi-variable and sub-linear function for monotone dynamical systems or for systems of ordinary differential equations which generate an order preserving flow [29,30,48].
In order to investigate the effects of the environmental contamination on the transmission of EVD, it is reasonable to consider the sub-model of system (1) without the environment compartment. Note that, even though the full model (which couples many subsystems) could have two equilibria (namely, the disease free and the interior equilibria), it is not obvious that all its sub-models will exhibit the same property since the coupling can reduce or increase for example the number of equilibrium points. Below is the sub-model involving only human, animal and bat populations, but excluding the environment influence.
4. The full model (1) without the environmental contamination
Here the environmental transmission is neglected. This assumption reflects the disease transmission cycles in [26,51], where the indirect contamination is not explicitly mentioned. This amounts to getting rid of the last terms in Eqs. (2)-(4) of the forces of infection. The model in this setting reads therefore:
|
$
\dfrac{dS_h}{dt} = \Lambda_h - \dfrac{\beta_{hh}\Phi_hS_hI_h}{N_h} - \dfrac{\beta_{ha}\Phi_aS_hI_a}{N_h} - \dfrac{\beta_{hb}S_h I_b}{N_h} - \mu_hS_h
$
|
(19a)
|
|
$
\dfrac{dE_h}{dt} = \dfrac{\beta_{hh}\Phi_hS_hI_h}{N_h} + \dfrac{\beta_{ha}\Phi_aS_hI_a}{N_h} +\dfrac{\beta_{hb}S_h I_b}{N_h} - \left(\mu_h + \omega\right)E_h
$
|
(19b)
|
|
$
\dfrac{dI_h}{dt} = \omega E_h - \left( \mu_h+\gamma \right)I_h
$
|
(19c)
|
|
$
\dfrac{dR_h}{dt} = \gamma(1-f)\, I_h - \mu_hR_h
$
|
(19d)
|
|
$
\dfrac{dS_a}{dt} = \Lambda_a - \dfrac{\beta_{aa}\Phi_a S_a I_a}{N_a} - \dfrac{\beta_{ab} S_a I_b}{N_a} - \mu_a S_a
$
|
(19e)
|
|
$
\dfrac{dI_a}{dt} = \dfrac{\beta_{aa}\Phi_a S_a I_a}{N_a} + \dfrac{\beta_{ab} S_a I_b}{N_a} - (\mu_a +\delta_a ) I_a
$
|
(19f)
|
|
$
\dfrac{dS_b}{dt} = \Lambda_b - \beta_{bb} S_b I_b - \mu_bS_b
$
|
(19g)
|
|
$
\dfrac{dI_b}{dt} = \beta_{bb} S_b I_b - \mu_b I_b
$
|
(19h)
|
The corresponding basic reproduction for this model is easily computed as
|
$
\mathcal R_{0, hab} = \max\left\{\mathcal R_{0, h}\;, \; \mathcal R_{0, a} \;, \; \mathcal R_{0, b} \right\}
$
|
(20)
|
where,
|
$
\mathcal R_{0, h} = \dfrac{\beta_{hh}\Phi_h\omega}{(\mu_h+\omega)(\mu_h+\gamma)},\;\; \mathcal R_{0, a}= \dfrac{\beta_{aa}\Phi_a}{\mu_a +\delta_a} \: \: \text{and} \: \: \mathcal R_{0, b} = \dfrac{\beta_{bb}\Lambda_b}{\mu^2_b}.
$
|
(21)
|
Actually, $\mathcal R_{0, h}$, $\mathcal R_{0, a}$ and $\mathcal R_{0, b}$ are the intra-specific basic reproduction numbers for human, animal and bat sub-populations given earlier by Eq. (10) and Eq. (15), respectively.
Remark 4. Note that the non-negative matrix $\mathcal{G}$ in (8) has diagonal entries $\mathcal R^{hhv}_{0}, \, \mathcal R^{aav}_{0}$ and $\mathcal R^{bbv}_{0}$ that are larger than $\mathcal R_{0, h}, \, \mathcal R_{0, a}$ and $\mathcal R_{0, b}$, respectively. This, together with the fact that the spectral radius of a non-negative matrix is an increasing function of its entries yields
|
$ \mathcal R_{0} = \rho{(\mathcal G)} \geq \mathcal R_{0, hab}.$
|
Consequently, the indirect environmental contamination enhances the transmissibility of EVD, and thus it increases the epidemic/endemic level of the disease.
The dynamics of sub-system (19) are confined in the biological feasible compact set subset of $\Gamma_{hab}$ given by
|
$
\Gamma_{hab} = \left\{(S_h, E_h, I_h, R_h, S_a, I_a, S_b, I_b) \in \mathbb R^5_+ : N_h\leq \dfrac{\Lambda_h}{\mu_h }, \;\; N_a\leq \dfrac{\Lambda_a}{\mu_a }, \: \, N_b\leq \dfrac{\Lambda_b}{\mu_b } \right\}.
$
|
(22)
|
Sub-model (19) is triangular. Indeed the variables ($S_h, E_h, I_h, R_h$) do not appear in the last fourth equations. Moreover, the variables ($S_a, I_a)$ do not appear in the last two equations. Therefore, in order to address the long run behavior of system (19), we shall make use of the decomposition techniques by applying repeatedly the following theorem [54].
Theorem 4.1. ([54], Theorem 3.1) Consider the system
|
$
\left\{dxdt=f(x),x∈Rn,dydt=g(x,y),x∈Rn,y∈Rm,withright−handsideofclassC1,and(x∗,y∗)anequilibriumpoint,i.e.,f(x∗)=0=g(x∗,y∗). \right.
$
|
(23)
|
1.If $x^*$ is globally asymptotically stable (GAS) in $\mathbb{R}^n$ for subsystem $\dfrac{dx}{dt} = f(x)$ and if $y^*$ is GAS in $\mathbb{R}^m$ for the subsystem $\dfrac{dy}{dt} = g(x^*, y)$, then $(x^*, y^*)$ is (locally) asymptotically stable for system (23).
2. Moreover, if all the trajectories of system (23) are forward bounded, then $(x^*, y^*)$ is GAS for the system (23).
In order to apply Theorem 4.1, we need to study some sub-systems of Eq. (19).
4.1. Dynamics of the bat sub-model (19g)-(19h)
We give here the long run behavior of the sub-model
|
$
\left\{dSbdt=Λb−βbbSbIb−μbSb,dIbdt=βbbSbIb−μbIb,\right.
$
|
(24)
|
by establishing the global stability of its equilibrium points. Obviously this system (24) has two equilibria; namely, the disease-free equilibrium $P^0_b = (S^0_b, I^0_b)$, whose coordinates are
|
$ S^0_b= \dfrac{\Lambda_b}{\mu_b},\;\; I^0_b=0 $
|
and the endemic equilibrium
|
$ \overline{P}_b = \left(\overline{S}_b, \, \overline{I}_b \right), $
|
which exists whenever $\mathcal R_{0, b} > 1$ and whose components are
|
$
\overline{S}_b = \dfrac{\mu_b}{\beta_{bb}},\;\; \overline{I}_b = \dfrac{ \mu_b\left(\mathcal R_{0, b}-1\right)}{\beta_{bb}}.
$
|
(25)
|
Obviously the dynamics of sub-model (24) are confined in the biological feasible compact set
|
$\Omega_b = \left\{ (S_b, I_b)\in \mathbb R^2_+ : S_b+I_b \leq \dfrac{\Lambda_b}{\mu_b}\right\}.$
|
Looking at model (24) in which the mass action law is applied, it is standard to deduce from the Lyapunov-LaSalle techniques its asymptotic behavior summarized in the result below.
Proposition 1. The following statements hold:
● If $\mathcal R_{0, b}\leq1$, then the disease-free equilibrium $P^0_b$ for subsystem (24) is GAS. It is unstable whenever $\mathcal R_{0, b} >1$.
● If $\mathcal R_{0, b} > 1$, then the equilibrium $ \overline{P}_b$ is GAS.
4.2. Dynamics of the animal sub-model (19e)-(19f) with the bat population at equilibrium points
Here, we consider the subsystem (19e)-(19f)
|
$
\left\{dSadt=Λa−βaaΦaSaIaNa−βabSaIbNa−μaSa,dIadt=βaaΦaSaIaNa+βabSaIbNa−(μa+δa)Ia.\right.
$
|
(26)
|
The dynamics of sub-model (26) are confined in the biological feasible compact set
|
$\Omega_a = \left\{ (S_a, I_a)\in \mathbb R^2_+ : S_a+I_a \leq \dfrac{\Lambda_a}{\mu_a}\right\}.$
|
Using the global asymptotic stability of equilibria for subsystem (24), the following two subsystems will be considered.
4.2.1. Dynamics of (26) with the bat population at equilibrium point $ P^0_b$
The variables $S_b$ and $ I_b$ are substituted in (26) by their corresponding values at the disease-free equilibrium $P^0_b$. This leads us to the system
|
$
\left\{dSadt=Λa−βaaΦaSaIaNa−μaSa,dIadt=βaaΦaSaIaNa−(μa+δa)Ia.\right.
$
|
(27)
|
Direct calculations show that model (27) has two possible non-negative equilibrium states: the disease-free equilibrium $P^0_a = \left(S^0_a = \dfrac{\Lambda_a}{\mu_a}, \, I^0_a = 0 \right)$ and a unique endemic equilibrium $\overline{P}_a = \left(\overline{S}_a, \overline{I}_a\right)$, with
|
$
\left\{¯Sa=Λaμa+(μa+δa)(R0,a−1),¯Ia=Λa(R0,a−1)μa+(μa+δa)(R0,a−1).\right.
$
|
We have the following proposition:
Proposition 2. The following statements are satisfied.
● If $\mathcal R_{0, a} \leq 1$, then for the subsystem (27), the disease free equilibrium $P^0_a$ is GAS. It is unstable whenever $\mathcal R_{0, a} >1$.
● When $\mathcal R_{0, a} > 1$, there exists an unique endemic equilibrium $\overline{P}_a$ which is GAS.
Proof. The GAS of the disease-free equilibrium $P^0_a$ is established using the quadratic Lyapunov function
|
$V_0(S_a, I_a) = \dfrac{1}{2}I^2_a. $
|
The directional derivative of $V_0$ towards the vector field given in the right-hand side of (27) is
|
$˙V0(Sa,Ia)=[βaΦaSa−(μa+δa)Na]I2aNa,=−(μa+δa)[Ia+(R0,a−1)Sa]I2aNa.$
|
Thus, $\dot{V}_0 \leq 0$ whenever $\mathcal R_{0, a} \leq 1 $. Observe that $\dot{V}_0(S_a, I_a) = 0$ if and only if, either $I_a =0$ or $\mathcal R_{0, a}=1$ and $I_a=0$. In both cases, it is easy to see that the largest invariant set contained in $\left\{\dot{V}_0(S_a, I_a) = 0\right\}$ is reduced to the disease-free equilibrium $P^0_a$. Hence, by LaSalle Invariance Principle [34], $P^0_a$ is GAS.
For the GAS of the endemic equilibrium $\overline{P}_a$, we propose the following Lyapunov function candidate.
|
$Q(Sa,Ia)=(Sa+Ia)−(¯Sa+¯Ia)−(¯Sa+¯Ia)ln(Sa+Ia¯Sa+¯Ia)+k(Ia−¯Ia−¯IalnIa¯Ia),=Na−¯Na−¯NalnNa¯Na+k(Ia−¯Ia−¯IalnIa¯Ia), $
|
defined in the set $\{(S_a, I_a) \in \Omega_a: S_a >0, I_a>0\}$. The positive constant $k$ will be determined shortly. Since $(\overline{S}_a, \overline{I}_a)$ is an equilibrium of (27) we have
|
$ \Lambda_a = \mu_a\overline{N}_a -\delta_a\overline{I}_a, (\mu_a+\delta_a) = \dfrac{\beta_{aa}\Phi_a\overline{S}_a}{\overline{N}_a}.$
|
With this in mind and the fact that
|
$\dfrac{S_a}{S_a+I_a} - \dfrac{\overline{S}_a}{\overline{S}_a+\overline{I}_a} = \dfrac{\overline{I}_a(S_a - \overline{S}_a) - \overline{S}_a(I_a-\overline{I}_a)}{(S_a+I_a)(\overline{S}_a+\overline{I}_a)}, $
|
the directional derivative $\dot Q$ of $Q$ towards the vector field given in the right-hand side of (27) is
|
$˙Q=−μa(Sa−¯Sa)2Sa+Ia−(μa+δa+kβaaΦa¯Sa¯Sa+¯Ia)(Ia−¯Ia)2Sa+Ia,−(2μa+δa−kβaaΦa¯Ia¯Sa+¯Ia)(Ia−¯Ia)(Sa−¯Sa)Sa+Ia. $
|
Choose the constant $k$ such that
|
$2\mu_a +\delta_a - \dfrac{k\beta_{aa}\Phi_a\overline{I}_a}{\overline{S}_a+\overline{I}_a} = 0, $
|
or equivalently
|
$ k= \dfrac{(2\mu_a +\delta_a)\overline{S}_a+\overline{I}_a}{\beta_{aa}\Phi_a\overline{I}_a}. $
|
Thus, the directional derivative of $Q$ becomes
|
$\dot Q = - \dfrac{\mu_a(S_a-\overline{S}_a)^2}{S_a+I_a} - \left(\mu_a +\delta_a + \dfrac{k\beta_{aa}\Phi_a\overline{S}_a}{\overline{S}_a+\overline{I}_a}\right) \dfrac{(I_a-\overline{I}_a)^2}{S_a +I_a}, $
|
from which we can see clearly that $\dot Q <0$ except at the endemic equilibrium where it is zero. Therefore, $\overline{P}_a$ is GAS.
4.2.2. Dynamics of (26) with the bat population at equilibrium point $ \overline{P}_b$
Sub-model (26) is considered when the bat population is at endemic state $ \overline{P}_b$. That is the variables $S_b$ and $ I_b$ are replaced in (26) by $\overline{S}_b$ and $\overline{I}_b$, respectively. This gives to the following subsystem:
|
$
\left\{dSadt=Λa−βaaΦaSaIaNa−βabSa¯IbNa−μaSa,dIadt=βaaΦaSaIaNa+βabSa¯IbNa−(μa+δa)Ia.\right.
$
|
(28)
|
Since $\overline{I}_b > 0$, (28) has no disease free equilibrium. We study the existence of endemic equilibria.
Let $\overline{D}_b$ be defined by
|
$
\overline{D}_b= \beta_{ab}\overline{I}_b.
$
|
(29)
|
$\widehat {E}_a = \left(\widehat{S}_a, \widehat{I}_a\right)$ is an equilibrium point of (28) if and only if
|
$
\left\{Λa−(βaaΦaˆIa+¯Db)ˆSaˆNa−μaˆSa=0,(βaaΦaˆIa+¯Db)ˆSaˆNa−(μa+δa)ˆIa=0.\right.
$
|
(30)
|
Set
|
$
\widehat{\lambda}_a =\dfrac{\beta_{aa}\Phi_a \widehat{I}_a + \overline{D}_b}{\widehat{N}_a}.
$
|
(31)
|
Then, from (30) and (31), we have
|
$
\widehat{S}_a = \dfrac{\Lambda_a}{\mu_a + \widehat{\lambda}_a}, \;\;
\widehat{I}_a = \dfrac{\Lambda_a\widehat{\lambda}_a}{\left(\mu_a + \delta_a\right)\left(\mu_a + \widehat{\lambda}_a\right)}, \;\;
\widehat{N}_a = \dfrac{\Lambda_a\left(\mu_a + \delta_a + \widehat{\lambda}_a\right)}{\left(\mu_a + \delta_a\right)\left(\mu_a + \widehat{\lambda}_a\right)}.
$
|
(32)
|
Substituting (32) into (31) yields
|
$
\widehat{\lambda}_a =\dfrac{\beta_{aa}\Phi_a \Lambda_a\widehat{\lambda}_a + \overline{D}_b\left(\mu_a + \delta_a\right)\left(\mu_a + \widehat{\lambda}_a\right)}{\Lambda_a\left(\mu_a + \delta_a + \widehat{\lambda}_a\right)}.
$
|
From this latter expression, we derive the quadratic equation
|
$
\Lambda_a \left(\widehat{\lambda}_a\right)^2 + \left[\Lambda_a\left(\mu_a + \delta_a \right)-\overline{D}_b(\mu_a+\delta_a)-\beta_{aa}\Phi_a \Lambda_a \right] \widehat{\lambda}_a - \mu_a\left(\mu_a + \delta_a \right)\overline{D}_b = 0.
$
|
(33)
|
Denote the discriminant of Eq. (33) by
|
$
\Delta_a = \left[\Lambda_a\left(\mu_a + \delta_a \right)-\overline{D}_b(\mu_a+\delta_a)-\beta_{aa}\Phi_a \Lambda_a \right]^2 + 4\mu_a\Lambda_a\left(\mu_a+\delta_a\right)\overline{D}_b >0.
$
|
(34)
|
Then, the unique positive root of Eq. (33) is
|
$
\widehat{\lambda}_a = \dfrac{ \left(\beta_{aa}\Phi_a - \mu_a - \delta_a\right) \Lambda_a + \overline{D}_b(\mu_a+\delta_a)+ \sqrt{\Delta_a}}{2\Lambda_a}.
$
|
(35)
|
Thus, the components of the unique equilibrium point $\widehat{E}_{a}$, obtained by substituting (35) into (32) are
|
$
\left\{ˆSa=2Λ2a2μaΛa+(βaaΦa−μa−δa)Λa+¯Db(μa+δa)+√Δa,ˆIa=Λa[(βaaΦa−μa−δa)Λa+¯Db(μa+δa)+√Δa](μa+δa)[2μaΛa+(βaaΦa−μa−δa)Λa+¯Db(μa+δa)+√Δa].\right.
$
|
(36)
|
Proposition 3. The endemic equilibrium $\widehat{E}_a$ for subsystem (28) is GAS whenever $\mathcal R_{0, a} \leq 1$.
Proof. We first establish the LAS of $\widehat{E}_{a}$ when $\mathcal R_{0, a}\leq 1$. Let $J(\widehat {E}_a)$ be the Jacobian matrix at any equilibrium point $\widehat {E}_a$ of (28). We have
|
$
J(\widehat {E}_a) = (−βaaΦa(ˆIa)2(ˆNa)2−¯DbˆIa(ˆNa)2−μa− βaaΦa(ˆSa)2(ˆNa)2+¯DbˆSa(ˆNa)2βaaΦa(ˆIa)2(ˆNa)2+¯DbˆIa(ˆNa)2βaaΦa(ˆSa)2(ˆNa)2−¯DbˆSa(ˆNa)2−(μa+δa)).
$
|
Since $\widehat {E}_a$ is an equilibrium point, it can be shown that the trace of $J(\widehat {E}_a)$ is
|
$
trace(J(ˆEa))=βaaΦa(ˆSa−ˆIa)−(δa+2μa)ˆNa−¯DbˆNa,=−[(μa+δa)(1−R0,a)+μa]ˆSa−[βaaΦa+2μa+δa]ˆIa−¯DbˆNa,<0.
$
|
(37)
|
Furthermore, the determinant $\det(J(\widehat {E}_a))$ of $J(\widehat {E}_a)$ is
|
$
det(J(ˆEa))=βaaΦa(μa+δa)(ˆIa)2+¯Db(μa+δa)ˆIa−μaβaaΦa(ˆSa)2(ˆNa)2+μa¯DbˆSa+μa(μa+δa)(ˆNa)2(ˆNa)2,=(μa+δa)[βaaΦa(ˆIa)2+μa(ˆIa)2+¯DbˆIa+2μaˆSaˆIa](ˆNa)2+(μa+δa)μaˆSa(1−R0,a)+¯Dbμaδa(ˆNa)2,
$
|
(38)
|
which is positive whenever $\mathcal R_{0, a}\leq 1$. This proves the LAS of $\widehat {E}_a$.
Secondly, we prove the global attractiveness of $\widehat {E}_a$. To achieve this, we use the Dulac criterion [27] to rule out the existence of periodic solutions. Consider the Dulac function
|
$ g(S_a, I_a) = \dfrac{1}{I_a}, $
|
defined on the connected region $\left(0, \dfrac{\Lambda_a}{\mu_a}\right)\times \left(0, \dfrac{\Lambda_a}{\mu_a}\right)$ containing the interior of $\Omega_a$. Let $X(S_a, I_a)= \left(X_1(S_a, I_a), X_2(S_a, I_a)\right)^T$ be the right hand side of (28). It is easily shown that
|
$\dfrac{\partial(gX_1)}{\partial S_a} + \dfrac{\partial(gX_2)}{\partial I_a} = - \dfrac{\beta_{aa}\Phi_a}{N_a} - \dfrac{\overline{D}_b}{I^2_a} - \dfrac{\mu_a}{I_a} < 0.$
|
Hence, by Dulac's criterion, there is no periodic solution in the interior of $\Omega_a$. Hence $\widehat {E}_a$ is GAS whenever $\mathcal R_{0, a} \leq 1$. This completes the proof.
4.3. Dynamics of human sub-model (19a)-(19d) when bat and animal subpopulations are evaluated at steady states
We conclude the series of sub-models by studying the dynamics of the human subpopulation when the other subpopulations (bats and animals) are at their different equilibrium states. The subsystem under investigation is constituted of Eqs. (19a)-(19d) given below.
|
$
\left\{dShdt=Λh−βhhΦhShIhNh−βhaΦaShIaNh−βhbShIbNh−μhSh,dEhdt=βhhΦhShIhNh+βhaΦaShIaNh+βhbShIbNh−(μh+ω)Eh,dIhdt=ωEh−(μh+γ)Ih,dRhdt=γ(1−f)Ih−μhRh. \right.
$
|
(39)
|
4.3.1. Dynamics of subsystem (39) when bats and animals are evaluated at the equilibrium point $\left(P^0_a, P^0_b\right)$
Consider the subsystem (19a)-(19d) dealing with human subpopulation, where the animals and bats subpopulations are at disease-free equilibrium $(P^0_a, P^0_b)$:
|
$
\left\{dShdt=Λh−βhhΦhShIhNh−μhSh,dEhdt=βhhΦhShIhNh−(μh+ω)Eh,dIhdt=ωEh−(μh+γ)Ih,dRhdt=γ(1−f)Ih−μhRh. \right.
$
|
(40)
|
Model (40) is well posed mathematically and biologically in the compact set
|
$
\Omega_h = \left\{ (S_h, E_h, I_h, R_h)\in \mathbb R^4_+ : N_h= S_h+E_h+I_h+R_h \leq \dfrac{\Lambda_h}{\mu_h}\right\}.
$
|
(41)
|
System (40) has two equilibrium points, namely the disease-free
|
$P^0_h= \left(\dfrac{\Lambda_h}{\mu_h}, 0, 0, 0\right), $
|
which always exists and the endemic equilibrium point $\overline{E}_h = \left(\overline{S}_h, \overline{E}_h, \overline{I}_h\overline{R}_h\right)$, which exists whenever the human intra-specific basic reproduction number
|
$\mathcal{R}^0_{0h} = \frac{\beta_{hh}\Phi_h\omega}{\left(\mu_h+\omega\right)\left(\mu_h+\gamma\right)} >1. $
|
Set
|
$B_h = \left(\mu_h+\omega\right)\left(\mu_h+\gamma\right).$
|
Then the components of $\overline{E}_h$ are:
|
$
¯Sh=Λh[μh(μh+ω+γ)+γω(1−f)]μh[Bh(R00h−1)+μh(μh+ω+γ)+γω(1−f)],¯Eh=Λh(μh+γ)(R00h−1)Bh(R00h−1)+μh(μh+ω+γ)+γω(1−f),¯Ih=ωΛh(μh+γ)(R00h−1)(μh+γ)[Bh(R00h−1)+μh(μh+ω+γ)+γω(1−f)],¯Rh=γ(1−f)ωΛh(μh+γ)(R00h−1)μh(μh+γ)[Bh(R00h−1)+μh(μh+ω+γ)+γω(1−f)].
$
|
The asymptotic behavior of model (40) is completely described by
Theorem 4.2. The following statements hold true:
(1) The disease-free equilibrium point $P^0_h$ is GAS when $\mathcal R_{0, h} \leq 1$ and unstable if $\mathcal R_{0h} > 1$.
(2) The endemic equilibrium point $\overline{E}_h $ is GAS whenever $\mathcal R_{0h} > 1$.
Proof. The first item is established using the Lyapunov function
|
$L_h= L_h\left(S_h, E_h, I_h, R_h\right) = \dfrac{\omega}{B_h}E_h + \dfrac{1}{\mu_h+\gamma} I_h.$
|
The Lie derivative of $L_h$ with respect to the vector field given by the right hand side of (40) is
|
$\dot{L}_h = \left[\dfrac{\beta_{hh}\Phi_h\omega S_h}{B_hN_h}-1 \right]I_h = - \left[\left(1-\mathcal R_{0, h}\right)S_h + E_h+I_h+R_h \right]\dfrac{I_h}{N_h}.$
|
Clearly $\dot{L}_h \leq 0$ in $\Omega_h$, and $\dot{L}_h = 0$ if and only if $I_h=0$ or $\mathcal R_{0, h} = 1$ and $ E_h+I_h+R_h = 0$. In both cases, the largest invariant set in $M_h= \left\{\left(S_h, E_h, I_h, R_h\right)\in\right.$ $ \left.\Omega_h / \ \dot{L}_h = 0\right\}$ is the disease-free equilibrium point $P^0_h$. Indeed, suppose $I_h = 0$, then replace it in the first, second and fourth equations of (40) and solve. One has $S_h(t) =\Lambda_h/\mu_h + \left[S_h(0)-\Lambda_h/\mu_h\right] e^{-\mu_h t}$, $E_h(t) = E_h(0)e^{-(\mu_h+\gamma)t}$ and $R_h(t) = R_h(0)e^{-\mu_h t}$. Thus, as $t\to \infty$, $S_h(t)\to \Lambda_h/\mu_h $, and $\left(E_h(t), E_h(t)\right) \to \left(0, 0\right)$. Hence $M_h= \left\{P^0_h\right\}$. The conclusion for the GAS of $P^0_h$ follows by LaSalle's Invariance Principle.
As for the second item of Theorem 4.2, the proof of the global asymptotic stability is quiet long and challenging. We refer the interested reader to [39,61] where the proof is provided using a geometrical approach [40].
Thanks to Theorem 4.1 and combining Proposition 1, Proposition 2 and Proposition 4.2 we are now able state the first main result regarding the asymptotic behavior of the environmental-free model (19).
Theorem 4.3. For system (19), the following statements hold true:
1. If $\mathcal R_{0, h} \leq 1$, $\mathcal R_{0, a}\leq 1$, and $\mathcal R_{0, b}\leq1$, then $\left(P^0_h, \, P^0_a, \, P^0_b\right)$ is GAS.
2. If $\mathcal R_{0, h} > 1$, $\mathcal R_{0, a}\leq 1$, and $\mathcal R_{0, b} \leq 1$, then $\left(\overline{P}_h, \, P^0_a, \, P^0_b\right)$ is GAS.
4.3.2. Dynamics of (39) with the bats and animals at steady state $\left(\overline{P}_a, P^0_b\right)$
The model under consideration in this section is
|
$
\left\{dShdt=Λh−βhhΦhShIhNh−¯DaShNh−μhSh,dEhdt=βhhΦhShIhNh+¯DaShNh−(μh+ω)Eh,dIhdt=ωEh−(μh+γ)Ih,dRhdt=γ(1−f)Ih−μhRh, \right.
$
|
(42)
|
where the constant $\overline{D}_a$ is giving by
|
$
\overline{D}_a = \beta_{ha}\Phi_a\overline{I}_a.
$
|
(43)
|
This model is obviously a dynamical system on the biological feasible domain given in (41).
Due to the fact $\overline{I}_a > 0$, model (42) cannot exhibit a disease free equilibrium. We shall therefore focus on the existence and stability of possible endemic equilibrium points. Let $E^{**}_h= \left(S^{**}_h, E^{**}_h, I^{**}_h, R^{**}_h\right)$ be an equilibrium of (42). Set
|
$
\lambda^{**}_h = \dfrac{\beta_{hh}\Phi_h I^{**}_h + \overline{D}_a}{N^{**}_h}.
$
|
(44)
|
Then $\left(S^{**}_h, E^{**}_h, I^{**}_h, R^{**}_h\right)$ is a positive solution of
|
$
\left\{Λh−(λ∗∗h+μh)S∗∗h=0,λ∗∗hS∗∗h−(μh+ω)E∗∗h=0,ωE∗∗h−(μh+γ)I∗∗h=0,γ(1−f)I∗∗h−μhR∗∗h=0. \right.
$
|
(45)
|
From (45), we have
|
$
\left\{S∗∗h=Λhμh+λ∗∗h,E∗∗h=Λhλ∗∗h(μh+ω)(μh+λ∗∗h),I∗∗h=ωΛhλ∗∗hBh(μh+λ∗∗h),R∗∗h=γ(1−f)ωΛhλ∗∗hμhBh(μh+λ∗∗h),N∗∗h=[μhBh(μh+λ∗∗h)+μh(μh+γ)λ∗∗h+μhωλ∗∗h+γ(1−f)ωλ∗∗h]μhBh(μh+λ∗∗h). \right.
$
|
(46)
|
Putting the above expressions (46) in (44), yields the following quadratic equation with respect to $\lambda^{**}_h$
|
$
a_h \left(\lambda^{**}_h\right)^2 + b_h\lambda^{**}_h + c_h = 0,
$
|
(47)
|
where the constant coefficients $a_h, b_h, c_h$ are:
|
$
\left\{ah=Λh[μhBh+μh(μh+γ)+μhω+γ(1−f)ω],bh=μ2hBhΛh−μhβhhΦhωΛa+μhω−μh(μh+γ)(μh+ω)¯Da,ch=−μ2hBh¯Da. \right.
$
|
(48)
|
Since, $a_h>0$ and $c_h<0$, the quadratic equation (47) has one positive solution $\lambda^{**}_h$ to which corresponds the unique endemic equilibrium point $E^{**}_h$ of subsystem (42) giving by (46).
Similar arguments to those in [39,61] can be used to prove the global asymptotic stability of the unique endemic equilibrium point $E^{**}_h$ of subsystem (42). Hence, thanks to Theorem 4.1, we can give the second main theorem of this section.
Theorem 4.4. If $\mathcal R_{0, a} > 1$ and $\mathcal R_{0, b}\leq 1$, then the equilibrium point $\left(E^{**}_h, \, \overline{P}_a, \, P^0_b\right)$ for subsystem (42) is GAS.
4.3.3. Dynamics of (39) with the bats and animals at steady state $\left(\widehat{E}_a, \overline{P}_b \right)$
Replacing $\left(\widehat{I}_{a}, \overline{I}_b \right)$ in subsystem (39) above, yields the following system
|
$
\left\{dShdt=Λh−βhhΦhShIhNh−(ˆDa+¯Db)ShNh−μhSh,dEhdt=βhhΦhShIhNh+(ˆDa+¯Db)ShNh−(μh+ω)Eh,dIhdt=ωEh−(μh+γ)Ih,dRhdt=γ(1−f)Ih−μhRh, \right.
$
|
(49)
|
where $\widehat{D}_{a}$ is the constant defined by
|
$
\widehat{D}_{a} = \beta_{ha}\Phi_a\widehat{I}_{a}.
$
|
(50)
|
The theoretical analysis of subsystem (49) is similar to that of subsystem (42). Denoting by $E^{***}_h= \left(S^{***}_h, E^{***}_h, I^{***}_h, R^{***}_h\right)$ its unique endemic equilibrium defined in terms of the analogues for (42) of Eqs. (44) and (47), we obtain the following result.
Theorem 4.5. If $\mathcal R_{0, a} \leq 1$ and $\mathcal R_{0, b} > 1$, then the equilibrium $\left(E^{***}_h, \, \widehat{E}_a, \, \overline{P}_b\right) $ for subsystem (49) is GAS.
We summarize the existence of the four equilibria of system (19) and their stability properties in the following table.
Table 3. Existence, conditions for existence and stability of equilibria.
| Equilibria | |
Conditions of existence |
Stability |
| $\left(P^0_h, P^0_a, P^0_b \right)$ | |
$ \mathcal R_{0, h}>1, \mathcal R_{0, a}\leq 1, \mathcal R_{0, b} \leq 1 $ |
GAS |
| $\left(\overline{E}_h, P^0_a, P^0_b \right)$ | |
$ \mathcal R_{0, h} \leq 1, \mathcal R_{0, a}\leq 1, \mathcal R_{0, b} \leq 1 $ |
GAS |
| $\left(E^{**}_h, \overline{P}_a, P^0_b \right)$ | |
$ \mathcal R_{0, a}>1, \mathcal R_{0, b} \leq 1 $ |
GAS |
| $\left(E^{***}_h, \widehat{E}_a, \overline{P}_b\right)$ | |
$ \mathcal R_{0, a}\leq 1, \mathcal R_{0, b} > 1 $ |
GAS |
5. Sensitivity analysis
We carried out a sensitivity analysis. This allows to identify the parameters that are most influential in determining population dynamics [42,43]. A Latin Hypercube Sampling (LHS) scheme [15,43] samples $1000$ values for each input parameter using a uniform distribution over the range of biologically realistic values, listed in Table 7. Using system (1), $1000$ model simulations are performed by randomly pairing sampled values for all LHS parameters. Outcome measures are calculated for each run: Exposed individuals to EVD, infected individuals, virus concentration, infected animals and infected bats. Partial Rank Correlation Coefficients (PRCC) and corresponding $p$-values are computed. An output is assumed sensitive to an input if the corresponding PRCC is less than $-0.50$ or greater than $+0.50$, and the corresponding $p$-values is less than $5\%$. The results are displayed in Table 4, Table 5 and Table 6. From these tables, it can be seen that the effective contact rate between humans and fruit bats and the bat mortality rate are the most influential parameters on the latent and infected human individuals.
Table 4. PRCCs of full model's parameters.
| Parameters | $E_h$ | $I_h$ | $V$ | $I_a$ | $I_b$ |
| $\Lambda_{h}$ | $0.7624^{**}$ | 0.2343 | 0.1922 | 0.0124 | 0.0172 |
| $\Lambda_a$ | -0.1822 | 0.2005 | 0.1610 | $0.8914^{**}$ | 0.0180 |
| $\Lambda_b$ | -0.3116 | $0.4407^*$ | 0.3008 | $-0.5346^{**}$ | 0.0132 |
| $\mu_{h}$ | $-0.8657^{**}$ | $-0.8588^{**}$ | $-0.9438^{**}$ | -0.0341 | 0.0329 |
| $\mu_{a}$ | 0.1060 | -0.1786 | -0.1134 | $-0.4854^*$ | -0.0148 |
| $\mu_{b}$ | $0.5677^{**}$ | $-0.6054^{**}$ | $-0.4335^*$ | $0.7106^{**}$ | $0.8966^{**}$ |
| $\mu_{v}$ | -0.0143 | -0.0493 | -0.0453 | -0.0530 | 0.0202 |
| $\xi_{h}$ | 0.0030 | -0.0099 | 0.284 | -0.0491 | -0.0250 |
| $\xi_{a}$ | -0.0107 | 0.0630 | 0.0010 | -0.1381 | 0.0356 |
| $\nu_{h}$ | -0.0218 | 0.0572 | 0.0200 | -0.0509 | -0.0518 |
| $\nu_{a}$ | -0.1213 | 0.1149 | 0.0410 | -0.1530 | 0.0256 |
| $\omega $ | -0.1299 | -0.2465 | $0.5385^{**}$ | 0.0513 | -0.0613 |
| $\gamma$ | 0.0463 | -0.0623 | 0.1735 | 0.0108 | 0.0092 |
| $\delta_a$ | 0.0239 | -0.0450 | -0.0185 | -0.325 | -0.0044 |
| $\alpha_h$ | 0.0143 | 0.0490 | -0.0125 | 0.0067 | 0.0154 |
| $\alpha_a$ | 0.043 | 0.0177 | 0.1003 | -0.0653 | -0.0434 |
| $\alpha_b$ | 0.0078 | -0.0041 | -0.0254 | -0.0113 | -0.0506 |
| $\theta_h$ | 0.0133 | 0.0073 | 0.0845 | -0.0410 | -0.0025 |
| $f$ | 0.0142 | -0.0065 | $-0.4980^{*}$ | -0.0320 | -0.0106 |
| $K$ | 0.0375 | -0.0581 | 0.0141 | 0.0003 | 0.0263 |
| $\beta_{hh}$ | -0.2682 | 0.3205 | 0.1217 | 0.0220 | 0.0038 |
| $\beta_{hb}$ | -0.3700 | $0.5287^{**}$ | 0.3747 | -0.0114 | 0.0125 |
| $\beta_{hv}$ | 0.0785 | 0.0106 | 0.0022 | -0.0824 | -0.0129 |
| $\beta_{ha}$ | -0.1816 | 0.2399 | 0.1559 | -0.0395 | -0.0448 |
| $\beta_{bb}$ | 0.0196 | 0.0757 | 0.1389 | -0.0976 | $-0.8883^{**}$ |
| $\beta_{ab}$ | -0.0242 | 0.0984 | 0.0080 | $-0.6039^{**}$ | -0.0030 |
| $\beta_{bv}$ | -0.0214 | -0.0310 | -0.0280 | -0.0071 | 0.0391 |
| $\beta_{aa}$ | -0.0145 | 0.1266 | -0.0036 | $-0.4099^{*}$ | -0.0596 |
| $\beta_{av}$ | -0.0214 | 0.0150 | 0.0718 | 0.0737 | 0.0339 |
Table 5. PRCCs of model's parameters without environment.
| Parameters | $E_h$ | $I_h$ | $I_a$ | $I_b$ |
| $\Lambda_{h}$ | $0.7897^{**}$ | 0.3341 | 0.0602 | 0.0406 |
| $\Lambda_a$ | -0.1412 | 0.2206 | 0.8767 | -0.0122 |
| $\Lambda_b$ | -0.3108 | $0.4231^*$ | $-0.4185^*$ | -0.0214 |
| $\mu_{h}$ | $-0.8755^{**}$ | $-0.8466^{***}$ | 0.0180 | 0.0341 |
| $\mu_{a}$ | 0.0936 | -0.2108 | $-0.4814^{*}$ | -0.0046 |
| $\mu_{b}$ | $0.5727^{**}$ | $-0.6096^{**}$ | $0.7117^{***}$ | $0.9040^{***}$ |
| $\xi_{h}$ | 0.0055 | 0.0391 | -0.0337 | -0.0270 |
| $\xi_{a}$ | -0.0913 | 0.1327 | -0.0923 | -0.0041 |
| $\nu_{h}$ | -0.0183 | 0.0184 | 0.0608 | -0.0183 |
| $\nu_{a}$ | -0.0483 | 0.0745 | -0.0953 | -0.0253 |
| $\omega $ | -0.1496 | -0.2233 | 0.0116 | 0.0046 |
| $\gamma$ | 0.0124 | -0.0410 | 0.0286 | -0.0295 |
| $\delta_a$ | 0.0690 | -0.0647 | -0.3869 | 0.0175 |
| $\theta_h$ | -0.0221 | 0.0308 | 0.0099 | 0.0539 |
| $f$ | 0.0035 | -0.0057 | 0.0042 | 0.0170 |
| $\beta_{hh}$ | -0.2865 | 0.3144 | -0.0275 | -0.0105 |
| $\beta_{hb}$ | -0.3649 | $0.4837^{*}$ | -0.0063 | -0.0131 |
| $\beta_{ha}$ | -0.2057 | 0.3168 | 0.0372 | 0.0050 |
| $\beta_{bb}$ | -0.0686 | 0.0757 | -0.2270 | $-0.8988^{***}$ |
| $\beta_{ab}$ | -0.0719 | 0.0684 | $-0.5291^{**}$ | -0.0245 |
| $\beta_{aa}$ | 0.0063 | 0.0049 | -0.2936 | 0.0053 |
Table 6. PRCCs of model's parameters without animals.
| Parameters | $E_h$ | $I_h$ | $V$ | $I_b$ |
| $\Lambda_{h}$ | $0.7853^{**}$ | 0.2046 | 0.1034 | 0.0202 |
| $\Lambda_b$ | -0.3295 | $0.4674^*$ | 0.3423 | -0.0096 |
| $\mu_{h}$ | $-0.8726^{**}$ | $-0.8067^{**}$ | $-0.9046^{**}$ | 0.0203 |
| $\mu_{b}$ | $0.6098^{**}$ | $-0.6607^{**}$ | $-0.5215^{**}$ | $0.8990^{**}$ |
| $\mu_{v}$ | 0.01 | 0.0066 | 0.0254 | -0.0085 |
| $\xi_{h}$ | -0.0047 | 0.0470 | 0.0421 | -0.0097 |
| $\nu_{h}$ | -0.0110 | 0.0116 | -0.0052 | 0.0244 |
| $\omega $ | -0.1750 | -0.1661 | $0.4079^{*}$ | -0.0014 |
| $\gamma$ | 0.0404 | 0.0196 | 0.1127 | -0.0412 |
| $\alpha_h$ | -0.0375 | -0.0105 | 0.0071 | 0.0263 |
| $\alpha_b$ | 0.0091 | -0.0128 | -0.0147 | 0.0408 |
| $\theta_h$ | -0.0182 | 0.0316 | 0.0038 | -0.0090 |
| $f$ | 0.0037 | 0.0187 | $-0.4368^{*}$ | -0.0041 |
| $K$ | -0.0096 | -0.0177 | 0.0319 | -0.0294 |
| $\beta_{hh}$ | -0.2646 | 0.3093 | 0.2130 | 0.0209 |
| $\beta_{hb}$ | -0.3794 | $0.5955^{**}$ | $0.4528^*$ | 0.0162 |
| $\beta_{hv}$ | 0.0055 | 0.0171 | -0.0102 | -0.0538 |
| $\beta_{bb}$ | -0.0803 | 0.0556 | 0.0875 | $-0.8952^{***}$ |
| $\beta_{bv}$ | -0.0094 | 0.0178 | -0.0178 | 0.0804 |
Table 7. Baseline numerical values for the parameters of system (1).
| Parameters | Range | Values | Units | Source |
| $\Lambda_{h}$ | Variable | 100 | $indiv.day^{-1}$ | N/A |
| $\Lambda_a$ | Variable | 5 | $indiv.day^{-1}$ | N/A |
| $\Lambda_b$ | Variable | 10 | $indiv.day^{-1}$ | N/A |
| $\mu_{h}$ | 0-1 | 0.33/365 | $day^{-1}$ | [57] |
| $\mu_{a}$ | 0-1 | 0.4/365 | $day^{-1}$ | Assumed |
| $\mu_{b}$ | 0-1 | 0.5/365 | $day^{-1}$ | Assumed |
| $\mu_{v}$ | 0-1 | 0.85/30 | $day^{-1}$ | Assumed [10,46] |
| $\xi_{h}= 1/\tau_h$ | 0-1 | 1/2.5 | $day^{-1}$ | [50,57] |
| $\tau_h$ | 1-7 | 2.5 | $day$ | [50,57] |
| $\xi_{a} =1/\tau_a$ | 0-1 | 1/7 | $day^{-1}$ | Assumed |
| $\tau_a$ | 1-14 | 7 | $day$ | Assumed |
| $\nu_{h}$ | 1-5 | 1.2 | $day^{-2}$ | Assumed |
| $\nu_{a}$ | 1-5 | 1.3 | $day^{-2}$ | Assumed |
| $\omega $ | 1/2-1/21 | 1/21 | $day^{-1}$ | [22,50] |
| $\gamma$ | 1/7-1/14 | 1/14 | $day^{-1}$ | [57] |
| $\delta_a$ | 0-1 | 0.5/365 | $day^{-1}$ | Assumed |
| $\alpha_h$ | 10-100 | 50 | $cells.(ml.day.indiv)^{-1}$ | [8] |
| $\alpha_a$ | 20-200 | 100 | $cells.(ml.day.indiv)^{-1}$ | Assumed |
| $\alpha_b$ | 50-400 | 200 | $cells.(ml.day.indiv)^{-1}$ | Assumed |
| $\theta_h = 1/r_h$ | 1/81-1 | 1/61 | $day^{-1}$ | [50] |
| $r_h$ | 1-81 | 61 | $day$ | [50] |
| $f$ | 0.4-0.9 | 0.70 | dimensionless | [50,52,57] |
| $K$ | $10^6$-$10^9$ | $10^6$ | $cells.ml^{-1}$ | [8] |
| $\beta_{hh}$ | 0-1 | | $day^{-1}$ | Variable |
| $\beta_{hb}$ | 0-1 | | $day^{-1}$ | Variable |
| $\beta_{hv}$ | 0-1 | | $day^{-1}$ | Variable |
| $\beta_{ha}$ | 0-1 | | $day^{-1}$ | Variable |
| $\beta_{bb}$ | 0-1 | | $day^{-1}$ | Variable |
| $\beta_{ab}$ | 0-1 | | $day^{-1}$ | Variable |
| $\beta_{bv}$ | 0-1 | | $day^{-1}$ | Variable |
| $\beta_{aa}$ | 0-1 | | $day^{-1}$ | Variable |
| $\beta_{av}$ | 0-1 | | $day^{-1}$ | Variable |
6. Numerical simulations
In this section, we give numerical simulations that support the theory presented in the previous sections. The simulations are produced by MatLab. While the parameters values for human-to-human transmission are mostly taken from [50,57], we have proposed almost all the parameter values regarding animal-to-human, bat-to-human, environment-to-human, environment-to-animal, environment-to-bat, animal-to-animal, animal-to-bat and bat-to-bat transmission mechanisms.
6.1. General dynamics
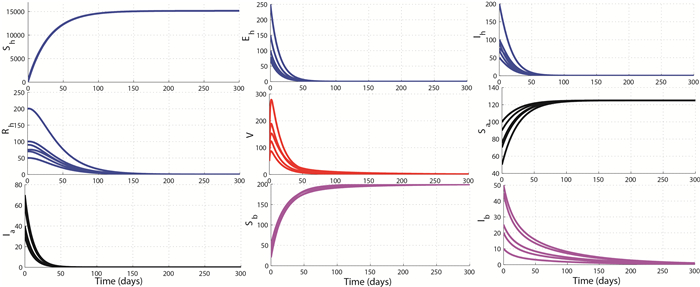
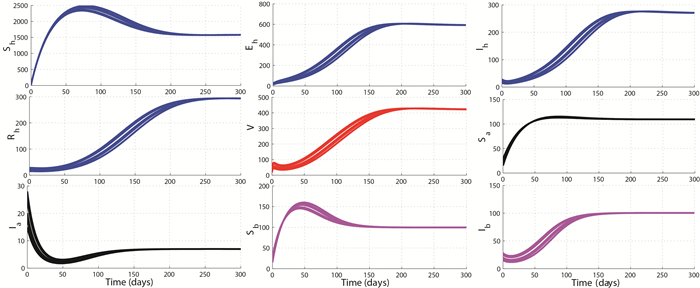
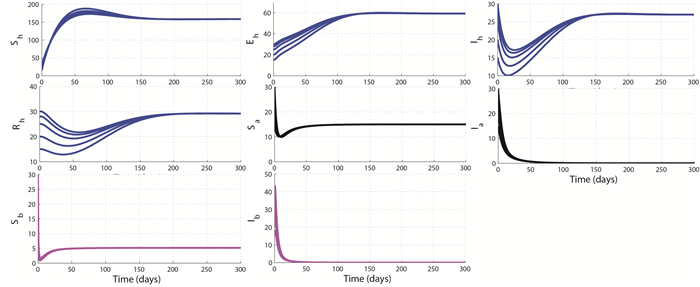
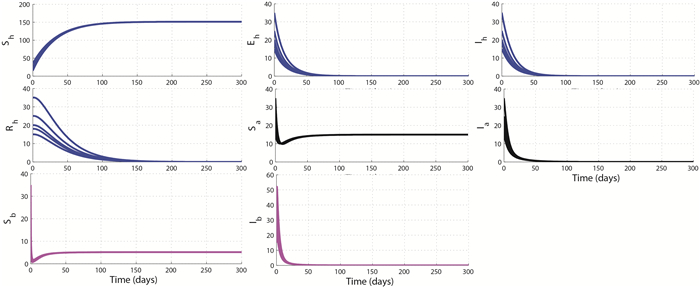
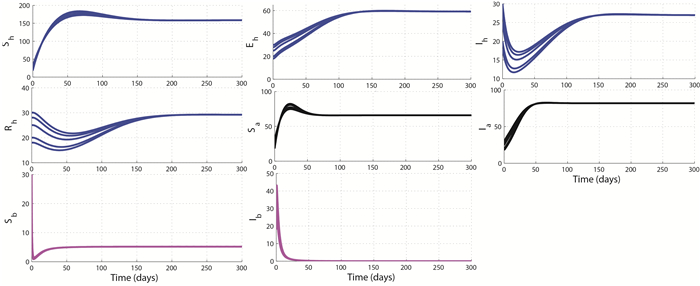
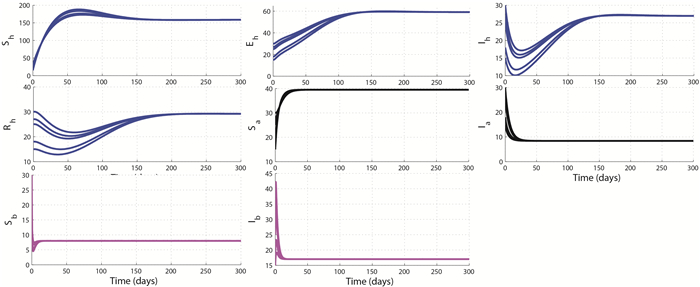
We numerically illustrate the asymptotic behavior of the full model and the sub-model without the environmental contamination. The GAS of the disease-free equilibrium $P_0$ demonstrated in Theorem 3.4 and the existence and stability of a unique endemic equilibrium as stated in Conjecture 1 for the model with the environmental contamination are numerically shown on Figure 2 and Figure 3, respectively. However, Figure 4 further suggests the GAS of $(\overline{P}_h, P_a^0, P_b^0)$. Figure 5 illustrates the GAS of $(P_h^0, P_a^0, P_b^0)$ for the free-environmental contamination sub-model (19) as established in Theorem 4.3. Figure 6 supports the stability of $(E^{**}_h, \overline{P}_a, P_b^0)$ as shown in Theorem 4.4, while Figure 7 illustrates the stability of $(E^{***}_h, \widehat{E}_a, \overline{P}_b)$ as shown in Theorem 4.5.
6.2. Impact of the contaminated environment on the infected level of EVD
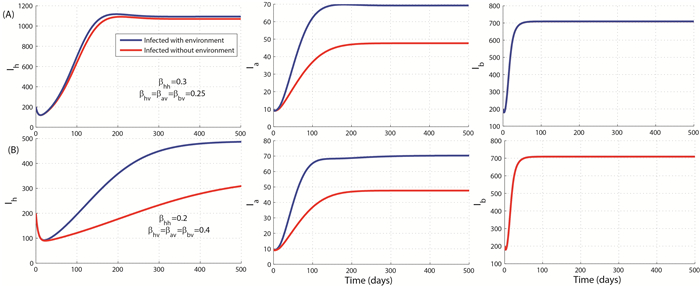
We numerically assess the impact of the contaminated environment on the severity/endemicity of EVD, as well as the effects of bats and animals on the long run and severity/endemicity of EVD.
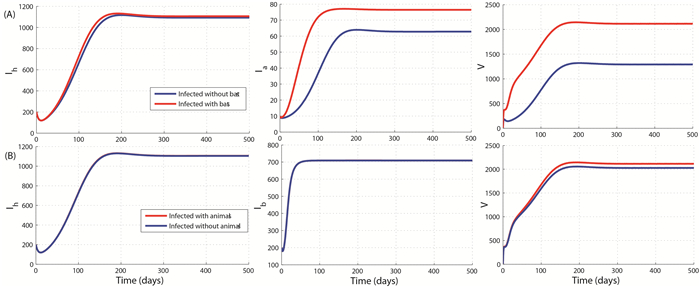
Figure 8 and Figure 9 show the increasing behavior of the full model-related infected component with respect to the indirect effective contact rates $\beta_{hv}$, $\beta_{av}$ and $\beta_{bv}$. This highlights the detrimental role of the contaminated environment on the transmission dynamics of EVD. Moreover, one observes from Figure 8 that, the infected bats are not influenced by the environmental contamination, which suggests that the indirect route of transmission for bats can be neglected. Similarly Figure 9 shows that the infected humans and bats are not significantly influenced by the incorporation of animals species in the model development. This suggests and confirms in some sense (see [37]) the fact that the bats are reservoir of Ebola viruses. Therefore, it may be more suitable to build a model involving only two hosts: namely, humans and fruit bats.
To illustrate the effects of bats and animals on the dynamics of EVD, Figure 9 is the simulation of the model (1) with and without bats on the one hand and with and without animals on the other hand. It can be seen that the incorporation of bats increases significantly the endemic level of EVD in the human population, while the involvement of animals does not.
7. Conclusion
The main purpose of this paper was to build and analyze a mathematical model for the transmission dynamics of EVD in a complex Ebola virus life ecology. We have then developed and analyzed both theoretically and numerically a new model by taking into account the known, the probable/suspected and the hypothetical mechanisms of transmission of EVD [26,37,51]. The proposed model captures as much as possible the essential patterns of the disease evolution as a three cycle transmission process in the following two ways:
1. It involves the interplay between the epizootic phase (during which the disease circulates periodically amongst non-human primates populations and decimates them), the enzootic phase (during which the disease always remains in fruit bats population) and the epidemic phase (during which the EVD threatens and decimates the human beings).
2. It includes the direct transmission mechanism between and within the three different types of populations which are humans, animals and fruit bats, as well as the indirect route of infection through a contaminated environment.
More precisely, we have extended and enriched the few existing SEIR-type human models for EVD with five additional compartments which model the direct transmissions within/between animal and fruit bat populations as well as the environmental indirect contamination. In this double setting of direct and indirect transmissions, our major findings from the theoretical, numerical and computational point of view read as follows:
From the theoretical perspective, our results are two-fold:
● For the full model with the environmental contamination, we have computed the basic reproduction number $\mathcal R_0$ and used it to prove the global asymptotic stability of the disease free equilibrium, whenever $\mathcal R_0 < 1$. Furthermore, when $\mathcal R_0 > 1$ the existence and the stability of an endemic equilibrium is investigated and conjectured.
● The sub-model without the environmental contamination exhibits one globally asymptotically stable disease-free equilibrium whenever the host-specific basic reproduction numbers, $\mathcal R_{0, h}$, $\mathcal R_{0, a}$ and $\mathcal R_{0, b} $ are less than or equal to the unity. We have also shown that a such sub-model has three additional endemic equilibria which are all globally asymptotical stable.
From the numerical and computational point of view, the following three facts were addressed:
● In order to assess the role of a contaminated environment on the spreading of EVD, the infected human component resulting from sub-model without the environmental contamination was compared with that of the full model. Similarly, we have considered the sub model without animals on the one hand, and the sub model without bats on the other hand, and found that bats influence more the dynamics of EVD than animals. This is probably because almost all EVD outbreaks were due to consumption and manipulation of fruits bats.
● Global sensitivity analyses were performed to identify the most influential model parameters on the model variables. It shows that the effective contact rate between humans and fruit bats and the bat mortality rate were the most influential parameters on the latent and infected human individuals. This is probably because almost all EVD outbreaks were due to consumption and manipulation of fruits bats.
● Numerical simulations, apart from supporting the theoretical results and the existence of a unique global stable endemic equilibrium for the full model (when $\mathcal R_0 > 1$), have further suggested the following two important statements: (1)-fruit bats are more important in the transmission processes and the endemicity of EVD than the animal species. This is in line with biological findings through which fruit bats were identified as the reservoir of Ebola viruses. (2)-the indirect environmental contamination is detrimental to human beings and is almost insignificant for the transmission in bats. From all these investigations, we believe that a more realistic mathematical model will involve only human beings and fruit bats.
Despite the high level of generalization and complexity of our work, it still offers many opportunities for extensions. Theses include:
(ⅰ) The incorporation of the Ebola-deceased compartments to better capture the transmission mechanisms of EVD during funerals [9].
(ⅱ) The incorporation of the transmission in health care centers in which medical staff can be infected as well [58].
(ⅲ) The incorporation of patches to account for the internationalization of EVD as it is the case in Western Africa [13,23,31].
(ⅳ) The modeling of multi-species transmission mechanism in the case where the same region is threaten by more than one Ebola virus strain.
(ⅴ) The incorporation of the human behavior. For instance, there were evidence of behavioral reaction and self-protection measures: people were scared, they panicked and left care centers, etc...Thus the need to fill the gap of lack of modeling human behavior [11,21]. This important feature calls for a modeling approach based on "Behavioral Epidemiology" developed in [41], which we are already addressing in another work which takes into account self-protection measures driven by human behavior.
(ⅵ) The modeling of some optimal control strategies such as vaccination, isolation, quarantine, treatment, early detection, environmental decontamination.
Acknowledgments
This work was initiated and mostly developed during the postdoctoral fellowship of the first author (T.B.) at the University of Pretoria in South Africa. (T.B.) and the third author (J.L.) would like to acknowledge the support of the South African Research Chairs Initiative in Mathematical Models and Methods in Bioengineering and Biosciences at the University of Pretoria. The authors are grateful to two anonymous referees whose comments helped to substantially improve this work.









 DownLoad:
DownLoad: