The practice of clinical genetics in the context of breast cancer predisposition has reached another critical point in its evolution. For the past two decades, genetic testing offered to women attending clinics has been limited to BRCA1 and BRCA2 unless other syndromic indicators have been evident (e.g. PTEN and TP53 for Cowden and Li-Fraumeni syndrome, respectively). Women (and their families) who are concerned about their personal and/or family history of breast and ovarian cancer have enthusiastically engaged with clinical genetics services, anticipating a genetic cause for their cancer predisposition will be identified and to receive clinical guidance for their risk management and treatment options. Genetic testing laboratories have demonstrated similar enthusiasm for transitioning from single gene to gene panel testing that now provide opportunities for the large number of women found not to carry mutations in BRCA1 and BRCA2, enabling them to undergo additional genetic testing. However, these panel tests have limited clinical utility until more is understood about the cancer risks (if any) associated with the genetic variation observed in the genes included on these panels. New data is urgently needed to improve the interpretation of the genetic variation data that is already reported from these panels and to inform the selection of genes included in gene panel tests in the future. To address this issue, large internationally coordinated research studies are required to provide the evidence-base from which clinical genetics for breast cancer susceptibility can be practiced in the era of gene panel testing and oncogenetic practice.
Two significant steps associated with this process include i) validating the genes on these panels (and those likely to be added in the future) as bona fide breast cancer predisposition genes and ii) interpreting the variation, on a variant-by-variant basis in terms of their likely “pathogenicity” ― a process commonly referred to as “variant classification” that will enable this new genetic information to be used at an individual level in clinical genetics services. Neither of these fundamental steps have been achieved for the majority of genes included on the panels.
We are thus at a critical point for translational research in breast cancer clinical genetics ― how can rare genetic variants be interpreted such that they can be used in clinical genetics services and oncogenetic practice to identify and to inform the management of families that carry these variants?
1.
Introduction
GH4169 (Ni-Fe-Cr) superalloy is broadly applied to modern aero engines, gas turbines and high-temperature applications because of its excellent radiation resistance, fatigue resistance, high temperatures strength, corrosion resistance and good welding performance [1,2,3]. The components in many industrial applications need suitable microstructure, favourable mechanical properties and excellent dimensional stability [4]. Understanding of the behavior of materials' deformation can contribute to the shape prediction and property control for the components during deformation process. Generally, a relationship between the flow stress and the strain rate and the deformation temperature can be used to be a constitutive model. Constitutive [5,6,7] and artificial neural network (ANN) models [8,9,10] are broadly used in recent years to study the deformation behavior of the materials. Processing map is based on dynamic material models (DMM) [11], and is considered to be an important model for optimizing hot parameters and for controlling microstructure during hot working processes [12,13]. Based on processing maps, both the deformation mechanisms in different deformation conditions and the instable deformation zones can be predicted, which can improves the reliability and the quality of the components. In addition, FEM simulation is also an effective method to investigate the hot working processes. Hot isothermal compression tests are adopted to generate flow stress data for the finite element modeling and this technique is particularly suitable for modeling processes such as upsetting, heat bending [14,15].
In this paper, hot compression tests have been employed to investigate the flow behavior of GH4169 superalloy at temperature range of 970–1150 ℃ and strain rate range of 0.001–10 s−1. The effects of deformation temperature, strain and strain rate on the flow stress were investigated using true stress-true strain data from compression tests. The Arrhenius-type constitutive and ANN models were respectively established to predict the flow behavior of GH4169 superalloy. The processing maps at different strains were established to optimize the processing parameters. Finally, based on ABAQUS software, a 3D finite element method (FEM) model is established to simulate the extrusion process of this superalloy during hot deformation process, and this 3D model were verified.
2.
Experimental procedures
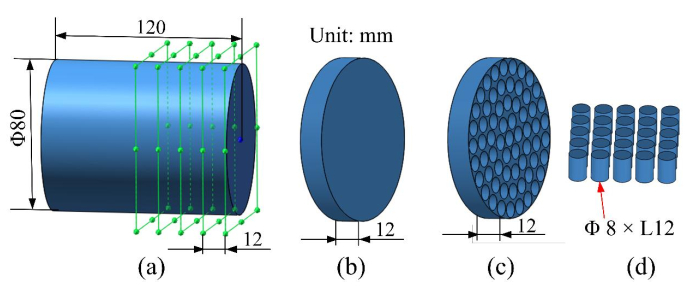
The chemical composition (wt.%) of GH4169 superalloy in this paper is given as follows: Ni 52.69, Cr 18.43, Nb 5.17, Mo 2.90, Ti 0.98, Al 0.60, Co 0.18, C 0.04 and Fe bal. The original material has a cylindrical shape and its dimensions are shown in Figure 1a. Cylindrical samples (Φ8 × L12 mm, Figure 1d) were machined from the original material using a wire-electrode cutting machine. Details of the positions and directions of samples are given in Figures 1b, c. Hot compression tests were carried out in different strain rates (0.001, 0.01, 0.1, 1 and 10 s−1) and temperatures (970, 1000, 1050, 1100 and 1150 ℃) in a Gleeble-3500 thermal simulator. The engineering compressive strain was set as 60%. A lubricant mixed with graphite and mechanical oil was adopted to reduce the friction of specimen/die. The specimens were heated to the set temperature, and then maintained for 120 s for microstructural uniformity and finally compressed by the thermal simulator.
The specimens had been treated by water proof abrasive papers (grits of 80 to 600#). Metallographic specimens were prepared by standard mechanical polishing procedures and were then etched in this reagent (5 g CuCl2 + 100 ml HCl + 100 ml ethyl alcohol).
3.
ANN model
A back propagation (BP) ANN model was built to predict the flow stress of GH4169 superalloy during compression process. The BP model consists of an input layer, an output layer and one or more hidden layers. The input variables of this model are strain, strain rate and deformation temperature, and the output is the flow stress. The compression tests' data were separated into two sub-sets (a training set and a testing set). In order to speed the converging of training process, the original data must be normalized. The normalized equation can be written as Eq 1.
Where X are the original data from compression tests. Xi, Xmax and Xmin are the normalized, maximum and minimum values of X, respectively. When the high precision of network is attained, the data of trained and tested results converted to their original form, which can be indicated as:
The transfer function in output layer obeyed a linear function. Sigmoidal functions were selected as transfer functions in hidden layers. Mean square error, shorted as MSE, is adopted for performance assessment of network training, and it can be defined as:
Where N is the number of sample set,
d(i) is the desired output value and a(i) is the actual output value.
4.
Experimental results and discussion
4.1. Flow curves and flow characteristics of the GH4169 superalloy
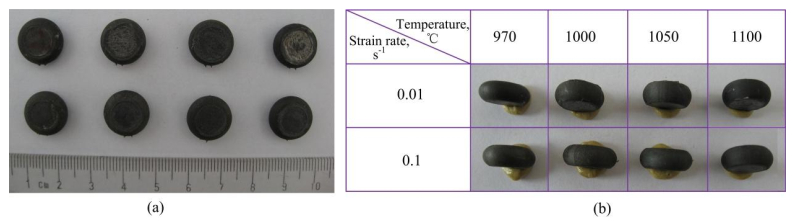
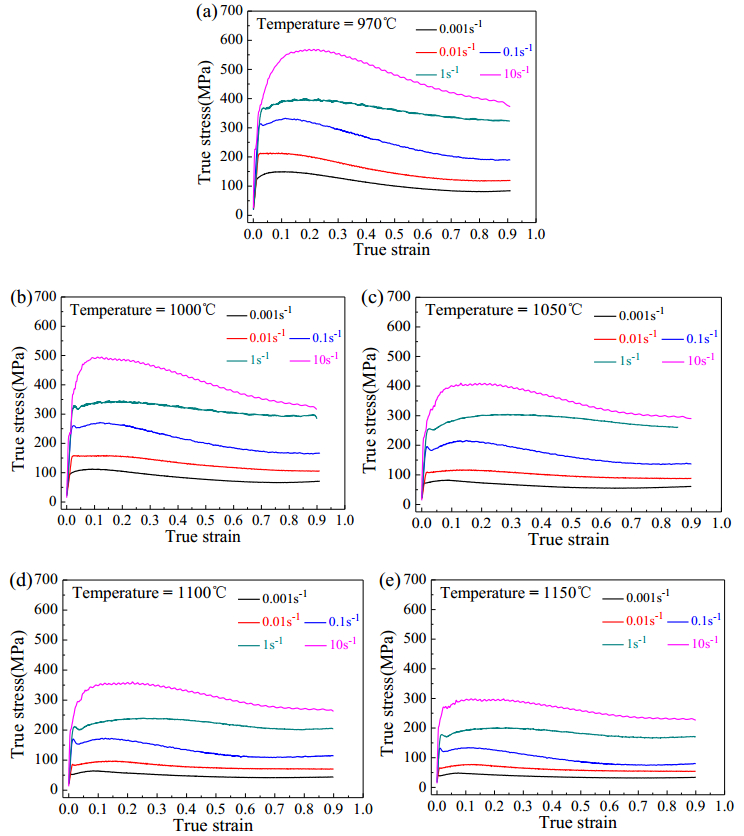
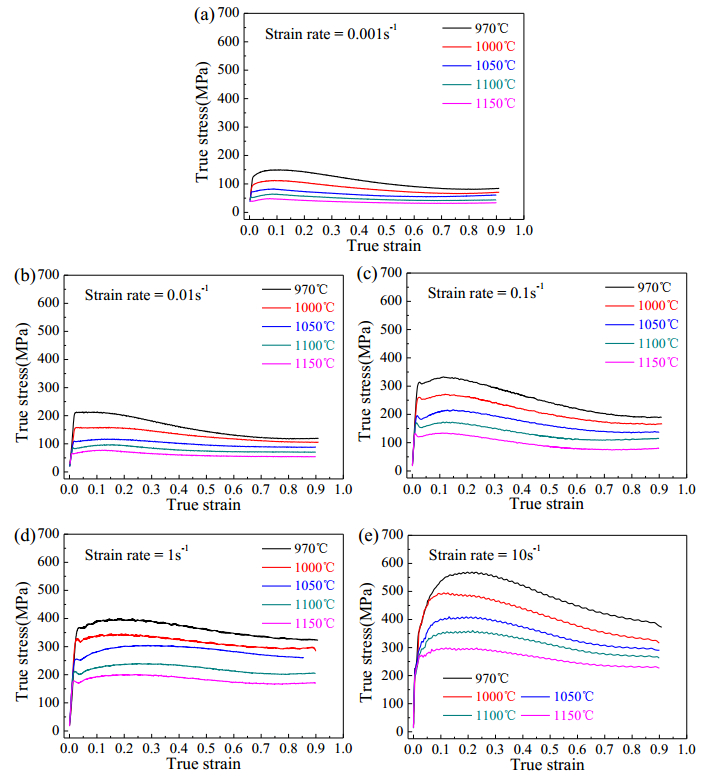
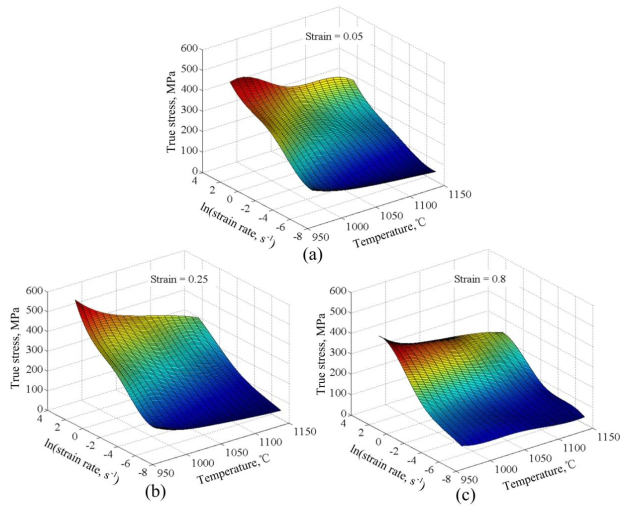
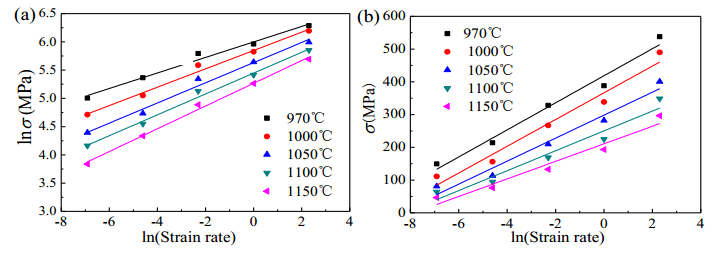
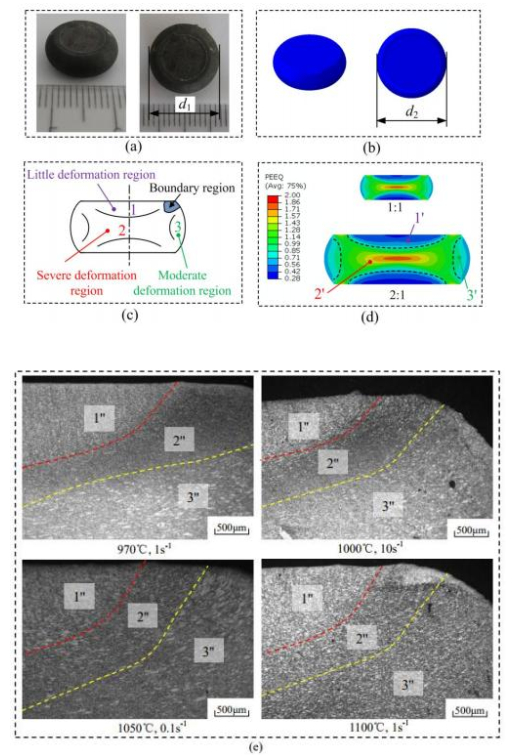
Figure 2 shows the photos of the compressed samples. As shown in Figure 2, there are no cracks on the side of the compressed samples. Figures 3, 4 show the true stress-true strain curves of the GH4169 superalloy for a wide range of deformation temperature and strain rate conditions. As shown in these two pictures, as the strain increases, the flow stress rapidly increases and quickly reaches a peak value, and then decreases. For the same temperature, the flow stress increases with increasing strain rate (Figure 3). For the same strain rate, the flow stress increases with increasing deformation temperature (Figure 4). As shown in Figure 3, for a particular deformation temperature condition, the strain corresponding to the peak flow stress increases with the increase of the strain rate. As shown in Figure 4d, at the highest strain rate (10 s−1) and the two lower deformation temperatures (970 ℃ and 1000 ℃), the GH4169 superalloy shows an evident peak stress, and then shows a sharply decrease of flow stress. As shown in Figures 4a, b, at the two lower strain rates (0.001 s−1 and 0.01 s−1) and the two higher deformation temperatures (1100 ℃ and 1150 ℃), no evident peak stress appears in stress-strain curves. Figure 5 shows the effect of deformation temperatures and strain rates on the flow stress at strains 0.05, 0.25, and 0.8. As can be seen from Figure 5, the flow stress generally increases with the increasing strain rate at a given deformation temperature and decreases with the increase of deformation temperature at a given strain rate.
4.2. Constitutive equation for compression
Several basic constitutive equations are shown as follows [15,16,17]:
Where $\dot \varepsilon $ is strain rate (s−1),
σ is flow stress (MPa), A1, n1, A2,
A3, n, α and β are material constants. T is absolute temperature (K). Q is deformation activation energy (kJ/mol). R is gas constant (8.3154 J·mol−1·K−1). Z is Zener-Hollomon parameter (s−1). α (α = β/n1) is an adjustable constant (MPa−1).
Eq 8 and Eq 9 are respectively derived by taking natural logarithm of Eq 4 and Eq 5.
Here, σ is the flow stress at a strain 0.1. n1 is obtained from the slope of the plot of ln($\dot \varepsilon $) against lnσ (Figure 6a). β is obtained from the slope of the plot of ln($\dot \varepsilon $) against σ (Figure 6b). The values of n1 and β are respectively 5.788 and 0.029 MPa−1. Therefore, α is calculated by α = β/n1, and it is 0.005 mm2/N.
Eq 6 can also be expressed as:
For a particular temperature, differentiating Eq 10, n is described as:
For a particular strain rate, differentiating Eq 10, Q is described as:
Therefore, Q is described as:
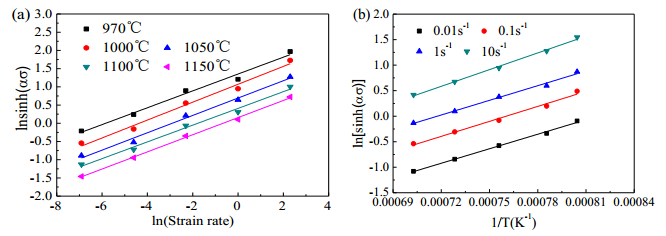
The relationship between ln[sinh (ασ)]-ln(strain rate), and the relationship between ln[sinh (ασ)]-1/T are respectively shown in Figures 7a, b. Q is calculated by Eq 13, and it is 257.657 kJ/mol. Z is calculated by using Eq 7.
Eq 14 can be obtained by logarithmic transformation of the Eq 6.
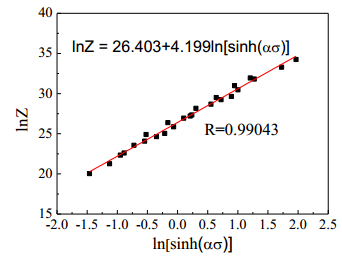
Figure 8 shows the relationship between lnZ and ln [sinh (ασ)].
A3, n and the correlation coefficient are respectively obtained from Figure 8. They are 2.929 × 1011, 4.199 and 0.99043, respectively. Good linear relation between lnZ and ln [sinh (ασ)] is obtained due to the high value of correlation coefficient.
Thus, when strain is 0.1, constitutive model is described as:
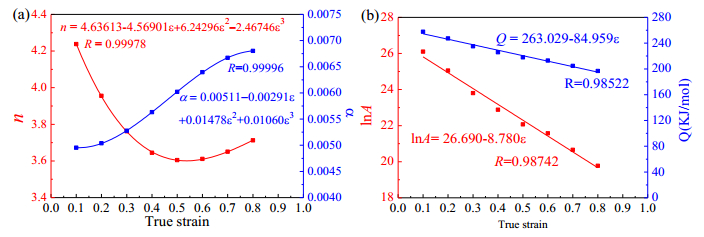
Figure 9 shows the materials constants (n, α, lnA and Q) values of constitutive model of GH4169 superalloy under different strains (0.1–0.8, interval of 0.1). It is seen from Figure 9a that the maximum and the minimum values of n respectively appear in the strain 0.1 and 0.5. When the strain is in the range of 0.1–0.4, n value decreases sharply by the increase of the strain. When the strain is in the range of 0.4–0.5, the decreasing extent of n with increasing strain is less than that in the strain range of 0.1–0.4. When the strain is over 0.5, n value increases by the increase of the strain. When the strain is in the range of 0.5–0.6, with the increase of strain, n increases by a small margin. When the strain is in the range of 0.6–0.8, the increasing extent of n with increasing strain is slightly higher than that in the strain range of 0.5–0.6. As shown in Figure 9a, at the strain range 0.1–0.2, α increases slowly with increasing the strain, and it increases in a large scale at strain range of 0.2 to 0.3 and increases sharply at the strain range of 0.3 to 0.6, and then its increasing extent shows a slightly decrease at the strain range of 0.6 to 0.7. Finally, the increasing extent of n with the increase of strain (strain range of 0.7–0.8) indicates a greater degree of decline. As shown in Figure 9b, both Q and ln A values decrease with increasing strain. ln A—strain or Q—strain curve can be plotted by a straight line, indicating that n—strain curve or α-strain curve is more complicated than ln A—strain curve or Q-strain curve.
4.3. Validation for constitutive equation
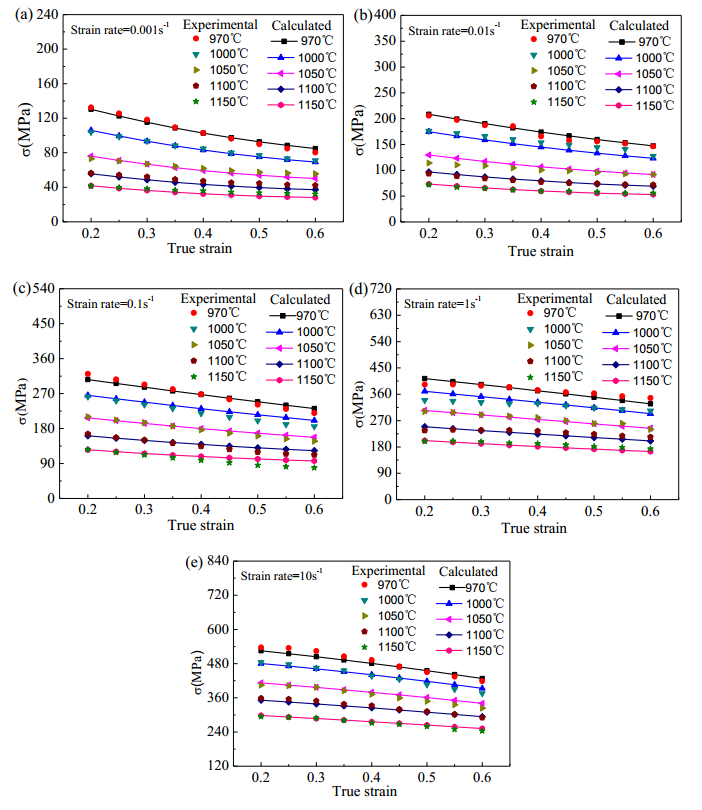
Figure 10 shows comparison of flow stress between experimental and calculated data at different strain rates. As shown in Figure 10, the experimental results agree well with the calculation data. The maximum relative error between calculated and experimental values is 18.3% and the mean relative error is at approximately 3.8%, which indicates the constitutive model of GH4169 with high precision is obtained by this paper.
4.4. ANN results and validation
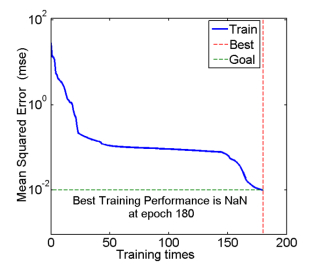
After training, a momentum rate 0.6, a learning rate 0.1, an MSE 0.01 and epochs 10000 were adopted in the network model. 6 and 12 neurons were respectively adopted in the hidden layer 1 and in the hidden layer 2, respectively. The result of MSE for training is shown in Figure 11. It can be seen that the training process terminated at 180 epochs when the error goal was set as 0.01.
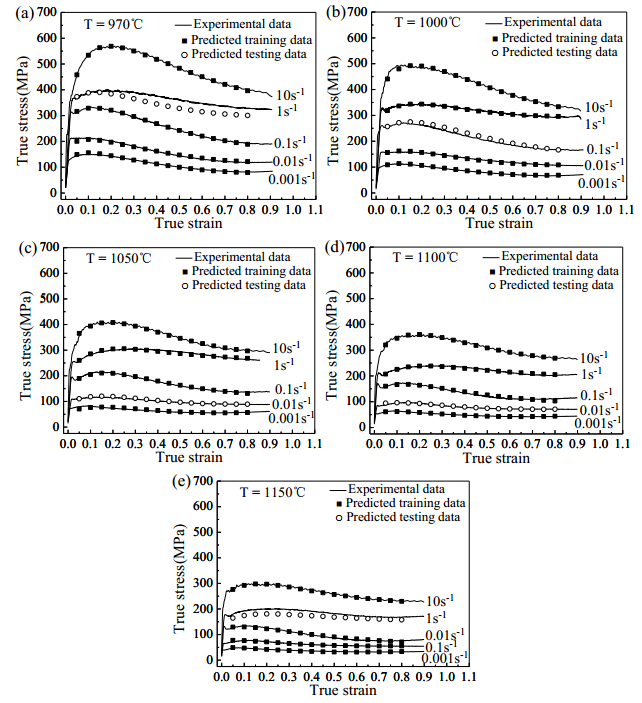
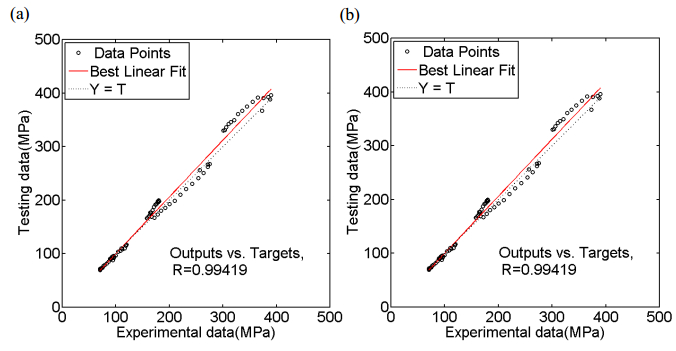
Figure 12 shows comparison of predicted data with experimental flow stresses. It can be seen from Figure 12 that the predicted data are basically in consistence with the experimental flow stresses. The maximum relative error between calculated and experimental values is 9.85% and the average absolute relative error is 4.12%. Figures 13a, b show the correlation coefficient between the experimental and predicted data for both training and testing sets, respectively. It can be seen from Figure 13 that the correlation coefficient of 0.9997 for training and of 0.9942 for testing processes. According to the result of error and correlation coefficient analysis, it can be obtained that the network model is very stable and it has high precision. Table 1 shows error of constitutive equation model and ANN model for prediction of flow stress. It can be seen from Table 1 that although the maximum relative error of constitutive equation model is larger than that of the ANN model, but the average absolute relative error of constitutive equation model is lower than that of the ANN model. So the prediction precision of constitutive equation model is higher than that of to the ANN model.
4.5. Processing map
4.5.1. Principles of processing maps
According to DMM, the workpiece under hot deformation process is considered as a nonlinear dissipate of the power and the total power dissipation P. P is divided into two functions (G content and J co-content). P is given by [16]:
Where σ is the flow stresss (Mpa). $\dot \varepsilon $ is the strain rate (s−1).
G content stands for the power dissipation due to plastic deformation, J co-content stands for the power dissipation through metallurgical process.
The strain rate sensitivity m can be given as follows [16]:
The J co-content can be written as follows:
By comparison of J co-content with the maximum possible dissipation Jmax (m = 1 and ${J_{max}} = \frac{{\sigma \dot \varepsilon }}{2}$), the efficiency of power dissipation η can be given by:
Based on the maximum entropy principle, a continuum criterion based on irreversible thermodynamic for the occurrence of flow instabilities is defined by:
The instability map is obtained by plotting $\xi $ at different strain rates and temperatures when $\xi $ is negative [17]. $\xi $ varies with temperature and strain rate. η and $\xi (\dot \varepsilon)$ can be calculated by a series of m values. So the power dissipation and instability maps are obtained. A processing map is obtained by superposing the unstable map on the power dissipation map.
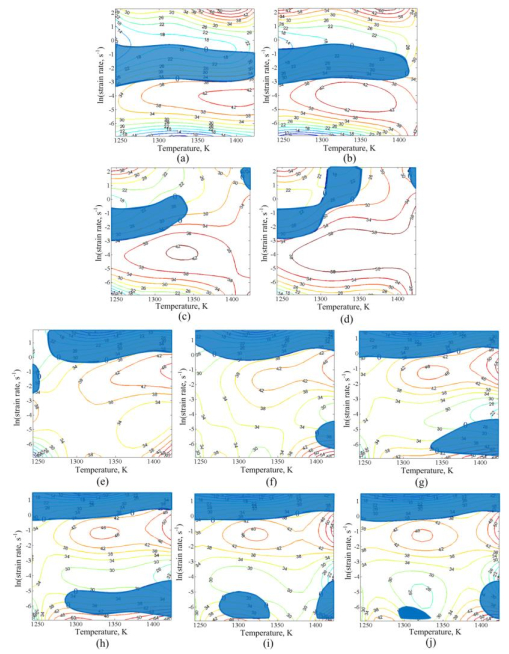
4.5.2. Influences of strain on processing maps
Figure 14 shows the processing maps in the strain rate range of 0.001 to 10 s−1 and temperature range of 1243 to 1423 K at the strains 0.05, 0.15, 0.25, 0.3, 0.45, 0.5, 0.6, 0.65, 0.75 and 0.8. The different color contours in Figure 14 indicate the efficiency of power dissipation, and the blue shaded regions represent the flow instability domains. The distributions of the efficiency of power dissipation are different in different strains. The flow instability domains are different in different strains. As shown in Figures 14a, b, the distributions of the efficiency of power dissipation under strain 0.05 is similar to the strain 0.15, namely the appearance regions of peak value of the efficiency of power dissipation is similar between these two strains. Meanwhile, the distributions of the flow instability under strain 0.05 are also similar to the strain 0.15. When the strain is 0.05, the only region of the flow instability appears in a very broad area, which is in the whole temperature range of 1243 K to 1423 K and in the strain rate range of 0.038 s−1 to 0.827 s−1. When the strain is 0.15, the only region of the flow instability appears also in a very broad area, which is in the broad temperature range of 1243 K to 1413 K and in the strain rate range of 0.041 s−1 to 0.515 s−1.As shown in Figures 14c, d, the distributions of the efficiency of power dissipation under strain 0.25 is similar to strain 0.3, while the distributions of the flow instability under these two strains have a relatively big difference. As shown in Figures 14e, f, when the strains are 0.45 and 0.5, the distributions of the efficiency of power dissipation are similar each other. As shown in Figures 14g, h and i, when the strains are 0.6, 0.65 and 0.75, the distributions of the power dissipation efficiency are similar each other.
5.
Simulation for the compression tests and verification
5.1. FEM model of compression test
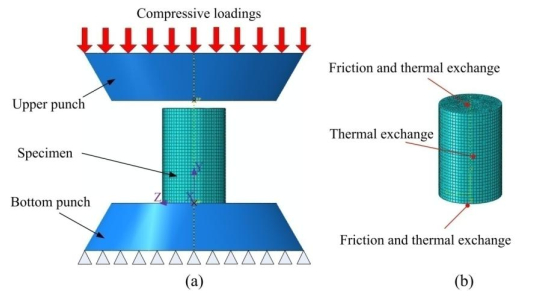
Figure 15 shows FEM model of hot compression process of GH4169 superalloy. Three-dimensional (3D) deformable type in the FEM model was selected for the specimen, while 3D analytical rigid type was used for upper and bottom punches. Stress-strain data are obtained from the constitutive equation model. The red arrows in Figure 15 indicate the moving direction of upper punch. Advancing front algorithm, sweep technique and hex element shape were selected as the model meshes.
5.2. Simulation results and verification
Experimental observation, numerical simulation and theoretical analysis are three type methods to research the scientific issues. Figure 16 shows the macroscopic photos from experimental results (Figure 16a) and FEM simulation (Figure 16b), the theoretical analysis for the deformation regions (Figure 16c), and the simulated equivalent plastic strain (Figure 16d). Here the deformation parameters is strain rate 0.1 s−1 and temperature 970 ℃. The contour in Figure 16d represents the PEEQ (equivalent plastic strain) distribution after hot deformation of GH4169 superalloy. The PEEQ in ABAQUS is defined as [18].
Where ${\left. {{{\bar \varepsilon }^{pl}}} \right|_0}$ is the initial equivalent plastic strain. ${\dot {\bar \varepsilon} ^{pl}}$ depends on the material model and it is described as:
The maximum diameter of the bulging deformation of specimen acquired from experimental and simulation results are respectively expressed by signals d1 (Figure 16a) and d2 (Figure 16b). It can be seen that d1 is substantially equal to d2 value when the experimental were conducted at 970 ℃ and 0.1 s−1. Here an error statistical analysis was made between d1 and d2 under the whole deformation parameters (temperature range of 970 to 1150 ℃ and strain rate range of 0.001 to 10 s−1). The results show that the average absolute relative error between d1 and d2 is less than 6%, indicating that the FEM model developed in this paper has high accuracy to simulate the hot compression process for GH4169 superalloy.
Figure 16c shows the deformed specimen that is divided into three regions. In Figure 16c, Regions 1, 2 and 3 are respectively called little deformation region, severe deformation region and moderate deformation region. In Figure 16d, the different colour contours of PEEQ can evidently divide the deformed specimen into three regions. The regions in Figure 16d are marked by 1', 2' and 3', whose are respectively corresponding to the regions 1, 2 and 3(Figure 16c). Figure 16e shows the microstructure of the deformed specimen in boundary region at four sets of parameters (970 ℃, 1 s−1; 1000 ℃, 10 s−1; 1050 ℃, 0.1 s−1; 1100 ℃, 1 s−1). The red and yellow dotted lines are shown in Figure 16e, and it is found that the microstructure in boundary region is seperated into three regions (regions 1'', 2'' and 3''). The grain sizes in these three regions are different. It is not difficult to find the difference in brightness between different regions on the image.
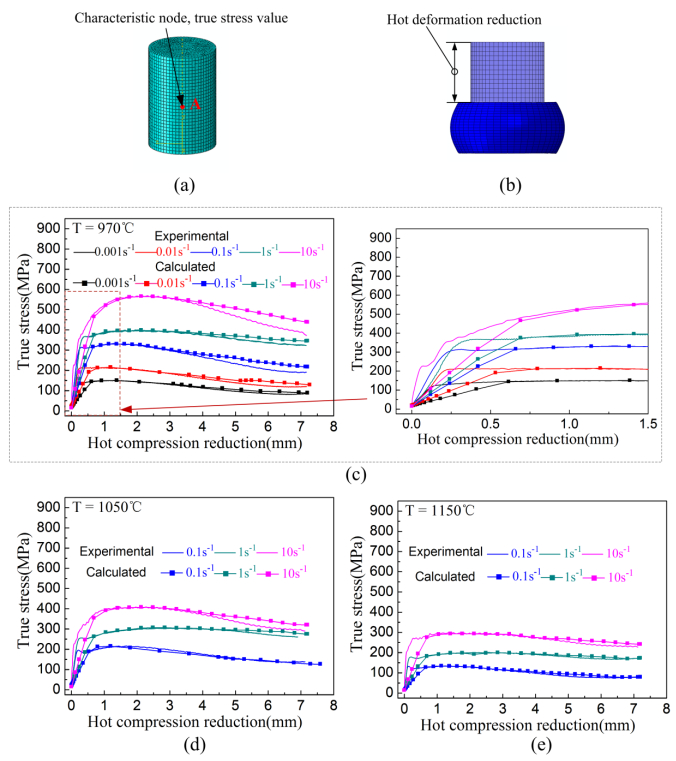
Figure 17 shows the microstructure of the deformed specimen in the three characteristic regions at 1100 ℃ and 1 s−1. As shown in Figures 17b, c, both the grains in severe deformation region and moderate deformation region were dramatically extruded along radial direction. And the elongated degree of the grains in severe deformation region is obviously larger than that in moderate deformation region. The true stresses values of the characteristic node A in Figure 18a were recorded by the thermal simulator and the FEM model. In Figure 18b, the hot compression reduction values of the specimens during deformation process can be also obtained from the thermal physical simulator and the FEM model. From Figures 18c, d and e, the calculated true stress-hot deformation reductions curves are basically conform to the experimental results. The curves can be divided into three intervals based on the error values size between calculated and experimental data. As shown in Figure 18c, the highest error values appear in the initial stage (reduction range of 0–0.7) of the compression process, and this stage is regarded as the first interval. The smallest error values appear when the hot compression reduction is in the range of 0.7–3.0, and this stage is regarded as the second interval. When the reduction is over than 3.0, the error values increase with the increase of the reduction, and this stage is regarded as the third interval. The rule of the highest error values appear in the initial stage also can be found from Figures 18d, e. As shown in Figures 18c, d and e, when the parameter for simulation is 1050 ℃/0.1 s−1, 1150 ℃/0.1 s−1 or 1150 ℃/1 s−1, the rule is not the same with other parameters except the first interval, while it has no evident effect on the error values of the curves.
6.
Conclusions
(1) The constitutive model parameters (a, Q, lnA3, and n) of GH4169 superalloy were calculated by a constitutive equation model. The mean relative error between experimental and predicted data is at approximately 3.8%, which indicates that the calculated curves agree well with the experimental curves.
(2) A BP model was built for prediction of the flow stress in hot compression of GH4169 superalloy. The mean relative error between predicted and experimental data is at approximately 4.6%, which indicates that the BP model has a high accuracy for prediction of the flow stress. The prediction precision of the constitutive equation model is higher than that of the BP model.
(3) The processing maps were plotted in the temperature range of 1243–1423 K and strain rate range of 0.001–10 s−1 at the strains 0.05, 0.15, 0.25, 0.3, 0.45, 0.5, 0.6, 0.65, 0.75 and 0.8. Both the distributions of power dissipation efficiency and the flow instability under strain 0.05 are similar to the strain 0.15. The distributions of power dissipation efficiency under strain 0.25 are similar to strain 0.3, while the distributions of the flow instability under these two strains have a relatively big difference. When the strains are 0.45 and 0.5, the distributions of the efficiency of power dissipation are similar each other. When the strains are 0.6, 0.65 and 0.75, the distributions of power dissipation efficiency are similar each other.
(4) An FEM model was successfully created to describe the hot compression process of GH4169 superalloy. It can be applied to predict the residual stresses and distortions of components.
Acknowledgements
The authors would like to acknowledge the financial support from the National Natural Science Foundation of China (No. 51875470, No. 51405389), the Natural Science Foundation of Shaanxi Province(No. 2018JM5159), the Fundamental Research Funds for the Central Universities (No. 3102017ZY005).
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: