Modeling growth of Alicyclobacillus acidoterrestris DSM 3922 type strain vegetative cells in the apple juice with nisin and lysozyme

1.   Introduction

We consider the system of difference equations

where $\varepsilon \in \lbrack 0, 1]$ is a coupling parameter and $f_{\mu }(x) = \mu x(1-x)$, $\mu \in (0, 4]$, $x\in [0, 1]$, is the classical logistic family widely studied ^[7,25,26]. This model was proposed and studied in ^[17,18] and it is motivated by difference equations associated to the Belousov-Zhabotinsky chemical reaction ^{[11,12,20,21]}. This model is included in the family of the so-called dynamics of coupled map lattices (see e.g. ^[13,10,5]).

This model can be seen as a convex deformation between two well-known systems. When $\varepsilon = 0$, the systems reads as

and so is the product map $f_{\mu }\times f_{\mu }$, while if $\varepsilon = 1$, we have the model

called antitriangular ^[4]. This kind of map appears naturally in some economic models called duopolies ^[19,14]. In both cases, the dynamics of this model is deeply connected with that of $f_{\mu }$. In particular, attractors or limit sets of the orbits have been analyzed ^[1], ^[4], ^[19]. From these papers, one can see that a rectangle contained in $[0, 1]^{2}$ can be an attractor or a limit set of these models and suggest a response to the question raised in ^[17] about the synchronization of the model Eq (1.1). In general, some orbits do not synchronize. We will check this by proving the existence and asymptotic stability of fixed points out of the diagonal $\Delta = \{(x, x):x\in \lbrack 0, 1]\}$ in Section 2 and by studying the local stability of the diagonal utilizing Lyapunov exponents in Section 3. The paper finishes with a section in which we study the bifurcation scenarios of the model Eq (1.1) to illustrate and complete the results of the two previous sections.

Of course, a lot of work is left to understand these systems' dynamics. For instance, a complete characterization of the attractors, the existence of chaotic dynamics when simple maps $f_{\mu }$ are considered, and how is the chaotic dynamics outside the diagonal $\Delta$. In some sense, this paper is a partial advance for these and other possible questions.

We organize this paper divided into the three sections mentioned above. Each section contains the basic definitions necessary to understand the presented results.

2.   Periodic points: existence and stability

Given a map $f:X\rightarrow X$, $X\subset \mathbb{R}^n$, $n \in \mathbb{N}$, we denote by $f^0$ the identity on $X$, by $f^1 = f$, and define inductively $f^n = f\circ f^{n-1}$. The solution of the difference equation

is called the orbit of $x_0$ by $f$. The set of the limit points of the orbit of $x_0$ is called the attractor or the $\omega$-limit set of $x_0$ by $f$, denoted by $\omega (x_0, f)$. We say $x\in X$ is periodic of period $n\in \mathbb{N}$ if $f^n(x) = x$ and $f^i(x)\neq x$ for $1\leq i < n$. If $n = 1$ we say that $x$ is a fixed point of $f$. According to ^[8], a fixed point $x_0$ is said to be:

1. Locally stable if for each $\varepsilon > 0$ there exists a neighborhood $V$ of $x_0$ such that for any $x\in V$, then $||f^{n}(x)-x_0|| < \varepsilon$, for each $n\in\mathbb{N}$.

2. Attracting if there exists a neighborhood $V$ of $x_0$ such that $\lim_{n\rightarrow +\infty} f^{n}(x) = x_0$ for each $x\in V$.

3. Locally asymptotically stable (LAS) if it is both, locally stable and attracting.

4. Furthermore, if a fixed point $x_0$ is LAS, then $|Jf(x_0)|\leq1$ whenever $f$ is differentiable and $Jf(x_0)$ denotes the Jacobian matrix.

Now, fix $f_{\mu }(x) = \mu x(1-x)$, $\mu \in (0, 4]$, $x\in [0, 1]$. For $\varepsilon \in [0, 1]$, we define

defined on $[0, 1]^{2}$. The diagonal set

is invariant by $F_{\varepsilon, \mu }$, i.e., $F_{\varepsilon, \mu }(\Delta)\subseteq \Delta$ and the dynamics on this invariant set is independent on $\varepsilon$ and given by $f_{\mu }$ since

In addition, the map $F_{\varepsilon, \mu }$ is symmetric with respect to $\Delta$, that is, $F_{\varepsilon, \mu }(x, y) = F_{\varepsilon, \mu }(1-x, 1-y)$ for all $x, y\in [0, 1]$.

The equation

gives us the fixed points of $F_{\varepsilon, \mu }$. It is easy to see that this equation has at most four solutions $P_{i}$, $i = 1, 2, 3, 4$, given by

● $P_{1} = (0, 0).$

● $P_{2} = \left(\frac{\mu -1}{\mu }, \frac{\mu -1}{\mu }\right).$

● $P_{3} = \left(\frac{1+(2\varepsilon -1)\mu -\sqrt{(1+2\varepsilon (\mu -2)-\mu)(1+(2\varepsilon -1)\mu)}}{2(2\varepsilon -1)\mu }, \frac{ 1+(2\varepsilon -1)\mu +\sqrt{(1+2\varepsilon (\mu -2)-\mu)(1+(2\varepsilon -1)\mu)}}{2(2\varepsilon -1)\mu }\right).$

● $P_{4} = \left(\frac{1+(2\varepsilon -1)\mu +\sqrt{(1+2\varepsilon (\mu -2)-\mu)(1+(2\varepsilon -1)\mu)}}{2(2\varepsilon -1)\mu }, \frac{ 1+(2\varepsilon -1)\mu -\sqrt{(1+2\varepsilon (\mu -2)-\mu)(1+(2\varepsilon -1)\mu)}}{2(2\varepsilon -1)\mu }\right).$

Clearly, $P_{1}$ and $P_{2}$ belong to $\Delta$ and $P_{2}$ exists and it is different from $P_{1}$ if and only if $\mu \leq 1$. $P_{3}$ and $P_{4}$ are symmetric with respect to $\Delta$ and do exist whenever

Note that the equation

has solutions

and

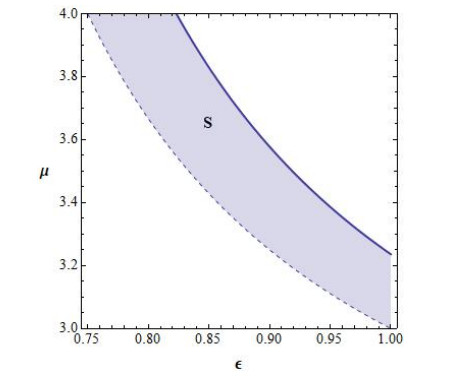
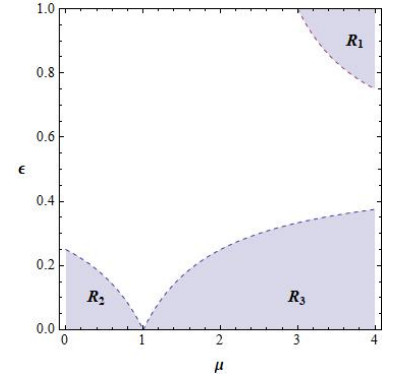
If the conditions Eq (2.1) and Eq (2.2) are fulfilled, then $P_{3} = P_{4} = P_{2}$. The region where both $P_{3}$ and $P_{4}$ exist and are different from $P_{2}$ can be seen in Figure 1.

However, as

in the regions $R_{2}$ and $R_{3}$, the points $P_{3}$ and $P_{4}$ have negative coordinates except when $\varepsilon = 0$ and $\mu > 3$, where the fixed points are $P_{3} = \left(0, \frac{\mu -1}{\mu }\right)$ and $P_{4} = \left(\frac{\mu -1}{\mu }, 0\right)$. Therefore, the region where fixed points $P_{3}$ and $P_{4}$ exist and are different from $P_{2}$ is

where

The Jacobian matrix is

We use it to study the local asymptotic stability of the fixed points of $F_{\varepsilon, \mu }$.

2.1.   The fixed point $P_{1}$

The Jacobian matrix reads as

with eigenvalues $\mu$ and $\mu (1-2\varepsilon)$. As $|1-2\varepsilon |\leq 1$, it turns out that if $\mu < 1$, then $P_{1}$ is LAS.

2.2.   The fixed point $P_{2}$

The Jacobian matrix reads as

with eigenvalues $2-\mu$ and $(2-\mu)(1-2\varepsilon)$. As $|1-2\varepsilon |\leq 1$, it turns out that if $1 < \mu < 3$, then $P_{2}$ is LAS.

2.3.   The fixed points $P_{3}$ and $P_{4}$

By symmetry, the analysis for $P_{4}$ is the same than that of $P_{3}$. So, we will study the stability for $P_{3}$. The Jacobian matrix reads as

with eigenvalues

and

These eigenvalues are real when

The equation

gives the solutions

and

It can be seen that $\mu _{1} < 0$ while the graph of $\min \{4, \mu _{2}\}$ can be seen in Figure 2, jointly with the region $S$ such that $\lambda _{1}$ and $\lambda _{2}$ are real.

In this case, note that $\lambda _{1}\geq \lambda _{2}$ and the equality holds when $\lambda _{1} = \lambda _{2} = \frac{1-\varepsilon }{1-2\varepsilon }$. The equations

and

are the boundaries of the region with real eigenvalues with modulus smaller than one. The solutions of the equation Eq (2.3) are the ones of the conditions Eq (2.1) and Eq (2.2), while the solutions of the Eq (2.4) are

The first solution satisfies that $\mu < 0$. Hence, when the eigenvalues are real, the stability region is given by the inequality

When the eigenvalues are complex, the border of the stability region is given by the equation

which reduces to

with solutions

The first solution satisfies that $\mu < 0$. Hence, when the eigenvalues are complex, the stability region is given by the inequality

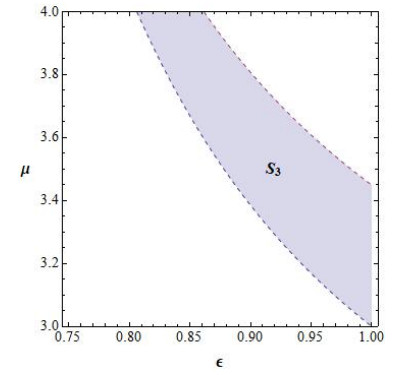
Hence, the stability region of $P_{3}$ is the set

This region can be see in Figure 3.

Then, we can summarize the above results as follows.

Theorem 1. Let $P_{1}$, $P_{2}$, $P_{3}$ and $P_{4}$ be the fixed points of the map $F_{\varepsilon, \mu }$. Then:

(a) The fixed point $P_{1}$ is LAS if $\mu < 1$.

(b) The fixed point $P_{2}$ is LAS if $1 < \mu < 3$.

(c) The fixed points $P_{3}$ and $P_{4}$ are LAS if either $\varepsilon > 0$ and $(\varepsilon, \mu)\in S_{3}$.

Proof. The cases (a), (b) and case (c) when $\varepsilon > 0$ have been studied above. When $\varepsilon = 0$, note that $P_{3}$ and $P_{4}$ cannot be LAS since the stability conditions of the map $f_{\mu }$ to have $0$ and $\frac{\mu -1}{\mu }$ cannot be fulfilled simultaneously.

3.   Synchronization

We say that an orbit of $F_{\varepsilon, \mu }$ synchronizes if its attractor is contained in the diagonal line $\Delta$. The orbit converges therefore to an attractor of the map $(1-\varepsilon)f_\mu +\varepsilon f_\mu$. Here one can identify the diagonal $\Delta$ with the interval $[0, 1]$. The attractors of this kind of maps are well-known (cf. ^[9].). They are of the following types:

1. a periodic orbit;

2. a finite union of pairwise disjoint subintervals $I_{1}, I_{2}, \dots, I_{k}$ such that $f^{k}(I_{i}) = I_{i}$ and $f^{k}_{|_{I_{i}}}$ has a dense orbit for $i\in\{1, \dots, k\}$;

3. a Cantor set,

and there is at most one metric attractor of a type different from type (1).

Following [3,§2.1], see also ^[24], for a given $v = \sum_{i = 1}^{2}a_{i}{\bf v}_{i-1} = (a_{1}, a_{2})_{\beta }\in \mathbb{R} ^{2}$ (here, we use the subindex $\beta$ to indicate that its coordinates are expressed in terms of the basis $\beta = \{(1, 1), (1-, 1)\}$), we define the tangential Lyapunov exponent at $\bar{x}$ in the direction of $v$ to be

where $\Pi _{\Delta }$ is meant the projection of a vector of $\mathbb{R}^{2}$ in the subspace $\Delta$ and $dF_{\bar{x}}^{n}$ denotes the differential of $F$ at $\bar{x} = (x, y)$. On the other hand, again following [3,§2.1], we define the normal Lyapunov exponent at $\bar{x}\in \Delta$ in the direction of $v$ to be

The existence of fixed points $P_{3}$ and $P_{4}$ proves that the dynamics of $F_{\varepsilon, \mu }$ when $\mu > \mu _{0} = 3.5699...$ need not converge to the diagonal $\Delta$. This fact solves a question stated in ^[17]. In this section, we will explore when the synchronization of $F_{\varepsilon, \mu }$ is possible. For that, note that the Jacobian matrix at $\Delta$, given by

is circulant (see ^[6]). Then,

and

Note that $(1, 1)$ is a basis of $\Delta$ and $(1, -1)$ is normal to $\Delta$.

Following the ideas from ^[5], we can prove that

and

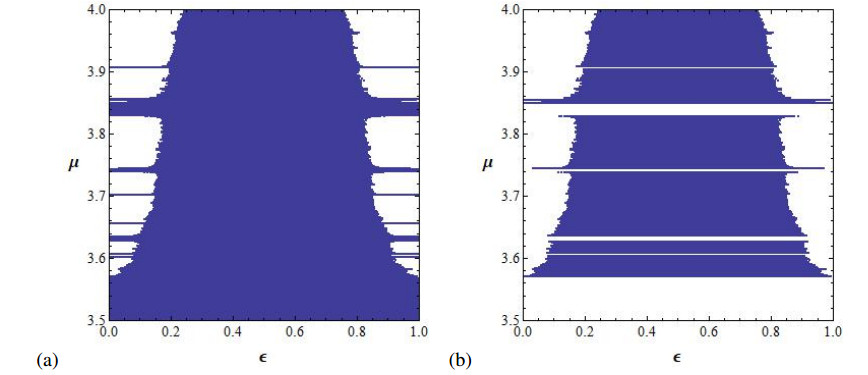
It is known, see ^[2], [3,Theorem 2.8 and Proposition 2.21], that $LE_{\parallel }(x)$ measures the complexity along the trajectory of $x$ and $LE_{\perp }(x)$ measures the convergence to $\Delta$, i.e. the synchronization, which is possible when $LE_{\perp }(x) < 0$. A chaotic synchronization is possible when $LE_{\parallel }(x) > 0$. In Figure 4, we will show the values in the parameter space $(\varepsilon, \mu)$ where the synchronization is possible.

Note that when $\varepsilon = 0$, the map $F_{0, \mu }$ is the product map $f_{\mu }\times f_{\mu }$. When $\varepsilon = 1$ we have that $F_{0, \mu }(x, y) = (f_{\mu }(y), f_{\mu }(x))$, and it is known as antitriangular map. The attractors of product and antitriangular maps have been studied in several papers (see, e.g. ^[1]).

It is clear that if $f_{\mu }$ has two fixed points ($\mu > 1$) and $\varepsilon = 0$, then there exist orbits of $F_{0, \mu }$ that do not synchronize: the fixed points $P_{3} = \left(0, \frac{\mu -1}{\mu }\right)$ and $P_{4} = \left(\frac{\mu -1}{\mu }, 0\right)$. When $\mu \in (1, 3]$, the fixed point $P_{2} = \left(\frac{\mu -1}{\mu }, \frac{\mu -1}{\mu } \right)$ attracts the orbits of all the points with a positive initial conditions while $P_{3}$ and $P_{4}$ attract the orbits with initial with one coordinate equal to zero. It is clear that the orbits which do not synchronize increase when $\mu > 3$.

4.   Attractors and bifurcation scenarios

Below we show the behaviour of the attractors when $\varepsilon$ ranges the interval $[0, 1]$. We see the typical attractor of the product map when $\varepsilon = 0$; this attractor is perturbed until the parameter $\varepsilon$ enters a region of synchronization, and synchronized attractors contained in $\Delta$ are shown. After that, the parameter enters the region $S_{3}$, where the fixed point $P_{3}$ is LAS, leaving the stability region via a Neimark-Sacker bifurcation given by complex eigenvalues with modulus one ^[15]. After that, the circle is perturbed and the attractors evolve to finish when $\varepsilon = 1$ of a well-known attractor of an antitriangular map. Figure 5 shows bifurcation diagrams on the variable $x$ for fixed values of $\mu$ and $\varepsilon$ ranging the interval $[0, 1]$.

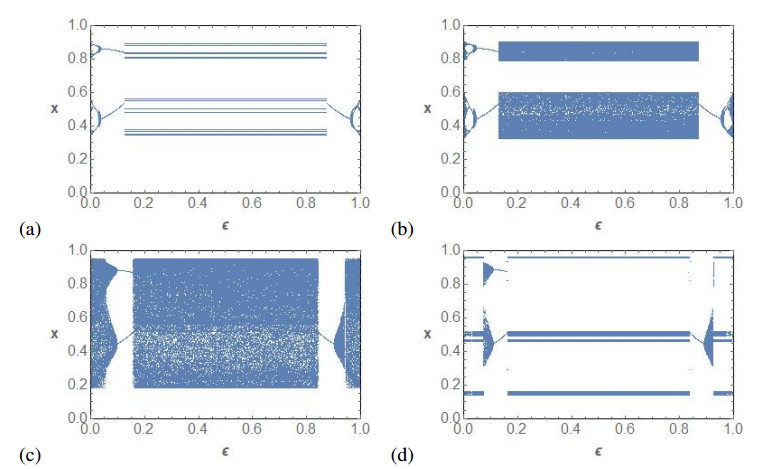
The information of Figure 5 is not complete. Only the variable $x$ is shown, and some additional information is necessary to have a complete picture of know the shape of the attractors. So, we add figures of different orbits with both coordinates and explain how the bifurcations behave. It is important to realize that Figure 5 is shown the projection to the X-axis of attractors of the plane and that different shapes can give rise to the same projection. For instance, the projections on the X-axis of a closed curve and a rectangle can be the same interval, although the dynamics can be completely different. So, Figures 6–9 are useful for a better understanding of Figure 5.

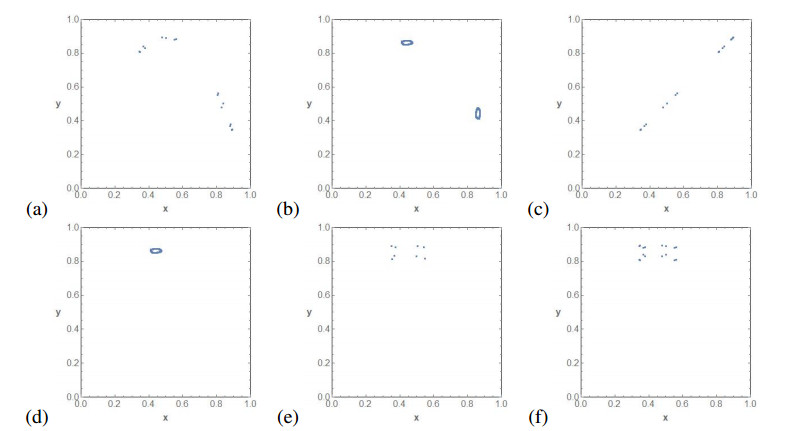
Figure 6 completes the bifurcation diagram of Figure 5a. We show six phase space plots for several values of $\varepsilon$ when $\mu = 3.568$. Note that for $\mu = 3.568$, the map $f_{\mu}$ is not chaotic and almost all the orbits all attracted by a periodic orbit. So, in (a) we can see a periodic attractor of $F_{0, \mu}$, which evolves periodically until we meet a Neimark-Sacker bifurcation in which a two periodic orbit bifurcates into two periodic curves. The curves collapse to a two periodic orbit until we reach the synchronization. When $\varepsilon$ is big enough, so no synchronization is possible, we have fixed points which evolve to an invariant curve via a Neimark-Sacker bifurcation. When the invariant curve disappears, we have periodic orbits again.

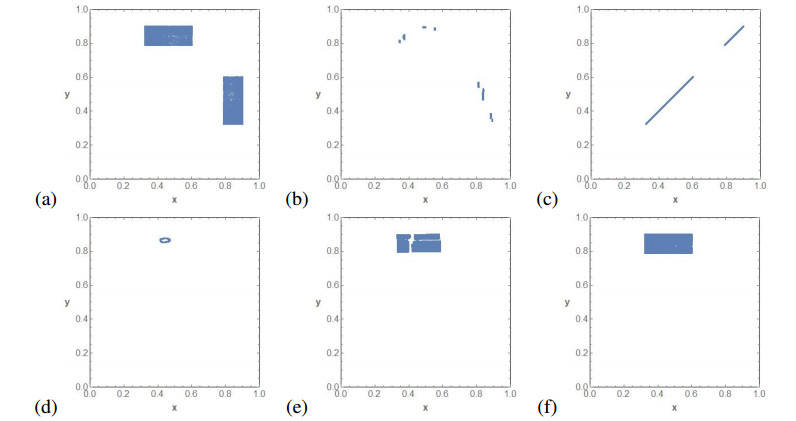
Figure 7 completes the bifurcation diagram of Figure 5b. First, we have a non-synchronized orbit of $F_{0, \mu}$ shown in Figure 7a, which evolves until we enter the parameter region where synchronization is possible. In Figure 7b, we show an intermediate attractor. This region of synchronization is reached by a periodic orbit of period two. The attractor in $\Delta$ is shown in Figure 7c. The region where synchronization is possible breaks to a fixed point, and after a Neimark-Sacker bifurcation Figure 7d, and then the attractors evolve to get a typical attractor with a non-empty interior of the antitriangular map $F_{1, \mu}$ in Figure 7f. Figure 7e shows an intermediate step between the synchronization region and the antitriangular map.

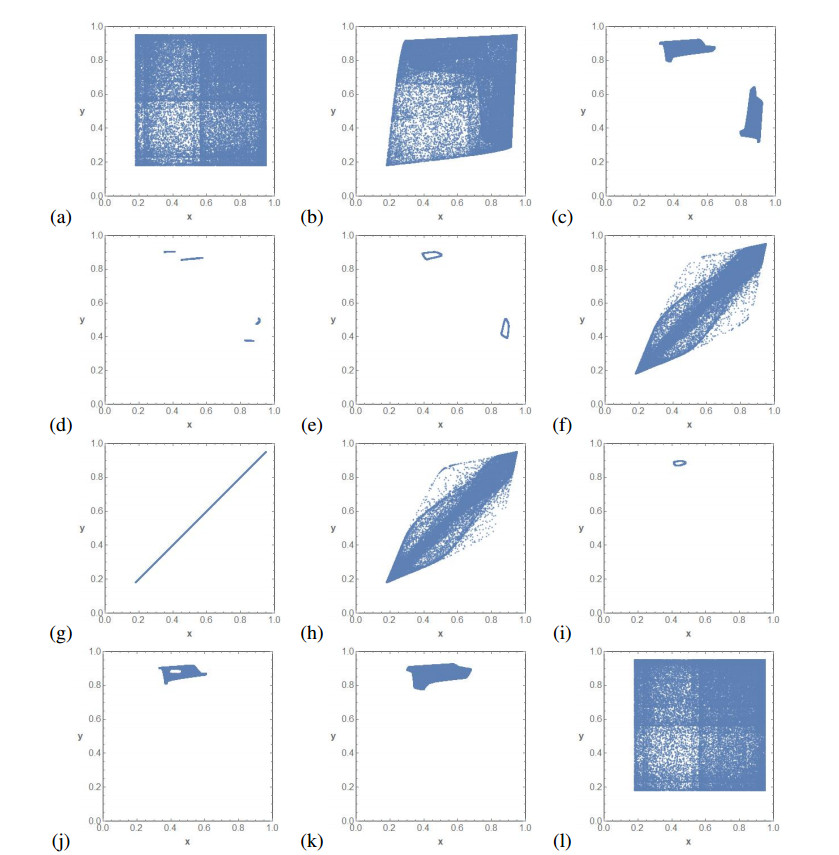
Figure 8 completes the bifurcation diagram of Figure 5c. We start by showing the attractor of $F_{0, \mu}$, which evolves following Figures 8b–d and degenerates to a periodic orbit via a Neimark-Sacker bifurcation Figure 8e. When the parameter $\varepsilon$ enters the region where synchronization is possible, we have Figure 8f. Then, the system synchronizes Figures 8g and leaves the synchronization region Figure 8h, followed by a fixed orbit which bifurcates to a closed curve via a Neimark-Sacker bifurcation. The curve degenerates to several attractors, Figure 8j and Figure 8k until we arrive at the final attractor of the antitriangular map Figure 8l. It is worth pointing out Figures 8f, h. They indicate that when the parameter $\varepsilon$ is going to enter the synchronization region, a two periodic orbit "explodes" to an attractor with unclear structure. The same happens when $\varepsilon$ leaves the parameter region where the orbits of $x$ and $y$ synchronize in $\Delta$.

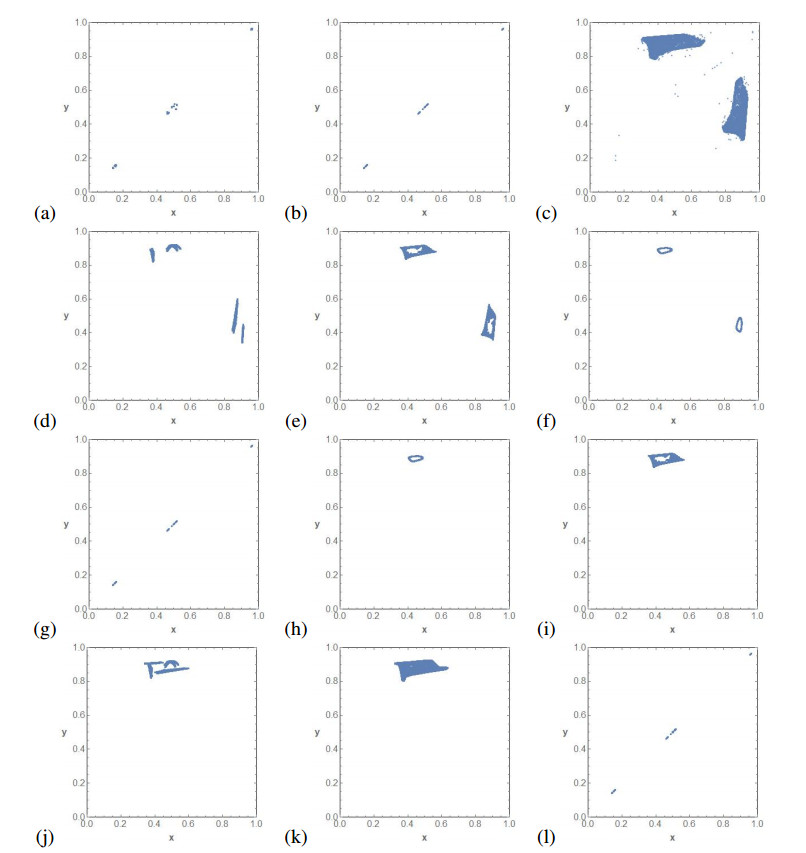
Figure 9 completes the bifurcation diagram of Figure 5d. Figure 9a shows the attractor of $F_{0, \mu}$. Then, Figures 9b–f show the route to synchronization parameters Figure 9g. Note that we arrive at this parameter region after a Neimark-Sacker bifurcation of a periodic point of period two. After the synchronization, we have a fixed point which bifurcates to a periodic curve Figure 9h, which degenerates Figures 9i–k. Finally, we get the attractor of the antitriangular map Figure 9l.

Remark 1. As stated in ^[17], since $\Delta$ is invariant by $F_{\varepsilon, \mu }$ and the dynamics restricted to $\Delta$ is given by the dynamics of $f_{\mu }$, we know that some complex behavior can found when $\mu > \mu _{0} = 3.5699...$ as the topological entropy of $f_{\mu }$ is positive (see ^[5] for further discussions on this issue). When $\mu < \mu _{0}$ the topological entropy of $f_{\mu }$ is zero and the Lyapunov exponents are negative, and the unique possible attractors are periodic orbits. Thus the diagonal $\Delta$ is free of complexity, but it is unclear whether it is possible to have a complicated behavior when the dynamics are outside $\Delta$. Figure 6 shows the existence of an invariant closed curve. Still, it is unclear whether the dynamics on this curve are complicated or not since it could be conjugate to an irrational rotation. Additionally, we did not observe the existence of attractors that can have positive two-dimensional Lebesgue measure.

5.   Discussion

Although this paper considers the logistic map, we present a general method to decide whether a coupled two-dimensional system can locally synchronize to the diagonal. This result completes the paper ^[5], where the method was presented for dimensions greater than two. The process to estimate Lyapunov exponents depends on the fact that the Jacobian matrix on the diagonal is circulant and can be easily adapted for different types of coupling, for instance, linear coupling. The bifurcation diagrams, jointly with the shown orbits, illustrate the results. This author would be surprised if significant new phenomena are shown when the logistic map is replaced with another regular enough one-dimensional map. It is substantial to find conditions to guarantee that almost all orbits in the system converge to the diagonal. Still, this question is challenging to solve because the dynamics of two-dimensional systems are far from being characterized.

6.   Conclusion

We have considered a two-dimensional coupled map based on the one-dimensional logistic family. We can see this system as a deformation through the coupling parameter $\varepsilon$ with a product map from one side and an antitriangular map from the other. Then, we use the fact that the Jacobian matrix at the diagonal is circular to give an explicit formula to estimate Lyapunov exponents and analyze when the system can locally evolve to synchronize their orbits in both chaotic and non-chaotic ways. We have obtained evidence that the dynamics when $\varepsilon$ is close to zero are a distortion of the dynamics when $\varepsilon = 0$. A similar result is obtained for $\varepsilon = 1$. So, the dynamics evolve from the case $\varepsilon = 0$ to $\varepsilon = 1$ through a huge parameter region where orbits synchronize. We must emphasize that the method described in this paper can be easily adapted for systems based on regular enough one-dimensional maps different from the logistic family considered in this paper.

Acknowledgements

I thank the two anonymous referees for their comments and suggestions to improve this manuscript.

This work has been supported by the grant MTM2017-84079-P funded by MCIN/AEI/10.13039/501100011033 and by "ERDF A way of making Europe", by the "European Union".