Changes in nucleosome formation at gene promoters in the archiascomycetous yeast <em>Saitoella complicata</em>

Hikaru Nakamiya; Saeka Ijima; Hiromi Nishida; Hikaru Nakamiya; Saeka Ijima; Hiromi Nishida

doi:10.3934/microbiol.2017.2.136

AIMS Microbiology

2017, Volume 3, Issue 2: 136-142. doi: 10.3934/microbiol.2017.2.136

Previous Article Next Article

Research article Topical Sections

Changes in nucleosome formation at gene promoters in the archiascomycetous yeast Saitoella complicata

Department of Biotechnology, Toyama Prefectural University, Imizu, Toyama 939-0398, Japan

Received: 08 December 2016 Accepted: 09 March 2017 Published: 16 March 2017

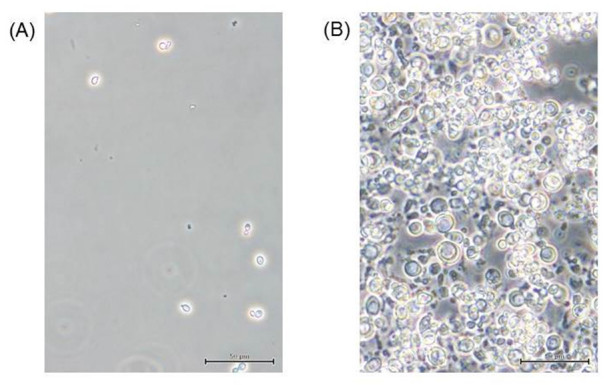
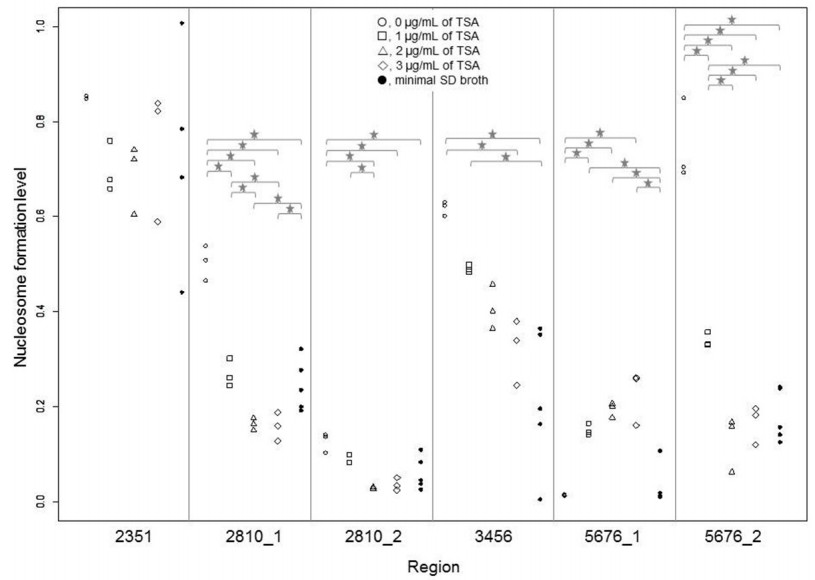
We measured the degree of nucleosome formation at the gene promoters in trichostatin A-treated (1, 2, and 3 μg/mL) cells of the archiascomycete Saitoella complicata and those in enlarged S. complicata cells after zymolyase treatment. TSA-treated and enlarged cells showed similar changes in nucleosome occupancy in five out of six positions in the gene promoters. These results suggest that changes in nucleosome formation at the gene promoters could serve as stress response mechanisms elicited in response to spheroplast (zymolyase treatment) and TSA treatment. In addition, we demonstrated that changes in nucleosome position occurred mainly in cells treated with 1 μg/mL TSA, whereas cells treated with 2 and 3 μg/mL TSA did not exhibit significant changes in the degree of nucleosome formation.

Keywords:

Citation: Hikaru Nakamiya, Saeka Ijima, Hiromi Nishida. Changes in nucleosome formation at gene promoters in the archiascomycetous yeast Saitoella complicata[J]. AIMS Microbiology, 2017, 3(2): 136-142. doi: 10.3934/microbiol.2017.2.136

Related Papers:

[1]	Wenbin Gong, Yaqiang Wang . Some new criteria for judging $\mathcal{H}$ -tensors and their applications. AIMS Mathematics, 2023, 8(4): 7606-7617. doi: 10.3934/math.2023381
[2]	Tinglan Yao . An optimal $Z$ -eigenvalue inclusion interval for a sixth-order tensor and its an application. AIMS Mathematics, 2022, 7(1): 967-985. doi: 10.3934/math.2022058
[3]	Sourav Shil, Hemant Kumar Nashine . Positive definite solution of non-linear matrix equations through fixed point technique. AIMS Mathematics, 2022, 7(4): 6259-6281. doi: 10.3934/math.2022348
[4]	Shiyu Lin, Shilin Yang . A new family of positively based algebras ${\mathcal{H}}_n$ . AIMS Mathematics, 2024, 9(2): 2602-2618. doi: 10.3934/math.2024128
[5]	Jie Zhou, Tianxiu Lu, Jiazheng Zhao . The expansivity and sensitivity of the set-valued discrete dynamical systems. AIMS Mathematics, 2024, 9(9): 24089-24108. doi: 10.3934/math.20241171
[6]	Panpan Liu, Hongbin Lv . An algorithm for calculating spectral radius of $s$ -index weakly positive tensors. AIMS Mathematics, 2024, 9(1): 205-217. doi: 10.3934/math.2024012
[7]	Reena Jain, Hemant Kumar Nashine, Jung Rye Lee, Choonkil Park . Unified relational-theoretic approach in metric-like spaces with an application. AIMS Mathematics, 2021, 6(8): 8959-8977. doi: 10.3934/math.2021520
[8]	Keun Young Lee, Gwanghyun Jo . The dual of a space of compact operators. AIMS Mathematics, 2024, 9(4): 9682-9691. doi: 10.3934/math.2024473
[9]	Shengying Mu, Yanhui Zhou . An analysis of the isoparametric bilinear finite volume element method by applying the Simpson rule to quadrilateral meshes. AIMS Mathematics, 2023, 8(10): 22507-22537. doi: 10.3934/math.20231147
[10]	Salma Aljawi, Kais Feki, Hranislav Stanković . Jointly $A$ -hyponormal $m$ -tuple of commuting operators and related results. AIMS Mathematics, 2024, 9(11): 30348-30363. doi: 10.3934/math.20241464

Abstract

1. Introduction

Consider the following $m$ th degree homogeneous polynomial of $n$ variables $f(x)$ as

$f(x) = \sum\limits_{i_{1}, i_2, \ldots, i_{m}\in N} a_{i_{1}i_2\cdots i_{m}}x_{i_{1}}x_{i_{2}}\cdots x_{i_{m}},$

(1.1)

where $x = (x_{1}, x_{2}, \cdots, x_{n})\in R^n$ . When $m$ is even, $f(x)$ is called positive definite if

$f(x) > 0, \; \; for \; any \; x \in R^n, \; \; x\neq 0.$

The homogeneous polynomial $f(x)$ in $(1.1)$ can be expressed as the tensor product of a symmetric tensor $\mathcal{A}$ with $m$ -order, $n$ -dimension and $x^{m}$ defined by

$\begin{eqnarray} f(x)\equiv\mathcal{A}x^{m} = \sum\limits_{i_{1}, i_2, \ldots, i_{m}\in N} a_{i_{1}i_2\cdots i_{m}}x_{i_{1}}x_{i_{2}}\cdots x_{i_{m}}, \end{eqnarray}$

(1.2)

where

$\begin{array}{l} \mathcal{A} = (a_{i_{1}i_2 \cdots i_{m}}), \; \; \; a_{i_{1}i_2\cdots i_{m}}\in C(R), \; \; \; i_{j} = 1, 2, \cdots, n, \; \; \; j = 1, 2, \cdots, m, \end{array}$

$C(R)$ presents complex (real) number fields. The symmetric tensor $\mathcal {A}$ is called positive definite if $f(x)$ in $(1.2)$ is positive definite ^[1]. Moreover, a tensor $\mathcal {I} = (\delta_{i_{1}i_2\cdots i_{m}})$ is called the unit tensor^[2], where

$\delta_{i_{1}i_2\cdots i_{m}} = \left\{ \begin{array}{cc} 1, &\; \; \; \; \; \; if \; i_{1} = \cdots = i_{m}, \\ 0, &otherwise. \end{array} \right.$

The positive definiteness of tensor has received much attention of researchers' in recent decade ^[3,4,5]. Based on the Sturm theorem, the positive definiteness of a multivariate polynomial form can be checked for $n\leq3$ ^[6]. For $n > 3$ and $m\geq 4$ , it is difficult to determine the positive definiteness of $f(x)$ in $(2)$ . Ni et al.^[1] provided an eigenvalue method for identifying positive definiteness of a multivariate form. However, all the eigenvalues of the tensor are needed in this method, thus the method is not practical when tensor order or dimension is large.

Recently, based on the criteria of $\mathcal {H}$ -tensors, Li et al.^[7] provided a practical method for identifying the positive definiteness of an even-order symmetric tensor. $\mathcal {H}$ -tensor is a special kind of tensors and an even order symmetric $\mathcal {H}$ -tensor with positive diagonal entries is positive definite. Due to this, we may identify the positive definiteness of a tensor via identifying $\mathcal {H}$ -tensor. For the latter, with the help of generalized diagonally dominant tensor, various criteria for $\mathcal {H}$ -tensors and $\mathcal {M}$ -tensors is established ^{[8,9,10,11,12,13,14,15,16]}, which only depends on the elements of the tensors and is more effective to determine whether a given tensor is an $\mathcal {H}$ -tensor ( $\mathcal {M}$ -tensor) or not. For example, the following result is given in ^[16]:

Theorem 1. Let $\mathcal {A} = (a_{i_1\cdots i_m})$ be a complex tensor with $m$ -order, $n$ -dimension. If

$\begin{array}{l} |a_{ii\cdots i}| > \sum\limits_{i_2, {i_3}, \ldots, i_m\in {N^{m-1}}\backslash N_{3}^{m-1} \atop \delta_{ii_2\ldots i_m} = 0} |a_{ii_2\cdots i_m}|+\sum\limits_{i_2i_3\cdots i_m\in N_3^{m-1} }\max\limits_{j\in \{i_2, i_3, \cdots, i_m\}} \frac{{{\Lambda_j}( \mathcal{A})}}{|a_{jj\cdots j}|} |a_{ii_2\cdots i_m}|, \ \ \ \ \forall i \in N_{1}\cup N_{2}, \end{array}$

then $\mathcal{A}$ is an $\mathcal{H}$ -tensor.

In this paper, we continue to present new criterions based on $\mathcal{H}$ -tensors for identifying positive definiteness of homogeneous polynomial forms. The obtained results extend the corresponding conclusions ^[16,17,18]. The validity of our proposed methods are theoretically guaranteed and the numerical experiments show their effciency.

2. Preliminaries

In this section, some notation, definitions and lemmas are given.

Let $S$ be a nonempty subset of $N = \{1, 2, \cdots, n\}$ and let $N \backslash S$ be the complement of $S$ in $N$ . Given an $m$ -order $n$ -dimension complex tensor $\mathcal {A} = (a_{i_1\cdots i_m})$ , we denote

$\begin{array}{l} \Lambda_i(\mathcal {A})& = &\sum\limits_{i_2, \ldots, i_m\in N \atop \delta_{ii_2\ldots i_m} = 0} |a_{ii_2\cdots i_m}| = \sum\limits_{i_2, \ldots, i_m\in N} |a_{ii_2\cdots i_m}|-|a_{ii\cdots i}|;\\ N_1& = &N_1(\mathcal {A}) = \{i\in N: 0 < |a_{ii\cdots i}| = \Lambda_i(\mathcal {A})\};\\ N_2& = &N_2(\mathcal {A}) = \{i\in N: 0 < |a_{ii\cdots i}| < \Lambda_i(\mathcal {A})\};\\ N_3& = &N_3(\mathcal {A}) = \{i\in N: |a_{ii\cdots i}| > \Lambda_i(\mathcal {A})\};\\ N_{0}^{m-1}& = &N^{m-1}\setminus(N_{2}^{m-1}\cup N_{3}^{m-1});\\ q & = &\mathop {\max }\limits_{i \in {N _2}} {\frac{{{\Lambda_i}\left( {\cal A} \right) - \left| {{a_{ii \cdots i}}} \right|}}{{{\Lambda_i}\left( {\cal A} \right)}}};\\ P_i(\mathcal {A})& = & q \left(\sum\limits_{i_2, \ldots, i_m\in N_{0}^{m-1}}\left| {{a_{i{i_2} \cdots {i_m}}}} \right| +\sum\limits_{i_2, \ldots, i_m\in N_{2}^{m-1}} \left| {{a_{i{i_2} \cdots {i_m}}}} \right| + \sum\limits_{i_2, \ldots, i_m\in N_{3}^{m-1} \atop \delta_{ii_2\ldots i_m} = 0} |a_{ii_2\cdots i_m}|\right), \; \; \; \; \; \; \forall i \in N_{3};\\ t & = & \mathop {\max }\limits_{i \in {N _3}} {\frac{{q\left( {\sum\limits_{{i_2} \cdots {i_m} \in N _0^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} + \sum\limits_{{i_2} \cdots {i_m} \in N _2^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} } \right)}}{{{P_i}\left( {\cal A} \right) - \sum\limits_{ {i_2} \cdots {i_m} \in N _3^{m - 1} \atop {\delta _{i{i_2} \cdots {i_m}}} = 0 } {\mathop {\max }\limits_{j \in \left\{ {{i_2}, {i_3}, \cdots , {i_m}} \right\}} \frac{{{P_j}\left( {\cal A} \right)}}{{\left| {{a_{jj \cdots j}}} \right|}}\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} }}}. \end{array}$

In this paper, we always assume that neither $N_1$ or $N_2$ is empty. Otherwise, we assume that $\mathcal {A}$ satisfies: $a_{ii\cdots i}\neq 0, \Lambda_i(\mathcal {A})\neq 0, \forall i\in N.$

we may define the following structured tensors extended from matrices.

Definition 1. ^[10] Let $\mathcal {A} = (a_{i_1i_2\cdots i_m})$ be an $m$ -order $n$ -dimension complex tensor. $\mathcal{A}$ is called an $\mathcal{H}$ -tensor if there is a positive vector $x = (x_1, x_2, \cdots, x_n)^{T}\in R^n$ such that

$\begin{array}{l} |a_{ii\cdots i}|x_{i}^{m-1} > \sum\limits_{i_2, \ldots, i_m\in N \atop \delta_{ii_2\ldots i_m} = 0} |a_{ii_2\cdots i_m}|x_{i_{2}}\cdots x_{i_{m}}, \; \; \; \; \forall i \in N. \end{array}$

Definition 2. ^[2] An $m$ -order $n$ -dimension complex tensor $\mathcal {A} = (a_{i_1i_2\cdots i_m})$ is called reducible if there exists a nonempty proper index subset $I\subset N$ such that

$\begin{array}{l} a_{i_1i_2\cdots i_m} = 0, \; \; \forall i_{1}\in I, \; \; \forall i_2, \cdots, i_m\notin I. \end{array}$

Otherwise, we say $\mathcal{A}$ is irreducible.

Example 1. Consider the $4$ -order $4$ -dimension tensor $\mathcal{A}$ given

$\begin{array}{l} a_{1111} = a_{2222} = a_{3333} = a_{4444} = a_{1444} = a_{2333} = 2, \end{array}$

and zero elsewhere. Then $a_{i_{1}i_{2}i_{3} i_{4}} = 0$ for all $i_1\in \{1, 4\}$ and for all $i_2, i_3, i_4\in \{2, 3\}$ . From Definition $2$ , we have that $\mathcal {A}$ is reducible.

Definition 3. ^[12] Let $\mathcal {A} = (a_{i_1i_2\cdots i_m})$ be an $m$ -order $n$ -dimension complex tensor, for $i, j\in N (i\neq j)$ , if there exist indices $k_{1}, k_{2}, \cdots, k_{r}$ with

$\begin{array}{l} \sum\limits_{i_2, \ldots, i_m\in N \atop \delta_{k_{s}i_2\ldots i_m} = 0 , k_{s+1}\in\{i_2, \ldots, i_m\}} |a_{k_{s}i_2\cdots i_m}|\neq 0, \; \; \; \; s = 0, 1, \ldots, r, \end{array}$

where $k_{0} = i, k_{r+1} = j$ , we call that there is a nonzero elements chain from $i$ to $j$ .

It is shown that for any $\mathcal {H}$ -tensor, there exists at least one strictly diagonally dominant row ^[7]. Further, we have the following conclusion.

Lemma 1. ^[10] If $\mathcal{A}$ is a strictly diagonally dominant tensor, then $\mathcal {A}$ is an $\mathcal {H}$ -tensor.

Lemma 2. ^[7] Let $\mathcal {A} = (a_{i_1\cdots i_m})$ be a complex tensor with $m$ -order, $n$ -dimension. If there exists a positive diagonal matrix $X$ such that $\mathcal {A}X^{m-1}$ is an $\mathcal {H}$ -tensor, then $\mathcal{A}$ is an $\mathcal {H}$ -tensor.

Lemma 3. ^[7] Let $\mathcal {A} = (a_{i_1\cdots i_m})$ be a complex tensor with $m$ -order, $n$ -dimension. If $\mathcal {A}$ is irreducible,

$|a_{i\cdots i}|\geq \Lambda_i(\mathcal{A}), \; \; \; \; \forall i \in N,$

and strictly inequality holds for at least one $i$ , then $\mathcal{A}$ is an $\mathcal {H}$ -tensor.

Lemma 4. ^[12] Let $\mathcal{A} = (a_{i_{1}\cdots i_{m}})$ be a complex tensor with $m$ -order, $n$ -dimension. If

● $(i)$ $|a_{ii\cdots i}|\geq \Lambda_i(\mathcal{A}), \; \; \; \; \forall i\in N$ ,

● $(ii)$ $N_3 = \{i\in N: |a_{ii\cdots i}| > \Lambda_i(\mathcal{A}) \}\neq \emptyset$ ,

● $(iii)$ For any $i\notin N_3$ , there exists a nonzero elements chain from $i$ to $j$ such that $j\in N_3$ ,

then $\mathcal {A}$ is an $\mathcal {H}$ -tensor.

3. Criteria for identifying $\mathcal {H}$ -tensors

In this section, we give some new criteria for $\mathcal{H}$ -tensors.

Theorem 2. Let $\mathcal{A} = (a_{i_{1}\cdots i_{m}})$ be a complex tensor with $m$ -order, $n$ -dimension. If for $i\in N_2$ ,

$\begin{eqnarray} |a_{ii\cdots i}| & > & \frac{\Lambda_i(\mathcal{A}) }{\Lambda_i(\mathcal{A})-|a_{ii\cdots i}|}\left[ q\left( \sum\limits_{i_2i_3\cdots i_m\in N_0^{m-1} } |a_{ii_2\cdots i_m}|+\sum\limits_{i_2i_3\cdots i_m\in N_2^{m-1} \atop\delta_{ii_2\cdots i_m} = 0} |a_{ii_2\cdots i_m}| \right) \right.\\ &&+ \left. \sum\limits_{i_2i_3\cdots i_m\in N_3^{m-1} }\max\limits_{j\in \{i_2, i_3, \cdots, i_m\}} \frac{tP_{j}(\mathcal {A}) }{|a_{jj\cdots j}|} |a_{ii_2\cdots i_m}|\right], \end{eqnarray}$

(3.1)

and for $i\in N_1$ , $|a_{ii\cdots i}|\neq \sum\limits_{i_2i_3\cdots i_m\in N_0^{m-1} \atop\delta_{ii_2\cdots i_m} = 0} |a_{ii_2\cdots i_m}|$ , then $\mathcal {A}$ is an $\mathcal{H}$ -tensor.

Proof. From the definition of $q$ , we know that $0\leq q < 1$ , $q \geq \frac{\Lambda_i(\mathcal{A})-|a_{ii\cdots i}|}{\Lambda_i(\mathcal{A}) }(\forall i \in N_2)$ , so for any $i\in N_3$ ,

$\begin{array}{l} P_i(\mathcal {A})& = & q \left(\sum\limits_{i_2, \ldots, i_m\in N_{0}^{m-1}}\left| {{a_{i{i_2} \cdots {i_m}}}} \right| +\sum\limits_{i_2, \ldots, i_m\in N_{2}^{m-1}} \left| {{a_{i{i_2} \cdots {i_m}}}} \right| \right. \\ &&+ \left.\sum\limits_{i_2, \ldots, i_m\in N_{3}^{m-1} \atop \delta_{ii_2\ldots i_m} = 0} |a_{ii_2\cdots i_m}|\right) = q\Lambda_i(\mathcal {A}) < q|a_{ii\cdots i}|, \end{array}$

that is

$\begin{eqnarray} q > \frac{P_i(\mathcal{A})}{|a_{ii\cdots i}|}. \end{eqnarray}$

(3.2)

By the definition of $P_i(\mathcal{A})$ , we have

$\begin{array}{l} \frac{q\left( \sum\limits_{i_2i_3\cdots i_m\in N_0^{m-1} } |a_{ii_2\cdots i_m}|+\sum\limits_{i_2i_3\cdots i_m\in N_2^{m-1} } |a_{ii_2\cdots i_m}| \right)}{P_i(\mathcal{A})-\sum\limits_{i_2i_3\cdots i_m\in N_3^{m-1}\atop\delta_{ii_2\cdots i_m} = 0 }\max\limits_{j\in \{i_2, i_3, \cdots, i_m\}} \frac{P_{j}(\mathcal {A}) }{|a_{jj\cdots j}|} |a_{ii_2\cdots i_m}|} = \frac{P_i(\mathcal{A})-q\sum\limits_{i_2\ldots i_m\in N_{3}^{m-1} \atop \delta_{ii_2\ldots i_m} = 0 } |a_{ii_2\cdots i_m}| }{P_i(\mathcal{A})-\sum\limits_{i_2i_3\cdots i_m\in N_3^{m-1} \atop \delta_{ii_2\ldots i_m} = 0 }\max\limits_{j\in \{i_2, i_3, \cdots, i_m\}} \frac{P_{j}(\mathcal {A}) }{|a_{jj\cdots j}|} |a_{ii_2\cdots i_m}|} \leq 1. \end{array}$

For any $i\in N_{3}$ , from Inequality (3.2) and $0\leq t \leq 1$ , we conclude that

$\begin{eqnarray} q > \frac{tP_{i}(\mathcal {A}) }{|a_{ii\cdots i}|}, \; \; \; \; \; \; \forall i\in N_{3}. \end{eqnarray}$

(3.3)

For any $i \in N _2$ , by Inequality (3.1), it holds that

$\begin{eqnarray} \left| {{a_{ii \cdots i}}} \right|\frac{{{\Lambda_i}\left( A \right) - \left| {{a_{ii \cdots i}}} \right|}}{{{\Lambda_i}\left( A \right)}} & > & q\left( {\sum\limits_{{i_2} \cdots {i_m} \in N _0^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} + \sum\limits_{ {i_2} \cdots {i_m} \in N _2^{m - 1} \atop {\delta _{i{i_2} \cdots {i_m}}} = 0 } {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} } \right)\\ &&+ \sum\limits_{{i_2} \cdots {i_m} \in N _3^{m - 1}} {\mathop {\max }\limits_{j \in \left\{ {{i_2}, {i_3}, \cdots , {i_m}} \right\}} \frac{{t{P_j}\left( A \right)}}{{\left| {{a_{jj \cdots j}}} \right|}}\left| {{a_{i{i_2} \cdots {i_m}}}} \right|}. \end{eqnarray}$

(3.4)

By Inequality (3.3) and Inequality (3.4), there exists a sufficiently small positive number $\varepsilon$ such that

$\begin{eqnarray} q > \frac{tP_{i}(\mathcal {A}) }{|a_{ii\cdots i}|}+\varepsilon, \; \; \; \; \; \; \forall i\in N_{3}, \end{eqnarray}$

(3.5)

and

$\begin{array}{l} \left| {{a_{ii \cdots i}}} \right|\frac{{{\Lambda_i}\left( A \right) - \left| {{a_{ii \cdots i}}} \right|}}{{{\Lambda_i}\left( A \right)}} & > & q\left( {\sum\limits_{{i_2} \cdots {i_m} \in N _0^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} + \sum\limits_{ {i_2} \cdots {i_m} \in N _2^{m - 1} \atop {\delta _{i{i_2} \cdots {i_m}}} = 0 } {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} } \right)\\ &&+ \sum\limits_{{i_2} \cdots {i_m} \in N _3^{m - 1}} {\mathop {\max }\limits_{j \in \left\{ {{i_2}, {i_3}, \cdots , {i_m}} \right\}} \frac{{t{P_j}\left( A \right)}}{{\left| {{a_{jj \cdots j}}} \right|}}\left| {{a_{i{i_2} \cdots {i_m}}}} \right|}\\ &&+ \varepsilon\sum\limits_{{i_2} \cdots {i_m} \in N _3^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|}, \; \; \; \; \; \; {\kern 1pt} {\kern 1pt} {\forall i \in {N _2}}, \end{array}$

that is,

$\varepsilon\sum\limits_{{i_2} \cdots {i_m} \in N _3^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} < \left| {{a_{ii \cdots i}}} \right|\frac{{{\Lambda_i}\left( A \right) - \left| {{a_{ii \cdots i}}} \right|}}{{{\Lambda_i}\left( A \right)}} - q\left( {\sum\limits_{{i_2} \cdots {i_m} \in N _0^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} + \sum\limits_{ {i_2} \cdots {i_m} \in N _2^{m - 1} \atop {\delta _{i{i_2} \cdots {i_m}}} = 0 } {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} } \right)\\ - \sum\limits_{{i_2} \cdots {i_m} \in N _3^{m - 1}} {\mathop {\max }\limits_{j \in \left\{ {{i_2}, {i_3}, \cdots , {i_m}} \right\}} \frac{{t{P_j}\left( A \right)}}{{\left| {{a_{jj \cdots j}}} \right|}}\left| {{a_{i{i_2} \cdots {i_m}}}} \right|}\text{, } \; \; \; \; \; \; {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\forall i \in {N _2}}.$

(3.6)

By the definition of $t$ , it holds that

$t \geq {\frac{{q\left( {\sum\limits_{{i_2} \cdots {i_m} \in N _0^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} + \sum\limits_{{i_2} \cdots {i_m} \in N _2^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} } \right)}}{{{P_i}\left( {\cal A} \right) - \sum\limits_{ {i_2} \cdots {i_m} \in N _3^{m - 1} \atop {\delta _{i{i_2} \cdots {i_m}}} = 0 } {\mathop {\max }\limits_{j \in \left\{ {{i_2}, {i_3}, \cdots , {i_m}} \right\}} \frac{{{P_j}\left( {\cal A} \right)}}{{\left| {{a_{jj \cdots j}}} \right|}}\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} }}}, \; \; \; \; \; \; \; \; \; \; {\forall i \in {N _2}},$

that is

$q\left( {\sum\limits_{{i_2} \cdots {i_m} \in N _0^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} + \sum\limits_{{i_2} \cdots {i_m} \in N _2^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} } \right) + \\ t\sum\limits_{ {i_2} \cdots {i_m} \in N _3^{m - 1} \atop {\delta _{i{i_2} \cdots {i_m}}} = 0 } {\mathop {\max }\limits_{j \in \left\{ {{i_2}, {i_3}, \cdots , {i_m}} \right\}} \frac{{{P_j}\left( {\cal A} \right)}}{{\left| {{a_{jj \cdots j}}} \right|}}\left| {{a_{i{i_2} \cdots {i_m}}}} \right| } \leq t{P_i}\left( {\cal A} \right), \; \; {\forall i \in {N _2}}.$

(3.7)

Let the matrix $D = diag(d_1, d_2, \cdots, d_n)$ , and denote $\mathcal {B} = \mathcal {A}D^{m-1} = (b_{i_1i_2\cdots i_m}),$ where

$d_i = \left\{\begin{array}{cc} q^{\frac{1}{m-1}}, &i\in N_1, \\ \left(\frac{\Lambda_{i}(\mathcal {A})- |a_{ii\cdots i}| }{\Lambda_{i}(\mathcal {A})}\right)^{\frac{1}{m-1}}, &i\in N_2, \\ \left(\varepsilon+\frac{t P_{i}(\mathcal {A}) }{|a_{ii\cdots i}|}\right)^{\frac{1}{m-1}}, &i\in N_3. \end{array} \right.$

For any $i\in N_1$ , by $q > \frac{tP_{i}(\mathcal {A}) }{|a_{ii\cdots i}|}(\forall i\in N_{3})$ , we conclude that

$\begin{array}{l} {\Lambda_i}\left( {\cal B} \right) & = & q {\sum\limits_{ {i_2} \cdots {i_m} \in N _0^{m - 1} \atop {\delta _{i{i_2} \cdots {i_m}}} = 0 } {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} }\\ &&+ \sum\limits_{{i_2} \cdots {i_m} \in N _2^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} \left( \frac{\Lambda_{i_2}\left( {\cal A} \right)-\left| a_{{i_2}{i_2} \cdots {i_2}} \right|}{\Lambda_{i_2}\left( {\cal A} \right)} \right) ^{\frac{1}{{m - 1}}} \cdots \left( \frac{\Lambda_{i_m}\left( {\cal A} \right)-\left| a_{{i_m}{i_m} \cdots {i_m}} \right|}{\Lambda_{i_m}\left( {\cal A} \right)} \right) ^{\frac{1}{{m - 1}}} \\ &&+ \sum\limits_{{i_2} \cdots {i_m} \in N _3^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} \left( {\frac{{t{P_{{i_2}}}\left( {\cal A} \right)}}{{\left| {{a_{{i_2}{i_2} \cdots {i_2}}}} \right|}} + \varepsilon } \right) ^{\frac{1}{{m - 1}}} \cdots \left( {\frac{{t{P_{{i_m}}}\left( {\cal A} \right)}}{{\left| {{a_{{i_m}{i_m} \cdots {i_m}}}} \right|}} + \varepsilon } \right) ^{\frac{1}{{m - 1}}}\\ &\leq& q\left( {\sum\limits_{ {i_2} \cdots {i_m} \in N _0^{m - 1} \atop {\delta _{i{i_2} \cdots {i_m}}} = 0 } {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} + \sum\limits_{{i_2} \cdots {i_m} \in N _2^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} } \right) \\ &&+ \sum\limits_{{i_2} \cdots {i_m} \in N _3^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} \left( \max\limits_{j\in \{i_2, i_3, \cdots, i_m\}} \frac{{{tP_j}\left( {\cal A} \right)}}{{\left| {{a_{jj \cdots j}}} \right|}} +\varepsilon \right) \\ & < & q\left( {\sum\limits_{ {i_2} \cdots {i_m} \in N _0^{m - 1} \atop {\delta _{i{i_2} \cdots {i_m}}} = 0 } {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} + \sum\limits_{{i_2} \cdots {i_m} \in N _2^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} } \right) + q\sum\limits_{{i_2} \cdots {i_m} \in N _3^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|}\\ & = & q\left| a_{ii\cdots i} \right| = \left| b_{ii\cdots i} \right|. \end{array}$

For $\forall i\in N_2$ , by Inequality (3.6), then

$\begin{array}{l} {\Lambda_i}\left( {\cal B} \right) & = & q \sum\limits_{{i_2} \cdots {i_m} \in N _0^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} \\ &&+ \sum\limits_{{i_2} \cdots {i_m} \in N _2^{m - 1}\atop{\delta _{i{i_2} \cdots {i_m}}} = 0} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} \left( \frac{\Lambda_{i_2}\left( {\cal A} \right)-\left| a_{{i_2}{i_2} \cdots {i_2}} \right|}{\Lambda_{i_2}\left( {\cal A} \right)} \right) ^{\frac{1}{{m - 1}}} \cdots \left( \frac{\Lambda_{i_m}\left( {\cal A} \right)-\left| a_{{i_m}{i_m} \cdots {i_m}} \right|}{\Lambda_{i_m}\left( {\cal A} \right)} \right) ^{\frac{1}{{m - 1}}} \\ &&+ \sum\limits_{{i_2} \cdots {i_m} \in N _3^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} \left( {\frac{{t{P_{{i_2}}}\left( {\cal A} \right)}}{{\left| {{a_{{i_2}{i_2} \cdots {i_2}}}} \right|}} + \varepsilon } \right) ^{\frac{1}{{m - 1}}} \cdots \left( {\frac{{t{P_{{i_m}}}\left( {\cal A} \right)}}{{\left| {{a_{{i_m}{i_m} \cdots {i_m}}}} \right|}} + \varepsilon } \right) ^{\frac{1}{{m - 1}}}\\ &\leq& q\left( {\sum\limits_{ {i_2} \cdots {i_m} \in N _0^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} + \sum\limits_{{i_2} \cdots {i_m} \in N _2^{m - 1} \atop {\delta _{i{i_2} \cdots {i_m}}} = 0 } {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} } \right) \\ &&+ \sum\limits_{{i_2} \cdots {i_m} \in N _3^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} \left( \max\limits_{j\in \{i_2, i_3, \cdots, i_m\}} \frac{{{tP_j}\left( {\cal A} \right)}}{{\left| {{a_{jj \cdots j}}} \right|}} +\varepsilon \right) \\ & = & q\left( {\sum\limits_{ {i_2} \cdots {i_m} \in N _0^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} + \sum\limits_{{i_2} \cdots {i_m} \in N _2^{m - 1} \atop {\delta _{i{i_2} \cdots {i_m}}} = 0 } {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} } \right) \\ &&+\sum\limits_{{i_2} \cdots {i_m} \in N _3^{m - 1}} \max\limits_{j\in \{i_2, i_3, \cdots, i_m\}} \frac{{{tP_j}\left( {\cal A} \right)}}{{\left| {{a_{jj \cdots j}}} \right|}}{\left| {{a_{i{i_2} \cdots {i_m}}}} \right|}+ \varepsilon\sum\limits_{{i_2} \cdots {i_m} \in N _3^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|}\\ & < & q\left( {\sum\limits_{ {i_2} \cdots {i_m} \in N _0^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} + \sum\limits_{{i_2} \cdots {i_m} \in N _2^{m - 1} \atop {\delta _{i{i_2} \cdots {i_m}}} = 0 } {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} } \right) \\ &&+\sum\limits_{{i_2} \cdots {i_m} \in N _3^{m - 1}} \max\limits_{j\in \{i_2, i_3, \cdots, i_m\}} \frac{{{tP_j}\left( {\cal A} \right)}}{{\left| {{a_{jj \cdots j}}} \right|}}{\left| {{a_{i{i_2} \cdots {i_m}}}} \right|}\\ &&+ \left[ \left| {{a_{ii \cdots i}}} \right|\frac{{{\Lambda_i}\left( A \right) - \left| {{a_{ii \cdots i}}} \right|}}{{{\Lambda_i}\left( A \right)}} - q\left( {\sum\limits_{{i_2} \cdots {i_m} \in N _0^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} + \sum\limits_{ {i_2} \cdots {i_m} \in N _2^{m - 1} \atop {\delta _{i{i_2} \cdots {i_m}}} = 0 } {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} } \right) \right.\\ &&\; \; \; \; \; - \left. \sum\limits_{{i_2} \cdots {i_m} \in N _3^{m - 1}} {\mathop {\max }\limits_{j \in \left\{ {{i_2}, {i_3}, \cdots , {i_m}} \right\}} \frac{{t{P_j}\left( A \right)}}{{\left| {{a_{jj \cdots j}}} \right|}}\left| {{a_{i{i_2} \cdots {i_m}}}} \right|}\right]\\ & = & \left| a_{ii\cdots i} \right|\frac{\Lambda_{i}(\mathcal {A})- |a_{ii\cdots i}| }{\Lambda_{i}(\mathcal {A})} = \left| b_{ii\cdots i} \right|. \end{array}$

Finally, for any $i\in N_3$ , by Inequality (3.7), thus

$\begin{array}{l} {\Lambda_i}\left( {\cal B} \right) & = & q \sum\limits_{{i_2} \cdots {i_m} \in N _0^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} \\ &&+ \sum\limits_{{i_2} \cdots {i_m} \in N _2^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} \left( \frac{\Lambda_{i_2}\left( {\cal A} \right)-\left| a_{{i_2}{i_2} \cdots {i_2}} \right|}{\Lambda_{i_2}\left( {\cal A} \right)} \right) ^{\frac{1}{{m - 1}}} \cdots \left( \frac{\Lambda_{i_m}\left( {\cal A} \right)-\left| a_{{i_m}{i_m} \cdots {i_m}} \right|}{\Lambda_{i_m}\left( {\cal A} \right)} \right) ^{\frac{1}{{m - 1}}} \\ &&+ \sum\limits_{{i_2} \cdots {i_m} \in N _3^{m - 1}\atop{\delta _{i{i_2} \cdots {i_m}}} = 0} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} \left( {\frac{{t{P_{{i_2}}}\left( {\cal A} \right)}}{{\left| {{a_{{i_2}{i_2} \cdots {i_2}}}} \right|}} + \varepsilon } \right) ^{\frac{1}{{m - 1}}} \cdots \left( {\frac{{t{P_{{i_m}}}\left( {\cal A} \right)}}{{\left| {{a_{{i_m}{i_m} \cdots {i_m}}}} \right|}} + \varepsilon } \right) ^{\frac{1}{{m - 1}}}\\ &\leq& q\left( {\sum\limits_{ {i_2} \cdots {i_m} \in N _0^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} + \sum\limits_{{i_2} \cdots {i_m} \in N _2^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} } \right) \\ &&+ \sum\limits_{{i_2} \cdots {i_m} \in N _3^{m - 1} \atop {\delta _{i{i_2} \cdots {i_m}}} = 0 } {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} \left( \max\limits_{j\in \{i_2, i_3, \cdots, i_m\}} \frac{{{tP_j}\left( {\cal A} \right)}}{{\left| {{a_{jj \cdots j}}} \right|}} +\varepsilon \right) \\ & = & q\left( {\sum\limits_{ {i_2} \cdots {i_m} \in N _0^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} + \sum\limits_{{i_2} \cdots {i_m} \in N _2^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} } \right) \\ &&+\sum\limits_{{i_2} \cdots {i_m} \in N _3^{m - 1} \atop {\delta _{i{i_2} \cdots {i_m}}} = 0 } \max\limits_{j\in \{i_2, i_3, \cdots, i_m\}} \frac{{{tP_j}\left( {\cal A} \right)}}{{\left| {{a_{jj \cdots j}}} \right|}}{\left| {{a_{i{i_2} \cdots {i_m}}}} \right|}+ \varepsilon\sum\limits_{{i_2} \cdots {i_m} \in N _3^{m - 1} \atop {\delta _{i{i_2} \cdots {i_m}}} = 0 } {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|}\\ &\leq& {tP_i}\left( {\mathcal A} \right)+\varepsilon\sum\limits_{{i_2} \cdots {i_m} \in N _3^{m - 1} \atop {\delta _{i{i_2} \cdots {i_m}}} = 0 } {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|}\\ & < & {tP_i}\left( {\mathcal A} \right)+\varepsilon{\left| {{a_{ii \cdots i}}} \right|} = \left| b_{ii\cdots i} \right|. \end{array}$

Therefore, we obtain that $|b_{ii\cdots i}| > \Lambda_i(\mathcal {B}) (\forall i\in N)$ . From Lemma 1, $\mathcal {B}$ is an $\mathcal {H}$ -tensor. Further, by Lemma 2, $\mathcal {A}$ is an $\mathcal {H}$ -tensor.

Remark 1. From Theorem $2$ , we conclude that $0\leq p < 1$ , $0\leq t\leq1$ , and for any $i\in N_3$ ,

$\begin{array}{l} \frac{tP_i(\mathcal{A})}{|a_{ii\cdots i}|} < \frac{\Lambda_i(\mathcal{A})}{|a_{ii\cdots i}|} < 1. \end{array}$

Thus, all conditions in Theorem $2$ are weaker than that in Theorem $1$ . Example $2$ illustrates the superiority of Theorem $2$ .

Theorem 3. Let $\mathcal{A} = (a_{i_{1}\cdots i_{m}})$ be a complex tensor with $m$ -order, $n$ -dimension. If $\mathcal {A}$ is irreducible, and for all $i\in N_2,$

$\begin{eqnarray} |a_{ii\cdots i}| &\geq& \frac{\Lambda_i(\mathcal{A}) }{\Lambda_i(\mathcal{A})-|a_{ii\cdots i}|}\left[ q\left( \sum\limits_{i_2i_3\cdots i_m\in N_0^{m-1} } |a_{ii_2\cdots i_m}|+\sum\limits_{i_2i_3\cdots i_m\in N_2^{m-1} \atop\delta_{ii_2\cdots i_m} = 0} |a_{ii_2\cdots i_m}| \right) \right.\\ &&+ \left. \sum\limits_{i_2i_3\cdots i_m\in N_3^{m-1} }\max\limits_{j\in \{i_2, i_3, \cdots, i_m\}} \frac{tP_{j}(\mathcal {A}) }{|a_{jj\cdots j}|} |a_{ii_2\cdots i_m}|\right], \end{eqnarray}$

(3.8)

and at least one strict inequality in $(3.8)$ holds, then $\mathcal {A}$ is an $\mathcal{H}$ -tensor.

Proof. Notice that $\mathcal {A}$ is irreducible, this implies that for any $i \in N_3$ , $P_{i}(\mathcal {A}) > 0\text{, }\; t > 0$ (Otherwise, $\mathcal{A}$ is reducible).

For any $i \in N_2$ , by Inequality (3.8), we obtain

$\begin{eqnarray} |a_{ii\cdots i}|\frac{\Lambda_i(\mathcal{A})-|a_{ii\cdots i}|}{\Lambda_i(\mathcal{A}) } &\geq& q\left( \sum\limits_{i_2i_3\cdots i_m\in N_0^{m-1} } |a_{ii_2\cdots i_m}|+\sum\limits_{i_2i_3\cdots i_m\in N_2^{m-1} \atop\delta_{ii_2\cdots i_m} = 0} |a_{ii_2\cdots i_m}| \right) \\ &&+ \sum\limits_{i_2i_3\cdots i_m\in N_3^{m-1} }\max\limits_{j\in \{i_2, i_3, \cdots, i_m\}} \frac{tP_{j}(\mathcal {A}) }{|a_{jj\cdots j}|} |a_{ii_2\cdots i_m}|. \end{eqnarray}$

(3.9)

Let the matrix $D = diag(d_1, d_2, \cdots, d_n)$ , denote $\mathcal {B} = \mathcal {A}D^{m-1} = (b_{i_1i_2\cdots i_m}),$ where

$d_i = \left\{\begin{array}{cc} q^{\frac{1}{m-1}}, &i\in N_1, \\ \left(\frac{\Lambda_{i}(\mathcal {A})- |a_{ii\cdots i}| }{\Lambda_{i}(\mathcal {A})}\right)^{\frac{1}{m-1}}, &i\in N_2, \\ \left(\frac{t P_{i}(\mathcal {A}) }{|a_{ii\cdots i}|}\right)^{\frac{1}{m-1}}, &i\in N_3. \end{array} \right.$

For any $i\in N_1$ , by $q > \frac{tP_{i}(\mathcal {A})}{|a_{ii\cdots i}|}(\forall i\in N_{3})$ , we conclude that

$\begin{array}{l} {\Lambda_i}\left( {\cal B} \right) & = & q {\sum\limits_{ {i_2} \cdots {i_m} \in N _0^{m - 1} \atop {\delta _{i{i_2} \cdots {i_m}}} = 0 } {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} }\\ &&+ \sum\limits_{{i_2} \cdots {i_m} \in N _2^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} \left( \frac{\Lambda_{i_2}\left( {\cal A} \right)-\left| a_{{i_2}{i_2} \cdots {i_2}} \right|}{\Lambda_{i_2}\left( {\cal A} \right)} \right) ^{\frac{1}{{m - 1}}} \cdots \left( \frac{\Lambda_{i_m}\left( {\cal A} \right)-\left| a_{{i_m}{i_m} \cdots {i_m}} \right|}{\Lambda_{i_m}\left( {\cal A} \right)} \right) ^{\frac{1}{{m - 1}}} \\ &&+ \sum\limits_{{i_2} \cdots {i_m} \in N _3^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} \left( {\frac{{t{P_{{i_2}}}\left( {\cal A} \right)}}{{\left| {{a_{{i_2}{i_2} \cdots {i_2}}}} \right|}} } \right) ^{\frac{1}{{m - 1}}} \cdots \left( {\frac{{t{P_{{i_m}}}\left( {\cal A} \right)}}{{\left| {{a_{{i_m}{i_m} \cdots {i_m}}}} \right|}} } \right) ^{\frac{1}{{m - 1}}}\\ &\leq& q\left( {\sum\limits_{ {i_2} \cdots {i_m} \in N _0^{m - 1} \atop {\delta _{i{i_2} \cdots {i_m}}} = 0 } {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} + \sum\limits_{{i_2} \cdots {i_m} \in N _2^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} } \right) \\ &&+ \sum\limits_{{i_2} \cdots {i_m} \in N _3^{m - 1}} \max\limits_{j\in \{i_2, i_3, \cdots, i_m\}} \frac{{{tP_j}\left( {\cal A} \right)}}{{\left| {{a_{jj \cdots j}}} \right|}}{\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} \\ & < & q\left( {\sum\limits_{ {i_2} \cdots {i_m} \in N _0^{m - 1} \atop {\delta _{i{i_2} \cdots {i_m}}} = 0 } {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} + \sum\limits_{{i_2} \cdots {i_m} \in N _2^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|} } \right) + q\sum\limits_{{i_2} \cdots {i_m} \in N _3^{m - 1}} {\left| {{a_{i{i_2} \cdots {i_m}}}} \right|}\\ & = & q\left| a_{ii\cdots i} \right| = \left| b_{ii\cdots i} \right|. \end{array}$

For any $i\in N_2$ , by Inequality $(3.9)$ , it holds that

Next, for any $i\in N_3$ , by Inequality $(3.7)$ , then

Therefore, $|b_{ii\cdots i}|\geq \Lambda_i(\mathcal {B})$ ( $\forall i\in N$ ), and for all $\forall i\in N_2$ , at least one strict inequality in (10) holds, that is, there exists an $i_0\in N_2$ such that $|b_{i_0i_0\cdots i_0}| > \Lambda_{i_0}(\mathcal {B})$ .

On the other hand, since $\mathcal {A}$ is irreducible and so is $\mathcal {B}$ . Then, by Lemma 3, we have that $\mathcal {B}$ is an $\mathcal {H}$ -tensor. By Lemma 2, $\mathcal {A}$ is also an $\mathcal {H}$ -tensor.

Let

$\begin{array}{l} K(\mathcal{A})& = &\left\{i\in N_2: |a_{ii\cdots i}| > \frac{\Lambda_i(\mathcal{A}) }{\Lambda_i(\mathcal{A})-|a_{ii\cdots i}|}\left[ q\left( \sum\limits_{i_2i_3\cdots i_m\in N_0^{m-1} } |a_{ii_2\cdots i_m}| + \sum\limits_{i_2i_3\cdots i_m\in N_2^{m-1} \atop\delta_{ii_2\cdots i_m} = 0} |a_{ii_2\cdots i_m}| \right) \right. \right.\\ &&+ \left.\left. \sum\limits_{i_2i_3\cdots i_m\in N_3^{m-1} }\max\limits_{j\in \{i_2, i_3, \cdots, i_m\}} \frac{tP_{j}(\mathcal {A}) }{|a_{jj\cdots j}|} |a_{ii_2\cdots i_m}|\right]\right\}. \end{array}$

Theorem 4. Let $\mathcal{A} = (a_{i_{1}\cdots i_{m}})$ be a complex tensor with $m$ -order, $n$ -dimension. For any $i\in N_2$ ,

$\begin{array}{l} |a_{ii\cdots i}|\nonumber &\geq& \frac{\Lambda_i(\mathcal{A}) }{\Lambda_i(\mathcal{A})-|a_{ii\cdots i}|}\left[ q\left( \sum\limits_{i_2i_3\cdots i_m\in N_0^{m-1} } |a_{ii_2\cdots i_m}|+\sum\limits_{i_2i_3\cdots i_m\in N_2^{m-1} \atop\delta_{ii_2\cdots i_m} = 0} |a_{ii_2\cdots i_m}| \right) \right.\\ &&+ \left. \sum\limits_{i_2i_3\cdots i_m\in N_3^{m-1} }\max\limits_{j\in \{i_2, i_3, \cdots, i_m\}} \frac{tP_{j}(\mathcal {A}) }{|a_{jj\cdots j}|} |a_{ii_2\cdots i_m}|\right], \end{array}$

and if for any $i \in N\setminus K(\mathcal{A})\neq \emptyset$ , there exists a nonzero elements chain from $i$ to $j$ such that $j\in K(\mathcal{A})\neq \emptyset$ , then $\mathcal {A}$ is an $\mathcal {H}$ -tensor.

Proof. Let the matrix $D = diag(d_1, d_2, \cdots, d_n)$ , and denote $\mathcal {B} = \mathcal {A}D^{m-1} = (b_{i_1i_2\cdots i_m}),$ where

$d_i = \left\{\begin{array}{cc} q^{\frac{1}{m-1}}, &i\in N_1, \\ \left(\frac{\Lambda_{i}(\mathcal {A})- |a_{ii\cdots i}| }{\Lambda_{i}(\mathcal {A})}\right)^{\frac{1}{m-1}}, &i\in N_2, \\ \left(\frac{t P_{i}(\mathcal {A}) }{|a_{ii\cdots i}|}\right)^{\frac{1}{m-1}}, &i\in N_3. \end{array} \right.$

A similar argument to that of Theorem 2, we can prove that $|b_{ii\cdots i}|\geq \Lambda_i(\mathcal {B}) (\forall i\in N)$ , and there exists at least an $i \in N_2$ such that $|b_{ii\cdots i}| > \Lambda_i(\mathcal {B})$ .

On the other hand, if $|b_{ii\cdots i}| = \Lambda_i(\mathcal {B})$ , then $i \in N\setminus K(\mathcal{A})$ , by the assumption, we know that there exists a nonzero elements chain of $\mathcal {A}$ from $i$ to $j$ , such that $j\in K(\mathcal{A})$ . Hence, there exists a nonzero elements chain of $\mathcal {B}$ from $i$ to $j$ , such that $j$ satisfying $|b_{jj\cdots j}| > \Lambda_j(\mathcal {B})$ .

Based on above analysis, we get that $\mathcal {B}$ satisfies the conditions of Lemma 4, so $\mathcal {B}$ is an $\mathcal {H}$ -tensor. By Lemma 2, $\mathcal {A}$ is an $\mathcal {H}$ -tensor.

Example 2. Consider the $3$ -order $3$ -dimension tensor $\mathcal {A} = (a_{ijk})$ defined as follows:

$\mathcal {A} = [A(1, :, :), A(2, :, :), A(3, :, :)],$

$A(1, :, :) = \left(\begin{array}{cccc} 12 &1 &0 \\ 1 &6 &0 \\ 1 &0 &15 \end{array} \right), A(2, :, :) = \left(\begin{array}{cccc} 1 &1 &0 \\ 0 &6 &0 \\ 0 &0 &1 \end{array} \right), A(3, :, :) = \left(\begin{array}{cccc} 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &16 \end{array} \right).$

Obviously,

$|a_{111}| = 12, \ \ \Lambda_1(\mathcal {A}) = 24, \ \ |a_{222}| = 6, \ \ \Lambda_2(\mathcal {A}) = 3, \ \ |a_{333}| = 16, \ \ \Lambda_3(\mathcal {A}) = 2.$

so $N_1 = \emptyset, N_2 = \{1\}, N_3 = \{2, 3\}$ . By calculations, we have

$q_{i = 1} = \frac{24-12}{24} = \frac{1}{2} = q, \ \ \ \ \$

$P_{2}(\mathcal{A}) = \frac{1}{2}(1+1+1) = \frac{3}{2}, \ \ \ \ \ P_{3}(\mathcal{A}) = \frac{1}{2}(0+1+1) = 1,$

$\frac{P_{2}(\mathcal{A})}{|a_{222}|} = \frac{\frac{3}{2}}{6} = \frac{1}{4}, \ \ \ \ \ \frac{P_{3}(\mathcal{A})}{|a_{333}|} = \frac{1}{16},$

$t_{i = 2} = \frac{\frac{1}{2}(1+1)}{\frac{3}{2}-\frac{1}{4}\times 1} = \frac{4}{5}, \ \ \ \ \ t_{i = 3} = \frac{\frac{1}{2}(0+1)}{1-\frac{1}{4}\times 1} = \frac{2}{3}, \ \ \ \ \ t = \frac{4}{5}.$

When $i = 1$ , we get

$\begin{array}{l} &&\frac{\Lambda_1(\mathcal{A})}{\Lambda_1(\mathcal{A})-|a_{111}|}\left[ q\left( \sum\limits_{i_2i_3 \in N_0^{2} } |a_{1i_2 i_3}|+\sum\limits_{i_2i_3\in N_2^{2} \atop\delta_{1i_2 i_3} = 0} |a_{1i_2i_3}| \right) + \sum\limits_{i_2i_3\in N_3^{2} }\max\limits_{j\in \{i_2, i_3\}} \frac{tP_{j}(\mathcal {A}) }{|a_{jj j}|} |a_{1i_2i_3}|\right] \\ & = & \frac{24}{24-12}\left[ \frac{1}{2}(3+0)+\frac{4}{5} \times\frac{1}{4}\times 21 \right] = \frac{57}{5} < 12 = |a_{111}|, \end{array}$

so $\mathcal {A}$ satisfies the conditions of Theorem $2$ , then $\mathcal {A}$ is an $\mathcal {H}$ -tensor. However,

$\begin{array}{l} \sum\limits_{ {i_2}{i_3} \in {N^{2}}\backslash N _3^{2} \atop {\delta _{1{i_2} i_3}} = 0 } {\left| {{a_{1{i_2} i_3}}} \right|} + \sum\limits_{{{i_2}{i_3} } \in N_3^{2} }{\mathop {\max }\limits_{j \in \left\{ {{i_2}, {i_3}} \right\}}} \frac{{{\Lambda_j}\left( A \right)}}{{\left| {{a_{jj j}}} \right|}}\left| {a_{1{i_2} i_3}} \right| = 3+ \frac{1}{2} \times 21 = \frac{27}{2} > 12 = \left| {a_{111}} \right|, \end{array}$

so $\mathcal {A}$ does not satisfy the conditions of Theorem $1$ .

4. An application: the positive definiteness of homogeneous polynomial forms

Based on the criteria of $\mathcal {H}$ -tensors in Section $3$ , we present some criteria for identifying the positive definiteness of an even-order real symmetric tensor. First, we recall the following lemma.

Lemma 5. ^[7] Let $\mathcal{A} = (a_{i_{1}i_2\cdots i_{m}})$ be an even-order real symmetric tensor with $m$ -order, $n$ -dimension, and $a_{k\cdots k} > 0$ for all $k \in N$ . If $\mathcal {A}$ is an $\mathcal{H}$ -tensor, then $\mathcal {A}$ is positive definite.

From Theorems $2-4$ and Lemma $5$ , we obtain easily the following result.

Theorem 5. Let $\mathcal{A} = (a_{i_{1}i_2\cdots i_{m}})$ be an even-order real symmetric tensor with $m$ -order, $n$ -dimension, and $a_{ii\cdots i} > 0$ for all $i \in N$ . If one of the following holds:

● $(i)$ $\mathcal {A}$ satisfies all the conditions of Theorem $2$ ,

● $(ii)$ $\mathcal {A}$ satisfies all the conditions of Theorem $3$ ,

● $(iii)$ $\mathcal {A}$ satisfies all the conditions of Theorem $4$ ,

then $\mathcal {A}$ is positive definite.

Example 3. Let

$\begin{array}{l} f(x)& = &\mathcal{A}x^{4} = 16x_{1}^4+20x_{2}^4+30x_{3}^4+33x_{4}^4-8x_{1}^{3}x_{4}+12x_{1}^{2}x_{2}x_{3}-12x_{2}x_{3}^2x_{4} -24x_{1}x_{2}x_{3}x_{4} \end{array}$

be a $4$ th-degree homogeneous polynomial. We can get the $4$ -order $4$ -dimension real symmetric tensor $\mathcal{A} = (a_{i_{1}i_{2}i_{3} i_{4}})$ , where

$\begin{array}{l} &&a_{1111} = 16, \ \ a_{2222} = 20, \ \ a_{3333} = 30, \ \ a_{4444} = 33, \\ &&a_{1114} = a_{1141} = a_{1411} = a_{4111} = -2, \\ &&a_{1123} = a_{1132} = a_{1213} = a_{1312} = a_{1231} = a_{1321} = 1, \\ &&a_{2113} = a_{2131} = a_{2311} = a_{3112} = a_{3121} = a_{3211} = 1, \\ &&a_{2334} = a_{2343} = a_{2433} = a_{4233} = a_{4323} = a_{4332} = -1, \\ &&a_{3234} = a_{3243} = a_{3324} = a_{3342} = a_{3423} = a_{3432} = -1, \\ &&a_{1234} = a_{1243} = a_{1324} = a_{1342} = a_{1423} = a_{1432} = -1, \\ &&a_{2134} = a_{2143} = a_{2314} = a_{2341} = a_{2413} = a_{2431} = -1, \\ &&a_{3124} = a_{3142} = a_{3214} = a_{3241} = a_{3412} = a_{3421} = -1, \\ &&a_{4123} = a_{4132} = a_{4213} = a_{4231} = a_{4312} = a_{4321} = -1, \end{array}$

and zero elsewhere. By calculations, we have

$a_{1111} = 16 < 18 = \Lambda_1(\mathcal{A}),$

and

$a_{4444}\left( a_{1111}-\Lambda_1(\mathcal{A})+|a_{1444}|\right) = -66 < 0 = \Lambda_4(\mathcal{A})|a_{1444}|.$

Then $\mathcal{A}$ is not strictly diagonally dominate as defined in ^[17] or quasidoubly strictly diagonally dominant as defined in ^[18]. Hence, we cannot use Theorem 3 in ^[17] and Theorem 4 in ^[18] to identify the positive definiteness of $\mathcal{A}$ . However, it can be verified that $\mathcal {A}$ satisfies all the conditions of Theorem $2$ .

$\Lambda_1(\mathcal {A}) = 18, \ \ \Lambda_2(\mathcal {A}) = 12, \ \ \Lambda_3(\mathcal {A}) = 15, \ \ \Lambda_4(\mathcal {A}) = 11,$

so $N_1 = \emptyset, N_2 = \{1\}, N_3 = \{ 2, 3, 4\}$ . By calculations, we have

$q_{i = 1} = \frac{18-16}{18} = \frac{1}{9} = q, \ \ \ \ \$

$P_{2}(\mathcal{A}) = \frac{1}{9}(9+0+3) = \frac{4}{3}, \ \ \ \ \ P_{3}(\mathcal{A}) = \frac{1}{9}(9+0+6) = \frac{5}{3}, \ \ \ \ \ P_{4}(\mathcal{A}) = \frac{1}{9}(6+2+3) = \frac{11}{9},$

$\frac{P_{2}(\mathcal{A})}{|a_{2222}|} = \frac{\frac{4}{3}}{20} = \frac{1}{15}, \ \ \ \ \ \frac{P_{3}(\mathcal{A})}{|a_{3333}|} = \frac{\frac{5}{3}}{30} = \frac{1}{18}, \ \ \ \ \ \frac{P_{4}(\mathcal{A})}{|a_{4444}|} = \frac{\frac{11}{9}}{33} = \frac{1}{27},$

$t_{i = 2} = \frac{\frac{1}{9}(9+0)}{\frac{4}{3}-\frac{1}{15}\times 3} = \frac{15}{17}, \ \ \ \ \ t_{i = 3} = \frac{\frac{1}{9}(9+1)}{\frac{5}{3}-\frac{1}{15}\times 6} = \frac{15}{19},$

$t_{i = 4} = \frac{\frac{1}{9}(6+2)}{\frac{11}{9}-\frac{1}{15}\times 3} = \frac{10}{13}, \ \ \ \ \ t = \frac{15}{17}.$

When $i = 1$ , we get

$\begin{array}{l} &&\frac{\Lambda_1(\mathcal{A})}{\Lambda_1(\mathcal{A})-|a_{1111}|}\left[ q\left( \sum\limits_{i_2i_3 i_4\in N_0^{3} } |a_{1i_2 i_3i_4}|+\sum\limits_{i_2i_3i_4\in N_2^{3} \atop\delta_{1i_2 i_3i_4} = 0} |a_{1i_2i_3i_4}| \right) + \sum\limits_{i_2i_3i_4\in N_3^{3} }\max\limits_{j\in \{i_2, i_3, i_4\}} \frac{tP_{j}(\mathcal {A}) }{|a_{jjj j}|} |a_{1i_2i_3i_4}|\right] \\ & = & \frac{18}{18-16}\left[ \frac{1}{9}(12+0)+\frac{15}{17} \times\frac{1}{15}\times 6 \right] = \frac{258}{17} < 16 = |a_{1111}|. \end{array}$

Therefore, from Theorem $5$ , we have that $\mathcal {A}$ is positive definite, that is, $f(x)$ is positive definite.

5. Conclusions

In this paper, we given some inequalities to identify whether a tensor is an $\mathcal {H}$ -tensor, which was also used to identify the positive definiteness of an even degree homogeneous polynomial $f(x)\equiv\mathcal{A}x^{m}$ . These inequalities were expressed in terms of the elements of $\mathcal{A}$ , so they can be checked easily.

Acknowledgments

The authors wish to give their sincere thanks to the anonymous referees for their valuable suggestions and helpful comments, which help improve the quality of the paper significantly. This work was supported by the National Natural Science Foundation of China (11861077), the Foundation of Science and Technology Department of Guizhou Province (20191161, 20181079), the Talent Growth Project Department of Guizhou Province ([2016]168) and the Research Foundation of Guizhou Minzu University (2019YB08).

Conflict of interest

The authors declare that they have no competing interests.

References

[1]	Luger K, Mäder AW, Richmond RK, et al. (1997) Crystal structure of the nucleosome core particle at 2.8 Å resolution. Nature 389: 251–260.
[2]	Yuan GC, Liu YJ, Dion MF, et al. (2005) Genome-scale identification of nucleosome positions in S. cerevisiae. Science 309: 626–630.
[3]	Tsankov AM, Thompson DA, Socha A, et al. (2010) The role of nucleosome positioning in the evolution of gene regulation. PLOS Biol 8: e1000414. doi: 10.1371/journal.pbio.1000414
[4]	Huebert DJ, Kuan PF, Keleş S, et al. (2012) Dynamic changes in nucleosome occupancy are not predictive of gene expression in dynamics but are linked to transcription and chromatin regulators. Mol Cell Biol 32: 1645–1653. doi: 10.1128/MCB.06170-11
[5]	Small EC, Xi L, Wang JP, et al. (2014) Single-cell nucleosome mapping reveals the molecular basis of gene expression heterogeneity. Proc Natl Acad Sci USA 111: E2462–E2471. doi: 10.1073/pnas.1400517111
[6]	Nishida H (2012) Conservation of nucleosome positions in duplicated and orthologous gene pairs. Scientific World J 2012: 298174.
[7]	Yoshida M, Horinouchi S, Beppu T (1995) Trichostatin A and trapoxin: novel chemical probes for the role of histone acetylation in chromatin structure and function. Bioessays 17: 423–430. doi: 10.1002/bies.950170510
[8]	Nishida H, Motoyama T, Suzuki Y, et al. (2010) Genome-wide maps of mononucleosomes and dinucleosomes containing hyperacetylated histones of Aspergillus fumigatus. PLOS One 5: e9916. doi: 10.1371/journal.pone.0009916
[9]	Li B, Workman JL (2007) The role of chromatin during transcription. Cell 128: 707–719. doi: 10.1016/j.cell.2007.01.015
[10]	Yamauchi K, Kondo S, Hamamoto M, et al. (2016) Genome-wide maps of nucleosomes of the trichostatin A treated and untreated archiascomycetous yeast Saitoella complicata. AIMS Microbiol 2: 69–91. doi: 10.3934/microbiol.2016.1.69
[11]	Nishida H, Sugiyama J (1994) Archiascomycetes: detection of a major new linage within the Ascomycota. Mycoscience 35: 361–366. doi: 10.1007/BF02268506
[12]	Liu Y, Leigh JW, Brinkmann H, et al. (2009) Phylogenomic analyses support the monophyly of Taphrinomycotina, including Schizosaccharomyces fission yeasts. Mol Biol Evol 26: 27–34.
[13]	Yabe I, Horiuchi KI, Nakahara K, et al. (1999) Patch clamp studies on V-type ATPase of vacuolar membrane of haploid Saccharomyces cerevisiae. J Biol Chem 274: 34903–34910. doi: 10.1074/jbc.274.49.34903
[14]	Fukudomi T, Kotani T, Miyakawa I (2011) A simple method for culture and stable maintenance of giant spheroplasts from the yeast Saccharomyces cerevisiae. J Gen Appl Microbiol 57: 177–182. doi: 10.2323/jgam.57.177
[15]	Takahashi S, Takayanagi A, Takahashi Y, et al. (2016) Comparison of transcriptomes of enlarged spheroplasts of Erythrobacter litoralis and Lelliottia amnigena. AIMS Microbiol 2: 152–189. doi: 10.3934/microbiol.2016.2.152

This article has been cited by:

1.	Dongjian Bai, Feng Wang, New Criterions-Based H-Tensors for Testing the Positive Definiteness of Multivariate Homogeneous Forms, 2022, 10, 2227-7390, 2416, 10.3390/math10142416
2.	鹏程赵, New Criterions for H-Tensors and Its Applications, 2022, 11, 2324-7991, 5727, 10.12677/AAM.2022.118604
3.	Wenbin Gong, Yan Li, Weiting Duan, Tao Wang, Yaqiang Wang, New iterative schemes for identifying strong $\mathcal{H}$ -tensors and their applications, 2025, 0, 1547-5816, 0, 10.3934/jimo.2025050

Reader Comments

Your name:*

Email:*
© 2017 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Microbiology

2.7 7.0

Metrics

Article views(5040) PDF downloads(768) Cited by(0)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(2) / Tables(1)

AIMS Microbiology

Changes in nucleosome formation at gene promoters in the archiascomycetous yeast Saitoella complicata

Related Papers:

Abstract

1. Introduction

2. Preliminaries

3. Criteria for identifying $\mathcal {H}$ -tensors

4. An application: the positive definiteness of homogeneous polynomial forms

5. Conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Microbiology

Changes in nucleosome formation at gene promoters in the archiascomycetous yeast Saitoella complicata

Related Papers:

Abstract

1. Introduction

2. Preliminaries

3. Criteria for identifying H \mathcal {H} -tensors

4. An application: the positive definiteness of homogeneous polynomial forms

5. Conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

3. Criteria for identifying $\mathcal {H}$ -tensors