The expansivity and sensitivity of the set-valued discrete dynamical systems

1.   Introduction

Discrete dynamical systems use iterative functions to model dynamic changes in both natural and engineering contexts. Within these systems, chaotic systems form a distinctive category, notable for their sensitivity to initial conditions, which is often summarized by the adage "small discrepancies lead to significant divergences" ^[1].

Based on whether the iterative mapping varies, dynamical systems can be divided into two categories: autonomous dynamical systems (abbreviated as ADDSs) ^[2] and non-autonomous dynamical systems (abbreviated as NDDSs) ^[3]. ADDSs were initially the primary focus of the study. They feature invariant evolutionary rules, with their behavior dictated by the constant equation $x_{n+1} = f(x_n)$, reflecting a process dependent exclusively on the state. In contrast, NDDSs adapt to time-dependent changes such as daily and seasonal variations, placing them at the forefront of research into dynamic processes. Expansivity, characterized by a system's acute sensitivity to initial conditions, is a pivotal concept in the study of dynamical systems, thoroughly examined in references ^[4,5]. This concept has evolved into various broader forms such as $n$-expansivity, $\aleph_0$-expansivity, continuous expansivity, and sparse expansivity, which are discussed in detail by ^{[6,7,8,9,10,11,12]}.

Sensitivity in chaos theory, on the other hand, deals with how dynamical systems respond over time. The sensitivity of dynamical systems is discussed in ^{[13,14,15,16,17]}, while the concept of Li-Yorke sensitivity is elaborated in ^[18,19,20]. The study of $(\mathcal{H}(X), \bar{f}_{1, \infty})$ (a non-autonomous set-valued discrete dynamical system) has emerged as a significant advancement in understanding the behaviors of complex systems. These systems are characterized by mappings between sets rather than mere point-to-point transitions and have become a crucial area of research. Their dynamic properties such as transitivity and chaotic behavior have been scrutinized in ^{[21,22,23,24]}. Discussions on various chaotic dynamics in set-valued systems can be found in ^{[25,26,27,28]}, with specific focus on the chaotic properties associated with the Furstenberg families detailed in ^[29,30]. Furthermore, their topological entropy is explored in ^{[31,32,33,34]}.

In section 3 of this article, we delve into various expansivities of the space $(\mathcal{H}(X), \bar{f}_{1, \infty})$. Moving to section 4, the discussion shifts to examining a range of sensitivities that manifest within the framework of $(\mathcal{H}(X), \bar{f}_{1, \infty})$. Section 5 focuses on analyzing the interplay between expansivity and sensitivity. Section 6 further extends the exploration to include the concept of topological conjugacy, specifically applied to $(\mathcal{H}(X), \bar{f}_{1, \infty})$.

2.   Preliminaries

In mathematical terms, an NDDS is a compact metric space $X$ with a series of time-dependent maps $f_{n}: X \rightarrow X$, defining $(X, f_{1, \infty})$. The orbit of $x$ is

where $f^{n}_1 = f_{n} \circ \cdots \circ f_{1}$ for $n \geq 1$, and $f^{0}_1$ serves as the identity.

Let $\mathcal{H}(X)$ denote the collection of all compact and non-empty subsets in $X$. Given $A, B \in \mathcal{H}(X)$, the Hausdorff metric between them is designated as

For $A \in \mathcal{H}(X)$, the $\epsilon$-ball in the $d_\mathcal{H}$ is denoted as $B(A, \epsilon)$. The dilation by $\delta$ of the set $A$ is defined by

Consider a set-valued NDDS governed by $(\bar{f}_{1, \infty}, \mathcal{H}(X))$, with state evolution,

To enhance the rigor of the analysis, this study ensures that the sequence $(\bar{f}_{1, \infty}, \mathcal{H}(X))$ preserves the topological properties such as continuity, compactness, and openness, and each $f_n$ is a homeomorphism.

Definition 2.1. (^[21]) Let $C$ be a subset of $X$, defining the extension of $C$ within $\mathcal{H}(X)$ as

Lemma 2.1. Let $C$ be a subset of $X$. The following properties are established.

(1) The set $e(C)$ is non-empty if and only if $C$ is non-empty;

(2) $e(C)$ forms an open subset within $\mathcal{H}(X)$ when $A$ itself is open in $X$;

(3) $e(C \cap D) = e(C) \cap e(D)$;

(4) $\bar{f}_i(e(C)) \subseteq e(\bar{f}_i(C))$ with $i = 1, 2, 3...$;

(5) The operation $\overline{f_1^n} = \bar{f}_1^n$ holds for all $n$ in $\mathbb{N}$.

Proof. The argument for this lemma closely mirrors that presented for Lemma 3.5 in ^[21].

Theorem 2.1. If $(f_{1, \infty}, X)$ exhibits uniform continuity, it follows that $(\bar{f}_{1, \infty}, \mathcal{H}(X))$ also maintains uniform continuity.

Proof. Since $X$ is compact and each $f_n$ is uniformly continuous, consider all $\epsilon > 0$. There exists a $\delta > 0$ such that for each $x, y \in X$ and $n\in \mathbb{N}$, if $d(x, y) < \delta$, then $d(f_n(x), f_n(y)) < \epsilon$. For any compact sets $A, B$ within $\mathcal{H}(X)$, we calculate the following formulation for the Hausdorff distance between $\bar{f}_n(A)$ and $\bar{f}_n(B)$.

Given $\epsilon>0$, select $\delta>0$ due to the uniform continuity of $\bar{f}_{1, \infty}$. If $d_\mathcal{H}(A, B) < \delta$, then for every $a \in A$ and $n\in \mathbb{N}$, one can find a $b \in B: d(a, b) < \delta$ and consequently,

Since $a$ can take any point in $A$, this demonstrates that

Similarly, for every $b \in B$, one can find an $a \in A$ that satisfies

This demonstrates that

Combining the results

it is easy to obtain that

which shows that $\bar{f}_n$ maintains uniform continuity across $\mathcal{H}(X)$.

3.   Expansivity

Definition 3.1. (^[8,10,11,27]) A map sequence (or system $(X, f_{1, \infty})$) is said to be

(1) expansive if there exists a sequence of real constants $\{\lambda_n\}_{n = 1}^\infty$ with each $\lambda_n > 1 (n\in \mathbb{N})$ such that, for all $x, y \in X$ and for each $n \in \mathbb{N}$,

(2) positively expansive if an expansivity constant $\rho > 0$ is found such that, for any two distinct points $x, y$ in $X$, there exists an $n \in \mathbb{N}$ that satisfies

(3) n-expansive if a constant $c > 0$ is designated as an $n$-expansivity constant, whereby for each $x \in X$, the set $\{y \in X : d(f_{1}^i(x), f_{1}^i(y)) \leq c, i \in \mathbb{N}\}$ contains no more than $n$ elements.

(4) $\aleph_0$-expansive if a constant $c > 0$ (designated as an $\aleph_0$-expansivity constant) exists such that for any $x \in X$, the set $\{y \in X : d(f_{1}^i(x), f_{1}^i(y)) \leq c, i \in \mathbb{N}\}$ is countable.

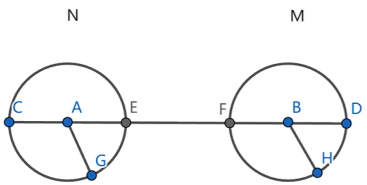
Lemma 3.1. Let $x$ and $y$ be two distinct points in the space $X$, and $d(x, y) = \delta > 0$. Then for any $\epsilon > 0$, $d_\mathcal{H}(B_\epsilon(\{x\}), B_\epsilon(\{y\})) = \delta$.

For this, a simple example in the two-dimensional plane can be given (see Figure 1). Consider two circles with the same radius ($AG = BH = \delta$), and centers are designated as $A$ and $B$, respectively. The distance between $A$ and $B$ is $\epsilon$ units. The points $C$, $A$, $E$, $F$, $B$, and $D$ lie on the same straight line.

Now, let $X$ be a two-dimensional space with $x = A$ and $y = B$. According to our assumption, $d(x, y) = d(A, B) = \delta$. In accordance with the defined properties of the $d_\mathcal{H}$ and the given illustration, one can readily derive that the $d_\mathcal{H}$ between $B_\epsilon(x)$ and $B_\epsilon(y)$ is

Since the radii of the two circles are the same, then $CF = ED = \delta.$ Hence, $d_\mathcal{H}(B_\epsilon(\{x\}), B_\epsilon(\{y\})) = \delta$.

Theorem 3.1. ${f}_{1, \infty}$ is expansive for space $X$ if and only if $\bar{f}_{1, \infty}$ is expansive for the space $\mathcal{H}(X)$.

Proof. (Necessity) Assume that $f_{1, \infty}$ is expansive for the space $X$. For any two sets $A, B \in \mathcal{H}(X)$, the images under $f_n(n \in \mathbb{N})$ are denoted by $\bar{f}_n(A)$ and $\bar{f}_n(B)$. In accordance with the definition of the $d_\mathcal{H}$, one has

By the expansivity of $f_{1, \infty}$, for each $a \in A$ and $b \in B$, one finds that

Therefore,

which implies

so

This completes the proof that $\bar{f}_{1, \infty}$ is expansive for $\mathcal{H}(X)$ endowed with the $d_\mathcal{H}$.

(Sufficiency) Let us posit a sequence of real constants $\{\lambda_n\}_{n = 1}^{\infty}$ with $\lambda_n > 1$ for all $n \in \mathbb{N}$ such that $\bar{f}_{1, \infty}$ is expansive, that is, for any two sets $A, B \in \mathcal{H}(X)$ and for every $n \in \mathbb{N}$,

Based on the expansivity of the system $\bar{f}_{1, \infty}$ for two distinct sets $x, y \in X$, consider them as single-element sets in $\mathcal{H}(X)$. In terms of the $d_\mathcal{H}$ definition, $d_\mathcal{H}(\{x\}, \{y\}) = d(x, y)$. Since $\bar{f}_{1\infty}$ is expansive,

This implies that

which reduces to

Hence, $f_{1, \infty}$ is expansive.

Remark. $\bar{f}_{1, \infty}$ being $n$-expansive with constant $c$ does not necessarily imply that ${f}_{1, \infty}$ is $n$-expansive with the same constant.

In fact, if $\bar{f}_{1, \infty}$ is $n$-expansive, for any $x \in X$, consider $A_x = \{x\}$. By the $n$-expansivity, for each $x \in X$ and $i \in \mathbb{N}$, there exist infinitely many points $y \in X$ such that $d(f_i(x), f_i(y)) \leq c$. Hence ${f}_{1, \infty}$ is not $n$-expansive with constant $c$.

However, since the set-valued system acts on finite compact subsets, let

thus, if $\bar{f}_{1, \infty}$ is $n$-expansive, one can infer that ${f}_{1, \infty}$ is also $n$-expansive.

Theorem 3.2. If $(\mathcal{H}_{F}(X), \bar{f}_{1, \infty})$ is $n$-expansive, then $X, ({f}_{1, \infty})$ is $n'$-expansive for some $n'\geq n$.

Proof. $(\mathcal{H}_{F}(X), \bar{f}_{1, \infty})$ exhibits $n$-expansivity. For any $x \in X$, consider $A_x = \{x\}$. Since $n$-expansivity implies that for every $A \in \mathcal{H}_F(X)$, there exist at most $n (n \in \mathbb{N})$ finite compact subsets $\{M\}_1^n \in \mathcal{H}_F(X)$ such that

For $A_x$, this means that there exist at most $n (n \in \mathbb{N})$ finite compact subsets $\{M\}_1^n \in \mathcal{H}_F(X)$ characterized by

If the maximum number of points in all $M$ is $m$, let $n' = m \cdot n$, and one can find that for each $x \in X$, there are at most $n'$ points $\{y\}_1^{n'} \in X$ whereby

This demonstrates ${f}_{1, \infty}$ is $n'$-sensitive with the constant $c$.

It should be noted that the converse of Theorem 3.2 is not valid for the reason that $n$-expansivity for $f_{1, \infty}$ does not imply $n$-expansivity for $\bar{f}_{1, \infty}$.

In fact, given $(X, f_{1, \infty})$ is $n$-expansive, then, for all $x \in X$,

Being $n$-expansive implies that for every $x \in X$, at most $n (n \in \mathbb{N})$ finite points $\{y\}_1^n \in X$ exist whereby

Let us denote these $n$ points as $\{y\}_1^n$. For any $y_j$, it holds that

However, for $A_x = x$, it is possible to find infinitely many sets $\{B_1, B_2\ldots \}$ such that

Therefore, $\bar{f}_{1, \infty}$ is not $n$-expansive.

Theorem 3.3. If $(\mathcal{H}_{F}(X), \bar{f}_{1, \infty})$ is $\aleph_0$-expansive with expansivity constant $c$, then $(X, f_{1, \infty})$ is also $\aleph_0$-expansive with the same constant.

Proof. Assume that $(\mathcal{H}_{F}(X), \bar{f}_{1, \infty})$ is $\aleph_0$-expansive. For each point $x \in X$, let us define the singleton set $A_x = \{x\}$ in $\mathcal{H}(X)$. Due to the $\aleph_0$-expansivity of $(\mathcal{H}_{F}(X), \bar{f}_{1, \infty})$, the collection of sets

is at most countable.

Continuing further, write the countable sets in $\bar{N}_c(A_x)$ as $\{B_m\}_{i = m}^{\infty}$, and for any given $m\in \mathbb{N}$, since $B_m$ is a finite compact subset, the number of points in $B_m$ is finite.

Let the cardinality of $\{B_m\}_{i = 1}^{\infty}$ be $\aleph'$, and the maximum cardinality of $B_m(m\in \mathbb{N})$ be $\aleph''$. Let $\aleph = \aleph' \times \aleph''$.

Since both $\aleph'$ and $\aleph''$ are countable, then $\aleph$ is also countable. Therefore, in point systems, one can only find some countable number of points $y_1, y_2, \ldots$ such that the elements in

are fewer than $\aleph$.

Hence, the system $(X, f_{1, \infty})$ is $\aleph_0$-expansive.

Unfortunately, similar to $n$-expansivity, even if $(\mathcal{H}_{F}(X), \bar{f}_{1, \infty})$ is $\aleph_0$-expansive, it still does not imply that $f_{1, \infty}$ is $\aleph_0$-expansive. The proof is analogous to the case with $n$-expansivity.

Theorem 3.4. If $(\mathcal{H}(X), \bar{f}_{1, \infty})$ is positively expansive, then $(X, f_{1, \infty})$ is also positively expansive.

Proof. Assume that $\bar{f}_{1, \infty}$ on the compact set space $\mathcal{H}(X)$ is positively expansive, meaning that a positive constant $\rho$ can be identified such that, for any two distinct compact sets $A, B \in \mathcal{H}(X)$, there exists some $n \in \mathbb{N}$ whereby

where $d_\mathcal{H}$ denotes the Hausdorff distance.

To prove that $f_{1, \infty}$ is also positively expansive on $X$, we consider any two distinct points $x, y \in X$. The $\epsilon$-neighborhoods of $x$ and $y$ are denoted by $N(x, \epsilon)$ and $N(y, \epsilon)$. Let $\overline{N(x, \epsilon)} = K_x$ and $\overline{N(y, \epsilon)} = K_y$ denote their closures, respectively.

By the positive expansivity of the set-valued system, for these two compact spaces $K_x, K_y$, an $n_1 \in \mathbb{N}$ can be found for which

Due to the special structure of $K_x, K_y$, applying Lemma 3.1 one can get that

Due to the continuous nature of $\bar{f}_{1, \infty}$, then

Thus, $(X, f_{1, \infty})$ is also positively expansive.

Theorem 3.5. If $f_{1, \infty}$ is expansive, then $f_{1, \infty}$ being positively expansive implies $\bar{f}_{1, \infty}$ is also positively expansive.

Proof. Consider any two distinct non-empty compact sets $A, B \in \mathcal{H}(X)$. For any $a \in A$ and $b \in B$, by the positive expansivity of $f_{1, \infty}$, there exists an $n_0 \in \mathbb{N}$, such that

Since $f_{1, \infty}$ is also expansive, for any $n_1 \in \mathbb{N}: n_1 > n_0$, one has

Then, it can be concluded that

Hence, one can find a suitable $n \in \mathbb{N}$ ensuring that, for any two different points $x, y \in X$, regardless of how $x$ and $y$ vary, there exists some $n \in \mathbb{N}$ ensuring that

According to the defined properties of the $d_\mathcal{H}$ and the fact that $f_1^n$ is continuous, then, for all two non-empty compact sets, given the continuity of $\bar{f}_1^n$, it consequently follows that

This means that $\bar{f}_{1, \infty}$ is positively expansive.

4.   Sensitivity

Definition 4.1. (^[16]) The mapping sequence (or $(X, f_{1, \infty})$) is called sensitive if there exists an $\eta > 0$ such that, for any $a \in X$ and any $\epsilon>0$, one can find $b \in B(a, \epsilon)$ and $n \in \mathbb{N}$ satisfying $d(f^n_1(a), f^n_1(b)) > \eta$.

Definition 4.2. (^[14]) The sequence of mappings (or system $(X, f_{1, \infty})$) is designated as collectively sensitive if there exists an $\eta > 0$ such that, for each $\epsilon>0$ and every set of distinct finite points $a_1, a_2, \ldots, a_k$ within $X$, there are $k$ distinct points $b_1, b_2, \ldots, b_k \in X$ meeting the following conditions:

(1) $d(a_i, b_i) < \epsilon$ for each $1 \leq i \leq k$;

(2) there exists $1 \leq i_0, j_0 \leq k$ and an integer greater than zero $n \in \mathbb{N}$ whereby

Definition 4.3. (^[18]) $f_{1, \infty}$ is defined as Li-Yorke sensitive if an $\epsilon > 0$ exists such that, for every $x \in X$ and any neighborhood $U(x)$ of $x$, there can be found $y \in U(x)$ where the pair $(x, y)$ is proximal but its orbit is frequently at least $\epsilon$ apart. That is, the subsequent conditions are satisfied:

and

Definition 4.4. (^[14]) A set $S \subseteq \mathbb{N}$ is said to be

(1) syndetic if $k$ is a positive integer that can be established so that for any $j \in \mathbb{N}$, the intersection $\{j, j + 1, \ldots, j + k\} \cap S$ is non-empty.

(2) thick if, for each $n \in \mathbb{N}$, one can identify an $m \in \mathbb{N}$ such that the set $\{m, m+1, m+2, \ldots, m+n\}$ forms a subset of $S$.

(3) thickly syndetic if, for every $l \in \mathbb{N}$, an $m \in \mathbb{N}$ can be found such that $\{m + j : 0 \leq j \leq l\} \subseteq S$, where $S$ is syndetic.

Denote

for any non-empty open subset $V$ in $X$.

Definition 4.5. Consider an NDDS $(X, f_{1, \infty})$. The system can exhibit various types of sensitivity, and $(X, f_{1, \infty})$ is said to be

(1) multi-sensitive if a $\delta > 0$, designated as a multi-sensitivity constant, can be identified, whereby for any $n \in \mathbb{N}$ and each group of non-empty open subsets $V_1, V_2, \ldots, V_n$ in $X$, the intersection $\bigcap_{i = 1}^{n} N_{f_{1, \infty}}(V_i, \delta)$ remains non-empty;

(2) syndetically sensitive if for some $\delta > 0$, it holds that for every non-empty open subset $V$ of $X$, the set $N_{f_{1, \infty}}(V, \delta)$ is syndetic for some $\delta > 0$;

(3) thickly sensitive if for any non-empty open subset $V$ of $X$, the set $N_{f_{1, \infty}}(V, \delta)$ is thick for some $\delta > 0$;

(4) thickly syndetically sensitive if for each non-empty open subset $V$ of $X$, the set $N_{f_{1, \infty}}(V, \delta)$ is thickly syndetic for some $\delta > 0$;

(5) cofinitely sensitive if there exists a constant $\delta > 0$, termed a sensitive constant, whereby for every non-empty relative open subset $V$ within $X$, there is an $N \geq 1$ such that $N_{f_{1, \infty}}(V, \delta)$ includes $[N, +\infty) \cap \mathbb{N}$.

Theorem 4.1. The system $(\mathcal{H}(X), \bar{f}_{1, \infty})$ exhibits multi-sensitivity if and only if the system $(X, f_{1, \infty})$ demonstrates multi-sensitivity.

Proof. (Necessity) Consider every group of open subsets that are not empty $V_1, V_2, \ldots, V_n$ in $X$. For each $V_i$, $e(V_i)$ represents the ensemble of all compact subsets within $V_i$. Assume $(\mathcal{H}(X), \bar{f}_{1, \infty})$ exhibits multi-sensitivity with sensitivity constant $\delta > 0$. Then, for every collection of open sets $e(V_1), e(V_2), \ldots, e(V_n)$ in $\mathcal{H}(X)$, one can identify an $n$ in $\mathbb{N}$ whereby

So for any $i = 1, \ldots, n$, there are two sets $M, N\in V_i$ whereby

According to the definition of $d_\mathcal{H}$ and the continuity of $\bar{f}_{1, \infty}$, one can certainly find two points $x \in M \subset V_i$, $y \in N \subset V_i$ whereby

Thus, regarding any collection of open sets $V_1, V_2, \ldots, V_n$ in $X$, there exists an $n \in \mathbb{N}$ such that the intersection

Therefore, $f_{1, \infty}$ is also multi-sensitive.

(Sufficiency) Assume that $(X, f_{1, \infty})$ exhibits multi-sensitivity. That is, regarding any assembly of open subsets that are not empty $\{V_i\}_{i = 1}^{m}$ in $X$, one can identify an $n \in \mathbb{N}$ such that for at least one $i$, there are points $x, y \in V_i$ satisfying $d(f_1^n(x), f_1^n(y)) > \delta$.

For points $x, y$ in $V_i$ that satisfy $d(f_1^n(x), f_1^n(y)) > \delta$, construct $K_x$ and $K_y$ as follows

(1) Choose $\epsilon$-neighborhoods $B_\epsilon(x)$ and $B_\epsilon(y)$ in $e(V_i)$, where $\epsilon$ is small enough such that $\overline{B_\epsilon(x)}$ and $\overline{B_\epsilon(y)}$ are entirely contained within $e(V_i)$. Let $\overline{B_\epsilon(x)} = K_x$ and $\overline{B_\epsilon(y)} = K_y$.

(2) Due to the multi-sensitivity of $f_{1, \infty}$, for the chosen $n \in \mathbb{N}$, one has

Let $d(x, y) = \delta_1 \ (\delta_1 > \delta)$, then by the continuity of $\bar{f}_{1, \infty}$ and Lemma 3.1, one can easily obtain that

This means that

Therefore, $\bar{f}_{1, \infty}$ is also demonstrated to be multi-sensitive.

Theorem 4.2. The system $(\mathcal{H}(X), \bar{f}_{1, \infty})$ demonstrates syndetic sensitivity with a specified sensitivity constant $\delta > 0$ if and only if the system $(X, f_{1, \infty})$ also exhibits syndetic sensitivity.

Proof. (Necessity) Assuming the system $(\mathcal{H}(X), \bar{f}_{1, \infty})$ is syndetically sensitive, for some $\delta > 0$, it holds that for each open subset $V \subseteq X$ that is not empty, the set

is syndetic, where $e(V) = \{ K \in \mathcal{H}(X) : K \subseteq V \}$.

For any $k \in N_{\bar{f}_{1, \infty}}(e(V), \delta)$, define $\{x\} = K_1 \subset V$, then there exists a $K_2 \subset V$ such that

By the compactness of $V$ and the continuity of $\bar{f}_{1, \infty}$, there exists a $y_0 \in K_2$ such that:

Therefore

is syndetic. Hence $(X, f_{1, \infty})$ is syndetically sensitive.

(Sufficiency) Assuming that the system $(X, f_{1, \infty})$ exhibits syndetic sensitivity, it follows that a constant $\delta > 0$ exists, ensuring that for every non-empty open set $V \subset X$, the set

is syndetic. This means that a $k$ can be found within $\mathbb{N}$ such that for each $j\in\mathbb{N}$, the intersection $\{j, j + 1, \ldots, j + k\} \cap N_{f_{1, \infty}}(V, \delta)$ is non-empty.

For each index $n \in N_{f_{1, \infty}}(V, \delta)$, there are points $x, y \in V$ for which $d(f_1^n(x), f_1^n(y)) > \delta$. To demonstrate syndetic sensitivity of $(\mathcal{H}(X), \bar{f}_{1, \infty})$, consider any open set that is not empty $e(V)$ in $\mathcal{H}(X)$. Let $e(V) = \{ K \in \mathcal{H}(X) : K \subseteq V \}$. Thus, for the compact sets $K_x = \{x\}$ and $K_y = \{y\}$, one has

Given the same $k$, one can observe that the set $\{j, j+1, \ldots, j+k\} \cap N_{\bar{f}_{1, \infty}}(e(U), \delta)$ is not empty. Consequently, $N_{\bar{f}_{1, \infty}}(e(U), \delta)$ is syndetic, which confirms that $(\mathcal{H}(X), \bar{f}_{1, \infty})$ exhibits syndetic sensitivity.

Theorem 4.3. The system $(\mathcal{H}(X), \bar{f}_{1, \infty})$ is thickly sensitive if and only if the system $(X, f_{1, \infty})$ is also thickly sensitive.

Proof. (Necessity) Assume that the set-valued system $(\mathcal{H}(X), \bar{f}_{1, \infty})$ is thickly sensitive with a sensitivity constant $\delta > 0$, and it implies that for any open set $e(V) = \{K \in \mathcal{H}(X) : K \subset V\}$ in $\mathcal{H}(X)$, the set

is thick.

To prove that the point dynamical system $(X, f_{1, \infty})$ is also thickly sensitive, we consider any open set $V \subset X$.

For all pairs $x, y$ in set $V$, should there exist an $n \in \mathbb{N}$ such that $d(f_1^n(x), f_1^n(y)) > \delta$, given $K_x = \{x\}$ and $K_y = \{y\}$ as elements in $e(V)$, for every $n \in N_{\bar{f}_{1, \infty}}(e(V), \delta)$, one has

This ensures that

is thick. So $(X, f_{1, \infty})$ exhibits thick sensitivity as well.

(Sufficiency) The methodology of this proof closely mirrors that of necessity.

Theorem 4.4. The system $(\mathcal{H}(X), \bar{f}_{1, \infty})$ exhibits thickly syndetic sensitivity if and only if the system $(X, f_{1, \infty})$ exhibits thickly syndetic sensitivity behavior.

Proof. (Necessity) Assume that the system $(\mathcal{H}(X), \bar{f}_{1, \infty})$ is thickly syndetically sensitive and equipped with a sensitivity constant $\delta > 0$. For every open set $V \subset X$, the corresponding open set $e(V) \in \mathcal{H}(X)$.

The thickly syndetically sensitive nature of $(\mathcal{H}(X), \bar{f}_{1, \infty})$ implies that for every length $l \in \mathbb{N}$, a natural number $m$ can be identified such that, for each $k$ within the set $\{m, m+1, \ldots, m+l\}$, $N_{\bar{f}_{1, \infty}}(e(V), \delta)$ is syndetic. Specifically, there exist two subsets $M, N \in e(V)$ such that, for any $k \in \{m, m+1, \ldots, m+l\}$,

By the definition of $d_\mathcal{H}$ and the continuity of $\bar{f}_{1, \infty}$, for the aforementioned $k$, there exist points $x \in M \subset V$, $y \in N \subset V$ ensuring that

By the arbitrariness of $k$,

where $N_{f_{1, \infty}}(V, \delta)$ demonstrates syndetic properties. Consequently, the system $(X, f_{1, \infty})$ exhibits thickly syndetic sensitivity.

(Sufficiency) Given that the system $(X, f_{1, \infty})$ exhibits thickly syndetic sensitivity, for each open subset $V$ of $X$, one has a sensitivity constant $\delta > 0$. This implies that there exists a thickly syndetic set $S \subseteq \mathbb{N}$ for which, there are points $x, y \in V$ satisfying $d(f_1^n(x), f_1^n(y)) > \delta$ for every $n \in S$.

To construct corresponding compact sets $K_1$ and $K_2$ in $e(V) = \{K \in \mathcal{H}(X) : K \subseteq V\}$, we select small enough neighborhoods around $x$ and $y$, denoted as $B_\epsilon(x)$ and $B_\epsilon(y)$, and take their closures to form $K_1 = \overline{B_\epsilon(x)}$ and $K_2 = \overline{B_\epsilon(y)}$.

By the compactness of $K_1$ and $K_2$, along with the continuity of $\bar{f}_{1, \infty}$, according to Lemma 3.1 and the definition of $d_\mathcal{H}$, it is straightforward to deduce that

For every $n \in S$, it holds that

which satisfies the condition of thick syndetic sensitivity for $(\mathcal{H}(X), \bar{f}_{1, \infty})$.

Theorem 4.5. $(X, f_{1, \infty})$ is cofinitely sensitive if and only if the system $(\mathcal{H}(X), \bar{f}_{1, \infty})$ exhibits the same property.

Proof. The proof method follows closely with that of Theorem 4.4.

Theorem 4.6. The system $(\mathcal{H}(X), \bar{f}_{1, \infty})$ exhibits collective sensitivity with a sensitivity constant $\eta > 0$ if and only if the system $(X, f_{1, \infty})$ also exhibits collective sensitivity with the same sensitivity constant.

Proof. (Necessity) Assume that $(\mathcal{H}(X), \bar{f}_{1, \infty})$ exhibits collective sensitivity, implying that for each $\epsilon>0$, and any finite collection of compact sets $\{A_1, A_2, \ldots, A_k\}$ in $\mathcal{H}(X)$, there exists a corresponding collection $\{B_1, B_2, \ldots, B_k\}$ in $\mathcal{H}(X)$ satisfying:

(1) $d_\mathcal{H}(A_i, B_i) < \epsilon$ holds for every $1 \leq i \leq k$,

(2) there exist indices $1 \leq i_0, j_0 \leq k$ and $n \in \mathbb{N}$ such that $d_\mathcal{H}(\bar{f}^n_1(A_{i_0}), \bar{f}^n_1(B_{j_0})) > \eta$.

Considering any finite distinct points $\{a_1, a_2, \ldots, a_k\}$ in $X$, where $a_i\in A_i$ for all $1 \leq i \leq k$, for each point $a_i$, select a point $b_i\in B_i$ satisfying $d(a_i, b_i) < \epsilon \; \text{for all}\; 1 \leq i \leq k.$

If there exist indices $1 \leq i_1, j_1 \leq k$ and $n \in \mathbb{N}$ such that

then for $B(x_{i_1}, \delta) = A_{i_1}$ and $B(y_{j_1}, \delta) = B_{j_1}$, one has

Thus,

(1) each pair $(a_i, b_i)$ satisfies $d(a_i, b_i) < \epsilon$ for all $1 \leq i \leq k$;

(2) there exists at least one pair of indices $1 \leq i_0, j_0 \leq k$ and an $n \in \mathbb{N}$ such that

Therefore, $(X, f_{1, \infty})$ exhibits collective sensitivity.

(Sufficiency) For all $\epsilon>0$ and each finite collection of compact sets $\{A_1, A_2, \ldots, A_k\}$ in $\mathcal{H}(X)$, there exists a corresponding collection $\{B_1, B_2, \ldots, B_k\}$ in $\mathcal{H}(X)$ satisfying

According to the definition of the $d_\mathcal{H}$, one can find $a_i\in A_i$ and $b_i\in B_i$ $(1 \leq i \leq k)$ satisfying

Since $f_{1, \infty}$ is collectively sensitive, then one can ascertain the existence of at least one pair of indices $1 \leq i_0, j_0 \leq k$ and an $n \in \mathbb{N}$ such that

Due to the continuity of $f_{1, \infty}$ and the compactness of $A_{i_0}$ and $B_{j_0}$ for any $m \in \mathbb{N}$, there always exist fixed $x \in A_{i_0}$ and $y \in B_{j_0}$ such that

Therefore, there always exists an $m_0 \in \mathbb{N}$ such that

That is to say,

Thus, $(\mathcal{H}(X), \bar{f}_{1, \infty})$ also exhibits collective sensitivity.

Theorem 4.7. If the system $(\mathcal{H}(X), \bar{f}_{1, \infty})$ exhibits Li-Yorke sensitivity, then the system $(X, f_{1, \infty})$ is also Li-Yorke sensitive.

Proof. Assume that $(\mathcal{H}(X), \bar{f}_{1, \infty})$ demonstrates Li-Yorke sensitivity. Then, for any given point $y \in X$ and for each $\delta > 0$, one can find a compact set $K \subset X$ such that the $d_\mathcal{H}$ $H(\{y\}, K)$ is less than $\delta$, and the pair $(\{y\}, K)$ forms an $\epsilon$-Li-Yorke sensitive pair under the map sequence $\bar{f}_{1, \infty}$.

This implies that, for any $\epsilon > 0$ and point $y \in X$, the Li-Yorke sensitivity of $\bar{f}_{1, \infty}$ guarantees the existence of a point $y'$ within $X$ such that the orbit of $y'$ intermittently approaches and recedes from that of $x$, that is,

and

Consequently, the system $(X, f_{1, \infty})$ exhibits Li-Yorke sensitivity.

The example below demonstrates that Li-Yorke sensitivity in $f_{1, \infty}$ does not automatically confer Li-Yorke sensitivity in $\bar{f}_{1, \infty}$, if $X$ is a linear space containing $\frac{2}{3}$ of the closed convex subsets therein. Let

Example 4.1. Examine the mapping of the interval $f: [0, 1] \to [0, 1]$ defined by

This function is commonly referred to as the tent map. It is topologically transitive on $(0, 1)$, contains periodic points, and exhibits Li-Yorke sensitivity. For every point $x \in (0, 1)$, an interval neighborhood $U(x)$ can be found whereby, for some $y \in U(x)$, the duo $(x, y)$ constitutes a Li-Yorke pair. That is,

and

However, the point $x = \frac{2}{3}$ is a fixed point of $f$. Now, let $K$, a subset that is both compact and convex, reside within $[0, 1]$, which contains the fixed point $\frac{2}{3}$. It follows that if $K$, a compact and convex subset, is contained within the interval $[0, 1]$, consequently, $\bar{f}(K)$, resulting from the function application, remains a subset that is both compact and convex within the interval $[0, 1]$ and contains the fixed point $\frac{2}{3}$. Therefore, $\bar{f}$ can extend as a map $\bar{f}: \mathcal{H}_c([0, 1]) \to \mathcal{H}_c([0, 1])$, where $\mathcal{H}_c([0, 1])$ denotes the assembly of all subsets that are both compact and convex of the interval $[0, 1]$. $\mathcal{H}^{\frac{2}{3}}_c([0, 1])$ denotes the collection of all subsets of $[0, 1]$ that are compact and convex that contain the point $\frac{2}{3}$.

For the compact convex set $\{\frac{2}{3}\} \in \mathcal{H}^{\frac{2}{3}}_c([0, 1])$ and its neighborhood $B(\{\frac{2}{3}\}, \frac{1}{5})$, for any $M \in B(\{\frac{2}{3}\}, \frac{1}{5})$ containing $\frac{2}{3}$ and $i \in \mathbb{N}$, one has that

fails to meet one of the conditions for Li-Yorke sensitivity. Specifically, it does not satisfy the requirement that for any $\epsilon>0$,

Hence, $\bar{f} \big|_{\mathcal{H}^{\frac{2}{3}}_c([0, 1])}: \mathcal{H}^{\frac{2}{3}}_c([0, 1])$$\rightarrow$ $\mathcal{H}^{\frac{2}{3}}_c([0, 1])$ is not Li-Yorke sensitive.

5.   The relationship between expansive and sensitive

In ADDSs, expansive implies sensitive (see Theorem 5.1).

Theorem 5.1. $f$ being expansive implies that $\bar{f}$ is sensitive.

Proof. Define $f: X \rightarrow X$ as an expansive function within the metric space $(X, d)$. Then, for each pair of distinct points $x, y$ in $X$, the distance between their images under $f$ expands by a factor $\lambda > 1$, i.e.,

For any point $x \in X$ and any $\epsilon > 0$, it is possible to identify a point $y \in X$ and a natural number $n \in \mathbb{N}$ such that

For a given $\delta > 0$, by choosing an $n \in \mathbb{N}$ sufficiently large to satisfy $\lambda^n \epsilon > \delta$, it follows that

This demonstrates that $f$ is sensitive. In fact, since the expansivity guarantees that after $n$ iterations, the separation between the trajectories of $x$ and $y$ exceeds $\delta$, specifically,

Hence, $f$ exhibits sensitivity.

However, in NDDSs, expansivity does not necessarily imply sensitivity. Here is a counterexample.

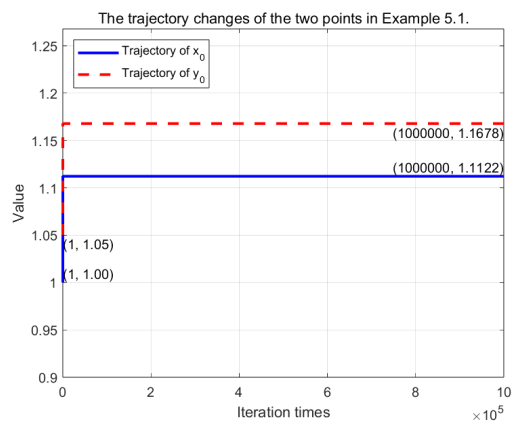
Example 5.1. Consider the metric space $X = \mathbb{R}$ equipped with the metric $d(a, b) = \mid a - b\mid$, a non-autonomous system is structured with a sequence of functions $\{f_n\}$, where $f_n(x) = (1 + \frac{1}{10^n})x$ $(n\in \mathbb{N})$. The expansivity factor for this system is $\lambda_n = 1 + \frac{1}{10^n}$, which satisfies the expansivity definition.

As shown in the images (see Figure 2), after 1,000,000 iterations, the distance between the trajectories of two points $x_0 = 1.00$ and $y_0 = 1.05$ has not significantly increased. This indicates that the function lacks sensitivity.

This example illustrates that despite the system being expansive by definition, the particular nature of the non-autonomous expansivity factors $\{\lambda_n\}$ approaching 1 prevents the system from exhibiting sensitivity to initial conditions in the long term. For more complex NDDSs, this conclusion needs to be slightly modified so that $\lambda_n > 1$ does not converge to 1 as time varies. Even though the function changes over time, expansivity still implies sensitivity. Below is a simple proof (Theorem 5.1$'$).

Theorem 5.1$'$. Let $\lambda_n > 1$ and assume it does not converge to 1. If the dynamical system $f_{1, \infty}$ is expansive, then it is also sensitive.

Proof. The premise that $\lambda_n > 1$ and does not converge to 1 guarantees that for each pair of points $x, y$ within $X$, a certain condition holds, such as $d(x, y) < \epsilon$ for some $\epsilon > 0$. For all $n \in \mathbb{N}$, one has

Based on the proof approach for ADDSs, we have proved the sensitivity.

This property can be naturally applied to $(\mathcal{H}(X), \bar{f}_{1, \infty})$.

Theorem 5.2. Suppose that the expansivity constant $\lambda_n > 1$ does not converge to 1. If $\bar{f}_{1, \infty}$ is expansive under this condition, then $\bar{f}_{1, \infty}$ is also sensitive.

Proof. Suppose there exists a series of real constants $\{\lambda_n\}_{n = 1}^{\infty}$ where $\lambda_n > 1$ for all $n \in \mathbb{N}$, and that the map $\bar{f}_{1, \infty}$ is expansive in the context that for each pair of sets $A$ and $B$ that belong to $\mathcal{H}(X)$, and for all $n \in \mathbb{N}$,

To show sensitivity, let $\epsilon > 0$ and consider any set $A \in \mathcal{H}(X)$. Choose any set $B \in \mathcal{H}(X)$ such that the $d_\mathcal{H}$ $D(A, B) < \epsilon$. Given the expansivity condition, for any given $\eta > 0$, one can find a suitable $n_0$ such that

ensuring that

thereby proving that $\bar{f}_{1, \infty}$ is sensitive.

6.   Topological conjugacy

Topological conjugacy is crucial in dynamical systems analysis because it preserves key properties such as periodicity, chaoticity, and stability.

Definition 6.1. Let $(X, d_1)$ and $(Y, d_2)$ each be defined as a metric space. Consider sequences $f_{1, \infty}$ and $g_{1, \infty}$ of time-varying homeomorphisms on $X$ and $Y$, respectively. $f_{1, \infty}$ and $g_{1, \infty}$ are called conjugate with respect to a homeomorphism $T$ if there exists a homeomorphism $T$ from $X$ to $Y$ such that

for all $n \in \mathbb{N}$.

Conjugation can naturally be expanded to include the context of set values.

Suppose $f_{1, \infty}$ and $g_{1, \infty}$ are sequences of mappings where $\bar{f}_{1, \infty}: \mathcal{H}(X) \rightarrow \mathcal{H}(X)$ and $\bar{g}_{1, \infty}: \mathcal{H}(Y) \rightarrow \mathcal{H}(Y)$.

The sequences are said to be conjugate with respect to a set-valued homeomorphism $\mathcal{T}$, satisfying

for all $A \in \mathcal{H}(X)$ and for all $n \in \mathbb{N}$.

Theorem 6.1. Suppose $\bar{f}_{1, \infty}$ and $\bar{g}_{1, \infty}$ are mappings on $\mathcal{H}(X)$ and $\mathcal{H}(Y)$, conjugate via $\mathcal{T}$. If the function $\bar{f}_{1, \infty}$ exhibits expansivity, then the function $\bar{g}_{1, \infty}$ also exhibits expansivity, and vice versa.

Proof. Given that $\bar{f}_{1, \infty}$ and $\bar{g}_{1, \infty}$ are conjugate, a homeomorphism $\mathcal{T}$ can be found ensuring that $\mathcal{T} \circ \bar{f}_n = \bar{g}_n \circ \mathcal{T}$ holds for every $n \in \mathbb{N}$. This relationship further implies that the inverse $\mathcal{T}^{-1}$ satisfies $\mathcal{T}^{-1} \circ \bar{g}_n = \bar{f}_n \circ \mathcal{T}^{-1}$ for each $n \in \mathbb{N}$, demonstrating the bijective nature of the conjugacy.

(Necessity) Assume the function $\bar{f}_{1, \infty}$ exhibits expansivity on the compact sets $\mathcal{H}(X)$, characterized by an expansive constant $\epsilon>0$. Then for each pair of distinct sets $A$ and $B$ within $\mathcal{H}(X)$, an $n \in \mathbb{N}$ can be identified such that $d_1(\bar{f}_n(A), \bar{f}_n(B))>\epsilon$.

Given two distinct sets $C, D \in \mathcal{H}(Y)$, since $\mathcal{T}$ is a homeomorphism, then $\mathcal{T}^{-1}(C)$ and $\mathcal{T}^{-1}(D)$ are distinct sets in $\mathcal{H}(X)$. By the expansivity of $\bar{f}_{1, \infty}$, for some $n \in \mathbb{N}$, it holds that

According to the definition of conjugacy, for all $n \in \mathbb{N}$, one has

This implies that

Since $\mathcal{T}$ is a bijective homeomorphism, applying $\mathcal{T}$ and $\mathcal{T}^{-1}$ to $\bar{f}_n(\mathcal{T}^{-1}(C))$ and $\bar{f}_n(\mathcal{T}^{-1}(D))$ in $(Y, d_2)$ yields

This proves that $\bar{g}_{1, \infty}$ is expansive on $\mathcal{H}(Y)$.

(Sufficiency) Conversely, if $\bar{g}_{1, \infty}$ is expansive on $\mathcal{H}(Y)$, there exists $\epsilon>0$ ensuring for distinct $C, D \in \mathcal{H}(Y)$, there is an $n \in \mathbb{Z}$ such that

By the conjugacy definition,

which implies

Since $\mathcal{T}$ is a continuous bijection, applying $\mathcal{T}$ and $\mathcal{T}^{-1}$ to $\bar{g}_n(\mathcal{T}(A))$ and $\bar{g}_n(\mathcal{T}(B))$ in $(X, d_1)$, one can get

Thus, the expansivity of $\bar{g}_{1, \infty}$ on $Y$ ensures that of $\bar{f}_{1, \infty}$ on $\mathcal{H}(X)$.

Theorem 6.2. Let $\bar{f}_{1, \infty}$ and $\bar{g}_{1, \infty}$ be on $\mathcal{H}(X)$ and $\mathcal{H}(Y)$, conjugate via $\mathcal{T}$. If $\bar{g}_{1, \infty}$ is sensitive to initial conditions, then so is $\bar{g}_{1, \infty}$, and vice versa.

Proof. We are given that $\bar{f}_{1, \infty}$ and $\bar{g}_{1, \infty}$ are conjugate via $\mathcal{T}$, indicating $\bar{g}_1^n = \mathcal{T} \bar{f}_1^n \mathcal{T}^{-1}$ for all $n \in \mathbb{N}$.

(Necessity) Assume $\delta>0$ for the sensitivity of $\bar{f}_{1, \infty}$ on $\mathcal{H}(X)$. For any $A\in\mathcal{H}(X)$ and any $\epsilon>0$, one can find a set $B \in \mathcal{H}(X)$ such that $d_{H_1}(A, B) < \epsilon$.

Given the uniform continuity of $\mathcal{T}$, one can select $\epsilon'>0$ sufficiently small enough such that $d_{H_2}(\mathcal{T}(A), \mathcal{T}(B)) < \epsilon$. For this pair $A$ and $B$, it is possible to identify an $n$ in $\mathbb{N}$ whereby

Applying the conjugacy mapping $\mathcal{T}$, one has

thus demonstrating that $\bar{g}_{1, \infty}$ also exhibits sensitivity.

(Sufficiency) Conversely, assume $\delta>0$ for the sensitivity of $\bar{g}_{1, \infty}$ on $\mathcal{H}(Y)$. For any $C \in \mathcal{H}(Y)$ and any $\epsilon>0$, one can find a set $D \in \mathcal{H}(Y)$ such that $d_{H_2}(C, D) < \epsilon$.

Given the uniform continuity of $\mathcal{T}^{-1}$, one can choose $\epsilon'>0$ small enough such that $d_{H_1}(\mathcal{T}^{-1}(C), \mathcal{T}^{-1}(D)) < \epsilon$. For this pair $C$ and $D$, one can identify an $n$ in $\mathbb{N}$ whereby

Applying the inverse conjugacy mapping $\mathcal{T}^{-1}$, one has

thus demonstrating that $\bar{f}_{1, \infty}$ also exhibits sensitivity on $\mathcal{H}(X)$.

The conjugate invariance of sensitivity and expansivity in set-valued systems are proved above. Similarly, for the chaos properties mentioned, such as positive expansivity, $n$-expansivity, and $\aleph_0$-expansivity, as well as multi-sensitivity and syndetic sensitivity, one can also demonstrate using the same method that these properties remain invariant under topological conjugacy. This demonstrates a fundamental characteristic of dynamical systems, showing that certain complex behaviors, when transformed through a topological conjugacy, preserve their intrinsic chaotic nature. This invariance under topological conjugacy is crucial for understanding the robustness and universality of chaotic dynamics across different mathematical models.

7.   Conclusions

This study explores the expansive and sensitive properties of $(\bar{f}_{1, \infty}, \mathcal{H}(X))$, detailing through comprehensive analysis how various forms of expansivity and sensitivity, from basic expansivity to complex concepts like $\aleph_0$-expansivity and multi-sensitivity, fundamentally characterize the dynamical behavior and shed light on the underlying topological and dynamical complexities. Our investigations reveal the intricate relationship between expansivity and sensitivity in NDDSs, showing that under certain conditions, expansivity also implies sensitivity. Additionally, we extend the concept of topological conjugacy to $(\bar{f}_{1, \infty}, \mathcal{H}(X))$, demonstrating that dynamical properties are preserved under topologically conjugate transformations.

Author contributions

J.Z.(Zhou): conceptualization, validation, writing original draft; T.L.(Lu): writing review and editing, supervision, funding acquisition; J. Z.(Zhao): formal analysis, investigation. All authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by Sichuan Science and Technology Program (No. 2023NSFSC0070), the Scientific Research and Innovation Team Program of Sichuan University of Science and Engineering (No. SUSE652B002), and the Graduate Student Innovation Fundings (No. Y2024335).

Conflict of interest

The authors declare no conflicts of interest regarding the publication of this paper.