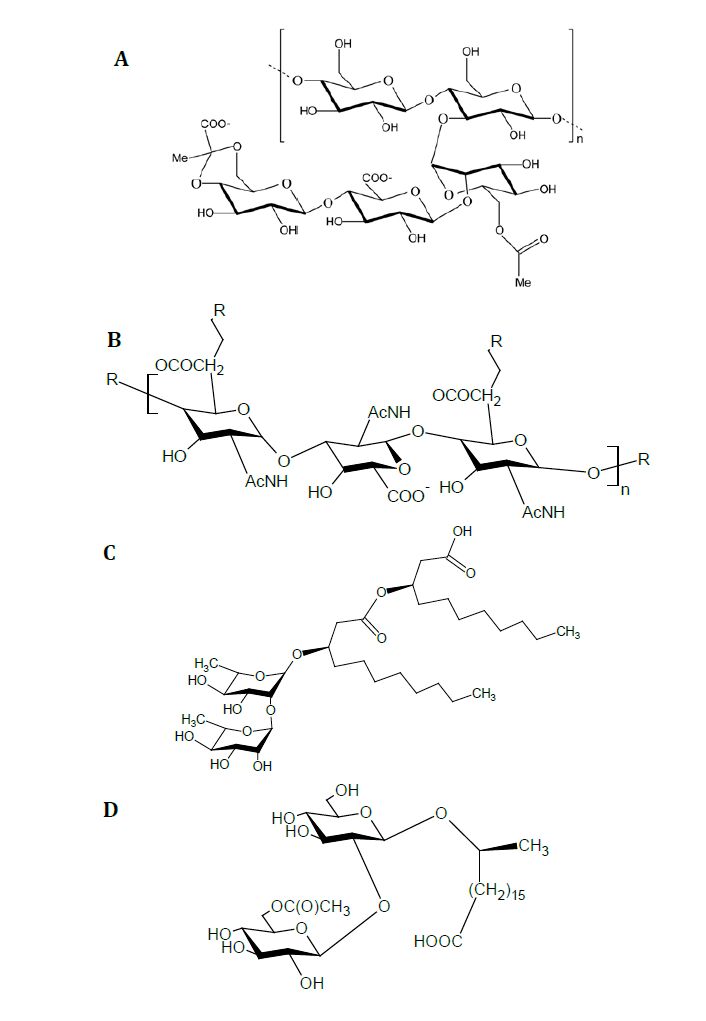
Surface-active agents are amphiphilic chemicals that are used in almost every sector of modern industry, the bulk of which are produced by organo-chemical synthesis. Those produced from biological sources (biosurfactants and bioemulsifiers), however, have gained increasing interest in recent years due to their wide structural and functional diversity, lower toxicities and high biodegradability, compared to their chemically-synthesised counterparts. This review aims to present a general overview on surface-active agents, including their classification, where new types of these biomolecules may lay awaiting discovery, and some of the main bottlenecks for their industrial-scale production. In particular, the marine environment is highlighted as a largely untapped source for discovering new types of surface-active agents. Marine bacteria, especially those living associated with micro-algae (eukaryotic phytoplankton), are a highly promising source of polymeric surface-active agents with potential biotechnological applications. The high uronic acids content of these macromolecules has been linked to conferring them with amphiphilic qualities, and their high structural diversity and polyanionic nature endows them with the potential to exhibit a wide range of functional diversity. Production yields (e.g. by fermentation) for most microbial surface-active agents have often been too low to meet the volume demands of industry, and this principally remains as the most important bottleneck for their further commercial development. However, new developments in recombinant and synthetic biology approaches can offer significant promise to alleviate this bottleneck. This review highlights a particular biotope in the marine environment that offers promise for discovering novel surface-active biomolecules, and gives a general overview on specific areas that researchers and the industry could focus work towards increasing the production yields of microbial surface-active agents.
1.
Introduction
1.1. State of play
The global climate crisis has brought ever increasing attention to the need to rapidly decarbonise the world's economies, with one of the major sectors of concern being energy production. Much of the focus of the energy transition has to date been on wind and solar energy. However, as the use of these technologies expands, an increasing awareness of the inherent limits that intermittency imposes, and their reliance on grid scale storage systems to pick up the slack, has led many to seek out clean, renewable energy sources which are also capable of providing the kind of baseload power supply that traditional fossil fuel plants excel at.
One of the most promising answers to this need is deep geothermal energy, which taps into a source of effectively limitless heat within the Earth. This energy has been used for centuries on a small scale, and in recent decades has been utilised for electrical power production in volcanic regions such as Iceland and New Zealand. These very high-enthalpy resources can be thought of as relatively low-hanging fruit, with geothermal struggling to become established in other parts of the world, where only low-enthalpy resources exist in the shallow subsurface and deeper, higher-enthalpy resources are too difficult to exploit. Geothermal energy is presently only a minor contributor to global heat and power generation, and only saw a growth in installed capacity of 2.3% from 1990 to 2016, according to the IEA [1].
This lack of development stems from some key limitations of the technology, which have only recently begun to be addressed. Historically, closed-loop geothermal energy systems have been restricted to low-enthalpy resources, except where high temperatures are present close to the surface. Traditional drilling techniques have not been able to create lateral wellbores at the kind of depths where temperatures become high enough for power production at average geothermal gradients. Existing deep geothermal systems have an open-loop design with at least two vertical wells injecting into and abstracting water from either confined saline aquifers or fractured basement rock, with direct interaction between the water and the rock formations at depth [2]. This direct interaction brings many risks, such as contamination of potable groundwater aquifers, mineral scaling of the wells [3], and where hydraulic fracturing is employed to create an enhanced geothermal system (EGS), the inducement of potentially damaging seismic events [4]. In addition to the environmental hazards, there is serious financial risk when sinking exploratory wells as there are several documented instances of huge sums being spent on drilling wells which fail to bring sufficient geothermal brine to the surface. This was the case with the Newcastle Science Central project [5] for example, and also the Geretsried site in Germany, about which more later.
According to [6], 98% of the Earth's available geothermal energy is present in Hot Dry Rock or Hot Sedimentary Aquifers. EGS in these systems is dependent on the development of suitable groundwater flow conditions through fracturing technology. Closed-loop systems could allow access to these resources without the need for fracturing.
This study evaluates the Eavor-Loop, a deep closed-loop geothermal energy system (DCLGS) which uses a water-based, "benign" heat-bearing fluid. The risk of groundwater contamination in this design is very low, even if there were to be a leak from the loop [7], although exactly what the fluid composition referred to by the terms "water-based" and "benign" is, is not publicly available.
The boom in unconventional hydrocarbon extraction, which occurred mainly in North America, fuelled some major advances in drilling technology, particularly in the capability to drill lateral wells, which are necessary to reach the most inaccessible hydrocarbon deposits. Eavor Technologies Inc. claims it will leverage these advances to build the first scalable, dispatchable, zero-emission baseload power plants. The power plant at the surface will operate an organic Rankine cycle which exchanges heat from the abstracted geothermal brine into an organic compound such as perfluoropentane. These compounds have a much lower boiling point than water, allowing turbines to be driven by rapidly boiling and expanding the fluid before recondensing it to be recycled. The cycle is roughly 13% efficient at converting thermal to gross electrical power when the input temperature is 150 ℃ [8]. Higher efficiencies can be achieved with higher input temperatures.
Eavor state the advantages of DCLGS as being unbound to particular hydrogeological conditions, and as eventually outperforming both fossil-fuel plants and wind or solar energy with grid storage, all while requiring a much smaller surface footprint [9]. In fact, geothermal in general has been shown to have what Matuszewska et al. [10] term the smallest "relative aggregate lifecycle footprint" of any energy source, taking into account total land area used for power plants but also mining of fuel and materials for example. Eavor have suggested that they can produce fluid from their system up to a maximum temperature of 180 ℃ [11]. Another key selling point of the Eavor-Loop is that its power is dispatchable, meaning that it can readily follow the energy demands of the grid by simply controlling the flow rate into the system [12]. A clear sign of confidence in DCLGS technology and an indication of repositioning in the oil and gas industry came in early 2021, when it was announced that Chevron and BP now held shares in Eavor Technologies Ltd [13].
1.2. The Eavor-Lite demonstration plant
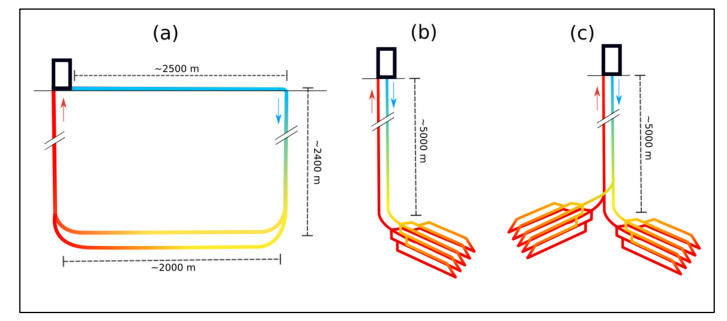
Eavor has already built and operated a small-scale version of their system at a demonstration plant close to their base of operations in Alberta, Canada. The installation is named Eavor-Lite (Figure 1a) and was completed in 2020. The Eavor-Lite plant bares a pared-down design compared to the full commercial proposals, featuring just two lateral sections connecting to two vertical wells at a separation of around 2000 m at a depth of 2400 m. All of the central technological principles of the Eavor-Loop have been successfully proven at this site, while avoiding the high capital expenditure required to develop a full-scale commercial power plant. Although the Eavor-Lite is a scaled-down version of the technology, it was designed with the capability to generate enough thermal energy to heat the equivalent of 16,000 homes. The key technological features which have been proven are the ability to drill and successfully intersect the lateral wellbore sections with the vertical wells using magnetic ranging technology, the use of the proprietary Rock-Pipe sealing system to line the uncased lateral sections as they are drilled, and the inducing of a thermosiphon effect in the system [14]. Establishing a thermosiphon means that unlike other geothermal systems which can expend a significant amount of their power output and money on pumping, the Eavor-Loop can operate without what are termed parasitic pumping costs [15]. Although the specifications of the Rock-Pipe system are not available, Van Horn et al. [9] report that alongside developments in drilling technology in recent years, advances have been made in the development of cement materials which can operate under immense heat and pressure conditions with reduced likelihood of failure over traditional cements. One advance in pipe sealing technology has been the use of a robot to deploy the cement with another robot following which quickly cures the cement using UV light. As to whether these methods are being used by Eavor, that information is not available.
1.3. Geretsried, the first commercial plant
A failed EGS project in Geretsried in the state of Bavaria, Germany has provided Eavor with an opportunity to develop their first commercial power plant. Two attempts were made at this site to produce geothermal brine to the surface, but flow rates were found to be too low, leaving the company responsible with two very expensive dry wells. Eavor's proposal is to rehabilitate the site by converting it into an Eavor-Loop. They are currently looking at a number of other unproductive well sites which could benefit from retrofitting with DCLGS technology. Development licenses have already been granted for Geretsried, with construction slated to commence in early 2022. An initial power output of 10 MW is expected from the site, later to be increased by drilling additional lateral arrays (Figure 1c) [16]. Eavor have stated that by adding further arrays, they hope to eventually increase the total output of the site to 200 MW. This expansion is projected to cost €2.4bn [13], which is significantly more expensive per MW than other renewable energy sources but doesn't necessitate the construction of grid storage solutions to combat intermittency.
One of the driving factors behind Eavor's decision to locate its first commercial power plant in Germany is the opportunity to benefit from the Renewable Energy Sources Act. This government policy guarantees a feed-in tariff of over €200 per MWh to encourage the development of clean renewable energy sources in the country. This highlights the need for favourable regulatory frameworks to be in place if emerging clean energy technologies are to be able to gain a foothold in the market.
Each Eavor-Loop is projected to produce 3–8 MW of power, with up to 10 such arrays being placed around shared vertical wells from a single drill site. They state that stacking the lateral arrays in this way would mean up to 50 km of pipework while maintaining the same small surface footprint [17]. This configuration with folded multilateral sections and closely spaced vertical wells is called the "James Joyce" design (Figure 1b), named for the pub in which it was conceived, rather than for its labyrinthine design.
1.4. Existing literature on DCLGS
The novelty of DCLGS technology means that literature which deals specifically with geothermal systems of the kind dealt with in this study is quite scarce. One of the most relevant published studies is by Yuan et al. [18], who used two different analytical methods to model the output of a DCLGS, also based on the Eavor-Loop, namely Duhamel's convolution theory method and the natural coupling method. They modelled the system over 30 years, experimenting with various parameters to find those which held most sway over the system performance. Their conclusion was that thermal conductivity is the primary factor determining output and the extent of thermal interference between the laterals. They modelled different spacings between laterals and different flow rates, demonstrating that the efficiency of the system can be greatly improved by optimising these parameters. Their model with 10 lateral wells gave a sustained output of 9–11 MW over a 30-year period. A different study by Van Oort et al. [3] suggests that approximately 25–30 MW could be produced from a single DCGLS borehole.
Geoscientists from Eavor themselves have produced a paper about the characterisation of the subsurface, based around the Eavor-Lite demonstration plant in Alberta, Canada. They explain how the geophysical and geological techniques used for hydrocarbon prospecting can readily be applied to the assessment of suitability for DCLGS. Methods of gaining essential knowledge of the subsurface such as the geothermal gradient, thermal conductivity and rock characterisation are shown to be well established in the oil and gas sector. The placement of Eavor-Lite in an active hydrocarbon play is therefore no coincidence.
Van Horn et al. [9] produced a review of the state of DCGLS in conjunction with GreenFire, a company based in California, USA which is designing DCLGS that uses supercritical CO2 as the heat-bearing fluid. This paper highlights the potential of using closed-loop systems to retrofit unproductive oil and gas wells, as well as failed conventional geothermal wells. They note that the World Bank has stated that globally around 22% of all geothermal wells that have been drilled have failed. If DCLGS can be used to retrofit these wells and make them productive, then this could go some way to recouping sunk costs while also avoiding the increasing costs incurred by abandoning unproductive wells. Another application is that, in addition to electrical power production, DCGLS is an ideal candidate to provide precise, high pressure heat flow to industrial processes such as hydrogen production or lithium extraction from brines, both of which are very high-value processes with increasing importance to the energy market [9].
The previously mentioned GreenFire Energy Inc. have produced their own report on experiments carried out for the California Energy Commission in 2019 [7]. They constructed a field-scale test of their closed-loop design using supercritical CO2 as the heat-bearing fluid. The experiments were designed to validate a numerical modelling method and showed good agreement. Like Eavor, GreenFire are now seeking investment and are in talks to begin commercial roll-out of their technology in the near future.
By contrast to the rather optimistic forecasts of the previously mentioned papers, McClure [19], writing for hydraulic fracturing simulator ResFrac, insists that DCLGS is guaranteed to fail because it relies solely on heat conduction through the rock without the aid of convection that EGS harnesses. By their calculation this means that the thermal transport through the rock is too slow for a sustained power output of any economically viable magnitude to be sustained over a period of years. This they claim is even the case when taking technological advances and lowering costs of drilling into account.
Although the effect of groundwater flow on the power output and thermal regime development in DCLGS has not been greatly studied, Tolooiyan and Hemmingway [20] have investigated this problem as it relates to single and multiple borehole heat exchangers. They too used the finite element method to model a scenario with groundwater flow and a control scenario with static groundwater, similarly to the approach taken in this study. They found that even modest flow rates around the boreholes could have a significant impact on output and thermal interaction between multiple boreholes. They conclude that the optimum orientation of the boreholes is perpendicular to the direction of groundwater flow, suggesting that if groundwater flow were a variable of concern to DCLGS, then orientation of wellbores may be a consideration when optimising the system design.
Wu et al. [21] created numerical models of a DCLGS design consisting of an injection well, a lateral well and a production well connected in a U-shaped configuration. They investigated the effects of varying a number of variables to test the impact on power output. Flow rates in increments ranging from 0.01 m3/s to 0.14 m3/s were tested and they found that at the beginning of the simulation, production temperatures peaked before rapidly falling to a level which was then more or less maintained for the 30-year duration of the simulation. Their results showed that the lower the injection flow rate, the lower the power output, but the higher the production temperatures achieved over time. Ultimately, they concluded that injection flow rate is the main controlling variable on the output performance of the system.
Wu et al. [21] also trialled various injection temperatures from 30 ℃ to 70 ℃ and found a similar trend to the flow rate. The lowest injection temperature produced the largest power output, due in theory to the greater temperature difference, but also saw the greatest cooling of the domain with the result that production temperatures rapidly fell and remained low for the rest of the 30-year run.
A study by Chen et al. [22] modelled what they term a deep enhanced U-tube borehole heat exchanger (EUBHE) system in OpenGeoSys and noted a decline in output over time, much like studies on DCLGS.
Wang et al. [16] propose a coaxial design which, like other models discussed, produces a significant zone of thermal drawdown around the wellbores. They found that after 30 years, the cooled region extended to 100 m away from the wells. Also similarly to other models, the initial power output is high but rapidly declines over the first year of operation. The rate of decline eventually levels off and then remains relatively stable over the next few years as it approaches an equilibrium with the heat flux. The effects of adding additional lateral sections is also discussed in this paper, and they found that when adding more than five laterals, the rate of increase in output reduced due to thermal interference between the laterals. This implies that an optimal number and arrangement of lateral wellbores could be defined.
1.5. Research questions
Here are the main research questions which we used to guide the shape of this study, along with a brief statement on the approach taken to answer each of them:
Q1—Are the power output claims realistic?
An approximation of the Eavor-Loop system is modelled to ascertain whether the 3–8 MW output claim for a single lateral array design is credible.
Q2—How does stacking additional lateral arrays affect power output?
A model is created with 10 lateral arrays and the total power output of the system is calculated. This value is compared against the output of the single array model.
Q3—What is the effect of groundwater flow on the performance of the system?
Two models are created, one with and one without groundwater flow. The power outputs of the two are compared over time.
Q4—Does controlling the flow rate make this a dispatchable technology?
A model is created which allows for the control of flow rate through a section of pipe. The effect of flow rate on power output over time is calculated. An accompanying model allows for the results of the controlled flow rate model to be tied into the other models.
2.
Methodology
2.1. The finite element method
This study employed the finite element method (FEM) to numerically model heat transport in and around the geothermal system. This was achieved by discretising the study domain into elements with increased density of elements, and therefore resolution of output, closer to the geothermal wells where changes are expected to be greatest. Changes in temperature and groundwater head were then calculated across these elements for each timestep in the simulation. The elements are defined by a mesh of nodes at which the new temperature and head values are output. The meshes were created for each model in the Gmsh software [23] by specifying the geometry of the domain and node density at each point. Polylines within the volume are used to represent the pipework [24]. These polylines can be assigned boundary conditions to specify temperature or head values and source terms to instruct the solver to add heat or water into the system at the adjacent nodes. The work of Chen et al. [22] was referenced when initially conceptualising the models. The differential equations used to calculate the node values were solved in the OpenGeoSys numerical simulation program. Model file manipulation was done via the graphical user interface GINA_OGS, which creates a visualisation of the model during construction and aids in the manipulation of FEM parameters.
Developing an FEM model necessitates the balancing of model size, and therefore simulation run-time, with accuracy of results. Increasing the density of nodes in the mesh introduces more degrees of freedom into the model, which will capture the behaviour of the processes with more fidelity. However, this added complexity increases the time needed to solve for every node in the model. Time and hardware constraints therefore place a limit on the size and density of a domain mesh.
Before arriving at the final models used in this study, several iterations were run with a reduced domain volume and varying mesh densities to check for stability in the simulation. Another stability consideration was the length of time-step which OpenGeoSys would solve for. In order to allow for the running of the simulations over a period of 10 years without extending the solve-time beyond what was practical, while also allowing for a relatively fine-grained view on the evolution of the system, a time-step of 1 day was used. The models were stable at this time-step size and varying it in the scaled-down iterations demonstrated that the results obtained at 1-day intervals were independent of variations in time-step, and that reducing the time-step size below 1 day did not result in any greater accuracy of results.
2.2. Governing equations
The first stage of processing done by OpenGeoSys is to calculate the groundwater flow within each discrete element of the model. In more specific terms, this is done by solving the following mass balance equation [25]:
where $ {S}_{s} $ is specific storage, $ p $ is pressure head, $ t $ is time, $ k $ is intrinsic permeability, $ \mu $ is fluid viscosity, $ \rho $ is fluid density, $ g $ is acceleration due to gravity, $ z $ is height above datum, and $ Q $ is flow rate.
The node values resulting from the solution of this equation can be used to derive flow velocities within the elements using interpolation. These velocities are then fed into the next stage of processing, which involves solving the following thermal energy balance equation [26]:
where $ c $ is the specific heat of the saturated rock, $ \rho $ is the rock density, $ T $ is temperature, $ t $ is time, $ {c}^{w} $ is the specific heat of the fluid, $ {\rho }^{w} $ is fluid density, $ \upsilon $ is flow velocity, $ D $ is the thermal diffusion dispersion tensor and $ {Q}_{T} $ is the heat source or sink.
The elements of the above conservation equations contain the following constitutive equations.
2.2.1. Fluid density ($ \mathrm{\rho } $)
The density of a typical saline groundwater is a function of temperature, pressure, and salinity, and can be expressed as follows [27]:
Where $ \psi $ is the reduced pressure, $ \tau $ is the inverse reduced temperature, $ p $ is pressure, $ R $ is the specific gas constant for pure water, $ T $ is temperature, and $ {g}_{s} $ is salinity.
2.2.2. Fluid dynamic viscosity ($ \mu $)
The viscosity of a groundwater fluid is also a function of temperature, pressure, and salinity. Wagner and Kruse [27] produced the following formulation for given ranges of pressure and temperature:
2.2.3. Specific heat capacity ($ {c}_{p} $)
Specific heat capacity is a function of pressure and temperature. Wagner and Kruse [27] formulated isobaric specific heat capacity for non-critical conditions in the following equation:
where
2.2.4. Thermal conductivity ($ \lambda $)
Thermal conductivity is defined by the equation $ \lambda = \rho {c}_{p}D $, where $ \rho $ is the material density, $ {c}_{p} $ is the isobaric specific heat capacity described above, and $ D $ is the thermal diffusivity.
These equations are used to determine static values in the simulation. This modelling method is not fully coupled between the processes of the reservoir and the wellbore, and the behaviour of the fluid in the wellbore is not modelled in this study.
2.3. Overview of model design
In order to address each of the research questions, we created a series of models based on a conceptual model for each scenario. Early iterations of the models were first created to fine tune the approach taken with the final models. These initial models began in 2 dimensions with greatly reduced scale, before being extended into 3-dimensional versions and then ultimately, the full-scale 3-dimensional models used in the study were created.
Models SLA (single lateral array model) and MLA (multiple lateral arrays model) were designed to approximate the maximum possible power output of the system by setting a constant temperature in the wells to simulate flushing with cool water. The first model, SLA, acts as the "baseline" model for evaluating the output potential of a single "James Joyce" Eavor-Loop type design. The next model, MLA, addresses the question of stacking additional multilateral arrays around shared vertical wells and the impact that this has on system power output.
The final pair of models, CF (controlled flow model) and FT (fixed temperature model), were designed to calculate an adjustment factor to these maximum values which can be used to attain a more realistic approximation of power output over time. These two models have identical 2-dimensional geometries representing a short length of pipe in a block of rock, except that CF models the injection of water at one end of the pipe at a constant temperature with an equal rate of extraction at the other end, whereas FT employs the same constant temperature method as SLA and MLA. These models were designed to allow a direct comparison between the power outputs of the two methods, the CF water injection method more accurately approximating the real-world conditions but being prohibitively complex to model on the scale of an entire geothermal system.
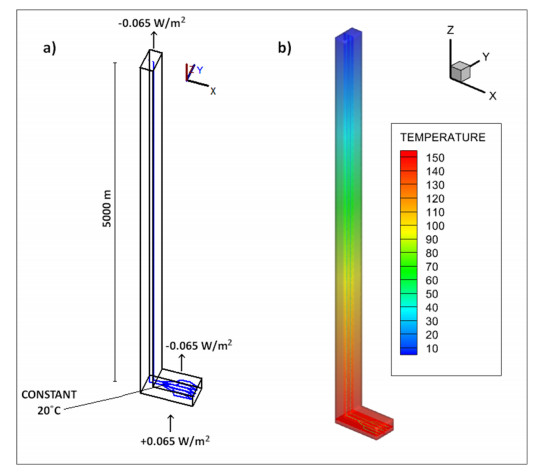
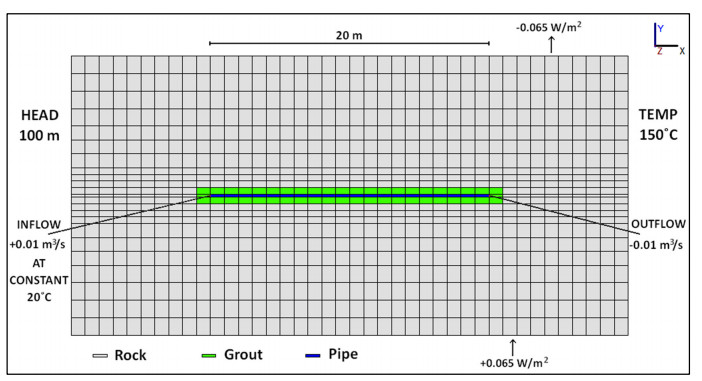
2.4. Model SLA—single lateral array (Q1)
The SLA model (Figure 2) is based on a single "James Joyce" Eavor-Loop design with two vertical wells placed 50 m apart and extending to a depth of 5000 m. At this depth, the injection well fans out horizontally into a five-tine multilateral array which folds back under itself before remerging and connecting into the production well. The dimensions of this model are based on comments made in Eavor press-releases [13] which suggested that they would be drilling up to 5 km depth and targeting temperatures of 150 ℃. For this and the following models, we therefore chose to use a geothermal gradient of 0.03 K/m (Figure 2b). In addition, we added source terms to replicate a constant geothermal heat flux of 0.065 W/m2 [28] into the system from the centre of the Earth, with an equal flux from the top of the model as though being radiated from the Earth's surface. This model has static groundwater with no hydraulic gradient across the domain.
The length of pipe in the multilateral sections is based on a statement from Eavor [17] that up to 10 lateral arrays (Eavor-Loops) could be added to the same vertical wells, amounting to 50,000 m of pipework in total. Subtracting the length of the two vertical wells and dividing the remainder by 10 suggested 4000 m of pipework in each multilateral section.
The entire domain was constructed from a 3-dimensional mesh with tetrahedral elements. The pipework sits within a block of rock which extends 50 m in each direction, including a "toe" section to accommodate the lateral array section.
The boundary condition which governs heat transport in this model is that all pipes are set at a constant 20 ℃. This causes cooling of the surrounding rock from its initial temperature, removing heat from the system. As the geothermal heat flux into and out of the model is net zero, the cooling around the pipes is the only source of net energy loss from the domain, allowing the calculation of the amount of energy transferred from the rock and "into" the pipes per second. We will describe the process of outputting and manipulating this data in more detail later.
The parameters assigned to the model were chosen to represent typical geological and hydraulic fluid properties which are likely to be encountered at depth. The full list of parameter values for the model are set out in Table 1.
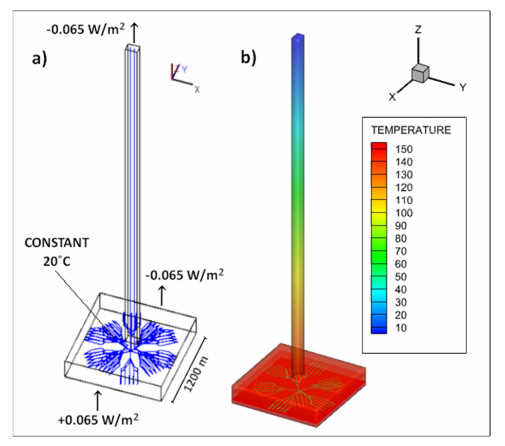
2.5. Model MLA - multiple lateral arrays (Q2)
In a press release [17], Eavor have claimed that up to 10 Eavor-Loops could be emplaced from a single drill location, all sharing the same vertical wells, when utilising the "James Joyce" design. To that effect, the MLA model was designed to evaluate the power output which could be achieved by adding 9 additional multilateral arrays (Eavor-Loops) to the single-array system modelled in SLA. This was achieved by duplicating the lateral section of the SLA pipework geometry and rotating the newly created arrays such that there are five arrays spaced evenly at 2π/5 radians separation. A second layer was created with a gap of 50 m above the first layer and was rotationally offset by π/5 radians. To accommodate this enlarged arrangement, the basal portion of the domain has a width of 1200 m. This configuration was designed to take advantage of the high temperatures at the deepest part of the domain, while also attempting to maximise spacing between the arrays to reduce the risk of excessive thermal interference between them.
As with model SLA, a boundary condition maintains the pipes at a constant 20 ℃ and a constant geothermal heat flux of 0.065 W/m2 (Figure 3a). The domain has a geothermal gradient of 0.03 K/m (Figure 3b). The parameters assigned to the model were chosen to represent typical geological and hydrothermal fluid properties which are likely to be encountered at depth. All of the model parameter values are set out in Table 2.
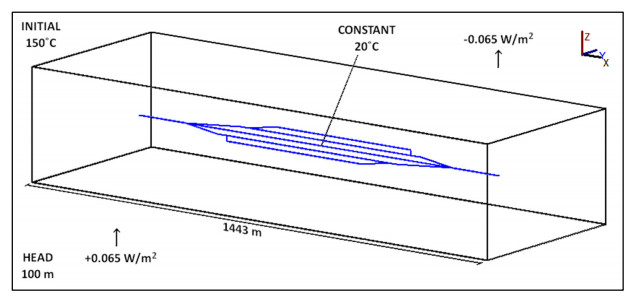
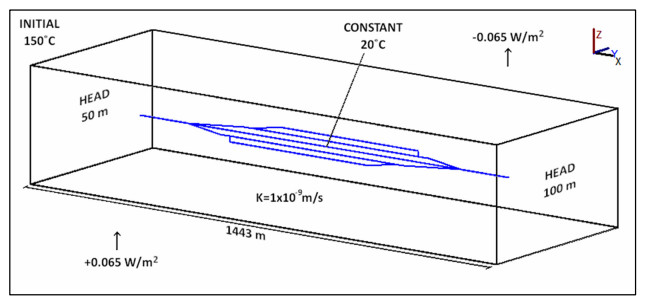
2.6. Models SG & FG—static vs flowing groundwater (Q3)
Part of Eavor's claim for their technology is that as it is a closed loop, it can be situated almost anywhere, independent of local geological considerations. While there is no direct contact between the heat-bearing fluid in the system and the groundwater, the thermal properties and movement of groundwater in the vicinity of the system may affect the transport of heat to the wells. These interactions have been examined in shallow ground source heat pump settings but there is scant literature on groundwater interactions with deep closed-loop systems. Models SG and FG were designed to investigate these interactions. These models have a flattened lateral array design, though it identical in dimensions to the folded "James Joyce" design used in models SLA and MLA. Similarly to models SA and MLA, these models have a constant heat flux through the domain and pipes set at a constant 20 ℃. Model SG has static groundwater (Figure 4) whereas FG has boundary conditions which set differing constant head values either side of the domain, creating a hydraulic gradient of 0.035, thus inducing groundwater flow (Figure 5). The hydraulic conductivity of the rock in these models is set to 1 × 10−6 m/s. This value is typical of fractured crystalline basement [29], but it is likely to be at the very top of the realistic range for 5 km depth. Work by Kuang and Jiao [30] suggests that intrinsic permeability, a major component of hydraulic conductivity, decreases with depth due to the increased confining pressure, which forces fractures to close.
The parameters assigned to the models were chosen to represent typical geological and hydraulic fluid properties which are likely to be encountered at depth. These values are set out in Table 3 for model SG and Table 4 for model FG.
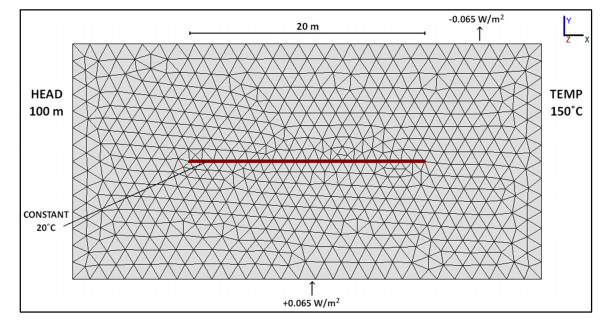
2.7. Model CF—controlled flow (Q4)
The constant well temperature boundary condition used in the previous models provides an upper limit of energy available to the pipes, given the conditions present in the models. Model CF (Figure 6) was designed with a different mechanism which attempts to create a more realistic simulation of heat transfer to the heat-bearing fluid within the pipes. This design comprises a 20 m length of pipe with a diameter of 0.2 m, as stated by Eavor [22]. The pipe section is assigned its own material group with a porosity of 1.0, i.e. 100% void space.
One end of the pipe section has an inflow of water at a constant 20 ℃, and the other end has an outflow at an equal flow rate. This model was run at three flow rates, 0.01 m3/s, 0.05 m3/s and 0.1 m3/s. Eavor have stated simply that their heat-bearing fluid is benign and water-based. For the purposes of this study, we have therefore assumed that its properties are similar enough to water that the simulation can operate with water without serious divergence in behaviour from Eavor's system.
Further, to best recreate the closed-loop conditions and prevent direct interaction between the heat-bearing fluid and the surrounding rock and groundwater, an additional material group was created to emulate the grout or "Rock-Pipe" which constitutes the wall of the pipe in the Eavor designs. The exact properties of this material have not been made public but for the purposes of this model, the grout is given an equal thermal conductivity to the rock and a very low hydraulic conductivity to prevent leakage.
The 20 m length of pipe in CF sits within a 2-dimensional slice of rock which extends 10 m away from the pipe in each direction. The model has a 2-dimensional structured rectangular mesh. The nodes within this mesh are regularly spaced at 1 m intervals in the x direction, and in the y dimension the spacing gets closer with proximity to the pipe.
The parameters assigned to the model were chosen to represent typical geological and fluid properties which are likely to be encountered at depth. The model parameter values are set out in Table 5.
2.8. Model FT—fixed temperature
The companion model to CF is FT (Figure 7). This model features identical dimensions and material properties to CF, but where CF has flow within a separate pipe material group, FT has a single 20 m polyline representing the same pipe section. This polyline has a boundary condition setting it at a constant temperature of 20 ℃, similarly to models SLA and MLA. Likewise, FT is constructed from an unstructured triangular 2-dimensional mesh, but with the same node spacing at the pipe to CF. The model parameter values are set out in Table 6.
2.9. Application of adjustment factor
Comparison of the outputs for models CF and FT allows for an adjustment factor to be derived. This factor is calculated by taking the difference of the mean power output of each model in watts. As the mechanism employed in CF is reasoned to give a more realistic estimate of actual output than that used in the other models, this adjustment factor is then applied to the maximum output values obtained in models SLA and MLA.
2.10. Data output and manipulation
All of these models have two types of data output. The first is a text file containing the total energy in joules for each material group, at each timestep. The second is a Tecplot.tec file which contains all of the values of temperature and head for each node at each selected timestep. The.tec files allow for the thermal and hydraulic evolution of the simulation to be visualised in the Tecplot software.
Each of the models was run for 3650 timesteps of 1 day (10 years), so in order to efficiently handle such a large number of values, a Python script was written which reads the input text file, extracts the individual data points and writes the times and energies as lists into separate, newly created text files. The contents of the new text files can then be copied directly into Excel for manipulation. Once the raw output data is in a spreadsheet, the power output in watts (J/s) is obtained by first calculating the difference in total energy between each timestep. The resultant values are then divided by the duration of the timestep in seconds (86,400 seconds per day) to give a wattage for each timestep
3.
Results
Here we present the results of the numerical modelling and data manipulation, in order of the research questions which they are intended to address.
3.1. Model SLA—single lateral array (Q1)
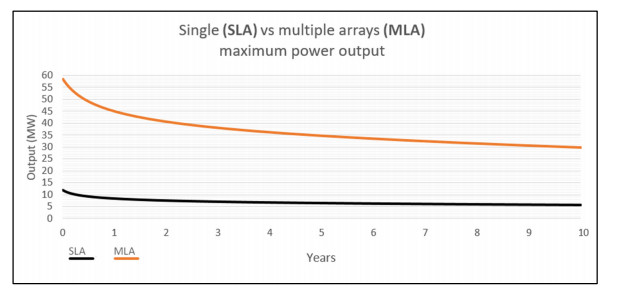
Figure 8 shows the power output in megawatts of the SLA model over a duration of 10 years, representing the total amount of energy lost from the domain per timestep by maintaining a single "James Joyce" type Eavor-Loop system at a constant 20 ℃. The power output after the first one-day timestep is 11.9 MWth (megawatts thermal). This falls steeply by 3.5 MWth to 8.4 MWth by the end of the first year. The power output continues to fall but the rate of decline slows over the remainder of the simulation's run. After 10 years, 5.8 MWth are being extracted from the domain.
Table 7 shows the output values in megawatts of the SLA model at intervals of 1 year, 5 years and 10 years of operation. It also shows the mean power output of the system over the entire 10-year duration of the simulation. The average rate of decline over the course of the simulation is a 0.61 MWth reduction in output per year.
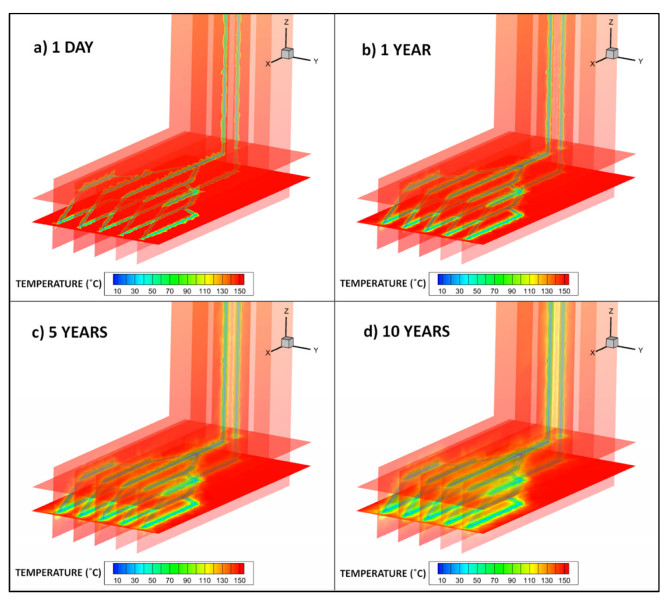
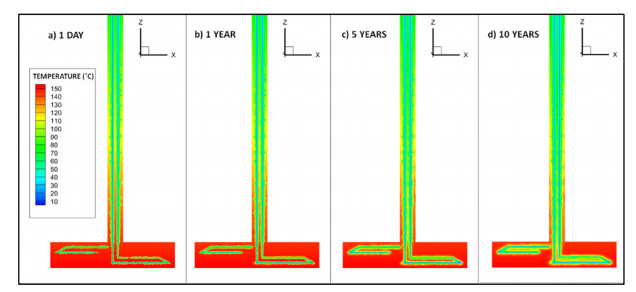
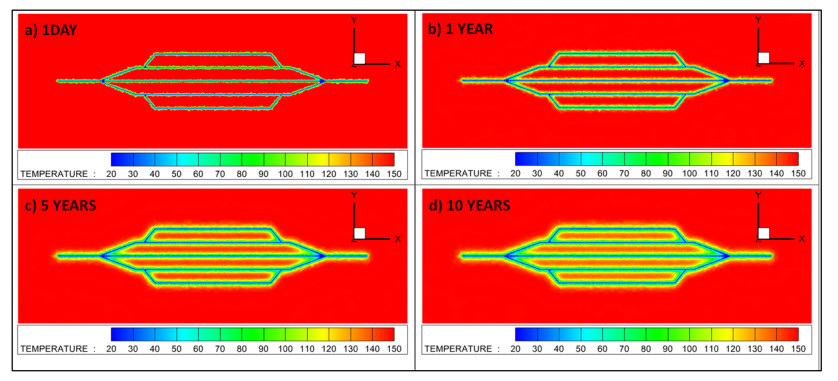
Figure 9 is a visualisation of the temperature distribution in the lower portion of the SLA model. Multiple slices are taken through the domain volume perpendicular to the y- and z-axes. The geothermal gradient of 0.03 K/m means an initial temperature of 150 ℃ at 5000 m depth, where the lowest part of the lateral array is positioned. The polylines representing the pipes are maintained at a constant 20 ℃, which has an immediate cooling effect on the surrounding rock. After a timestep of 1 day (a), a significant region of cooling is already observable in the immediate vicinity of the pipes. Across the following time intervals of 1 year (b), 5 years (c) and 10 years (d), this zone of thermal drawdown can be seen to expand until after 10 years, the cooling extends approximately 15–20 m away from the pipe.
3.2. Model MLA - multiple lateral arrays (Q2)
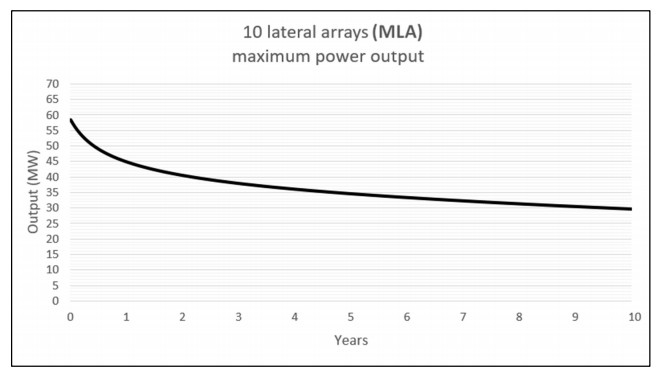
Figure 10 shows the power output in megawatts of the MLA model over a duration of 10 years, representing the total amount of energy lost from the domain per timestep by maintaining an Eavor-Loop system with 10 stacked lateral arrays at a constant 20 ℃. The power output after the first one-day timestep is 58.5 MWth. This falls by 13.6 MWth to 44.9 MWth by the end of the first year. The power output continues to fall but the rate of decline slows over the remainder of the simulation's run. After 10 years, 29.7 MWth are being extracted from the domain.
Table 8 shows the output values in megawatts of the MLA model at intervals of 1 year, 5 years and 10 years of operation. It also shows the mean power output of the system over the entire 10-year duration of the simulation. The average rate of decline over the course of the simulation is a 2.88 MWth reduction in output per year.
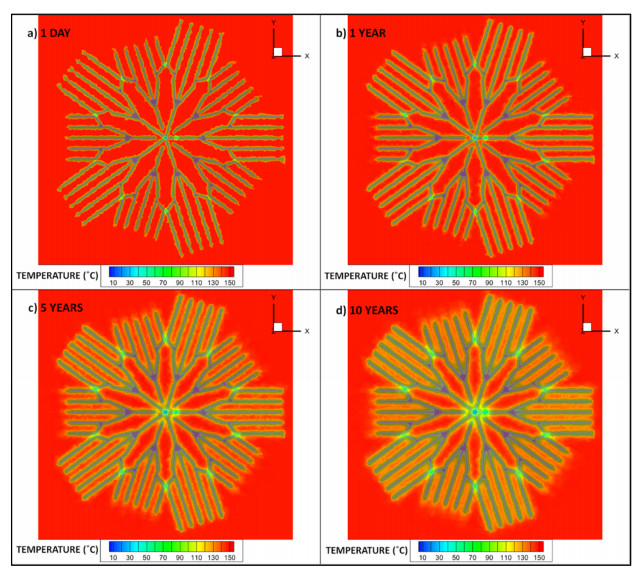
Figure 11 is a visualisation of the temperature distribution in the lateral array section of the MLA model. Slices are taken through the domain volume perpendicular to the z-axis, for each timestep there is a slice at 5000 m depth intersecting the base of the lower set of 5 arrays, and another slice at 4850 m depth intersecting the top of the upper set of 5 arrays. The geothermal gradient of 0.03 K/m means an initial temperature of 150 ℃ at 5000 m depth, where the lowest part of the lateral array is positioned. The polylines representing the pipes are maintained at a constant 20 ℃, which has an immediate cooling effect on the surrounding rock. After a timestep of 1 day (a), a significant region of cooling is already observable in the immediate vicinity of the pipes. Across the following time intervals of 1 year (b), 5 years (c) and 10 years (d), this zone of thermal drawdown can be seen to expand until after 10 years, the cooling extends approximately 20 m away from the pipe. Increased cooling can be observed at and around the junction points, particularly where the vertical wells join the lateral array.
Figure 12 is a visualisation of the temperature distribution in the lower portion of the MLA model. A slice is taken through the domain volume perpendicular to the y-axis, intersecting one array from each of the upper and lower tiers, as well as a portion of the two vertical wells. The geothermal gradient of 0.03 K/m means an initial temperature of 150 ℃ at 5000 m depth, where the lowest part of the lateral array is positioned. The polylines representing the pipes are maintained at a constant 20 ℃, which has an immediate cooling effect on the surrounding rock. After a timestep of 1 day (a), a significant region of cooling is already observable in the immediate vicinity of the pipes. Across the following time intervals of 1 year (b), 5 years (c) and 10 years (d), this zone of thermal drawdown can be seen to expand until after 10 years, the cooling extends approximately 20 m away from the pipe.
3.3. Models SG & FG—static vs flowing groundwater (Q3)
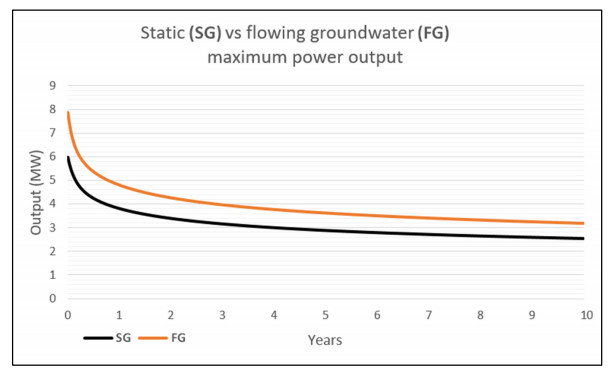
Figure 13 shows the power output in megawatts of both the SG and FG models over a duration of 10 years, representing the total amount of energy lost from the domain per timestep by maintaining a single lateral array section at a constant 20 ℃. The power output after the first one-day timestep is 6 MWth for model SG and 7.9 MWth for model FG. For SG, this falls by 2.2 MWth to 3.8 MWth by the end of the first year. The power outputs of both models continue to fall but the rate of decline slows over the remainder of the simulation's run. After 10 years, 2.5 MWth are being extracted from model SG and 3.2 MWth from model FG.
Table 9 shows the output values in megawatts of both the SG and FG models at intervals of 1 year, 5 years and 10 years of operation. It also shows the mean power output of each model over the entire 10-year duration of the simulation. The average annual rate of decline over the course of the two simulations is a 0.35 MWth reduction for SG and a 0.47 MWth reduction for FG. The difference in power output between the two models is initially 1.9 MWth, narrowing to 0.7 MWth by the tenth year. The difference between the mean outputs of the two models after 10 years is 0.8 MWth, or in percentage terms, the model with groundwater flow through the domain (FG) has a 26% higher average wattage than the static groundwater model (SG).
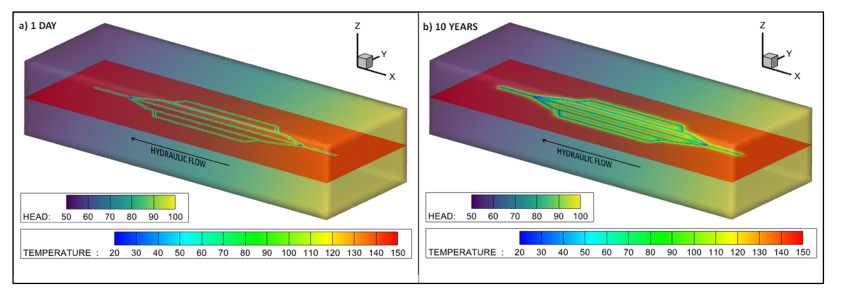
Figure 14 is a visualisation of the temperature distribution in the lateral array section of the SG model. A slice is taken through the domain volume perpendicular to the z-axis at four time intervals, 1 day (a), 1 year (b), 5 years (c) and 10 years (d). The model represents the lateral array at 5000 m depth and an initial domain temperature of 150 ℃. The polylines representing the pipes are maintained at a constant 20 ℃, which has an immediate cooling effect on the surrounding rock. After a timestep of 1 day (a), a region of cooling is observable in the immediate vicinity of the pipes. Across the following time intervals of 1 year (b), 5 years (c) and 10 years (d), this zone of thermal drawdown can be seen to expand until after 10 years, the cooling extends approximately 15 m away from the pipe. Increased cooling can be observed at and around the junction points.
Figure 15 is a visualisation of both the temperature and head distributions in the FG model. A slice is taken through the domain volume perpendicular to the z-axis at two time intervals, 1 day (a) and 10 years (b). The hydraulic head at one face of the model domain is set to a constant 100 m, while the opposite face is set at a constant 50 m, inducing a hydraulic gradient of 0.035 which persists for the duration of the simulation. The model represents the lateral array at 5000 m depth and an initial domain temperature of 150 ℃. The polylines representing the pipes are maintained at a constant 20 ℃, which has an immediate cooling effect on the surrounding rock. After a timestep of 1 day (a), a region of cooling is observable in the immediate vicinity of the pipes. After 10 years (d), this zone of thermal drawdown can be seen to expand until the cooling extends approximately 15 m away from the pipe. Increased cooling can be observed at and around the junction points. The temperature mapping of the two models after 10 years look similar, although the power output data indicate that model FG must be cooled further overall.
3.4. Model CF—controlled flow (Q4)
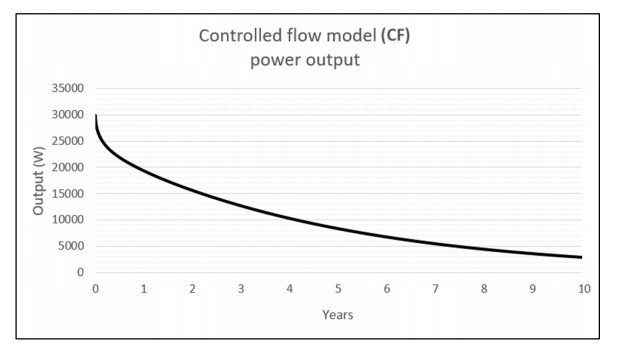
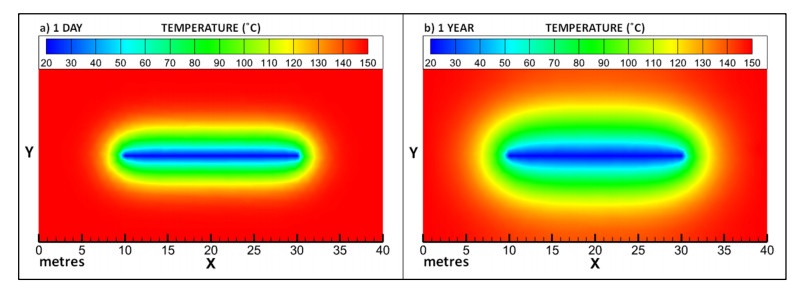
Figure 16 shows the power output in watts of the CF model over a duration of 10 years, representing the total amount of energy lost from the domain per timestep by pumping water through a 20 m section of pipe at a constant flow rate of 0.1 m3/s and a constant inflow temperature of 20 ℃. The power output after the first one-day timestep is 29,786 W. This falls by 10,454 W to 19,332 W by the end of the first year. The power output continues to fall but the rate of decline slows over the remainder of the simulation's run. After 10 years, just 2853 W are being extracted from the domain.
Table 10 shows the output values in watts of the CF model at intervals of 1 year, 5 years and 10 years of operation. It also shows the mean power output of the system over the entire 10-year duration of the simulation. The average rate of decline over the course of the simulation is a 2693 W reduction in output per year.
Table 11 shows the output values in watts of the CF model after 10 years of operation at three different flow rates, 0.01 m3/s, 0.05 m3/s and 0.1 m3/s. These data show an increase in power output with increased flow rate, though the rate of increase is only 0.465 W per 0.1 m3/s, or in percentage terms, approximately 0.1% increase in power output per 0.01 m3/s increase
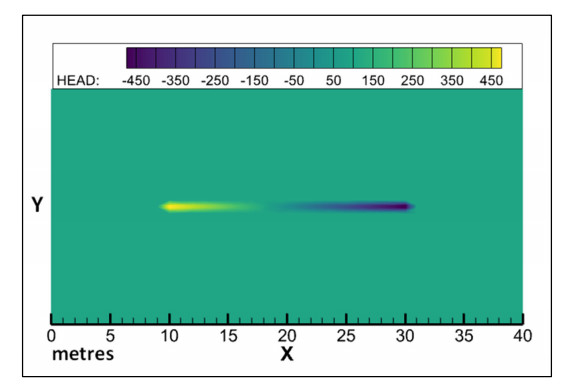
Figure 17 is a visualisation of the head distribution in the CF model. A region of very high pressure can be seen peaking at the pipe inflow point, with the pressure decreasing along the length of the pipe into a region of very low pressure which nadirs at the pipe outflow point. The rest of the domain remains at a constant 100 m head. This pressure regime persists with only minor fluctuations for the duration of the simulation.
Figure 18 is a visualisation of the temperature distribution in the CF model at two different time intervals, 1 day (a) and 1 year (b). The model represents a 20 m section of pipe at 5000 m depth and with an initial domain temperature of 150 ℃. There is an inflow of water a constant flow rate of 0.1 m3/s and at a constant inflow temperature of 20 ℃, which has an immediate cooling effect on the surrounding rock. After a timestep of 1 day (a), a region of cooling is observable in the immediate vicinity of the pipe section. After 1 year (b), this zone of thermal drawdown can be seen to expand to approximately 5 m distance from the pipe. This cooling appears symmetrical about the pipe, with no visible effect from the geothermal heat flux into the base of the model.
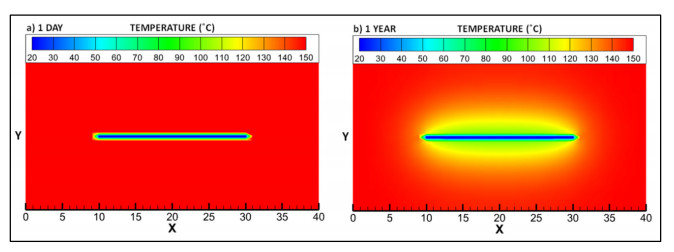
3.5. Model FT—fixed temperature
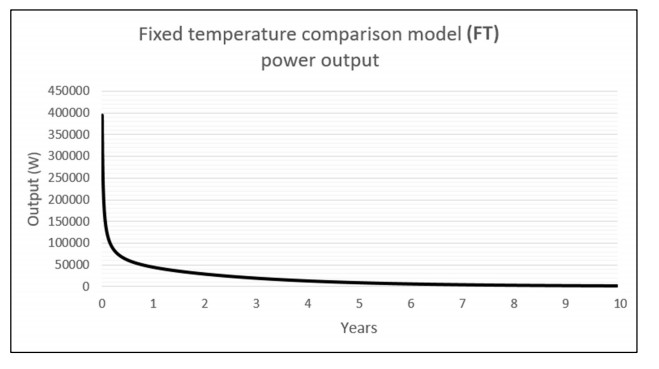
Figure 19 shows the power output in watts of the FT model over a duration of 10 years, representing the total amount of energy lost from the domain per timestep by maintaining the polyline representing the 20 m pipe section at a constant temperature of 20 ℃. The power output after the first one-day timestep is 395,004 W. This falls sharply by 350,962 W to 44,042 W by the end of the first year. The power output continues to fall but the rate of decline slows over the remainder of the simulation's run. After 10 years, just 1051 W are being extracted from the domain.
Table 12 shows the output values in watts of the FT model at intervals of 1 year, 5 years and 10 years of operation. It also shows the mean power output of the system over the entire 10-year duration of the simulation. The average rate of decline over 10 years is a 39,395 W reduction in output per year.
Figure 20 is a visualisation of the temperature distribution in the FT model at two different time intervals, 1 day (a) and 1 year (b). The model represents a 20 m section of pipe at 5000 m depth and with an initial domain temperature of 150 ℃. The polyline representing the pipe is set at a constant temperature of 20 ℃, which has an immediate cooling effect on the surrounding rock. After a timestep of 1 day (a), a region of cooling is observable in the immediate vicinity of the pipe section. After 1 year (b), this zone of thermal drawdown can be seen to expand to approximately 15 m distance from the pipe. After 10 years the cooled region extends up to the top and bottom edges of the domain. This cooling appears symmetrical about the pipe, with no visible effect from the geothermal heat flux into the base of the model.
3.6. Models CF & FT—controlled flow vs fixed temperature
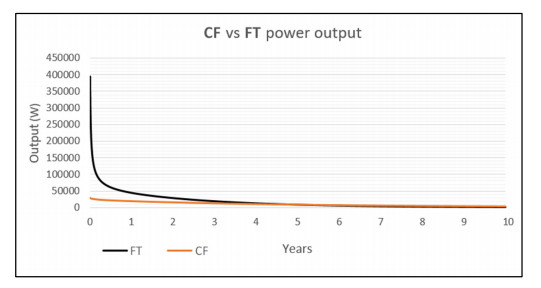
Figure 21 shows the power output in watts of both the CF and FT models over a duration of 10 years, allowing the performance of the controlled flow and fixed temperature methods to be directly compared. The model FT output is initially very high but sharply declines as it rapidly cools the surrounding rock. Model CF conversely, has an a much lower initial output but maintains a much steadier output with a slower rate of decline than FT. Around the 5 years mark, the output of FT dips below that of CF, having depleted much of the energy supply within the first year.
Table 13 shows the output values in watts of both the CF and FT models at intervals of 1 year, 5 years and 10 years of operation. It also shows the mean power output of each model over the entire 10-year duration of the simulation. Initially, the output of model FT is 365,218 W greater than that of CF, but after 10 years the CF model output is 1802 W greater than that of FT. The difference between the mean outputs of the two models after 10 years is 7719 W, or in percentage terms, the average power output of the controlled flow method is approximately 56% that of the fixed temperature method. This gives what will be referred to as the CF adjustment factor of 0.56.
3.7. Models SLA & MLA—single array vs 10 stacked arrays (Q2)
Figure 22 shows the power output in megawatts of both the SLA and MLA models over a duration of 10 years, allowing the performance of 10 lateral arrays to be directly compared to that of a single array. The difference in output between the two models is initially 46.6 MWth, narrowing to 23.9 MWth by the tenth year. The difference between the mean outputs of the two models is 29.5 MWth.
Table 14 shows the output values in watts of both the SLA and MLA models at intervals of 1 year, 5 years and 10 years of operation. It also shows the mean power output of each model over the entire 10-year duration of the simulation.
Using the mean power output from the vertical section of SLA only (1.7 MWth) and subtracting that from the mean MLA output gives a mean output of 34.7 MWth for the 10 lateral array sections only. Comparing the performance of 10 arrays to that of a single array (5.2 MWth), it is therefore calculated that increasing the number of arrays tenfold only increases the power output by a factor of approximately 6.7.
3.8. Models SLA & MLA—adjusted by CF factor
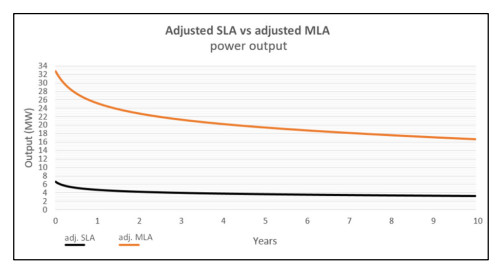
Figure 23 shows the power output in megawatts of both the SLA and MLA models adjusted by the CF adjustment factor of 0.56. The power output after the first one-day timestep of SLA is now 6.6 MWth. After 10 years, the adjusted output of SLA is 3.2 MWth. The power output after the first one-day timestep of MLA is now 32.7 MWth. After 10 years, the adjusted output of MLA is 16.7 MWth.
Table 15 shows the output values in watts of both the SLA and MLA models at intervals of 1 year, 5 years and 10 years of operation. It also shows the mean power output of each model over the entire 10-year duration of the simulation. The power output range of model SLA is now 3.2 to 6.6 MW. The adjusted range for model MLA is 16.7 to 32.7.
4.
Discussion
Here we will discuss the findings of this study and present an analysis of the mechanisms which could be behind the modelling results, addressing each research question in turn. We will also describe the limitations of the study and suggest several avenues for further investigation.
4.1. Are the power output claims realistic? (Q1)
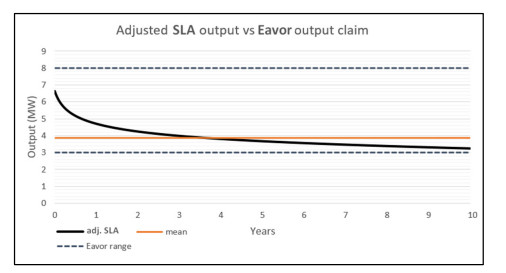
Figure 24 shows the mean and per timestep power output of the SLA model once processed by the adjustment factor of 0.56 derived from models CF and FT. Eavor have claimed in press releases that a single Eavor-Loop, the design approximated by model SLA, will produce between 3 and 8 MW of power. The upper and lower bounds of this range are also shown on the graph. The modelled output begins towards the upper part of Eavor's range at 6.6 MWth but declines over the 10-year run to just 3.1 MWth, only slightly above the lower bound of the claimed range. These results appear to verify to some degree Eavor's power output claims, falling as they do within the stated limits, although the mean output is very close to the lower bound at 3.9 MWth. While this study has used a maximum temperature of 150 ℃, Eavor have stated that they could operate production temperatures of up to 180 ℃. It is possible that modelling at these temperatures is the source for the upper bound of their power output claims.
The low value achieved by this study may in large part be a function of the limits to the modelling method used. Setting a fixed temperature of 20 ℃ in the entire length of the loop is analogous to flushing the system with 20 ℃ water at such a high rate that this temperature is maintained without warming through the entire length of its path. This is not a plausible scenario, and it is for this reason that the results are treated as an absolute maximum, and the CF and FT models were constructed to provide a calibration to more realistic levels. Although this adjustment improves the accuracy of the results, the greatly reduced scale of CF and FT means that longitudinal temperature changes are not properly accounted for, and so these output values remain only an upper bound on the power that could be produced by such a system. The output profile, though lowered by the CF adjustment factor, retains its shape and rate of decline. The decline is a result of the rapid cooling which occurs in the rock immediately adjacent to the pipes. This severe thermal drawdown critically impacts the longevity of the system's power output as it removes the thermal energy that is available to the pipes at a faster rate than the heat in that region can be replenished.
Model CF showed that flowing water through a pipe with a constant inflow temperature removes heat at a steadier rate than setting a fixed temperature. It therefore follows that in practice, the initial output might be somewhat lower than modelled in SLA, but due to the slower thermal drawdown, the replenishment of heat into the cooled zone will more readily be able to keep pace, leading to a higher sustained power output over time. Eavor has claimed that they can create a truly dispatchable power source by simply controlling the flow rate in the Eavor-Loop system. The findings of this study suggest that while this could be possible, a higher heat extraction rate appears likely to negatively impact the overall performance of the system.
4.2. How does stacking additional lateral arrays affect power output? (Q2)
One of the pillars of Eavor's pitch is the scalability of the Eavor-Loop technology. They have claimed [17] that the James Joyce configuration could allow for up to ten lateral arrays to be stacked around shared vertical injection and production wells. The results of the MLA model reveal that 10 stacked lateral arrays generate only 6.7 times the power output of a single lateral array, as represented by model SLA. This non-linear relationship suggests that there is thermal interference between the arrays in the modelled configuration, with each array reducing the pool of thermal energy available to its neighbours. This reduced efficiency means that the adjusted mean power output for each lateral array in the MLA model is roughly 1.9 MWth, as compared to around 2.9 MWth for the isolated output of the lateral array in SLA. The stacked lateral array configuration modelled in MLA can therefore be regarded as approximately 66% as efficient as a single lateral array.
Another possible cause of the reduced efficiency could be the geometry of the model domain. To keep processing times to a minimum, the volume of rock surrounding the system was kept as small as possible without the zones of thermal drawdown reaching the edge of the domain. As the cross-section of the domain through the z-axis is square while the footprint of the pipework is decagonal, some of the arrays are closer to the edge than others and may have had a slightly smaller pool of available thermal energy to draw from.
Eavor's proposed first commercial plant at the Geretsried site in Germany is expected to generate 60 MW. If the results from the MLA model are accurate, with a mean output of 20.4 MW, 3 separate drill locations would be required to reach this target output. It is reported that the site already has two dry exploratory wells which Eavor intends to rehabilitate, so this could be their intention. They have further stated that 200 MW could be possible from the Geretsried location alone. The results of this study suggest that although this may be technically feasible, and with a relatively small surface footprint, the total area of the site would have to be very large to accommodate all of the lateral arrays in the subsurface.
4.3. What is the effect of groundwater flow on the performance of the system? (Q3)
A stated advantage of Eavor's deep closed-loop geothermal design, and closed-loop geothermal energy more broadly, is that it is not tied to locations with particular hydrogeological conditions. While it is true that the technology does not require aquifers or areas with favourable fracture flow rates to function, work on borehole heat exchangers has shown that the movement of groundwater in the vicinity of a geothermal system does have the capacity to significantly affect the system performance [20]. Comparison of the results from models SG and FG show that at a hydraulic conductivity of 1 × 10−6, and with a hydraulic gradient of 0.035 across the domain, the flow of groundwater around the system increases the power output by 26% as compared to a static groundwater scenario. This appears to be a result of the groundwater aiding the replenishment of heat in the zone of cooling around the pipes. Another consideration is the effect that cooling from 150 ℃ to 20 ℃ would have on the dynamic viscosity of the groundwater. This could greatly alter the hydraulic conductivity and therefore the groundwater flow in the vicinity of the wellbores.
The same model was run with a hydraulic conductivity (K) in the rock of 1 × 10−9 and there was almost no difference in power output. A K value of 1 × 10−6 lies in the middle of the typical range for fractured basement, according to Freeze & Cherry [29], whereas 1 × 10−9 is just below the lower limit for this rock type. Whether K values of 1 × 10−6 are likely to be found at the kinds of depths targeted by an Eavor-Loop system is uncertain as data from several deep drilling projects indicates that this may not be the case. Work by Kuang and Jiao [30] shows that at these depths, the intrinsic permeability of the rocks, a key component of hydraulic conductivity, is much lower due to the immense confining pressure forcing fractures closed. K values of 1 × 10−12 would be more likely at a depth of 5 km. It therefore seems likely that the hydrogeological conditions of a target site will not be of primary concern. In addition, for most locations, information on hydraulic conductivity at the target depths will not be available so using this to inform decisions on drill locations will not be possible, except where DCLGS is being retrofitted to an unproductive geothermal, oil or gas well.
4.4. Does controlling the flow rate make this a dispatchable technology? (Q4)
The Eavor-Loop system is described as fully dispatchable, meaning that it is capable of following peaks and troughs in energy demand. The claim is that this can be achieved by way of a simple valve system at the top of the injection well which allows the flow rate through the system to be controlled. Increasing the flow rate should immediately increase the power output of the system. Indeed, the results of model CF when run at three different flow rates showed an increase in wattage of approximately 0.1% per 0.01 m3/s increase in flow rate. This increase would not be enough to be usefully load-following, but these values were obtained from a model of just 20 m of pipe and are therefore hardly representative of an entire Eavor-Loop. At such a small scale the entire pipe is kept close to a constant 20 ℃ temperature. In a longer section of pipe, the travel time of the water within the pipe would increase such that the water is able to be warmed further by the surrounding rock before reaching the outflow. Work by Wu et al. [21] finds marked differences in power output at different flow rates and shows that while a higher flow rate means a higher output, it also means a poorer performance over a longer time span with lower production temperatures. This is an issue which would have to be carefully monitored when altering the flow rate to meet demand. Overproduction at peak times could cool the rock so that the long-term performance of the system is compromised. A study which models flow rates which follow typical changes in energy demand over time in a DCLGS and monitors the effect on the thermal regime and long-term performance would be a very useful tool for assessing the true dispatchability of DCLGS technology.
Another limitation on the CF and FT model is that they were constructed in 2D, whereas the models to which the CF adjustment factor was applied were constructed in 3D. These models were created in 2D, and at a reduced scale, to compensate for the increased complexity of the CF modelling method. Applying this method to a larger system would have been prohibitively time intensive for this study. Although the comparison between CF and FT is fair given that they have near identical geometries to one another, constructing similar models in 3D would mean a greater amount of thermal energy available to the system and a better representation of the dynamics in a real system. Adapting the CF method to a 3D domain is beyond the scope of this study, however.
4.5. Study limitations and suggested further investigation
While modelling 10 stacked arrays showed a drop-off in efficiency compared to a single lateral array, the details of the interaction between additional arrays and overall power output has not been established. Further modelling of this type of system could sequentially add arrays to find a "sweet spot" where power output is increased with a minimum overall reduction in efficiency. Another facet of this line of enquiry could be to experiment with different multiple array configurations.
Wanju et al. [18] found that manipulating the lateral wellbore spacings could have a large impact on thermal interference and loss of output over time. This study used two tiers of five evenly spaced arrays with the intention of keeping as much of the system in the highest temperature portion of the domain as possible. It could be possible that placing some arrays at shallower depths but with more space between them gives a higher overall power output due to reduced thermal interference between the lateral arrays.
Another avenue of study might be the effect of groundwater flow on the power output of closed-loop geothermal systems. It could be useful to the field of closed-loop geothermal development to model various scenarios with different hydrological regimes, i.e. hydraulic conductivities, hydraulic gradients etc. The FEM modelling by Tolooiyan and Hemmingway [20] demonstrated that in shallower settings, a small amount of groundwater flow can have a significant impact of the thermal regime in the subsurface. If it can be determined that groundwater flow can help to reduce thermal drawdown in DCLGS, or perhaps even exacerbate it, this could inform future decisions about the siting of closed-loop systems.
While the parameters chosen for the models in this study are typical of real-world values and are based on empirical data, the study domains were simplified with no geological variation. All models were entirely homogeneous and isotropic with only one material group for the entire domain, with the exception of the grout and pipe in model CF. While no single model can fully capture the complexity of real hydrogeology, a series of models constructed using data from known locations could better test the idea that this technology can effectively be sited anywhere in the world. Many locations around the globe have a wealth of data about the lithologies and hydrological conditions in the subsurface down to considerable depth, especially in those areas that have been explored or exploited for oil and natural gas. Simplifications are inevitable and necessary when constructing numerical models, but borehole data could be used to inform somewhat more representative model designs.
The main limit on the controlled flow model, CF, was the small scale of it, modelling as it did only a 20 m length of pipe. While scaling this model up would pose problems in terms of processing capacity, a much longer length of pipe could effectively be modelled by splitting it into several smaller sections and using the outflow temperature of the first section as the inflow temperature of the following section, and so on. This is similar to the approach taken by Wu et al. [21], who split their model of a U-shaped DCLGS into three sections, the injection well, the lateral well and the production well. The combined power outputs of a series of modelled sections of this kind could provide a much more accurate representation of the interaction between the flow of the heat-bearing fluid and heat transport from the surrounding rock.
Each of the models in this study were simulated for a duration of 10 years to provide a picture of changes in the system's performance over time. However, after 10 years the models continued to put out power, with the rate of decline having shallowed but not levelled. The study conducted by Wu et al. [21] gave power output results with a very similar profile to the results of the models in this study, but their simulation was run for a duration of 30 years, as compared to the 10 years used here. Using the trajectory of 30-year output data as a guide, it is reasonable to extrapolate that the SLA and MLA models, if run for 30 years, would close to level out beyond the 10-year mark. However, as the methods used are not identical, and any commercial power plant must have estimates of the longevity of the site, and it would therefore be beneficial to model these systems over longer durations to determine whether equilibrium is ever reached between heat extraction and recharge, and if not, after how many years might the plant become economically unviable due to reduced power output.
As discussed previously, the method of maintaining a fixed temperature in the pipes provides an absolute maximum value for available thermal energy while also dramatically cooling the surrounding rock and subsequently seeing the power output sharply decline. A model which sets a source term to extract heat at set rates from the pipes could be developed. Experimenting with various extraction rates could allow for optimisation of the system to find how much energy can be removed before the rock is overcooled and system performance diminished. Future work on this question could build on this study by extracting at rates from within the range resulting from model SLA. Taking the midpoint of the Eavor claim at 5.5 MW for example and dividing that output over the length of the pipework, would generate a constant heat sink term that does not diminish over time. If thermal recharge is insufficient to resupply the cooled region, the thermal drawdown will continue to expand, providing another view on the bounds of possible power outputs from the system.
This study used a somewhat arbitrary inflow temperature of 20 ℃ for all models as this is a typical ambient temperature at surface. Wu et al. [21] suggest that this could be an important parameter for determining the performance of a closed-loop system. Injecting water at higher temperatures might reduce the immediate power output but prevent excessive cooling over time by reducing the temperature differential between the heat-bearing fluid in the pipe and the surrounding rock. Further work on this problem might run similar models to those used in this study but at a range of different inflow temperatures. Also regarding temperature parameters, while Eavor have stated that they will target temperatures of 150 ℃, they have also suggested that temperatures as high as 180 ℃ could be accessed. The models run at 150 ℃ could be compared to new models at higher temperatures to assess the impact of a greater temperature differential between the wells and the surrounding rock, and a greater total energy in the system.
5.
Conclusions
This study constitutes a rather broad appraisal of the novel Eavor-Loop DCLGS technology. It uses typical parameter values to model various facets of the technology's mechanics. This breadth means that each variable studied lacks the depth of insight that a dedicated investigation would yield. However, as a first-pass evaluation of an as-yet little studied technology, it could serve as a jumping off point for future validation or rebuttal of the claims made by Eavor.
The key findings of the study are:
ⅰ. The 3–8 MW per Eavor-Loop figure claimed by Eavor's press releases is supported by the numerical modelling results of model SLA, in so far as they fall within this range. However, the modelled results lie in the lower half of the range and higher output figures are therefore not supported by this study, at least in the modelled conditions. Modelling at higher temperatures would likely achieve the higher outputs.
ⅱ. Provided that the technological and financial limits are not too great, Eavor-Loop technology could indeed be scalable, model MLA suggests that adding additional lateral wellbore arrays will likely not provide a linear increase in power output. Thermal interference between the arrays could reduce the overall efficiency of the system by approximately 34%, although optimising the spacing of wellbores could mitigate some of these losses.
ⅲ. While claims that DCLGS technology is free from the restraints of local hydrogeological conditions is true in the broad sense, the results of models SG and FG indicate that targeting sites with high enough groundwater flow could increase power output by up to 26%. The literature poses some doubt over whether that hydraulic conductivity values used in model FG could realistically be expected to be found at depths of around 5 km, as confining pressure greatly reduces permeability.
ⅳ. Eavor's claim that they can provide dispatchable power to the grid by controlling the flow rate through the system cannot be clearly verified by this study, although some literature shows that this may be possible if carefully monitored. The model CF demonstrated that power output does increase with higher flow rates, however the scale of the model makes it unreasonable to draw definite conclusions about the range of outputs which could be safely operated without jeopardising the longevity of the site.
ⅴ. This study opens the doors to many other avenues of investigation with possibilities for more in-depth analysis of each variable in the system. One of the more pressing tasks would be to build on the maximum power output assessments by using the results of models SLA and MLA to decide on heat extraction rates, then set these as sink terms in new models of the system. This would allow a more realistic picture of the performance of the Eavor-Loop over time. Another important variable that this study does not adequately address is the role of flow rate in governing power output. Any attempt to tackle this problem would require the creation of new designs using different modelling methods to those used in this study.
Acknowledgements
Joseph Kelly would like to thank Elliot Ferryman-Avery for his support.
Conflict of interest
The author declares no conflict of interest.









 DownLoad:
DownLoad: