1.
Introduction
Epidemics have posed a significant threat to global public health over the years. The emergence of COVID-19 in 2019 has had a profound impact on human health, the global economy, and social behavior. Nevertheless, the effective addressing of disease transmission remains a challenge. Mathematical modeling has emerged as a crucial tool in tackling this challenge. Numerous disease models have been developed in existing literature to study and control the spread of epidemics. It is important to note that mathematical models based on ordinary differential equations (i.e., classical derivatives) have their limitations and may not accurately capture biological phenomena. On the other hand, fractional models can offer a relatively more accurate understanding of disease outbreaks. Therefore, they are increasingly being used to simulate disease transmission with higher accuracy. Relevant literature on fractional models can be found in [1,2,3,4,5]. In addition, as another epidemic that endangers human health, the acute viral infection caused by the human immunodeficiency virus (HIV) studied in this paper is also a hot issue in society. Many researchers aim to capture the dynamics between viral and antiviral immune responses through mathematical modeling.
As we all know, HIV, which causes AIDS, can directly infect the immune system (mainly regulating CD$ {4^ + } $ T cells). The consequences of this impact are a continuous decrease in the number of CD$ {4^ + } $ T cells, ultimately leading to the death of infected individuals due to immune system collapse. The highly active antiretroviral therapy (HAART) currently in widespread use has been shown to improve the survival probability of HIV patients and reduce the incidence rate [6,7]. This therapy effectively suppresses the plasma virus to levels below the standard detection for extended periods and even halts viral evolution [8,9]. However, many complex problems arise after long-term use, such as obvious drug resistance, and, due to the side effects of antiviral drugs, some AIDS patients have poor compliance with antiviral therapy [10,11,12].
In fact, numerous mathematical models have been put forth to describe the dynamics of HIV and elucidate various phenomena. The effect of antiviral therapy has been investigated by some researchers [13,14,15,16]. In their work, Xiao et al.[13] analyzed the free terminal time optimal tracking control problem to determine the optimal multidrug therapy for HIV, considering both the optimal time frame and therapeutic strategies. The literature [17,18,19,20,21,22,23,24] incorporated the expansion delay of immune cells to discuss the local and global stability of equilibrium solutions. In particular, [17] indicates that such an unstable equilibrium will exhibit oscillatory solutions of increasing amplitude. In recent years, realizing gradually the multiple effects of spatial heterogeneity and mobility, many scholars utilized the reaction-diffusion equation to investigate the spatial effect of viral infection [23,24,25].
Several recent clinical studies have exhibited that structured treatment interruptions (STIs) can be used for early treatment of HIV infection to achieve sustained specific immunity. For some chronically infected individuals who may require lifelong medication, this may be a beneficial option as it can help patients rebuild their immune system during periods of non-medication[26]. While numerous mathematical models have been employed for simulating continuous therapy [27,28,29], there is scant investigation on modeling structured interruptions in treatment.
To investigate strategies for STIs, Tang et al.[30] suggested a piecewise model for delineating CD4 cell-guided STIs. The system provides an explanation for some controversial clinical research results. In 2017, Tang et al.[31] proposed a mathematical model to describe the dynamics of the interplay between the virus and the immune system. This model takes into consideration the structured treatment guided by effector cells while also incorporating the use of combined antiretroviral therapy and interleukin (IL)-2 treatment. However, they posit a linear growth pattern for the HIV virus [31], which does not accurately reflect the true dynamics of the virus. Some clinical facts show that the growth of HIV may have a saturation effect[32].
To better illustrate the non-linear evolutionary characteristics of the interplay between virus and immune response, the immunosuppressive infection model was devised by Komarova et al.[33]. The model is given as follows:
The assumptions in model (1.1) are as follows:
❑ $ y $ and $ z $ represent the population sizes of the virus and immune cells, respectively. The virus population is assumed to grow logistically: The replication rate at low viral loads, denoted as $ r $, is expected to decrease linearly with an increase in the viral load until it becomes zero at a viral load $ K $.
❑ $ c $ represents the immune intensity, while the proliferation term is denoted as $cyz / (1 + hy)$. Thus, the assessment of immune cell proliferation depends on both the immune cells and the virus. The inhibitory effect of the virus on the proliferation of immune cells is represented by the variable $ \eta $.
❑ The viral elimination rate, denoted as $ a $, is a result of natural decay and antiretroviral therapy. Immune cells, which have the ability to kill the virus at a rate $ pyz $, also have a death rate $ b $. Furthermore, these immune cells can be inhibited by the virus at a rate $ qyz $.
The study conducted in [33] aimed to investigate the optimal timing and duration of antiviral treatment. The research elucidates the presence of bistability dynamics, wherein a stable state without immunity coexists alongside a stable state with immunity. Meanwhile, this model demonstrates the attainment of sustained immunity following the interruption of therapy. Additionally, Wang et al.[34] expanded on this model and uncovered that bistability arises within the range delineated by the post-treatment control threshold and the elite control threshold.
Following the pioneer works above[30,31,32,33,34], in this thesis, we extend model (1.1) by proposing a Filippov immunosuppressive infection model with viral logistic growth and effector cell-guided therapy. We have proposed the following model:
We assume that the sole course of action is to administer antiretroviral therapy to the patient if the number of effector cells exceeds the critical value $ {E_T} $. Conversely, when the count falls below the $ {E_T} $ threshold, a combination of antiretroviral therapy and immune therapy is concurrently implemented. In this context, $ \varepsilon $ represents the rate at which effector cells grow as a result of immune therapy, like the treatment of interleukin (IL)-2. As the interpretation of other parameters is consistent with a model (1.1), all parameters in (1.2) remain nonnegative.
This paper presents a switching model with viral load logistic growth to analyze effector cell-guided treatment and assess the threshold strategy's effectiveness. The following section provides an overview of the model, defining the switching system, and summarizing the dynamic behavior of the subsystems. Additionally, in Section 3, there is a discussion on sliding mode and dynamics, exploring the presence of a sliding domain and pseudo-equilibrium. The global dynamics of the proposed model are examined in Section 4, while Section 5 focuses on the boundary equilibrium bifurcation of the system. Finally, the paper concludes with discussions and biological implications.
2.
Filippov model and preliminaries
2.1. Model formulation
By rearranging the system (1.2), we can obtain a generic planar system in the form of Filippov given by
with
Systems (2.1) and (2.2) describe a Filippov immunosuppressive infection model where (2.1) is considered a free system when $ \phi = 0\left({i.e., z > {E_T}} \right) $, indicating that the patient receives antiretroviral therapy. On the other hand, (2.1) as a control system when $ \phi = 1\left({i.e., z < {E_T}} \right) $ reflects the simultaneous utilization of antiretroviral therapy and immune therapy.
Let $ R_ + ^2 = \left\{ {\left. {X = {{\left({y, z} \right)}^T}} \right|y \geqslant 0, z \geqslant 0} \right\}, $ $ {S^1} = \left\{ {\left. {X \in R_ + ^2} \right|H(X) > 0} \right\}, $ and $ {S^2} = \left\{ {\left. {X \in R_ + ^2} \right|H(X) < 0} \right\} $ with $ {H(X)} $ being a smooth scale function. For convenience, we further denote
We can rewrite model (1.2) to represent the Filippov system as follows:
The discontinuous boundary $ \Sigma $ that separates the two areas can be represented as:
It is evident that $ R_ + ^2 = {S^1}\cup\Sigma\cup{S^2} $. Henceforth, we shall designate the Filippov system (2.4) as subsystem $ \mathbb{S}^1 $ when it is defined within region $ {S^1} $, and as subsystem $ \mathbb{S}^2 $ when defined within region $ {S^2} $.
Let
where $ \langle { \cdot, \cdot } \rangle $ represents the standard scalar product and $ {H_X}(X) $ denotes the gradient of $ {H(X)} $ that remains nonvanishing on $ \Sigma $. $ F_{S^i}H(X) = F_{S^i}\cdot {\rm grad} H(X) $ is the Lie derivative of $ H $ with respect to the vector field $ F_{S^i} $ $ \left({i = 1, 2} \right) $ at $ X $. To analyze the direction of the vector field $ \left[{{F_{{S^1}}}\left(X \right), {F_{{S^2}}}\left(X \right)} \right] $, through a specific point $ X \in \Sigma $, we categorize the areas on $ \Sigma $ based on whether the vector field points towards it:
(a) Crossing region:
(b) Sliding region:
(c) Escaping region:
Throughout the paper, it is crucial to have a clear understanding of the definitions regarding all types of equilibria in Filippov systems [35,36].
Definition 2.1. If $ F_{S^1}(X_*) = 0, H(X_*) > 0 $, or $ F_{S^2}(X_*) = 0 $, $ \; H(X_*) < 0 $, then $ X_* $ is defined as a real equilibrium of the Filippov system (2.4). Analogously, if $ F_{S^1}(X_*) = 0 $, $ H(X_*) < 0 $, or $ F_{S^2}(X_*) = 0, H(X_*) > 0 $, then $ X_* $ is a virtual equilibrium. Both the real and virtual equilibriums are named as regular equilibria.
Definition 2.2. If $ X_* $ is an equilibrium of the sliding mode of system (2.4), and satisfies $ (1-\lambda) F_{S^1}(X_*)+ \lambda F_{S^2}(X_*) = 0, H(X_*) = 0 $ with $ 0 < \lambda < 1 $, then $ X_* $ is a pseudo-equilibrium, where
Definition 2.3. If $ F_{S^1}(X_*) = 0, H(X_*) = 0 $, or $ F_{S^2}(X_*) = 0, H(X_*) = 0 $, then $ X_* $ is defined a boundary equilibrium of Filippov system (2.4).
Definition 2.4. If $ F_{S^1}H(X_*) = 0 $ but $ F_{{S^1}}^2H({X_ * }) > 0\left({F_{{S^1}}^2H({X_ * }) < 0} \right) $, then $ X_* $ is a visible (invisible) $ \Sigma $-fold point of $ F_{S^1} $. The same definition applies to $ F_{S^2} $.
Definition 2.5. If $ X_*\in\Sigma_s $ and $ F_{S^1}H(X_*) = 0 $ or $ F_{S^2}H(X_*) = 0 $, then $ X_* $ is defined a tangent point of Filippov system (2.4).
2.2. Qualitative analysis of subsystems
The model equation for the free system $ \mathbb{S}^1 $ is as follows:
We can easily define a threshold $ {R_0} = \frac{r}{a} $. If $ {R_0} < 1 $, subsystem $ \mathbb{S}^1 $ has only one uninfected equilibrium $ E_0^1 = \left({0, 0} \right) $; if $ {R_0} > 1 $, then subsystem $ \mathbb{S}^1 $ also has an immune-free equilibrium $ E_1^1 = \left({{y_1}, 0} \right) = \left({K\left({1 - \frac{a}{r}} \right), 0} \right) $.
We certainly get an equation for $ y $
It can be confirmed that $ {S_1}\left(y \right) = 0 $ has a sole solution when $ c = q + b\eta \pm 2\sqrt {bq\eta } $. Denote $ {c_1} = q + b\eta - 2\sqrt {bq\eta } $ and $ {c_2} = q + b\eta + 2\sqrt {bq\eta } $. Thus, we have two possible positive roots
when $ c > {c_2} $, where $ B = c - q - b\eta $. Substituting $ {y_{11}} $ or $ {y_{12}} $ into the first equation of (2.11), we get
Let $ R_i^1 = \frac{r}{a}\left({1 - \frac{{{y_{1i}}}}{K}} \right)\left({i = 1, 2} \right) $. Hence, the subsystem $ \mathbb{S}^1 $ has two immune equilibriums $ {E_{11}} = \left({{y_{11}}, {z_{11}}} \right) $ and $ {E_{12}} = \left({{y_{12}}, {z_{12}}} \right) $ when $ R_i^1 > 1 $ and $ c > {c_2} $ are satisfied.
In fact, subsystem $ \mathbb{S}^1 $ has been extensively examined in a previous study. Therefore, we will provide an overview of the main findings without delving into specific calculations. For more details on the discussion of the stability analysis of this system, please consult [34]. Here, we define three thresholds by referring [34], i.e., $ {c^ * } = q{\rm{ + }}b\eta {\rm{ + }}2q\eta K\left({1 - \frac{a}{r}} \right), $ $ {c^{ * * }} = q{\rm{ + }}b\eta {\rm{ + }}\frac{b}{{K\left({1 - \frac{a}{r}} \right)}}{\rm{ + }}q\eta K\left({1 - \frac{a}{r}} \right) $, and threshold $ {R_{{c_1}}} = 1 + \frac{{r\sqrt {bq\eta } }}{{aq\eta K}} $. Moreover, we have the following
Lemma 2.1. If $ {R_0} < 1 $, the infection-free equilibrium $ E_0^1 $ is globally asymptotically stable $ \left({GAS} \right) $. If $ {R_0} > 1 $, we have $ E_1^1 $ as locally asymptotically stable $ \left({LAS} \right) $ when $ 0 < c < {c_2} $ or $ {c_2} < c < {c^{ * * }} $, and $ E_1^1 $ is unstable when $ c > {c^{ * * }} $. The immune equilibrium $ {E_{11}} $ is $ LAS $ when $ {R_{{c_1}}} > {R_0} > 1 $ and $ c > {c^{ * * }} $ or $ {R_0} > {R_{{c_1}}} $ and $ {c_2} < c $. Suppose $ {R_0} > {R_{{c_1}}} > 1 $ and $ {c_2} < c < {c^ * } $, then positive equilibrium $ {E_{11}} $ is $ LAS $ and $ {E_{12}} $ is a unstable saddle.
Remark 2.1. For $ {R_0} > {R_{{c_1}}} > 1 $ and $ {c_2} < c < {c^{ * * }} $, subsystem $ \mathbb{S}^1 $ has bistable behavior, i.e., $ E_1^1 $ and $ {E_{11}} $ are bistable but the equilibrium $ {E_{12}} $ is an unstable saddle. In other cases, subsystem $ \mathbb{S}^1 $ does not exhibit bistable behavior. Note that the post-treatment control threshold is represented by $ {c_2} $, while the elite control threshold is denoted as $ {c^{ * * }} $. The range between $ {c_2} $ and $ {c^{ * * }} $ is referred to as the bistable interval.
Dynamical analysis of the subsystem $ \mathbb{S}^1 $ is presented in Table 1.
Control system $ \mathbb{S}^2 $ gives
The basic reproduction number is also $ {R_0} = \frac{r}{a} $ for subsystem $ \mathbb{S}^2 $. Similarly, we can get uninfected equilibrium $ E_0^2 = \left({0, 0} \right) $ and the immune-free equilibrium $ E_1^2 = \left({K\left({1 - \frac{a}{r}} \right), 0} \right) $. Thus, we use $ E_0^1 = E_0^2 = {E_0} $ and $ E_1^2 = E_1^1 = {E_1} $ in the following.
Using the same method as subsystem $ \mathbb{S}^1 $, we can derive the following quadratic equation for $ y $
Let $ {c_3} = q + \left({b - \varepsilon } \right)\eta - 2\sqrt {q\eta \left({b - \varepsilon } \right)} $ and $ {c_4} = q + \left({b - \varepsilon } \right)\eta {\rm{ + }}2\sqrt {q\eta \left({b - \varepsilon } \right)} $, then there are two possible positive roots
when $ c > {c_4} $, where $ D = c - q - b\eta + \varepsilon \eta $. It follows that
In fact, we can obtain $ {y_{21}} < {y_{11}} < {y_{12}} < {y_{22}} $ by doing a simple calculation. Now, we define $ R_i^2 = \frac{r}{a}\left({1 - \frac{{{y_{2i}}}}{K}} \right)\left({i = 1, 2} \right) $. For subsystem $ \mathbb{S}^2 $, we have two positive equilibriums $ {E_{21}} = \left({{y_{21}}, {z_{21}}} \right) $ and $ {E_{22}} = \left({{y_{22}}, {z_{22}}} \right) $ when $ c > {c_4} $, $ b > \varepsilon $ and $ R_i^2 > 1\left({i = 1, 2} \right) $ hold. Furthermore, following a similar approach to subsystem $ \mathbb{S}^1 $, we can also define thresholds $ {c^\dagger } = q + \left({b - \varepsilon } \right)\eta + 2q\eta K\left({1 - \frac{a}{r}} \right) $, $ {c^{\dagger \dagger }} = q + \left({b - \varepsilon } \right)\eta + \frac{{b - \varepsilon }}{{K\left({1 - \frac{a}{r}} \right)}} + q\eta K\left({1 - \frac{a}{r}} \right) $, and $ {R_{{c_2}}} = 1 + \frac{{r\sqrt {q\eta \left({b - \varepsilon } \right)} }}{{aq\eta K}} $. Meanwhile, we have the following results about the behaviors of subsystem $ \mathbb{S}^2 $ by using the consistent method with $ \mathbb{S}^1 $.
Lemma 2.2. Suppose $ {R_0} < 1 $, the equilibrium $ E_0^2 $ is $ GAS $. Suppose $ {R_0} > 1 $, then $ E_1^2 $ is $ LAS $ when $ 0 < c < {c_4} $ or $ {c_4} < c < {c^{\dagger \dagger }} $, and $ E_1^2 $ is unstable when $ c > {c^{\dagger \dagger }} $. If $ {R_{{c_2}}} > {R_0} > 1 $ and $ c > {c^{\dagger \dagger }} $ or $ {R_0} > {R_{{c_2}}} $ and $ {c_4} < c $, the subsystem $ \mathbb{S}^2 $ has a locally asymptotically stable immune equilibrium $ {E_{21}} $; if $ {R_0} > {R_{{c_2}}} > 1 $ and $ {c_4} < c < {c^\dagger } $, then positive equilibrium $ {E_{21}} $ is $ LAS $ and $ {E_{22}} $ is an unstable saddle.
Dynamical analysis of the subsystem $ \mathbb{S}^2 $ is shown in Table 2.
3.
Sliding mode dynamics
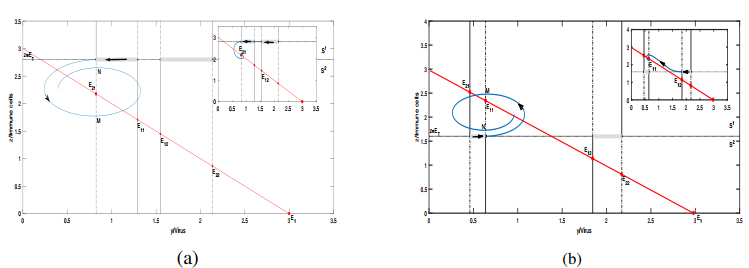
In this section, we will provide a brief overview of the definitions pertaining to the sliding segment and crossing segment discussed in Section 2. We have $ \sigma \left(X \right) = \langle {{H_X}(X), {F_{{S^1}}}(X)} \rangle \cdot \langle {{H_X}(X), {F_{{S^2}}}(X)} \rangle $. Here, $ {H_X}(X) = \left({\frac{{\partial H}}{{\partial y}}, \frac{{\partial H}}{{\partial z}}} \right) $ is the non-vanishing gradient on the discontinuity boundary $ \Sigma $, where $ H = z - {E_T} $. Therefore, we denote
and calculating the inequality $ \sigma \left(X \right) < 0 $ obtains $ {y_{21}} < y < {y_{11}} $ and $ {y_{12}} < y < {y_{22}} $. Naturally, we can verify that there are $ \langle {{F_{{S^1}}}, {H_X}(X)} \rangle = \frac{{cyz}}{{1 + \eta y}} - bz - qyz < 0 $ and $ \langle {{F_{{S^2}}}, {H_X}(X)} \rangle = \frac{{cyz}}{{1 + \eta y}} - bz - qyz + \varepsilon z > 0 $ for $ {y_{21}} < y < {y_{11}} $ or $ {y_{12}} < y < {y_{22}} $. Therefore, the Filippov system (2.4) always comprises two sliding segments, which can be obtained as
Naturally, the crossing region we can get is $ {\Sigma _c} = \left\{ {\left. {\left({y, z} \right) \in R_ + ^2} \right|0 < y < {y_{21}}, } \right. $ or $ {{y_{11}} < y < {y_{12}}, } $ or $ y > {y_{22}}, \left. {z = {E_T}} \right\} $. Notably, every trajectory within the segment $ \left\{ {\left. {\left({y, z} \right) \in R_ + ^2} \right|0 < y < {y_{21}}} \right. $ or $ y > {y_{22}}, \left. {z = {E_T}} \right\} $ will intersect the $ {z = {E_T}} $ line, moving from region $ {S^1} $ to $ {S^2} $. Similarly, the trajectory within the segment $ \left\{ {\left. {\left({y, z} \right) \in R_ + ^2} \right|{y_{11}} < y < {y_{12}}, z = {E_T}} \right\} $ will cross the $ {z = {E_T}} $ line, transitioning from region $ {S^2} $ to $ {S^1} $.
The Filippov convex method is employed in this study to analyze the sliding domain and sliding mode dynamics of the switching system (2.4). According to Definition 2.2, we have
By a straightforward calculation, one can get
It follows that
Therefore, the dynamic equation of the switching system (2.4) on the sliding mode domain is
There exists one positive equilibrium $ {E_c} = \left({{y_c}, {E_T}} \right) $, where $ {y_c} = K\left({1 - \frac{{a + p{E_T}}}{r}} \right) $. We can easily obtain that $ r > a + p{E_T} $. According to Definition 2.2, the equilibrium $ {E_c} $ is referred to as a pseudo-equilibrium.
When $ {y_{21}} < {y_c} < {y_{11}} $, we have
and
Clearly, $ {y_{21}} < {y_c} < {y_{11}} $ is equivalent to
$ \left({i.e., {z_{11}} < {E_T} < {z_{21}}} \right) $. Thus, the equilibrium $ {E_c} $ is located on the sliding segment $ \Sigma _s^1 $ when $ {{z_{11}} < {E_T} < {z_{21}}} $. It can be readily confirmed that $ {cyz}/{(1+hy)} < 0 $ holds on the segment $ \Sigma _s^2 $. Similariy, if $ {y_{12}} < {y_c} < {y_{22}} $, we conclude that
$ \left({i.e., {z_{22}} < {E_T} < {z_{12}}} \right) $. Under this circumstance, the pseudo-equilibrium $ {E_c} $ is located on the sliding segment $ \Sigma _s^2 = \left\{ {\left. {\left({y, z} \right)} \right|{y_{12}} < y < {y_{22}}, z = {E_T}} \right\} $ for $ {{z_{22}} < {E_T} < {z_{12}}} $, meanwhile, we can get $ {cyz}/{(1+hy)} > 0 $ holds on the segment $ \Sigma _s^1 $.
Theorem 3.1. If $ {{z_{11}} < {E_T} < {z_{21}}} $, system (2.4) has one pseudo-equilibrium $ {E_c} = \left({K\left({1 - \frac{{a + p{E_T}}}{r}} \right), {E_T}} \right) $ on the sliding segment $ \Sigma _s^1 $, which is always $ LAS $ when it exists; analogously, if $ {{z_{22}} < {E_T} < {z_{12}}} $, then pseudo-equilibrium $ {E_c} $ is $ LAS $ on the sliding segment $ \Sigma _s^2 $.
Proof. Without loss of generality, we only consider the proof for the first case. Let $ y' = ry\left({1 - \frac{y}{K}} \right) - ay - pyz \buildrel.\over = g\left(y \right) $. Substituting $ H = z-{E_T} = 0 $ into the $ g\left(y \right) $, we will get $ g\left(y \right) = - \frac{r}{K}{y^2} + \left({r - a - p{E_T}} \right)y $. Based on the function $ g\left(y \right) $, we know $ g\left({{y_{21}}} \right) > 0, g\left({{y_{11}}} \right) < 0 $. Further, we note that $ y' = g\left(y \right) $, then $ g'\left(y \right) = - \frac{{2r}}{K}y + \left({r - a - p{E_T}} \right) $. Naturally $ g'\left({{y_c}} \right) = - \frac{{2r}}{K} \cdot K\left({1 - \frac{{a + p{E_T}}}{r}} \right) + \left({r - a - p{E_T}} \right) = - r + a + p{E_T} < 0 $, which implies that $ {E_c} $ is $ LAS $. Thus, the equilibrium $ {E_c} $ is locally stable provided it is feasible. Likewise, we can use a similar method to prove $ {E_c} $ is $ LAS $ on the $ \Sigma _s^2 $.
4.
Global dynamics of system (2.3)
This part focuses on examining the global dynamics of a switching system. To certify the global stability of the equilibrium of the system (2.4), it is necessary to rule out the presence of limit cycles. Firstly, we let the Dulac function be $ V\left({y, z} \right) = {1}/{yz} $. For subsystem $ \mathbb{S}^i $$ \left({i = 1, 2} \right) $, this gives $ \frac{\partial }{{\partial y}}\left({V\left({y, z} \right)\frac{{dy}}{{dt}}} \right){\rm{ + }}\frac{\partial }{{\partial z}}\left({V\left({y, z} \right)\frac{{dz}}{{dt}}} \right) = - \frac{r}{{zK}} < 0 $. Based on the Dulac-Bendixson criterion, it can be concluded that there are no limit cycles present. Consequently, we can derive the following Lemma 4.1.
Lemma 4.1. There exists no limit cycle that is entirely situated within the region $ S^i $$ \left({i = 1, 2} \right) $.
Next, we will exclude limit cycles that intersect with the sliding segment or surrounding the whole sliding segment. Note that this exclusion is necessary for us to follow up with better explanations.
Lemma 4.2. There does not exist a limit cycle that includes a portion of the sliding segment.
Proof. We need to establish the proofs of Lemma 4.2 for the cases $ {E_T} > {z_{21}} $, $ {z_{11}} < {E_T} < {z_{21}} $, $ {z_{12}} < {E_T} < {z_{11}} $, $ {z_{22}} < {E_T} < {z_{12}} $, and $ 0 < {E_T} < {z_{22}} $.
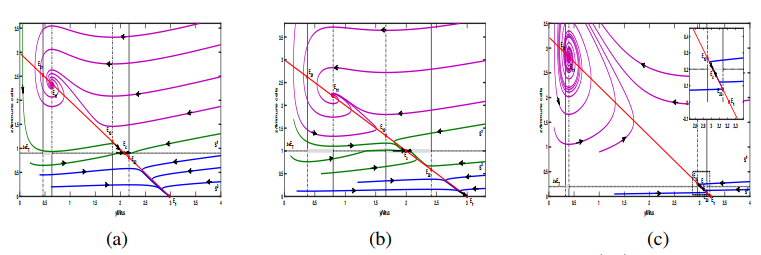
If $ {E_T} > {z_{21}}, $ the absence of pseudo-equilibrium is deduced from the demonstration of Theorem 3.1, which indicates the presence of $ dy/dt < 0 $ on the sliding segments $ \Sigma _s^i\left({i = 1, 2} \right) $ under such circumstances. Therefore, any trajectory reaching $ \Sigma _s^1 $ or $ \Sigma _s^2 $ will approach the boundary points $ \left({{y_{21}}, {E_T}} \right) $, and $ {E_{21}} $ is a real stable node. Note that $ \left({{y_{21}}, {E_T}} \right) $ is visible $ \Sigma $-fold points of subsystem $ \mathbb{S}^2 $ (see Definition 2.4 in Section 2). Thus, the trajectory initiating at $ \left({{y_{21}}, {E_T}} \right) $ tends to either approach the stable state $ {E_{21}} $ directly or in a spiral manner [shown in Figure 1(a)], without touching the switching line again. Therefore, there are no closed orbits that include any part of the sliding segment.
If $ {z_{11}} < {E_T} < {z_{21}} $, we know that the pseudo-equilibrium $ {E_c} $ is $ LAS $ on the segment $ \Sigma _s^1 $ (see Theorem 3.1 in Section 3) under this scenario, which means the nonexistence of a limit cycle that contains part of the sliding segment $ \Sigma _s^1 $. Beyond that, there is $ dy/dt < 0 $ on the segment $ \left\{ {\left. {\left({y, z} \right)} \right|{y_{12}} < y < {y_{22}}, z = {E_T}} \right\} $ when $ {z_{11}} < {E_T} < {z_{21}} $. This implies that the orbits reaching sliding segment $ \Sigma _s^2 $ firstly slide towards the boundary point $ \left({{y_{12}}, {E_T}} \right) $, which is a visible $ \Sigma $-fold point as well, enter into the $ {S^1} $, and then tend to $ {E_c} $. Therefore, there exists no limit cycle incorporating any portion of the sliding segment.
If $ {z_{12}} < {E_T} < {z_{11}} $, there exists one real stable equilibrium $ {E_{11}} $ in region $ {S^1} $. Thus, we can employ a way similar to that applied in the first case to demonstrate the conclusion [shown in Figure 1(b)].
If $ {z_{22}} < {E_T} < {z_{12}} $, we have that pseudo-equilibrium $ {E_c} $ is $ LAS $ on the sliding segment $ \Sigma _s^2 $. We get $ dy/dt > 0 $ on the segment $ \Sigma _s^1 $ in this case. Clearly, the proof process is similar to the second case, so we have omitted here.
If $ 0 < {E_T} < {z_{22}} $, we know that there is no pseudo-equilibrium, and $ dy/dt > 0 $ holds on the sliding segments $ \Sigma _s^i\left({i = 1, 2} \right) $, since there exists a stable equilibrium $ {E_{1}} $, and $ \left({{y_{22}}, {E_T}} \right) $ is visible $ \Sigma $-fold point. Thus, the orbits starting from segments $ \Sigma _s^i\left({i = 1, 2} \right) $ move from the left to the right along the sliding line to the boundary point $ \left({{y_{22}}, {E_T}} \right) $. Then, they proceed into region $ {S^1} $ and eventually converge to $ {E_{1}} $, without experiencing hitting the switching line $ z = {E_T} $ again. Thus, the proof for Lemma 4.2 is thereby completed.
Significantly, the following lemma is similar to previous studies [37,38], which is obtained by constructing a cycle around the sliding segment and then using the method of counter-evidence to draw a contradiction.
Lemma 4.3. There exists no closed orbit containing the whole sliding segment.
Combined with analysis in Section 2, we obtain the two sets of key parameters, i.e., $ {R_0}, {R_{{c_1}}}, {R_{{c_2}}} $, and $ {c_2}, {c_4}, {c^ * }, {c^{ * * }}, {c^\dagger }, {c^{\dagger \dagger }} $. They are the crucial elements that determine the dynamic behavior of the system (2.4). Next, we will discuss the global dynamics of the proposed piecewise system based on the relationships between the parameters mentioned earlier. Considering that there exists only one uninfected equilibrium $ {E_0} $ for both subsystem $ \mathbb{S}^1 $ and $ \mathbb{S}^2 $ when $ {R_0} < 1 $, we will not delve further into it. Here, we will focus on the following situations:
Case(a): $ {R_0} > {R_{{c_1}}} > {R_{{c_2}}} > 1 $,
Case(b): $ {R_{{c_1}}} > {R_{{c_2}}} > {R_0} > 1 $,
Case(c): $ {R_{{c_1}}} > {R_0} > {R_{{c_2}}} > 1 $.
4.1. The global dynamics for Case $ \left(a \right) $
The global dynamics for Case $ \left(a \right) $ are the main focus of this section. Note that the analysis methods for the three cases are analogous, thus we have omitted detailed proofs for the other cases. According to the results in Section 2, it can be seen that the relationship between immune intensity $ c $ and parameters $ {c_2}, {c_4}, {c^ * }, {c^{ * * }}, {c^\dagger }, {c^{\dagger \dagger }} $ have a significant impact on the dynamics of the system (2.4). Through direct analysis, we will consider the under situations:
To understand the dynamics of the system (2.4) more comprehensively, we present the stabilities of various equilibriums completely in Table 3, considering that the dynamics of the system also depend on the relationship between threshold $ {{E_T}} $ and $ {z_{11}}, {z_{12}}, {z_{21}} $, and $ {z_{22}} $. Thus, we have the following threshold levels:
4.1.1. $ Case\left({a1} \right): {E_T} > {z_{21}} $
In such a case, if equilibriums $ {E_{11}}, {E_{12}}, {E_{21}} $, and $ {E_{22}} $ exist, it can be noted that $ {E_{11}} $ and $ {E_{12}} $ are virtual, whereas $ {E_{21}} $ and $ {E_{22}} $ are real, with $ {E_{21}} $ being $ LAS $. We will examine the following six cases in the light of the connections between $ c $ and $ {c_4}, {c_2}, {c^{\dagger \dagger }}, {c^{ * * }}, {c^\dagger }, {c^ * } $.
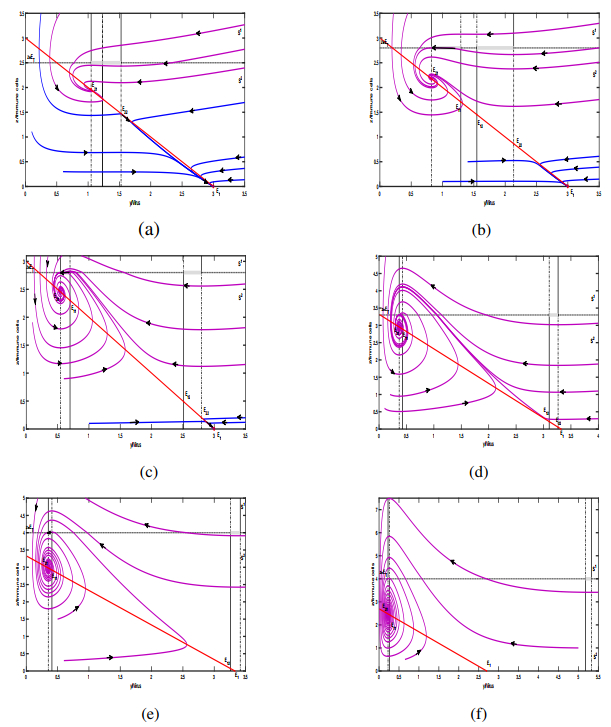
Subcase (ⅰ): Assume $ {c_4} < c < {c_2} $, here we know $ {E_1} $ is $ LAS $. Note that equilibria $ {E_{11}} $ and $ {E_{12}} $ do not exist under this scenario. All the orbits in $ {S^1} $ will reach the switching line $ z = {E_T} $ within a finite amount of time, then firstly enter $ {S^2} $ and ultimately approach either $ {E_{21}} $ or $ {E_{1}} $ [shown in Figure 2(a)], contingent upon their initial positions. Thus, the $ {E_{21}} $ and $ {E_{1}} $ are bistable in this particular scenario.
Subcase (ⅱ): Assume $ {c_2} < c < {c^{\dagger \dagger }} $, we have immune-free equilibrium $ {E_1} $ is $ LAS $ in subsystem $ \mathbb{S}^2 $. According to Lemma 4.2, there exists $ dy/dt < 0 $ on the $ \Sigma _s^i\left({i = 1, 2} \right) $ when ET exceeds $ {z_{21}} $. Therefore, all the orbits of subsystem $ \mathbb{S}^1 $ will slide from right to left to the $ \left({{y_{21}}, {E_T}} \right) $ or $ \left({{y_{12}}, {E_T}} \right) $ when they reach the sliding segments, and finally tend to $ {E_{21}} $. Hence, $ {E_{21}} $ and $ {E_{1}} $ are bistable [illustrated in Figure 2(b)].
Subcase (ⅲ): Assume $ {c^{\dagger \dagger }} < c < {c^{ * * }} $, here we have equilibrium $ {E_1} $, real equilibrium $ {E_{21}} $ are $ LAS $. In this subcase, system (2.4) has the same bistable behavior as the previous case [shown in Figure 2(c)].
Subcase (ⅳ): Assume $ {c^{ * * }} < c < {c^\dagger } $, we get that $ {E_1} $ is $ US $, and there is only one stable equilibrium $ {E_{21}} $. Thus, any orbit starting from region $ {S^1} $ firstly crosses the switching line $ z = {E_T} $ and enters $ {S^2} $, following the dynamics of $ \mathbb{S}^2 $ tends to $ {E_{21}} $. Additionally, Lemmas 4.1–4.3 confirms the absence of a limit cycle, implying that all trajectories ultimately converge to $ {E_{21}} $. Therefore, it can be concluded that the equilibrium $ {E_{21}} $ is $ GAS $ [shown in Figure 2(d)].
Subcase (ⅴ): Assume $ {c^\dagger } < c < {c^ * } $. In such a subcase, we know equilibrium $ {E_{22}} $ does not exist. In consideration of the nonexistence of the limit cycle, $ {E_{21}} $ becomes a glocally stable equilibrium [shown in Figure 2(e)].
Subcase (ⅵ): Assume $ c > {c^ * } $. Under this scenario, we know equilibria $ {E_{12}} $ and $ {E_{22}} $ do not exist. That is, there exists not any other stable equilibrium other than $ {E_{21}} $. Considering that the existence of the limit cycle is excluded, endemic equilibrium $ {E_{21}} $ is $ GAS $ [shown in Figure 2(f)]. The dynamics of the system (2.4) can be summarized below when $ {E_T} > {z_{21}} $.
Theorem 4.1. Suppose $ {E_T} > {z_{21}} $, it can be deduced that both $ {E_{21}} $ and $ {E_1} $ are bistable for $ {c_4} < c < {c_2}, {c_2} < c < {c^{\dagger \dagger }}, {c^{\dagger \dagger }} < c < {c^{ * * }} $; positive equilibrium $ {E_{21}} $ is $ GAS $ for $ {c^{ * * }} < c < {c^\dagger } $, $ {c^\dagger } < c < {c^ * } $ and $ c > {c^ * } $.
4.1.2. $ Case\left({a2} \right) $: $ {z_{11}} < {E_T} < {z_{21}} $
In such a case, if equilibriums $ {E_{11}}, {E_{12}}, {E_{21}} $, and $ {E_{22}} $ exist, we have $ {E_{11}} $, $ {E_{12}} $, $ {E_{21}} $ are virtual, while $ {E_{22}} $ is real but $ US $. Meanwhile, our analysis reveals the occurrence of sliding mode and the emergence of pseudo-equilibrium within the sliding segment $ \Sigma _s^1 = \left\{ {\left. {\left({y, z} \right)} \right|{y_{21}} < y < {y_{11}}, z = {E_T}} \right\} $. By Theorem 3.1, we know that the pseudo-equilibrium $ {E_c} $ is $ LAS $ when it exists. Likewise, we will analyze the following six scenarios.
Subcase (ⅰ): Assume $ {c_4} < c < {c_2} $. We know equilibria $ {E_{11}} $ and $ {E_{12}} $ do not exist, then we have omitted the description for this case.
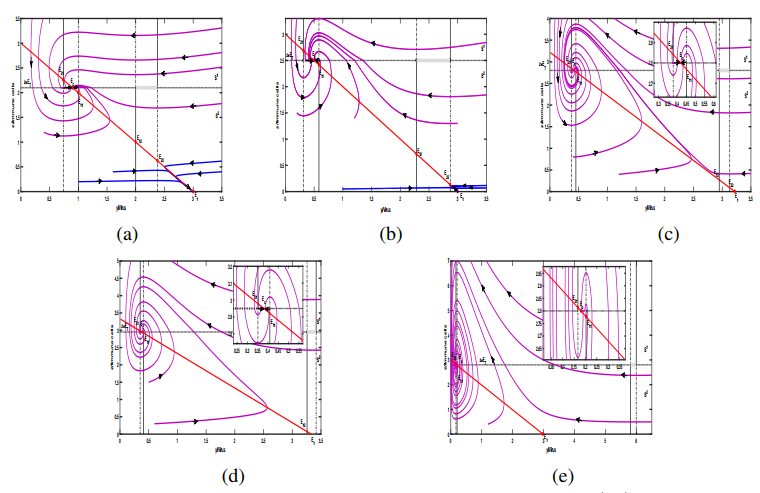
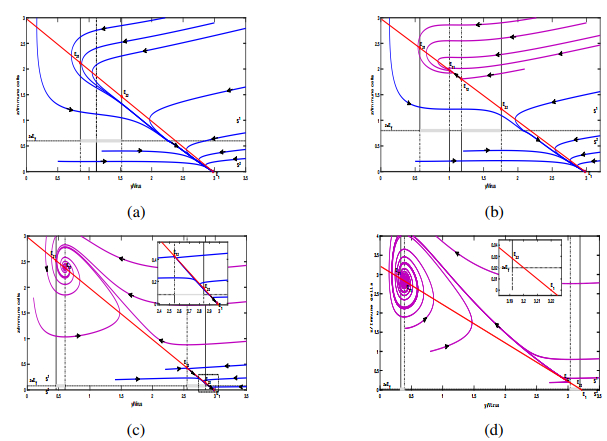
Subcase (ⅱ): Assume $ {c_2} < c < {c^{\dagger \dagger }} $. In such a subcase, $ {E_1} $ is $ LAS $ in the subsystem $ \mathbb{S}^2 $ and the pseudo-equilibrium will appear on the sliding segment $ \Sigma _s^1 $. Thus, the partial orbits starting from region $ {S^1} $ will follow the dynamics of $ \mathbb{S}^1 $ to the sliding segment $ \left\{ {\left. {\left({y, z} \right)} \right|{y_{21}} < y < {y_c}, z = {E_T}} \right\} $, whereas partial trajectories starting from subsystem $ \mathbb{S}^2 $ will arrive at the segment $ \left\{ {\left. {\left({y, z} \right)} \right|{y_c} < y < {y_{11}}, z = {E_T}} \right\} $ along the $ \mathbb{S}^2 $, depending on the initial point, and both types of orbits will eventually converge toward pseudo-equilibrium $ {E_c} $. Therefore, we conclude that $ {E_c} $ and $ {E_1} $ are bistable [shown in Figure 3(a)].
Subcase (ⅲ): Assume $ {c^{\dagger \dagger }} < c < {c^{ * * }} $. In such a subcase, we get that both pseudo-equilibrium $ {E_c} $ on the sliding segment $ \Sigma _s^1 $ and equilibrium $ {E_1} $ are $ LAS $. Thus, we can obtain the coincident conclusion by using similar ways of discussion. That is, the orbits will either go to $ {E_c} $ or tend to $ {E_1} $ along the subsystem $ \mathbb{S}^1 $ and $ \mathbb{S}^2 $, respectively [shown in Figure 3(b)].
Subcase (ⅳ): Assume $ {c^{ * * }} < c < {c^\dagger } $. In such a subcase, $ {E_c} $ is the only stable equilibrium for the system (2.4). Our findings reveal that all trajectories intersecting with the line $ z = {E_T} $ and following the sliding segment $ \Sigma _s^1 $ reach the pseudo-equilibrium $ {E_c} $. Considering that a limit cycle does not exist for the entire system, we can conclude that $ {E_c} $ is $ GAS $ [illustrated in Figure 3(c)].
Subcase (ⅴ): Assume $ {c^\dagger } < c < {c^ * } $. In such a subcase, we know $ {E_{22}} $ does not exist and the pseudo-equilibrium $ {E_c} $ is $ LAS $. Here, we have immune-free equilibrium $ {E_1} $ is $ US $. Equally, system (2.4) does not exist any limit cycle. Then the equilibrium $ {E_c} $ is $ GAS $ [shown in Figure 3(d)].
Subcase (ⅵ): Assume $ c > {c^ * } $. Under this condition, equilibria $ {E_{12}} $ and $ {E_{22}} $ do not exist. There is only one stable equilibrium $ {E_c} $ in the switching system (2.4). Considering the exclusion of closed orbit, then $ {E_c} $ is $ GAS $ [illustrated in Figure 3(e)]. Hence, we summarize the aforementioned conclusion of system (2.4) to the following when $ {z_{11}} < {E_T} < {z_{21}} $.
Theorem 4.2. Suppose $ {z_{11}} < {E_T} < {z_{21}} $, we can conclude that system (2.4) has bistable behavior, i.e., immune-free equilibrium $ {E_1} $ and pseudo-equilibrium $ {E_c} $ are $ LAS $ for $ {c_2} < c < {c^{\dagger \dagger }}, {c^{\dagger \dagger }} < c < {c^{ * * }} $; equilibrium $ {E_c} $ is $ GAS $ for $ {c^{ * * }} < c < {c^\dagger } $, $ {c^\dagger } < c < {c^ * } $ and $ c > {c^ * } $.
4.1.3. $ Case\left({a3} \right) $: $ {z_{12}} < {E_T} < {z_{11}} $
In such a case, if equilibriums $ {E_{11}}, {E_{12}}, {E_{21}}, {E_{22}} $ exist, we get $ {E_{12}} $ and $ {E_{21}} $ are virtual, but $ {E_{11}} $ and $ {E_{22}} $ are real, where $ {E_{11}} $ is $ LAS $ in the $ \mathbb{S}^1 $. We prove the existence of sliding mode but there is no pseudo-equilibrium. Next, we will analyze the stability of equilibria based on the connections between $ c $ and $ {c_4}, {c_2}, {c^{\dagger \dagger }}, {c^{ * * }}, {c^\dagger }, {c^ * } $.
Subcase (ⅰ): Assume $ {c_4} < c < {c_2} $. Under this scenario, it follows from Section 2 that the two equilibria $ {E_{11}} $ and $ {E_{12}} $ are not feasible. So we can omit the description for this case.
Subcase (ⅱ): Assume $ {c_2} < c < {c^{\dagger \dagger }} $. In such a subcase, $ {E_1} $ is $ LAS $ and $ {E_{11}} $ is a real and stable equilibrium, since subsystem $ \mathbb{S}^1 $ has only one stable endemic state. Thus, trajectories initiating from $ \mathbb{S}^1 $ will intend to approach the equilibrium $ {E_{11}} $. In this scenario, the endemic equilibrium $ {E_{11}} $ can coexist with the immune-free equilibrium $ {E_1} $. That is, system (2.4) has bistable behavior [shown in Figure 4(a)].
Subcase (ⅲ): Assume $ {c^{\dagger \dagger }} < c < {c^{ * * }} $. Regarding the presence and stability of the equilibriums, the dynamics exhibited by subsystems $ \mathbb{S}^1 $ and $ \mathbb{S}^2 $ resemble those of the former scenario [shown in Figure 4(b)]. Thus, we get that $ {E_{11}} $ and $ {E_1} $ are bistable for the Filippov system (2.4).
Subcase (ⅳ): Assume $ {c^{ * * }} < c < {c^\dagger } $. In this subcase, the equilibrium $ {E_{21}} $ is virtual and the system (2.4) only exhibits one stable endemic equilibrium $ {E_{11}} $. As there is no limit cycle, then $ {E_{11}} $ is GAS [shown in Figure 4(c)].
Subcase (ⅴ): Assume $ {c^\dagger } < c < {c^ * } $. Analogously, there exists only one stable equilibrium point $ {E_{11}} $ in subsystem $ \mathbb{S}^1 $. It should be noted that the endemic equilibrium $ {E_{11}} $ functions as an attractor. We have excluded the existence of limit cycles. Consequently, any orbit starting from region $ \mathbb{S}^1 $ or $ \mathbb{S}^2 $ will approach the equilibrium point $ {E_{11}} $ [shown in Figure 4(d)]. Thus, the equilibrium $ {E_{11}} $ is $ GAS $.
Subcase (ⅵ): Assume $ c > {c^ * } $. In this scenario, since the equilibria $ {E_{12}} $ and $ {E_{22}} $ do not exist, we have omitted the description for this case and we get the following conclusion.
Theorem 4.3. Suppose $ {z_{12}} < {E_T} < {z_{11}} $, we can conclude that immune-free equilibrium $ {E_1} $ and endemic equilibrium $ {E_{11}} $ are bistable for $ {c_2} < c < {c^{\dagger \dagger }} $ and $ {c^{\dagger \dagger }} < c < {c^{ * * }} $; equilibrium $ {E_{11}} $ is $ GAS $ for $ {c^{ * * }} < c < {c^\dagger } $ and $ {c^\dagger } < c < {c^ * } $.
4.1.4. $ Case\left({a4} \right) $: $ {z_{22}} < {E_T} < {z_{12}} $
In such a case, if equilibriums $ {E_{11}}, {E_{12}}, {E_{21}} $, and $ {E_{22}} $ exist, we have $ {E_{21}} $ is virtual, while $ {E_{11}} $, $ {E_{12}} $, and $ {E_{22}} $ are real. Note that both equilibriums $ {E_{12}} $ and $ {E_{22}} $ are $ US $. Furthermore, the sliding mode does exist, and the pseudo-equilibrium $ {E_c} $ is $ LAS $ on the $ \Sigma _s^2 $. A similar discussion works for $ {z_{22}} < {E_T} < {z_{12}} $.
Subcase (ⅰ): Assume $ {c_4} < c < {c_2} $, we know equilibria $ {E_{11}} $ and $ {E_{12}} $ do not exist according to Section 2. Therefore, we can ignore the explanation of this situation.
Subcase (ⅱ): Assume $ {c_2} < c < {c^{\dagger \dagger }} $. In such a subcase, $ {E_1} $ is $ LAS $ and $ {E_{11}} $ is real and stable in $ \mathbb{S}^1 $. As mentioned above, the pseudo-equilibrium $ {E_c} $ is $ LAS $. From the dynamics of subsystems $ \mathbb{S}^2 $ and $ \mathbb{S}^1 $, it can be deduced that the orbits will either directly reach the $ {E_{11}} $, $ {E_1} $ or firstly arrive at the line $ z = {E_T} $ on the segment $ \left\{ {\left. {\left({y, z} \right)} \right|{y_{12}} < y < {y_{22}}, z = {E_T}} \right\} $, then slide to the $ {E_c} $ along sliding segment $ \Sigma _s^2 $, depending on the initiating points. Hence, as is shown in Figure 5(a), the equilibriums $ {E_{11}} $, $ {E_c} $, and $ {E_1} $ are tristable.
Subcase (ⅲ): Assume $ {c^{\dagger \dagger }} < c < {c^{ * * }} $. In such a subcase, we get that the equilibrium $ {E_1} $ is $ LAS $, and there exist two equilibria $ {E_{11}} $ and $ {E_c} $, which are locally stable in their respective regions. Thus, we can conclude that the dynamic behaviors in this scenario are consistent with the former subcase. That is, system (2.4) has tristable behavior in this case [shown in Figure 5(b)].
Subcase (ⅳ): Assume $ {c^{ * * }} < c < {c^\dagger } $. Note that the locally stable equilibrium $ {E_{21}} $ is virtual, then cannot be attained. Part of the trajectories starting from subsystem $ \mathbb{S}^1 $ will approach the equilibrium $ {E_{11}} $, while certain trajectories will collide on the switching line at finite time, and the locally stable pseudo-equilibrium $ {E_c} $ appears ultimately on the segment $ \Sigma _s^2 = \left\{ {\left. {\left({y, z} \right)} \right|{y_{12}} < y < {y_{22}}, z = {E_T}} \right\} $. Hence, they are bistable for the switching system (2.4) [shown in Figure 5(c)].
Subcase (ⅴ): Assume $ {c^\dagger } < c < {c^ * } $. We know equilibrium $ {E_{22}} $ does not exist, then we rule this out.
Subcase (ⅵ): Assume $ c > {c^ * } $. In such a subcase, we know equilibria $ {E_{12}} $ and $ {E_{22}} $ do not exist, so we have omitted the description in this case as well. To sum up, we can derive the conclusion as follows.
Theorem 4.4. Suppose $ {z_{22}} < {E_T} < {z_{12}} $, we can conclude that the real equilibrium $ {E_{11}} $, pseudo-equilibrium $ {E_c} $, and the immune-free equilibrium $ {E_1} $ are tristable for $ {c_2} < c < {c^{\dagger \dagger }} $ and $ {c^{\dagger \dagger }} < c < {c^{ * * }} $; immune-free equilibrium $ {E_{11}} $ and pseudo-equilibrium $ {E_c} $ are bistable for $ {c^{ * * }} < c < {c^\dagger } $.
4.1.5. $ Case\left({a5} \right) $: $ 0 < {E_T} < {z_{22}} $
In such a case, if equilibriums $ {E_{11}}, {E_{12}}, {E_{21}} $, and $ {E_{22}} $ exist, we have $ {E_{21}} $ and $ {E_{22}} $ are virtual, but $ {E_{11}} $, $ {E_{12}} $ are real, where $ {E_{11}} $ is $ LAS $ in the $ \mathbb{S}^1 $. Under this scenario, there is no pseudo-equilibrium for the Filippov system (2.3). Subsequently, we will analyze the following situations based on the relationships between immune intensity $ c $ and $ {c_4}, {c_2}, {c^{\dagger \dagger }}, {c^{ * * }}, {c^\dagger }, {c^ * } $.
Subcase (ⅰ): Assume $ {c_4} < c < {c_2} $. In this condition, we get that equilibria $ {E_{11}} $ and $ {E_{12}} $ do not exist on the basis of the discussion of Section 2. Note that the locally stable equilibrium $ {E_{21}} $ is virtual. Thus, there is not any other stable equilibrium besides $ {E_1} $, as all the possible limit cycles have been excluded. Hence, we have $ {E_1} $ is $ GAS $ [shown in Figure 6(a)].
Subcase (ⅱ): Assume $ {c_2} < c < {c^{\dagger \dagger }} $. In such a subcase, $ {E_1} $ is $ LAS $ and $ {E_{11}} $ is a real and stable equilibrium. However, $ {E_{21}} $ is virtual in $ \mathbb{S}^1 $. Thus, positive equilibrium $ {E_{11}} $ and immune-free equilibrium $ {E_1} $ are bistable for $ {c_2} < c < {c^{\dagger \dagger }} $ being satisfied [shown in Figure 6(b)].
Subcase (ⅲ): Assume $ {c^{\dagger \dagger }} < c < {c^{ * * }} $. We know that equilibria $ {E_{11}} $ and $ {E_1} $ are $ LAS $ as well. Thus, the dynamics of this case are similar to the former, i.e., the bistable behavior occurs [shown in Figure 6(c)].
Subcase (ⅳ): Assume $ {c^{ * * }} < c < {c^\dagger } $. In such a subcase, note that locally stable equilibrium $ {E_{21}} $ is virtual and then cannot be attained. There exists only one stable equilibrium point $ {E_{11}} $ in subsystem $ \mathbb{S}^1 $. As there is no limit cycle, we obtain that the equilibrium $ {E_{11}} $ is $ GAS $ [illustrated in Figure 6(d)].
Subcase (ⅴ): Assume $ {c^\dagger } < c < {c^ * } $. In such a subcase, we know that equilibrium $ {E_{22}} $ does not exist, so we have ignored the description of this situation.
Subcase (ⅵ): Assume $ c > {c^ * } $. In such a subcase, both $ {E_{12}} $ and $ {E_{22}} $ do not exist, therefore, the explanation for this case is omitted. Consequently, we arrive at the subsequent conclusion.
Theorem 4.5. Suppose $ 0 < {E_T} < {z_{22}} $, we can conclude that immune-free equilibrium $ {E_1} $ is $ GAS $ for $ {c_4} < c < {c_2} $; the real equilibrium $ {E_{11}} $ and immune-free equilibrium $ {E_1} $ are bistable for $ {c_2} < c < {c^{\dagger \dagger }} $ and $ {c^{\dagger \dagger }} < c < {c^{ * * }} $; the equilibrium $ {E_{11}} $ is $ GAS $ for $ {c^{ * * }} < c < {c^\dagger } $.
In fact, extensive discussions have been conducted on the stability of various equilibriums for the switching system (2.4) under Case(a). Furthermore, Table 4 provides a comprehensive summary of the global dynamics associated with these specific cases.
5.
Boundary equilibrium bifurcation
Notably, the collision of pseudo-equilibrium, tangent point, and regular equilibrium (or tangent point and regular equilibrium) in switching systems occurs when $ {{E_T}} $ reaches a critical value, leading to boundary equilibrium bifurcations on the discontinuity surface [as shown in Figure 7]. The understanding and analysis of these boundary equilibrium bifurcations are crucial in studying the dynamical behavior of the Filippov system. To verify the boundary equilibrium bifurcation, we select $ {{E_T}} $ as the bifurcation parameter while keeping all other parameters constant. Detailed explanations of the boundary equilibrium and the tangent point are shown in Definitions 2.3 and 2.5.
Boundary equilibrium of the Filippov system (2.4) satisfies
where $ \phi = 0 $ or $ \phi = 1 $. By solving the equations provided in (5.1), it is possible to obtain four potential boundary equilibria
Tangent points of the Filippov system (2.4) satisfy
Thus, the potential tangent points can be denoted as
which are the solutions of (5.4) corresponding to $ \phi = 0 $ and $ \phi = 1 $.
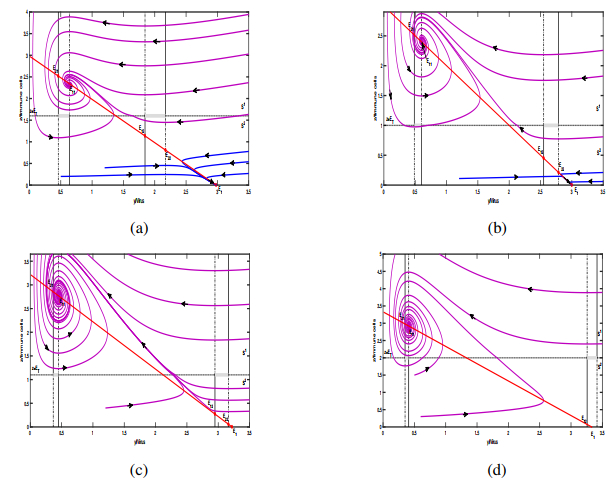
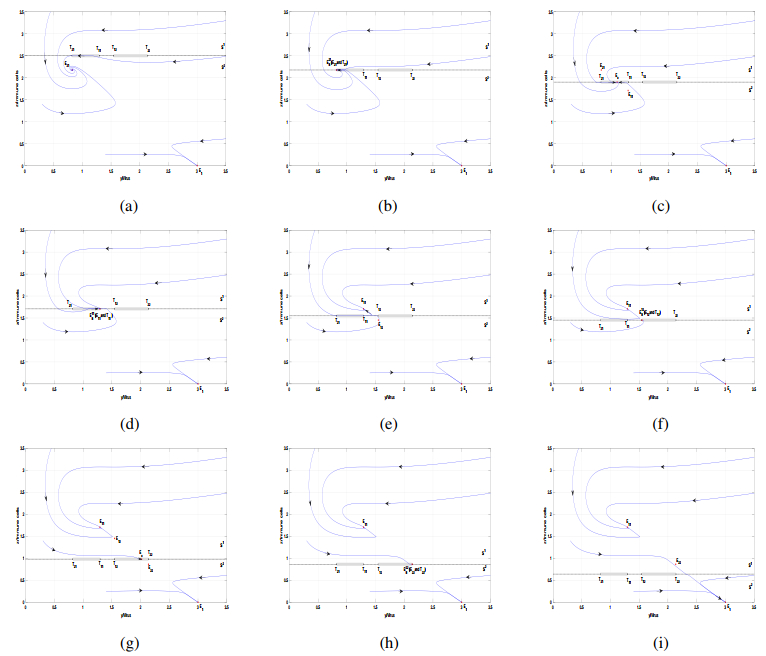
Figure 7 examines a series of boundary equilibrium bifurcations when $ {c_2} < c < {c^{\dagger \dagger }} $. In this case, both subsystems have two positive equilibria. The real and stable equilibrium $ {E_{21}} $ coexists simultaneously with the visible tangent point $ {T_{21}} $ when $ {E_T} > {z_{21}} $ [shown in Figure 7(a)]. As $ {{E_T}} $ decreases from $ {E_T} > {z_{21}} $ to $ {z_{21}} $, $ {E_{21}} $ collides with $ {T_{21}} $ [shown in Figure 7(b)]. With the threshold $ {{E_T}} $ decreasing further to $ {z_{11}} < {E_T} < {z_{21}} $, a stable pseudo-equilibrium $ {E_c} $ emerges and $ {T_{21}} $ transforms into an invisible tangent point [as depicted in Figure 7(c)]. This bifurcation exhibits the progress of the formation of $ {E_c} $. Furthermore, boundary bifurcation takes place again when $ {{E_T}} $ through the critical value $ {z_{11}} $. This case results in the collision of the tangent point $ {T_{11}} $, the equilibrium point $ {E_{11}} $ with the pseudo-equilibrium point $ {E_c} $ [as depicted in Figure 7(d)]. Subsequently, the $ {E_c} $ vanishes, and the stable point $ {E_{11}} $ transforms into the local attractor [as illustrated in Figure 7(e)]. When $ {{E_T}} $ drops consistently until $ {z_{12}} $, the third boundary bifurcation takes place, leading to the collision of the visible tangent point $ {T_{12}} $ with the equilibriums $ {E_{12}} $ [as depicted in Figure 7(f)].
Provided $ {{E_T}} $ continues to decrease until $ {z_{22}} < {E_T} < {z_{12}} $, a locally stable pseudo-equilibrium $ {E_c} $ appears [as shown in Figure 7(g)] and a tristable phenomenon ($ {E_c} $, $ {E_{11}} $, and the immune-free equilibrium $ {E_1} $) occurs. When $ {{E_T}} $ passes $ {E_{22}} $, the fourth boundary equilibrium bifurcation occurs. In this scenario, the pseudo-equilibrium $ {E_c} $ will collide with the equilibrium point $ {E_{22}} $ and tangent point $ {T_{22}} $ if $ {E_T} = {z_{22}} $ [illustrated in Figure 7(h)]. However, as the threshold $ {{E_T}} $ continues to decrease, the equilibrium $ {E_c} $ disappears, and the tangent point $ {T_{22}} $ becomes invisible [illustrated in Figure 7(i)]. Here, the equilibriums $ {E_1} $ and $ {E_{11}} $ exhibit bistability under this scenario.
6.
The influence of the pivotal parameters of the system (2.4)
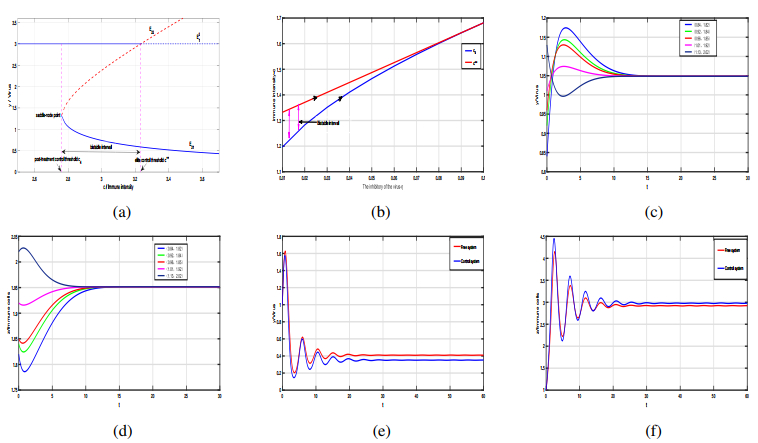
In order to stabilize the HIV viral loads and effector cell counts within the required predetermined level, it is crucial to implement a control strategy for the switching system (2.4) by setting an appropriate threshold $ {E_T} $. The dynamics of the system are influenced by two key parameters: The immune intensity $ c $ and the inhibition of the virus on the proliferation of immune cells $ \eta $. Therefore, it is important to study the impact of these parameters on the system's dynamics. Note that the parameters in this study are based on the findings of Komarova[33] and colleagues. A direct calculation reveals that the bistable interval is (2.7666, 3.2333) [shown in Figure 8(a)]. From this figure, it is evident that system (2.4) has the potential to have either one or two nontrivial $ LAS $ equilibria depending on the value of $ c $. In detail, two stable equilibriums $ E_1^2 $ and $ {E_{21}} $ coexist when $ {c_4} < c < {c^{\dagger \dagger }} $. As established in Section 2, there is a unique $ LAS $ equilibrium $ {E_{21}} $ if $ c > {c^{\dagger \dagger }} $. It is important to note that a saddle-node bifurcation occurs at $ c = {c_4} $. Generally, a longer bistable interval implies a wider range of variation for the proliferation coefficient $ c $ of immune cells. In this context, a lower viral inhibition intensity $ \eta $ [shown in Figure 8(b)] is more advantageous for immune control. This indicates the necessity of developing medications aimed at diminishing the viral inhibitory effect on immune cells. The phase portrait of this system reveals that both variables $ y $ and $ z $ will gradually tend to a stable value over time $ t $ changed [shown in Figures 8(c) and (d)]. In subsystem $ \mathbb{S}^2 $, the combination of antiretroviral therapy and immunotherapy not only controlled the number of viruses better but also stabilized the immune cell count at a more reliable level than the free system, as can be seen in Figures 8(e) and (f).
7.
Conclusions
Given the immunosuppressive HIV infection model[32,33,34], it is suggested that the threshold policy control (TPC) method for treating infected patients should be based on the number of immune cells. Thus, we propose a piecewise immunosuppressive infection system. We call model (2.4) a discontinuous right-hand side dynamical system under TPC, which consists of two subsystems. Specifically, it is recommended to initiate a combination of antiretroviral therapy and immune therapy when the value drops below a certain threshold $ {E_T} $, which includes the usage of antiretroviral medications and interleukin (IL)-2. This leads to the emergence of a nonsmooth system. Unlike [31], we consider the logical growth of HIV rather than linear growth in this paper. Some clinical facts indicate that the saturated growth of HIV is reasonable.
Initially, we provide a concise overview of the dynamics exhibited by the two subsystems. Through the subsystems $ \mathbb{S}^i $$ \left({i = 1, 2} \right) $, we derive the thresholds $ {R_0} $, $ {R_{{c_1}}} $, and $ {R_{{c_2}}} $. It becomes evident that $ {R_0} $ plays a pivotal part in determining the eradication of the virus. We also obtain the post-treatment control thresholds $ {c_2} $($ {c_4} $) and the elite control threshold $ {c^{ * * }} $($ {{c^{\dagger \dagger }}} $) for subsystems $ \mathbb{S}^1 $ ($ \mathbb{S}^2 $). According to [34], there exists a bistable behavior between these two threshold intervals. The sliding dynamics and sliding domain of the system (2.4) are studied in the subsequent analysis. Our purpose is to demonstrate the existence of two sliding segments $ \Sigma _s^i\left({i = 1, 2} \right) $. By employing the Filippov convex approach, we investigate the possibility and local asymptotic stability of the pseudo-equilibrium $ {E_c} $ on the sliding segment $ \Sigma _s^1 $ under the $ {z_{11}} < {E_T} < {z_{21}} $, or on the sliding segment $ \Sigma _s^2 $ under the $ {z_{22}} < {E_T} < {z_{12}} $. Significantly, we have primarily focused on Case (a) and discussed the global dynamics of the system in this paper. To investigate the global dynamic behavior of the system, we have excluded the existence of three types of limit cycles. It is important to understand the relationship not only among $ {R_0}, {R_{{c_1}}}, {R_{{c_2}}} $, and $ 1 $ but also among immune intensity $ c $ and $ {c_4}, {c_2}, {c^{\dagger \dagger }}, {c^{ * * }}, {c^\dagger }, {c^ * } $. Subsequently, the bifurcation theories were utilized to address the dynamics of sliding mode and local sliding bifurcations.
The analysis reveals that the system can demonstrate diverse and complex dynamic behaviors: (ⅰ) One of the equilibria in the system is $ GAS $, which can manifest as the immune-free equilibrium $ {E_1} $, pseudo-equilibrium $ {E_c} $, or even as the positive equilibrium $ {E_{11}} $ or $ {E_{21}} $ within subsystems $ \mathbb{S}^1 $ or $ \mathbb{S}^2 $; (ⅱ) There are two possible equilibria in this system that exhibit bistability, namely the immune-free equilibrium $ {E_1} $ and equilibrium $ {E_{21}} $ (or $ {E_c} $ or $ {E_{11}} $), or the positive equilibrium $ {E_{11}} $, which is bistable alongside the pseudo-equilibrium $ {E_c} $; (ⅳ) Three equilibria are tristable, i.e., immune-free equilibrium $ {E_1} $, positive equilibrium $ {E_{11}} $, and the pseudo-equilibrium $ {E_c} $ are stable for $ {z_{22}} < {E_T} < {z_{12}} $ and $ {c_2} < c < {c^{ * * }} $. Our work demonstrates that the utilization of effector cell-guided therapy leads to an expansion of the controllable area of initial values for patients, generating a more complex Filippov dynamics system when compared with [35]. Interestingly, we find that there exists an optimal threshold interval for immune intensity that can maximize the controllable area of initial values. This highlights the importance of considering the effects of effector cell-guided therapy and immune intensity when studying the dynamics of the switching system. It suggests that maximizing the controllable area of initial values can potentially improve the effectiveness of treatment strategies for patients.
In this paper, the existence of three types of equilibria including pseudo-equilibrium is explored. These equilibria can exhibit bistability or tristability, meaning that the HIV viral loads and effector cell counts can be stabilized at a preset level. Achieving these stable states depends on factors such as the threshold level, immune intensity, and the initial values of the system. Consequently, determining the optimal strategy for immune intensity and the threshold conditions should still take into account the individual characteristics of the patients. In the case of boundary $ H\left(X \right) $, the selection of parameter values is crucial in stabilizing different equilibria within the system. From a biological standpoint, employing rational control intensity and intervention is highly effective in ensuring the control and management of diseases.
Although our research has an impact on HIV disease control, it is still insufficient. We only consider the relationship between the number of effector cells and the threshold level to construct switching conditions. The actual disease control strategy should also take into account the change rate of effector cell count, which will be our next work. By considering these factors, we aim to further provide insights into the effectiveness and impact of this treatment approach on the virus-immune system dynamics. This mathematical model could potentially contribute to the improvement of treatment strategies for viral infections.
Use of AI tools declaration
The authors declare that no Artificial Intelligence (AI) tools were used in the creation of this article.
Acknowledgments
This work was supported by The National Natural Science Foundation of China (Grant No. 12261033).
The authors would like to thank the editor and anonymous referees for their valuable comments and suggestions, which have led to an improvement of the paper.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: