A review on tissue-needle interaction and path planning models for bevel tip type flexible needle minimal intervention

1.   Introduction

For the benefit of both the present and future generations, protecting endangered plants and animals as well as maximizing the preservation of the planet's unique biological resources are the main objectives of biodiversity conservation. An increasing number of empirical findings indicate that human-caused environmental deterioration has impacted natural population habitats ^[1]. The habitat of populations is fragmented, split into patches and the populations become extinct. Numerous studies ^[2,3,4] have shown that the creation of ecological corridors between patches is more favorable to the survival of species. Therefore, it is of great importance to study the dispersal behavior of populations.

In 1977, Freedman and Waltman ^[5] studied a source–source system with dispersal. Their study indicated that under certain conditions, the total population abundance of dispersed species may be greater than that of non-dispersed species. Holt ^[6] considered a sink–source system:

where $N_i$ represents the population density of the species in the patch $i$, $i = 1, 2$. The first patch is a sink patch which is not self-sustaining and the second patch is a source. $r_1$ represents the species' death rate in patch 1. Here, the dispersal rate $D$ is symmetric. $\phi_2(N_2)$ is the per-capita growth rate of the species in patch 2, which monotonically declines due to intraspecific competition. Holt showed that if the death rate in the sink patch and the dispersal rate are small, the species persists in the two patches. Otherwise, the species went to extinction in both patches. After that, more and more scholars studied the different types of diffusion between patches. Wang et al. ^[7,8,9] did a series of work on two-species competitive systems with one-species' diffusion between patches. In ^[10], the authors analyzed linear dispersal (the diffusion coefficient is constant) in predator-prey systems with Holling II functional response as follows.

Their study showed that there exists an optimal dispersal that drives the predator into extinction and makes the prey reach the maximal abundance. These results are biologically important when preserving endangered species. On the basis of ^[10], Xia et al. ^[11] proposed and studied a predator-prey model with the prey's dispersal and counter-attack behavior as follows.

Here $k$ is the fear factor and $c$ is the counter-attack rate. Compared with a single strategy, the multiple anti-predator strategies are more beneficial to the persistence and the population density of prey. We notice that in ^[10] and ^[11], the dispersal of the prey between the two patches is linear. Actually, there are several scholars who investigated the non-constant case, i.e., nonlinear dispersal. For example, Xia et al. ^[12] proposed a two-patch model with the Allee effect and nonlinear dispersal:

where $A$ is the Allee effect constant. $D$ is the dispersal coefficient and dispersal is affected by population density. The authors found that the diffusion rate has a certain influence on the solution of the system. When dispersal is high, nonlinear dispersal is more favorable to population survival than linear dispersal. Kang et al. ^[13] formulated a Rosenzweig-MacArthur prey-predator two-patch model with mobility only in the predator and assumed that the predator moves toward patches with more concentrated prey-predator interactions:

where $r_i$ is the intrinsic growth of prey at patch $i$; $k_i$ is the prey carrying capacity in patch $i$; $b_i$ is the predator attacking rate in patch $i$; $h_i$ is the predator handling time in patch $i$; $c_i$ is the energy conversion rate in patch $i$; and $\delta_i$ is the mortality of the predators in patch $i \; (i = 1, 2)$. In the presence of dispersal, the dispersal rate of the predators from patch $i$ to patch $j$ depends on the prey-predator interaction term $\frac{b_jx_jy_j}{1+b_jh_jx_j}$ in patch $j$, and the dispersal term of predators from patch $i$ to patch $j$ is modeled by $\frac{b_jx_jy_j}{1+b_jh_jx_j}\rho_{ij}y_i$ which gives the net dispersal of the predator at patch $i$ as follows: $\frac{b_jx_jy_j}{1+b_jh_jx_j}\rho_{ij}y_i-\frac{b_ix_iy_i}{1+b_ih_ix_i}\rho_{ji}y_j$, where $\rho_{ij}$ is the dispersal constant of predators in patch $j$ moving to patch $i$. The authors showed that dispersal may stabilize or destabilize the coupled system and dispersal may generate multiple interior equilibria that lead to rich bistable dynamics or may destroy interior equilibria that lead to the extinction of predators in one patch or both patches. In 2019, Mai ^[14] proposed the following predator-prey metapopulation model over an arbitrary number of patches:

where $h_i$ and $p_i$ denote the densities of prey and predators in patch $i \ (i = 1, 2, ..., n)$, respectively. $n$ is the total number of patches, $d > 0$ is the rescaled dispersal rate; $\alpha\in[0, 1]$ denotes the fraction of dispersal due to predation avoidance; $\varepsilon > 0$ and $\kappa > 0$ are the rescaled intrinsic growth rate and carrying capacity of the prey, respectively; and a Holling type II functional response function is used where $\gamma > 0$ is the scaling factor associated with the maximum consumption rate and yield constant. The prey's dispersal is due to random effect and avoidance from predators. The authors' results showed that the delay and the patterns of prey dispersal jointly affect the stability of predator-prey metacommunities and can induce multiple stability switches. For more relevant works, one can see ^[15,16,17].

In natural ecosystems, the interaction between predator and prey is one of the most important roles, the predator-prey model has been extensively studied ^[18,19,20]. Some scholars ^[21,22] have argued that the mere presence of a predator may alter the prey's behavior and physiology. Its presence has even more impact than direct predation. In 2016, Wang et al. ^[23] first proposed the following predator–prey model with a fear effect on prey:

where $f(k, v) = \frac{1}{1+kv}$ and the parameter $k$ reflect the degree of the fear effect on the prey from the predators. Furthermore, for the above system, the authors introduced the Holling type II functional response and concluded that the fear effect can lead to population oscillation from supercritical Hopf bifurcation to subcritical Hopf bifurcation. In recent years, more and more works have focused on the fear effect. Liu et al. ^[24,25] proposed a Leslie–Gower model with the Allee effect on prey and fear effect on the predator. Their study demonatrates that compared with the case without a fear effect on the predator, the new model has richer dynamic behavior and various kinds of bifurcations will occur. About the impact of the fear effect on dynamic behaviors of different ecosystems, one can refer to ^[26,27,28] for details. Sarkar et al. ^[29] thought that the fear effect function proposed by Wang et al. ^[23] was not consistent with the ecological status. The authors introduced the fear effect function $f(k, \eta, P) = \eta+\frac{k(1-\eta)}{k+P}$ and proposed the following predator–prey model:

where $k$ represents the level of the fear and $\eta\in[0, 1]$ indicates the minimum cost of the fear effect. $\beta$, $\xi$, $d$, and $\theta$ are the per-capita consumption rate of the predator, the processing time to capture each prey, the mortality rate of the predator, and the conversion rate of prey biomass to predator biomass, respectively. The authors obtained that the fear effect can stabilize the predator-prey system at an interior steady state, or it can create the oscillatory coexistence of all the populations. $f(k, \eta, P)$ is a monotone increasing function with respect to $k$. Namely, as the level of fear effect $k$ increases, the prey reproduction rate increases. From the ecological point of view, the above fear effect function is not reasonable. Dong et al. ^[30] proposed a new fear function $f(k, \eta, y) = \eta+\frac{1-\eta}{1+ky}$ and created a new model as follows.

where $\alpha > 0$ is the predator-taxis sensitivity, which has a positive effect on prey and a negative effect on predator population. For the fear function $f(k, \eta, y) = \eta+\frac{1-\eta}{1+ky}$, it is easy to obtain that $f(k, y)\rightarrow \eta$ as $k\rightarrow \infty$ or $y\rightarrow \infty$. This is why the authors call the parameter $\eta$ the saturated fear cost. The authors found that the fear effect from predators does not cause the extinction of the prey population. Even if the fear effect is sufficiently large, the prey can survive under the saturated fear cost. Furthermore, when choosing the fear level $k$ as a bifurcation parameter, the model will arise a Hopf bifurcation point. However, when the predator-taxis sensitivity $\alpha$ is chosen as a bifurcation parameter, the model will arise two Hopf bifurcation points. The predator-taxis sensitivity determines the success or failure of the predator invasion under an appropriate fear level. After that, Meng et al. ^[31] investigated a predator-prey system incorporating asymmetric dispersal and the fear effect, which influences the birth and death rates of the prey species as follows.

The authors revealed that the fear effect and its maximum cost exhibit significant negative impacts on predator abundance, but they do not influence the density of the prey.

Through the above literature survey, we know that the population dispersal considered in the patchy model may be related with multiple factors. It is often recognized that when there is a fear effect from the predator, the prey is more likely to scatter. For example, in Yellowstone National Park, due to the fear of being preyed upon by wolves, the elk evades the open river valleys (where wolves are most active in hunting), and migrate to areas such as the forest edges or steep mountains where it is difficult for wolves to track them. Furthermore, the dispersal rate increases with the degree of the fear effect. So what happens to the dynamic behavior when we consider the case where prey dispersal is affected by the fear effect? In this paper, we propose the following predator-prey model with dispersal subject to the fear effect in a two-patch environment:

where $x_i$ represents the density of species $x$ in patch $i$ ($i = 1, 2$), and $y$ represents the density of the predator in patch 1. $r_1$ is the intrinsic growth rate of species $x$ in patch 1, and $r_2$ is the death rate of species $x$ in patch 2. $K_1$ is the carrying capacity of species $x$ in patch 1. $a_1$ is the maximal per-capita consumption rate, i.e., the maximum number of prey that can be eaten in each unit time. $a_2$ denotes the conversion of nutrients into the reproduction of the predators. $d$ and $e$ are the natural mortality rate and the intra-species competition coefficient of species $y$, respectively. $D_1 (D_2)$ is the dispersal rate of species $x$ from patch 1(2) to patch 2(1). It is worth noting that the dispersal rate of the prey increases as predator biomass increases. The dispersal rate deduced by the fear effect from the predator is not likely to increase indefinitely; instead, it may reach a finite value. Thus, we consider the dispersal rate of prey by multiplying a function $f(k, \eta, y) = 1+\eta(1-\frac{1}{1+ky})$, where $k$ is the level of the fear effect and $\eta$ is the maximum cost of the fear effect.

To simplify the parameters of system (1.1), the following dimensionless quantities are applied:

and

With bars dropped, system (1.1) can be rewrittten as

All parameters in system (1.2) are positive and $0 < d < 1$. The initial conditions are

To the best of our knowledge, this is the first study to discuss a patchy model in which the migration is induced by the fear effect of the predator. Unlike most studies in which the fear effect influences the birth rate of prey, we will investigate how the fear effect from the predator impacts the diffusion rate of prey populations. In fact, our results obtained in this paper can be seen as an important expansion and supplement to those in ^[13] and ^[14].

The rest of the paper is organized as follows. In Section 2, we obtain the permanence of the system (1.2). Existence and local stability of the equilibria are given in Section 3 and Section 4 demonstrates the global stability. In Section 5, we show that system (1.2) undergoes transcritical bifurcation. Also, some numerical simulation results are shown to verify the analytical results in Section 6. Finally, we give a brief discussion in Section 7.

2.   Preliminaries

2.1.   Nonnegativity and boundedness of the solutions

Theorem 2.1. All solutions of system (1.2) with initial conditions (1.3) are nonnegative and ultimately bounded for ${t > 0}$.

Proof. According to Proposition A.17 of ^[32], it is not difficult to obtain that all the solutions of system (1.2) are always nonnegative. Next, we define a function

Then, by differentiating (2.1) with respect to $t$, we obtain

where $\bar r = \mathrm{min}\{1, r_2, d\alpha_2 \}$. Thus, we obtain

So all solutions of system (1.2) with initial conditions (1.3) are ultimately bounded. This completes the proof.

2.2.   Uniform persistence of the system (1.2)

Theorem 2.2. System (1.2) is uniformly persistent if $0 < D_1 < D^+$, where $D^+ = \frac{(1-d-\alpha_1G_0)(\alpha_1+k{\alpha_2}G_0)}{\alpha_1+(\eta+1)k{\alpha_2}G_0}$, $\alpha_1 < \frac{1-d}{G_0}$.

Proof. From (2.1), for $\varepsilon > 0$ small enough, there is $T > 0$ such that, for $t > T$, we have

According to the first equation of system (1.2),

Setting $\varepsilon \rightarrow0$ in the above inequality leads to

Similarly, according to the third equation of system (1.2),

Then we have

Finally, it follows from the second equation of system (1.2) and the above results that

We get

When $0 < D_1 < D^+$, we have $m_1 > d$ and then $m_2, m_3 > 0$. The above implies that system (1.2) is uniformly persistent. This ends the proof.

3.   Existence and local stability of the equilibria

In the following we present five conditions, i.e.,

One can get the equilibria by setting the right-hand sides of system (1.2) equal to zero. Obviously, the trivial equilibrium $E_0(0, 0, 0)$ always exists. If $(H_1)$, $(H_2)$, or $(H_3)$ holds, system (1.2) also has a predator-extinction equilibrium $E_1(\bar x_1, \bar x_2, 0)$, where $\bar x_1 = 1-\frac{D_1r_2}{r_2+D_2}$ and $\bar x_2 = \frac{D_1\bar x_1}{r_2+D_2}$.

For the potential coexistence equilibrium $E_2(x_1^*, x_2^*, y^*)$, we have

and $y^*$ is the positive root of the the following equation:

where

If $D_1\ge(1-d) (1+\frac{D_2}{r_2})$, one has $P_2 > 0$ and $P_3\ge0$. Then Eq. (3.1) has no positive real root. If $(H_1)$ holds, it has a unique positive real root $y^*$, where

Therefore, we can state the following theorem:

Theorem 3.1. System (1.2) has a unique co-existence equilibrium $E_2(x_1^*, x_2^*, y^*)$ if $(H_1)$ holds.

In the next section, we will discuss the local stability of all equilibria. The Jacobian matrix at the equilibrium $E(x_1, x_2, y)$ of system (1.2) is calculated as

We then have the following result:

Theorem 3.2. The trivial equilibrium $E_0(0, 0, 0)$ is

(i) unstable if $(H_1)$, $(H_2)$, or $(H_3)$ holds;

(ii) locally asymptotically stable if $(H_5)$ holds;

(iii) a saddle-node if $(H_4)$ holds.

Proof. For the trivial equilibrium $E_0(0, 0, 0)$, the Jacobian matrix is given by

The corresponding characteristic equation is

We know that Eq. (3.2) has a positive root and two negative roots if $(H_i)(i = 1, 2, 3)$ holds, thus, $E_0$ is unstable. If $(H_5)$ holds, one can verify that the three roots of Eq. (3.2) are negative, thus $E_0$ is locally asymptotically stable. Notice that Eq. (3.2) has two negative roots and a unique zero root when $(H_4)$ holds. Applying the Taylor expansion of $\frac{1}{1+ky}$ at the origin, system (1.2) can be rewritten as

where

Then we make the following transformation:

and system (3.3) becomes

where

For $X_1\sim0$, there exists a center manifold

Then on the center manifold, system (3.4) becomes

Obviously, the coefficient of $X_1^2$ is $\hat a_{200} = -\frac{\left({r_2}+{D_2}\right) {r_2^2} }{{D_2} {r_2}+{r_2}^{2}+{D_2}} < 0$. Therefore, $E_0$ is a saddle-node. This ends the proof of Theorem 3.2. □

Theorem 3.3. The predator-extinction equilibrium $E_1(\bar x_1, \bar x_2, 0)$ is

(i) unstable if $(H_1)$ holds;

(ii) locally asymptotically stable if $(H_3)$ holds;

(iii) a saddle-node if $(H_2)$ holds.

Proof. For the predator-extinction equilibrium $E_1(\bar x_1, \bar x_2, 0)$, the Jacobian matrix is given by

$J_{E_1}$ always has an eigenvalue $\lambda = \alpha_2\left(1-\frac{D_1r_2}{r_2+D_2}-d\right)$.

(i) If $(H_1)$ holds, one can verify that $\lambda > 0$, thus $E_1(\bar x_1, \bar x_2, 0)$ is unstable.

(ii) If $(H_3)$ holds, then we have $\lambda < 0$. Define

The determinant and trace of $J_1$ can be simplified as

Combining with the conditions for the existence of $E_1$, we obtain $Det\left(J_1\right) > 0$ and $Tr\left(J_1 \right) < 0$. It follows that $J_1$ has two negative eigenvalues. Hence, if $(H_3)$ holds, $J_{E_1}$ has three negative eigenvalues which implies that $E_1$ is locally asymptotically stable.

(iii) If $(H_2)$ holds, we also can deduce that $Det\left(J_1\right) > 0$ and $Tr\left(J_1 \right) < 0$. Now, $J_{E_1}$ has a unique zero eigenvalue $\lambda = 0$. Using the same method of proof as in Theorem 3.2, we can get that $E_1$ is a saddle-node. This completes the proof. □

Theorem 3.4. When $(H_1)$ holds, the co-existence equilibrium $E_2(x_1^*, x_2^*, y^*)$ exists and is always locally asymptotically stable.

Proof. The Jacobian matrix at $E_2(x_1^*, x_2^*, y^*)$ can be calculated as

The corresponding characteristic equation is

where

After a simple calculation, we obtain that

Applying the Routh-Hurwitz criteria^[33], when $E_2$ exists, i.e., $(H_1)$ holds, we can verify that $E_2$ is locally asymptotically stable. This completes the proof. □

The existence and stability conditions for all equilibria are given in Table 1.

4.   Global stability analysis

In this section we shall analyze the global stability of all the equilibria under some conditions. Consider the following equations:

Let $U_1 = x_1$ and $U_2 = x_1+x_2$. Then model (4.1) can be transformed into the following system:

By the nonnegativity of the solutions, from Eq. (4.2), we obtain

Applying the comparison theorem for differential equations, we establish the comparison equation:

Then, for model (4.3), we can obtain the following lemmas:

Lemma 4.1. System (4.3) has a trivial equilibrium $P_0(0, 0)$. If $(H_1)$, $(H_2)$, or $(H_3)$ holds, system (4.3) has a unique positive equilibrium $P_1(N_1^+, N_2^+)$, where $N_1^+ = 1-\frac{D_1r_2}{r_2+D_2}, N_2^+ = \frac{D_1N_1^+}{r_2+D_2}+N_1^+$.

Lemma 4.2. The trivial equilibrium $P_0(0, 0)$ is globally asymptotically stable if $(H_5)$ holds.

Proof. The Jacobian matrix of model (4.3) at $P_0(0, 0)$ is given by

The two eigenvalues of $J_{P_0}$ satisfy the following equations:

If $(H_5)$ holds, $J_{P_0}$ has two negative eigenvalues, thus, $P_0(0, 0)$ is locally asymptotically stable. Furthermore, there is no positive equilibrium when $(H_5)$ holds, and then there exists no limit cycle in the first quadrant. So $P_0(0, 0)$ is globally asymptotically stable. □

Lemma 4.3. The positive equilibrium $P_1(N_1^+, N_2^+)$ is globally asymptotically stable if $(H_1)$, $(H_2)$, or $(H_3)$ holds.

Proof. The Jacobian matrix at $P_1(N_1^+, N_2^+)$ is

The two eigenvalues of $J_{P_1}$ satisfy the following equations:

Therefore, by some simple calculations, if $(H_1)$, $(H_2)$, or $(H_3)$ holds, the two eigenvalues $\lambda_{1, 2} < 0$ hold, and obviously, $P_1(N_1^+, N_2^+)$ is locally asymptotically stable. Next, from (4.3), we have

Hence, as $t\rightarrow \infty$,

Then, we denote the right-hand side of system (4.3) as $F(N_1, N_2)$ and $G(N_1, N_2)$, respectively. Introduce a Dulac function $B(N_1, N_2) = \frac{1}{N_1N_2}$. It follows that

Applying the Bendixson-Dulac discriminant, system (4.3) has no limit cycle in the first quadrant. Therefore, when $P_1(N_1^+, N_2^+)$ exists, i.e., $(H_1)$, $(H_2)$, or $(H_3)$ holds, $P_1(N_1^+, N_2^+)$ is globally asymptotically stable. □

According to Lemma 4.2, we can get

The third equation of system (1.2) can be rewritten as the following limit equation:

Then we can obtain

Combining the above results, we have the following theorem:

Theorem 4.1. For system (1.2), the trivial equilibrium $E_0$ is globally asymptotically stable if $(H_5)$ holds.

Further, Lemma 4.3 yields that

Assume that $d > 1-\frac{D_1r_2}{r_2+D_2}$, i.e., $(H_3)$, $(H_4)$, or $(H_5)$ holds. Thus, there is $\varepsilon_0 > 0$ small enough such that $1-\frac{D_1r_2}{r_2+D_2}+\varepsilon_0-d < 0$. From Eq. (4.5), for $\varepsilon_0 > 0$, there is $T > 0$ such that, for $t > T$, we have $x_1(t) < 1-\frac{D_1r_2}{r_2+D_2}+\varepsilon_0$. Then the third equation of system (1.2) can be rewritten as

It follows that

Thus, when $y(t)\to 0$, the limit equation of system (1.2) is

Combining with Theorem 2.2 in ^[9], we obtain

In summary, we can state the following theorem:

Theorem 4.2. For system (1.2), the predator-extinction equilibrium $E_1$ is globally asymptotically stable if $(H_3)$ holds.

Next, by using the geometric approach ^[34,35], we will discuss the global stability of the positive equilibrium $E_2$. We denote the variational matrix of the system (1.2) by $V$ as

Then the second additive compound matrix of $V$ is given by

where $M = 1-2x_1-\alpha_1y-D_1\left[1+\eta\left(1-\frac{1}{1+ky}\right)\right]-r_2-D_2$ and $N = 1-2x_1-\alpha_1y-D_1\left[1+\eta\left(1-\frac{1}{1+ky}\right)\right]+\alpha_2(x_1-d)$. We define a diagonal matrix $P$ = diag$\left\{1, \frac{x_1}{y}, \frac{x_1}{y}\right\}$. It can be obtained that $P^{-1}$ = diag$\left\{1, \frac{y}{x_1}, \frac{y}{x_1}\right\}$ and

Hence

Then we state

where

Next, let $(u, v, w)$ be a vector in $R^3$ and its norm $|.|$ is defined as $|(u, v, w)| = \mathrm{max}\{|u|, |v+w|\}$. Denote the Lozinski measures with respect to this norm and with respect to the $L^1$ norm by $\mu$ and $\mu_1$, respectively. Then

where $|a_{12}|, |a_{21}|$ are matrix norms with respect to the $L^1$ vector norm. We have

Using equations of system (1.2) and with further simplification, we get the following:

Therefore, we have

where

Now, we denote $\gamma_1 = \liminf\limits_{t\rightarrow +\infty}\{x_1(t), x_2(t), y(t)\}$ and $\gamma_2 = -\mathrm{max}\{1-(2+\alpha_1-\alpha_2)\gamma_1, -r_2+\frac{G_0\alpha_2^2}{\alpha_1}\}$, where $G_0 = \limsup\limits_{t\rightarrow +\infty} y(t)$. So we can deduce that

where

Then we define

Thus, by the above discussion, we state

Therefore, if $\gamma_3 > 0$, we have

Then we can state the following theorem:

Theorem 4.3. For system (1.2), the co-existence equilibrium $E_2$ is globally asymptotically stable if $(H_1)$ holds and $\gamma_3 > 0$, where $\gamma_3 = \mathrm{min}\{\delta_1, \gamma_2\}$, $\gamma_2 = -\mathrm{max}\{1-(2+\alpha_1-\alpha_2)\gamma_1, -r_2+\frac{G_0\alpha_2^2}{\alpha_1}\}$ and $\gamma_1 = \liminf\limits_{t\rightarrow +\infty}\{x_1(t), x_2(t), y(t)\}$.

Remark 4.1. Specially, when $D_1\le\frac{1-\alpha_1}{k\eta}, \ \alpha_1 < 1$, $\gamma_1 > \frac{1}{2+\alpha_1-\alpha_2}, \ \alpha_2^2 < \frac{\alpha_1r_2}{G_0}$, the conditions of Theorem 4.3 hold. In other words, when the prey's dispersal from the source to the sink $({i.e.}, D_1)$ is small, the maximal per-capita consumption rate and the conversion of nutrients into the reproduction of the predators are not large, all species in both patches can coexist. Through numerical simulations in Section 6, we find that when $E_2$ exists, i.e., $(H_1)$ holds, the uinque positive equilibrium is globally asymptotically stable. However, we cannot present the rigorous proof. We will investigate the above in future work.

5.   Bifurcation analysis

From Section 3, we can see that the predator-extinction equilibrium $E_1\left(1-\frac{D_1r_2}{r_2+D_2}, \frac{D_1\left(1-\frac{D_1r_2}{r_2+D_2}\right)}{r_2+D_2}, 0\right)$ coincides with the trivial equilibrium $E_0(0, 0, 0)$ if $(H_4)$ holds. In the following, we will investigate the existence of transcritical bifurcation in system (1.2) by using the standard Sotomayor theorem ^[36].

Theorem 5.1. System (1.2) experiences a transcritical bifurcation around the trivial equilibrium $E_0$ when $D_1 = D_1^* = 1+\frac{D_2}{r_2}$ and $D_2\ne\frac{r_2^2}{1-r_2}$.

Proof. Notice that the Jacobi matrix $J_{E_{1}^*}$ possesses a unique zero eigenvalue when $D_1 = D_1^*$. Let

be the eigenvectors of $J_{E_{1}}$ and $J^T_{E_{1}}$ corresponding to a zero eigenvalue, respectively. Denote

Then we have

It follows from above that

Therefore, according to the Sotomayor theorem, we know that system (1.2) experiences a transcritical bifurcation at $E_0$ if $D_2\ne\frac{r_2^2}{1-r_2}$. Theorem 5.1 is proved. □

6.   Numerical simulations

To validate the theoretical findings in the preceding parts, we will present the MATLAB numerical simulations of system (1.2) in this section.

Case I. Stability of the equilibria

Here we take the parameters of system (1.2) as follows:

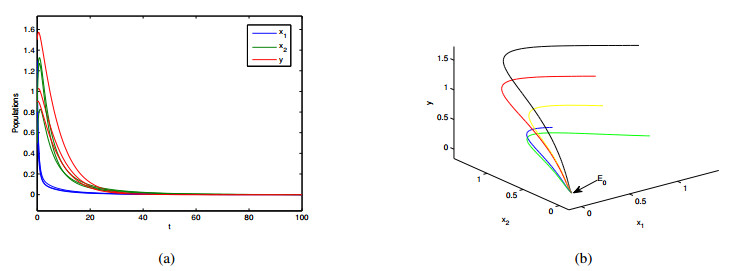
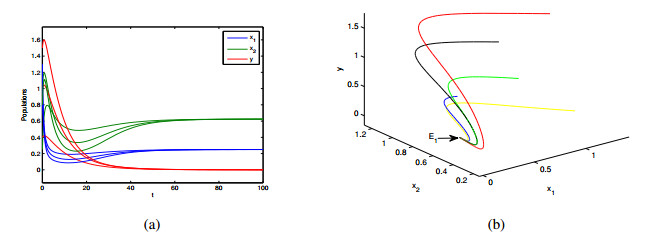
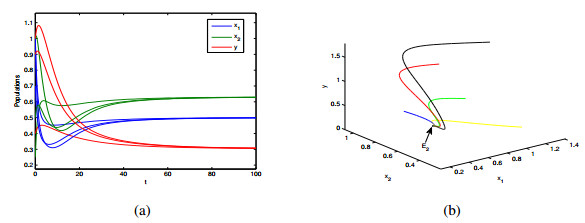
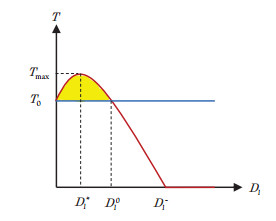
In Figures 1–3, the equilibria $E_0(0, 0, 0)$, $E_1(0.25, 0.625, 0)$, and $E_2(0.5, 0.6319969406, 0.3952971308)$ are globally asymptotically stable, respectively. The ecological significance of these results are well understood as follows. First, when the prey's dispersal from the source to the sink is large $(\mathrm{i.e.}, D_1 > 1+\frac{D_2}{r_2})$, all populations will be extinct (see Figure 1). Second, when the dispersal is intermediate, i.e., $(1-d) (1+\frac{D_2}{r_2}) < D_1 < 1+\frac{D_2}{r_2}$, the predator goes to extinction and the prey persists in the two patches (see Figure 2). The total prey population abundance is $T(D_1) = \left(1-\frac{D_1r_2}{r_2+D_2}\right)\left(1+\frac{D_1}{r_2+D_2}\right)$. Figure 4 shows the trajectory of $T$ about $D_1$, where $D_1^* = \frac{1-r_2}{2r_2}, D_1^0 = 2D_1^*$, and $T_{\mathrm{max}} = T(D_1^*)$. If $0 < D_1 < D_1^0$, the population density of the prey with diffusion is higher than that without diffusion. Furthermore, we can infer that there is an optimal diffusion coefficient $D_1^*$ that maximizes the total population density of the prey. Third, when the dispersal is small $(\mathrm{i.e.}, 0 < D_1 < (1-d) (1+\frac{D_2}{r_2}))$, the species in both patches will be permanent (see Figure 3).

Case II. Impact of the fear effect on system (1.2)

For this purpose, we take the following parameters:

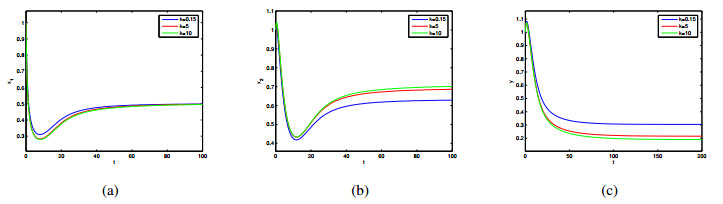
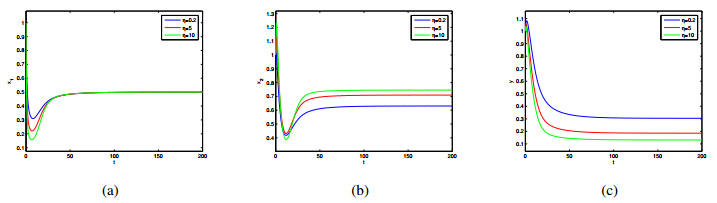
When the dispersal is small $(\mathrm{e.g.}, 0 < D_1 < (1-d) (1+\frac{D_2}{r_2}))$, the prey and predator coexist at the equilibrium $E_2(x_1^*, x_2^*, y^*)$. Then we know that the fear effect $k$ has no impact on the existence and local stability of the co-existence equilibrium. It only influences the population densities of species $x_2, y$. In Figure 5, we present the dynamic behavior of $x_1$, $x_2$, and $y$ for different levels of fear effect $k$ over time $t$, respectively. We observe that as $k$ increases, the steady state level of $y$ gradually decreases, but the steady state level of $x_2$ will increase. In Figure 6, we give the dynamic behavior of the populations for different values of $\eta$, i.e., the maximum cost of fear. Similarly, we find that as $\eta$ increases, the steady state level of $y$ will decrease and the steady state level of $x_2$ will increase. In other words, from Figures 5–6, we obtain that the fear effect plays a negative role for specie $y$ in the first patch. The higher the cost of the prey's fear effect from the predator, the lower the density will be of the population $y$. In contrast, for specie $x$ in the two patches, the fear effect has a beneficial impact on the total density.

7.   Conclusion

In this paper, we have analyzed a patchy model in which the migration is induced by the fear effect from the predator. We have investigated that prey species in the source patch can migrate to the sink patch at a faster rate due to the fear effect. Meanwhile, the dispersal rate induced by the fear effect does not increase indefinitely; instead, it may reach a finite value. In other words, we have introduced a fear effect factor $k$ and a maximum fear cost $\eta$ in our model.

We have explored the nonnegativity and boundedness of model (1.2). Also, we have obtained that the model is uniformly persistent when $0 < D_1 < D^+$. For system (1.2), it always has a trivial equilibrium. There exists a predator-extinction equilibrium if $(H_1)$, $(H_2)$, or $(H_3)$ holds and a unique co-existence equilibrium if $(H_1)$ holds. By calculating the eigenvalues of the Jacobian matrices at each equilibrium, and combining with the central mainfold theorem, we have obtained the local stability of all equilibria. Then, using the comparison theorem and Dulac's theorem, we have obtained the global stability of the boundary equilibrium. Moreover, a geometric approach in ^[34,35] has been used to prove the global stability of a unique co-existence equilibrium $E_2(x_1^*, x_2^*, y^*)$. Choosing the diffusion coefficient $D_1$ as the bifurcation parameter, we can conclude that system (1.2) undergoes a transcritical bifurcation. The biological implication of the existence of transcritical bifurcation is that, when $(H_1)$, $(H_2)$, or $(H_3)$ holds, the predator goes extinct, but the species $x$ still exists. If $D_1$ increases, species $x$ easily migrates to patch 2 and will go extinct.

After that, we have verified the obtained theoretical results by performing numerical simulations through MATLAB. We have selected suitable parameters and analyzed the global stability of all equilibria, which is in agreement with our theoretical results. When the dispersal is intermediate, we find an optimal diffusion coefficient to make the density of the prey population reach its maximum. In Figures 5–6, we have explored the impacts of fear effect $k$ and maximum fear cost $\eta$ on the dynamic behavior of system (1.2). They play a negative role for specie $y$ in the first patch and have a beneficial impact on the total density of the prey.

Unlike ^[13], we consider the prey's dispersal instead of the predator's disperal between patches. Also, unlike ^[14], the prey's dispersal rate is affected by the fear effect from the predator in our paper. This is the first time that this type of dispersal has been considered. Overall, this paper extends the literatures ^[13,14] by considering the impact of dispersal induced by the fear effect. In our model (1.2), dispersal plays a significant role in a the persistence of populations in a source-sink patch. Furthermore, our results show that the fear effect is beneficial to the total population density of the prey, which is different from the results that the fear effect has no influence on the density of prey in ^[31]. This is because we posit that fear does not directly influence the birth and death rates of the prey species but instead induces prey migration as a response to predation risk. In other words, the prey successfully evades the predator, thereby the dispersal deduced by the fear effect contributes to an increase in prey population density. Our research has important ramifications for protecting threatened and endangered species. By creating ecological corridors and regulating the rate of species movement across patches, we can lessen the consequences of isolated patches and eventually raise the overall abundance of endangered species.

Our research shows that the fear effect only impacts the total population density, and it has no influence on the existence and stability of the equilibria. This is possibly explained by the fact that we considered the Holling type I functional response between the prey and the predator. Therefore, in future research, we will consider other functional responses. Furthermore, we have noticed that some scholars focused on inverse problems ^[37,38,39] and boundary observation ^[40,41,42] in studying multi-population aggregations. Their goal was to reconstruct the diffusion coefficient, advection coefficient, and interaction kernels of the aggregation system, which characterize the dynamics of different populations. In future work, we will connect our study on inverse problems in mathematical biology with more application backgrounds.

Author contributions

Jin Zhong: writing-original draft; Lijuan Chen and Fengde Chen: supervision, writing-review and editing. All authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgment

This work was supported by the National Natural Science Foundation of China (11601085) and the Natural Science Foundation of Fujian Province (2021J01614, 2021J01613).

Conflict of interest

The authors declare there is no conflict of interest.