Dynamic analysis of sheep Brucellosis model with environmental infection pathways

1.   Introduction

Brucellae are Gram-negative coccobacilli causing brucellosis, a serious chronic zoonotic infectious disease. The World Organization for Animal Health classifies brucellosis as a notifiable infectious disease category Ⅰ, and China classifies it as a category Ⅱ infectious disease ^[1]. In China, the main sources of the disease are cattle, sheep and pigs, with brucellosis being the most transmissible, pathogenic and dangerous disease in sheep. Brucellae are resistant to external factors such as dryness and cold, but not to moisture and heat, and die immediately after boiling. Commonly used disinfectants can kill brucellae within a few hours ^[2]. Brucellosis may be transmitted directly way through the gastrointestinal and respiratory tracts, the genitourinary tract, and infections of damaged or undamaged skin and mucous membranes. There is also an indirect channel of infection through direct contact or contact with the secretions and excretions of diseased animals ^[3,4]. It is estimated that the disease is endemic in humans and animals in more than 170 countries and territories, with more than 500,000 new cases of brucellosis worldwide each year ^[5].

Studying the spread of infectious diseases using dynamical models is an important avenue of research that can provide referable advice for disease control. Of course, when building a model, it is important to include the transmission pattern of the disease, especially the main transmission routes. In the study of brucellosis, the indirect transmission pathway of the bacteria from the environment is a non-negligible part of brucellosis transmission, so the exposure infection function of environmental infection needs to be determined in the modeling analysis. A simple model of Brucella transmission that takes into account both routes of transmission may be written as

where $S(t), I(t), W(t)$ represents the susceptible flock, the infected flock, and the concentration of bacteria in the environment, respectively. The parameter $\alpha$ denotes the birth rate, $A$ is the recruitment rate of the flock, $g(s, I)$ is the contact infection function between susceptible and infected sheep, $f(w)$ is the environmental exposure function, and $d$ is the mortality rate of the flock per unit time. Sheep with brucellosis spread Brucella in the environment at rate $k$ and environmental Brucella had a mortality rate $\delta$. The number of disinfection per unit time is $l$. The efficiency of each disinfection is $\eta$.

One of the things that we are more interested in is how the environmental exposure function may be described. Li et al. ^[6] proposed a dynamicak model of brucellosis in sheep consideredin the environmental indirect infection. They used three common environmental exposure functions, which are also present in the literature:

Case 1. Standard incidence: $f(W) = \frac{W}{N}$ ^[6];

Case 2. Incidence of saturation: $f(W) = \frac{W}{W+\epsilon_1}$ ^[7,8,9];

Case 3. Incidence of mass action: $f(W) = \frac{W}{M}$ ^{[10,11,12,13,14,15,16]}.

Here, $\epsilon_1$ and $M$ are scaling factors for the Brucella concentration in the environment.

In ref ^[6], the authors compared three forms of environmental exposure functions using real data, and indicate the first environmental exposure function as the proper choice. The second environmental exposure function was used by Li et al. ^[8] to develop a sheep-human Brucella infection model, with particular attention to the role of ewe flocks in disease transmission. Meng et al. ^[12] used the third environment exposure function to develop a multi-stage dynamic model. Sun et al. ^[16] used the third environmental exposure function to develop a five-step model of brucellosis transmission based on model (1.1), taking into account vaccination as well as latent period transmission. In fact, the third environmental exposure function is the most used in current literature. Looking at the results obtained so far from a dynamical point of view, the behavior of the models resulting from using the three above environmental exposure functions is relatively similar. The existence and stability of disease-free equilibrium and endemic equilibrium points are determined by the critical values, i.e., the basic reproduction number $R_0$.

The spread of brucellosis in sheep has actually some specific characteristics. Sheep are managed as domestic animals, so there are some human factors involved, e.g., addition of new sheep, slaughter of adult sheep, environmental disinfection and testing, trapping and killing of infected sheep, etc. In addition, sheep brucellosis has a very obvious stage structure ^[17], i.e., the probability of lambs being infected by brucellosis in sheep is very low, while adult sheep are easily infected. Morevover, owing to the growing demand for dairy and meat products, large scale live sheep trading and trafficking activities are increasing. Due to lack of disease prevention awareness and lax management, some infected sheep are introduced from outside to the original farming area and spread the disease. Based on the presence of these factors, we here develop a model of brucellosis transmission considering stage structure, external inputs and immune control. In order to describe environmental exposure, unlike in other works, we take an abstract function. Our goals include to study of the transmission pattern of brucellosis and to propose control measures, as well as to examine whether the use of different environmental infection exposure functions has a significant effect on the selection and the strength of the possible control measures.

This paper is structured as follows. In Section 2, we introduce our models and a unified abstract expression for the environmental exposure function. In Section 3, the stability and persistence of the models are investigated. In Section 4, numerical simulations of our models are performed, and the sensitivities of the models resulting from using three different environmental exposure functions are analyzed and compared. Finally, Section 5 closes the paper with some concluding remarks.

2.   Mathematical model

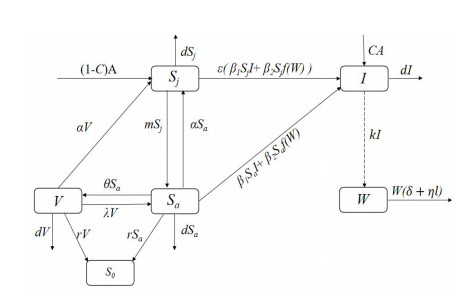
Sheep are divided into four classes: susceptible young sheep $S_j(t)$, susceptible adult sheep $S_a(t)$, immune sheep $V(t)$ and infected sheep $I(t)$. Let $W(t)$ denote the density of Brucella in the environment, $S_0(t)$ the quantity of slaughter sheep, and $f(W)$ the environmental infection exposure function. We also assume that the introduction rate of external sheep per unit time is $A$, the birth rate of sheep is $\alpha$, which is limited by the natural mortality rate of sheep $d$. The probability of external introduction into the infected flock is $C$, the conversion rate of lambs to adults is $m$, and the immune loss rate is $\lambda$. The ratio of infection rate in adult sheep to lambs is denoted by $\epsilon$, and te slaughter rate by $r$. Sheep with brucellosis spread Brucella in the environment at rate $k$ and environmental Brucella had a mortality rate $\delta$. The number of disinfection per unit time is $l$, and the efficiency of each disinfection is $\eta$. Direct infection rate is $\beta_1$, indirect infection rate is $\beta_2$.

Some assumptions are embedded in our model:

1) Brucellosis in the exposure period is hardly detected, hence, we ignore this period in the sheep population.

2) Once the ewes are infected with brucellosis, they will not be able to reproduce.

3) All parameters above are non-negative and $0 < \alpha < d < 1$, $0 \le C \le1$, $0 < \epsilon$, $r < 1$.

According to the flow chart of transmission (see Figure 1), the dynamics of brucellosis is modeled as follows

The non-negative functions $f(W)$ and $W$ are differentiable. Based on the three common forms of $f(W)$, we assume that the function $f(W)$ has the following properties.

(H1) $f(W) \ge 0$ with equality if and only if $W = 0$;

(H2) $f(W)$ is monotone nondecreasing with $W$;

(H3) $\frac{f(W)}{W}$ is monotone nonincreasing.

Lemma 1. Supposing all parameters are non-negative and $0 < \alpha < d < 1$, $0 \le C \le1$, $0 < \epsilon$, $r < 1$, then the closed set

is a positive invariant set of the model (2.1) if system (2.1) satisfied initial conditions $S_j(0) > 0$, $S_a(0) > 0$, $S_0(0) > 0$, $I(0) > 0$, $V(0) > 0$, $W(0) > 0$.

Proof. Let $N(t) = S_j(t)+S_a(t)+I(t)+V(t)$, it is easy to obtain

then we have

Hence, we have that $S_a(t), V(t)$ are bounded. Suppose $0 < V(t)+S_a(t) \le M_0 \le \frac{A}{d-\alpha}$, then we have

It follows that there is a sufficiently large $T$ such that the following expression holds when $t\ge T > 0$:

then, when $t\rightarrow \infty$, we get

According to the last equation of model (2.1), we have

then we have

By (2.3)–(2.5), we arrive at (2.2), i.e., the solutions of model (2.1) are non-negative for all time $t > 0$ and all solutions are uniformly bounded. The region $\Omega$ is a positive invariant. The proof is completed.

3.   Dynamical behavior of virus transmission

In fact, according to the formulation of model (2.1), it can be seen that $S_0$ is not related to the rest of the variables. We may consider the following equivalent model to describe the dynamics of disease transmission:

3.1.   Basic reproduction number and disease-free equilibrium

If $C = 0$, it is easy to get the disease-free equilibrium (DFE) $E_0 = (S_{j}^0, S_{a}^0, 0, V^0, 0)$, from the equations

In particular, we have the following theorem

Theorem 2. If $C = 0$ and $0 < \alpha < d < 1$, the model (3.1) has one disease-free equilibrium $E_0 = (S_{j}^0, S_{a}^0, 0, V^0, 0)$, where

We derive the basic reproduction number of system (3.1) using the next generation matrix method formulated by Diekmann et al. ^[18,19]. We order the infection variables first by disease state, only needing the vector $X(t) = (I(t), W(t))^T$. Then, considering the following auxiliary system:

According to the recipe of van den Driessche and James, the Watmough ^[20] matrices $F$ and $V$ are given by

Here $f^{'}(0)$ is the derivative of $f(W(t))$ with respect to $W(t)$ at disease-free equilibrium. The basic reproduction number is defined as the spectral radius of the nonnegative matrix $FV^{-1}$ which is given by

Therefore

where $R_{0}^i = \frac{\epsilon \beta_1 S_{j}^0+\beta_1 S_{a}^0}{d+e}$ and $R_{0}^e = \frac{k[\epsilon \beta_2 S_{j}^0 f^{'}(0)+\beta_2 S_{a}^0 f^{'}(0)]}{(d+e)(\delta+\eta l)}$ are the partial reproduction numbers due to environment-to-individual and individual-to-individual transmission, respectively.

Notice that

and thus $R_0$ can be written as

If we now insert the expression $S_{j}^0 = \frac {A(d+r)} {d^2+(d-\alpha)m+r(d+m)}$ in the above equation, we arrive at

3.2.   Stability of disease-free equilibrium

Theorem 3. If the assumptions (H1)–(H3), $0 < \alpha < d < 1$ and $C = 0$, then the disease-free equilibrium of model (3.1) is globally asymptotically stable in the region $\Omega$ if $R_0 < 1$ and unstable if $R_0 > 1$.

Proof. By using assumptions (H1) and (H3), we have

Thus by (3.11), we have $f^{'}(0)W \ge f(W)$. Hence, for model (3.4), denoting $X(t) = (I(t), W(t))^T$, it is easy to prove that

Let $b \ge 0$ be the left eigenvector of the nonnegative matrix $V^{-1} F$, which satisfies $b V^{-1} F = R_0 b^T$, and define the Lyapunov function $L = b^T V^{-1} X(t)$. Taking derivative of $L$ and use (3.3) we arrive at

Then $\frac{dL}{dt} \le 0$ fpr $R_0 < 1$. Let $\Omega^{*} = \{(S_j(t), S_a(t), I(t), V(t), W(t))\in X(t) | \frac{dL}{dt} = 0\}$, we have $\frac{dL}{dt} = 0$ if $R_0 = 1$. This implies that $X(t) = 0$, i.e., $I(t) = 0, W(t) = 0$. Therefore, the largest invariant set of $\Omega^{*}$ is the singleton $E_0$. According to LaSalle's invariance principle ^[21], $E_0$ is globally asymptotically stable in the region $\Omega$.

Obviously, if $R_0 > 1$ and $X(t) > 0$, then $(R_0-1)b^T X(t) > 0$. In this case, there must exist a small enough neighborhood of $E_0$ in which $\frac{dL}{dt} > 0$ holds. Therefore, $E_0$ is unstable. The proof is completed.

3.3.   Endemic equilibrium points

Theorem 4. If the assumptions (H1)–(H3) and $0 < \alpha < d < 1$ hold,

(a) if $0 < C < 1$, the model (3.1) has a unique endemic equilibrium $E^* = (S_{j}^*, S_{a}^*, I^*, V^*, W^*)$;

(b) if $C = 0$ and $R_0 > 1$, the model (3.1) has a unique endemic equilibrium $E^* = (S_{j}^*, S_{a}^*, I^*, V^*, W^*)$;

(c) if $C = 0$ and $R_0\le1$, the model (3.1) has no endemic equilibrium.

(d) if $C = 1$, the model (3.1) has a boundary point $(0, 0, \frac{A}{d+e}, 0, \frac{A k}{(d+e)(\delta +\eta l)})$, and has no endemic equilibrium $E^*$.

Proof. The endemic equilibrium of model (3.1) satisfies the following equilibrium equations:

Thus, we have

where

From the third equation of (3.14) and Eq (3.15), we also obtain that $S_{a}^*$ should satisfy

Assuming $I$ as the independent variable and $S_a$ as the dependent variable, we may write the two following functional expressions

where $H(I) = \beta_1 I+\beta_2 f(W) = \beta_1 I+\beta_2 f(\frac{kI}{\delta +\eta l})$. Since $f(W)$ is a monotonic function of $W$, $H(I)$ is an increasing function. Moreover

It is now clear that $F_1^{'}(I) < 0$ for all $I \in \Gamma$. In other words, $F_1(I)$ decreases monotonically in $\Gamma$.

The derivative of $F_2(I)$ is

By noticing that

and $(\frac{f(W)}{I})^{'} \le 0$, $(\frac{I}{f(W)})^{'} = \frac{f(W)-If^{'}(\frac{kI}{\delta +\eta l})\frac{k}{\delta +\eta l}}{f^{2}(W)} \ge 0$ for all $I \in \Gamma$, we have that $F_2^{'}(I) > 0$.

Let

This means that

Thus, we have $G^{'}(I) = F_1^{'}(I)-F_2^{'}(I) < 0$. $G(I)$ is a monotonically decreasing function when $0 < I < \frac{A}{d-\alpha}$. If the function $G(I)$ has a zero point, it must be unique. This means that if model (3.1) has a positive equilibrium point, it must be unique. Let us now address the value of the G function at $G(\frac{A}{d+e})$ and $G(0^+)$. First we consider $G(\frac{A}{d+e})$,

Next, consider $G(\frac{A}{d+e})$ as a function on $C$, say $J(C)$. Then $J(1) = 0$, and

where

Since $d > \alpha$, we havet $p > 0$, i.e., $J^{'}(C) > 0$. If $0\le C < 1, J(C) < J(1) = 0$ always holds. Therefore $G(\frac{A}{d+e}) < 0$. When $C = 1$, $G(\frac{A}{d+e}) = 0$.

Let us now focus on the sign of $G(0)$. There are three cases: $0 < C < 1$, $C = 1$ and $C = 0$.

Case1 $0 < C < 1$. Noticing that $H(0) = 0$, we have $I\rightarrow0$, $G(0)\rightarrow +\infty$, i.e., $\exists \delta_1 > 0$ s.t. as $I \in (0, \delta_1)$, $G(I) > 0$ holds. The function $G(I)$ has a unique zero point between $0$ and $\frac{A}{d+e}$.

Case2 $C = 1$. $G(\frac{A}{d+e}) = 0$, and $G(I)$ is a monotonically decreasing function when $0 < I < \frac{A}{d-\alpha}$. The function $G(I)$ has thus a unique zero point at $I = \frac{A}{d+e}$, and model (3.1) has only one boundary equilibrium point $(0, 0, \frac{A}{d+e}, 0, \frac{A k}{(d+e)(\delta +\eta l)})$.

Case3 $C = 0$. We have

Since

Thus $G(0^+) > 0$ if and only if $R_0 > 1$. The function $G(I)$ has a unique zero point between $0$ and $\frac{A}{d+e}$ if $R_0 > 1$. When $R_0 = 1$ or $R_0 < 1$, there are no zero points for $G(I)$. The proof is completed.

Remark. From the above proof, it can be seen that the model (3.1) does not have a disease-free equilibrium point when $0 < C \le 1$. When $C = 0$, the disease-free equilibrium point exists if and only if $R_0\le1$. When $C = 1$, the model (3.1) has only one boundary equilibrium point.

Next we prove the global stability of the endemic equilibrium point. For the sake of convenience, we omit the t-dependence and use $S_j$, $S_a$, $I$, $V$, $W$ to denote $S_j(t)$, $S_a(t)$, $I(t)$, $V(t)$, $W(t)$. The following lemma will be useful later.

Lemma 5. ^[22] Supposing that assumptions (H1)–(H3) hold,

where $\phi$ is defined by $\phi(x) = x-1-ln(x)$.

Theorem 6. Assuming (H1)–(H3) and $0 < \alpha < d < 1$, the endemic equilibrium $E^*$ of system (3.1) is globally asymptotically stable if any one of the following conditions holds: (a) $0 < C < 1$; (b) $C = 0$ and $R_0 > 1$.

Proof. For model (3.1), we construct the following Lyapunov function:

where

The derivative of $L$, according to (3.7), is

Moreover, we have that:

Let us now introduce the quantities

which allow us to rewrite the derivative as

Noticing that

and

Then, we have

According to Lemma 5, we have $\frac{dL}{dt}\le0$. On the other hand $\frac{dL}{dt} = 0$ holds if and only if $(S_j, S_a, I, V, W) = (S_j^*, S_a^*, I^*, V^*, W^*)$. From Lyapunov's Direct Method, one concludes that $E^* = (S_j^*, S_a^*, I^*, V^*, W^*)$ is globally asymptotically stable if it exists. The proof is completed.

Remark. From the above theorem, it can be seen that endemic equilibrum is globally asymptotically stable iff it exist.

Theorem 7. Supposing that assumptions (H1)–(H3), $0 < \alpha < d < 1$ and $C = 1$ hold, the boundary equilibrium point $E_1 = (0, 0, \frac{A}{d+e}, 0, \frac{Ak}{(d+e)(\delta+\eta l)})$ of system (3.1) is globally asymptotically stable.

Proof. For model (3.1), we construct the following Lyapunov function:

where

The derivative of $L_1$ along model is

Moreover, we have that

Thus

We get $\frac{dL}{dt} \le 0$. And $\frac{dL}{dt} = 0$ holds if and only if $I = I_1$, $W = W_1$. From Lyapunovs Direct Method, the boundary equilibrium point $E_1$ is globally asymptotically stable if it exists. The proof is completed.

4.   Numerical results

In this section, we first study the dynamics of the model using the value of parameters from references ^[6,12] as well as hypothetical data. We then fit the model to real data provided by our collaborators about sheep infections in the Yulin region of China from 2005 to 2014. Finally, we perform some numerical analysis to assess the effects of the control measures using different environmental infection functions.

4.1.   Dynamics of the model

Taking $f(W) = \frac{W}{N}$ as an example, the parameters are selected as in Table 1. In this paper all the parameters are measured in years, in addition to environmental disinfection frequency units is times/year.

We assume that the initial values are $S_j(0) = 1860$, $S_a(0) = 1845$, $I(0) = 110$, $V(0) = 1185$, $W(0) = 50$ and the exposure infection rates are given by $\beta_1 = 0.000038$, $\beta_2 = 0.0000135$.

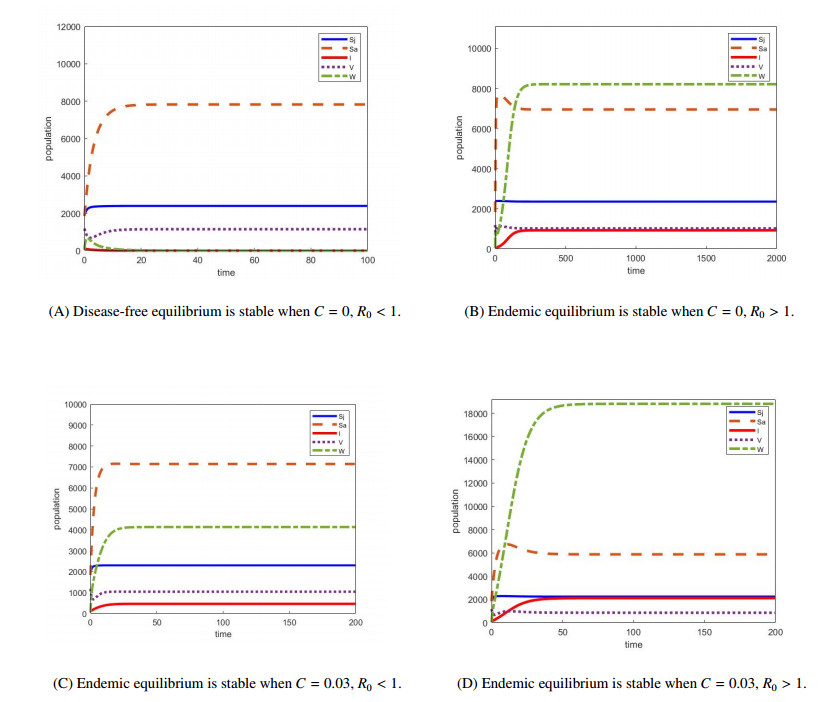
Example 1: Let $C = 0$, $A = 3000$, $e = 0.25$, then $R_0 = 0.7455 < 1$. Figure 2 shows that the disease-free equilibrium point of the model is globally asymptotically stable.

Example 2: Let $C = 0$, $A = 3000$, $e = 0.05$, then $R_0 = 1.24244 > 1$. The presence and stability of the positive equilibrium point in Figure 3 can be observed.

Example 3: Let $C = 0.03$, at this point, the endemic equilibrium point is always present and globally stable, which is independent of whether $R_0$ is larger than one or not.

4.2.   Data fitting

In order to simulate real-world situations, one set a specific environmental exposure function. The results of the previous Sections show that the three commonly used environmental exposure functions lead to consistent results for the dynamics of the model. A question however arises abut the sensitivity the models employing different exposure functions with respect to control parameters In order to facilitate the comparison, we use flock data from Yulin, China and establish a common range of variations.

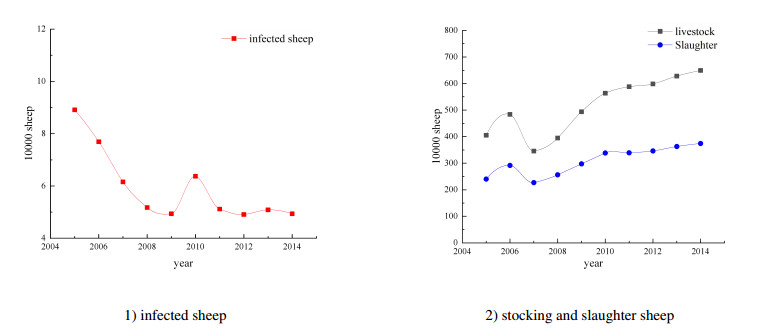
Using the statistical bulletin of national economic and social development of Yulin City [from the website of Yulin municipal government (www.yl.gov.cn)], we obtain the stock and slaughter of sheep for each year from 2005 to 2014, and combined with the annual infection rate of sheep, we get the number of infected sheep, see the Figure below.

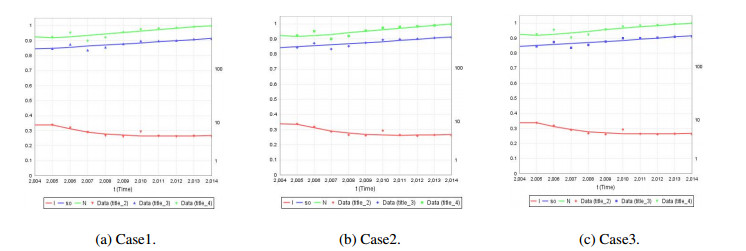
We use the least square method to estimate the parameters. Through DEDiscover software (DEDiscover is a general-purpose tool to perform simulation), we fit each of the three cases to find a combination of parameters that is closer to the actual results. The fit parameters can be seen in Tables 2–4. Figure 4 illustrates the results of the three fits against the actual data, and show the good quality of the fits. The sum of squared residuals for all three sets of parameters is about 0.044. Using the method of Akaike information criterion (AIC) ^[23,24] to compare the three models, we get $AIC_1 = -162.832$, $AIC_2 = -162.401$, $AIC_3 = -162.609$. Case 1 is more suitable for the data, but the three values do not differ much.

In order to put the three sets of values in a unified coordinate system, we used logarithmic values and then compared them. From Figure 4, we conclude that in three cases, there is no obvious difference in the simulation results.

4.3.   Simulation analysis of model sensitivity to parameters

In this section, we numerically compare and analyze results from the perspective of disease control. Our main concern is to assess how sensitive are the different environmental infection exposure functions to control measures. If the magnitude of the variation is comparable, then we can choose the first form containing fewer parameters. However, if the variations are larger, then we are also reminded that the formulation of the environmental infection pathway is something that needs to be chosen carefully in the modeling stage.

The following control measures are investigated:

1) Improve source management efforts of sheep to control the inflow of diseased sheep.

2) Increase culling of diseased sheep to reduce the infection base.

3) Standardize the disinfection of the environment to reduce the risk of environmental infection.

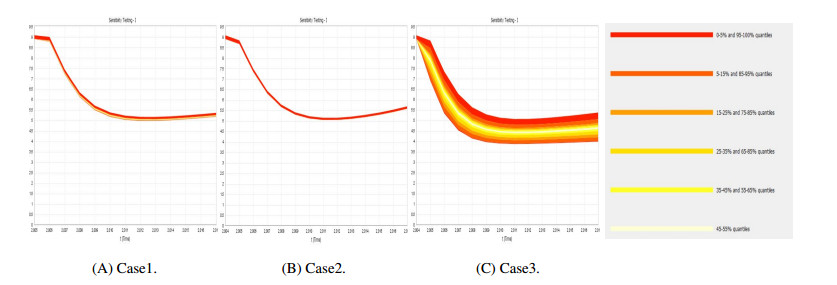
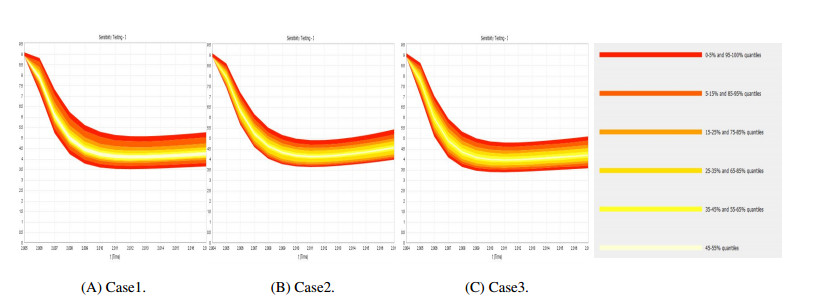
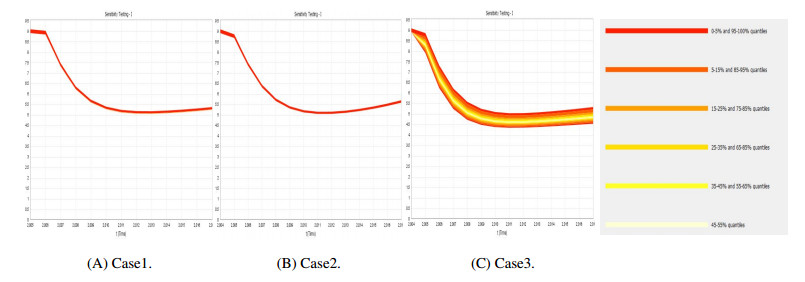
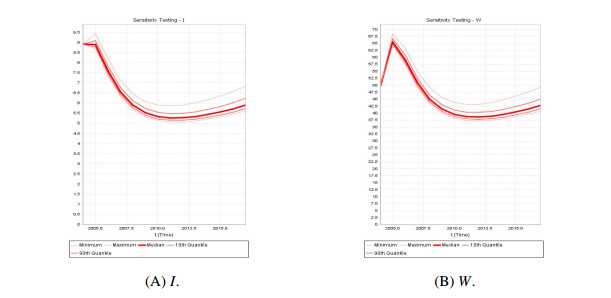
Based on the assumed values of the model parameters, we then change the control parameters in the above strategies to achieve a reduction in the number of infected sheep $(I)$. Obviously, some of these parameters need to be increased (such as $e$ and $l$) and some need to be decreased (such as $\beta_2$ and $C$). Here, we consider a 50$\%$ range of parameter changes to analyze the changes in the number of infected sheep.

In the above plots, we use a superimposed quantized visualization to show the range and the magnitude of the variationa of $I$ across the parameter range. This facilitates the comparison of three models.

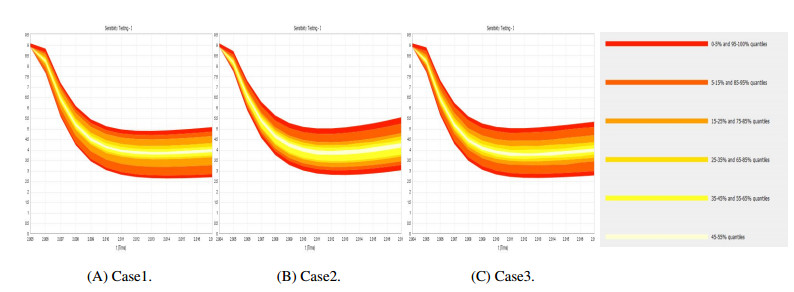
As can be seen in Figures 5–8, all the control measures lead to a decrease in the number of infected sheep. However, the dynamics of the model is different for the three functions. In particular, the magnitude of the change of $I$ with the parameters is different. The effects of parameters $C$ and $e$ is not much different in the three cases, whereas for parameter $\beta_2$, the magnitude of change in $I$ is significantly greater in case 3 than in the first two cases, with case 2 being almost insensitive. Concerning parameter $l$, case 2 remains insensitive, whereas in case 3 the number of infected sheep can be reduced by 50$\%$ of the initial value, while this is not possible in the first two cases. For case 2, we scaled the upper limit of the environmental exposure rate to 0.0078 and scaled the environmental modulation parameter $\epsilon_1$ to a range of values of $(0,150)$. As it can be seen in Figure 9, the magnitude of the change in $I$ is small and still reflects the insensitivity to the environmental modulation parameter.

5.   Conclusions

In this paper, a stage-specific dynamic model of brucellosis in sheep has been suggested and analyzed. Due to the constant input of infected sheep, there is no disease-free equilibrium point in the model, which means that Brucella is always transmitted in the flock. Numerical simulationz show that the following measures can effectively reduce the scale of the epidemic and control the occurrence of brucellosis: 1) Strengthen the monitoring of imported individuals; 2) Disinfect the environment regularly; 3) Once infected sheep are found, they should be promptly slaughtered.

Looking at the index parameters of the fitting for the three models, we have found that case l is closer to actual data, and this is consistent with the conclusions of reference ^[6]. If the second environmental exposure function is chosen, for $C = 0$, our results are consistent with the results of reference ^[8]. If the third environmental exposure function is chosen our results are consistent with those of reference ^[12] for $C = 0$. However, when $0 < C < 1$, we have found that the epidemic of persists because a disease-free equilibrium points does not exist. In particular, when $C = 1$, the disease-free equilibrium point, and the positive equilibrium point do not exist. On the contrary, there exists a boundary equilibrium point with global asymptotic stability, which corresponds to a situation in which all sheep are eventually infected.

Although the dynamical behavior is similar for the three environmental exposure functions, we have found that the sensitivity may be considerably different. Results from numerical simulations for cases 1 and 2 have shown that the number of infections is not much affected by changes in the environmental control parameters. On the contrary, in case 3 the sensitivity is significant. In particular, in the third case it is possible to achieve a control goal to reduce the number of infections to less than half of the initial value.

In the literature about infections by Brucellae, specific functional expressions of environmental infections have been.employed and pathways of environmental infection are considered. However, little attention has been paid to the variability exhibited by the different environmental functional expressions. To fill this gap, we have compared those common forms and found that their differences have a significant effect on the selection of optimal control methods. Our results clearly show that different function expressions yield different optimal control results, and that the expressions of environmental infection pathwayswe should be chosen carefully.

In this paper we have adopted a relatively simple ODE model for the spread of brucellosis virus in sheep, unifying the results of the analysis of the dynamical behavior of the environmental exposure function under certain characteristics. However, in practice, there is a certain time delay from exposure to the virus to infection with the virus, and this phenomenon is more common in disease transmission including pathogenic infections ^{[25,26,27,28]}. Then whether different environmental infection exposure functions will show greater variability under the infectious disease model of delayed infection or delayed distribution will be the next step of our research.

Acknowledgments

The authors acknowledge the useful suggestions and thoughtful comments made by the referees on their earlier version of this work. This work has been supported by the Industry-University-Research project of science and technology plan of Yulin City, Shaanxi Province (CXY-2020-087), Natural Science Foundation Project of Shaanxi Province, China (2023-JC-YB-084).

Conflict of interest

The authors declare there is no conflict of interest.