Modelling and stability analysis of ASFV with swill and the virus in the environment

1.   Introduction

African swine fever virus (ASFV) is an ancient virus and was first discovered in 1921 in Kenya. African swine fever (ASF) is caused by ASFV which is a large double-stranded DNA virus, and ASF is a highly contagious hemorrhagic disease of pigs ^[1,2]. Pigs of all breeds and ages can be infected ^[3], and the outbreaks of ASF lead to a mass of death of pigs ^[4,5]. The clinical manifestation includes high fever, bleeding, and other symptoms ^[6]. In general, the incubation period ranges from 4 to 19 days ^[2]. For highly pathogenic ASFV strains, the fatality rate could reach 100% ^[7]. Since the outbreak in East Africa in the 1900s, the spread of ASF ranges from Africa and Europe to South America and Caribbean ^[8]. Ever since the first outbreak was reported in Shenyang in August 2018, ASF has quickly spread in China and led to millions of pigs culled ^[9]. In the absence of a vaccine, ASF poses a serious threat to the domestic and foreign trade of pigs and pork products ^[10,11].

ASF could be transmitted by direct transmission and indirect transmission. The direct transmission includes the direct contact between susceptible pigs and infected pigs (effective transmission distance within 1 km), and feeding contaminated pig products ^[12,13,14]. The indirect transmission occurs by the virus in the environment and ticks ^[4]. The important routes of transmission of ASF may be feeding noxious swill and exposure to the virus from infected pigs, and other possible routes for the spread of ASFV in China may be the widespread use of contaminated swill and pig products ^[15]. Thus, the virus in the environment and contaminated swill play an important role in the ASFV transmission.

Mathematical modeling is an important method to explore the spread of diseases such as ASF, and prevent and control the disease spreading using public information ^{[16,17,18,19,20,21,22,23,24]}. Guinat et al. ^[25] used a stochastic SEIR model to estimate the basic reproduction number in Georgia. Barongo et al.^[26] developed a stochastic dynamical model to evaluate the impact of control strategies at different times on disease-related mortality. O'Neill et al. ^[27] developed a wild boar ASF model to explore the pivotal transmission and infection maintenance processes. Based on the effectiveness of control measures, Li et al. ^[28] proposed a generalized SEIR model and estimated the important epidemiological parameter values. Although some research focuses on the dynamics of ASFV transmission, little research contributes to the impact of contaminated swill and virus in the environment on the ASFV transmission so far.

In this paper, to examine the impact of contaminated swill and virus in the environment on the ASFV transmission, we propose an ASFV transmission model with swill and virus in the environment. The basic reproduction number is computed using the next-generation matrix. We prove the global stability of the disease-free equilibrium and endemic equilibrium by constructing the Lyapunov function. Based on the public information, parameter values are estimated, and sensitivity analysis will be performed by PRCC and eFAST. Numerical simulations are implemented to validate the theoretical results and assess the impact of contaminated swill and virus in the environment on the ASFV transmission.

This paper is organized as follows. In Section 2, we formulate an ASF transmission dynamics model, and the nonnegativeness and boundedness of solutions are proved. In Section 3, the basic reproduction number is calculated, and the global dynamics are proved. In Section 4, parameter values are estimated using the reported cases in Aijuan, and sensitivity analysis and numerical simulations are implemented. Section 5 gives the conclusion and discussion.

2.   Model formulation

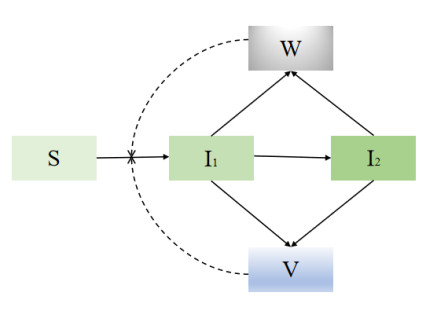
Based on the mechanism of ASFV transmission ^[29,30], the population of the pig is divided into susceptible pigs (S), asymptomatic infectious pigs ($I_1$) and symptomatic infectious pigs ($I_2$). Also, ASFV is transmitted by feeding contaminated swill and contact with the virus in the environment. Then we assume that $V$ denotes the virus load in the environment and $W$ denotes the amount of contaminated swills. Given the mechanism of ASFV transmission and previous work ^[27,28], we build the ASFV transmission model

with nonnegative initial values

where $p_1 = p d_1, p_2 = p d_2$. The detailed descriptions of state variables and related parameters in model (2.1) are shown in Table 1. The flow chart in Figure 1 depicts the transmission of ASFV.

Theorem 2.1. The solutions of the model (2.1) with nonnegative initial values (2.2) are nonnegative and ultimately bounded.

Proof. Form model (2.1) with nonnegative initial values (2.2), we can get

where

where

and

with $S(t)\geq0, I_1(t)\geq0, I_2(t)\geq0, V(t)\geq0 \ \text{and}\ W(t)\geq0$. Therefore, the nonnegativity of solutions is proved.

Now, we prove the ultimate boundedness of solutions. From the model (2.1),

where $d = \min\{d_1, d_2\}$. According to the comparison theorem ^[31], we have

Therefore, the nonnegativity and boundedness of solutions of model (2.1) are proved.

The feasible region

is the positive invariant set of model (2.1).

3.   Threshold dynamics

3.1.   The basic reproduction number and equilibria

Obviously, system (2.1) always has a disease-free equilibrium $E_0 = (S_0, 0, 0, 0, 0)$, where $S_0 = b/d_1$. Using the theory in ^[32], we could compute the basic reproduction number. Let $X = (I_1, I_2, V, W)$, then model (2.1) can be expressed as

where

The Jacobian matrices of $\mathscr{F}$ and $\mathscr{V}$ at $E_0$ gives

Using the spectral radius of the matrix $FV^{-1}$, we have the basic reproduction number

When $R_0 > 1$, the unique endemic equilibrium of model (2.1) is $E_1(S^*, I_1^*, I_2^*, V^*, W^*)$, where

3.2.   Local stability

Theorem 3.1. When $R_0 < 1$, the disease-free equilibrium $E_0 = (S_0, 0, 0, 0, 0)$ of model (2.1) is locally asymptotically stable in $\Omega$.

Proof. The Jacobian matrix $J_1$ at $E_0$ gives

Obviously, the characteristic equation of $J_1$ always has a negative real root $\lambda_1 = -d_1$, and the other roots are determined by the following equation

Assume that $Re(\lambda)\geq0$. Then we can divide by $(\lambda+\alpha+d_1)(\lambda+d_2)(\lambda+c_1)(\lambda+c_2)$ and take absolute values on both sides of the equation, and we have

If $\lambda = x+yi$, where $i$ is the imaginary unit, then

Hence,

which contradicts with $R_0 < 1$. All roots of characteristic equation have negative parts when $R_0 < 1$. Thus, the disease-free equilibrium of model (2.1) is locally asymptotically stable in $\Omega$.

Theorem 3.2. When $R_0 > 1$, the unique endemic equilibrium $E_1(S^*, I_1^*, I_2^*, V^*, W^*)$ of model (2.1) is locally asymptotically stable in $\Omega$.

Proof. The Jacobian matrix $J_2$ at $E_1$ gives

The characteristic equation of $J_2$ leads to

where

Using the similar discussion in Theorem 3.1, we assume that $Re(\lambda)\geq0$. Then we can divide the two sides of the above equation by $A$ and take the absolute value of both sides of this equation, and we have

The right side of equation gives

which leads to a contradiction. All roots of characteristic equation have negative parts when $R_0 > 1$. Thus, the unique endemic equilibrium of model (2.1) is locally asymptotically stable in $\Omega$.

3.3.   Global dynamics

In this section, we prove that the disease-free equilibrium and endemic equilibrium of model (2.1) are globally asymptotically stable by constructing Lyapunov function. Let

Note that $F(x)\geq0$ when $x > 0$, and $F_{\min}(x) = F(1) = 0$.

Theorem 3.3. When $R_0 < 1$, the disease-free equilibrium $E_0 = (S_0, 0, 0, 0, 0)$ of model (2.1) is globally asymptotically stable in $\Omega$.

Proof. Define the Lyapunov function

The time derivative of $L_0$ along the solution of model (2.1) gives

Note that $L'_0(t) < 0$ when $R_0 < 1$. In addition, $L'_0(t) = 0$ if and only if $S = S_0, I_1 = 0, I_2 = 0, V = 0, W = 0$. The single point set ${E_0}$ is the largest invariant set of model (2.1) on set $\{(S(t), I_1(t), I_2(t), V(t), W(t))\in\Omega\mid L'_0(t) = 0\}$. Using LaSalle's Invariance Principle ^[33] and the local stability of $E_0$, then the disease-free equilibrium $E_0$ is globally asymptotically stable in $\Omega$ when $R_0 < 1$.

Theorem 3.4. When $R_0 > 1$, the unique endemic equilibrium $E_1(S^*, I_1^*, I_2^*, V^*, W^*)$ of model (2.1) is globally asymptotically stable in $\Omega$.

Proof. Define the Lyapunov function

Calculating the derivative of $L_1(t)$ along the solution of model (2.1) gives

Using $F(x) = x-1-\ln x, x\in(0, \infty)$, we have

Note that $L'_1(t) < 0$ when $R_0 > 1$. Besides, $L'_1(t) = 0$ if and only if $S(t) = S^*, I_1(t) = I_1^*, I_2(t) = I_2^*, V(t) = V^*, W(t) = W^*$. The single point set ${E_1}$ is the largest invariant set of model (2.1) on set $\{(S(t), I_1(t), I_2(t), V(t), W(t))\in\Omega\mid L'_1(t) = 0\}$. Using LaSalle's Invariance Principle ^[33] and the local stability of $E_1$, then the endemic equilibrium $E_1$ is globally asymptotically stable in $\Omega$ when $R_0 > 1$.

4.   Numerical simulations

Using the public information, parameter values and initial values are estimated. This section gives the sensitivity indexes of the basic reproduction number $R_0$ and state variables $I_1$, $I_2$, $V$ and $W$. Numerical simulations are implemented to illustrate our theoretical results and assess the impact of the virus in the environment and swill on the ASFV transmission. All simulations are conducted by Matlab.

4.1.   Parameter estimation

4.1.1.   Data source

In August 2018, an ASF outbreak occurred at an Aiyuan farm of Jiangsu Jiahua Breeding Pig Company in Siyang County, China. There are 14929 pigs in the 13 pigpens. The ASF outbreak is possibly caused by the introduction of contaminated vehicles and employees. The data from January 8, 2019 to January 11, 2019 are obtained from the China Animal Health Endemic Center (CAHEC) ^[34] and reference^[35]. Our data includes new ASF cases in Table 2. All data used are from the public information.

It is worth noting that as a major pig producing country in the world, China has suffered great economic losses from the ASF outbreaks to her domestic pig market. Since there is no effective treatment for ASFV at present, the Chinese government attaches great importance to the prevention and control of ASF at an early stage. For example, when pig farmers are suspected of being infected with ASFV, the relevant departments will immediately conduct an epidemiological investigation and clinical diagnosis, and collect samples for testing in a short time. Once the outbreak of the epidemic is determined, all pigs in the epidemic site and within a certain range should be culled immediately ^[10]. At the same time, carcasses and pollutants should be destroyed innocuously, and vehicles, facilities and relevant personnel in the epidemic site should be disinfected and cleaned. Further intervention measures will be implemented according to the development of the epidemic, including restrictions on the movement of pigs and pork products, timely monitoring and quarantine. Therefore, the epidemic foci usually only have time series data within a few days.

4.1.2.   Parameter estimation

Based on our mathematical model and the cumulative number of ASF cases and using the Least Square method (LSM), our model is fitted to the real data. Parameters values $\beta_3$ and $\alpha$ and initial values $I_1(0)$ with 95% confidence interval (CI) are estimated in Tables 3 and 4. Other parameter values are obtained from the real data and references.

4.1.3.   Fitting results

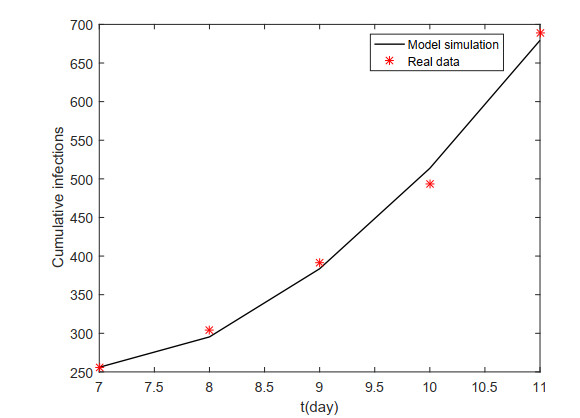
Given the uncertainty of parameter values and initial values, LSM is used to assess our model with evaluated parameter values and initial values in Tables 3 and 4. Figure 2 gives the estimated cumulative number of ASF cases with real data on the Aiyuan pig farm. Our simulations are consistent with the real data, which verifies the accuracy of the model.

4.2.   Sensitivity analysis

Partial rank correlation coefficients (PRCCs) and variance decomposition (obtained by an extended version of the Fourier Amplitude Sensitivity Test (eFAST)) are used to carry out the sensitivity analysis ^[38]. We calculate PRCCs and eFAST sensitivity indexes of $R_0$ and $I_1$, $I_2$, $V$, $W$ to have a complete and informative uncertainty and sensitivity (US) analysis.

4.2.1.   Sensitivity indexes of $R_0$

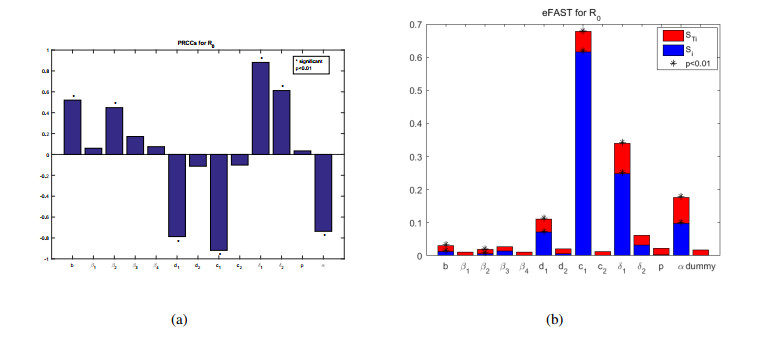
The PRCCs and eFAST sensitivity results about $R_0$ are illustrated in Figure 3 using the bar charts. PRCCs in Figure 3 give that $b, \beta_2, \delta_1$, $d_1, c_1$, $\alpha$ and $\delta_2$ have a significant impact on $R_0$. The first order $S_i$ and the total order $S_{Ti}$ are given for each parameter (including a dummy parameter) in Figure 3. The red bar represents the sum of the influence of a single parameter and its interaction with other parameters, denoted as $S_{Ti}$ (total order sensitivity index) and the blue bar indicates the sensitivity of the independent effect of a single parameter, expressed as $S_i$ (first-order sensitivity index). Considering only $p < 0.01$, the relationship of $S_i$ is $c_1 > \delta_1 > \alpha > d_1 > b > \beta_2$, and the size relationship of $S_{Ti}$ is $\delta_1 > \alpha > c_1 > d_1 > b > \beta_2$.

Therefore, Figure 3 finds that $b, \beta_2, \delta_1$ and $\delta_2$ have a significant positive impact on $R_0$, while $d_1, c_1$ and $\alpha$ have a significant negative impact on $R_0$. However, $b$ and $\beta_2$ have high PRCCs sensitivity indexes and low eFAST sensitivity indexes.

4.2.2.   Sensitivity indexes of $I_1$, $I_2$, $V$, $W$

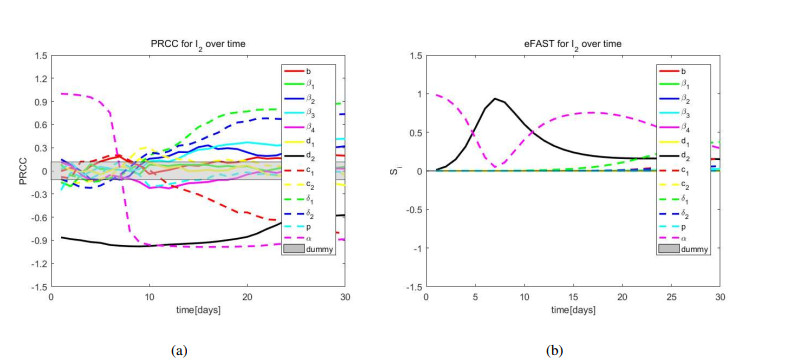
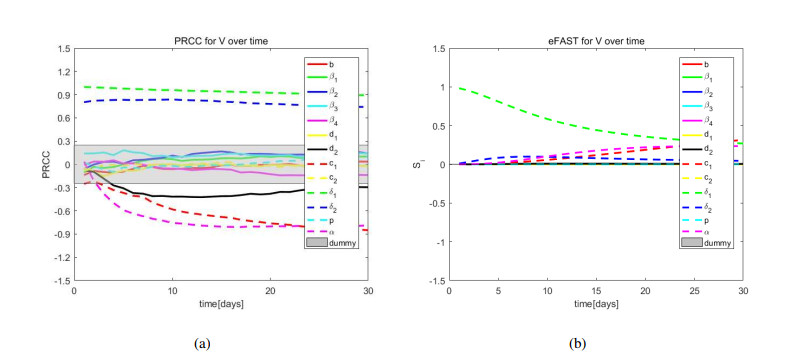
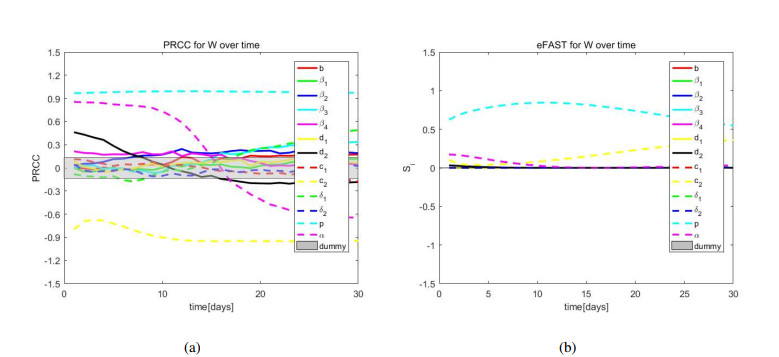
To evaluate whether the importance of a parameter appears in the entire time interval during the dynamics process, we focus on state variables $I_1, I_2, V$ and $W$. We assume that the PRCCs and eFAST time ranges from 0 to 30, and parameter values are chosen from Table 1. We calculate the PRCCs and eFAST ($S_i$) indexes at multiple time points and plot the time series about state variables $I_1, I_2, V$ and $W$. The gray area indicates that there is no significant difference from zero.

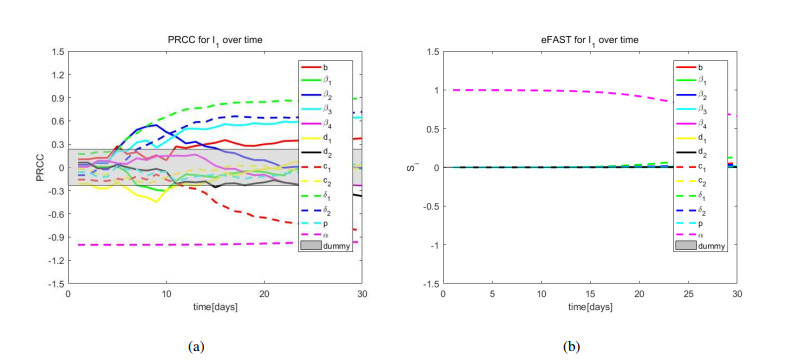
In Figure 4(a), the parameters are divided into four categories. The PRCCs index values of the first category including $\delta_1, \delta_2, \beta_3, b$ and $c_1$ firstly rise or fall to a value over time, and then gradually stabilize. The PRCCs index values of the second category including $\beta_2$ rise to a peak at an average speed, and then decrease rapidly until there is no significant difference from zero. The PRCCs index values of the third category including $\alpha$ always remain in a steady correlation with $I_1$. The fourth category containing $\beta_4, d_2, c_2, d_1, \beta_1$ and $p$ have no effect on $I_1$. Figure 4(b) reveals that the curve of the parameter $\alpha$ is very stable at early time points, and declines after 15 days and then stabilize in the future.

Figure 5(a) shows that the curve of parameter $\alpha$ is positively correlated with $I_2$ at the initial stage, and then decreases rapidly to negative correlation until gradually reaches a stable state. Figure 5(b) shows that $\alpha$ and $d_2$ have a significant impact on $I_2$.

Figure 6(a) demonstrates that $\delta_1$ and $\delta_2$ have a strong positive impact on $V$ and $c_1$ is negatively correlated with $V$. Figure 6(b) demonstrates that $\delta_1$ has a strong positive impact on $V$.

Figure 7(a) explains that $\alpha$ and $p$ have a strong positive impact on $W$ and $c_2$ is negatively correlated with $W$. Figure 7(b) explains that $p$ has a strong positive impact on $W$.

4.3.   Numerical simulations

In this section, numerical simulations are implemented to illustrate our theoretical results and assess the impact of the virus in the environment and swill on the ASFV transmission.

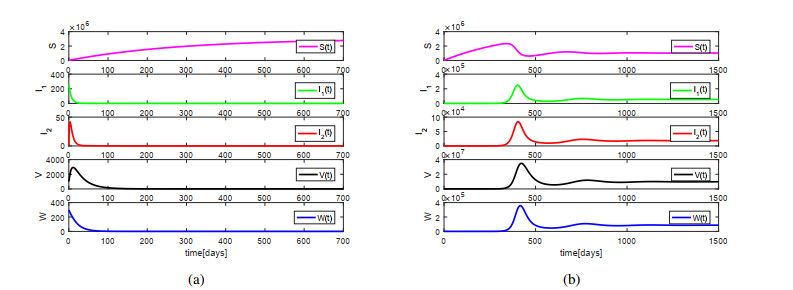
Set parameters $b = 10587$, $\beta_1 = 1.0004\times10^{-8}$, $\beta_2 = 5.5410\times10^{-8}$, $\beta_3 = 3.0947\times10^{-10}$, $\beta_4 = 3.2320\times10^{-10}$, $c_1 = 0.0391, c_2 = 0.0545$, $d_1 = 0.0035$, $d_2 = 0.5885$, $\delta_1 = 1.5977$, $\delta_2 = 2.4596$, $p = 0.1285$, $\alpha = 0.1555$, and the initial values $S(0) = 10000$, $I_1(0) = 256$, $I_2(0) = 0$, $V(0) = 1000$, $W(0) = 300$. We get that the basic reproduction number $R_0 = 0.8015 < 1$, and the disease-free equilibrium of model (2.1) is globally asymptotically stable (Figure 8(a)), which illustrates the results in Theorem 3.3.

Set parameters $b = 10358$, $\beta_1 = 1.0272\times10^{-8}$, $\beta_2 = 1.5669\times10^{-7}$, $\beta_3 = 4.2918\times10^{-10}$, $\beta_4 = 3.1256\times10^{-10}$, $c_1 = 0.0377, c_2 = 0.0725$, $d_1 = 0.0024$, $d_2 = 0.4239$, $\delta_1 = 4.6698$, $\delta_2 = 6.2956$, $p = 0.7933$, $\alpha = 0.1439$, and the initial values $S(0) = 10000$, $I_1(0) = 256$, $I_2(0) = 0$, $V(0) = 1000$, $W(0) = 300$. We obtain that the basic reproduction number $R_0 = 4.1865 > 1$, and the unique endemic equilibrium is globally asymptotically stable (Figure 8(b)), which illustrates the results in Theorem 3.4.

4.3.1.   The effect of the virus in the environment on the ASFV transmission

The effect of the virus in the environment on the ASFV transmission is assessed by the impact of $\delta_1$ and $\delta_2$ on the symptomatic ASF cases. Set $\delta_1 = 9$, $\delta_1 = 6$ and $\delta_1 = 3$, the peak value and peak time of symptomatic ASF cases could reach 780, 660, 570 and 60, 63, 65 days, respectively. If $\delta_2 = 9$, $\delta_2 = 6$ and $\delta_2 = 3$, the peak value of symptomatic ASF cases could reach 630, 590 and 550, respectively, and the peak time of symptomatic ASF cases could roughly the same. Figure 9 reveals that virus in the environment increases the peak value of symptomatic ASF cases.

4.3.2.   The effect of swill on the ASFV transmission

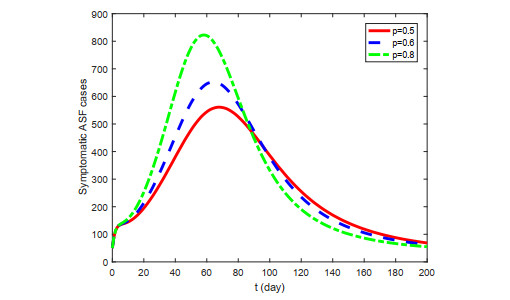
The effect of swill on the ASFV transmission is assessed by the impact of $p$ on the symptomatic ASF cases. If $p = 0.8$, $p = 0.6$ and $p = 0.5$, the peak value of symptomatic ASF cases could reach 820, 650, 550 and 59, 65, 70 days, respectively. Figure 10 reveals that contaminated swill increases the peak value of symptomatic ASF cases and makes the peak time in advance.

5.   Conclusions

African swine fever is listed as an animal disease that must be reported by the World Organization of Animal Health (OIE), and is a class I animal disease in China. The early epidemic in China mainly occurred in small and medium-sized pig farms, which was mainly caused by swill feeding ^[28]. Due to the 100% mortality rate, ASF seriously threatens the pig industry. The virus in the environment and contaminated swill contribute to the ASFV transmission. To study the impact of the virus in the environment and contaminated swill on the ASFV transmission, we build the ASFV transmission model with the virus in the environment and swill.

This is the first study to show the global dynamics of the ASFV transmission model. We compute the basic reproduction number, and prove the global stability of disease-free equilibrium and endemic equilibrium. When $R_0 < 1$, the disease-free equilibrium $E_0$ is globally asymptotically stable. When $R_0 > 1$, the unique endemic equilibrium $E_1$ is globally asymptotically stable.

Our findings reveal that the release rate of ASFV from asymptomatic and symptomatic infectious pigs and the proportion of pig products from infectious pigs to swill have a significant impact on the ASFV transmission. We use the PRCCs and eFAST to evaluate the impact of parameters on $R_0$ and $I_1$, $I_2$, $V$, $W$. PRCCs and eFAST sensitivity analysis reveals that parameters $b$, $\beta_2$ and $\delta_1$ have a significant positive effect on $R_0$, and parameters $d_1$, $c_1$ and $\alpha$ have a significant negative effect on $R_0$. The sensitivity indexes at multiple time points give that the release rate of ASFV from asymptomatic and symptomatic infectious pigs and the proportion of pig products from infectious pigs to swill have a significant impact on $I_1$, $I_2$, $V$ and $W$.

The results show that viruses in the environment and contaminated swill contribute to the ASFV transmission. PRCCs and eAFST indicate that $\delta_1$ and $c_1$ have a significant effect on $R_0$, which means that the virus in the environment exerts a major influence on $R_0$. PRCCs and eAFST indicate that $\delta_1$, $\delta_2$ and $p$ have a significant impact on $I_1$, $I_2$, $V$ and $W$, which means that the virus in the environment and contaminated swill exert a major influence on $I_1$, $I_2$, $V$ and $W$. Numerical simulations reveal that reducing $\delta_1$ and $\delta_2$ could effectively cut down the peak value of symptomatic ASF cases, and increasing $p$ could reduce the peak value of symptomatic ASF cases by over 30%.

Our results indicate that contaminated swill contributes to the ASFV transmission, which is consistent with the results in ^[28]. Therefore, banning swill feeding, improving farmers' awareness of swill transmission and large-scale breeding are very necessary for prevention and control measures, which can effectively reduce the risk of ASFV transmission. Furthermore, our results show that the virus in the environment greatly accelerates ASFV transmission. By increasing the frequency and efficiency of disinfection, removing dead pigs in time, and strictly testing the vehicles and staff entering and leaving the pig farm, the virus in the environment could be cleared to control the epidemic.

It is of great significance to study the impact of culling on ASFV transmission. Millions of pigs are culled to contain the ASFV transmission in China. For future work, we may evaluate the impact of culling on the ASFV transmission. In this paper, our findings may help animal health to prevent and control the ASFV transmission.

Acknowledgments

The research is supported by the National Natural Science Foundation of China (12171291, 11871179, 61873154), the Fund Program for the Scientific Activities of Selected Returned Overseas Professionals in Shanxi Province (20200001), the Fundamental Research Program of Shanxi Province (20210302124018), the Shanxi Scholarship Council of China (HGKY2019004), and the Scientific and Technological Innovation Programs (STIP) of Higher Education Institutions in Shanxi (2019L0082).

Conflict of interest

The authors declare there is no conflict of interest.

Availability of data and materials

The ASF reported data used in this work were freely obtained from the China Animal Health Endemic Center via https://www.cahec.cn/ and reference ^[35].