New insights on novel coronavirus 2019-nCoV/SARS-CoV-2 modelling in the aspect of fractional derivatives and fixed points

1.   Introduction

In very recent years, the world has encountered with a deadly outbreak due to attack of a strange virus named novel coronavirus^[1]. Initially, the outbreak started in Wuhan city of China, and rapidly spread to all parts of the world. The deadly infectious disease has already taken lives of thousands of people around the globe. It could be observed that the virus had hugely effected aged people and people with chronic health issues. It is believed that the spread is more aggressive in low temperatures; however, the science behind this has not been found yet. Despite many studies carried out on the origin and the spread of the virus, the researcher could not determine the exact cause of the spread of the virus including the finding up the life span of virus on surface. Some people believe that such a virus is from bats, pangolins, seafood, and others strongly believed the virus is man-made. The spread and fatality of the Coronavirus has made this world hostile place to live in. The spread of the strange virus within humans is a clear indication that mankind must have limits to interact with living beings. But the precautions taken against the virus prevented the severe spread of virus. Therefore, humans should take necessary care while interacting with other humans in day to day life. So far, there are many studies carried out to understand structure, the life span, the mode of transmission, effect on the human body, in terms of the affluence of temperature, age, etc^[2,3,4]. However, to understand properly the spread, many researchers attempt to develop a mathematical model using the concept of differentiation and further some facts were derived through the observation. This observed factual information helps the mathematicians to come up with a suitable model with a solution that could show the predictable behaviour of the real-world problem as a function of time. Mathematicians can use this solution to understand, control, and predict the behavior of the real-world problem for a set of given data and parameters. In a latest study by Altaf and Atangana^[5] suggested a mathematical model could depict the spread of the novel coronavirus, many factors are considered for the following model. The readers can refer to ^[5] to understand more about the variables in below mathematical model.

Above all these studies suggested with help of the data sources, a reproductive number around 2.4, which was in good accordance with the value suggested by the World Health Organization(WHO).

Further, fractional calculus plays a pivotal role in the mathematical modeling of many bio-medical and engineering disciplines. The following is detailed review of literature with references connected to the study.

● In ^[6,7,8], we can see that, new fractional derivatives with nonlocal and non-singular kernel and their properties.

● In ^[9,10,11,12], there is a vigorous study via numerical and/or computational methods for various fractional derivatives with nonlocal and non-singular kernel and also for ordinary differential equations.

● Addressed the integro-differential equations utilizing the Atangana-Baleanu fractional derivatives, that will have the generalised Mittag-Leffler functions in their kernels and have been studied extensively. They investigated the existence and uniqueness of solutions to such equations in Banach spaces using fixed point approach in ^[13,14].

● We can see valid discussions and new results on nonlocal functional integro-differential equations with different kind of approaches such as non-compactness, with impulsive conditions and Hilfer fractional derivative in ^[15,16,17].

● In ^[18,19,20], using the concept of fractional differentiation based on the generalized Mittag-Leffler function, they presented some interesting simulations.

● Applied various methods such as fractal-fractional Atangana-Baleanunu order, Atangana-Baleanu Caputo (ABC) derivative and stationary distribution extinction and optimal control in mathematical modelling for hepatitis B and drinking alcohol in ^{[21,22,23,24,25]}.

However, the analysis presented in their paper is based on numerical approximation, the numerical methods have been promising to be effective mathematical tools that could be used where analytical techniques failed. It is essential that, to note that, the exact solution of given model with its proof is important to be observed. Therefore in this paper, extended orthogonal spaces are adopted and established valid fixed point results. Afterward, using fractional derivatives, we present an overview of the existence of solutions for the novel coronavirus 2019-nCoV/SARS-CoV-2 model. An investigation of the proposed model's existence of solutions is presented. Furthermore, we use a numerical approach to address the proposed model using several forms of differential operators.

2.   An extended orthogonal space and fixed points

The accessible collected works show that there is a clear connection between Metric Fixed Point Theory and many academic fields including but not limited to engineering, sciences, and technology. One of the clear applications of this is found in the theory of ordinary and partial differential equations. These equations are used to model real-world problems, thus their exact solutions are requested to be compared with experimental data. However on many occasions, exact solutions are impossible to be obtained, thus researchers relied on numerical approximation to provide a numerical solution that can be used for comparison with data. However, it is at least useful to provide conditions under which the model has an exact solution, in this case, metric fixed point theory is very useful. Several extensions or generalizations have been made and extensions have been done to capture problems that are more complex.

In recent past, Kamran et al. ^[26] introduced a novel approach to the study of $b$-metric space as below:

Definition 2.1 (see ^[26]). Let $\mathcal{S}$ be a non-empty set and $\mu {}:\mathcal{S}\times \mathcal{S}\rightarrow [1, \infty)$. A function $\mathscr{D}:\mathcal{S}\times \mathcal{S}\rightarrow [0, \infty)$ is called an extended $b$-metric if, for all $u, v, w\in \mathcal{S},$ it satisfies

(i). $\mathscr{D}(u, v) = 0$ if and only if $u = v$;

(ii). $\mathscr{D}(u, v) = \mathscr{D}(v, u)$;

(iii). $\mathscr{D}(u, v)\leq \mu (u, v)[\mathscr{D}(u, w)+\mathscr{D}(w, v)].$

The pair $(\mathcal{S}, \mathscr{D})$ is called an extended $b$-metric space.

His findings and/or methods also laid the groundwork for the observation of the role of extended dislocated $b$-metric^[27], extended complex $b$-metric^[28], controlled metric type^[29], extended $F$-metric^[30] and many more (For more info, reader can refer ^[31,32,33] and ^[34,35].

Definition 2.2. Let $\mathbb{S}\neq \emptyset$ and $\bot\subseteq \mathbb{S}\times\mathbb{S}$ be a binary relation. If $\bot$ satisfies the below assertion:

i.e., there exist $u_{0}$ such that for all $v\in \mathbb{S}, v\bot u_{0}$ or for all $v\in \mathbb{S}, u_{0}\bot v$, then it is called an orthogonal set (clearly, $\mathcal{O}$-set) and $u_{0}$ is called an orthogonal element. We denote this $\mathcal{O}$-set by $(\mathbb{S}, \bot)$.

Example 2.1. Let $\mathbb{S} = \mathcal{W}$. Define the binary relation $\bot$ on $\mathbb{S}$ by $m\bot n$ if there exist $k\in \mathcal{W}$ such that $m = kn$. It is easy to see that $\mathcal{O}\bot n$ for all $n\in \mathcal{W}$. Hence $(\mathbb{S}, \bot)$ is an $\mathcal{O}$-set.

Example 2.2. Let $\mathcal{A} = \{1, 2, 3\}$. Then the power set of $\mathcal{A}$ is $\mathcal{P}(\mathcal{A}) = \{\emptyset, \{1\}, \{2\}, \{3\}, \{1, 2\}, \{1, 3\}, \\ \{2, 3\}, \{1, 2, 3\}\}$. Define the binary relation $\bot$ on $\mathcal{P}(\mathcal{A})$ by $C\bot D$ such that $\emptyset = C\cap D$. It is easy to see that $\emptyset\bot D$ for all $D\in \mathcal{P}(\mathcal{A})$. Hence $(\mathcal{P}(\mathcal{A}), \bot)$ is an $\mathcal{O}$-set.

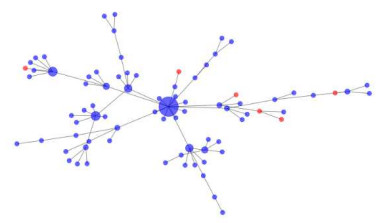
Example 2.3. Let $\mathbb{S}$ be the set of all peoples in the world. Define the binary relation $\bot$ on $\mathbb{S}$ by $u\bot v$ if $u$ can get novel coronavirus 2019-nCoV/SARS-CoV-2 infection by $u$. If $u_{0}$ is a person such that he/she infected by novel coronavirus 2019-nCoV/SARS-CoV-2, then we have $u_{0}\bot v$ for all $v\in \mathbb{S}$. Thus $(\mathbb{S}, \bot)$ is an $\mathcal{O}$-set. In this regard $\mathcal{O}$-set, $u_{0}$ is not unique.

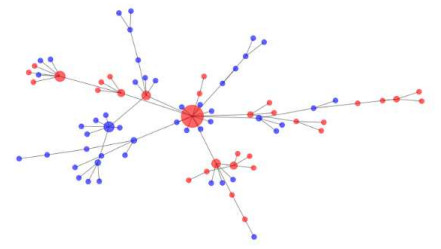
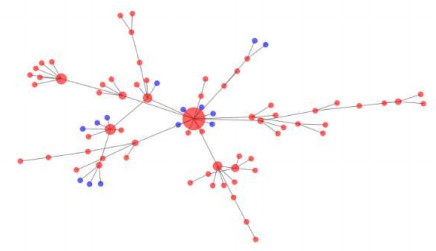
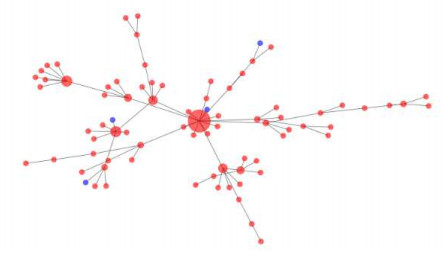
More clearly, If we consider a social network of a particular person:

The huge hub in the outline is a super-spreader, an individual who associates with numerous others, and along these lines can possibly spread the novel coronavirus 2019-nCoV/SARS-CoV-2 infection. Two spots are associated by a line on the off chance that they are in contact with one another, and the more contacts an individual has, the bigger their hub is on the network.

Example 2.4. Let $\mathbb{S}$ be the set of all peoples who effected by any one of the listed diseases, so called: EBOV-Ebola virus, MERS-CoV, SARS-CoV and FECV-feline enteric conronavirus. Define the binary relation $\bot$ on $\mathbb{S}$ by $u\bot v$ if $u$ and $v$ will hit/target the disease module by drug combination for all $u, v\in \mathbb{S}$. According to below given table, Antineoplastic drugs may furnish a synergistic repercussions in vigorously treating above mentioned EBOV-Ebola virus, MERS-CoV, SARS-CoV and FECV-feline enteric conronavirus diseases as in Table.1 (For more about eight potential repurposable drugs, the reader can refer ^[36]). Thus, $(\mathbb{S}, \bot)$ is an $\mathcal{O}$-set.

Now we give the concepts of an extended $\mathcal{O}$-sequence, an extended $\bot$-continuous mapping, an extended $\mathcal{O}$-complete orthogonal space, an extended $\bot$-preserving mapping.

Definition 2.3. The triplet $(\mathbb{S}, \bot, \mathscr{D})$ is called an extended orthogonal space if $(\mathbb{S}, \bot)$ is an $\mathcal{O}$-set and $(\mathbb{S})$ is an extended orthogonal space.

Definition 2.4. Let $(\mathbb{S}, \bot, \mathscr{D})$ be an extended orthogonal space. A sequence $\{u_{n}\}$ is called an extended orthogonal sequence (shortly, $\mathcal{E}_{\mathcal{O}}$-sequence) if for all $n\in \mathbb{N}, u_{n}\bot u_{n+1}$ (or) $n\in \mathbb{N}, u_{n+1}\bot u_{n}$

Definition 2.5. Let $(\mathbb{S}, \bot, \mathscr{D})$ be an extended orthogonal space. Then a mapping $\chi:\mathbb{S}\rightarrow \mathbb{S}$ is said to be an extended orthogonally continuous (shortly, $\mathcal{E}_{\bot}$-continuous) in $u\in \mathbb{S}$, if for each $\mathcal{E}_{\mathcal{O}}$-sequence $\{u_{n}\}$ in $\mathbb{S}$ with $u_{n}\rightarrow u$ as $n\rightarrow \infty$, we have $\chi(u_{n})\rightarrow \chi(u)$ as $n\rightarrow \infty$. Also $\chi$ is said to be $\mathcal{E}_{\bot}$-continuous on $\mathbb{S}$ if $\chi$ is $\mathcal{E}_{\bot}$-continuous in each $u\in \mathbb{S}$.

Remark 1.1. Every continuous mapping is $\mathcal{E}_{\bot}$-continuous and the converse is not true.

Definition 2.6. Let $(\mathbb{S}, \bot, \mathscr{D})$ be an extended orthogonal space. Then $\mathbb{S}$ is said to be an extended orthogonally complete (shortly, $\mathcal{E}_{\mathcal{O}}$-complete) if every Cauchy $\mathcal{E}_{\mathcal{O}}$-sequence is convergent.

Remark 1.2. Every complete extended space is $\mathcal{E}_{\mathcal{O}}$-complete space and the converse is need not to true.

Definition 2.7. Let $(\mathbb{S}, \bot)$ be an $\mathcal{O}$-set. A mapping $\chi:\mathbb{S}\rightarrow \mathbb{S}$ is said to be $\bot$-preserving if $\chi(u)\bot \chi(v)$ whenever $u\bot v$. Also, $\chi:\mathbb{S}\rightarrow \mathbb{S}$ is said to be weakly $\bot$-preserving if $\chi(u)\bot \chi(v)$ or $\chi(v)\bot \chi(u)$ whenever $u\bot v$.

Theorem 2.1. Let $(\mathbb{S}, \bot, \mathscr{D})$ be a complete extended orthogonal space. Suppose that $\mathscr{H}:\mathbb{S}\rightarrow \mathbb{S}$ is an $\mathcal{E}_{\bot}$-continuous mapping such that the following assertions hold:

(i) there exists $0 < k < 1$ such that $\mathscr{D}(\mathscr{H} u, \mathscr{H} v)\leq k\mathscr{D}(u, v)$ for all $u, v\in \mathbb{S}$ with $u\bot v$ and for each $n_{0}\in \mathbb{S}, \ \lim_{n, m\rightarrow \infty}\mathscr{D}(u_{n}, u_{m}) < \frac{1}{k}$, here $u_{n} = \mathscr{H}^{n}u_{0}, \ n = 1, 2, 3...$

(ii) $\mathscr{H}$ is $\mathcal{E}_{\bot}$-preserving.

Then $\mathscr{H}$ has a unique fixed point in $\mathbb{S}$. Also the picard sequence $\{\mathscr{H}^{n}u_{0}\}$ converges to the fixed point of $\mathscr{H}$.

Proof. From the definition of the orthogonality, it follows that $u_{0}\bot \mathscr{H}(u_{0})$ or $\mathscr{H}(u_{0})\bot u_{0}$.

Let,

If $u_{n^{*}} = u_{n^{*}+1}$ for some $n^{*}\in \mathbb{N}\cup \{0\},$ then $u_{n^{*}}$ is a fixed point of $\mathscr{H}$ and so the proof is completed. So, we may assume that $u_{n}\neq u_{n+1}$ for all $n\in \mathbb{N}\cup \{0\}$. Thus we have $\mathscr{D}(\mathscr{H} u_{n}, \mathscr{H} u_{n+1}) > 0$ for all $n\in \mathbb{N}\cup \{0\}$. Since $\mathscr{H}$ is $\bot$-preserving, we have $u_{n}\bot u_{n+1}$ or $u_{n+1}\bot u_{n}$ for all $n\in \mathbb{N}\cup \{0\}$. This implies that $\{u_{n}\}$ is an $\mathcal{E}_{\mathcal{O}}$-sequence.

Consider,

By triangular inequality and Eq (2.1), we have,

This will leads to,

Since $\lim_{n, m\rightarrow \infty} \mu {}(u_{n+1}, u_{m})k < 1$, the series $\Sigma_{n = 1}^{\infty}k^{n}\prod _{i = 1}^{n} \mu {}(u_{i}, u_{m})$ converges by ratio test for each $m\in \mathbb{N}$.

Let

Thus, for $m > n$, above inequality (2.2) implies

Letting $n\rightarrow \infty$, it follows that $\{u_{n}\}$ is a Cauchy $\mathcal{E}_{\mathcal{O}}$-sequence in $\mathbb{S}$. Since $\mathbb{S}$ is $\mathcal{E}_{\mathcal{O}}$-complete, there exists $u^{\star}\in \mathcal{S}$ such that $u_{n}\rightarrow u^{\star}$ as $n\rightarrow \infty$. Since $\mathscr{H}$ is $\mathcal{E}_{\bot}$-continuous, we have,

and so $u^{\star}$ is a fixed point of $\mathscr{H}$.

Next we prove the uniqueness of fixed point of $\mathscr{H}$.

Assume that $u^{*}$ is an another fixed point of $\mathscr{H}$. If $u_{n}\rightarrow u^{*}$ as $n\rightarrow \infty$, we have $u^{\star} = u^{*}$. If $u_{n}$ does not converge to $u^{*}$ as $n\rightarrow \infty$, there is a subsequence $\{u_{n_{\alpha}}\}$ such that

By the choice of $u_{0}$, we have $u_{0}\bot u^{*}$ or $u^{*}\bot u_{0}.$ Since $\mathscr{H}$ is $\mathcal{E}_{\bot}$-preserving and $\mathscr{H}^{n}u^{*} = u^{*}$ for all $n\in \mathbb{N}$, we have $\mathscr{H}^{n} u_{0}\bot u^{*}$ or $u^{*}\bot \mathscr{H}^{n} u_{0}$ for all $n\in \mathbb{N}$.

Consider,

This implies that $\mathscr{D}(\mathscr{H}^{n_{\alpha}}u_{0}, u^{*})\rightarrow 0$ as $n\rightarrow \infty$ since $u_{0}\bot u^{*}$, which is a contradiction to Eq (2.3).

This yields $u_{n}\rightarrow u^{*}$ as $n\rightarrow \infty$. Hence $u^{\star} = u^{*}$. Thus $\mathscr{H}$ has a unique fixed point.

Example 2.5. Let $\mathbb{S} = [0, \infty)$. Define $\mathscr{D}:\mathbb{S}\times\mathbb{S}\rightarrow \mathbb{R}^{+}$ and $\mu {}:\mathbb{S}\times\mathbb{S}\rightarrow [1, \infty)$ as $\mathscr{D}(u, v) = (u-v)^{2}$, $\mu {}(u, v) = 2u+3y+5$ for all $u, v\in \mathbb{S}$.

Consider the sequence $\{\Delta_{n}\}_{n\in \mathbb{N}}$ defined as $\Delta_{n} = \frac{n}{6}(2n+1)(n+1)$ for all $n\in \mathbb{N}\cup\{0\}$.

Define a relation $\bot$ on $\mathbb{S}$ by $u\bot v \Leftrightarrow uv\in\{u, v\}\subseteq \{\Delta_{n}\}$. Thus $(\mathbb{S}, \bot, \mathscr{D})$ is $\mathcal{E}_{\mathcal{O}}$-complete space. Now define a mapping $\mathscr{H}:\mathbb{S}\times\mathbb{S}$ by

It is easy to see that $\mathscr{H}$ is $\mathcal{E}_{\bot}$-continuous and $\mathscr{H}$ is $\mathcal{E}_{\bot}$-preserving.

Let $u, v\in \mathbb{S}$ with $u\bot v$ and $\mathscr{D}(\mathscr{H}u, \mathscr{H}v) > 0$. Without loss of generality we assume that $u < v$. This implies that $u\in \{\Delta_{0}, \Delta_{1}\}$ and $v = \Delta_{i}$ for some $i\in \mathbb{N}\backslash\{1\}$.

Then,

Thus $\mathscr{D}(\mathscr{H}u, \mathscr{H}v)\leq k \mathscr{D}(u, v)$. Therefore, all the assertions managed by above theorem satisfied and so $\mathscr{H}$ has a unique fixed point $u = \Delta_{0}$.

By applying various setting on above Theorem 2.1 we may get below corollaries. For suppose, if we consider $\mu {}(u, v) = b(\geq1)$, then we can reduce above theorem to below corollary.

Corollary 2.1. Let $(\mathbb{S}, \bot, \mathscr{D})$ be a $\mathcal{O}$-complete $b$-metric space. Suppose that $\mathscr{H}:\mathbb{S}\rightarrow \mathbb{S}$ is an $\bot$-continuous mapping such that the following assertions hold:

(i) there exists $0 < k < 1$ such that $\mathscr{D}(\mathscr{H} u, \mathscr{H} v)\leq k\mathscr{D}(u, v)$ for all $u, v\in \mathbb{S}$ with $u\bot v$ and for each $n_{0}\in \mathbb{S}, \ \lim_{n, m\rightarrow \infty}\mathscr{D}(u_{n}, u_{m}) < \frac{1}{k}$, here $u_{n} = \mathscr{H}^{n}u_{0}, \ n = 1, 2, 3...$

(ii) $\mathscr{H}$ is $\bot$-preserving.

Then $\mathscr{H}$ has a unique fixed point in $\mathbb{S}$.

If we consider $\mu {}(u, v) = 1$, then we can reduce above theorem to below corollary.

Corollary 2.2. Let $(\mathbb{S}, \bot, \mathscr{D})$ be a $\mathcal{O}$-complete metric space. Suppose that $\mathscr{H}:\mathbb{S}\rightarrow \mathbb{S}$ is an $\bot$-continuous mapping such that the following assertions hold:

(i) there exists $0 < k < 1$ such that $\mathscr{D}(\mathscr{H} u, \mathscr{H} v)\leq k\mathscr{D}(u, v)$ for all $u, v\in \mathbb{S}$ with $u\bot v$ and for each $n_{0}\in \mathbb{S}, \ \lim_{n, m\rightarrow \infty}\mathscr{D}(u_{n}, u_{m}) < \frac{1}{k}$, here $u_{n} = \mathscr{H}^{n}u_{0}, \ n = 1, 2, 3...$

(ii) $\mathscr{H}$ is $\bot$-preserving.

Then $\mathscr{H}$ has a unique fixed point in $\mathbb{S}$.

3.   Existence of solutions for novel coronavirus 2019-nCoV/SARS-CoV-2 model in fractional scenario

Although humans have advanced their technologies and their medicine to protect the mankind, it is important to note that there are still diseases that continue to spread across the world that up to now humans have not found a permanent solution to eradicating these diseases. A few examples can be noted including HIV, malaria, Ebola, and other well-known infectious diseases that continue to take much life daily. In addition to these existing diseases, humans continue to be surprised by new ones that lead them to double their efforts to make their environment more saver, however, diseases are known to be the main source of death across the world. For example, information released by the WHO in 2001 indicated that diseases have added 26% of global mortality. From 2003, the world has witnessed a rise of different types of viruses for example SARS-CoV in 2003, Mers-CoV in 2012, Ebola in 2014, and now SARS-CoV-2 and others that are not listed here. Researchers from different backgrounds have investigated the biological structures, mode of transmission, and life span of these viruses. On the other hand, to protect life and livelihood medical bodies have developed several vaccines that could help prevent the spread of these diseases. Nevertheless, to have an idea of what could happen in a near future, mathematicians have developed some mathematical models that could be used first to provide the reproductive number of these diseases, second to predict the numbers of infected, recovery, and death cases. This was also valid with the breakout of the new virus known as covid-19, several investigations have been done, vaccines have been developed and some mathematical models have been proposed in the last two years with the aim to predict future behaviors of the spread. It's important to note that the use of mathematical modeling in the analysis of epidemiological disorders has risen significantly. In this work, we propose solutions for fractional-order models of the novel coronavirus 2019-nCoV/SARS-CoV-2.

3.1.   Existence of solution for novel coronavirus 2019-nCoV/SARS-CoV-2 model via Atangana-Baleanu fractional integral operator

Let $\mathbb{S} = \{\mathbb{A}\in \mathcal{C}(I, \mathbb{R}): \mathbb{A}(t) > 0$ for all $t\in I = [0, \mathscr{H}], \mathscr{H} > 0\}$. Define the orthogonality relation $\bot$ on $\mathbb{S}$ by $u\bot v\Leftrightarrow u(t)v(t)\geq u(t)$ or $u(t)v(t)\geq v(t)$ for all $t\in I$.

Define a mapping $\mathscr{D}:\mathbb{S}\times\mathbb{S}\rightarrow [0, \infty)$ and $\mu {}:\mathbb{S}\times\mathbb{S}\rightarrow [0, \infty)$ as $\mathscr{D}(u, v) = |u-v|$ for all $u, v\in \mathbb{S}$. Then $(\mathbb{S}, \bot, \mathscr{D})$ is a $\mathcal{O}$-complete metric space. Define a mapping $\mathscr{H}:\mathbb{S}\times\mathbb{S}$ by,

Then, we see that $\mathscr{H}$ is $\bot$-continuous. Now we show that $\mathscr{H}$ is $\bot$-preserving. For each $u, v\in \mathbb{S}$ with $u\bot v$ and $t\in I$, we have,

It follows that, $[\mathscr{H}\mathcal{S}_{p}(t)][\mathscr{H}\mathcal{S}_{q}(t)]\geq [\mathscr{H}\mathcal{S}_{q}(t)]$ and so $[\mathscr{H}\mathcal{S}_{p}(t)]\bot[\mathscr{H}\mathcal{S}_{q}(t)]$. Then $\mathscr{H}$ is $\bot$-preserving.

In this section, by using Corollary 2.2, we prove the existence and uniqueness of solutions of Eq (3.1) provided the following conditions satisfied:

1) $|\mathbb{A}(t_{1}, \mathcal{S}_{p})-\mathbb{A}(t_{2}, \mathcal{S}_{p})|\leq |\mathcal{S}_{p}(t_{1})-\mathcal{S}_{p}(t_{2})|$;

2) $\bigg|\frac{\mathbb{A}(k, \mathcal{S}_{p})}{\Lambda}\bigg| < 1$;

3) $|t_{1}^{\Lambda}-t_{2}^{\Lambda}|\leq |\mathcal{S}_{p}(t_{1})-\mathcal{S}_{p}(t_{2})|$;

4) $\bigg|\frac{(1-\Lambda)\Gamma(\Lambda)+\Lambda}{\mathscr{AB}(\Lambda)\Gamma(\Lambda)}\bigg| < \gamma; \ \ \text{where} \ 0 < \gamma < 1.$

Now consider,

This can be reduced in to:

Therefore,

By following the same pattern as above, we get,

From Eq (3.2), we can write, $\mathscr{D}(\mathscr{H}\mathcal{S}_{p}(t_{1}), \mathscr{H}\mathcal{S}_{p}(t_{2}))\leq k\mathscr{D}(\mathcal{S}_{p}(t_{1}), \mathcal{S}_{p}(t_{2}))$. Similarly, we can get,

Hence the system of novel corona virus model gratified all the assertions of Corollary 2.2. Hence Eq (3.1) has unique fixed point. Thus Eq (3.1) has a unique solution.

3.2.   Existence of solution for novel coronavirus 2019-nCoV/SARS-CoV-2 model via Caputo-Fabrizio fractional derivative operator

In this section, we replace Atangana-Baleanu derivative with Caputo-Fabrizio fractional derivative and generalized model (1.1) in the following way:

By applying fractional integral operator, we convert model (3.3) into below integral form:

Let $\mathbb{S} = \{\mathbb{A}\in \mathcal{C}(I, \mathbb{R}): \mathbb{A}(t) > 0$ for all $t\in I = [0, \mathscr{H}], \mathscr{H} > 0\}$. Define the orthogonality relation $\bot$ on $\mathbb{S}$ by $u\bot v\Leftrightarrow u(t)v(t)\geq u(t)$ or $u(t)v(t)\geq v(t)$ for all $t\in I$.

Define a mapping $\mathscr{D}:\mathbb{S}\times\mathbb{S}\rightarrow [0, \infty)$ and $\mu {}:\mathbb{S}\times\mathbb{S}\rightarrow [0, \infty)$ as $\mathscr{D}(u, v) = |u-v|^{2}$ and $\mu {}(u, v) = u(t)+v(t)+2$ for all $u, v\in \mathbb{S}$. Then $(\mathbb{S}, \bot, \mathscr{D})$ is a complete extended orthogonal space. Define a mapping $\mathscr{H}:\mathbb{S}\times\mathbb{S}$ by,

Then, we see that $\mathscr{H}$ is $\mathcal{E}_{\bot}$-continuous. Now we show that $\mathscr{H}$ is $\mathcal{E}_{\bot}$-preserving. For each $u, v\in \mathbb{S}$ with $u\bot v$ and $t\in I$, we have,

It follows that, $[\mathscr{H}\mathcal{S}_{p_{1}}(t)][\mathscr{H}\mathcal{S}_{q_{1}}(t)]\geq [\mathscr{H}\mathcal{S}_{q_{1}}(t)]$ and so $[\mathscr{H}\mathcal{S}_{p_{1}}(t)]\bot[\mathscr{H}\mathcal{S}_{q_{1}}(t)]$. Then $\mathscr{H}$ is $\mathcal{E}_{\bot}$-preserving.

In this section, by using Theorem 2.1, we prove the existence and uniqueness of solutions of Eq (3.5) provided the following conditions satisfied:

1) $|\mathbb{A}(t, \mathcal{S}_{p_{1}}(t))-\mathbb{A}(t, \mathcal{S}_{p_{2}}(t))|^{2}\leq |\mathcal{S}_{p_{1}}(t)-\mathcal{S}_{p_{2}}(t)|^{2}$

2) $\bigg(\frac{1-\Lambda+\sigma t}{\mathscr{B}(\Lambda)}\bigg)^{2} < \xi, \ \ \text{where} \ \ 0 < \xi < 1$

Now consider,

Therefore,

By following the same pattern as above, we get,

From Eq (3.6) we can write, $\mathscr{D}(\mathscr{H}\mathcal{S}_{p_{1}}(t), \mathscr{H}\mathcal{S}_{p_{2}}(t))\leq \xi\mathscr{D}(\mathcal{S}_{p_{1}}(t), \mathcal{S}_{p_{2}}(t))$.

Similarly,

Hence the system of novel corona virus model gratified all the assertions of Theorem 2.1. Hence Eq (3.5) has unique fixed point. Thus Eq (3.5) has a unique solution.

3.3.   Existence of solution for novel coronavirus 2019-nCoV/SARS-CoV-2 model via Caputo fractional derivative operator

Let $\mathbb{S} = \{\mathbb{A}\in \mathcal{C}(I, \mathbb{R}): \mathbb{A}(t) > 0$ for all $t\in I = [0, \mathscr{H}], \mathscr{H} > 0\}$.

Define the orthogonality relation $\bot$ on $\mathbb{S}$ by $u\bot v\Leftrightarrow u(t)v(t)\geq u(t)$ or $u(t)v(t)\geq v(t)$ for all $t\in I$.

Define a mapping $\mathscr{D}:\mathbb{S}\times\mathbb{S}\rightarrow [0, \infty)$ and $\mu {}:\mathbb{S}\times\mathbb{S}\rightarrow [0, \infty)$ as $\mathscr{D}(u, v) = |u-v|$ for all $u, v\in \mathbb{S}$. Then $(\mathbb{S}, \bot, \mathscr{D})$ is a $\mathcal{O}$-complete metric space. Define a mapping $\mathscr{H}:\mathbb{S}\times\mathbb{S}$ by,

Then, we see that $\mathscr{H}$ is $\bot$-continuous. Now we show that $\mathscr{H}$ is $\bot$-preserving. For each $u, v\in \mathbb{S}$ with $u\bot v$ and $t\in I$, we have,

It follows that, $[\mathscr{H}\mathcal{S}_{p_{1}}(t)][\mathscr{H}\mathcal{S}_{q_{1}}(t)]\geq [\mathscr{H}\mathcal{S}_{q_{1}}(t)]$ and so $[\mathscr{H}\mathcal{S}_{p_{1}}(t)]\bot[\mathscr{H}\mathcal{S}_{q_{1}}(t)]$. Then $\mathscr{H}$ is $\bot$-preserving.

In this section, by using Corollary 2.2, we prove the existence and uniqueness of solutions of Eq (3.8) provided the following conditions satisfied:

1) $|\mathbb{A}(\tau, \mathcal{S}_{p_{1}}, \mathcal{E}_{p_{1}}, \mathcal{I}_{p_{1}}, \mathcal{A}_{p_{1}}, \mathcal{R}_{p_{1}}, \mathcal{M}_{p_{1}})-\mathbb{A}(\tau, \mathcal{S}_{p_{2}}, \mathcal{E}_{p_{2}}, \mathcal{I}_{p_{2}}, \mathcal{A}_{p_{2}}, \mathcal{R}_{p_{2}}, \mathcal{M}_{p_{2}})| < |\mathcal{S}_{p_{1}}(t)-\mathcal{S}_{p_{2}}(t)|$

2) $\frac{t^{\Lambda}}{\Gamma(\Lambda+1)} < \rho, \ \ \text{where} \ \ 0 < \rho < 1$

Now consider,

Therefore,

By following the same pattern as above, we get,

From Eq.(3.6) we can write, $\mathscr{D}(\mathscr{H}\mathcal{S}_{p_{1}}(t), \mathscr{H}\mathcal{S}_{p_{2}}(t))\leq \rho\mathscr{D}(\mathcal{S}_{p_{1}}(t), \mathcal{S}_{p_{2}}(t))$. Similarly,

Hence the system of novel corona virus model gratified all the assertions of Corollary 2.2. Hence Eq (3.8) has unique fixed point. Thus Eq (3.8) has a unique solution.

4.   Numerical experiments for novel coronavirus 2019-nCoV/SARS-CoV-2 model via various fractional derivatives

4.1.   Atangana-Baleanu fractional derivative sense

It has been recognized that dynamical spread exhibits nonlocal behaviors resembling processes like that of a power-law, fatigue, and crossover. These patterns are well described by some mathematical functions, for example, the power-law function is known to replicate power-law behaviors as time and power change. The fatigue effect can be well explained using an exponential decay function. The generalized Mittag-Leffler has been recognized to depict a passage from stretched fatigue effect to power-law. From these functions and the convolution, concepts of fractional differentiation and integration have been introduced and applied in many problems in the last decades. In this section, we investigate the model of 2019-nCoV/SARS-CoV-2 using differential operators based on the generalized Mittag-Leffler kernel.

The novel coronavirus 2019-nCoV/SARS-CoV-2 model further can be written as:

Hence we only consider the $t = \Delta t(n+1) = t_{n+1}$,

Applying the method to our system, we get

4.2.   Caputo-Fabrizio fractional derivative sense

In this section, we presented the numerical solution of the suggested model by employing the newly established predictor-corrector numerical scheme. Since our equations are non-linear, we present the method for a general non-linear fractional differential equation with power-law and exponential kernal. We start with the following general equation.

Applying the associated integral operator, we obtain,

at the point $t = t_{n+1} = \Delta t(n+1)$.

Our equation becomes,

Then, between $t_{n}$ and $t_{n+1}$, we approximate the function $\Lambda (\tau, v(\tau))$ using the Newton polynomial such that

After integration, we obtain,

where, $v_{n+1}^{p} = v_{0}+\frac{(1-\Lambda)\Lambda}{\mathscr{M}(\Lambda)}\Lambda(t_{n}, v(t_{n}))+\frac{\Lambda}{\mathscr{M}(\Lambda)}\sum_{k = 0}^{n}\Lambda(t_{k}, v(t_{k}))\Delta t$.

However, we need $v_{1}$ to start the process, here,

To apply this method to our system, we transform the system to

Applying the method to our system, we get,

where,

And,

4.3.   Caputo fractional derivative sense

Due to uncertainties associate with the etymology of the raise of infection, the initial time, within the Wuhan city, it is there for worth to include such uncertainty into a mathematical equation, additionally so far the world of research is very uncertain on when and how the curve of the spread will be flattened. To include such events into mathematical formulas, one should use a differential operator with a kernel that has similar properties, and the well-known differential operator with such is nothing else than the Caputo fractional derivative. In this section, we present the analysis with Caputo derivative

After integration, we have for the first equation

Hence we only consider the $t = \Delta t(n+1) = t_{n+1}$,

Approximating $\mathbb{A}_{p}(t) = \mathcal{P}_{p}(t)$ within $[t_{\sigma}, t_{\sigma+1}]$ following the work of Atangana and Seda^[11], we obtain,

Also,

The same with $\mathcal{I}_{p}(t_{n+1}), \mathcal{A}_{p}(t_{n+1}), \mathcal{R}_{p}(t_{n+1})$ and $\mathcal{M}_{p}(t_{n+1})$.

5.   Numerical representations

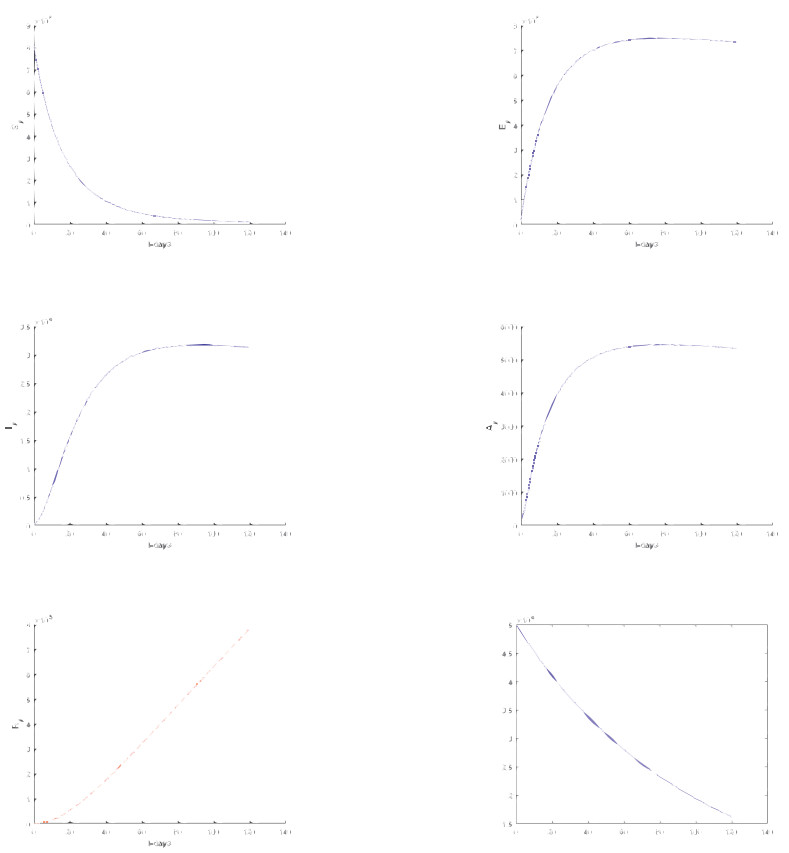
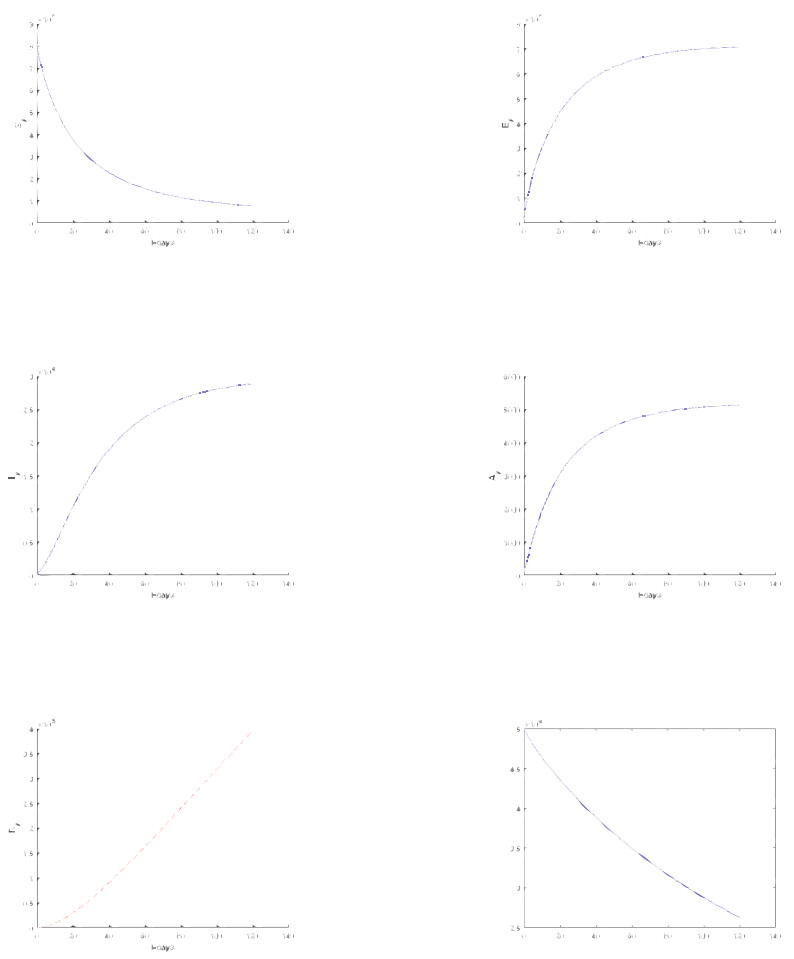
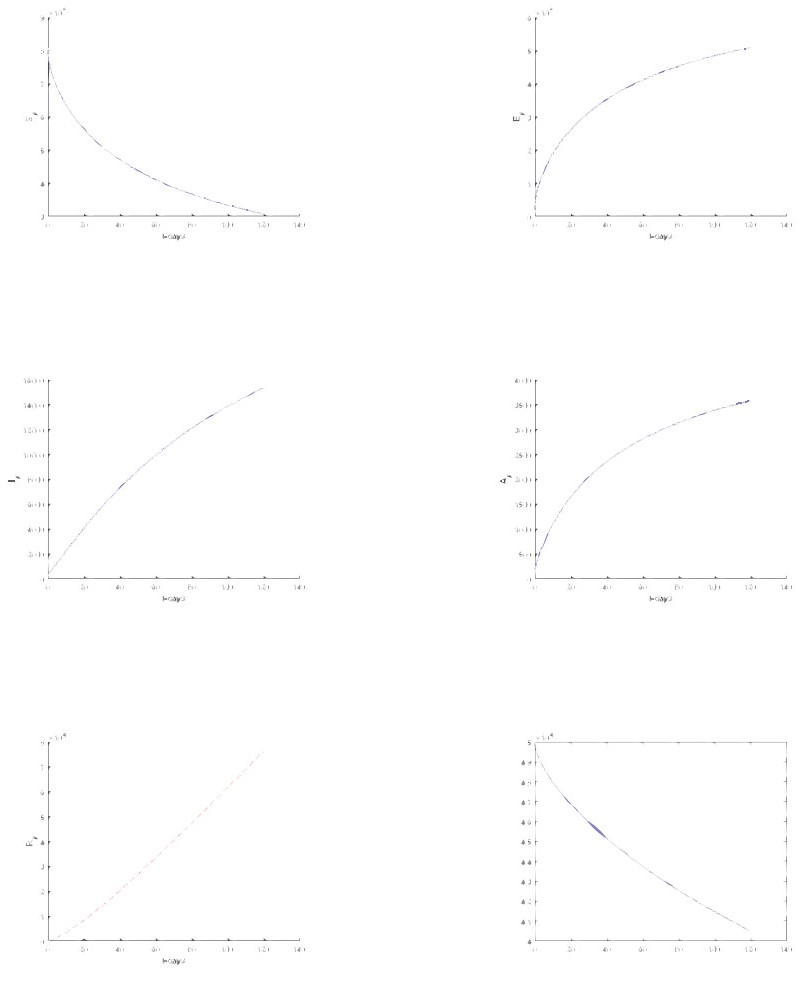
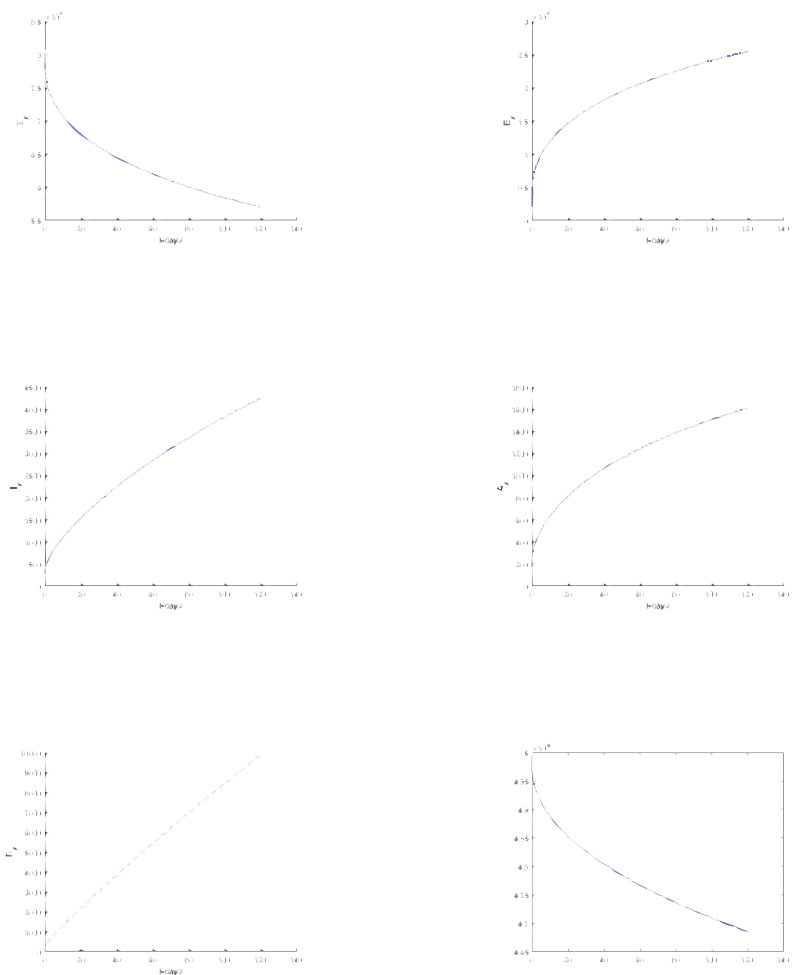
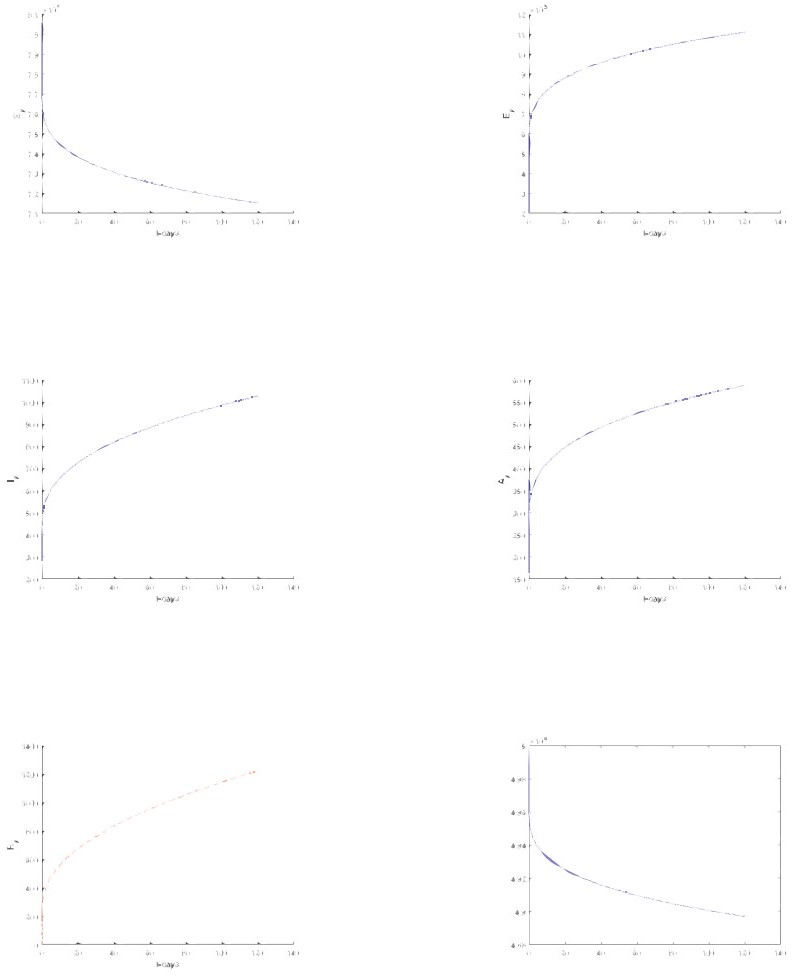
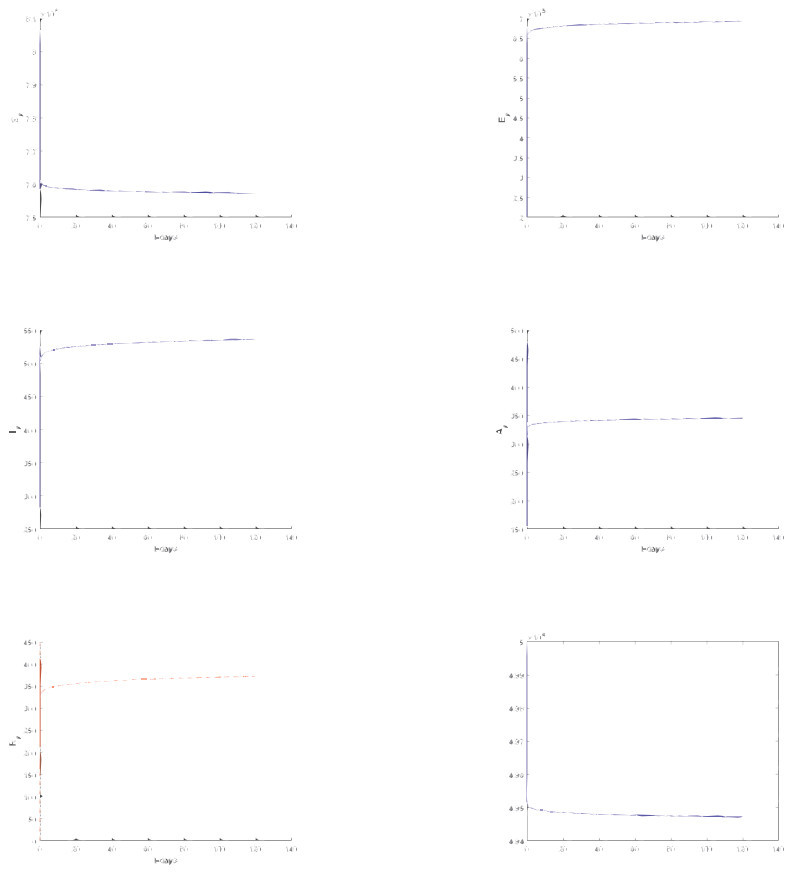
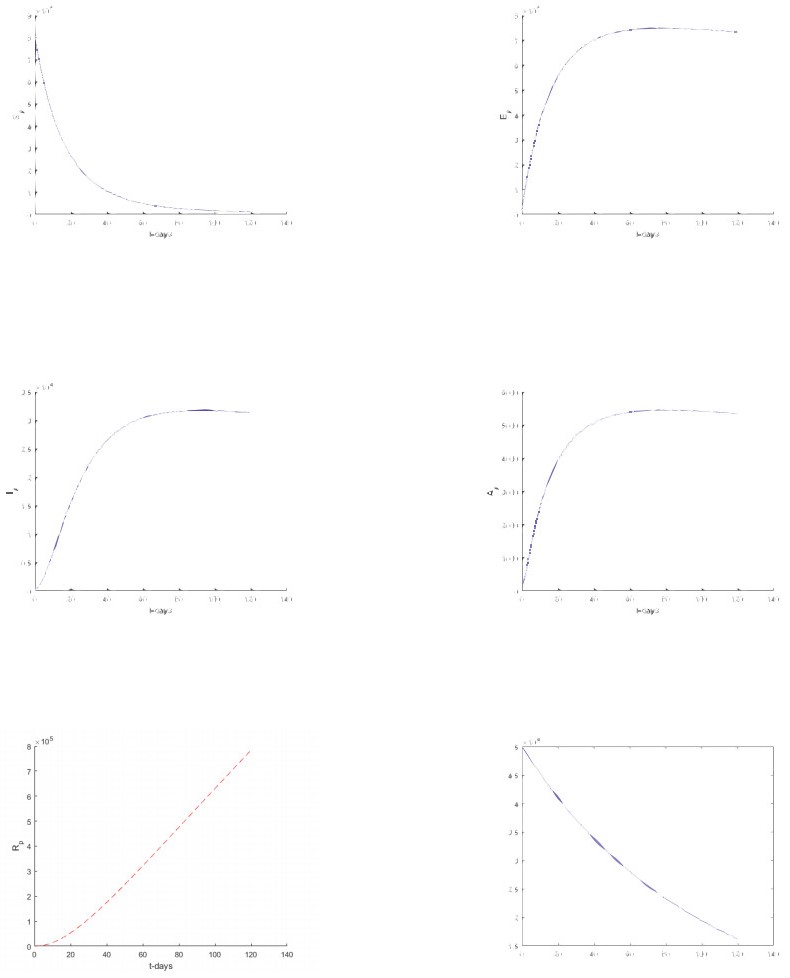
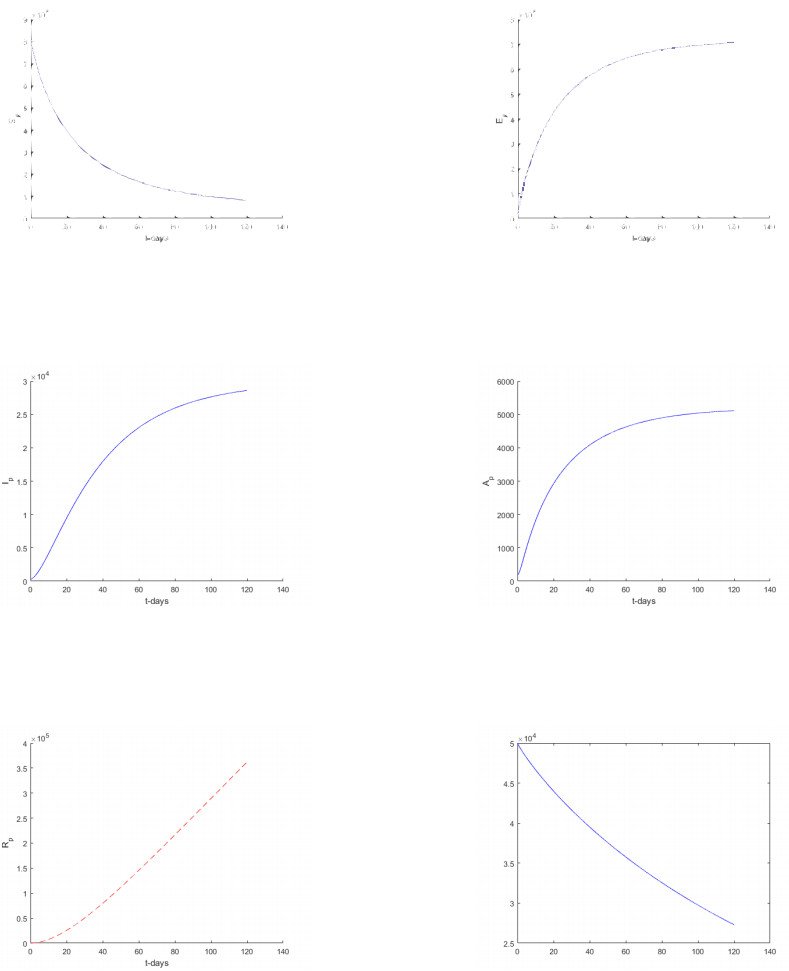
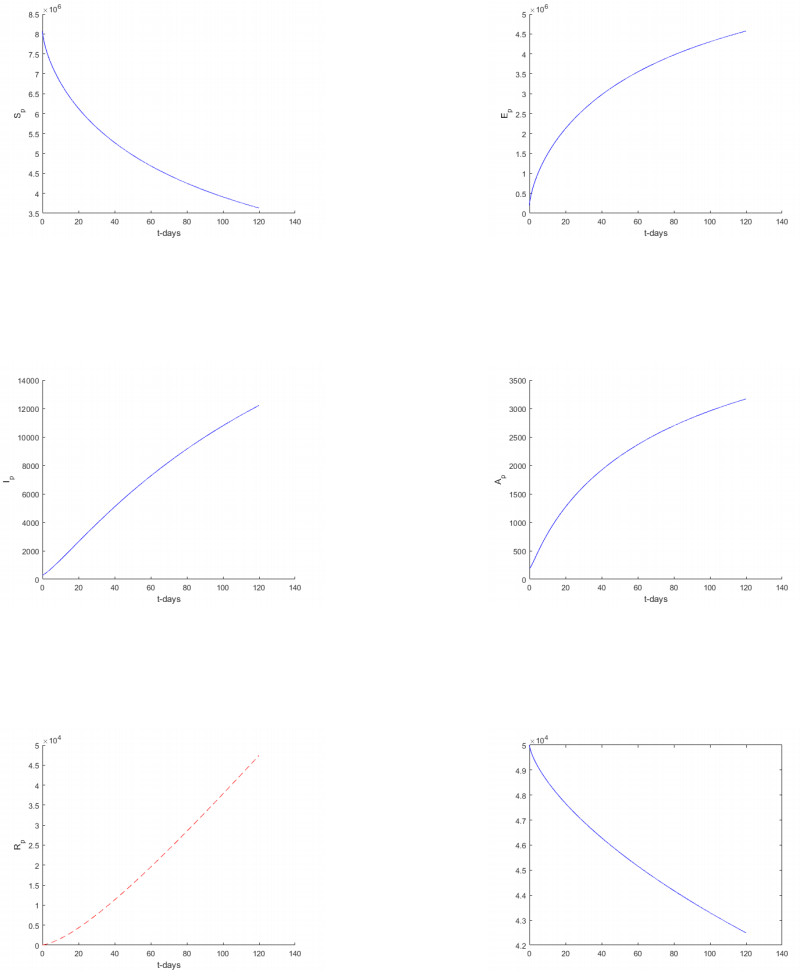
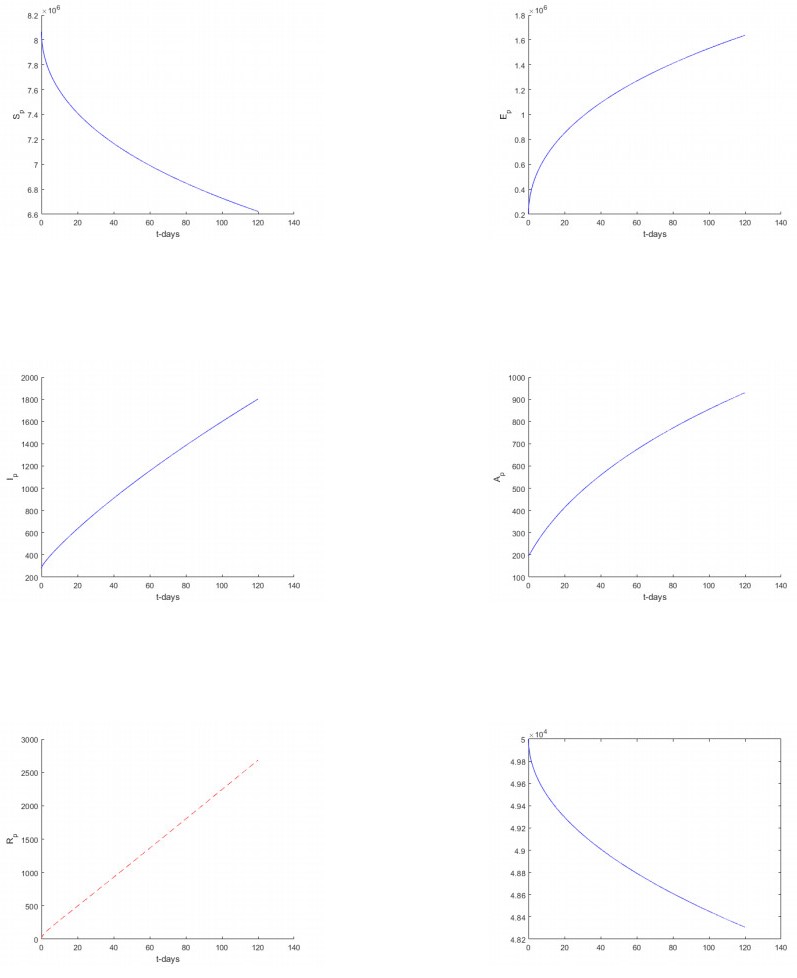
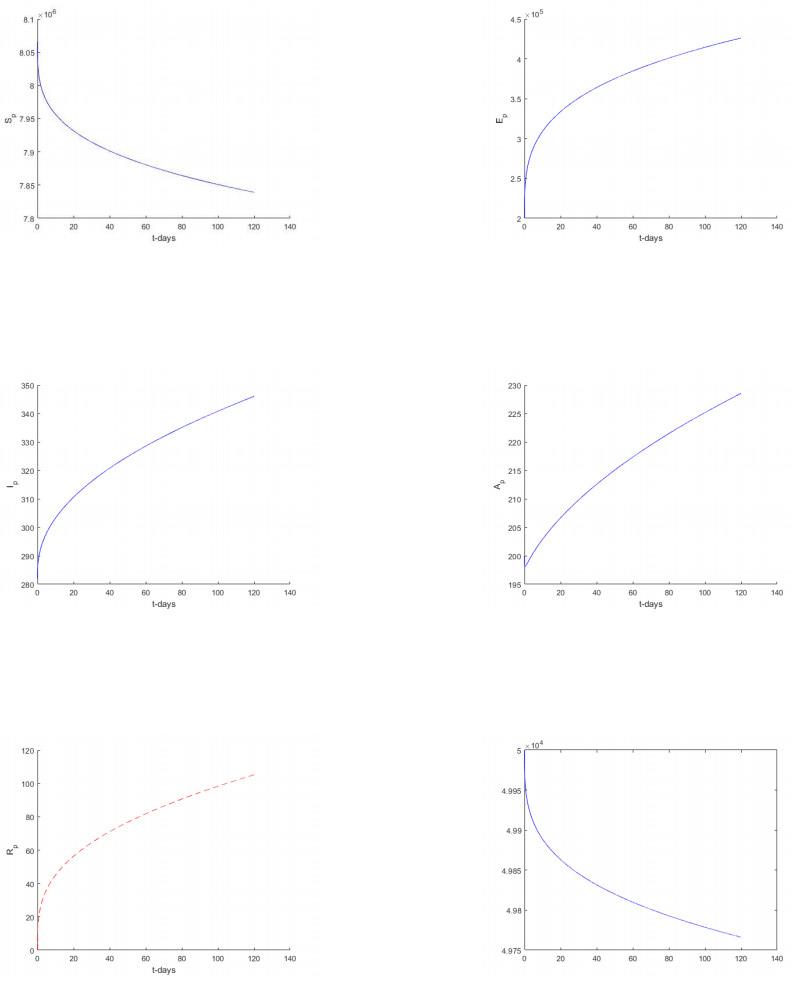
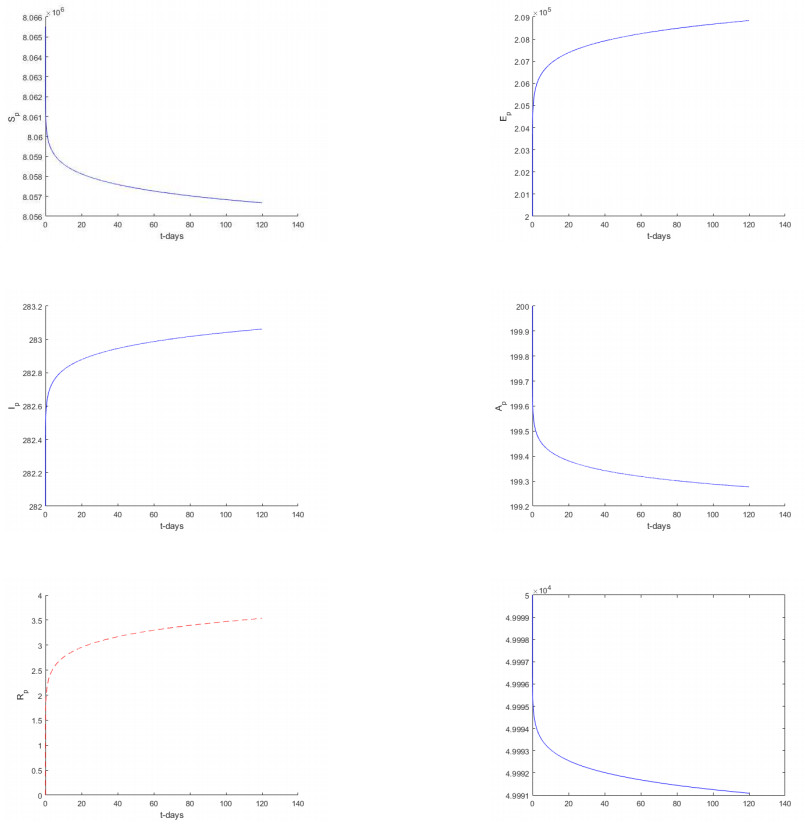
In this section, we considered only Atangana-Baleanu sense and Caputo sense. We represent $t$ numerical simulation of the suggested models using the software called Matlab. The numerical simulations are performed from the suggested numerical solutions obtained from the new suggested numerical schemes. The solutions are presented for different values of fractional orders including 1, 0.9, 0, 7, 0.5, 0.3 and 0.1 respectively. Starting with the model based on the Atangana-Baleanu fractional differential operator.

5.1.   Numerical verifications for Atangana-Baleanu Sense

Numerical simulation for Atangana-Baleanu based models are depicted in Figures 5–10 respectively.

5.2.   Numerical verifications for Caputo Sense

Numerical simulation for Caputo based models are depicted in Figures 11–16 respectively.

6.   Conclusions

Extended orthogonal spaces are used, and valid fixed point results are obtained. Thereafter, we use fractional derivatives to provide a summary of the novel coronavirus 2019-nCoV/SARS-CoV-2 model's existence and unique solutions. Additionally, the model employed in this study is dubious because we did not include all information about the propagation into mathematical equations, and there are still various misunderstandings about the virus's behavior and spread. Our goal with this study was not to present a method to assist stop the spread, but rather to demonstrate that the model proposed by Altaf and Atangana^[5] had unique solutions using a fixed-point technique using the initial conditions and theoretical values we utilized. In addition, to offer numerical solutions to the recommended models, a novel numerical scheme was applied. Most nonlinear systems require numerical simulations to analyze their behavior because their mathematical models are too complex to provide analytical answers. As a result of the numerical simulations produced, the virus is incredibly fast-spreading and can infect the entire world in a short period if precautions are not taken.

Acknowledgments

The research of JJN has been partially supported by the Agencia Estatal de Investigacion (AEI) of Spain, projects MTM2016-75140-P and PID2020-113275GB-I00 and by the European Fund for Regional Development (FEDER). Also by Xunta de Galicia under grant ED431C 2019/02.

Conflict of interests

The authors declare that they have no competing interests to influence the work reported in this paper.