Global dynamics of a Lotka-Volterra competition-diffusion-advection system for small diffusion rates in heterogenous environment

1.   Introduction 

Many ecologists and evolutionary biologists are attracted by the issue of why individuals disperse for a number of years. So far, a great deal of researches are addressed to understand the mechanism of dispersal ^[1,2]. Over the last few decades, researchers from both biology and mathematics have used the reaction-diffusion equations to model population dynamics in spatial ecology and evolution. Among these models, the two species Lotka-Volterra competition-diffusion system perhaps is the most salient example; refer to, e.g., the books ^[1,3] and some recent works in ^[4,5,6].

With further development, researchers become more interested in the study of spatial population dynamics in advective environments which forces organisms to move in certain directions(biased movements) modeled by reaction-diffusion-advection equations. For instance, a part of researchers pay attention to an active research area concerning the population dynamics in which the individuals are very intelligent so that they can sense the surroundings and move upward along the gradients of a resource distribution. Belgacem and Consner ^[7] was the first to raise the single species model and then Cantrell et al. ^[2] presented the two-species model. From the direction of different research, a portion of researchers investigate population dynamics of some aquatic ecosystem modeled by reaction-diffusion-advection equations. The aquatic ecosystems are environments which are featured by a predominantly unidirectional flow, such as rivers, water columns or streams ^{[8,9,10,11,12,13,14]}. The organisms will move passively toward the downstream end due to unidirectional water flow if species lives in rivers and streams, or move upward(downward) due to buoyancy(gravity) if species is in water columns. Specially, environmental conditions shift can produce biased motion, such as, the movement of temperature isoclines, which is caused by global climate change^[15]. Speirs and Gurney ^[16] proposed the following single compartment model with diffusion, advection and a logistic growth from river ecosystems.

where $u(x, t)$ denotes the population density at location $x$ and time $t$, $d$ is the diffusion rate, $L$ is the size of the habitat, and in the sequel, we call $x = 0$ the upstream end and $x = L$ the downstream end, $\alpha$ measures the tendency of the biased movement by water flow (sometimes we call $\alpha$ the advection speed/rate) and we point out here that $\alpha$ should be positive since it is defined that $x = L$ is the downstream end. At the upstream end $x = 0$, the no-flux type condition is imposed, which indicates that there is no individuals movement in or out through the upstream end. However, at the downstream end $x = L$, the hostile condition is assumed which means that once individuals pass through the downstream end they do not return back(e.g., stream to ocean ^[16]). The constant $m > 0$ accounts for intrinsic growth rate, which indicates that the environment is spatially homogeneous. However, as we know, spatial characteristics of the environment play a vital role in ecology and evolution, and the uneven distribution of resources caused by the effect of geological and environmental heterogeneity could create very interesting phenomena in population dynamics. Moreover, the phenomenon of spatial heterogeneity of resources will create more complexity to investigate the global dynamics.

Recently, Tang and Zhou ^[17] considered the situation where a new or exotic species invades such advective environment. They investigated the competitive consequence of two species model in nonhomogeneous environment, to be more specific, the following two-species Lotka-Volterra competition-diffusion-advection system:

where $u$ and $v$ stand for the population densities of two competing aquatic species with their inter-specific and intra-specific competition intensities all equal to 1. $d_{1}$, $d_{2}$ and $\alpha_{1}$, $\alpha_{2}$ are the diffusion and advection rates respectively. The functions $m_{1}(x)$ and $m_{2}(x)$ represent the intrinsic growth rates at location $x$ of these two competitors, which also reflect the distribution of resources. The parameter $L > 0$ measures the length of the one-dimensional habitat. And at the boundary of the habitat, it is assumed that there is no net flux across for either of the two species which implies that the environment is closed. In their study, they imposed that $m_{2} = M$ where $M$ is a constant, that is, the distribution of resources for the species $u$ is spatially uneven while for the species $v$ is homogeneous. By employing principal spectral theory, they investigated the global dynamics of system (1.2) on the condition that: $(H)\; \; \alpha_{1}/d_{1} = \alpha_{2}/d_{2} = : k > 0$ and found that the competitive result was depended on $d_{1}, d_{2}$ and $m_{1}$. However, for the general situation where $m_{1} \neq m_{2}$ and $m_{1}$ together with $m_{2}$ is the function of spatial variation $x$, the global dynamics of system (1.2) is far from being completely understood. It is common to ask if the outcome of competition when $m_{2}$ is a function with respect to $x$ is more complex than when $m_{2}$ is a constant. We will pursue further in this direction.

For the spatially homogeneous case $m_{1} = m_{2} \equiv m_{0}$ with $m_{0}$ being a positive constant, a lot of researchers are interested in it and have investigated it qualitatively ^{[18,19,20,21,22]}. In the case that $m_{1} = m_{2} = : m(x)$, non-constant, that is, spatially nonhomogeneous, system (1.2) is more difficult to handle and has been explored in many works. Lam et al. ^[23] seemed the first to try to discuss the case $d_{1}\neq d_{2}$ and $\alpha_{1} = \alpha_{2}$, which directed at the existence and diversity of evolutionarily stable strategies applying some limiting arguments (in the sense of both diffusion and advection rates are sufficiently small and comparable). Zhao and Zhou ^[24], considering on the special case $d_{1}\neq d_{2}$ and $\alpha_{1} = 0 < \alpha_{2}$, which meant that one species merely suffered random while the other one underwent both random and advective movements, attempted to uncover some various phenomena. For the general case $d_{1}\neq d_{2}$ and $\alpha_{1}\neq \alpha_{2}$, recently, Lou et al. ^[25], by developing new techniques to surmount the difficult caused by non-self-adjoint operators, obtained a profound understanding on the global dynamics. The more general case $m_{1} \neq m_{2}$ now is far from being understood completely. Zhou and Xiao ^[26] established a classification of all possible long time behaviors for a more general competitive system in the condition of $(H)$. Indeed, they discussed it in higher spatial dimensions.

Motivated by Tang and Zhou ^[17], in this paper, we mainly investigate the dynamical behaviors of system (1.2). Firstly, we need to make the following basic assumptions:

$(H_{1}) \; \alpha_{1}/d_{1} = \alpha_{2}/d_{2} = : k > 0$ (or equivalently, $d_{2}/d_{1} = \alpha_{2}/\alpha_{1} = : k^{*} > 0$);

$(H_{2}) \; m_{i} \in \mathcal{C}^{1 + \gamma}([0, L])$ with some $\gamma \in (0, 1)$ is nonconstant, $m_{i}(x) \geq 0$ in $[0, L]$, $m_{1}(x) \not\equiv m_{2}(x)$, $m_{i}(x) \neq c_{0}e^{kx}$, where $c_{0} = MLk/(e^{kL} - 1)$($i = 1, 2$) and

Condition $(H_{1})$, biologically, means that the movement strategies(random diffusion and advection rates) of two competitors are proportional, and it is a mathematically technical condition in the main body of this paper. In assumption $(H_{2})$, it means the two competing populations have the same amount of total resources and the distributions of resources are spatially heterogeneous as well as nonidentical. Moreover, we exclude the ideal free distribution introduced in ^[27].

According to the above hypotheses, system (1.2) changes to

where, the variables in the system (1.3) have the same meanings as in the system (1.2). Moreover, as we know, system (1.3) has one trivial steady state $(0, 0)$ (always linearly unstable) and two semi-trivial steady states respectively denoted by $(\theta_{d_{1}, k, m_{1}}, 0)$ and $(0, \theta_{d_{2}, k, m_{2}})$ in the sequel.

Following the approach in ^[22], we first give some notations:

and

$\Sigma_{u}$ : = $\{ (d_{1}, d_{2}) \in \Gamma: (\theta_{d_{1}, k, m_{1}}, 0)$ is linearly stable$\}$,

$\Sigma_{v}$ : = $\{ (d_{1}, d_{2}) \in \Gamma: (0, \theta_{d_{2}, k, m_{2}})$ is linearly stable$\}$,

$\tilde{\Sigma}_{u}$ : = $\{ (d_{1}, d_{2}) \in \Gamma: (\theta_{d_{1}, k, m_{1}}, 0)$ is neutrally stable$\}$,

$\tilde{\Sigma}_{v}$ : = $\{ (d_{1}, d_{2}) \in \Gamma: (0, \theta_{d_{2}, k, m_{2}})$ is neutrally stable$\}$,

$\tilde{\Sigma}_{u}^{v}$ : = $\tilde{\Sigma}_{u} \cap \tilde{\Sigma}_{v}$,

$\Sigma_{o}$ : = $\{ (d_{1}, d_{2}) \in \Gamma$: $(\theta_{d_{1}, k, m_{1}}, 0)$ and $(0, \theta_{d_{2}, k, m_{2}})$ are linearly unstable$\}$.

The definitions of the linear stability/instability and the neutrally stability of a steady state of system (1.3) will be given precisely in Section 2.

Due to assumption $(H_{1})$, the following complete classification on the global dynamics of system (1.3) can be obtained directly from (Theorem 1.2 ^[26]). It is a special case of (Theorem 1.2 ^[26]), where the advective direction $P(x) = x$, inter-specific competition ability $b = c = 1$, and the habitat $\Omega = [0, L]$.

Assume that $(H_{1})$ and $(H_{2})$ hold. Then for system (1.3), we have the following mutually disjoint decomposition of $\Gamma$:

Moreover,

(ⅰ') for all $(d_{1}, d_{2}) \in (\Sigma_{u} \cup \tilde{\Sigma}_{u}\setminus \tilde{\Sigma}_{u}^{v})$, $(\theta_{d_{1}, k, m_{1}}, 0)$ is g.a.s;

(ⅱ') for all $(d_{1}, d_{2}) \in (\Sigma_{v} \cup \tilde{\Sigma}_{v}\setminus \tilde{\Sigma}_{u}^{v})$, $(0, \theta_{d_{2}, k, m_{2}})$ is g.a.s;

(ⅲ') for all $(d_{1}, d_{2}) \in \Sigma_{o}$, system (1.3) has a coexistence steady state that is g.a.s;

(ⅳ') for all $(d_{1}, d_{2}) \in \tilde{\Sigma}_{u}^{v}$, $\theta_{d_{1}, k, m_{1}} = \theta_{d_{2}, k, m_{2}}$ in $(0, L)$ and system (1.3) has a compact global attractor consisting of a continuum of steady states

connecting the two semi-trivial steady states;

where g.a.s means that the steady state is globally asymptotically stable among all non-negative and nontrivial initial conditions.

A basic classification on all possible long time behaviors of system (1.3) is exhibited by the above statements. However, to obtain a transparent picture of the global dynamics of system (1.3), it remains to know explicitly when $\Sigma_{u}, \tilde{\Sigma}_{u}, \Sigma_{v}, \tilde{\Sigma}_{v}$ and $\Sigma_{o}$ will happen. Equivalently speaking, is it possible to provide a sharp division of these sets by using certain variable parameters? As mentioned in ^[26], each component of these sets could be empty, and more challengingly, it is hard to give a criteria guaranteeing the dynamics in these sets. Even for the non-advective case, it is not yet completely solved ^[4].

In this paper, we study the global dynamics of system (1.3) which contains two competing species. We assume that the two species both are in heterogeneous environment and denote their intrinsic growth rates by the functions $m_1(x)$ and $m_2(x)$, respectively. As we known, the distribution of resources is uneven in the natural environment, hence, this case is of more realistic significance. In the condition that $m_1 \not\equiv m_2$ and total resources of the two species are fixed at the same level($\int_{0}^{L}m_{1}(x)dx = \int_{0}^{L}m_{2}(x)dx$), we find that the sign of $\int_{0}^{L}(m_{1}-m_{2})e^{kx}dx$ plays an extremely important role in determining the global dynamics. This result indicates that the values of $m_1$ and $m_2$ influence the global dynamics of the system. Moreover, we obtain the limiting behaviour of the coexistence steady state when the diffusion rates($d_1$ and $d_2$) of the two species tend to zero.

The rest of this paper is organized as follows. Section 2 contains some preliminaries which are useful in later analysis and our main results. In Section 3, we will give the proof of Theorem 1.1. We prove Theorem 1.2 in Section 4. Finally, we give a short discussion.

2.   Preliminaries and main results 

This section is aim to display our main results and exhibit some fundamental results which will be utilized in later sections.

We obtain the following result when one of $d_{1}$ and $d_{2}$ tends to zero.

Theorem 1.1. Assume that $(H_{1})$ and $(H_{2})$ hold. The following statements are valid:

(ⅰ) Fix $d_{2} > 0$.

$(i_{1})$ If $\int_{0}^{L}(m_{1}-m_{2})e^{kx}dx \leq 0$, then for small $d_{1} > 0$, $(\theta_{d_{1}, k, m_{1}}, 0)$ is linearly unstable;

$(i_{2})$ If $\int_{0}^{L}(m_{1} - m_{2})e^{kx}dx > 0$, then for small $d_{1} > 0$, $(\theta_{d_{1}, k, m_{1}}, 0)$ is g.a.s provided $d_{2} > 1/\mu_{1}(m_{2} - m_{1})$ and linear unstable provided $d_{2} < 1/\mu_{1}(m_{2} - m_{1})$.

(ⅱ) Fix $d_{1} > 0.$

$(ii_{1})$ If $\int_{0}^{L}(m_{1} - m_{2})e^{kx}dx \geq 0$, then for small $d_{2} > 0$, $(0, \theta_{d_{2}, k, m_{2}})$ is linearly unstable;

$(ii_{2})$ If $\int_{0}^{L}(m_{1} - m_{2})e^{kx}dx < 0$, then for small $d_{2} > 0$, $(0, \theta_{d_{2}, k, m_{2}})$ is g.a.s provided $d_{1} > 1/\mu_{1}(m_{1} - m_{2})$ and linear unstable provided $d_{1} < 1/\mu_{1}(m_{1} - m_{2})$;

where $\mu(h)$ is the unique nonzero principal eigenvalue of problem (2.4).

Remark 1.1. In ^[17], the authors found that the outcome of competition in general heterogeneous distribution is very complicate: either $u$ wins, or $v$ wins, or $u-v$ coexists, depending on the size of diffusion rates $d_{1}$, $d_{2}$ and $m_{1}$. Similar to ^[17], Theorem 1.1 indicates that the outcome of competition depends on the size of diffusion rates $d_{1}$ and $d_{2}$; however, in this paper, because the resource functions of the two competing species $u$ and $v$ are both spatially nonhomogeneous, then the outcome of competition depends not only on the distribution of $m_{1}$ but also the distribution of $m_{2}$. Moreover, the competition outcome in this situation will be more abundant.

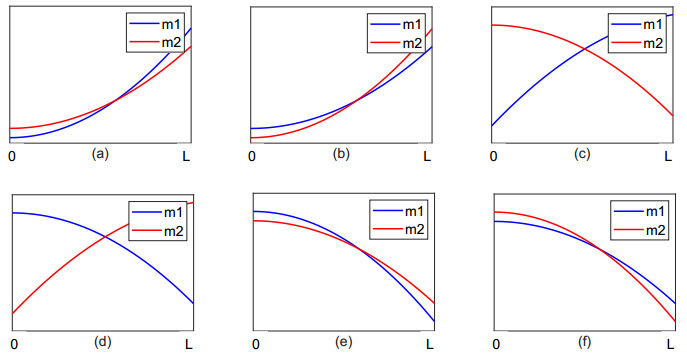
Remark 1.2. According to Theorem 1.1, we find that the sign of the quantity $\int_{0}^{L}(m_{1} - m_{2})e^{kx}dx$ plays a significant role in understanding the global dynamics of system (1.3) which is similarly to the description mentioned in ^[16]. Then we give some sufficient conditions about determining the sign of the quantity $\int_{0}^{L}(m_{1}-m_{2})e^{kx}dx$ on the condition that $m_{1}$ and $m_{2}$ are monotonic with respect to spatial variable $x$. In view of the monotonicity of $m_{1}$ and $m_{2}$, we can divide into six situations to talk about and the graphs of $m_{1}$ and $m_{2}$ are as follows Figure 1. From Figure 1, the following statements are true:

(ⅰ) In cases of $a$, $c$ and $f$, it holds that $\int_{0}^{L}(m_{1}-m_{2})e^{kx}dx < 0$;

(ⅱ) In cases of $b$, $d$ and $e$, we can obtain $\int_{0}^{L}(m_{1}-m_{2})e^{kx}dx > 0$.

In fact, since $m_{1}$ and $m_{2}$ are monotonic, there is a unique $x_{0} \in (0, L)$ such that $m_{1}(x) = m_{2}(x)$. Define

Then

which, by $q(0) = \int_{0}^{L}(m_{2} - m_{1})dx = 0$, implies

The desired result follows by letting $s = k$.

When $d_{1}$ and $d_{2}$ tend to zero meanwhile, the following result is true.

Theorem 1.2. Assume that $(H_{1})$ and $(H_{2})$ hold. Then we have:

(ⅰ) As $d_{1}$ and $d_{2}$ tend to 0, system (1.3) has a coexistence steady state that is g.a.s;

(ⅱ) Let us denote by $(u_{d_{1}, d_{2}}, v_{d_{1}, d_{2}})$ the unique coexistence stable state of system (1.3). Then we have

uniformly on compact subsets of $[0, L] \setminus \{x\in[0, L]:m_{1}(x) = m_{2}(x)\}$, where

and

Remark 1.3. From a biological perspective, Remark 1.2, together with Theorems 1.1 and 1.2 implies several interesting explanations. Back to Theorem 1.1 $(i_{1})$, if the resource $m_{1}$ of species $u$ is distributed decreasingly in spatial variable $x$ and $m_{2}$ of species $v$ is distributed increasingly in spatial variable $x$ or $m_{1}$ and $m_{2}$ increase in spatial variable meanwhile $m_{1}$ changes faster than $m_{2}$ or $m_{1}$ and $m_{2}$ decrease in spatial variable meanwhile $m_{1}$ changes slower than $m_{2}$, then $d_{1}k$ is not good for $u$ no matter how small $d_{1}$ is, however, in view of Theorem 1.1 $(ii_{2})$, it is good for $v$ if $d_{2}$ is suitably small. Otherwise, from Theorem 1.1 ($ii_{1})$, it is unfavorable for $v$ no matter how small $d_{2}$ is. In view of Theorem 1.1 $(i_{2})$, it is favorable for $u$ if $d_{1}$ is suitably small. Therefore, we can infer Theorem 1.2 (i), which says that both species will coexist if they nearly do not move ($d_{1}, d_{2}\rightarrow0$), regardless of the shape of $m_{1}$ and $m_{2}$.

Let us look at the following single-species model corresponding to system (1.3)

where $d, k > 0$, $m$ is in $\mathcal{C}^{1 + \gamma}([0, L])$ and $m > 0$ in $[0, L]$. Under these conditions, it is easy to see that problem (2.1) admits a unique positive steady state (see, e.g., [3]), denoted by $\theta_{d, k, m}$. By applying this fact to system (1.3), there are always two semi-trivial steady states $(\theta_{d_{1}, k, m_{1}}, 0)$ and $(0, \theta_{d_{2}, k, m_{2}})$ in the condition of $(H_{2})$.

About the positive steady solution $\theta_{d, k, m}$ of Eq (2.1), we have the following limiting profile. The limiting profile can be seen as an extension of the non-advective case (i.e., $k = 0$); see ^[28,29].

Lemma 2.1. The following statement on $\theta_{d, k, m}$ is true:

Proof. Denote $\theta_{d, k, m}$ by $\theta_{d}$ for simplicity. Let $\beta_{d}(x) = e^{-kx}\theta_{d}$. Then $\beta_{d}(x)$ satisfies

For any given $\epsilon > 0$, since $m$ is in $\mathcal{C}^{1 + \gamma}([0, L])$, there is some function $\xi$ in $C^{2}([0, L)]$ such that

Define $\beta^{+} : = \xi + 2\epsilon$ and $\beta^{-} : = \xi - 2\epsilon$. Then for $d$ sufficiently small, it is not difficult to prove that $\beta^{+}$ and $\beta^{-}$ are, respectively, super- and sub-solution of problem (2.2). That is to say, if $d > 0$ is small, we have

and therefore,

due to the arbitrariness of $\epsilon > 0$, the desired result is proved.

Next we consider an auxiliary eigenvalue problem. It is helpful for studying the existence and stability of semi-trivial steady states:

where $d, k > 0$ and $h$ is in $L^{\infty}([0, L])$. By employing the Krein-Rutman Theorem ^[30], it is simple to prove that problem (2.3) admits a principal eigenvalue(simple and has the least real part among all eigenvalues) which is denoted by $\lambda_{1}(d, k, h)$ in the sequel, and its corresponding eigenfunction $\phi_{1}(d, k, h)$ can be chosen strictly positive in $[0, L]$. Moreover, the linear stabilities of $(\theta_{d_{1}, k, m_{1}}, 0)$ and $(0, \theta_{d_{2}, k, m_{2}})$ are determined, respectively, by the sign of $\lambda_{1}(d_{2}, k, m_{2} - \theta_{d_{1}, k, m_{1}})$ and $\lambda_{1}(d_{1}, k, m_{1} - \theta_{d_{2}, k, m_{2}})$. Specifically, $(\theta_{d_{1}, k, m_{1}}, 0)$ is linearly stable (resp. linearly unstable) if $\lambda_{1}(d_{2}, k, m_{2} - \theta_{d_{1}, k, m_{1}}) > 0$ (resp. $\lambda_{1}(d_{2}, k, m_{2} - \theta_{d_{1}, k, m_{1}}) < 0$); $(0, \theta_{d_{2}, k, m_{2}})$ is linearly stable (resp. linearly unstable) if $\lambda_{1}(d_{1}, k, m_{1} - \theta_{d_{2}, k, m_{2}}) > 0$ (resp. $\lambda_{1}(d_{1}, k, m_{1} - \theta_{d_{2}, k, m_{2}}) < 0$). We say $(\theta_{d_{1}, k, m_{1}}, 0)$($(0, \theta_{d_{2}, k, m_{2}})$) is neutrally stable if $\lambda_{1}(d_{2}, k, m_{2} - \theta_{d_{1}, k, m_{1}}) = 0$($\lambda_{1}(d_{1}, k, m_{1} - \theta_{d_{2}, k, m_{2}})$ = 0).

By the variational approach, $\lambda_{1}(d, k, h)$ can be characterized by

The following Lemma 2.2 collects some important properties of $\lambda_{1}(d, k, h)$. The proof can be found in ^[1,17,31,32].

Lemma 2.2. The following statements on $\lambda_{1}(d, k, h)$ are true:

(ⅰ) $\lambda_{1}(d, k, h)$ and $\phi_{1}(d, k, h)$ depend continuously and differentially on parameters $d$ and $k$;

(ⅱ) $\lambda_{1}(d, k, h)$ is strictly increasing in the parameter $d$ provided $h$ is non-constant;

(ⅲ) $\lim_{d\rightarrow0}\lambda_{1}(d, k, h) = -\max\limits_{x\in[0, L]}h(x)$ and $\lim_{d\rightarrow\infty}\lambda_{1}(d, k, h) = -\int_{0}^{L}h(x)e^{kx}dx/\int_{0}^{L}e^{kx}dx$.

For later research, it is needed to introduce the following eigenvalue problem with indefinite weight

where $h\not\equiv0$, could change sign in $(0, L)$. If there is a positive solution for problem (2.5) we say $\mu_{1} = \mu_{1}(h)$ is a principal eigenvalue.(0 is always a principal eigenvalue.) The following result collects some important properties of $\mu_{1}(h)$ in connection with $\lambda_{1}(d, k, h)$. The eigenvalue problem (2.5) is a special case of a general problem studied in ^[33,34]. Indeed, by the transformation $\varrho = e^{-kx}\phi$, one can change problem (2.5) to a Neumann type problem.

Lemma 2.3. The problem (2.5) has a nonzero principal eigenvalue $\mu_{1} = \mu_{1}(h)$ if and only if $\int_{0}^{L}he^{kx}dx\neq 0$ and $h$ changes sign in $(0, L)$. More precisely, if $h$ changes sign in $(0, L)$, then

(ⅰ) $\int_{0}^{L}he^{kx}dx = 0 \Leftrightarrow 0$ is the only principal eigenvalue;

(ⅱ) $\int_{0}^{L}he^{kx}dx > 0 \Leftrightarrow \mu_{1}(h) < 0$;

(ⅲ) $\int_{0}^{L}he^{kx}dx < 0 \Leftrightarrow \mu_{1}(h) > 0$; and in this case, $\mu_{1}(h)$ can be characterized by

(ⅳ) $\int_{0}^{L}he^{kx}dx\geq 0 \Rightarrow \lambda_{1}(d, k, h) < 0$ for all $d > 0$, and

3.   Proof of Theorem 1.1 

For clarity, we proceed with the proof in the from of several claims.

Claim 1: There are two functions $\hat{d}_{2}^{*}$ = $\hat{d}_{2}^{*}(d_{1})$ and $\hat{d}_{1}^{*}$ = $\hat{d}_{1}^{*}(d_{2})$ defined by

and

such that

and the following statements are valid:

$(a)$ for all $(d_{1}, d_{2}) \in (\Sigma_{u} \cup \tilde{\Sigma}_{u})$, $(\theta_{d_{1}, k, m_{1}}, 0)$ is g.a.s;

$(b)$ for all $(d_{1}, d_{2}) \in (\Sigma_{v} \cup \tilde{\Sigma}_{v})$, $(0, \theta_{d_{2}, k, m_{2}})$ is g.a.s;

$(c)$ for all $(d_{1}, d_{2}) \in \Sigma_{o}$, system (1.3) has a coexistence steady state that is g.a.s.

Where $\mu_{h}$ is the nonzero principal eigenvalue of Eq (2.5).

We first assert that $\tilde{\Sigma}_{u}^{v} = \emptyset$. On the contrary, suppose that $\tilde{\Sigma}_{u}^{v} \neq \emptyset$. In view of statement $(iv')$, one finds that for some $d_{1}^{0}$ and $d_{2}^{0} > 0$, $\theta_{d_{1}^{0}, k, m_{1}} \equiv \theta_{d_{2}^{0}, k, m_{2}}$ in $[0, L]$.

If $(d_{2}^{0}-d_{1}^{0}) = 0$, by the equations of $\theta_{d_{1}^{0}, k, m_{1}}$ and $\theta_{d_{2}^{0}, k, m_{2}}$, it holds that

From the above equation, one can derive that $m_{1} \equiv m_{2}$ in $[0, L]$, which contradicts our assumption $(H_{2})$.

If $(d_{2}^{0}-d_{1}^{0}) \neq 0$, by the equations of $\theta_{d_{1}^{0}, k, m_{1}}$ and $\theta_{d_{2}^{0}, k, m_{2}}$ again, one arrives at

Because of the condition $(H_{2})$, the above equality can be rewritten as

which implies that

Dividing the first equation of Eq (2.1) by $e^{-kx}\theta_{d, k, m}$ and integrating over $[0, L]$, one deduces that

so the positive steady solution $\theta_{d, k, m}$ of problem (2.1) satisfies

and the equality is valid if and only if $m(x) = ce^{kx}$ for some $c > 0$.

Due to the assumption $(H_{2})$, there is a contradiction. This contradiction gives that $\tilde{\Sigma}_{u}^{v} = \emptyset$. Then statements $(a), (b)$ and $(c)$ follow directly from Theorem 1.1.

It is sufficient to prove Eqs (3.1) and (3.2) can be verified in the same manner so we omit here. Given any $d_{1} > 0$, as shown above, the sign of $\lambda_{1}(d_{2}, k, m_{2}-\theta_{d_{1}, k, m_{1}}$) determines the linear stability of $(\theta_{d_{1}, k, m_{1}}, 0)$, which, by Lemma 2.2 (ⅲ), we have

and

For the first case, if $\max\limits_{x\in[0, L]}(m_{2}-\theta_{d_{1}, k, m_{1}}) \leq 0$, by Lemma 2.2 (ⅱ) and the above first limit, $\lambda_{1}(d_{2}, k, m_{2}-\theta_{d_{1}, k, m_{1}}) > 0$ for every $d_{2}$, so we can define $\hat{d}_{2}^{*}(d_{1}) = 0$; similarly, for the second case, using Lemma 2.2 (ⅱ) again and the above second limit, one can define $\hat{d}_{2}^{*}(d_{1}) = \infty$ if $-\int_{0}^{L}(m_{2}-\theta_{d_{1}, k, m_{1}})e^{kx}dx/\int_{0}^{L}e^{kx}dx \leq 0$; for the rest case, from Lemma 2.3 (ⅳ) it can be defined that $\hat{d}_{2}^{*}(d_{1}) = 1/\mu_{1}(m_{2}-\theta_{d_{1}, k, m_{1}})\in(0, \infty)$.

By the above statements, the formula in Eq (3.1) is established.

In view of the definition of linear stability and unstability, it is easy to understand the sets described in Eq (3.3).

Claim 2: The following limiting behaviors of $\hat{d}_{2}^{*}(d_{1})$ and $\hat{d}_{1}^{*}(d_{2})$ hold true:

For $\hat{d}_{2}^{*}(d_{1})$, we have

For $\hat{d}_{1}^{*}(d_{2})$, we have

As mentioned above, the sign of $\lambda_{1}(d_{2}, k, m_{2}-\theta_{d_{1}, k, m_{1}})$ determines the linear stability of $(\theta_{d_{1}, k, m_{1}}, 0)$, which, from Lemma 2.1, satisfies

Using Lemma 2.2 (ⅲ), one has

and

Then we can infer the limit Eq (3.4) from Eqs (3.6) and (3.7) and Lemmas 2.2 (ⅱ) and 2.3 (ⅳ).

The limit Eq (3.5) can be obtained by the above ideas as in the proof of Eq (3.4). This finishes claim 2.

Now we are in a position to prove Theorem 1.1. We first prove statement (ⅰ) by fixing $d_{2} > 0$. If $\int_{0}^{L}(m_{1}-m_{2})e^{kx}dx \leq 0$, by Eq (3.4), for small $d_{1} > 0$ and $d_{2} < \hat{d}_{2}^{*}(d_{1})$, it can be obtained that $(\theta_{d_{1}, k, m_{1}}, 0)$ is linearly unstable. If $\int_{0}^{L}(m_{1}-m_{2})e^{kx}dx > 0$, using the second limit in Eqs (3.4) and (3.2), for small $d_{1} > 0$, it is easy to conclude the second result of statement (ⅰ).

Similar to the above argument, from Eqs (3.1) and (3.5), statement (ⅱ) could be obtained.

4.   Proof of Theorem 1.2 

In order to prove statement (ⅰ), the continuous dependence of the principal eigenvalue $\lambda_{1}(d, k, h)$ in the parameter $d$ as well as the weight function $h$ plays a vital role.

Specifically, in view of Lemmas 2.1 and 2.3 (ⅳ), one obtains

and

From the first inequality, $(\theta_{d_{1}, k, m_{1}}, 0)$ is linearly unstable and $(0, \theta_{d_{2}, k, m_{2}})$ is linearly unstable by the second inequality. Due to the statement $(c)$, it is easy to deduce that system 1.3 has a coexistence steady state that is g.a.s.

Next we prove the limiting behavior of coexistence steady state of system (1.3). Following the ideas in ^[35], we obtain the proof of this statement.

Lemma 4.1. (ⅰ) Consider the sequences $\{\overline{u}_{n}\}_{n = 1}^{n = \infty}$ and $\{\underline{v}_{n}\}_{n = 1}^{n = \infty}$ defined by

Then, for small $d_{1}, d_{2} > 0$, denote the coexistence state of system (1.3) by $(u, v)$, the following hold:

(ⅱ) Analogously for sequences $\{\underline{u}_{n}\}_{n = 1}^{n = \infty}$ and $\{\overline{v}_{n}\}_{n = 1}^{n = \infty}$ defined by

We have

Proof. It is enough to prove Eq (4.1) as the proof of Eq (4.2) follows by the symmetry. The proof is obtained by induction argument.

From the equation of $u$, we obtain

that is to say, $u$ is a sub-solution of

Therefore,

Now, substitute this inequality into the equation of $v$

that is, $v$ is a super-solution of

so

Back to the equations of $u$ and $v$, one can obtain

and

For small $d_{1}$ and $d_{2} > 0$, we have $\underline{v}_{1} > 0$ in $(0, L)$, so

which further implies

This completes the proof of Eq (4.1) for $n = 1$.

Now suppose that Eq (4.1) is true for some $N > 1$. Then it suffices to show that

From $v \geq \underline{v}_{N+1}$ in $(0, L)$,

so

Similarly, one can derive

Thus it is sufficient to show that

Since $\underline{v}_{N+1} \geq \underline{v}_{N}$ in $(0, L)$, we get

Similarly,

This completes the proof.

We now analyze the behavior of the scheme introduced by Lemma 4.1, Eqs (4.1) and (4.2) as $d_{1}$ and $d_{2}$ tend to $0$.

In consideration of Lemma 4.1, for each $n \geq 1$, one can define the following limits in the topology of $C([0, L])$:

As a matter of fact, these limits can be described detailedly.

Lemma 4.2. The following identities hold:

where $n \geq 1$.

Proof. First, using the same arguments as in proof of Lemma 2.1, if $\int_{0}^{L}m(x)dx > 0$ and the set $\{x : m(x) < 0\}$ has a positive measure, we can obtain $\|\theta_{d, k, m} - m^{+}\|_{L^{\infty}(0, L)} \rightarrow 0$ as $d \rightarrow 0$ with $m^{+}(x) = max\{m(x), 0\}$.

Due to assumption $(H_{2})$, Eq (4.3) is hold when $n = 1$. Suppose that Eq (4.3) is valid for every $1\leq n \leq N$. Then, by definition, $\overline{u}_{N+2} : = \theta_{d_{1}, k, m_{1}-\underline{v}_{N+1}}$. Using the argument above again, one obtains

We can demonstrate the rest ones in the similar manner. Hence, the proof is finished.

By the above result, it is allowable to get explicit formulas for each of the sequences $\overline{U}_{n}$, $\underline{U}_{n}$, $\overline{V}_{n}$ and $\underline{V}_{n}$. The following lemma makes these precisely.

Lemma 4.3. The following formulas for $\overline{U}_{n}, \underline{U}_{n}, \overline{V}_{n}$ and $\underline{V}_{n}$ are true:

where $n \geq 1$.

Proof. We only prove Eq (4.4) by the induction argument and Eqs (4.5), (4.6) and (4.7) can be verified similarly.

From Lemma 4.2, it can be inferred that

Hence for $n = 1$, Eq (4.4) is hold.

Now suppose that Eq (4.4) is true for every $1 \leq n \leq N$, then one has

By Lemma 4.2 again, it holds that

Due to the above two equalities, the following can be obtained that

This completes the proof.

Now it is in a position to prove

By Lemmas 4.1 and 4.2, for small $d_{1}, d_{2} > 0$,

Setting $d_{1}, d_{2} \rightarrow 0$, we have

and

By further letting $n \rightarrow \infty$ and by Lemma 4.3, one obtains

and

which completes the proof.

Remark 4.1. If $m_{i}(x)$ changes sign in $[0, L]$($i = 1, 2)$, we have

uniformly on compact subsets of $[0, L] \setminus \{x\in[0, L]:m_{1}(x) = m_{2}(x)\}$, where

and

5.   Discussions 

In this paper, motivated by Tang and Zhou ^[17], we studied a classical two-species Lotka-Volterra competition-diffusion-advection system in which the diffusion rates, advection rates and intrinsic growth rates are allowed to take on different values in the space(heterogeneity).

In the condition that total resources for two populations are fixed at the same level, we consider both species $u$ and $v$ are both in heterogeneous environment. We assume that the two competing species have different resource functions and the distributions of resources are uneven, which is different from the literature ^[17], where the authors supposed that one spatial distribution is even across space while the other one not. We find that the outcome of competition in this situation is very abundant: either one of the two competitors becomes the final single winner or both populations coexist eventually, which is dependent on the diffusion rates of both species and the specific shapes of $m_{1}$ and $m_{2}$; see Theorem 1.1. By limiting arguments, we investigate further the population dynamics when $d_{1}$ and $d_{2}$ tend to zero and give the asymptotic behaviour of coexistence steady state for small diffusion; see Theorem 1.2. These results partially generalizes Tang and Zhou ^[17]. In comparison with Tang and Zhou ^[17], we study a more general case. In their paper, they assume that the resource function of $v$ expressed as $m_2$ is a constant M. In our research, $m_2$ is a function of the spatial variable x. This case is more realistic. Moreover, our results indicate that the values of $m_1$ and $m_2$ have a significant impact on the global dynamics of (1.3) and the limiting behaviour of the coexistence steady state. Therefore a change in the value of $m_2$ will produce more complicated spatial population dynamics.

From the above research, we know that both $m_{1}$ and $m_{2}$ have effects on global dynamics of system (1.3). It seems that the spatial population dynamics will appear to be more abundant. Moveover, assumption $(H_{1})$ plays an important role in the proof process. When $(H_{1})$ fails, it is far away from a complete understanding and extremely challenging to deal with. We will continue to explore these problems in the future.

Acknowledgments 

The authors express their gratitude to the anonymous reviewers and editors for their valuable comments and suggestions which led to the improvement of the original manuscript.

This work was partially supported by NNSF of China(No. 11971185).

Conflict of interests 

All authors declare no conflicts of interest in this paper.